化工热力学第二章5
化工热力学第二章教案

授课内容第二章p-V-T关系和状态方程§2-1 引言1 流体最基本的性质有两大类,一类是p、V、T、组成和热容数据,另一类是热数据(如标准生成焓和标准生成熵等)。
本章重点讨论p-V-T关系和状态方程2 推算流体p-V-T行为的途径1)状态方程(EOS)p-V-T关系的解析式。
2)对应态原理(CSP)一种特别的状态方程,以对比参数来表达方程,使流体性质在对比状态下便于比较,并统一到较好的程度。
3 p-V-T关系和状态方程的重要性在计算热力学性质时需要输入流体最基本的性质以及表达系统特征的模型。
状态方程不仅本身是重要的p-V-T关系式,而且从p-V-T的角度反映了系统的特征,是经典热力学中推算其它性质不可缺少的模型之一。
4 本章主要内容1)纯物质的p-V-T行为2)常见的状态方程3)常用的对应态原理4)混合法则§2-2 p-V-T 相图该图是表示纯物质在平衡状态下压力、摩尔体积与温度关系的p-V-T 曲面。
包括: 1 单相区:S 、L 和V (G )分别表示固相、液相和蒸汽(气相); 2 两相共存区:S/L 、V/S 和V/L 分别代表固/液、汽/固、汽/液两相平衡区3 临界点C :汽/液共存的最高温度或压力点,该点的温度、压力和摩尔体积分别称为临界温度Tc 、临界压力Pc 和临界体积Vc 。
数学上表示为:(在C 点) 流体在临界的特性和临界参数在状态方程研究中有重要作用。
在T >T c 和p >pc 的区域内,气体和液体变得不可区分,称为超临界流体。
在临界点附近,流体的许多性质有突变的趋势,如密度、溶解其它物质的能力等,已开发的工业过程有超临界分离技术、超临界化学反应等 。
4 饱和线:ACB 是汽/液两相共存区的边界线。
AC 为饱和液体线也称为泡点线,BC 为饱和蒸汽线也称为露点线。
5 三相线:通过A 、B 的直线,是三个两相平衡区的交界线。
在三相线上有固定的温度、压力,此状态下的纯物质处于气-液-固三相平衡 。
化工热力学-第2章_流体的p –V -T关系-127128页PPT
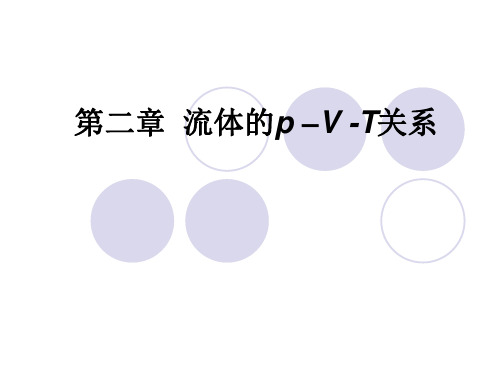
p V
T TC
0
(2-1)
2 p
V
2
T TC
0
(2-2)
式(2-1)和(2-2)对于不同物质都
成立,它们对状态方程等的研究意义重
大。
①纯物质的P-V图
临界点
PVT0 在 C点
2PV2T0 在 C点
超临界流体区 (T>Tc和P>Pc)
过冷液体区
汽液两相平衡区 F=C-P+2=1
过热蒸汽区
饱和液相线
饱和汽相线
作举例说明。
2、当压力大于临界压力时,纯物质是否就以液态存 在。
3、由于分子间相互作用力的存在,实际气体的摩尔 体积一定小于相同压力下的理想气体的摩尔体积, 所以理想气体的压缩因子等于1,实际气体的压缩因 子就一定小于1?
单相区 两相平衡线(饱和曲线)
汽化曲线、熔化曲线、升华曲线 三相点(Tt,Pt)和临界点(Tc,Pc,Vc) 等容线
临界等容线V=Vc、V>Vc、V<Vc
纯物质的p –T图
A
B 三相点
纯物质的p –T图
从 A 点到 B 点,即从液体到汽体,但 没有穿过相界面,这个变化过程是渐变的
过程,即从液体到流体或从气体到流体都
是渐变的过程,不存在突发的相变。超临
界流体的性质非常特殊,既不同于液体,
又不同于气体,它的密度接近于液体,而
传递性质则接近于气体,可作为特殊的萃
取溶剂和反应介质。近些年来,利用超临
界流体特殊性质开发的超临界分离技术和
反应技术成为引人注目的热点。
超临界流体-压缩流体,它既不同于气体。 也不同于液体,而是气液之间能进行无相变 转换的、高于临界温度和临界压力条件下存 在的物质。在pv图上pT略高于又接近于临界 点的流体。
化工热力学(第二版)第二章

0.5
2
1.2259
3648 8.314 408.1 b 0.08664 0.08058m3 / kmol 3648
a 0.42768
8.314 2 408.12
1.2259 1653.7kP m 6 / kmol2 a
a P V b V V b
立方型方程的发展是基于 vdW 方程,而 多常数状态方程是与Virial方程相联系的。
最初的 Virial 方程是以经验式提出的,
之后由统计力学得到证明。
1 Virial方程
Virial方程的两种形式
PV Z 1 B P C P 2 DP 3 RT PV B C D Z 1 2 3 RT V V V
ap Pr A 2 2 0.42748 2 T RT Tr bP Pr B 0.08664 RT Tr
SRK方程可以表示成压缩因子Z的三次方表达式:
Z 3 Z 2 A B B 2 Z AB 0
3 Peng - Robinson ( PR )方程
RT a P V b V V b bV b
给定T和V,由立方型状 态方程可直接求得P 。但大 多数情况是由T和P求 V 。 当T > Tc 时,立方型状 态方程有一个实根,它是气 体容积。 当T<Tc时,高压下立 方型状态方程有一个实根, 它是液体容积。低压存在三 个不同实根,最大的V值是蒸 气容积,最小的V值是液体容 积,中间的根无物理意义。
立方型状态方程的求根方法: (1)三次方程求根公式; (2)迭代法。 简单迭代法求立方型状态方程的根( 以RK 方程为例说明,其它立方型状态方程求解根方 法类似。)
化工热力学课件-第二章 流体的p-V-T关系

宏观定义
pV RT Z 1
物理意义
1. 分子间没有作用力 2. 分子本身不占有体积
1. 理想气体可否被液化(或固化)? 2. 实际气体何时可近似为理想气体?
非理想性
• 分子有大小和形状(几何特性):
硬球软球哑铃状链状拓扑结构….
• 分子间有作用力(化学特性):
作用力包括吸引与排斥两部分,吸引部分又可分解为: 色散、偶极和多极、 氢键、 链的连接性等
例2/4-1 已知SO2在431 K下,第二、三Virial系数分别为: B=-0.159 m3kmol-1 C=9.0×10-3 m6kmol-2 试计算SO2在431 K、1 MPa下的摩尔体积为多少?
解:
用舍项Virial方程:
Z
PV RT
1
B V
C V2
将p=1×106 Pa,R=8.314×103 m3 ·Pa·kmol-1K-1, B=-0.159 m3kmol-1,C=9.0×10-3 m6kmol-2,T=431 K 代入上式中并整理后得
及(b)饱和液相的摩尔体积。(正丁烷在此状况下适用RK状态 方程。)饱和汽相与液相的摩尔体积实验值分别为2482 cm3mol-1
和115.0 cm3mol-1。
解2/5-2:
由附录B1查得正丁烷的Tc及pc值,并求得:
Tr
350 425.2
0.8232
pr
0.9457 3.799
0.2489
由(2/5-14)式可求出参数q , :, 及(Tr)值由表2/5-1中查得
Tr=0.7时: 球形分子logprS = -1 其它流体的 logprS < -1
考虑到一般流体与简单 流体的差别,提出偏心 因子的概念。
化工热力学课件第二章

第二章 流体的p-V-T关系
——纯物质的p-V-T关系
第二章 流体的p-V-T关系
——纯物质的p-V-T关系
ห้องสมุดไป่ตู้
第二章 流体的p-V-T关系
——纯物质的p-V-T关系
第二章 流体的p-V-T
——纯物质的p-V-T关系
第二章 流体的p-V-T关系
——气体的状态方程
状态方程是流体p-V-T的解析表达式。
落 , 冬 季 无 雪时光 秃着枝 桠的树 木,此 时被雪 花装点 成琼装 玉树, 格外美 丽。
楚 博 、 孔 庙 、报恩 寺、清 真寺、 基督教 堂等在 雪花漫 舞中换 上白雪 装。那 青瓦、
红 墙 、 黄 墙 早就掩 隐雪中 ,只留 下一座 座白色 楼宇, 白雪建 筑惹得 游人竞 相拍照
留 存,记 载雪的 影子。
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
——气体的状态方程
第二章 流体的p-V-T关系
化工热力学讲义-1-第二章-流体的p-V-T关系

理想气体与实际气体差异
理想气体
理想气体是一种假设的流体模型,其分子间无相互作用力,分子本身无体积。理想气体的p-v-t关系符合 理想气体状态方程,因此在一些简单的计算和理论分析中,可以使用理想气体模型进行近似处理。
范德华方程的适用范围
范德华方程适用于中等压力、中等温度的气体,对于高压、低温或高温条件下的气体,其精度可能 有所下降。
范德华方程的参数
范德华方程中包含三个参数,分别是气体的摩尔体积、临界温度和临界压力,这些参数可以通过实 验测定得到。
维里方程
维里方程的形式和意义
维里方程是另一个用于描述真 实气体行为的状态方程,它通 过引入维里系数来考虑气体分 子间的相互作用力。
体积
体积是指流体所占据的空间大小,也是流体状态的重要参数之一。体积的大小与流体的密度 和数量有关,常用的体积单位有立方米(m³)、立方厘米(cm³)、升(L)等。
温度
温度是表示物体冷热程度的物理量,是流体状态的重要参数之一。在化工热力学中,常用的 温度单位有摄氏度(℃)、华氏度(℉)、开尔文度(K)等。
温度降低,气体分子的热运动减缓,分子间的相互作用力增强,实际气体与 理想气体的偏差增大,压缩因子增大。
膨胀系数及变化规律
80%
膨胀系数的定义
表示流体体积随温度或压力变化程 度的物理量。
100%
等压膨胀系数
在恒定压力下,流体体积随温度升 高而增大的程度。一般随温度升高 而增大。
80%
等温膨胀系数
在恒定温度下,流体体积随压力升 高而减小的程度。一般随压力升高 而减小。
化工热力学 第二章 流体的压力,体积,温度的关系:状态方程式
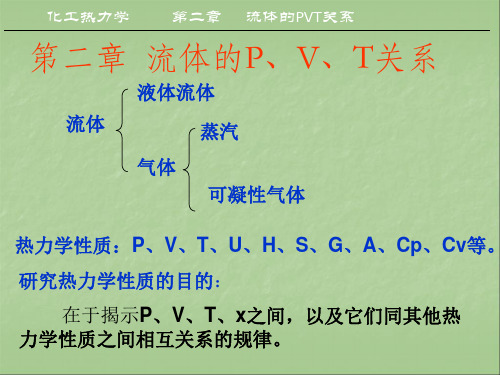
m 3 kmol
1 3
0.08664 a PC 2 b 0.42748 R
a 0.08664 1 TC b 0.42748 R
2 3
VC 3.847 b
化工热力学
第二章
流体的PVT关系
化工热力学
第二章
流体的PVT关系C 6a 4 3 VC b VC
两式相比得:
2
2a VC b TC 3 R VC
2
2 VC b VC 3
VC 3b
27 R 2TC a 64 PC
2
2a 4b 8a TC 3 R 27b 27bR
化工热力学
第二章
流体的PVT关系
(a)、求蒸汽的摩尔体积 将RK方程两端乘
V b 整理成:
P
aV b T PV V b
1 2
RT V b P
写成迭代形式:
RT Vi 1 b P
aVi b T PVi Vi b
1 2
化工热力学
化工热力学
3
第二章
2
流体的PVT关系
0 .5
PVi RTVi ab / T Vi 1 2 0.5 Pb bRT a / T
如令: b 2 C
3
bRT a ,则上式写成: 1 P PT 2
取初值:
RT 2 ab CVi 1 Vi Vi 1 P PT 2
2P 0 V 2 T Tc
27 R T a 64 PC
2
2 C
RTC b 8PC
化工热力学
第二章
化工热力学

8
第三章 流体的热力学性若为单位质量的性质,则为强度性质 ,如mol热力学能能,偏mol性质。
3.偏微分、全微分、点函数、状态函数的概念
4.剩余性质的定义式 M E M M
5. 热容的定义式
Cv
U T V
QR
8.正向卡诺循环、逆向卡诺循环
C
1 TC TH
C
TL TH TC
9.蒸汽动力循环,蒸汽压缩制冷循环,深度制冷
循环(林德、克劳特)的工作原理,能用T-S图表示,
会查用T-S图,主要设备与作用。
28
二.有关计算 ☆ 1. 制冷循环:
有关计算q0,qh,G,-ωS(Nt),ε等 ☆ 2. 蒸汽动力循环 :
10. 有效能与理想功的联系 ΔB=-Wid
11. 有效能衡算 可逆过程
B B
不可逆过程 B B D
12. 有效能效率
B
B
D
1 B
B 考虑数量、质量
13. 热力学效率 (仅考虑数量)
Wac
Wid
产功过程
Wid
Wac
耗功过程
14. 有效能、无效能、理想功、损失功
22
二.有关计算
8.活度与活度系数的概念及定义式
aˆi fˆi / fi 0
9.L—R定则表达式
i
aˆi Xi
xi
fˆi fi0
fˆi
/
fˆ i
id
fˆi id
x i
fi0
f
0 i
L
R
fi
f
0 i
HL
Ki
10. Q函数表达式
Q GE RT
X i ln i
【精品】化工热力学第二章习题解答

【精品】化工热力学第二章习题解答化工热力学第二章习题解答1.一个理想气体在恒定温度下,其压强与体积的关系如下所示:P = A / V^2其中P是压强,V是体积,A是常数。
求该气体的热力学过程方程。
解答:根据热力学第一定律,对于恒温过程,有dU = dq + dw = dq - PdV,其中U是内能,q是热量,w是对外界做的功。
由于该气体是理想气体,可以假设其内能只与温度有关,即dU = Cdt,其中C 是常数,t是温度。
将上式代入热力学第一定律中,得到Cdt = dq - PdV。
根据理想气体状态方程PV = nRT,其中n为物质的量,R为气体常数,T为温度。
将P = A / V^2代入上式,得到Cdt = dq - (A / V^2)dV。
对上式两边同时积分,得到∫Cdt = ∫dq - ∫(A / V^2)dV。
即Ct = q - A / V + B,其中B为常数。
综上所述,该气体的热力学过程方程为Ct = q - A / V + B。
2.一个气体在等体过程中,其压强与温度的关系如下所示:P = A * T^2其中P是压强,T是温度,A是常数。
求该气体的热力学过程方程。
解答:根据热力学第一定律,对于等体过程,有dU = dq + dw = dq - PdV,其中U是内能,q是热量,w是对外界做的功。
由于该气体是理想气体,可以假设其内能只与温度有关,即dU = Cdt,其中C 是常数,t是温度。
将上式代入热力学第一定律中,得到Cdt = dq - PdV。
根据理想气体状态方程PV = nRT,其中n为物质的量,R为气体常数,T为温度。
将P = A * T^2代入上式,得到Cdt = dq - (A * T^2)dV。
对上式两边同时积分,得到∫Cdt = ∫dq - ∫(A * T^2)dV。
即Ct = q - (A / 3)T^3 + B,其中B为常数。
综上所述,该气体的热力学过程方程为Ct = q - (A / 3)T^3 + B。
化工热力学第二章习题答案

习题:2-1.为什么要研究流体的pVT 关系?答:在化工过程的分析、研究与设计中,流体的压力p 、体积V 和温度T 是流体最基本的性质之一,并且是可以通过实验直接测量的。
而许多其它的热力学性质如内能U 、熵S 、Gibbs 自由能G 等都不方便直接测量,它们需要利用流体的p –V –T 数据和热力学基本关系式进行推算;此外,还有一些概念如逸度等也通过p –V –T 数据和热力学基本关系式进行计算。
因此,流体的p –V –T 关系的研究是一项重要的基础工作。
2-2.理想气体的特征是什么?答:假定分子的大小如同几何点一样,分子间不存在相互作用力,由这样的分子组成的气体叫做理想气体。
严格地说,理想气体是不存在的,在极低的压力下,真实气体是非常接近理想气体的,可以当作理想气体处理,以便简化问题。
理想气体状态方程是最简单的状态方程:RT pV =2-3.偏心因子的概念是什么?为什么要提出这个概念?它可以直接测量吗?答:纯物质的偏心因子ω是根据物质的蒸气压来定义的。
实验发现,纯态流体对比饱和蒸气压的对数与对比温度的倒数呈近似直线关系,即符合:⎪⎪⎭⎫ ⎝⎛-=r sr Tp 11log α 其中,c s s r p p p =对于不同的流体,α具有不同的值。
但Pitzer 发现,简单流体(氩、氪、氙)的所有蒸气压数据落在了同一条直线上,而且该直线通过r T =0.7,1log -=sr p 这一点。
对于给定流体对比蒸气压曲线的位置,能够用在r T =0.7的流体与氩、氪、氙(简单球形分子)的sr p log 值之差来表征。
Pitzer 把这一差值定义为偏心因子ω,即)7.0(00.1log =--=r s r T p ω任何流体的ω值都不是直接测量的,均由该流体的临界温度c T 、临界压力c p 值及r T =0.7时的饱和蒸气压s p 来确定。
2-4.纯物质的饱和液体的摩尔体积随着温度升高而增大,饱和蒸气的摩尔体积随着温度的升高而减小吗?答:正确。
化工热力学第三版课件第二章

取在303.6K、2.55MPa下的压缩因子。
[解题思路]
ZK 1
1
q
(ZK )
Zk ZK
bm p
RT
q am bm RT
聊城大学 化学化工学院
化工热力学 第二章 流体的热力学性质
第四节
[解]: 对RK方程有:
σ=1 , ε=0 ,Ω=0.08664 , ψ=0.42748 , α(Tr)=Tr-1/2
Zm
P nRT
Vi
P nRT
Zini RT P
Zi
ni n
Amagat 定律: Zm yi Zi
i
聊城大学 化学化工学院
组分 i 的压缩因子
化工热力学 第二章 流体的热力学性质
第四节
适用:非极性及弱极性气体 P 30MPa
(1) 由 T、P 求 V 的步骤:
Tri
T Tci
,
Pri
P Pci
0.288 0.285
0.286
ωij
0.007 0.091
0.049
聊城大学 化学化工学院
化工热力学 第二章 流体的热力学性质
第四节
1
Tc12 Tc1 Tc2 2 190.6 305.4 241.3
Vc12
1 Vc31
1
Vc32 2
3
991/3
1481/3 2
3
122
混合物的流率为:
n m 454 19.7Kmol h1 M 23.06
查附表1并计算得到的虚拟临界参数:
名称
ij
甲烷
11
乙烷
22
甲烷-乙烷 12
,ij/K
190.6 305.4
化工热力学课后答案完整版朱自强

第二章 流体压力、体积、浓度关系:状态方程式2-1 试分别用下述方法求出400℃、4.053MPa 下甲烷气体摩尔体积。
(1) 理想气体方程;(2) RK 方程;(3)PR 方程;(4) 维里截断式(2-7)。
其中B 用Pitzer 普遍化关联法计算。
[解] (1) 根据理想气体状态方程,可求出甲烷气体在理想情况下摩尔体积id V 为33168.314(400273.15) 1.381104.05310id RT V m mol p --⨯+===⨯⋅⨯ (2) 用RK 方程求摩尔体积将RK 方程稍加变形,可写为0.5()()RT a V b V b p T pV V b -=+-+(E1)其中从附表1查得甲烷临界温度和压力分别为c T =190.6K, c p =4.60MPa ,将它们代入a, b 表达式得2 2.56-20.560.427488.314190.6 3.2217m Pa mol K 4.6010a ⨯⨯==⋅⋅⋅⨯ 53160.086648.314190.6 2.9846104.6010b m mol --⨯⨯==⨯⋅⨯ 以理想气体状态方程求得id V 为初值,代入式(E1)中迭代求解,第一次迭代得到1V 值为5168.314673.15 2.9846104.05310V -⨯=+⨯⨯350.563353.2217(1.38110 2.984610)673.15 4.05310 1.38110(1.38110 2.984610)-----⨯⨯-⨯-⨯⨯⨯⨯⨯⨯+⨯ 3553311.381102.984610 2.1246101.389610m mol -----=⨯+⨯-⨯=⨯⋅ 第二次迭代得2V 为353520.563353553313.2217(1.389610 2.984610)1.381102.984610673.154.05310 1.389610(1.389610 2.984610)1.381102.984610 2.1120101.389710V m mol ------------⨯⨯-⨯=⨯+⨯-⨯⨯⨯⨯⨯⨯+⨯=⨯+⨯-⨯=⨯⋅1V 和2V 已经相差很小,可终止迭代。
化工热力学第二章

131.5267
131.5288
稍大 已接近
由此可计算出v=44.0686 cm3/mol
作图法: 若令y1=方程式左边=f1(V) 令y2=方程式右边=f2(V)
2.迭代法 :
A a 4.934 4.934 4.934 1.549 1.5 1.5 1.5 1.5 B bRT (T /T 2.164 273.15 c) 126 . 2 0.08664 Pr 101.33 B Pr T r 2.164 Tr 3.394
根据状态方程式的形式、结构进行分类可分为两类:
立方型:具有两个常数的EOS 精细型:多常数的EOS
二. 立方型(两常数)EOS
1. VDW Equation (1873) • 形式: RT
a P - 2 V-b V
a/V2 —
分子引力修正项。
由于分子相互吸引力存在,分子撞击器壁的力减小,造成压
◆目前已有300多种 EOS。
◆建立EOS的方法:或以理论法为主、或以经验法为主。
◆实际应用以半经验半理论和纯经验的EOS为主。
● 状态方程的分类:
1、立方型状态方程 2、多常数状态方程 3、理论型状态方程
一.维里方程(Virial Equation)
• (1901年,荷兰Leiden大
学Onness) • 由图2-3知,气相区,等 温线近似于双曲线,当 P↑时,V↓
实际气体的等温线
将范德华方程整理后得到: P(V-b)V2=RTV2-a(V-b) PV3-(bP+RT)V2+aV+ab=0 由这个方程可以看出,当温度不变时,是一个关于V的 三次方程,其解有三种情况:
P
• 三个不等的实根。
化工热力学第二章

流体p-V-T数据+状态方程EOS是计算热力学性质最 重要的模型之一。
EOS + Cpig →所有的热力学性质
2.2 纯物质的p-V-T关系
S-固相 L-液相 V-蒸气相(能够液化或凝固的气相) G-气相(不能液化的气相)
一、p-T图
单相区(4):f=C-P+2=2 两相平衡线(3) (饱和曲线):f=C-P+2=1 汽-固平衡线(升华曲线):1→2 液-固平衡线(熔化曲线):2→3 汽-液平衡线(汽化曲线):2→C 三相点2(Tt, pt):f=C-P+2=0
方程 vdW方程 引力修正项 a/V2 修正条件 没考虑温度的影响
RK方程
a/[T0.5V(V+b)]
考虑了温度的影响
RK方程如何使用 已知T、V,如何求p? 显压型,直接计算,但一定要注意单位。1 atm
=1.01325×105 Pa 已知p、V,求T? 已知p、T,如何求V? 工程上最常用的情况,因为p、T易测。用各种迭 代法求解。为了迭代方便,将RK方程对V的隐式, 变换成Z的显式,即:
状态方程的ZC值 对任何气体,范德华方程给出一个固定的ZC值,即ZC
=0.375,但大多数流体的ZC在0.23~0.29范围内变化 ; 根据气体的临界参数,即可求出范德华方程常数a,b, 从而可进行p-V-T关系的计算; ZC与实际ZC越接近,方程的精度就越高!
2. Redlich-Kwong( RK )方程(1949)
图2-2 p-V图
请思考:在其他条件不变的情况下,若容器的体积小
于或大于VC,加热过程的情况又将如何?请将变化过 程表示在p-V图和p-T图上。(作业2-1)
2.3 气体的状态方程
马沛生 主编 化工热力学 第二章习题解答

第二章习题解答一、问答题:2-1为什么要研究流体的pVT 关系?【参考答案】:流体p-V-T 关系是化工热力学的基石,是化工过程开发和设计、安全操作和科学研究必不可少的基础数据。
(1)流体的PVT 关系可以直接用于设计。
(2)利用可测的热力学性质(T ,P ,V 等)计算不可测的热力学性质(H ,S ,G ,等)。
只要有了p-V-T 关系加上理想气体的id p C ,可以解决化工热力学的大多数问题。
2-2在p -V 图上指出超临界萃取技术所处的区域,以及该区域的特征;同时指出其它重要的点、线、面以及它们的特征。
【参考答案】:1)超临界流体区的特征是:T >T c 、p >p c 。
2)临界点C 的数学特征:3)饱和液相线是不同压力下产生第一个气泡的那个点的连线;4)饱和汽相线是不同压力下产生第一个液滴点(或露点)那个点的连线。
5)过冷液体区的特征:给定压力下液体的温度低于该压力下的泡点温度。
6)过热蒸气区的特征:给定压力下蒸气的温度高于该压力下的露点温度。
7)汽液共存区:在此区域温度压力保持不变,只有体积在变化。
2-3 要满足什么条件,气体才能液化?【参考答案】:气体只有在低于T c 条件下才能被液化。
2-4 不同气体在相同温度压力下,偏离理想气体的程度是否相同?你认为哪些是决定偏离理想气体程度的最本质因素?【参考答案】:不同。
真实气体偏离理想气体程度不仅与T 、p 有关,而且与每个气体的临界特性有关,即最本质的因素是对比温度、对比压力以及偏心因子r T ,r P 和ω。
2-5 偏心因子的概念是什么?为什么要提出这个概念?它可以直接测量吗?()()()()点在点在C V P C V PTT 0022==∂∂∂【参考答案】:偏心因子ω为两个分子间的相互作用力偏离分子中心之间的作用力的程度。
其物理意义为:一般流体与球形非极性简单流体(氩,氪、氙)在形状和极性方面的偏心度。
为了提高计算复杂分子压缩因子的准确度。
气体压缩因子计算化工热力学-第二章

热力学第二定律
总结词:熵增原理
详细描述:热力学第二定律指出,在一个封闭系统中,自发过程总是向着熵增加 的方向进行,即系统总是向着更加混乱无序的状态发展。在化工热力学中,它用 于描述过程的方向和限度,以及能量的有效利用。
热力学第三定律
总结词
绝对熵的概念
详细描述
热力学第三定律指出,绝对零度(0K)是不可能达到的,因为在这个温度下,所有物质的熵变为零。这个定律建 立了绝对熵的概念,用于计算物质在低温下的熵值。在化工热力学中,它对于计算和优化化学反应过程具有重要 意义。
04
气体压缩因子在化工过程 中的应用
化工过程的热力学分析
化工过程热力学分析是利用热力学原理和方法,对化工过程进行能量转化和利用的分析。气体压缩因 子的计算是其中的重要环节,它能够反映气体在压缩过程中的能量变化和状态参数变化,为优化过程 提供理论依据。
在热力学分析中,气体压缩因子的计算需要考虑气体的性质、温度、压力等因素,通过相关公式和图 表进行计算,以获得准确的热力学数据。这些数据可以帮助我们了解化工过程的能量利用效率和可行 性,为优化过程提供指导。
保障安全
在化工生产中,气体压力的控制 直接关系到生产安全,精确计算 气体压缩因子有助于避免超压或 欠压等安全隐患。
应用领域
化工生产
在化工生产过程中,气体压缩因子的计算对 于精确控制气体压力、优化工艺流程和提高 产品质量具有重要意义。
石油天然气开采
石油天然气开采过程中涉及到大量的气体压力计算 和控制,气体压缩因子的计算有助于提高开采效率 和安全性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
化工热力学
第二章
流体的PVT关系
第五节
式中
Tcij 、Pcij 、 ij 按以下经验规则计算:
1 2
Tcij Tci Tcj 1 kij
1 1 3 3 Vci Vcj Vcij 2 Z ci Z cj Z cij 2
kij ——双元相互作用参数,
7.375 4.250 5.475
Vcij (m3 kmol1 )
0.0940 0.2030 0.1416
Z cij
0.274 0.281 0.278
ij
0.225 0.152 0.189
表中第4行数据是按式(2—35a)至式(2—35e)诸式求出的。 (a)用R-K方程求解 将表中有关数据代入式(2—37a)、式(2—37b),可得
III.
1 2
1 2 Q , m yiQi i
1 2
Q Q Qij 2
1 3 i
1 3 j
1 1 3 3 1 3 , Qm y i y j Qi Q j 8 i j
3
使用哪一种要根据方程的具体规定而定。
摩尔体积 m3 kmol1 偏差%
文献值
理想气体方程 阿玛格定律和Z图 虚拟临界参数法和Z图
0.1358
0.1176 0.1367 0.1376
——
-13.40 +0.66 +1.33
化工热力学
第二章
流体的PVT关系
第五节
三、真实气体混合物的状态方程式 Bm P 1、维里方程 Zm 1 RT Bm yi y j Bij ,(二次型混合规则)
0.04949 3 kmol1 m 2 2 am y1 a11 2 y1 y2a12 y1 a22
0.4 6.467 20.40.611.12 0.6 18.28
2 2
化工热力学
第二章
6
流体的PVT关系
1 12
第五节
12.95m MP kmol K a
0 22 1 22
Bij Pcij RTcij
Bij RTcij Pcij
0 1 Bij ij Bij
B
0 ij
ij B
1 ij
(其中 Tr
T ) Tcij
RTcij 0.422 0.172 0.083 1.6 ij 0.139 4.2 Pcij Tr Tr
化工热力学
第二章
流体的PVT关系
第五节
(摩尔比), 例 2-10 某合成氨厂原料气的配比是 N 2 : H 2 1 : 3 进合成塔前,先把混合气压缩到40.532MPa(400atm),并加热
到300℃。因混合气体的摩尔体积是合成塔尺寸设计的必要数据, 试用下列方法计算之。已知文献值 Zm 1.1155 。(a)用理想 气体方程;(b)阿玛格定律和普遍化Z图联用;(c)用虚拟临 界参数(Kay规则)计算。
化工热力学
第二章
流体的PVT关系
第五节
§2-5
一、混合规则
真实气体混合物
用纯物质性质来预测或推算混合物性质的函数式称为混合规则, 纯气体的关系式借助于混合规则可推广到气体混合物。
1、kay 规则(虚拟临界参数法) 若用 M m 代表 P 、Vcm、Tcm ,则: M m yi M i cm
i
化工热力学
第二章
流体的PVT关系
第五节
[解] 由附表1查得氢和氮的临界常数。
(a)理想气体方程
Vm
RT 8.314 10 300 273.2 0.1176m
3
3
P
40.532 106
kmol1
(b)用阿玛格定律和普遍化Z图 由临界常数求出氢和氮的 Tr 和 P r
(c)用普遍化维里系数关联
用式(2—24a)、式(2—24b)和式(2—23)以及前表中的
Zm 0.57 0.18120.16 0.5990
ij、Tcij、Pcij 等有关数据求出下列各第二维里系数值
ij
11 22 12
B
0
B1
和例2—3(a)的迭代解法相似,解得(迭代7次) m 和 Z m 之 h 值为
Zm 0.5791
hm 0.3241
Z m RT 0.5971 0.008314 424 0.1527 3 kml1 m Vm P 13.78
(b)用普遍化压缩因子关联 用虚拟临界参数法求出 Tcm 和 Pcm
bm P 0.04949 13.78 0.1935 RT 0.008314 424
将以上计算值代入式(2—18a)和式(2—18b),则可得
化工热力学
第二章
流体的PVT关系
第五节
hm 1 Zm 3.605 1 h 1 hm m 0.1935 hm Zm
573 .2 H 2:Tr 13.91 33.2 8
40.532 Pr 19.20 1.3 0.8106
化工热力学
第二章
流体的PVT关系
第五节
N 2:
573 .2 4.54 Tr 126 .2
40 .532 11.96 Pr 3.39
由图2—4(c)查得
Z H2 1.15
化工热力学
第二章
流体的PVT关系
第五节
Tcm y1Tc11 y2Tc 22 0.4304.2 0.6369.8 343 .6 K
Pcm y1Pc11 y2 Pc 22 0.47.375 0.64.25 5.500MPa 424 Trm 1.234 343 .6 13 .78 2.505 Prm 5.500
查图2—4(c)得
(c)用虚拟临界参数
Vm
1.178.314 103 573.2 0.1367m3 km ol1
40.532 10
6
Zm 1.170
将上述结果列成下表进行比较
化工热力学 计算方法
第二章
流体的PVT关系
第五节
Zm
1.155
1.000 1.163 1.170
Pcij Z cij RTcij Vcij
3
代表对 Tcij 几何平均值的偏差
ij
i j
2
化工热力学
第二章
流体的PVT关系
第五节
2、RK方程:
RT P Vm bm am T Vm Vm bm
1 2
am 、bm 为混合物的参数,按下面经验混合规则求得:
由
Trm 和 Prm 值从图2—7和图2—9查得
0
Z 1 0.16 Z 0.57 m y111 y222 0.40.225 0.60.152 0.1812
将以上数据代入式2—22,可得
化工热力学
第二章
流体的PVT关系
第五节
Z m RT 0.5990 0.008314 424 0.1532m3 kmol1 Vm P 13.78
bm yi bi
am yi y j aij
0.08664 ci RT b ( bi 为纯组分常数,按kay 规则求: i ) Pci 2 2.5 0.42748 R Tcij aij 为交叉常数,aij Pcij
i j
i
化工热力学
第二章
流体的PVT关系
第五节
(二版例2-7)试求在151℃、13.78MPa下二氧化碳(1)和丙烷
B B11 、 22 ——纯物质1、2的第二维里系数,
B12
——交叉维里系数。
化工热力学
第二章
流体的PVT关系
第五节
0 1 i=j(即纯物质), B11 B11 c 2 B22 B 2 B Pc 2 i j 时,Bij 的计算:B12 B21
Z N2 1.20
按式(2—70)求混合气体的压缩因子 Z m
Zm 1.15 0.75 1.20 0.25 1.163
Vm 40.532 106
1.1638.314 103 573.2 0.1367m3 km ol1
化工热力学
第二章
流体的PVT关系
Yi Y 2
1 3 1 3 j
Yi、j
———与体积有关的相互作用参数
3
2)、与相互作用能有关的参数(主要与T 的关系)
Qi、j Qi Q j
1 2
化工热力学
第二章
流体的PVT关系
第五节
3)R-K方程中的 am ,第二Virial 系数 Bm(采用组成的 二次型混合规则)
i j
对于二元混合物,有三种类型的两分子交互作用,
即: i i、j j、i 1、 j 1、 2; 2。
即: B y y B y y B y y B y y B m 1 1 11 1 2 12 2 1 21 2 2 22
2 y12 B11 2 y1 y2 B12 y2 B22
化工热力学
第二章
流体的PVT关系
第五节
二、Amagat(阿玛格)定律和普遍化压缩因子图联用
假设阿玛格分体积定律适用于真实气体混合物,则气体 混合物的体积 Vm 应为各组分在混合物的温度和总压力下测
得的体积 Vi 之和。
Z m nRT Vm Vi P
Z m ——混合物的压缩因子
PVm P Zm nRT nRT
Z i ni RT ni P Vi nRT P Z i n
