离散系统稳定性分析
合集下载
离散系统稳定性分析.ppt
(1-
-1 z )Z
2 s2
0.3
s
s0.140
0.1 s20
(1- z-1)(z2-1T)2z
0.3z z1
0.4z ze10T
0.1z ze20T
0z-.14
0.3
0.4(z1) z0.135
0.1(z1) z0.018
5
1 G(z) 0, 并代入
1 z
得
1
2.33 3 3 . 68 2 1 . 65 0 . 34 0
T0 kv 0
0
r(t) 12t2
T2 ka 0
例1.右图所示系统中的参数a=1,k=1,T=1, 试求在r(t)=1(t),r(t)=t及r(t)=t2/2时 的稳态误差.
1 e Ts s
K s(s a)
解:G(z)
0.3 6 8z0.2 6 4 (z1)(z0.3 6 8)
KP
l i mG(z) z1
3
2 .3 3
1 .6 5
2
3 .6 8
0 .3 4
1
1 .4 3
0
0
0 .3 4
0
系统是稳定的
例3:设采样系统的方框图如图所示,其中 稳定的K1值范围.
G(，s)采样s周(Ks期1T4=)0.25s,求能使系统
解:G ( z )
Z
[
s
(
K1 s
4
)
]
G(s)
C(s)
R(s) - T
K1 4
Z[
z2
，故1z离1散闭 环0系.0 统是7不,稳6z定2的 。4.876
三.Routh稳定判据
令z ωω11代入闭环采样系统征的方特程,进行z变换后, 既可用Rout判 h 据,其步骤如:下
自动控制原理离散系统知识点总结
自动控制原理离散系统知识点总结自动控制原理中的离散系统是指在时间域和数值范围上都是离散的系统。
在离散系统中，信号是以离散时间点的形式传递和处理的。
本文将对自动控制原理离散系统的知识点进行总结，包括离散系统的概念、离散信号与离散系统的数学表示、离散系统的稳定性分析与设计等。
一、离散系统的概念与特点离散系统是指系统输入、输出和状态在时间上都是以离散的方式存在的系统。
与连续系统相比，离散系统具有以下特点：1. 离散时间：离散系统的输入、输出和状态是在离散时间点上采样得到的，而不是连续的时间信号。
2. 离散数值：离散系统的输入、输出和状态都是以离散数值的形式存在的，而不是连续的模拟数值。
二、离散信号与离散系统的数学表示离散信号是指在离散时间点上采样得到的信号。
离散系统可以通过离散信号的输入与输出之间的关系进行描述。
常见的离散系统数学表示方法有差分方程和离散时间传递函数。
1. 差分方程表示：差分方程是通过离散时间点上的输入信号和输出信号之间的关系来描述离散系统的。
差分方程可以是线性的或非线性的，可以是时不变的或时变的。
2. 离散时间传递函数表示：离散时间传递函数描述了离散系统输入与输出之间的关系，类似于连续时间传递函数。
离散时间传递函数可以通过Z变换得到。
三、离散系统的稳定性分析与设计离散系统的稳定性是指系统的输出在有限时间内收敛到有限范围内，而不是无限增长或震荡。
离散系统的稳定性分析与设计是自动控制原理中的重要内容。
1. 稳定性分析：离散系统的稳定性可以通过判断系统的极点位置来进行分析。
若系统的所有极点都位于单位圆内，则系统是稳定的；若存在至少一个极点位于单位圆外，则系统是不稳定的。
2. 稳定性设计：若离散系统不稳定，可以通过调整系统的参数或设计控制器来实现稳定性。
常见的稳定性设计方法包括PID控制器调整、根轨迹设计等。
四、离散系统的性能指标与优化离散系统的性能指标与优化是指通过调整控制器参数或控制策略，使离散系统的性能得到优化。
《离散系统的稳定性》课件
离散系统稳定性控制的方法
极点配置法
通过选择适当的系统参数， 使得系统的极点位于复平面 的某一区域，从而实现系统 的稳定性。
反馈控制
利用负反馈原理，通过将系 统输出信号的一部分或全部 反馈到输入端，对系统进行 调节，使其达到稳定状态。
状态反馈控制
根据系统当前状态变量反馈 信息，计算出控制输入信号 ，使得系统状态变量能够跟 踪设定的参考轨迹。
离散系统的应用领域
• 离散系统广泛应用于工程、科学 、经济和社会等领域。例如，数 字信号处理、控制系统、计算机 仿真、经济模型等领域中经常涉 及到离散系统的分析和设计。
02 离散系统的稳定性分析
离散系统的稳定性定义
离散系统
离散系统是指系统的状态变量只在离 散时刻发生变化，如数字电路、控制 系统等。
05 离散系统稳定性的未来研 究方向
离散系统稳定性的深入研究
深入研究离散系统的稳定性理论，包括离散系统的稳定性判据、离散系统的稳定性分析方法等，以提 高对离散系统稳定性的认识和理解。
深入研究离散系统的动态行为，包括离散系统的响应特性、离散系统的控制性能等，以揭示离散系统 稳定性的内在机制。
离散系统稳定性与其他领域的交叉研究
离散系统的稳定性分析方法
直接法
直接法是通过分析系统状态方程的解的性质，判断系统是否稳定。例如，通过 求解状态方程的解，观察其收敛性或发散性，判断系统的稳定性。
频域分析法
频域分析法是通过将离散系统转化为频域表示形式，分析系统的频率响应特性 ，判断系统的稳定性。例如，通过绘制系统的频率响应曲线，观察其穿越频率 和阻尼比等参数，判断系统的稳定性。
鲁棒控制
针对具有不确定性的离散系 统，设计一种控制策略，使 得系统在各种不确定性条件 下都能保持稳定。
3.1 离散系统的稳定性分析
在Z 平面上，当δ为某个定值时z=eTs随ω 由-∞ 变到∞的轨迹是一个圆，圆心位于原点，半径为 z=eTs ，而圆心角是随线性增大的。 当δ=0时，|z|=1，即S平面上的虚轴映射到Z平 面上的是以原点为圆心的单位圆。 当δ<0时，|z|<1，即S平面的左半面映射到Z平 面上的是以原点为圆心单位圆的内部。 当δ>0时，|z|>1，即S平面的右半面映射到Z平 面上的是以原点为圆心单位圆的外部。
k 0.158kz G( z ) s( s 4) ( z 1)(z 0.368) 该系统的闭环Z传递函数为：
W ( z) G( z ) 0.158kz 1 G( z ) ( z 1)(z 0.368) 0.158kz
求得该系统的闭环Z特征方程为：
例3.1 某离散系统的闭环Z传递函数为
3.16z 1 w( z ) 1 1.792z 1 0.368z 1
解：根据已知条件w(z)的极点为 ：z1=0.237， z2=1.556 由于| z2 |=1.556＞1，故该系统是不稳定 的。
3.1.3 Routh稳定性准则在离散系统的应用
S平面与Z平面的映射关系如图3.1所示
jω [S] jIm j [Z]
-1 0
1
0 -j Re
δ
图3.1
S平面与Z平面的映射关系
于是得到下面结论：
1．S平面的虚轴对应于Z平面的单位圆的圆周。 在S平面上，ω每变化一个ωs时，则对应在Z平面上重 复画出一个单位圆，在S平面中-ωs/2～ωs/2
的频率范围内称为主频区，其余为辅频区（有无限多 个）。S平面的主频区和辅频区映射到Z平面的重迭称
面的左半部分，或者说它的闭环特征方程的根的实部小 于零，则该系统是稳定的。由此可以想见，离散系统的 闭环Z传递函数的全部极点（特征方程的根）必须在Z平 面中的单位圆内时，系统是稳定的。
自动控制原理第七章第二讲离散系统的稳定性分析
(a)
(b)
G(z) C(z) R(z)
图(b)情况下, 为了应用脉冲传递函数的概念, 可 以在输出端虚设一个采样开关, 并令其采样周期与输 入端采样开关的相同。
开环脉冲传递函数 1. 串联环节
C R((zz))G1(z)G2(z)G(z)
G(z)
G1(z)
G2(z)
C* (s)
R (s)
Kalz i1(m z1)2G(z)
单位反馈离散系统的稳态误差
例 设系统的结构图如下图所示，K=1, T=0.1s , r(t)=1(t)+t, 求系统的稳态误差。
R(s)
1 e Ts
K
C(s)
—
s
s(s 1)
解：系统的开环传递函数为
G (z ) (1 z 1 )Z s 2 (s 1 1 ) (1 z 1 ) (zT 1 )2 z (z (1 1 )e z T () e z T )
思路:找出与连续系统稳定性相关性, 用劳斯判据来判断其稳定性。
1）双线性变换
令： z w 1 w 1
则： w z 1 z 1
2）稳定性判据
将 z w1 w 1
代入特征方程中， 应用Routh判据判稳。
例 7-2 判断下图所示系统在采样周期T=1s ，T=4s，系统的稳定性。
K v T l z 1 i(z m 1 ) G (z ) 0 .1 l z 1 i(z m 1 )(z 1 )z( 0 .9)0 15
系统的稳态误差为 1 1
e() 1 Kp Kv
[注K ： aT 12lz i1(m z1)2G (z)]
把T=0.1代入化简得
§8-5离散系统稳定性分析
0.4 z-1
0.3
0.4( z1) z 0.1 3 5
0.1( z1) z 0.0 1 8 5
1 G(z) 0, 并代入
1
z
得
1
2.33 3 3.68 2 1.65 0.34 0
32Βιβλιοθήκη 331.652 3.68
0.34
1
1.43
0
0
0.34
0
系统是稳定的
例3:设采样系统的方框图如图所示,其中 稳定的K1值范围.
117( ωω11)2
119(
ω1 ω1
)
39
0
整理得: ω3 2ω2 2ω 40 0
ω3 1 2
ω2 2 40
ω1 - 18 0
ω0 40
系 统 不 稳 定, 有 两 根 在 单 位 圆 外
例2.判断如图所示系统的稳定性,采样周期T=0.2(秒)
r(t) T -
1e T s s
2 s (10.1s )(10.0 5s )
0.158K ω2 1.264ω (2.736 0.158K ) 0
1
1
ω2 0.158K 1
2.736- 0.158K 1
ω1 1.264
0
ω0 2.736- 0.158K 1
0.158K 0 , 2.736- 0.158K 0
1
1
解得 : 0 K 17.3
四、离散系统的稳态误差 稳态误差计算
1型系统
2型系统
3型系统
r(t)=1(t)
1 kp 0
0
0
r(t)=t
T0 kv
0
0
r(t)
1 2
t2
第七节 离散系统的稳定性分析
离散系统如上图所示，则
E(z) R(z) 1 Go (z)
若闭环系统稳定，则由终值定理
ess
lim e(k)
k
lim (z
z 1
1) E ( z )
lim (z
z 1
1) R(z) 1 Go (z)
将离散系统仿照连续系统分为0、1、2型：
若系统开环脉冲传递函数G0 (z)中含有 i(i=0,1,2)个|z|=1的极点，则系统称为i型
第七节 离散系统的稳定性分析
如上节所讲，采样会破坏系统的稳定性，所 以在设计采样系统时最先考虑的是稳定性。 对采样系统稳定性分析主要建立在Z变换的 基础上。
连续系统的稳定性
连续系统稳定
所有特征根均具有负实部
方法：劳斯判据,Hurwitz判据及奈氏判据。
在分析采样系统时，可以利用Z变换与拉氏变 换数学上的关系，找到Z平面与S平面之间的周 期映射关系，从而利用原有的各种判据来分析
0
2型
0
2 r(t)=t*1(t)时
静态速度误差系数
R(z)
Tz (z 1)2
, ess
lim [(z
z1
1) 1 1 Go(z)
Tz (z 1)2
]
T
lim z1 (z
1 1)Go ( z)
若定义KV
1 T
lim (z 1)Go (z)
z 1
，则ess
1 Kv
Kv
ess
0型
0
1型 2型
Bode Diagrams
50 40 30 20 10
Phase (deg); Magnitude (dB)
-100 -120 -140 -160
离散系统的稳定性分析
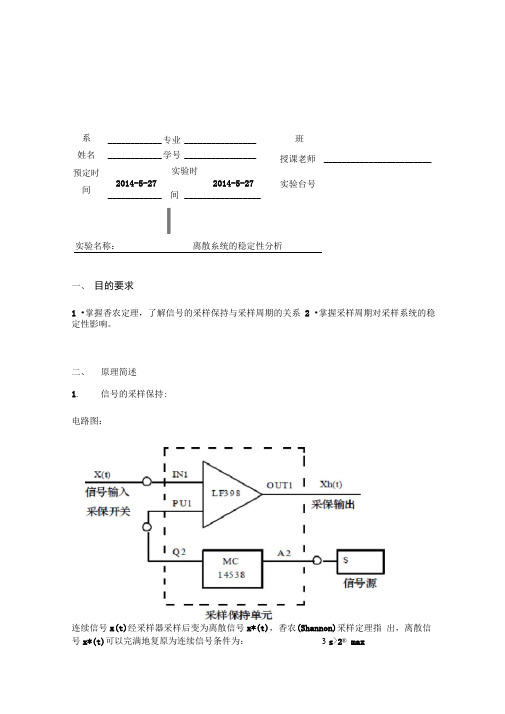
I实验名称：离散糸统的稳定性分析一、 目的要求1 •掌握香农定理，了解信号的采样保持与采样周期的关系2 •掌握采样周期对采样系统的稳定性影响。
二、 原理简述 1.信号的采样保持:电路图：连续信号x(t)经采样器采样后变为离散信号x*(t)，香农(Shannon)采样定理指 出，离散信号x*(t)可以完满地复原为连续信号条件为：3 s >2® max系姓名 预定时 间____________ 专业 ________________ ____________ 学号 ________________ 实验时2014-5-27 2014-5-27____________ 间 _________________班授课老师 ________________________ 实验台号I n I® = -------式中3 S为米样角频率，且',(T为米样周期),3 max为连续信号x (t)的幅频谱| x (j CD 的上限频率T s 若连续信号x (t)是角频率为D S = 22.5的正弦波，它经采样后变为x*(t)，则25（1-尹） ,1 _ 12 占[(2厂一1+訂巧二+ (1—訂「一 27＞力)]0-1)匕-严)闭环脉冲传递函数为：C ⑵12.5[(2厂-l + d + (l -严—22)]丽'一 X 匚(25丁二 13.5 — 11.牝引)二十(12.5 — 11.5邑血—25T 严) 闭环采样系统的特征方程式为：z 2 +(25T-13.5 1 L5e _2r )z+ Q2.5-11 .Se'3r -25Te^T ) = 0特征方程式的根与采样周期T 有关，若特征根的模均小于1,则系统稳定，若有 一个特征根的模大于1,则系统不稳定，因此系统的稳定性与采样周期 T 的大小 有关。
仪器设备PC 机一台，TD-ACC+ (或TD-ACS )教学实验系统一套。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R(s)
Y(s)
-
G1(s)
C(s) G2(s)
由 此 得 闭 环 系 统 的 特方 征程 为 1 G1G 2 H ( z ) 0
H(s)
设特征方程的根为 z1 , z 2 , z n , 则 线 性 数 字 控 制 系 统定 稳的 充要条件是 : 系 统 特 征 方 程 的 根 均于 位z平 面 的 单 位 圆 内 ,或全 部特征根的模小于 1.
例1.试分析特征方程为z2-z+0.632=0的系统的稳定性.
解:
z1,2
1 1 4 0.632 2
0.5 0.5 1.528 0.5 j 0.618
| z1 || z 2 |
2 2 0.5 0.618 0.795 1
系统是稳定的
例2: 设离散系统如下图所示，其中
§8-5 离散系统稳定性分析
一.s平面与z平面的映射关系 z e Ts s 2T
而 s j z e T e jT | z | e T z T
(1)
当 0 s j
当由 T T
| z | 1
[s]
z 由 - 因此s平面的虚轴对应 z平面的单位圆
系统不稳定 , 有两根在单位圆外
例2.判断如图所示系统的稳定性,采样周期T=0.2(秒)
r(t)
-
T
1 e Ts s
2 s ( 1 0.1 s )( 1 0.05 s )
解:
G(s)
(1- e -Ts ) s
-1 0.3 0.4 0.1 2 G( ， G ( s ) ， 。试分析闭环稳定性。 s ( s 1)
H (s) 1 T 1
解：G ( z ) Z
10 s ( s 1 )
10(1 e 1 ) z ( z 1)( z e 1 )
闭环特征方程为
1 G( z ) 0
三.Routh稳定判据
解:
令
1 得 45(ω1 ) 3 117( ω1 ) 2 119( ω1 ) 39 0 z ω ω1 ω1 ω1 ω1 3 2 整 理 得: ω 2ω 2ω 40 0 ω ω 3 2 1 2 - 18 40 2 40 0
1 ω ω 0
1 2 Ka lim ( z 1) G ( z ) 0 T 2 z 1 1 1 1 E( ) K K K P v a
Ⅰ型系统对于阶跃输入是无差的，对于斜坡输入是有差的，对于抛物线 输入的误差是无穷大。
1e Ts s
K s( s a)
解: G ( z )
0.368z 0.264 ( z 1)( z 0.368) 1 e ss K 0 P 0.623 1 e ss K 0.732 0.83 v e ss K a
1
K P lim G ( z ) z 1 Kv Ka 1
即
z 2 4.952z 0.368 0
解得特征根 因为
z2 1
，故离散闭环系统是不稳定的。
z1 0.076, z2 4.876
1 代入闭环采样系统的特 征方程 , 进行 z变换后 , 令z ω ω1 既可用 Routh 判据 , 其步骤如下 : (1) 求出采样系统的特征方 程D(z) 0 (2) 进行 ω变换 , 整理后得 D(ω) 0 判据判别采样系统的稳 定性 (3) 应用 Routh 例1.. 设闭环采样系统的特征方程为D(z)=45z3-117z2＋119z－39=0,判断其稳定性.
0.732 lim ( z 1)G ( z ) 0.623 T z 1 lim ( z 1) G ( z ) 0 T 2 z 1 1 2
例2：试计算如图所示系统，在输入
1 r (时的稳态误差。 t) 1 t t 2 2
-Ts 1 e 解：G ( z ) Z[ s s(sK ] 1) (1 - z -1 )Z[ K s 2 (s 1) ]
(1)输入信号为单位阶跃函数
E(S) R(S) - T
C(S) G(S)
r(t) 1(t), R(z) z 1 z z 1 1 1 e ss lim lim 1 G ( z ) K P z 1 1 G ( z ) z 1 ( z 1) K P lim [1 G(z)] 位置误差系数 z 1
1T=0.25s,求能使系统 G (，采样周期 s)
G(s) C(s)
K s ( s4)
K1 解:G ( z ) Z [ s ( s 4 ) ]
R(s)
- T
K1 K1 (1 e 4T ) z 1 1 4 Z[ s - s 4 ] 4 ( z 1)( z e 4T ) K1 4T ( 1 e )z C(z) G( z) 4 R(z) 1 G ( z ) K1 4T 4T ( z 1)( z e ) 4 (1 e )z K1 4T 则 1 G(z) (z - 1)( z e ) 4 (1 e )z 0 K1 (z - 1)(z - 0.368) 4 (1 0.368) z 0 1 令 z -1 代入上式得 1 1 1 ( -1 - 1)( -1 - 0.368) 0.158K1 -1 0 4T
(2)
当 1时 对应s平面的左半部 | z | e T 1 故对应于单位圆的内部 当 1时 对应s平面的右半部 | z | e T 1 故对应于单位圆的外部
[Z ]
(3)
结论：s平面的稳定区域在z平面上的影像是单位圆内部区域
二.离散系统稳定的充要条件
G G ( z) C(z) 1 2 R(z) 1G G H ( z ) 1 2
1 G(z) 0, 并代入 2.33 3 3.68 2
z
1 1
得
1.65 0.34 0 1.65 0.34 0 0
3 2
2.33 3.68 1.43 0.34
1 0
系统是稳定的
例3:设采样系统的方框图如图所示,其中 稳定的K1值范围.
两边同乘以 (ω - 1)2 并整理得 0.158K1 ω 2 1.264ω (2.736 0.158K 1 ) 0 ω2 ω1 ω0 0.158K1 1.264 2.736- 0.158K1 2.736- 0.158K1 0 2.736- 0.158K1 0
0.158K1 0 ,
2 lim ( z 1) G ( z ) T 2 z 1
稳态误差终值
输 入
系统类型 0型系统 1型系统 2型系统 3型系统
r(t)=1(t)
1 kp
r(t)=t
r (t ) 1 2t
2
T0 kv
0
T2 ka
0 0 0
0
0
例1.右图所示系统中的参数a=1,k=1,T=1, 试求在r(t)=1(t),r(t)=t及r(t)=t2/2时 的稳态误差.
2 z(z 1) T 2 1 r ( t ) 2 t , R(z) 2 ( z 1)3 T 2 z(z 1) ( z 1) 2 ( z 1)3 T2 1 lim Ka 1 G( z) z 1 ( z 1) 2 G ( z )
e ss lim z 1 Ka 1
解得 : 0 K 17.3
四、离散系统的稳态误差 稳态误差计算
e ss lim e ss ( t ) lim ( z 1) E ( z ) t z 1 R(z) E(z) 1 G ( z ) ( z 1) R ( z ) e ss lim z 1 1 G ( z )
z
(2)输入信号为单位斜坡函数
r(t) t, R(z)
Tz (z -1)2 Tz (z -1)2 T 1 lim ( z 1) G ( z ) K v 1 G ( z ) z 1
( z 1) e ss lim z 1 Kv 1
(3)输入信号为单位抛物线信号
lim ( z 1)G ( z ) 速度误差系数 T z 1
-Ts 400 2 (1 e ) 2 (1 0.1s )(1 0.05s ) s 2 ( s 10)( s 20)
-1 2Tz 0.3 z 0.4 z 0.1z (1 - z ) (z -1)2 z 1 z e10T z e20T 0.4 ( z 1) 0.1( z 1) 0.4 z -1 0.3 z 0.135 z 0.0185
(1 - z
-1
K ] )Z[ K - K s s 1 2 s
(T 1 e T ) z (1 Te T e T ) K (z - 1)(z - e T )
可见，系统是Ⅰ型系统
K P lim 1 G ( z ) 1 G (1) z 1 Kv 1 lim ( z 1)G ( z ) K T z 1
Y(s)
-
G1(s)
C(s) G2(s)
由 此 得 闭 环 系 统 的 特方 征程 为 1 G1G 2 H ( z ) 0
H(s)
设特征方程的根为 z1 , z 2 , z n , 则 线 性 数 字 控 制 系 统定 稳的 充要条件是 : 系 统 特 征 方 程 的 根 均于 位z平 面 的 单 位 圆 内 ,或全 部特征根的模小于 1.
例1.试分析特征方程为z2-z+0.632=0的系统的稳定性.
解:
z1,2
1 1 4 0.632 2
0.5 0.5 1.528 0.5 j 0.618
| z1 || z 2 |
2 2 0.5 0.618 0.795 1
系统是稳定的
例2: 设离散系统如下图所示，其中
§8-5 离散系统稳定性分析
一.s平面与z平面的映射关系 z e Ts s 2T
而 s j z e T e jT | z | e T z T
(1)
当 0 s j
当由 T T
| z | 1
[s]
z 由 - 因此s平面的虚轴对应 z平面的单位圆
系统不稳定 , 有两根在单位圆外
例2.判断如图所示系统的稳定性,采样周期T=0.2(秒)
r(t)
-
T
1 e Ts s
2 s ( 1 0.1 s )( 1 0.05 s )
解:
G(s)
(1- e -Ts ) s
-1 0.3 0.4 0.1 2 G( ， G ( s ) ， 。试分析闭环稳定性。 s ( s 1)
H (s) 1 T 1
解：G ( z ) Z
10 s ( s 1 )
10(1 e 1 ) z ( z 1)( z e 1 )
闭环特征方程为
1 G( z ) 0
三.Routh稳定判据
解:
令
1 得 45(ω1 ) 3 117( ω1 ) 2 119( ω1 ) 39 0 z ω ω1 ω1 ω1 ω1 3 2 整 理 得: ω 2ω 2ω 40 0 ω ω 3 2 1 2 - 18 40 2 40 0
1 ω ω 0
1 2 Ka lim ( z 1) G ( z ) 0 T 2 z 1 1 1 1 E( ) K K K P v a
Ⅰ型系统对于阶跃输入是无差的，对于斜坡输入是有差的，对于抛物线 输入的误差是无穷大。
1e Ts s
K s( s a)
解: G ( z )
0.368z 0.264 ( z 1)( z 0.368) 1 e ss K 0 P 0.623 1 e ss K 0.732 0.83 v e ss K a
1
K P lim G ( z ) z 1 Kv Ka 1
即
z 2 4.952z 0.368 0
解得特征根 因为
z2 1
，故离散闭环系统是不稳定的。
z1 0.076, z2 4.876
1 代入闭环采样系统的特 征方程 , 进行 z变换后 , 令z ω ω1 既可用 Routh 判据 , 其步骤如下 : (1) 求出采样系统的特征方 程D(z) 0 (2) 进行 ω变换 , 整理后得 D(ω) 0 判据判别采样系统的稳 定性 (3) 应用 Routh 例1.. 设闭环采样系统的特征方程为D(z)=45z3-117z2＋119z－39=0,判断其稳定性.
0.732 lim ( z 1)G ( z ) 0.623 T z 1 lim ( z 1) G ( z ) 0 T 2 z 1 1 2
例2：试计算如图所示系统，在输入
1 r (时的稳态误差。 t) 1 t t 2 2
-Ts 1 e 解：G ( z ) Z[ s s(sK ] 1) (1 - z -1 )Z[ K s 2 (s 1) ]
(1)输入信号为单位阶跃函数
E(S) R(S) - T
C(S) G(S)
r(t) 1(t), R(z) z 1 z z 1 1 1 e ss lim lim 1 G ( z ) K P z 1 1 G ( z ) z 1 ( z 1) K P lim [1 G(z)] 位置误差系数 z 1
1T=0.25s,求能使系统 G (，采样周期 s)
G(s) C(s)
K s ( s4)
K1 解:G ( z ) Z [ s ( s 4 ) ]
R(s)
- T
K1 K1 (1 e 4T ) z 1 1 4 Z[ s - s 4 ] 4 ( z 1)( z e 4T ) K1 4T ( 1 e )z C(z) G( z) 4 R(z) 1 G ( z ) K1 4T 4T ( z 1)( z e ) 4 (1 e )z K1 4T 则 1 G(z) (z - 1)( z e ) 4 (1 e )z 0 K1 (z - 1)(z - 0.368) 4 (1 0.368) z 0 1 令 z -1 代入上式得 1 1 1 ( -1 - 1)( -1 - 0.368) 0.158K1 -1 0 4T
(2)
当 1时 对应s平面的左半部 | z | e T 1 故对应于单位圆的内部 当 1时 对应s平面的右半部 | z | e T 1 故对应于单位圆的外部
[Z ]
(3)
结论：s平面的稳定区域在z平面上的影像是单位圆内部区域
二.离散系统稳定的充要条件
G G ( z) C(z) 1 2 R(z) 1G G H ( z ) 1 2
1 G(z) 0, 并代入 2.33 3 3.68 2
z
1 1
得
1.65 0.34 0 1.65 0.34 0 0
3 2
2.33 3.68 1.43 0.34
1 0
系统是稳定的
例3:设采样系统的方框图如图所示,其中 稳定的K1值范围.
两边同乘以 (ω - 1)2 并整理得 0.158K1 ω 2 1.264ω (2.736 0.158K 1 ) 0 ω2 ω1 ω0 0.158K1 1.264 2.736- 0.158K1 2.736- 0.158K1 0 2.736- 0.158K1 0
0.158K1 0 ,
2 lim ( z 1) G ( z ) T 2 z 1
稳态误差终值
输 入
系统类型 0型系统 1型系统 2型系统 3型系统
r(t)=1(t)
1 kp
r(t)=t
r (t ) 1 2t
2
T0 kv
0
T2 ka
0 0 0
0
0
例1.右图所示系统中的参数a=1,k=1,T=1, 试求在r(t)=1(t),r(t)=t及r(t)=t2/2时 的稳态误差.
2 z(z 1) T 2 1 r ( t ) 2 t , R(z) 2 ( z 1)3 T 2 z(z 1) ( z 1) 2 ( z 1)3 T2 1 lim Ka 1 G( z) z 1 ( z 1) 2 G ( z )
e ss lim z 1 Ka 1
解得 : 0 K 17.3
四、离散系统的稳态误差 稳态误差计算
e ss lim e ss ( t ) lim ( z 1) E ( z ) t z 1 R(z) E(z) 1 G ( z ) ( z 1) R ( z ) e ss lim z 1 1 G ( z )
z
(2)输入信号为单位斜坡函数
r(t) t, R(z)
Tz (z -1)2 Tz (z -1)2 T 1 lim ( z 1) G ( z ) K v 1 G ( z ) z 1
( z 1) e ss lim z 1 Kv 1
(3)输入信号为单位抛物线信号
lim ( z 1)G ( z ) 速度误差系数 T z 1
-Ts 400 2 (1 e ) 2 (1 0.1s )(1 0.05s ) s 2 ( s 10)( s 20)
-1 2Tz 0.3 z 0.4 z 0.1z (1 - z ) (z -1)2 z 1 z e10T z e20T 0.4 ( z 1) 0.1( z 1) 0.4 z -1 0.3 z 0.135 z 0.0185
(1 - z
-1
K ] )Z[ K - K s s 1 2 s
(T 1 e T ) z (1 Te T e T ) K (z - 1)(z - e T )
可见，系统是Ⅰ型系统
K P lim 1 G ( z ) 1 G (1) z 1 Kv 1 lim ( z 1)G ( z ) K T z 1