第二章 轴向拉压-习题答案
材料力学习题册答案-第2章-拉压

一、 选择题
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将(
A.平动
B.转动
C.不动
D.平动加转动
D)
2.轴向拉伸细长杆件如图 2 所示,则正确的说法是 ( C )
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布,2-2 面上应力均匀分布 D.1-1 面上应力均匀分布,2-2 面上应力非均匀分布
30KN 1
300mm
l1 解:(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
(2)
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示,试作图表示节点 C 的垂直位移,设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段:σ3= =
Pa=25MPa
2.图为变截面圆钢杆 ABCD,已知 =20KN, = =35KN, = =300mm, =400mm,
D
3
C
P3
2
,绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解:
-
50KN
l2 15KN
l1
20KN
+
AB 段:σ1=
=
=176.9MPa
BC 段:σ2=
反力均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力
。ห้องสมุดไป่ตู้
材料力学第二章 轴 向拉压习题及答案

第二章轴向拉压一、选择题1.图1所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将( D)A.平动B.转动C.不动D.平动加转动2.轴向拉伸细长杆件如图2所示,其中1-1面靠近集中力作用的左端面,则正确的说法应是( C)A.1-1、2-2面上应力皆均匀分布B.1-1、2-2面上应力皆非均匀分布C.1-1面上应力非均匀分布,2-2面上应力均匀分布D.1-1面上应力均匀分布,2-2面上应力非均匀分布(图1)(图2)3.有A、B、C三种材料,其拉伸应力—应变实验曲线如图3所示,曲线( B)材料的弹性模量E大,曲线( A )材料的强度高,曲线( C)材料的塑性好。
4.材料经过冷作硬化后,其( D)。
A.弹性模量提高,塑性降低B.弹性模量降低,塑性提高C.比例极限提高,塑性提高D.比例极限提高,塑性降低5.现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图4所示结构中两种合理选择方案是( A)。
A.1杆为钢,2杆为铸铁B.1杆为铸铁,2杆为钢C.2杆均为钢D.2杆均为铸铁(图3)(图4)(图5)6.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的是(B)。
A. 弹性阶段;B.屈服阶段;C.强化阶段;D.局部变形阶段。
7.铸铁试件压缩破坏(B)。
A. 断口与轴线垂直;B. 断口为与轴线大致呈450~550倾角的斜面;C. 断口呈螺旋面;D. 以上皆有可能。
8.为使材料有一定的强度储备,安全系数取值应( A )。
A .大于1; B. 等于1; C.小于1; D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向,过截面形心C 方向相对,作用线与杆轴线重合D 方向相对,沿同一直线作用10. 图6所示一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N 1,N 2和N 3,三者的关系为( B )。
《材料力学》第2章轴向拉(压)变形习题解答

其方向。 解:斜截面上的正应力与切应力的公式为:
ασσα20cos = αστα2sin 2 = 式中,MPa mm N A N 1001001000020===σ,把α的数值代入以上二式得:
[习题 2-7] 一根等直杆受力如图所示。已知杆的横截面面积 A 和材料的弹性模量 E 。试作轴力图,并求杆端点 D 的位移。 解: (1)作轴力图
[习题 2-9] 一根直径 mm d 16=、长 m l 3=的圆截面杆,承受轴 向拉力 kN F 30=,其伸长为 mm l 2.2=?。试求杆横截面上的应 力与材料的弹性模量 E 。 解:(1)求杆件横截面上的应力 MPa mm N A N 3.1491614.34 110302 23=???==σ (2)求弹性模量 因为:EA Nl l = ?, 所以:GPa MPa l l l A l N E 6.203)(9.2035902 .23000 3.149==?=??=???=σ。 [习题 2-10] (1)试证明受轴向拉伸(压缩)的圆截面杆横截 面沿圆周方向的线应变 s ε等于直径方向的线应变 d ε。 (2)一根直径为 mm d 10=的圆截面杆,在轴向力 F 作用下,直 径减小了 0.0025mm 。如材料 的弹性模量 GPa E 210=,泊松比 3.0=ν,试求该轴向拉力 F 。 (3)空心圆截面杆,外直径 mm D 120=,内直径 mm d 60=,材 料的泊松比 3.0=ν。当其轴向拉伸时,已知纵向线应变 001.0=, 试求其变形后的壁厚。 解:(1)证明 d s εε= 在圆形截面上取一点 A ,连结圆心 O 与 A 点,则 OA 即代表直 径方向。过 A 点作一条直线 AC 垂直于 OA ,则 AC 方向代表圆周方向。νεεε-==AC s(泊
轴向拉压习题答案2

第2章 轴向拉伸和压缩主要知识点:(1)轴向拉伸(压缩)时杆的内力和应力;(2)轴向拉伸(压缩)时杆的变形;(3)材料在轴向拉伸和压缩时的力学性能;(4)轴向拉压杆的强度计算;(5)简单拉压超静定问题。
轴向拉伸(压缩)时杆的变形4. 一钢制阶梯杆如图所示。
已知沿轴线方向外力F 1=50kN ,F 2=20kN ,各段杆长l 1=100mm ,l 2=l 3=80mm ,横截面面积A 1=A 2=400mm 2,A 3=250mm 2,钢的弹性模量E=200GP a ,试求各段杆的纵向变形、杆的总变形量及各段杆的线应变。
解:(1)首先作出轴力图如图4-11所示,由图知kN F N 301-=,kN F F N N 2032==。
(2)计算各段杆的纵向变形m m EA l F l N 5693311111075.31040010200101001030---⨯-=⨯⨯⨯⨯⨯⨯-==∆ m m EA l F l N 569332222100.2104001020010801020---⨯=⨯⨯⨯⨯⨯⨯==∆(3)杆的总变形量m l l l l 53211045.1-⨯=∆+∆+∆=∆。
(4)计算各段杆的线应变 451111075.310.01075.3--⨯-=⨯-=∆=l l ε 45222105.208.0100.2--⨯=⨯=∆=l l ε 45333100.408.0102.3--⨯=⨯=∆=l l ε材料在轴向拉伸和压缩时的力学性能5. 试述低碳钢拉伸试验中的四个阶段,其应力—应变图上四个特征点的物理意义是什么?答:低碳钢拉伸试验中的四个阶段为弹性阶段、屈服阶段、强化阶段和颈缩阶段。
在弹性阶段,当应力小于比例极限σp 时,材料服从虎克定律;当应力小于弹性极限σe 时,材料的变形仍是弹性变形。
屈服阶段的最低点对应的应力称为屈服极限,以σs 表示。
强化阶段最高点所对应的应力称为材料的强度极限,以σb 表示,它是材料所能承受的最大应力。
材料力学 轴向拉压 题目+答案详解
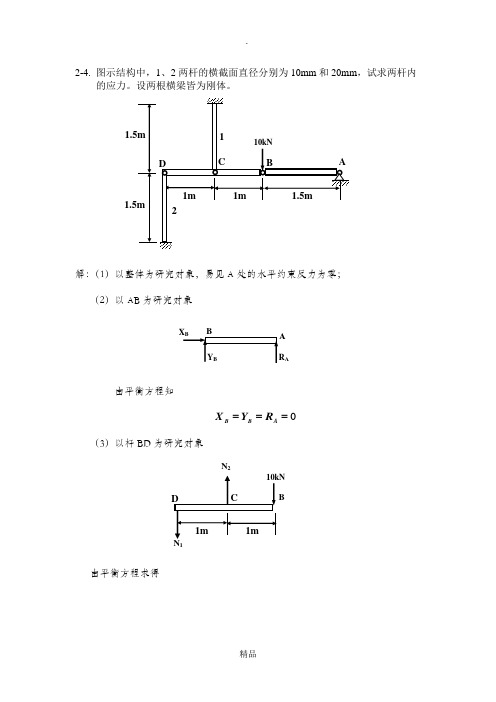
2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD 为研究对象由平衡方程求得1KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-19. 在图示结构中,设AB 和CD 为刚杆,重量不计。
铝杆EF 的l 1=1m ,A 1=500mm 2,E 1=70GPa 。
钢杆AC 的l 2=1.5m ,A 2=300mm 2,E 2=200GPa 。
若载荷作用点G 的垂直位移不得超过2.5mm 。
试求P 的数值。
解:(1)由平衡条件求出EF 和AC 杆的内力P N N N P N N AC EF AC4332 2112=====(2)求G 处的位移22221111212243)ΔΔ23(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +=+=+==(3)由题意kNP P P A E Pl A E Pl mml G 1125.2300102001500500107010009212143435.233222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中,设AB 和AC 分别是直径 为20mm 和24mm 的圆截面杆,E=200GPa ,P=5kN ,试求A 点的垂直位移。
解:(1)以铰A 为研究对象,计算杆AB 和杆AC 的受力kN N kN N AC AB 66.3 48.4==(2)两杆的变形为()伸长mm πEA l N l ABABAB AB 201.04201020045cos 20001048.42303=⨯⨯⨯⨯⨯==Δ ()缩短mm πEA l N l ACAC AC AC 0934.04241020030cos 20001066.32303=⨯⨯⨯⨯⨯==Δ(3)如图,A点受力后将位移至A’,所以A点的垂直位移为AA’’mmctg A A l A A AA A A mmA A ctg A A ctg A A A mm AA AA AA AA A A A A l l AB A AB AC 249.00355.0284.0 4545sin /Δ 035.04530A 0972.030sin /45sin /AΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中2-36. 在图示结构中,设AC 梁为刚杆,杆件1、2、3的横截面面积相等,材料相同。
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

习题2-1一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量MPa .如不计柱自重,试求:51010.0×=E (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(1)轴力图(2)AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=(3)AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε(4)总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为1cm 的圆杆,在拉力P =10kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为=30o 的斜截面上的正应力与剪应力。
α解:(1)最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−(2)界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
轴向拉伸及压缩习题及解答

轴向拉伸与压缩习题及解答一、判断改错1、构件力的大小不但与外力大小有关,还与材料的截面形状有关。
答:错。
静定构件力的大小之与外力的大小有关,与材料的截面无关。
2、杆件的某横截面上,假设各点的正应力均为零,那么该截面上的轴力为零。
答:对。
3、两根材料、长度都一样的等直柱子,一根的横截面积为1A ,另一根为2A ,且21A A >。
如下图。
两杆都受自重作用。
那么两杆最大压应力相等,最大压缩量也相等。
答:对。
自重作用时,最大压应力在两杆底端,即max max N All A Aνσν=== 也就是说,最大应力与面积无关,只与杆长有关。
所以两者的最大压应力相等。
最大压缩量为 2max max22N Al l l l A EA Eνν⋅∆===即最大压缩量与面积无关,只与杆长有关。
所以两杆的最大压缩量也相等。
4、受集中力轴向拉伸的等直杆,在变形中任意两个横截面一定保持平行。
所以宗乡纤维的伸长量都相等,从而在横截面上的力是均匀分布的。
答:错 。
在变形中,离开荷载作用处较远的两个横截面才保持平行,在荷载作用处,横截面不再保持平面,纵向纤维伸长不相等,应力分布复杂,不是均匀分布的。
5、假设受力物体某电测得x 和y 方向都有线应变x ε和y ε,那么x 和y 方向肯定有正应力x σ和y σ。
答:错, 不一定。
由于横向效应作用,轴在x 方向受拉〔压〕,那么有x σ;y 方向不受力,但横向效应使y 方向产生线应变,y x εενε'==-。
A 1(a) (b)二、填空题1、轴向拉伸的等直杆,杆的任一点处最大剪应力的方向与轴线成〔45〕2、受轴向拉伸的等直杆,在变形后其体积将〔增大〕3、低碳钢经过冷做硬化处理后,它的〔比例〕极限得到了明显的提高。
4、工程上通常把延伸率δ>〔5%〕的材料成为塑性材料。
5、 一空心圆截面直杆,其、外径之比为0.8,两端承受力力作用,如将外径增加一倍,那么其抗拉刚度将是原来的〔4〕倍。
材料力学练习册答案

第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑x F ,得 01=N F22-截面,取右段如)(b由0=∑x F ,得 P F N -=233-截面,取右段如)(c由0=∑x F ,得 03=N F2.2 图示杆件截面为正方形,边长cm a 20=,杆长m l 4=,kN P 10=,比重3/2m kN =γ。
在考虑杆本身自重时,11-和22-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑xF,得kN la F N 08.04/21==γ22-截面,取右段如)(b由0=∑xF,得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示,已知kN P 20=,kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解:轴力图如图。
杆的总伸长:m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力:MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示,已知直径mm d 40=,杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
(GPa E 80=铜,GPa E 200=钢)。
解:由∑=∆EAl F l N ,得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得: kN P 7.16= 杆内的最大正应力:MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时,在试件的某处分别安装两个杆件变形仪,其放大倍数各为1200=A k ,1000=B k ,标距长为cm s 20=,受压后变形仪的读数增量为mm n A 36-=∆,mm n B 10=∆,试求此材料的横向变形系数ν(即泊松比)。
材料力学第五版课后习题答案详解

Microsoft Corporation材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
返回2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)。
轴向拉伸和压缩习题集及讲解

第二章 轴向拉伸和压缩 第一节 轴向拉压杆的内力1.1 工程实际中的轴向受拉杆和轴向受压杆在工程实际中,经常有承受轴向拉伸荷载或轴向压缩荷载的等直杆。
例如图2-1a 所示桁架的竖杆、斜杆和上、下弦杆,图2-1b 所示起重机构架的各杆及起吊重物的钢索,图2-1c 所示的钢筋混凝土电杆上支承架空电缆的横担结构,BC 、AB 杆,此外,千斤顶的螺杆,连接气缸的螺栓及活塞连杆等都是轴间拉压杆。
钢木组合桁架d起重机图工程实际中的轴向受拉(压)杆1.2 轴向拉压杆的内力——轴力和轴力图bcx图用截面法求杆的内力为设计轴向拉压杆,需首先研究杆件的内力,为了显示杆中存在的内力和计算其大小,我们采用在上章中介绍过的截面法。
(如图2-2a )所示等直杆,假想地用一截面m -m 将杆分割为I 和II 两部分。
取其中的任一部分(例如I )为脱离体,并将另一部分(例如II )对脱离体部分的作用,用在截开面上的内力的合力N 来代替(图2-2b ),则可由静力学平衡条件:0 0X N P =-=∑求得内力N P =同样,若以部分II 为脱离体(图2-2c ),也可求得代表部分I 对部分II 作用的内力为N =P ,它与代表部分II 对部分I 的作用的内力等值而反向,因内力N 的作用线通过截面形心 即沿杆轴线作用,故称为轴力..。
轴力量纲为[力],在国际单位制中常用的单位是N (牛)或kN (千牛)。
为区别拉伸和压缩,并使同一截面内力符号一致,我们规定:轴力的指向离开截面时为正号轴力;指向朝向截面时为负号轴力。
即拉力符号为正,压力符号为负。
据此规定,图2-2所示m-m 截面的轴力无论取左脱离体还是右脱离体,其符号均为正。
1.3 轴力图当杆受多个轴向外力作用时,杆不同截面上的轴力各不相同。
为了形象表示轴力沿杆轴线的变化情况,以便于对杆进行强度计算,需要作出轴力图,通常用平行于杆轴线的坐标表示截面位置,用垂直杆轴线的坐标表示截面上轴力大小,从而给出表示轴力沿截面位置关系的图例,即为轴力图...。
材料力学内部习题集及答案

第二章 轴向拉伸和压缩2-1一圆截面直杆,其直径d =20mm,长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3,杆的上端固定,下端作用有拉力F =4KN ,试求此杆的:⑴最大正应力; ⑵最大线应变; ⑶最大切应力;⑷下端处横截面的位移∆。
解:首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 故最大正应力为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α(α为杆内斜截面与横截面的夹角)为45︒时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ,长度为L ,材料的容重为γ。
解:距离A 为x 处的轴力为 所以总伸长2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3图示结构,已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其方位角θ的大小。
解:由胡克定律得 相应杆上的轴力为取A 节点为研究对象,由力的平衡方程得解上述方程组得2-4图示杆受轴向荷载F 1、F 2作用,且F 1=F 2=F ,已知杆的横截面面积为A ,材料的应力-应变关系为ε=c σn,其中c 、n 为由试验测定的常数。
材料力学第2章答案

(2)若设计时取试验机的安全因数 n = 2 ,则杆 CD 的横截面面积为多少?
8
(3)若试样直径 d = 10 mm ,今欲测弹性模量 E ,则所加载荷最大不能超过多少?
解(1) σ
2-5 何谓失效?极限应力、安全因数和许用应力间有何关系?何谓强度条件?利用强度 条件可以解决哪些形式的强度问题?
答 失效(包括强度失效、刚度失效和稳定性失效)是指构件不能正常工作。 许用应力=极限应力/安全因数。 利用强度条件可以解决强度校核、截面设计和确定许用载荷等。
2-6 试指出下列概念的区别:比例极限与弹性极限;弹性变形与塑性变形;延伸率与正 应变;强度极限与极限应力;工作应力与许用应力。
α = 90° τ 90° = 0
2-5 图 示 拉 杆 沿 斜 截 面 m − m 由 两 部 分 胶 合 而 成 , 设 在 胶 合 面 上 许 用 拉 应 力 [σ ] = 100 MPa ,许用切应力[τ ] = 50 MPa 。并设胶合面的强度控制杆件的拉力。问:
(1)为使杆件承受最大拉力 F ,角α 的值应为多少? (2)若杆件横截面面积为 4 cm2,并规定α ≤ 60° ,确定许用载荷[F ] 。
∑ Fx = 0 , FCx = 0
图(c)
∑ M D = 0 , FC'y = 0
图(b)
∑ M B = 0 , FN1 = 10 kN (拉)
∑ Fy = 0 , FN2 = 20 kN (拉)
6
σ1
=
FN1 A1
=
4FN1 πd12
=
4 ×10 ×103 π ×102 ×10−6
= 127 MPa
材料力学第二章轴向拉伸与压缩作业习题

第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。
(1) (2)2、图示拉杆承受轴向拉力F =10kN ,杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。
如材料的弹性摸量E =210GPa ,泊松比ν=0.3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。
已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa,钢丝的自重不计。
试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。
6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。
《材料力学》第2章 轴向拉(压)变形 习题解讲解

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
轴向拉伸与压缩习题及解答

cos sin 3AyF F Fθθ轴向拉伸与压缩习题及解答计算题1:利用截面法,求图2. 1所示简支梁m — m 面的内力分量。
解:(1)将外力F 分解为两个分量,垂直于梁轴线的分量F sin θ,沿梁轴线的分量F cos θ. (2)求支座A 的约束反力:xF∑=0,AxF∑=cos F θB M ∑=0, Ay F L=sin 3L F θAy F =sin 3Fθ (3)切开m — m ,抛去右半部分,右半部分对左半部分的作用力N F ,S F 合力偶M 代替 (图1.12 )。
图 2.1 图2.1(a) 以左半段为研究对象,由平衡条件可以得到xF∑=0, N F =—Ax F =—cos F θ(负号表示与假设方向相反)y F ∑=0, s F =Ay F =sin 3Fθ 左半段所有力对截面m-m 德形心C 的合力距为零sin θC M ∑=0, M=AyF 2L =6FL sin θ 讨论 对平面问题,杆件截面上的内力分量只有三个:和截面外法线重合的内力称为轴力,矢量与外法线垂直的力偶距称为弯矩。
这些内力分量根据截面法很容易求得。
在材料力学课程中主要讨论平面问题。
计算题2:试求题2-2图所示的各杆1-1和2-2横截面上的轴力,并作轴力图。
解 (a )如图(a )所示,解除约束,代之以约束反力,作受力图,如题2-2图(1a )所示。
利用静力学平衡条件,确定约束反力的大小和方向,并标示在题2-2图(1a )中。
作杆左端面的外法线n ,将受力图中各力标以正负号,凡与外法线指向一致的力标以正号,反之标以负号,轴力图是平行于杆轴线的直线。
轴力图在有轴力作用处,要发生突变,突变量等与该处轴力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,如题2-2图(2a )所示,截面1和截面2上的轴力分别为1N F =F 和2N F =—F 。
(b)解题步骤与题2-2(a )相同,杆受力图和轴力图如题2-2(1b )、(2b )所示。
轴向拉伸和压缩习题附标准答案

第四章轴向拉伸和压缩、填空题1、杆件轴向拉伸或压缩时,其受力特点是:作用于杆件外力的合力的作用线与杆件轴线相_________ .2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面,并通过截面_____________ .4、杆件轴向拉伸或压缩时,其横截面上的正应力是___________ 分布的.7、在轴向拉,压斜截面上,有正应力也有剪应力,在正应力为最大的截面上剪应力为________ .8杆件轴向拉伸或压缩时,其斜截面上剪应力随截面方位不同而不同,而剪应力的最大值发生在与轴线间的夹角为________ 的斜截面上.矚慫润厲钐瘗睞枥庑赖。
9、杆件轴向拉伸或压缩时,在平行于杆件轴线的纵向截面上,其应力值为_______ .10、胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________ 极限.11、杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力,这说明杆件材料的弹性模量E值越大,其变形就越 ________ 聞創沟燴鐺險爱氇谴净。
12、在国际单位制中,弹性模量E的单位为________ .13、在应力不超过材料比例极限的范围内,若杆的抗拉(或抗压)刚度越_________ ,则变形就越小.15、低碳钢试样据拉伸时,在初始阶段应力和应变成___________ 关系,变形是弹性的,而这种弹性变形在卸载后能完全消失的特征一直要维持到应力为__________ 极限的时候.残骛楼諍锩瀨濟溆塹籟。
16、在低碳钢的应力一应变图上,开始的一段直线与横坐标夹角为a,由此可知其正切tg a在数值上相当于低碳钢的值.酽锕极額閉镇桧猪訣锥。
17、金属拉伸试样在屈服时会表现出明显的__________ 变形,如果金属零件有了这种变形就必然会影响机器正常工作.彈贸摄尔霁毙攬砖卤庑。
18、金属拉伸试样在进入屈服阶段后,其光滑表面将出现与轴线成_______ 角的系统条纹,此条纹称为__________ .謀养抟箧飆鐸怼类蒋薔。
材料力学第二章轴向拉伸与压缩习题答案

解:
设每个螺栓承受的剪力为 ,则由
可得
螺栓的切应力
MPa MPa
∴螺栓满足剪切强度条件。
3-11图示矩形截面木拉杆的接头。已知轴向拉力 ,截面的宽度 ,木材顺纹的许用挤压应力 ,顺纹的许用切应力 。试求接头处所需的尺寸l和a。
解:
1.求支反力,作剪力图和弯矩图。
,
2.按正应力强度条件选择工字钢型号
由 ≤ ,得到
≥
查表选 14工字钢,其
, ,
3.切应力强度校核
满足切应力强度条件。
∴选择 14工字钢。
5-17图示木梁受移动载荷 作用。已知木材的许用正应力 ,许用切应力 , ,木梁的横截面为矩形截面,其高宽比 。试选择此梁的横截面尺寸。
≤
可得 ≤ ①
D点受力如图(b)所示,由平衡条件可得:
CD杆受压,压力为 ,由压杆的强度条件
≤
可得 ≤ ②
由①②可得结构的许用载荷为 。
3-8图示横担结构,小车可在梁AC上移动。已知小车上作用的载荷 ,斜杆AB为圆截面钢杆,钢的许用应力 。若载荷F通过小车对梁AC的作用可简化为一集中力,试确定斜杆AB的直径d。
截面上的剪力和弯矩为: ,
2.求1-1横截面上a、b两点的应力
5-10为了改善载荷分布,在主梁AB上安置辅助梁CD。若主梁和辅助梁的抗弯截面系数分别为 和 ,材料相同,试求a的合理长度。
解:
1.作主梁AB和辅助梁CD的弯矩图
2.求主梁和辅助梁中的最大正应力
主梁:
辅助梁:
3.求 的合理长度
材料力学答案30581

第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布,集度为q。
题2-2图(a)解:由图2-2a(1)可知,=2()F-xqxqaN轴力图如图2-2a(2)所示,qa F 2m ax ,N =图2-2a(b)解:由图2-2b(2)可知, qa F =R qa F x F ==R 1N )(22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示,qa F =max N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N 10508263=⨯=⨯⨯==-A F σ斜截面m -m 的方位角,ο50-=α故有 MPa 3.41)50(cos MPa 100cos 22=-⋅==οασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅==οαστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa10220ΔΔ96=⨯=⨯≈=εσEMPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
2-7 一圆截面杆,材料的应力-应变曲线如题2-6图所示。
第二章轴向拉伸与压缩

第二章轴向拉伸与压缩(王永廉《材料力学》作业参考答案(第1-29题))2012-02-26 00:02:20| 分类:材料力学参答|字号订阅第二章轴向拉伸与压缩(第1-29题)习题2-1试绘制如图2-6所示各杆的轴力图。
图2-6解:由截面法,作出各杆轴力图如图2-7所示图2-7习题2-2 试计算图2-8所示结构中BC杆的轴力。
图2-8 a)解:(a)计算图2-8a中BC杆轴力截取图示研究对象并作受力图,由∑M D=0,即得BC杆轴力=25KN(拉)(b)计算图2-8 b中BC杆轴力图2-8b截取图示研究对象并作受力图,由∑MA=0,即得BC杆轴力=20KN(压)习题2-3在图2-8a中,若杆为直径的圆截面杆,试计算杆横截面上的正应力。
解:杆轴力在习题2-2中已求出,由公式(2-1)即得杆横截面上的正应力(拉)习题2-5图2-10所示钢板受到的轴向拉力,板上有三个对称分布的铆钉圆孔,已知钢板厚度为、宽度为,铆钉孔的直径为,试求钢板危险横截面上的应力(不考虑铆钉孔引起的应力集中)。
解:开孔截面为危险截面,其截面面积由公式(2-1)即得钢板危险横截面上的应力(拉)习题2-6如图2-11a所示,木杆由两段粘结而成。
已知杆的横截面面积A=1000 ,粘结面的方位角θ=45,杆所承受的轴向拉力F=10KN。
试计算粘结面上的正应力和切应力,并作图表示出应力的方向。
解:(1)计算横截面上的应力= = 10MPa(2)计算粘结面上的应力由式(2-2)、式(2-3),得粘结面上的正应力、切应力分别为cos245,=5 MPa45=sin(2*45。
)=5MPa45=其方向如图2-11b所示习题2-8 如图2-8所示,等直杆的横截面积A=40mm2,弹性模量E=200GPa,所受轴向载荷F1=1kN,F2=3kN,试计算杆内的最大正应力与杆的轴向变形。
解:(1)由截面法作出轴力图(2)计算应力由轴力图知,故得杆内的最大正应力(3)计算轴向变形轴力为分段常数,杆的轴向变形应分段计算,得杆的轴向变形习题2-9阶梯杆如图2-13a所示,已知段的横截面面积、段的横截面面积,材料的弹性模量,试计算该阶梯杆的轴向变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1a 求图示各杆指截面的轴力,并作轴力图。
(c ')(e ')(d ')N (kN)205455(f ')解:方法一:截面法(1)用假想截面将整根杆切开,取截面的右边为研究对象,受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力: (b) 图:)(20020011拉kN N NX =→=-→=∑(c) 图:)(5252002520022压kN N NX -=-=→=--→=∑(d) 图:)(455025200502520033拉kN N NX =+-=→=-+-→=∑(e) 图:)(540502520040502520044拉kN N NX =-+-=→=--+-→=∑(2)杆的轴力图如图(f )所示。
方法二:简便方法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图,作题的时候可用手蒙住丢弃的部份,并把手处视为固定端)(1)因为轴力等于截面一侧所有外力的代数和:∑=一侧FN 。
故:)(201拉kN N =)(525202压kN N -=-=)(455025203拉kN N =+-=)(5405025204拉kN N =-+-=(2)杆的轴力图如图(f ‘)所示。
2-2b 作图示杆的轴力图。
(c)图:(b)图:(3)杆的轴力图如图(d )所示。
2-5 图示两根截面为100mm ⅹ100mm 的木柱,分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题2-5-N图(kN)6108.5N图(kN)326.5-解:(1)梁与柱之间通过中间铰,可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁,柱可视为悬臂梁,受力如图所示。
列各梁、柱的平衡方程,可求中间铰对各梁、柱的约束反力,计算结果见上图。
(2)作柱的轴力图,如(e)、(f)所示。
(3)求柱各段的应力。
解:(1)用1-1截面将整个杆切开,取左边部分为研究对象;再用x -x 截面整个杆切开,取右边部分为研究对象,两脱离体受力如图(b)、(c),建立图示坐标。
(2)列平衡方程求杆的轴力 PN 图(d)题2-2b()2/0)(0011l x P N P N X <<=→=-→=∑拉()2/32/))(2/(0)2/(0l x l l x q N N l x q X x x <<-=→=--→=∑拉⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⨯⨯-==-=⨯⨯-==-=⨯⨯-==⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⨯⨯-==-=⨯⨯-==-=⨯⨯-==MPa Pa A N MPaPa A N MPa Pa A N MPa Pa A N MPaPa A N MPa Pa A N GH GH FG FG EF EF CD CD BC BC AB AB 65.001.001.0105.62.001.001.01023.001.001.010385.001.001.0105.8101.001.010106.001.001.0106333333σσσσσσ右柱左柱2-6一受轴向拉伸的杆件,横截面面积A =200mm 2,力P =10kN ,求法线与杆轴成30o 及45o 的斜截面上的正应力ασ和剪应力ατ。
解:(1)求轴向拉压杆横截面应力MPa Pa A N 5010200101063=⨯⨯==-σ(2)由轴向拉压杆斜截面上应力公式:⎪⎩⎪⎨⎧==αστασσαα2sin 2cos 2求得: ⎪⎩⎪⎨⎧=⨯=====⎪⎩⎪⎨⎧=⨯=====MPaMPaMPa MPa 25)452sin(2502sin 22545cos 50cos 65.21)302sin(2502sin 25.3730cos 50cos 452245302230οοοοοοοοαστασσαστασσ和2-9(1)证明轴向拉伸(或压缩)的圆截面杆,其横截面上沿圆周方向的线应变s ε等于沿直径方向的线应变d ε。
(2)一圆截面钢杆,直径d =10mm ,在轴向拉力P 作用下,直径减少了0.0025mm ,试求拉力P 。
(1)证明:ddddd d d s ∆=∆=∆=εππε,故,d s εε= (2)解:因4'105.2100025.0-⨯==∆==d d d εε,又01.025.0105.24''=⨯-==→-=-v v εεεε 故,kN N A E A P 7.151057.101.04001.010200429=⨯=⨯⨯⨯⨯=⋅=⋅=πεσ2-11图示结构中,刚性杆AB 由两根弹性杆AC 和BD 悬吊。
已知:P 、l 、E 1A 1和E 2A 2 ,试求x 等于多少时可使AB 杆保持水平?分析:两根杆的反力和x ,三个未知量,仅凭列AB 的平衡方程,无法求解。
显然要列变形协调方程。
解:(1)研究AB 杆,列平衡方程2N (b)题2-11⎩⎨⎧=+=⋅+⋅-P N N l N x P BD CABD 0,………(a ) 三个未知量,仅凭平衡方程无法求解。
(2)列变形协调方程AB 杆位置要水平,BD AC l l ∆=∆ 而:EAaN l EA a N l BD BD CD AC ⋅=∆⋅=∆,即EAaN EA a N l l BD CD BD AC ⋅=⋅=∆=∆………………………………………………(b ) (3)联解平衡方程式组和变形协调方程,可得:221111A E A E lA E x +=2-13 图示三角支架中,杆AB 由两根不等边角钢L63ⅹ40ⅹ4组成,当W =15kN 时,校核杆AB 的强度。
(3)强度校核:经查表,等边角钢的面积为4.058cm 2。
故,AB 杆的拉压强度足够。
2-14 图示桁架中,每根杆长均为1m ,并均由两根 Q 235等边角钢组成。
设P =400kN ,试选择AC 杆和CD 杆所用角钢的型号。
解:(1)求支反力R A 、R B :因屋架及荷载左右对称,所以:kN 200400212=⨯===P R R B A (2)求AC 杆和CD 杆的内力:用截面法1-1切开, 取截面的左边部分为研究对象,设三杆是拉杆,内力 沿截面外法线方向,脱离体受力如图(b )所示。
解:(1)拉紧的柔性约束对滑轮的作用,只相当于一个力矢2W ,而无主矩。
研究销钉,假设AB 、AC 为拉杆,受力如图(b),所示。
(注意:拉杆施与销钉的拉力是沿“背离销钉,指向杆内”) (2)列平衡方程,求AB 杆内力。
)(600230sin 0拉kN N W N Y AB AB =→=-→=∑οN AB题2-13(b)[]MPa MPa Pa A N AB AB 1609.7310058.42106043=≤=⨯⨯⨯==-σσ(b)列平衡方程求AC 杆和CD 杆的内力:⎪⎪⎩⎪⎪⎨⎧-=-=→⎪⎪⎩⎪⎪⎨⎧=⨯+=⨯⨯-⨯⨯-→⎪⎩⎪⎨⎧==∑∑332060sin 20)30cos 1(2)60sin 1(00)(P N P N N P P N Y F m DC AC DCAC D οοο (3)由强度条件选择等边角钢的型号:[][][][]⎪⎩⎪⎨⎧≥≥→⎪⎪⎪⎩⎪⎪⎪⎨⎧⨯⨯⨯=≥⨯⨯⨯=≥→⎪⎪⎪⎩⎪⎪⎪⎨⎧≤=≤=2226326322.761.310160131040021016013210400222cm cm m m A A N A N A A N A N AC DC DC AC AC DC DC DC AC AC AC σσσσσσ 故,AC 杆选两根L54040⨯⨯的等边角钢:。
CD 杆选两根L66363⨯⨯的等边角钢。
2-15图示三角架中,已知:[][]MPa ,A MPa A 100900,160,6002211====σσ22mm mm ,试求结构的许可荷载[P ]。
解:(1)求杆件的容许轴力[N ][][]kN 9696000106001016066111==⨯⨯⨯=⨯=-N A N σ[][]kN 9090000109001010066222==⨯⨯⨯=⨯=-N A N σ(2)求出内力N 与P 的关系,研究节点,受力如图(b): 由于结构对称,荷载对称,所示N 1=N 2)(06cos 20211拉P N N P N Y ==→=-→=∑π(3)由强度条件确定P :kN P kNP kNP kN N P N kN N P N 90909690][96][2211≤→⎩⎨⎧≤≤→⎩⎨⎧=≤==≤= 故,结构的容许荷载[]kN 90=P2-16 图示钢筋混凝土短柱,边长mm a 400=, 柱内有四根直径为mm d 30=的钢筋。
已知,柱 受压后混凝土的应力值为MPa h 6=σ,试求轴 向压力P 及钢筋的应力g σ。
解:方法一:钢筋混凝土短柱,下端固定,上端 为盖板覆盖,可认为短柱是由无数根纵向纤维组°N 2题2-15(b)N1成,各纵向纤维的线应变相同。
即g h εε=。
由胡虎定理εσE =可得:10102.01021111=⨯⨯===h g h h g g h g E E E E εεσσ故,MPa h g 6061010=⨯==σσ故, kN A A P g g h h 6.1129403.0106044.01062626=⨯⨯⨯⨯+⨯⨯=⋅+⋅=πσσ方法二: 由胡虎定理EA Nll =∆可得:gg g g h h h h A E l N l ,A E l N l =∆=∆ 而,钢筋和混凝土的纵向绝对伸长量相等。
044156.04.04/03.0102.01024/22111122=⨯⨯⨯⨯=⋅==→=ππa d E E A E A E N N A E l N A E l N h g h h g g h g g g g h h h 故:N N N kNN N h g h 39.42960044156.0044156.09604.010626=⨯===⨯⨯=kN N N P g h 6.112939.4249604=⨯+=⨯+=由轴向拉压杆的应力公式得:MPa Pa A N G gg 60403.01039.4223=⨯⨯==πσ 2-24 图示为低碳钢的εσ-曲线,若超过屈服极限后继续加载,当试件横截面上应力MPa 300=σ时,测得其轴向线应变3105.3-⨯=ε,然后立即卸载至0=σ,试求试件的轴向塑性应变P ε。
解:(1)卸载遵循弹性规律:卸卸εσE =。
查表可知低碳钢的弹性模量:E =200GPa3116105.110210300-⨯=→⨯=⨯→=e e E εεεσ卸卸(2)卸载前的轴向线应变3105.3-⨯=ε,则3102-⨯=-=e P εεε题2-25题2-242-25 图示拉杆为钢杆,测得表面上K 点处的横向线应变4'102-⨯-=ε,试求荷载P 和总伸长量l ∆。
