模式识别期末复习
模式识别期末考试题及答案

模式识别期末考试题及答案一、选择题(每题2分,共20分)1. 以下哪一项不是模式识别的主要任务?A. 分类B. 回归C. 聚类D. 预测答案:B2. 以下哪一种方法不属于统计模式识别方法?A. 最小二乘法B. 感知机C. 支持向量机D. 决策树答案:A3. 在模式识别中,以下哪种技术用于降低特征维度?A. 主成分分析(PCA)B. 线性判别分析(LDA)C. 神经网络D. K-均值聚类答案:A4. 以下哪一种模式识别方法适用于非线性问题?A. 线性判别分析(LDA)B. 支持向量机(SVM)C. 主成分分析(PCA)D. K-最近邻(K-NN)答案:B5. 以下哪一项不是模式识别的评价指标?A. 准确率B. 精确率C. 召回率D. 信息熵答案:D二、填空题(每题2分,共20分)6. 模式识别的主要任务包括分类、回归、聚类和________。
答案:预测7. 统计模式识别方法包括最小二乘法、感知机、________和决策树。
答案:支持向量机8. 主成分分析(PCA)的主要目的是________特征。
答案:降低维度9. 在模式识别中,________用于将样本分为不同的类别。
答案:分类器10. 支持向量机(SVM)的基本思想是找到一个________,使得不同类别的样本之间的间隔最大化。
答案:最优分割超平面三、简答题(每题10分,共30分)11. 请简述模式识别的主要步骤。
答案:(1)数据预处理:对原始数据进行清洗、标准化和降维等处理。
(2)特征提取:从原始数据中提取有助于分类的特征。
(3)模型训练:使用训练集对分类器进行训练。
(4)模型评估:使用测试集对分类器的性能进行评估。
(5)模型优化:根据评估结果对模型进行调整和优化。
12. 请简述支持向量机(SVM)的基本原理。
支持向量机是一种二分类模型,其基本思想是找到一个最优分割超平面,使得不同类别的样本之间的间隔最大化。
SVM通过求解一个凸二次规划问题来寻找最优分割超平面,从而实现分类任务。
模式识别期末试题及答案

模式识别期末试题及答案正文:模式识别期末试题及答案1. 选择题1.1 下列关于机器学习的说法中,正确的是:A. 机器学习是一种人工智能的应用领域B. 机器学习只能应用于结构化数据C. 机器学习不需要预先定义规则D. 机器学习只能处理监督学习问题答案:A1.2 在监督学习中,以下哪个选项描述了正确的训练过程?A. 通过输入特征和预期输出,训练一个模型来进行预测B. 通过输入特征和可能的输出,训练一个模型来进行预测C. 通过输入特征和无标签的数据,训练一个模型来进行预测D. 通过输入特征和已有标签的数据,训练一个模型来进行分类答案:D2. 简答题2.1 请解释什么是模式识别?模式识别是指在给定一组输入数据的情况下,通过学习和建模,识别和分类输入数据中的模式或规律。
通过模式识别算法,我们可以从数据中提取重要的特征,并根据这些特征进行分类、聚类或预测等任务。
2.2 请解释监督学习和无监督学习的区别。
监督学习是一种机器学习方法,其中训练数据包含了输入特征和对应的标签或输出。
通过给算法提供已知输入和输出的训练样本,监督学习的目标是学习一个函数,将新的输入映射到正确的输出。
而无监督学习则没有标签或输出信息。
无监督学习的目标是从未标记的数据中找到模式和结构。
这种学习方法通常用于聚类、降维和异常检测等任务。
3. 计算题3.1 请计算以下数据集的平均值:[2, 4, 6, 8, 10]答案:63.2 请计算以下数据集的标准差:[1, 3, 5, 7, 9]答案:2.834. 综合题4.1 对于一个二分类问题,我们可以使用逻辑回归模型进行预测。
请简要解释逻辑回归模型的原理,并说明它适用的场景。
逻辑回归模型是一种用于解决二分类问题的监督学习算法。
其基本原理是通过将特征的线性组合传递给一个非线性函数(称为sigmoid函数),将实数值映射到[0,1]之间的概率。
这个映射的概率可以被解释为某个样本属于正类的概率。
逻辑回归适用于需要估计二分类问题的概率的场景,例如垃圾邮件分类、欺诈检测等。
模式识别期末考试复习

题型:1.填空题5题填空题2.名词解释4题3.问答题4题4.计算作图题3题5.综合计算题1题备注1:没有整理第一章和第六章,老师说不考的备注2:非线性判别函数相关概念P69概率相关定义、性质、公式P83以后最小错误率贝叶斯决策公式P85最小风险贝叶斯P86正态贝叶斯P90综合计算有可能是第六次作业一、填空题物以类聚人以群分体现的是聚类分析的基本思想。
模式识别分类:1.从实现方法来分模式识别分为监督分类和非监督分类;2.从理论上来分,有统计模式识别,统计模式识别,模糊模式识别,神经网络模式识别法聚类分析是按照不同对象之间的差异,根据距离函数的规律做模式分类的。
模式的特性:可观察性、可区分性、相似性模式识别的任务:一是研究生物体(包括人)是如何感知对象的,二是如何用计算机实现模式识别的理论和方法。
计算机的发展方向:1.神经网络计算机--模拟人的大脑思维;2.生物计算机--运用生物工程技术、蛋白分子作芯片;3.光计算机--用光作为信息载体,通过对光的处理来完成对信息的处理。
训练学习方法:监督学习、无监督学习(无先验知识,甚至类别数也未知)。
统计模式识别有:1.聚类分析法(非监督);2.判决函数法/几何分类法(监督);3.基于统计决策的概率分类法- 以模式集在特征空间中分布的类概率密度函数为基础,对总体特征进行研究,以取得分类的方法数据的标准化目的:消除各个分量之间数值范围大小对算法的影响模式识别系统的基本构成:书P7聚类过程遵循的基本步骤:特征选择;近邻测度;聚类准则;聚类算法;结果验证;结果判定。
相似测度基础:以两矢量的方向是否相近作为考虑的基础,矢量长度并不重要。
确定聚类准则的两种方式:阈值准则,函数准则基于距离阈值的聚类算法——分解聚类:近邻聚类法;最大最小距离聚类法类间距离计算准则:1)最短距离法2)最长距离法 3)中间距离法4)重心法5)类平均距离法6)离差平方和法P24系统聚类法——合并的思想用于随机模式分类识别的方法,通常称为贝叶斯判决。
模式识别期末考试题及答案

模式识别期末考试题及答案一、选择题(每题2分,共20分)1. 以下哪项不属于模式识别的主要任务?A. 分类B. 回归C. 聚类D. 降维答案:B2. 以下哪种方法不属于模式识别的监督学习方法?A. 支持向量机B. 决策树C. 神经网络D. K-均值聚类答案:D3. 在模式识别中,特征选择和特征提取的主要目的是什么?A. 提高模型的泛化能力B. 减少模型的计算复杂度C. 提高模型的准确率D. 所有以上选项答案:D4. 以下哪种距离度量方法不适用于模式识别?A. 欧几里得距离B. 曼哈顿距离C. 余弦相似度D. 切比雪夫距离答案:C5. 以下哪种算法不属于模式识别中的分类算法?A. K-最近邻B. 支持向量机C. 线性回归D. 决策树答案:C二、填空题(每题2分,共20分)1. 模式识别的主要任务包括分类、回归、聚类和__________。
答案:降维2. 监督学习算法包括线性判别分析、__________、神经网络等。
答案:支持向量机3. 无监督学习算法包括K-均值聚类、层次聚类、__________等。
答案:DBSCAN4. 特征选择和特征提取的主要目的是降低数据的__________和__________。
答案:维度、计算复杂度5. 模式识别中常用的距离度量方法有欧几里得距离、曼哈顿距离、余弦相似度和__________。
答案:切比雪夫距离三、判断题(每题2分,共20分)1. 模式识别是人工智能领域中一个重要的分支,主要研究如何使计算机能够自动识别和处理模式。
()答案:√2. 监督学习算法和无监督学习算法在模式识别中具有相同的作用。
()答案:×3. 支持向量机是一种基于最大间隔的分类算法。
()答案:√4. K-均值聚类算法是一种基于距离度量的聚类算法。
()答案:√5. 特征选择和特征提取的主要目的是提高模型的泛化能力。
()答案:√四、简答题(每题10分,共30分)1. 简述模式识别的基本流程。
模式识别总复习题

总复习题1 简答题1、什么是模式与模式识别?2、一个典型的模式识别系统主要由哪几个部分组成?3、什么是后验概率?4、确定线性分类器的主要步骤?5、样本集推断总体概率分布的方法?6、近邻法的基本思想是什么?7、什么是K近邻法?1 简答题8、监督学习与非监督学习的区别?9、什么是误差平方和准则?10、分级聚类算法的2种基本途径是什么?11、特征抽取与特征选择的区别?12、什么是最优搜索算法?13、统计学习理论的核心问题?14、什么是支持向量机?2 问答题1、描述贝叶斯公式及其主要作用。
2、利用最大似然估计方法对单变量正态分布函数来估计其均值μ和方差σ2。
3 、请详细写出感知器训练算法步骤。
4 、请详细写出Fisher 算法实现步骤。
5 、什么是两分剪辑近邻法与压缩近邻法。
2 问答题6、请详细介绍初始聚类中心的选择方法。
7、请描述K均值聚类算法。
8、什么是离散K-L变换以及离散有限K-L展开。
9、必考:针对某个识别对象设计自己的模式识别系统,并叙述各步骤主要工作。
3 计算题1、在图像识别中,假定有灌木和坦克2种类型,它们的先验概率分别是0.7和0.3,损失函数如下表所示。
其中,类型w1和w2分别表示灌木和坦克,判决a1=w1,a2=w2。
现在做了2次实验,获得2个样本的类概率密度如下:3 计算题2、已知两类的训练样本:w1(0,0)T,(0,2)T;w2(2,0)T,(2,2)T,试用H-K 算法进行分类器训练,求解向量w*。
3、已知欧氏二维空间中两类9 个训练样本w1:(-1,0)T,(-2,0)T,(-2,1)T,(-2,-1)Tw2:(1,1)T,(2,0)T,(1,-1)T,(2,1)T,(2,2)T试分别用最近邻法和K 近邻法求测试样本(0,0)T的分类,取K=5,7。
3 计算题4、已知两类的数据:w1:(1,0),(2,0),(1,1)W2:(-1,0),(0,1),(-1,1)试求该组数据的类内与类间散布矩阵。
【模式识别】期末考试试卷01

《模式识别》期末考试试题(B )一、填空题(15个空,每空2分,共30分)1.基于机器学习的模式识别系统通常由两个过程组成, 即分类器设计和( )。
2.统计模式识别把( )表达为一个随机向量(即特征向量), 将模式类表达为由有穷或无穷个具有相似数值特性的模式组成的集合。
3.特征一般有两种表达方法:(1)将特征表达为数值;(2)将特征表达为( )。
4.特征提取是指采用( )实现由模式测量空间向特征空间的转变。
5.同一类模式类样本的分布比较集中,没有或临界样本很少,这样的模式类称为( )。
6.加权空间的所有分界面都通过( )。
7.线性多类判别: 若每两个模式类间可用判别平面分开, 在这种情况下,M 类有( )个判别函数,存在有不确定区域。
8.当取0-1损失函数时, 最小风险贝叶斯判决准则等价于( )判决准则。
9.Neyman-Pearson 决策的基本思想是( )某一错误率,同时追求另一错误率最小。
10.聚类/集群:用事先不知样本的类别,而利用样本的先验知识来构造分类器属于( )学习。
11.相似性测度、聚类准则和( )称为聚类分析的三要素。
12.K/C 均值算法使用的聚类准则函数是误差平方和准则,通过反复迭代优化聚类结果,使所有样本到各自所属类别的中心的( )达到最小。
13.根据神经元的不同连接方式,可将神经网络分为分层网络和相互连接型网络两大类。
其中分层网络可细分为前向网络、( )和层内互连前向网络三种互连方式。
14.神经网络的特性及能力主要取决于网络拓扑结构及( )。
15.BP 神经网络是采用误差反向传播算法的多层前向网络,其中,神经元的传输函数为S 型函数,网络的输入和输出是一种( )映射关系。
二、简答题(2题,每小题10分,共20分)1.两类问题的最小风险Bayes 决策的主要思想是什么? 2.已知一组数据的协方差矩阵为11/21/21⎡⎤⎢⎥⎣⎦,试问: (1)协方差矩阵中各元素的含义是什么? (2)K-L 变换的最佳准则是什么?(3)为什么说经K-L 变换后消除了各分量之间的相关性?三、 计算题(2题,每小题13分,共26分)1.已知有两类样本集,分别为ω1={x 1, x 2}={(1,2)T , (-1,0)T }; ω2={x 3, x 4} ={(-1,-2)T , (1,-1)T } 设初始权值w 1=(1,1,1)T , ρk =1,试用感知器固定增量法求判别函数,画出决策面。
模式识别期末复习总结

1、贝叶斯分类器贝叶斯分类器的定义:在具有模式的完整统计知识的条件下,按照贝叶斯决策理论进行设计的一种最优分类器。
贝叶斯分类器的分类原理:通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。
贝叶斯分类器是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。
贝叶斯的公式:什么情况下使用贝叶斯分类器:对先验概率和类概率密度有充分的先验知识,或者有足够多的样本,可以较好的进行概率密度估计,如果这些条件不满足,则采用最优方法设计出的分类器往往不具有最优性质。
2、K近邻法kNN算法的核心思想:如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
假设有N个已知样本分属c个类,考察新样本x在这些样本中的前K个近邻,设其中有个属于类,则类的判别函数就是决策规则:若则∈什么情况下使用K近邻法:kNN只是确定一种决策原则,在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别,并不需要利用已知数据事先训练出一个判别函数,这种方法不需要太多的先验知识。
在样本数量不足时,KNN法通常也可以得到不错的结果。
但是这种决策算法需要始终存储所有的已知样本,并将每一个新样本与所有已知样本进行比较和排序,其计算和存储的成本都很大。
对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
3、PCA和LDA的区别Principal Components Analysis(PCA):uses a signal representation criterionLinear Discriminant Analysis(LDA):uses a signal classification criterionLDA:线性判别分析,一种分类方法。
它寻找线性分类器最佳的法线向量方向,将高维数据投影到一维空间,使两类样本在该方向上的投影满足类内尽可能密集,类间尽可能分开。
模式识别期末考试试题

模式识别期末考试试题# 模式识别期末考试试题## 一、选择题(每题2分,共20分)1. 模式识别中,特征提取的目的是什么?A. 降低数据维度B. 提高计算效率C. 增强数据的可解释性D. 以上都是2. 在K-近邻算法中,K值的选择对结果的影响是什么?A. 无影响B. 影响分类的准确性C. 影响算法的运行时间D. 影响数据的可读性3. 决策树算法中,信息增益的计算是基于以下哪个概念?A. 熵B. 互信息C. 条件熵D. 联合熵4. 支持向量机(SVM)的主要思想是?A. 寻找数据点之间的最大间隔B. 寻找数据点之间的最小间隔C. 寻找数据点的平均间隔D. 寻找数据点的中心点5. 以下哪个算法属于聚类算法?A. K-近邻B. 决策树C. K-均值D. 支持向量机## 二、简答题(每题10分,共30分)1. 描述主成分分析(PCA)的基本原理及其在模式识别中的应用。
2. 解释什么是过拟合(Overfitting)现象,并给出避免过拟合的几种常用方法。
3. 给出神经网络在模式识别中的基本工作原理,并说明其优缺点。
## 三、计算题(每题25分,共50分)1. 给定以下数据点,使用K-均值算法将它们分为两个簇,并说明算法的步骤:- 数据点:(1, 2), (2, 3), (5, 6), (8, 7), (9, 8)2. 假设有一个二维数据集,其中包含两类数据点,分别用圆形和三角形表示。
数据点的特征如下表所示:| 特征1 | 特征2 | 类别 || | | - || 1.5 | 2.5 | 圆形 || 2.0 | 3.0 | 圆形 || 3.5 | 4.5 | 三角形 || 4.0 | 5.0 | 三角形 |使用线性判别分析(LDA)方法,找出最佳线性边界,并将数据点分为两类。
## 四、论述题(共30分)1. 论述深度学习在图像识别领域的应用,并讨论其与传统机器学习方法相比的优势和局限性。
## 五、案例分析题(共30分)1. 假设你是一名数据科学家,你的团队正在开发一个用于识别手写数字的系统。
模式识别复习资料

(4)如果 Z j( k 1 ) Z j( k )j 1 ,2 , ,K ,则回到(2),将模式 样本逐个重新分类,重复迭代计算。
.
15
例2.3:已知20个模式样本如下,试用K-均值算法分类。
X1 0,0T X2 1,0T X3 0,1T X4 1,1T X5 2,1T X6 1,2T X7 2,2T X8 3,2T
x1
20
8 聚类准则函数Jj与K的关系曲线
上述K-均值算法,其类型数目假定已知为K个。当K未知时,
可以令K逐渐增加, 此时J j 会单调减少。最初减小速度快,但当 K 增加到一定数值时,减小速度会减慢,直到K =总样本数N 时,
Jj = 0。Jj-K关系曲线如下图:
Jj
曲线的拐点 A 对应着接近最优
④ 判断:
Zj(2)Zj(1)
j 1,2 ,故返回第②步。 .
17
② 从新的聚类中心得:
X 1: D D12||||X X11ZZ12((22))|||| X1S1(2) ┋
X 20:D D12||||X X2200Z Z12((22))|||| X20S2(2) 有: S 1 ( 2 ) { X 1 ,X 2 , ,X 8 } N 1 8
(2)将最小距离 3 对应的类 G1(0) 和G2 (0) 合并为1类,得 新的分类。
G 1( 1 2 ) G 1 ( 0 )G , 2 ( 0 ) G 3(1)G 3(0) G 4(1 )G 4(0 ) G 5(1)G 5(0) G 6(1 )G 6(0)
计算聚类后的距离矩阵D(1): 由D(0) 递推出D(1) 。
3)计算合并后新类别之间的距离,得D(n+1)。
4)跳至第2步,重复计算及合并。
模式识别期末复习

1.模式是值得具体的摸一个物体,比如,李论是学生,李论是模式,学生是模式类。
2P134页5.23在图像识别中,假定有灌木丛和坦克两种类型,分别用ω1和ω2表示,它们的先验概率分别为0.7和0.3,损失函数如表所示。
现在做了四次试验,获得四个样本的类概率密度如下::0.1,0.15,0.3, 0.6:0.8,0.7,0.55, 0.3(1)试用贝叶斯最小误判概率准则判决四个样本各属于哪个类型;(2)假定只考虑前两种判决,试用贝叶斯最小风险准则判决四个样本各属于哪个类型;(3)将拒绝判决考虑在内,重新考核四次试验的结果。
表类型损失判决ω1 ω2a1 (判为ω1) 0.5 2.0a2 (判为ω2) 4.0 1.0a3 (拒绝判决) 1.5 1.5解:(1)两类问题的Bayes最小误判概率准则为如果,则判,否则判。
由已知数据,q12=0.3/0.7=3/7,样本x1:∵ l12(x1)=0.1/0.8<q12=3/7 \ x1Îω2样本x2:∵ l12(x2)=0.15/0.7<q12=3/7 \ x2Îω2样本x3:∵ l12(x3)=0.3/0.55>q12=3/7 \ x3Îω1样本x4:∵ l12(x4)=0.6/0.3>q12=3/7 \ x4Îω1(2)不含拒绝判决的两类问题的Bayes最小风险判决准则为如果,则判,否则判。
由已知数据,q12=0.3´(2 - 1)/[0.7´(4 - 0.5)]=3/24.5,样本x1:∵ l12(x1)=1/8>q12=6/49 \ x1Îω1样本x2:∵ l12(x2)=3/14>q12=6/49 \ x2Îω1样本x3:∵ l12(x3)=6/11>q12=6/49 \ x3Îω1样本x4:∵ l12(x4)=6/3>q12=6/49 \ x4Îω1(3)含拒绝判决的两类问题的Bayes最小风险判决准则为其中条件风险:后验概率:记 (4.7-1)则,含拒绝判决的两类问题的Bayes最小风险判决准则为对四个样本逐一列写下表,用(4.7-1)式计算r(aj|x)。
模式识别期末复习笔记

模式识别期末复习笔记模式识别ch2 贝叶斯决策1.贝叶斯公式2.贝叶斯决策的特例a)先验概率相同(均匀先验概率):决策仅依赖于类条件概率密度b)类条件概率密度相同:决策仅依赖于先验概率3.计算题(医学测试⽅法)4.计算题(车⾝⾼低)5.贝叶斯决策的最优性a)最⼩化误差概率的⾓度i.每次均选择概率⼤的类做判断结果,因此错误概率永远是最⼩的b)最⼩化风险的⾓度i.每次均选择条件风险最⼩的结果,因此总风险最⼩6.对于两类分类问题,最⼩风险贝叶斯决策a)可以基于似然⽐进⾏决策b)p(x|ω1)p(x|ω2)≥λ12?λ22λ21?λ11p(ω2)p(ω1)则判断为1类,否则为2类c)似然⽐超过某个阈值(θ),那么可判决为ω1类7.0-1损失(误判是等价的):最⼩化风险就是最⼤化后验,也就是选择后验最⼤的a)最⼩化误差概率与最⼩化风险等价,即选择最⼤后验的分类,即满⾜最⼩误差概率,也满⾜最⼩风险8.先验概率未知时如何设计风险最⼩的分类器?a)使先验概率取任意值时的总风险的最坏情况尽可能⼩b)极⼩化极⼤准则:i.极⼩化指的是贝叶斯风险,因为它是总风险的最⼩值ii.极⼤化指的是使贝叶斯风险达到最⼤iii.贝叶斯风险是和先验有关的,其最⼤也就是其极值,就是导数等于0 的时候c)极⼩化极⼤风险是最坏的贝叶斯风险9.从最⼩化误差概率的意义上讲,贝叶斯是最优的;贝叶斯决策得到的总风险也是最⼩的10.判别函数a)对于两类分类,根据判别函数的正负进⾏类的判断;对于多类问题,两两组成两类问题b)两类问题下:g(x)=g1(x)?g2(x)i.若g(x)≥0,即g1(x)≥g2(x),则判断为1类,否则为2类c)g1(x),g2(x)的设计i.最⼩总风险贝叶斯分类器1.g1(x)=?R(α1|x),风险的相反数ii.最⼩误差概率贝叶斯分类器1. g 1(x )=p (ω1|x )2. g 1(x )=p (x|ω1)p (ω1)3. g 1(x )=log(p (x|ω1))+log(p (ω1))11.12. 计算题(决策边界为何下偏)ch3 参数估计1. 模式分类的途径(截图)2. 当可⽤数据很多以⾄于减轻了先验知识的作⽤时,贝叶斯估计可退化为最⼤似然估计。
模式识别期末考试题及答案

模式识别期末考试题及答案一、填空题1. 模式识别是研究通过_________从观测数据中自动识别和分类模式的一种学科。
答案:计算机算法2. 在模式识别中,特征选择的主要目的是_________。
答案:降低数据的维度3. 支持向量机(SVM)的基本思想是找到一个最优的超平面,使得两类数据的_________最大化。
答案:间隔4. 主成分分析(PCA)是一种_________方法,用于降低数据的维度。
答案:线性降维5. 隐马尔可夫模型(HMM)是一种用于处理_________数据的统计模型。
答案:时序二、选择题6. 以下哪种方法不属于模式识别的监督学习方法?()A. 线性判别分析B. 支持向量机C. 神经网络D. K-means聚类答案:D7. 在以下哪种情况下,可以使用主成分分析(PCA)进行特征降维?()A. 数据维度较高,且特征之间存在线性关系B. 数据维度较高,且特征之间存在非线性关系C. 数据维度较低,且特征之间存在线性关系D. 数据维度较低,且特征之间存在非线性关系答案:A8. 以下哪个算法不属于聚类算法?()A. K-meansB. 层次聚类C. 判别分析D. 密度聚类答案:C三、判断题9. 模式识别的目的是将输入数据映射到事先定义的类别中。
()答案:正确10. 在模式识别中,特征提取和特征选择是两个不同的概念,其中特征提取是将原始特征转换为新的特征,而特征选择是从原始特征中筛选出有用的特征。
()答案:正确四、简答题11. 简述模式识别的主要任务。
答案:模式识别的主要任务包括:分类、回归、聚类、异常检测等。
其中,分类和回归任务属于监督学习,聚类和异常检测任务属于无监督学习。
12. 简述支持向量机(SVM)的基本原理。
答案:支持向量机的基本原理是找到一个最优的超平面,使得两类数据的间隔最大化。
具体来说,SVM通过求解一个凸二次规划问题来确定最优超平面,使得训练数据中的正类和负类数据点尽可能远离这个超平面。
大二上学期末模式识别与人工智能复习要点

大二上学期末模式识别与人工智能复习要点
一、数学基础
在学习模式识别与人工智能课程时,数学基础是非常重要的。
特别
是概率论、统计学和线性代数知识。
要重点复习和掌握这些数学概念,包括概率密度函数、条件概率、贝叶斯定理、协方差矩阵、特征值分
解等内容。
二、模式识别基础
模式识别的基本概念和方法也是复习的重点。
包括特征提取、特征
选择、模式分类、聚类分析等内容。
可以通过复习课本上的相关知识
和做一些练习题来加深对这些概念和方法的理解。
三、机器学习算法
在复习模式识别与人工智能课程时,机器学习算法是需要重点复习
的内容。
包括K近邻算法、支持向量机、决策树、神经网络等。
要对
这些算法的原理和应用有一个清晰的理解。
四、深度学习
近年来,深度学习在模式识别与人工智能领域得到了广泛的应用。
复习时要重点关注深度学习的基本概念、常见的深度学习模型以及它
们的训练和应用。
五、应用案例
复习模式识别与人工智能课程时,要结合一些实际的应用案例来加深对知识的理解。
比如人脸识别、字符识别、语音识别等。
可以通过相关的论文和实验来了解这些应用案例的原理和方法。
六、实践操作
最后,在复习模式识别与人工智能课程时,要进行一些实践操作。
可以通过编程实现一些经典的模式识别算法和人工智能模型,加深对知识的理解和掌握。
通过以上的复习要点,相信能够帮助大家更好地复习模式识别与人工智能课程,取得更好的成绩。
希望大家都能够在期末考试中取得优异的成绩,加油!。
模式识别复习要点

复习要点绪论1、举出日常生活或技术、学术领域中应用模式识别理论解决问题的实例。
答:语音识别,图像识别,车牌识别,文字识别,人脸识别,通信中的信号识别;① 文字识别汉字已有数千年的历史,也是世界上使用人数最多的文字,对于中华民族灿烂文化的形成和发展有着不可磨灭的功勋。
所以在信息技术及计算机技术日益普及的今天,如何将文字方便、快速地输入到计算机中已成为影响人机接口效率的一个重要瓶颈,也关系到计算机能否真正在我过得到普及的应用。
目前,汉字输入主要分为人工键盘输入和机器自动识别输入两种。
其中人工键入速度慢而且劳动强度大;自动输入又分为汉字识别输入及语音识别输入。
从识别技术的难度来说,手写体识别的难度高于印刷体识别,而在手写体识别中,脱机手写体的难度又远远超过了联机手写体识别。
到目前为止,除了脱机手写体数字的识别已有实际应用外,汉字等文字的脱机手写体识别还处在实验室阶段。
②语音识别语音识别技术技术所涉及的领域包括:信号处理、模式识别、概率论和信息论、发声机理和听觉机理、人工智能等等。
近年来,在生物识别技术领域中,声纹识别技术以其独特的方便性、经济性和准确性等优势受到世人瞩目,并日益成为人们日常生活和工作中重要且普及的安验证方式。
而且利用基因算法训练连续隐马尔柯夫模型的语音识别方法现已成为语音识别的主流技术,该方法在语音识别时识别速度较快,也有较高的识别率。
③ 指纹识别我们手掌及其手指、脚、脚趾内侧表面的皮肤凹凸不平产生的纹路会形成各种各样的图案。
而这些皮肤的纹路在图案、断点和交叉点上各不相同,是唯一的。
依靠这种唯一性,就可以将一个人同他的指纹对应起来,通过比较他的指纹和预先保存的指纹进行比较,便可以验证他的真实身份。
一般的指纹分成有以下几个大的类别:环型(loop),螺旋型(whorl),弓型(arch),这样就可以将每个人的指纹分别归类,进行检索。
指纹识别基本上可分成:预处理、特征选择和模式分类几个大的步骤。
模式识别期末试题

一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A→01, A→ 0A1 , A→ 1A0 , B→BA , B→ 0}, A)(2)({A}, {0, 1}, {A→0, A→ 0A}, A)(3)({S}, {a, b}, {S → 00S, S → 11S, S → 00, S → 11}, S)(4)({A}, {0, 1}, {A→01, A→ 0A1, A→ 1A0}, A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有( 1、2 );马式距离具有(1、2、3、4 )。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
模式识别复习重点总结85199

1.什么是模式及模式识别?模式识别的应用领域主要有哪些?模式:存在于时间,空间中可观察的事物,具有时间或空间分布的信息; 模式识别:用计算机实现人对各种事物或现象的分析,描述,判断,识别。
模式识别的应用领域:(1)字符识别;(2) 医疗诊断;(3)遥感; (4)指纹识别 脸形识别;(5)检测污染分析,大气,水源,环境监测;(6)自动检测;(7 )语声识别,机器翻译,电话号码自动查询,侦听,机器故障判断; (8)军事应用。
2.模式识别系统的基本组成是什么?(1) 信息的获取:是通过传感器,将光或声音等信息转化为电信息;(2) 预处理:包括A \D,二值化,图象的平滑,变换,增强,恢复,滤波等, 主要指图象处理;(3) 特征抽取和选择:在测量空间的原始数据通过变换获得在特征空间最能反映分类本质的特征;(4) 分类器设计:分类器设计的主要功能是通过训练确定判决规则,使按此类判决规则分类时,错误率最低。
把这些判决规则建成标准库; (5) 分类决策:在特征空间中对被识别对象进行分类。
3.模式识别的基本问题有哪些?(1)模式(样本)表示方法:(a)向量表示;(b)矩阵表示;(c)几何表示;(4)基元(链码)表示;(2)模式类的紧致性:模式识别的要求:满足紧致集,才能很好地分类;如果不满足紧致集,就要采取变换的方法,满足紧致集(3)相似与分类;(a)两个样本x i ,x j 之间的相似度量满足以下要求: ① 应为非负值② 样本本身相似性度量应最大 ③ 度量应满足对称性④ 在满足紧致性的条件下,相似性应该是点间距离的 单调函数(b)用各种距离表示相似性 (4)特征的生成:特征包括:(a)低层特征;(b)中层特征;(c)高层特征 (5) 数据的标准化:(a)极差标准化;(b)方差标准化4.线性判别方法(1)两类:二维及多维判别函数,判别边界,判别规则 二维情况:(a)判别函数: ( )(b)判别边界:g(x )=0; (c)判别规则:n 维情况:(a)判别函数:也可表示为:32211)(w x w x w x g ++=为坐标向量为参数,21,x x w 12211......)(+++++=n n n w x w x w x w x g X W x g T =)(为增值权向量,T T n n w w w w W ),,...,,(121=+(b)判别边界:g1(x ) =W TX =0 (c)判别规则:(2)多类:3种判别方法(函数、边界、规则)(A )第一种情况:(a)判别函数:M 类可有M 个判别函数(b) 判别边界:ωi (i=1,2,…,n )类与其它类之间的边界由 g i(x )=0确定(c)(B)第二种情况:(a)判别函数:有 M (M _1)/2个判别平面(b) 判别边界: (c )判别规则:(C)第三种情况:(a)判别函数: (b) 判别边界:g i (x ) =gj (x ) 或g i (x ) -gj (x ) =0(c)判别规则:5.什么是模式空间及加权空间,解向量及解区? (1)模式空间:由 构成的n 维欧氏空间;(2)加权空间:以为变量构成的欧氏空间; (3)解向量:分界面为H,W 与H 正交,W称为解向量; (4)解区:解向量的变动范围称为解区。
模式识别复习资料(1)
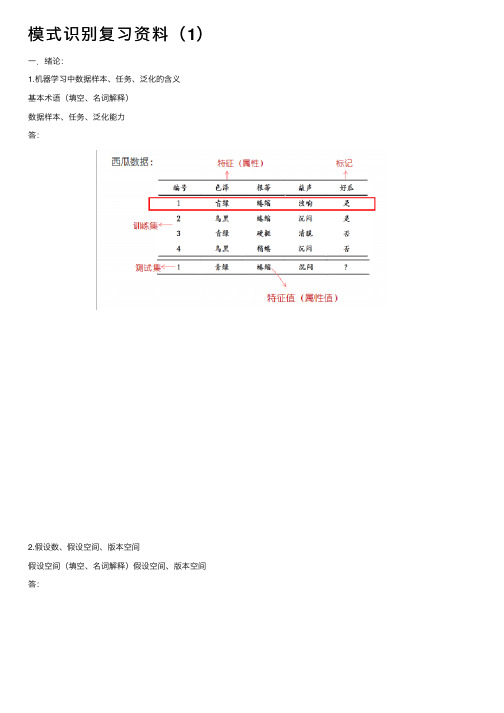
模式识别复习资料(1)⼀.绪论:1.机器学习中数据样本、任务、泛化的含义基本术语(填空、名词解释)数据样本、任务、泛化能⼒答:2.假设数、假设空间、版本空间假设空间(填空、名词解释)假设空间、版本空间答:3.归纳偏好:为什么要有偏好、偏好原则、偏好的决定因素归纳偏好(填空、名词解释、判断)为什么要有偏好、偏好原则、偏好的决定因素答:4.机器学习的应⽤与前景(开放)答:第⼀章练习:1、单选题(必做)请选出下列任务中属于回归的任务()A.分辨冬⽠、西⽠还是南⽠B.估计南⽠的成熟度C.将同类的⽠分成⼀堆D.以上都不是2、请写出以下训练集中的假设空间的假设总数,以及版本空间中所有的假设分别是什么(写出具体假设内容)。
认为训练集中的各属性值已经完备,不存在遗漏。
(必做)训练集1、青绿,蜷缩,浊响,是好⽠2、乌⿊,稍蜷,沉闷,不是好⽠3、⼆、模型评估与选择1.经验误差与过拟合错误率、误差、过拟合经验误差与过拟合(填空、名词解释)错误率、误差、过拟合答:2.评估⽅法留出法、交叉验证法、⾃助法评估⽅法(填空、计算、判断)留出法、交叉验证法、⾃助法答:3.性能度量错误率、P-R曲线、平衡点、ROC图性能度量(填空、问答)错误率、P-R曲线、平衡点、ROC图答:4.⽐较检验Friedman检验与Nemenyi后续检验、检验图⽐较检验(填空、计算、绘图)Friedman检验与Nemenyi后续检验、检验图答:第⼆章练习:1、数据集包含100个样本,其中正反例各⼀半,假定学习算法所产⽣的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进⾏随机猜测),试给出⽤10折交叉验证法和留⼀法分别对错误率进⾏评估所得的结果。
2、对于下列混淆矩阵,请计算查准率P和查全率R,可⽤分数表⽰,并计算出总样本数。
1、推导Fβ从调和平均到最终结果的过程2、针对下列混淆矩阵,计算TPR和FPR3、试举例说明为何TPR和FPR会同时增加或减少1、说明分类任务与回归任务的区别2、请计算下列样本集合对应的假设空间内假设数3、请简述奥卡姆剃⼑原理4、判断题:过拟合将训练样本本⾝的特点当做所有样本的⼀般性质,导致泛化性能下降,但可以通过设计彻底克服5、请写出学过的所有评估⽅法,并指出哪⼀个⽅法会因改变了数据分布⽽引⼊估计偏差在·6、请写出混淆矩阵的组成,并给出查准率P、查全率R、真正例率TPR、假正例率FPR的表达式和含义7、请写出Friedman检验和Nemenyi后续检验的步骤,并将下列参数画成Friedman检验图,其中,假设CD为1.28、请说出泛化误差由哪⼏部分组成,哪些可以通过设计进⾏优化三、线性模型1.基本形式线性模型基本形式(辨析)线性模型答:2.线性回归⽬的、算法线性回归(填空、计算)⽬的、算法答:3.对数⼏率回归对数⼏率函数、优点、极⼤似然对数⼏率回归(问答)对数⼏率函数、优点、极⼤似然答:4.线性判别分析(填空)答:5.多分类学习:概念、流程多分类学习(填空、问答、判断)OvO、OvR、MvM、ECOC 答:。
模式识别复习重点总结

1.什么是模式及模式识别?模式识别的应用领域主要有哪些?模式:存在于时间,空间中可观察的事物,具有时间或空间分布的信息; 模式识别:用计算机实现人对各种事物或现象的分析,描述,判断,识别。
模式识别的应用领域:(1)字符识别;(2) 医疗诊断;(3)遥感; (4)指纹识别 脸形识别;(5)检测污染分析,大气,水源,环境监测; (6)自动检测;(7 )语声识别,机器翻译,电话号码自动查询,侦听,机器故障判断; (8)军事应用。
2.模式识别系统的基本组成是什么?(1) 信息的获取:是通过传感器,将光或声音等信息转化为电信息;(2) 预处理:包括A\D,二值化,图象的平滑,变换,增强,恢复,滤波等, 主要指图象处理;(3) 特征抽取和选择:在测量空间的原始数据通过变换获得在特征空间最能反映分类本质的特征;(4) 分类器设计:分类器设计的主要功能是通过训练确定判决规则,使按此类判决规则分类时,错误率最低。
把这些判决规则建成标准库; (5) 分类决策:在特征空间中对被识别对象进行分类。
3.模式识别的基本问题有哪些? (1)模式(样本)表示方法:(a )向量表示;(b )矩阵表示;(c )几何表示;(4)基元(链码)表示;(2)模式类的紧致性:模式识别的要求:满足紧致集,才能很好地分类;如果不满足紧致集,就要采取变换的方法,满足紧致集(3)相似与分类;(a)两个样本x i ,x j 之间的相似度量满足以下要求: ① 应为非负值② 样本本身相似性度量应最大 ③ 度量应满足对称性④ 在满足紧致性的条件下,相似性应该是点间距离的 单调函数(b)用各种距离表示相似性(4)特征的生成:特征包括:(a)低层特征;(b)中层特征;(c)高层特征 (5) 数据的标准化:(a)极差标准化;(b)方差标准化4.线性判别方法(1)两类:二维及多维判别函数,判别边界,判别规则 二维情况:(a )判别函数: ( ) (b )判别边界:g(x)=0; (cn 维情况:(a )判别函数: 也可表示为: 32211)(w x w x w x g ++=为坐标向量为参数,21,x x w 12211......)(+++++=n n n w x w x w x w x g X W x g T =)(为增值模式向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模式识别期末复习1似然比决策准则为:若1221()()()()()p P l p P ωωωω=≥x x x ,则1ω∈x ;若1221()()()()()p P l p P ωωωω=≤x x x ,则2ω∈x 。
负对数似然比为[]()ln ()h l =-x x ,当()i p ωx 是均值向量为i μ和协方差矩阵为12=∑∑=∑的正态分布时:①试推导出()h x ,并指出其决策面规则; ②分析这种情况下的决策面类型。
解:①()()111112211()exp 2(2)T dp ωμμπ-⎛⎫=--∑- ⎪⎝⎭∑x x x ;()()122212211()exp 2(2)T dp ωμμπ-⎛⎫=--∑- ⎪⎝⎭∑x x x两边取自然对数()()111111ln ()ln 2ln 222Td p ωμμπ-=--∑---∑x x x ;()()122211ln ()ln 2ln 222Td p ωμμπ-=--∑---∑x x x[]()()()()()2111112211111111122211111211221210201()ln ()ln ()ln ()11221111222211()220 T TT T T T T T T T T T i i h l p p w w w ωωμμμμμμμμμμμμμμμμμ-------------=-=-=-∑---∑-⎛⎫⎛⎫=∑-∑+∑-∑-∑+∑ ⎪ ⎪⎝⎭⎝⎭=-∑-∑∑-∑--+-==∑Tx x x x x x x x x x x x x x x +=w w x w 1012T i i i μμ-=∑似然比决策准则为:若1221()()()()()p P l p P ωωωω=≥x x x ,则1ω∈x ;若1221()()()()()p P l p P ωωωω=≤x x x ,则2ω∈x即 若12()ln ()ln ()h P P ωω≤-x ,则1ω∈x ;若12()ln ()ln ()h P P ωω≥-x ,则2ω∈x ② 由上式所决定的决策面为超平面。
2 设在一维特征空间中两类样本服从正态分布,121σσ==,10μ=,23μ=,两类先验概率之比12()e ()P P ωω=,试求按基于最小错误率贝叶斯决策原则的决策分界 面的x 值。
解:由于按基于最小错误率的贝叶斯决策,则分界面上的点服从11221121222222()()()()()()() () e ()()11exp 1exp (3)2211111(3)226p P p P P p p p p P x x x x x ωωωωωωωωωω=⇒=⇒=⎡⎤⎡⎤⇒-+=--⎢⎥⎢⎥⎣⎦⎣⎦⇒-+=--⇒=x x x x x x3 对两类问题,若损失函数;11220λλ==,120λ≠,210λ≠,试求基于最小风险贝叶斯决策分界面处的两类错误率11()1()x P e P x ωω∈=-、22()1()x P e P x ωω∈=- 与12λ、21λ的关系解:由于在基于最小风险贝叶斯决策分界面处有1111122122221122221112122211()()()() ()()()()()()()()R P P P R P P P R R P P αλωλωλωαλωλωλωααλωλω=+==+==⇒=x x x x x x x x x x x x 而在两类问题中,112()1()()x P e P x P x ωωω∈=-=,221()1()()x P e P x P x ωωω∈=-=故122112()()x x P e P e ωωλλ∈∈=4 设一个二维空间中的两类样本服从正态分布,其参数分别为1(1=μ,0)T ,11001⎛⎫∑= ⎪⎝⎭,2(1=-μ,0)T ,22002⎛⎫∑= ⎪⎝⎭,,先验概率12()()P P ωω=。
试证明其基于最小错误率的贝叶斯决策分界面方程为一圆,并求其方程。
证明:先验概率相等条件下,基于最小错误率贝叶斯决策的分界面上两类条件概率密度函数相等。
因此有:()()()()1111112222222212121111ln ln 222211(1)(1)ln 422T T x x x x ----∑--∑=--∑--∑-+=+++x x x x μμμμ化简为2212(3)82ln 4x x -+=+,是一个圆的方程5对两类问题,若损失函数;11220λλ==,120λ≠,210λ≠,试求基于最小风险贝叶斯决策分界面处的两类错误率11()1()x P e P x ωω∈=-、22()1()x P e P x ωω∈=- 与12λ、21λ的关系。
解:由于在基于最小风险贝叶斯决策分界面处有1111122122221122221112122211()()()() ()()()()()()()()R P P P R P P P R R P P αλωλωλωαλωλωλωααλωλω=+==+==⇒=x x x x x x x x x x x x 而在两类问题中,112()1()()x P e P x P x ωωω∈=-=,221()1()()x P e P x P x ωωω∈=-=故122112()()x x P e P e ωωλλ∈∈=6 (1)指出从X 到超平面0()0T g w =+=X W X 的距离()g γ=X W是在()0q g =X 的约束条件下,使q -X X 达到极小的解;X 在超平面上的投影是2()q g =-X X X W W。
(2)对于二维线性判别函数12()22g x x =+-X ,将判别函数写成0()T g w =+X W X 的形式,并画出()0g =X 的几何图形;同时将其影射成增广齐次线性判别函数()T g =X A Y 。
(3)为什么说近邻法的分类器是线性分类器,试以以下样本数据集说明,并画出用近邻法得到的分类器。
第一类样本:(1,0) ,(0,1);第二类样本:(0,1)- ,(1-,0)。
解:(1)()0q g =X 表明q X 在超平面0()0T g w =+=X W X 上,当q -X X 达到极小时,q X 应是X 在超平面0()0T g w =+=X W X 上的投影。
那么p γ=+⇒W X X W00()T T T T p p g w w γγγγ⎛⎫=++=++== ⎪ ⎪⎝⎭W W W W W X W X W X WW W W 则()g γ=X W即q -X X 的极小解。
p γ=-W X X W 、()g γ=X W 则X 在超平面上的投影是2()q g =-X X X W W。
(2)这里21⎛⎫= ⎪⎝⎭W ,02w =-;若将其影射成增广齐次线性判别函数()T g =X A Y 则221-⎛⎫⎪= ⎪ ⎪⎝⎭A ,121x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭Y 。
(3)近邻法分类器的每条分界线必然由两个分别属于两类的样本点决定,故一定是线性的。
这些分界面拼接起来,就得到了分段线性的近邻法分类器。
本题的分类器如图所示。
7考虑基于具有先验知识12()()0.5P P ωω==和分布1 32 023() 0 x p ω≤≤⎧=⎨⎩x 其它和2 32 131() 0 x p ω≤≤⎧=⎨⎩x 其它的样本的分类器。
(1)在这种情况下,求Bayes 错误率;(2)求按最近邻法决策的渐近平均错误率。
解:12111, 0 0, 3()()112112() () , () ,2 3 3 2 33 ()()2 0, 1, 1 3 i i i c i i i x p P P P x P x p P x ωωωωωωω=⎧⎧≤≤⎪⎪⎪⎪⎪==≤≤=≤≤⎨⎨⎪⎪⎪⎪≤≤⎪⎩⎩∑x x x x x 其它其它1 3 1 , 04 3 3 12 , ()()() ()23 3 3 2 , 14 30, c i i i x x p p P p x ωω=⎧≤≤⎪⎪≤≤⎪==⎨⎪≤≤⎪⎪⎩∑x x x 其它1 1, 0 3 112 , ()23 3 2 1, 1 3 0, m x x P x ω⎧≤≤⎪⎪≤≤⎪=⎨⎪≤≤⎪⎪⎩x 其它 2313222311310, 0 3 112 , 3 1()1() ()()0.252 3 3 2 22 0, 1 31, 3 11()()10.252 2mi i x x P e P P P e p d d x P P p d d ωω***=⎧≤≤⎪⎪≤≤⎪=-===⨯=⎨⎪≤≤⎪⎪⎩⎡⎤⎡⎤=-=-⨯=⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰∑⎰⎰x x x x x x x x x x 其它8考虑一个对两类二维正态分布的样本进行分类的Bayes 分类器,设121001⎛⎫∑=∑= ⎪⎝⎭,101μ⎛⎫= ⎪⎝⎭,220μ⎛⎫= ⎪⎝⎭,而且1()0.25P ω=,2()0.75P ω=。
(1) 分别求出两类判别函数的表达式1()g x 与2()g x ;(已知1ln () 1.39P ω≈-,2ln ()0.29P ω≈-)(2) 求出两类样本之间的决策面方程,并根据该方程决定样本01⎛⎫ ⎪⎝⎭,21⎛⎫⎪⎝⎭的模式类别。
解:(1)两类判别函数的表达式()()()()1111()ln 2ln ln ()22211ln 2ln ln ()222Ti i i i i i T i i i d g P d P μμπωμμπω--=--∑---∑+=--∑---∑+x x x x x()()11()ln ()2Ti i i i g P μμω-⇒=--∑-+x x x()()()21211111211()ln ()1 1.3922T g P x x μμω-⎡⎤=--∑-+=-+--⎣⎦x x x()()()21222221211()ln ()20.2922T g P x x μμω-⎡⎤=--∑-+=--+-⎣⎦x x x(2)两类样本之间的决策面方程()()[][]2222121212121211()()21 1.390.2922114421 1.120.422g g x x x x x x x x ⎡⎤⎡⎤-=-+-+--+⎣⎦⎣⎦=-+--+-=-++x x01⎛⎫= ⎪⎝⎭x ,12121()()20.4 1.40 g g x x x ω-=-++=>⇒∈x x 21⎛⎫= ⎪⎝⎭x ,12122()()20.4 2.60 g g x x x ω-=-++=-<⇒∈x x。
