现代信号处理的理论和方法》Chapter+1
现代信号处理方法1_2

1.3.4 核函数的基本性质要求
由(1.3.5)式
( , v)
P(t , f )e j 2 ( vt f ) dtdf Az ( , v) P (t , f )e j 2 ( vt f ) dtdf
则(1.3.1)式化为
1 * 1 j 2f P(t , f ) z (t ) z (t )e d 2 2
(1.3.2)
上式就是著名的Wigner-Ville分布 .
记
上式是一个双线性变换(双时间信号)。关于 时间t作Fourier反变换
k z (t , ) z (t ) z (t ) 2 2
j 2 ( vt f )
如果时-频分布 p (t , 核函数的性质要求.
P (t , f )e z (u 2 ) z (u 2 )e
*
dtdf
(1.3.5)
j 2vu
du
f )有特定性质要求, 由上式可决定对
互时-频分布定义
两个连续信号 x(t ),y(t )的互时-频分布定义为:
P(t , ) 0
在上面的特性中,边缘特性和非负特性保 证了时-频分布准确反映信号的谱能量、瞬 时功率和总能量。边缘特性可以保证信号的 总体量(平均时间、平均频率、时宽和带宽 等)正确给定。非负性则可以进一步保证分 布的条件期望是切合实际的和物理解释。非 负性和边缘特性一起可以保证时-频分布的 强有限支撑。
2 2 * 1 2 z1 , z2 * 2 1 z2 , z1
胡广书《现代信号处理教程》第一章

1. 傅里叶变换在时间、频率“定位”的不足
如果我们想求一个信号,如 x(t ) ,在某一个频 率,如 0 处的值,则
X ( j0 ) x(t )e j 0t d t
需要
t ~
;
反之,如果我们想求某一个时刻,如 t 0
处的值,需要 ~
1 x(t0 ) 2
a: 是尺度定标常数,决定频率中心及带宽; b: 是位移,决定分析位置; (t ) : 又称为基本小波或母小波。
方法四、信号的子带分解
将信号的频谱均匀或非均匀地分解成若干部分, 每一个部分都对应一个时间信号,我们称它们为 原信号的子带信号 。
H0 ( z)
x ( n)
x0 (n)
M
v0 (n)
“分辨率(resolution)”是信号处理中的基本概念, 能作出辨别的时域或频域的最小间隔(又称最小分辨
细胞)。频率分辨率是通过一个频域的窗函数来观察 频谱时所看到的频率的宽度,时间分辨率是通过一个 时域的窗函数来观察信号时所看到的时间的宽度。显 然,这样的窗函数越窄,相应的分辨率就越好。分辨
能力的好坏一是取决于信号的特点,二是取决于信号
(二)多抽样率信号处理; (三)小波变换; (四)高阶统计量分析; (五)独立分量分析(ICA); (六)压缩感知理论(CS);
现代信号处理这十多年来的新进展
一、Hilbert-Huang变换 二、信号的稀疏表达 (sparse representations) -1998;
-1998;
三、压缩感知 ( compressed sensing,CS) -2006
g ( , ) 1 then
Cohen类分布变成Wigner-Ville分布
现代信号处理方法1-3
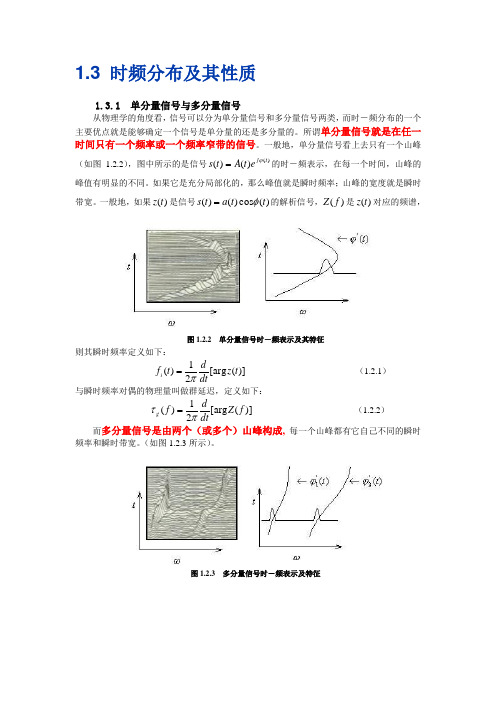
1.3 时频分布及其性质1.3.1 单分量信号与多分量信号从物理学的角度看,信号可以分为单分量信号和多分量信号两类,而时-频分布的一个主要优点就是能够确定一个信号是单分量的还是多分量的。
所谓单分量信号就是在任一时间只有一个频率或一个频率窄带的信号。
一般地,单分量信号看上去只有一个山峰(如图 1.2.2),图中所示的是信号)()()(t j e t A t s ϕ=的时-频表示,在每一个时间,山峰的峰值有明显的不同。
如果它是充分局部化的,那么峰值就是瞬时频率;山峰的宽度就是瞬时带宽。
一般地,如果)(t z 是信号)(cos )()(t t a t s φ=的解析信号,)(f Z 是)(t z 对应的频谱,图1.2.2 单分量信号时-频表示及其特征则其瞬时频率定义如下:)]([arg 21)(t z dtdt f i π=(1.2.1) 与瞬时频率对偶的物理量叫做群延迟,定义如下: )]([arg 21)(f Z dtdf g πτ=(1.2.2) 而多分量信号是由两个(或多个)山峰构成, 每一个山峰都有它自己不同的瞬时频率和瞬时带宽。
(如图1.2.3所示)。
图1.2.3 多分量信号时-频表示及特征1.3.2 时-频分布定义Fourier 变换的另一种形式⎰∞∞--=dt e t s f S ft j π2)()(⎰∞∞-=dfe f S t s tf j π2)()(Cohen 指出,尽管信号)(t z 的时-频分布有许多形式,但不同的时-频分布只是体现在积分变换核的函数形式上,而对于时-频分布各种性质的要求则反映在对核函数的约束条件上,因此它可以用一个统一形式来表示,通常把它叫做Cohen 类时-频分布,连续时间信号)(t z ()(t z 为连续时间信号)(t s 的解析信号)的Cohen 类时-频分布定义为ττφτττπdudvd e v u z u z f t P vu f vt j )(2*),()21()21(),(-+-∞∞-∞∞-∞∞--+=⎰⎰⎰(1.3.1) 式中),(v τφ称为核函数。
最新现代信号处理第1章ppt课件

信号处理的本质是信息的变换和提取。
信息的提取就要借助各种信号获取方法以及信号处理 技术。
信号测量系统和信号处理的工作内容的成本已达到装 备系统总成本的50%-70%。
1.1 现代信号处理的内容和意义
信号处理技术的应用领域:
电子通讯; 机械振动信号的分析与处理; 自动测量与控制工程领域; 语音分析、图像处理与声纳探测; 生物医学工程。
(1.4.4)
R x(y ) x ( t)y ( t)d t x ( t)y ( ,t)
(1.4.5)
内积可视为 x (t与) “基函数”关系紧密度或相似性的一种度量。
1.4 信号处理的内积与基函数
信号的内积与基函数
傅里叶变换是应用最为广泛的信号处理方法,函数 x (t ) 的傅里叶变换为
cn
1 T
T/2 x(t)eintdt
T/ 2
(1.3.6)
1.3 非平稳信号处理和信号的正交分解
1.3.2 信号的正交分解
傅里叶级数具有两个独特的性质:
1、函数 x (t ) 可分解为无限多个互相正交的分量 gn(t):cneint 的和,其中正交是指 g m 与 g n 的内积对所有 mn成立, 即
gm,gn:T 1 T T //2 2gm (t)gn(t)d t0
mn
2、正交分量 或 可用一个简单的基函数
的整数m
或n的膨胀g生m 成,g 线n 性累加逼近任何函数 g1(。t)
x(t) 小波变换中,通过母小波的伸缩和平移生成小波族。
1.3 非平稳信号处理和信号的正交分解
1.3.2 信号的正交分解
第一章 绪论
1.1 现代信号处理的内容和意义 1.2 信号的分类 1.3 非平稳信号处理和信号的正交分解 1.4 信号处理的内积与基函数 1.5 现代信号处理的应用现状与进展
现代信号处理1分析

5
根本概念
❖ 平稳过程与循环平稳过程
➢ 循环平稳过程
• 定义:统计特性随时间周期性变化的非平稳过程称为 循环
平稳或周期平稳(CS)过程。 • 循环平稳过程可进一步分为一阶(均值)循环平稳、二 阶循
环平稳(相关函数)和高阶循环平稳。循环二阶统计量 可用
现代信号处理1分析
主要内容
❖ 随机信号的最优预测和滤波 ❖ 最优滤波理论与维纳滤波器 ❖ 横向LMS自适应数字滤波器 ❖ 横向RLS自适应数字滤波器 ❖ 自适应格型滤波器 ❖ 自适应格-梯型滤波器 ❖ 无限脉冲响应自适应滤波器 ❖ 盲自适应信号处理 ❖ 自适应滤波器应用
2
盲自适应信号处理
❖ 引言 ❖ 根本概念 ❖ 根本思想 ❖ 盲自适应算法
成
序列 { x(n) }
系统 h
序列 { y(n) }
图1
➢问题:给定系统输出端的观测序列{y(n)},我们要恢复输入的信息 序列{x(n)}, 或等价地辨识系统h的逆系统h-1, 通常称为反卷积。
➢ 可行性 ➢ • 假设系统或信道h是最小相位的(即信道传递函数的所有零 极
➢ 点均位于z平面单位圆内), 那么不仅信道h是稳定的, 而且逆 信道
或
U () 1e j( D ) H ()
( 2 )
结论: 平衡器的目的就是实现上式所示的传递函数. 13
根本思想
❖ 盲平衡问题的数学描绘
➢ 盲平衡问题的求解(续)
上述表明, 我们希望设计均衡器的抽头系数 u i ,使得输 出序列{~x(n)}与输入序列{x(n)}满足式(1). 若令{ s i }代表信道 (滤波器)与均衡器(逆滤波器)的组合系统的抽头系数, 且
现代信号处理

R x(y)E {x(t)y*(t)}
互协方差函数
C x(y ) E {x ( [ t)x ]y ( [ t )y ] * } Rxy()x*y
互相关系数
xy()
Cxy()
Cxx(0)Cyy(0)
主要性质
1.对零均值随机信号,相关函数与协方差函数
非平稳即不具有广义平稳。 例1.1.1
随机信号的遍历性
均方遍历:一个平稳信号,其n阶矩及较
低阶的所有矩都与时间无关,对所k 有1, ,n
和所有整数 t1,,tk ,恒有
N l i E m 2 N 1 1t N N x (t t1) x (t tk)(t1, ,tk)2 0
及 ,其k阶矩有界,并满足
( t 1 , ,t k ) ( t 1 , ,t k )
广义平稳(协方差平稳、弱平稳):均值为常 数,二阶矩有界,协方差函数与时间无关。
严格平稳:概率密度函数与时间无关。
3者关系 广义平稳是n=2的n阶平稳; 严格平稳一定广义平稳,反之则不一定;
等价
2. 0 时,自相关函数退化为二阶矩
Rxx(0)E{x(t)2}
3. 0时,协方差函数退化为方差 Cx(x0)Rx(x0)x2
4. R* xx()Rxx() 5. C* xx()Cxx() 6. C x(x)C x(x 0),
R* xy()Ryx()
白噪声
互功率谱密度
定义
P x(yf) Cx(y )ej2fd
互功率谱的实部称为同相谱,虚部称为正交谱。
相干函数
定义 C(f) Pxy(f)
特点
汽车故障诊断技术-现代信号处理方法概论

250
300
0 样本点 n/个
检测出脉冲信号
并实例分析
模拟齿轮的裂纹故障 实验中采样频率为20kHz 转速1500r/min,齿数30 Wf(a,b)2
齿轮振动信号的尺度谱图
t=4ms, a=1.3~1.5
t=44ms, a=1.3~1.5
齿轮振动信号
齿轮振动信号时域图(a=1.3)
x(t)
X
200 a 1
连续小波---运算过程示意图
0
(s,t)
×
Inner product
x(t)
X
200 a 1
连续小波---运算过程示意图
(s,t)
×
Inner product
x(t)
X
0 a 10
连续小波---运算过程示意图
(s,t)
×
Inner product
x(t)
X
50 a 10
小波包
从时域来看小波包分解
每一层的小波包数目比上一层中的小波包数目增加一倍 每个小波包的数据长度比上一层小波包数据长度减半 每个小波包的时域分辨率比上一层小波包的时域分辨率减半
小波包
从频域来看小波包分解
每个小波包数据是原始信号在不同频率段上的成分 小波包的频带相邻,并且带宽相等 分解的层数越多,频率段划分得越细
第5层小波包分解 23号小波包重构
轴的转动周期
一个周期内约有9 个冲击,与理论分 析相符,说明小 波包分解有效
故障诊断中的应用---轴承外圈剥落
最高分析频率
f = fs /2 = 20/2 = 10 KHz 每个小波包的频率带宽为
d = f /32 =312.5 Hz 频谱图中的频率范围
中科院课件--《现代信号处理的理论和方法》Chapter+1

d3
0 -5 0 1 100 200 300 400
a4
0 -5 0 100 200 300 400
d4
0 -1 0 100 200 300 400
4、 盲信号处理技术
利用系统的输出观测数据,通过某种信号处 理的手段,获取我们感兴趣的有关信息。 盲源分离、盲均衡、盲系统辨识
第一章 信号分析基础
x(n)
↓2
d3(n)
H0(z)
↓2
H1(z)
↓2
H0(z)
↓2
a3(n)
j=1 j=2
H0(z) a2(n)
↓2
信号的二进制分解
j=3
x(t ) sin(2 f1t ) sin(2 f 2t ) sin(2 f3t ) s1 (t ) s2 (t ) s3 (t ) f1 1Hz, f 2 20Hz, f3 40Hz, f s 200 Hz, N 400
x ( n)
v0 (n)
↑M
u0 ( n )
G0(z)
x1 (n)
H1(z) ↓M
v1 (n)
↑M
u1 (n)
G1(z)
xM 1 (n)
HM-1(z) ↓M
vM 1 (n)
↑M
uM 1 (n)
GM-1(z)
ˆ ( n) x
M 通道滤波器组
例 假定要传输如图所示信号x(t),它由两个正弦信号加白噪 声组成。若用数字方法,其传输过程包括对x(t)的数字化、 量化、编码及调制等步骤。若对信号用抽样率fs进行抽样, 每一个抽样数据为16bit,那么其1s数据所需bit数是16fs。对 其抽样信号x(n)作傅里叶变换,频谱如图所示。
第1章 现代信号处理 (1)

ψ 若把ψ (t ) 看成一窗函数, (t / a ) 的宽度将随着的不同而不同, 看成一窗函数, 的宽度将随着的不同而不同, Ψ,由此我们可得到不同的 ( aΩ ) 这也同时影响到频域, 这也同时影响到频域,即 a 对应分析信号的高频部分, 时域分辨率和频域分辨率。 时域分辨率和频域分辨率。 小,对应分析信号的高频部分, a 对应分析信号的低频部分。 大,对应分析信号的低频部分。参数 是沿着时间轴的位 b x 尺度 位移” WTx ( a, b) 尺度- 移,所得结果 是信号 的“(t ) -位移”联合分 它也是时-频分布的一种。 析,它也是时-频分布的一种。
第1章 信号分析基础 章
Cohen时 Cohen时-频分布
C x (t , Ω : g ) =
1 2π
x (u + τ ) x * (u − τ ) g (θ ,τ )e − j (θt +Ωτ −uθ ) dudτdθ 2 2 ∫∫∫
Cohen分布即 式中g (θ , τ )是处在平面的权函数若g (θ , τ )=1,则Cohen分布即 变成Wigner-Ville分布,给定不同的权函数,我们可得到同 变成Wigner-Ville分布,给定不同的权函数, Wigner 分布 的时-频分布,统称为Cohen类时-频分布,简称Cohen类 的时-频分布,统称为Cohen类时-频分布,简称Cohen类, Cohen类时 Cohen
第1章 信号分析基础 章
小波变换
小波变换: 希望找到一个基本函 小波变换:对给定的信号 x (t ) ,希望找到一个基本函 数 ψ (t ) ,并记 ψ (t ) 的伸缩与位移
ψ a,b (t) = 1a ψ ( t −b ) a
x 为一族函数, 为一族函数,(t )和这一族函数的内积
现代信号与信息处理理论精品文档

x z / v
26
2019/10/4
估计理论
1 f(A)2A0
0
A0 AA0 其他
f(z|A) 21vexp (z2A v2)2
f(A| z) f(z| A)f(A) f (z)
Aˆmap zA0 A0
z A0 A0 z A0
z A0
2019/10/4
估计理论
估计量
A0
Aˆ m a p
Aˆ m l Aˆ m s
-A0
z 测量值
A0
-A0 估计图形
28
2019/10/4
估计理论
4 最大似然概率估计
例:z=+v
为待估计量,v为零均值 高斯白噪声,方差为2
f (z / )
f(z|)max
f(z/) 21vexp (z2v2)2
A~U(-A0,A0) 噪声为高斯的 v ~ N(0,v2)
1 f(A)2A0
0
A0 AA0 其他
f(z|A) 21vexp (z2A v2)2
f(A| z) f(z| A)f(A) f (z)
25
2019/10/4
估计理论
A ˆm s A f(A |z)d A A f(z|fA () z) f(A )d A A ff((z z||A A ))ff((A A )) d d A A
c(ˆ(z))f(| z)d f(z)dz
C ( ˆ|z)c( ˆ(z))f(|z)d
不同的代价函数得到不同的估计
20
2019/10/4
估计理论
1 最小均方估计 ——采用平方代价函数
现代信号处理

3. 宽平稳随机过程(广义平稳)
若一个随机过程的数学期望及方差与时间无关, 而其相关函数仅与有关,即我们就称这个随机过 程是广义平稳的。
不难看出,严平稳过程一定是宽平稳过程,反之, 不一定。但对于正态随机过程两者是等价的。后 面,若不加特别说明,平稳过程均指宽平稳过程。
4. 联合宽平稳随机过程 X(m),Y(n)是宽平稳过程 RXY (m, n) RXY ( )
典型:高斯白噪声
2. 移动平均处理
线性处理的过程,通过的是一个有限冲击响应滤波器
2
x[n] b(k)w[n k] k 0
w[n]
b(k )
x[n]
x[n] 1 w[n] 1 w[n 1] 1 w[n 2]
3
3
3
3. 自回归过程处理
P
x[n] a[k]x[n k] w[n] k 1
CXY [m, n] E{( X [m] X [m])(Y[n] Y [n])}
相关系数
X
Y
(m,
n)
CXY (m, n)
X (m)Y (n)
相互独立的X(m),Y(n)必定不相关;反之,不一定。 对于正态随机过程,不相关和独立是等价的。
2.2 平稳随机过程
1. 平稳随机过程在通信领域中占有重要地位。 其重要性来自两个方面:
5.平稳随机过程的各态历经性( 遍历性)
统计平均=时间平均
6.平稳随机过程的自相关函数特性
RX [0] E{( X [n] )} 0
| RX [ ] | RX [0] R RX [k] RX [k]
RXY [k ] RYX [k ]
举例 1. 白噪声 w[n]
特点:不相关,E(w[n])=0,Var (w[n])=
现代信号处理算法PPT课件

2
课程内容
第一章 概述 第二章 数字信号处理基础 第三章 自适应信号处理 第四章 现代谱估计 第五章 多速率信号处理与小波变换 第六章 数字语音信号处理
3
考核
读论文报告一篇—平时成绩 课程考试--2小时
The past, present, and future of image & multidimensional signal processing. IEEE SP Magazine, March 1998
The past, present, and future of speech processing. -, May 1998 Highlights of statistical signal & array processing. -, Sep. 1998 Highlights of signal processing for communication. -, March
13
信号处理发展趋势
特点 • 以算法为中心, 更加注重实现与应用 • 突出一个“非”, 呈现“智、多、新”
趋势 ➢ “非”
SP向着非平稳、非高斯、非线性方向发展 - 非线性信号处理 - 非平稳信号处理 - 多分辨信号处理
14
信号处理发展趋势(续)
➢ ”智“ 信号处理与智能技术相结合
• 各种智能及其关系 – 生物智能(BI) – 人工智能(AI): – 计算智能(CI): – 相互关系:BI >AI>CI
12
信号处理与现代通信(续)
信号处理与现代通信的密切关系还具体表现在通信的 如下方面: 接入网的宽带化-ADSL 骨干网的信道倍增-DCME 语音、图像和视频信息的压缩与传输 无线信道的估计、均衡与信道分配 3G/4G移动通信中的多用户检测和智能天线 软件无线电技术 加密、认证 网络信号处理
中科院课件---《现代信号处理的理论与方法》课程回顾祥解

时频分布 : P t,
R t, , e j
WVD :Wx t,
R t, , e j
AF : Ax , v R t, , e jvt
n
EMD : x t ck rn k 1
时频分析
❖ 线性时频分析方法(STFT,Gabor变换,WT) 使用时间和频率的联合函数描述信号的频谱 随时间的变化情况;
《现代信号处理的理论与方法》课程回顾
❖ 信号分析基础 ❖ 时频分析方法 ❖ 高阶统计和高阶谱方法 ❖ 多抽样率信号处理技术 ❖ 盲信号处理技术
解析信号
❖ 对于实信号s(t),它的Hilbert变换为:
sˆt
st ht
st 1
t
1
s
d
t
由此可得解析信号为:
zt st jsˆt ate jt
幅值和相位分别为:
at s2 t sˆ2 t
t
arctan
sˆt st
瞬时频率
❖ 瞬时频率:表征了信号在局部时间点上的瞬态频 率特性,整个持续期上的瞬时频率反映了信号频 率的时变规律。
fi
t
1
2
d dt
arg
zt
1
0 E
'(t) | x(t) |2 dt
➢ 信号的中心频率是其瞬时频率在整个时间轴上的加 权平均。
amn Gabor展开系数; g(t) 母函数;
gmn (t) m, n阶Gabor基函数,它是由g(t)做移位和调制生成的。
❖ Gabor变换与STFT的区别与联系:
➢ STFT的窗函数必须是窄窗,而Gabor变换的窗函数 无此限制,可以将Gabor变换看成是一种加窗的傅 立叶变换,它的适用范围比STFT适用范围更广泛;
chapter_1张贤达《现代信号处理》第二版

xi (ξ ) 都与另一个随机变量 y j (ξ ) 正交。
正交条件: R xy = E {x(ξ ) y H (ξ )} = 0 m×n (零矩阵)
正交的物理意义
两个向量正交 任何一个向量到另外一个向量的投影为零 两个向量互不干扰
正交的两个典型应用
1. 在多址通信技术中的应用 通信理论的基本结论:若多个用户的信号可以做到正交, 则这些用户可共享一个发射媒介。 时分多址(TDMA: time-division multiple access): 各个用户的信号波形在时域上无重叠 正交(时域正交)
按概率分布分类
随机信号:也叫随机过程、时间序列。 离散随机信号:x(k ) 离散时间序列: x(k )} , 其中 k = 1, 2,⋯ , N { 随机信号按概率密度分类,分为 高斯信号:概率密度函数服从正态(高斯) 分布的随机信号 非高斯信号:概率密度函数服从非正态(非 高斯)分布的随机信号。
i = m +1
∑
q iH E wi
{ }
2
qi =
i = 2
H i
qi
正交的两个典型应用( 正交的两个典型应用(续)
优化问题: min Em = min
i = m +1
∑
M
q iH R x q i
约束条件:q iH q i = 1 拉格朗日乘子法: 代价函数 J (q i ) =
成立,则称为n 阶平稳。
平稳信号( 平稳信号(续)
严格平稳 广义平稳,但反之一般不成立。 高斯信号:严格平稳=广义平稳 非平稳信号(nonstationary signal) 不是广义平稳的信号统称非平稳信号 遍历性
2 N 1 若 lim E ∑N x (t + t1 )⋯ x (t + tk ) − µ (t1 ,⋯ , tk ) = 0 N →∞ 2 N + 1 t =− 则{ x (t )}称为均方遍(态)历(经)信号。
现代信号处理的理论和方法》Chapter1PPT课件

信号的多分辨率分析
对频带的不均匀剖分产生了不同的时间、频率分辨 率,对快变信号需要好的时间分辨率,对慢变信号 需要好的频率分辨率。
d1(n)
H1(z)
↓2
x(n)
d2(n)
a1(n)
现代信号处理的理论与方法
预修课程
概率论与数理统计 信号与系统 数字信号处理 随机过程
课程特点及主要内容
以平稳随机信号处理技术为基础,主要讲授 现代数字信号处理的新理论和新技术。
非平稳随机信号的处理方法; 非高斯信号处理方法; 多抽样率信号处理技术; 盲信号处理技术
成绩评定
课堂作业 40% 闭卷考试 60%
盲源分离、盲均衡、盲系统辨识
第一章 信号分析基础
1.1 随机信号的统计描述 1.2 信号的时间和频率 1.3 信号的时间分辨率和频率分辨率 1.4 信号的时宽和带宽 1.5 信号的分解
1.1.1 信号的分类
信号的分类:
➢ 确定性信号 ➢ 随机信号:
✓ 平稳随机信号 ✓ 非平稳随机信号
1.1.2 随机信号的统计描述
➢均值、均方值和方差:
mx(n)E[X(n)] x(n)pXn(x,n)dx
Dx2(n)E[ X(n)2]
1、高阶统计和高阶谱方法
功率谱只揭示了该随机序列的幅度信息,而 没有反映出其相位信息。要准确描述随机信 号,仅使用二阶统计量是不够的,还要使用 高阶统计量。
2、 时频分析技术
有效地克服了傅里叶变换存在的不足
FT
X(j )x(t),ej t
X (t, ) x(t),t,
现代信号处理_2012-07

(11)
i 1) a (ji ) a (ji 1) ai(i ) ai( (12) j ( j 1,..., i 1)
(i ) (i 1) [1 (ai(i ) ) 2 ]
(13)
6) 置i =i+1; 7) 判别:若 i N 转3);否则,结束程序.
现代信号处理 7 现代信号处理 8
现代信号处理 4
1
Levinson算法
r (1) r (0) r (1) r (0) R ( k 1) r (k 1) r(k ) r ( k 1) r(k )
k
Levinson算法
由(5)式,(6)式和(9)式可得
(3)
r (k ) r ( k 1) 1 ( k 1) k ( k 1) r ( k ) a1( k 1) 0 ( k 1) r (0) r (1) ak 0 ( k 1) ak 1 r (1) r (0) 0
ai( i ) [ r (i ) a (ji 1) r (i j )] / ( i 1)
j 1 i 1
Levinson算法
Levinson算法第4步利用了一个重要递推关系(12) 通常称为Levinson关系式 递推过程产生一个滤波参数序列 通常称为偏相关系数 ai(i ) (i 1,..., N ) 递推过程产生的 ( i ) 可用来监视i阶信号模型的均方 误差估值 (N) 递推结果的最终解为 a j ( j 1,..., N ) 和 ( N ) 最后,计算功率谱密度:
(1)
最小方差谱估计
• 自相关矩阵的特征分解为
现代信号处理思考题(含问题详解)

第一章 绪论1、 试举例说明信号与信息这两个概念的区别与联系。
信息反映了一个物理系统的状态或特性,是自然界、人类社会和人类思维活动中普遍存在的物质和事物的属性。
信号是传载信息的物理量是信息的表现形式,如文字、语言、图像等。
如人们常用qq 聊天,即是用文字形式的信号将所要表达的信息传递给别人。
2、 什么是信号的正交分解?如何理解正交分解在机械故障诊断中的重要价值?P9正交函数的定义信号的正交分解如傅里叶变换、小波分解等,即将信号分解成多个独立的相互正交的信号的叠加。
从而将信号独立的分解到不同空间中去,通常指滤波器频域内正交以便于故障分析和故障特征的提取。
傅里叶变换将信号分解成各个正交的傅里叶级数,将信号从时域转换到频域从而得到信号中的各个信号的频率。
正交小波变换能够将任意信号(平稳或非平稳)分解到各自独立的频带中;正交性保证了这些独立频带中状态信息无冗余、无疏漏,排除了干扰,浓缩了了动态分析与监测诊断的信息。
3、 为什么要从内积变换的角度来认识常见的几种信号处理方法?如何选择合适的信号处理方法? 在信号处理各种运算中内积变换发挥了重要作用。
内积变换可视为信号与基函数关系紧密程度或相似性的一种度量。
对于平稳信号,是利用傅里叶变换将信号从时域变为频域函数实现的方式是信号函数x (t )与基函数i t e ω 通过内积运算。
匹配出信号x (t )中圆频率为w 的正弦波.而非平稳信号一般会用快速傅里叶变换、离散小波变换、连续小波变换等这些小波变换的内积变换内积运算旨在探求信号x (t )中包含与小波基函数最相关或最相似的分量。
“特征波形基函数信号分解”旨在灵活运用小波基函数 去更好地处理信号、提取故障特征。
用特定的基函数分解信号是为了获得具有不同物理意义的分类信息。
不同类型的机械故障会在动态信号中反应出不同的特征波形,如旋转机械失衡振动的波形与正弦波形有关,内燃机爆燃振动波形是具有钟形包络的高频波;齿轮轴承等机械零部件出现剥落。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d3
0 -5 0 1 100 200 300 400
a4
0 -5 0 100 200 300 400
d4
0 -1 0 100 200 300 400
4、 盲信号处理技术
利用系统的输出观测数据,通过某种信号处 理的手段,获取我们感兴趣的有关信息。 盲源分离、盲均衡、盲系统辨识
第一章 信号分析基础
x(n)
↓2
d3(n)
H0(z)
↓2
H1(z)
↓2
H0(z)
↓2
a3(n) H0(z) a2(n)
j=1
↓2
j=2
信号的二进制分解
j=3
x(t ) sin(2 f1t ) sin(2 f 2t ) sin(2 f3t ) s1 (t ) s2 (t ) s3 (t ) f1 1Hz, f 2 20Hz, f3 40Hz, f s 200 Hz, N 400
d t t dt
傅立叶频率和瞬时频率的区别:
傅立叶频率是一个独立的量,而瞬时频率是时间的 函数; 傅立叶频率和傅立叶变换相联系,而瞬时频率和 Hilbert变换相联系; 傅立叶频率是一个“全局性”的量,它是信号在整 个时间区间内的体现,而瞬时频率是信号在特定时 间上的“局部”体现,理论上讲,它应是信号在该 时刻所具有的频率。
课程主要内容
第一章 信号分析基础 第二章 高阶统计和高阶谱方法 第三章 时频分析 第四章 多抽样率信号处理 第五章 现代信号处理的前沿技术
1、高阶统计和高阶谱方法
功率谱只揭示了该随机序列的幅度信息,而 没有反映出其相位信息。要准确描述随机信 号,仅使用二阶统计量是不够的,还要使用 高阶统计量。
2、 时频分析技术
有效地克服了傅里叶变换存在的不足
FT
X ( j) x(t ), e jt
X (t, ) x(t ), t,
x( ), gt , ( ) x( ), g (t )e j STFT x( ) g (t )e
Linear scale
1
Real part
0 -1 |STFT| , Lh=48, Nf=192, lin. scale, contour, Thld=5%
2
Energy spectral density
0.4
Frequency [Hz]
159517975 0
0.3
0.2
0.1
0
50
100
150 200 Time [s]
* j
d STFTx (t , )
WT
* WTx (a, ) x(t ), a , (t ) x(t ) a , (t )dt
3、 多抽样率处理技术
信号的子带分解:将信号的频谱均匀或非均匀地分 解成若干部分,每一部分都对应一个时间信号。
x0 (n)
H0(z) ↓M
1
H ( ) X ( ) d
*
由Parseval’s定理,上式可写成
1 dx(t ) * 0 j x (t )dt E dt 1 ( j ) a '(t )e j (t ) ja(t ) (t )e j (t ) a(t )e j (t ) dt E 2 1 1 (t )[a(t )] dt j a '(t )a (t )dt E E 1 (t )a 2 (t )dt E 1 (t ) | x(t ) |2 dt E
现代信号处理的理论与方法
预修课程
概率论与数理统计 信号与系统 数字信号处理 随机过程
课程特点及主要内容
以平稳随机信号处理技术为基础,主要讲授 现代数字信号处理的新理论和新技术。 非平稳随机信号的处理方法; 非高斯信号处理方法; 多抽样率信号处理技术; 盲信号处理技术
成绩评定
课堂作业 40%
闭卷考试 60%
教材及参考书
张贤达,《现代信号处理》第二版,清华大学出版社,北 京,2002。 胡广书,《现代信号处理教程 》,清华大学出版社,北京, 2004。 邹谋炎,《反卷积和信号复原》,国防工业出版社,北京, 2001。 杨绿溪,《现代数字信号处理》,科学出版社,北京, 2007。 丁玉美,《数字信号处理—时域离散随机信号处理》,西 安电子科技大学出版社,2002。 Roberto Cristi, Modern Digital Signal Processing, Thomson-Brooks/Cole,2004。
这样,表示v0(n), v1(n)所需bit数是20fs/2= 10fs。比原来的 16fs,bit数下降了近40%。
信号的多分辨率分析
对频带的不均匀剖分产生了不同的时间、频率分辨 率,对快变信号需要好的时间分辨率,对慢变信号 需要好的频率分辨率。
d1(n) H1(z)
↓2
d2(n) a1(n) H1(z)
幅值和相位分别为:
ˆ at x t x t
2 2
j t
x t ˆ t arctan x t
1.2.3 瞬时频率
瞬时频率:表征了信号在局部时间点上的瞬态频 率特性,整个持续期上的瞬时频率反映了信号频 率的时变规律。
H1 ( z)
0
/2
2
6 4
1.5 1
x0(t)
0 -2 -4 0 100 200 300
x1(t)
2
0.5 0 -0.5 -1 0 100 200 300
60
40
the Spectrum of x0(t)
40 20 0 -20
the Spectrum of x1(t)
0 0.2 0.4 0.6 0.8
mx (n) E[ X (n)] x(n) p X n ( x, n)dx
2 2
D (n) E[ X (n) ] | x(n) |2 p X n ( x, n)dx
2 x
(n) E[ X (n) mx (n) ] E[| X n | ] m (n)
5
signal x(t)
0
-5
0
50
100
150
200
250
300
60
Spectrum of x(t)
40 20 0 -20
0
0.1
0.2
0.3
0.4
0.5
H0(z)
fs
x0 (n)
↓2
u0 ( n )
↓2
x ( n)
H1(z)
fs/2
x1 (n)
u1 (n)
H0 () H1()
H0 ( z)
是带限又是时限的信号波形。
1.4 信号的时宽和带宽
信号的“时间中心”及“时间宽度”,频率 的“频率中心”及“频带宽度”分别说明了 信号在时域和频域的中心位置及在两个域内 的扩展情况。 对给定的信号x(t) ,假定它是能量信号,即其 能量 1 2 2 2
E || x(t ) || | x(t ) | dt
250
300
350
1.2.2 解析信号
对于实信号x(t),它的Hilbert变换为:
1 1 x ˆ xt xt ht xt d t t
由此可得解析信号为:
ˆ z t xt jxt at e
| X ( j ) | 2
d
时域和频域的密度函数分别为
| x(t ) |2 / E 和
x(t)的“时间均值”
| X () |2 / E
1 2 (t ) t | x(t ) | dt t0 E
x(t)的“频率均值”
()
1 2 E
| X () |2 d 0
1. 2.1 信号的时间和频率
X ( j) x(t )e
jt
dt
x(t )
1 2
X ( j)e d
jt
傅立叶变换不具有时间和频率的“定位”功能
Signal in time
sin(1n), 0 n N1 1 x(n) sin(2 n), N1 n N 2 1 sin( n), N n N 1 3 2
x ( n)
v0 (n)
↑M
u0 ( n )
G0(z)
x1 (n)
H1(z) ↓M
v1 (n)
↑M
u1 (n)
G1(z)
xM 1 (n)
HM-1(z) ↓M
vM 1 (n)
↑M
uM 1 (n)
GM-1(z)
ˆ x ( n)
M 通道滤波器组
例 假定要传输如图所示信号x(t),它由两个正弦信号加白噪 声组成。若用数字方法,其传输过程包括对x(t)的数字化、 量化、编码及调制等步骤。若对信号用抽样率fs进行抽样, 每一个抽样数据为16bit,那么其1s数据所需bit数是16fs。对 其抽样信号x(n)作傅里叶变换,频谱如图所示。
x(t)
0 -5 10 100 200 300 400
a1
0 -5 50 100 200 300 400
d1
0 -1 50 100 200 300 400
a2
0 -5 50 100 200 300 400
