静定结构的影响线

合集下载

机动法作静定结构内力影响线依据

机动法作静定结构内力影响线依据机动法是结构力学中的一种常用方法，它通过对静定结构进行虚位移，得到结构内力的影响线。

影响线可以用来计算结构内力，分析结构的稳定性和安全性。

本文将以机动法作静定结构内力影响线为标题，详细介绍该方法的原理和应用。

一、机动法的原理机动法是一种基于虚位移原理的力学分析方法。

它假设结构处于静定平衡状态，通过施加虚位移，得到结构的内力分布情况。

具体的步骤如下：1. 建立坐标系：首先，需要建立合适的坐标系来描述结构的几何形状和受力情况。

2. 施加虚位移：在结构的每个节点处施加虚位移，可以是平移、转动或两者的组合。

虚位移是一个无限小的位移，它满足结构的约束条件。

3. 建立平衡方程：根据结构处于静定平衡状态，可以建立各个节点的平衡方程，包括力平衡和力矩平衡方程。

4. 求解内力影响线：通过解平衡方程，得到结构内力与虚位移之间的关系，即内力影响线。

内力影响线描述了不同位置处的虚位移对内力的影响程度。

5. 计算内力：利用内力影响线，可以计算出结构在不同位置处的内力大小和方向。

二、机动法的应用机动法作为一种常用的静力学方法，广泛应用于结构力学的研究和工程实践中。

具体应用包括以下几个方面：1. 内力分析：机动法可以用来计算结构在各个位置处的内力大小和方向。

通过分析内力的分布情况，可以评估结构的稳定性和安全性。

例如，在桥梁设计中，通过计算桥梁各个位置处的内力，可以确定桥梁的强度和刚度要求。

2. 结构优化：机动法可以用来评估不同结构方案的性能，从而进行结构优化设计。

通过分析不同虚位移对内力的影响，可以找到最优的结构形状和尺寸。

例如，在建筑设计中，可以通过机动法来评估不同楼板厚度对结构内力的影响，从而确定最经济的楼板厚度。

3. 结构安全评估：机动法可以用来评估结构的安全性。

通过分析内力的分布情况，可以确定结构是否存在超过设计强度的部分。

例如，在地震工程中，可以通过机动法来评估结构在地震荷载下的内力分布情况，从而确定结构的安全性。

10(超)静定结构的影响线解析

§9-5 超静定力的影响线1、影响线的特征与求解方法1）影响线的特征静定结构——反力、内力影响线均为直线；位移影响线为曲线。

超静定结构——各量值的影响线均为曲线。

2）影响线的求作方法静力法——利用静力平衡条件求影响线方程，进而绘制影响线。

但对超静定力的影响线须解超静定问题，复杂、少用。

机动法——利用影响线与移动载荷作用点位移（挠度）图的比拟关系，快速绘制影响线轮廓。

简便、实用。

2、机动法求作超静定力影响线以图9-14连续梁（超静定梁）M K的影响线为例，说明用机动法求作超静定力影响线的方法。

1）取基本结构（超静定、几何不变体系）图b——去掉与XK 相应的约束，代之以(暴露出)约束反力XK ；A B C D EF P=1K（a）原结构A B C D EF P=1X K(M K)(下拉为正)(b)基本结构图9-14§9-5 超静定力的影响线2）建立力法典型方程k kk kp X δδ+=1()kp k pk kk kkX x δδδδ∴=-=-⋅()()pk kp x x δδ=ABCD EF P =1K ABCD E F P =1X K (M K )(下拉为正)(b)基本结构§9-5 超静定力的影响线K 截面相对转角为0式中δkk ——常数,不随X 而变化。

δpk ——载荷F P =1位置参数X 的函数，即δPK =δPK (x)，其位移图如图9-14c 所示。

互等定理图9-14ABCDEX K (M K )(下拉为正)θB(c)挠度图⏹写成更明确的形式：()()1pk kkk x x X δδ=-ABCD EK+图9-15X k (M k )的影响线结论:X k 与δpk 成正比;挠度图即为影响线轮廓线图9-14ABCDEX K (M K )(下拉为正)θB(c)作用挠度图1kM=§9-5 超静定力的影响线X k 向上为正δpk 以向下为正(与p=1同向)X k 与δpk 反向3、求做超静定力影响线的步骤⏹1）撤去与所求约束力（或量值）相应的约束，代之以反力X K ；●2）使体系沿X K 正方向发生位移，作出移动载荷作用点的挠度δPK =δPK (x)（位移）图即为影响线X K (x)的形状；●3）将δPK 图除以常数δKK 使可确定影响线的具体数值；●4）横坐标以上图形为正号，横坐标以下图形为负号。

作静定结构影响线的三种简单方法

作静定结构影响线的三种简单⽅法作静定结构影响线的三种简单⽅法作影响线的基本⽅法有静⼒法和机动法，但是对于复杂的静定结构，仅仅运⽤静⼒法或机动法求解其内⼒影响线是不够的，往往不能迅速得到正确结果．我们参考资料归纳了三种简便⽅法，并借助例题进⾏阐述．这些⽅法均建⽴在静⼒法、机动法的基础之上，仍然遵循刚体的虚功原理，其处理问题的基本思路可归纳为：⾸先进⾏必要的静⼒计算或分析，考虑是否可以简化处理；再考虑辅以结构等效变形，进⾏结构简化；最后针对简化的机构运⽤机动法进⾏求作，便可迅速⽽⼜准确地确定复杂结构的内⼒影响线．这些⽅法的优点是既可以避开复杂静⼒计算、分段讨论，⼜可以解决机动法不能直接确定复杂静定结构内⼒影响线的难题。

1、结构等效法有些静定结构形式⽐较复杂，可以利⽤刚⽚法则进⾏等效，并且在静定结构中，若等效替代静定结构内部某⼀⼏何不变部分，则只能改变本部分的受⼒⽽不会改变其余部分的反⼒或内⼒．我们可以利⽤静定结构的这⼀特性并结合刚⽚组成法则，等效变形较复杂的静定结构，这样可以简化体系、利于快速求作结构内⼒影响线，这就是所谓的“结构等效法”．有时，复杂静定结构内⼒影响线⽆法直接利⽤机动法进⾏求解，灵活利⽤结构等效法可以解决这⼀难题，⽐如：不能直接利⽤机动法求作静定平⾏弦桁架内⼒影响线，可通过刚⽚法则简化并与相应机动简⽀梁⽐较，从⽽将机动法推⼴到静定平⾯桁架内⼒影响线的求作中；或抓住平⾏弦桁架荷载传递等效于结点荷载这⼀特点，分别考虑上弦承载及下弦承载的情形，并依据上、下弦杆结点位置确定对应结点荷载分布情况，然后借助结点荷载作⽤下的主梁某内⼒影响线求作桁架内⼒影响线．如图所⽰，求作图⽰结构HA的影响线．解：由刚⽚构造规则不难分析，△ADC及△BEC均可视为由铰接的三⾓形依次增加⼆元体形成的⼏何不变体系，故可以取L型刚⽚ADC及BEC进⾏等效替换，从⽽下部分的桁架可以运⽤三铰刚架进⾏等效替换，如下图所⽰．然后利⽤三铰刚架的关系式求作HA的影响线即可．2、斜率分析法由机动法作静定结构内⼒影响线的虚功原理可知：拟求静定结构内⼒Z的影响线，可以撤去与Z相应的约束并使体系沿着Z的正⽅向发⽣虚位移￡z=1，此时结构对应的荷载位移图为所求静定结构内⼒Z的影响线．也就是说，在竖向单位移动荷载P=1作⽤下，静定结构内⼒影响线取结构的竖向位移图；在⽔平单位移动荷载P=1作⽤下，静定结构内⼒影响线取结构的⽔平位移图；在单位移动⼒偶M=1作⽤下，静定结构内⼒影响线取结构的转⾓位移图，⽽当转⾓位移很⼩时，有等价关系，所以此时结构内⼒影响线可取竖向位移图的斜率．影响线竖距的正负号可规定如下：当结构转⾓位移⼝与单位移动⼒偶M=1⽅向⼀致时，取负号；反之，取正号．这就是所谓的“斜率法”，此种⽅法仅适⽤于求解静定结构在单位移动⼒偶M=1作⽤下的内⼒影响线．如图所⽰，试求作图⽰结构在单位移动⼒偶m=1作⽤下的Mc、Qc的影响线．解：分别撤去所⽰静定结构与Mc、Qc相应约束，并令结构分别沿其正⽅向发⽣的虚位移为“l”，然后分别作出结构的竖向位移图，如图所⽰，最后分别取结构竖向位移图的斜率即为所求图⽰结构Mc、Qc 的影响线，分别如图所⽰．3、联合分析法静定结构的内⼒影响线由分段的直线段组成，故可先运⽤机动法分析静定结构影响线的轮廓特征即影响线有⼏段及其相互位置关系(铰接或平⾏)，再利⽤静⼒法确定各直线段特征点竖标便可确定所求静定结构的内⼒影响线，这就是所谓的“联合分析法”。

静定结构某一截面某一内力的影响线

静定结构某一截面某一内力的影响线在结构力学中，影响线是一种描述结构内力和变形的图形工具。

在静定结构中，影响线的应用可以帮助我们快速而准确地计算结构的内力和变形。

本文将以静定结构某一截面某一内力的影响线为标题，为大家介绍影响线的原理、计算方法及应用。

我们需要了解什么是影响线。

影响线是指沿着结构中某个点或者某个截面上的一个虚拟荷载移动时，该点或该截面内力的变化情况。

影响线的作用是将实际荷载转化为相应的内力，从而方便我们进行计算。

在计算影响线时，我们需要使用弹性力学的基本原理。

根据弹性力学原理，结构内力与荷载的关系可以表示为：内力=荷载*影响线其中，影响线是一个比例系数，表示荷载作用在某一点或某一截面上时，该点或该截面内力的变化情况。

因此，我们可以通过计算影响线来求解结构的内力。

接下来，我们来看看如何计算影响线。

一般来说，计算影响线需要分为以下几个步骤：1.选择荷载的作用点或截面，确定荷载类型和大小。

2.在荷载作用点或截面上引入一个虚拟荷载，通常我们会选择一个单位荷载，即荷载大小为1。

3.计算结构在虚拟荷载作用下的内力和变形。

这一步需要使用力学知识和计算方法，例如静力平衡、弹性力学等。

4.根据弹性力学原理，计算虚拟荷载作用下的影响线。

影响线的计算公式为：影响线 = 内力/荷载5.重复以上步骤，分别在荷载作用点或截面的不同位置引入虚拟荷载，并计算其对应的影响线。

通过以上步骤，我们就可以得到荷载作用点或截面上不同位置的影响线。

影响线的图形通常为一条曲线，其纵坐标表示内力的大小，横坐标表示荷载作用点或截面的位置。

影响线的形状和位置与结构的刚度、荷载类型和大小等因素有关，因此我们需要针对不同的荷载类型和内力位置计算相应的影响线。

我们来看看影响线的应用。

在结构设计和分析中，影响线是一种常用的计算工具。

通过计算影响线，我们可以快速而准确地求解结构在不同荷载作用下的内力和变形，从而进行结构设计和分析。

例如，在桥梁设计中，我们可以通过计算不同位置的影响线，确定桥梁各部位的内力和变形，以保证桥梁的安全和稳定。

第八章静定结构影响线

P=1在C以右时 0 YbC=RA QBC P=1在B以左时 0 YbC=－RＧ QBC
A RA A a b 2 c d e f g
NbC
P=1 B
P=1 2
C
l=6d
D
D
E
F
可概括为一个式子
0 YbC QBC
B
C
P=1 E
F
G
x
RG 2/3
＋－1/6
平行弦桁架斜 RA 杆轴力的YbC影响线就是±梁的节间剪力QBC0影响线。右下斜为正，右上斜为负。
B
C
l=6d
D
E
F
10
h
G
§8-4静力法作桁架的影响线
任一轴力影响线在相邻结点之间为直线。反力影响线与简 A 支梁相同。平行弦桁架弦杆影响线可由相应梁结点的弯矩影响线竖标除以h得到。上弦杆为压下弦杆为拉。
RA a b N1 bc c d e P=1 D E F f g
B
NCD C 1
1
x a C i
P=1
l
x Z(x) 1
＋－
P=1 δP(x)
Z ( x) 1 1 P ( x) 0 Z ( x) P ( x)
Z 的影响线， P=1 作用点的竖基线以上的竖向虚位移图，向下为正（与P=1 标为正同向）。
于是得到：所得虚位移图即 Z 的影响线。基线以上的虚位移图是正影响线，基线以下的虚位移图是负影响线。
b/l + － a/l
ab/l
QC.I.L
－
+ Mc.I.L QD .I.L
MD.I.L
_
+ 1
-

第四章静定结构的影响线10

I.L M C
2012-3-22 扬州大学水利科学与工程学院 12
4.3
结构力学
A C
d
结点荷载作用下梁的影响线
P=1 E
d 2
D
2
B
（3）I.L MD，先假设主梁直接受荷载，D点的纵标值
yD = 1.5d × 2.5d 15 = d 4d 16 5d 3d , yE = 8 4
l=4d
5d 8
4.3
结构力学
A C
d
结点荷载作用下梁的影响线
P=1 E
d 2
D
2
B
（4）I.L FQD
左 I .L.FQE
l=4d 1
1 2
与 I.L FQD
1
右 I .L.FQE
静定结构的影响线
1 4
是否相同？
小结 1、先按直接荷载作用画出内力影响线； 2、投影各结点与影响线相交，各交点间连以直线。
Ｐ＝１在Ｃ以右：
A
FRA
2 3
B
FRG
F3Y = FRA
0 F3Y = FQBC
1
1 6
2012-3-22
I .L F3Y
1
扬州大学水利科学与工程学院
19
4.4 桁架影响线
结构力学
a b c FN4 4 A
FRA
d
e
f
g
5、竖杆FN4
h D l = 6d P=1 P=1 E F G
FRG
B
C
Ｐ＝１在C以左： F4 N = FRG Ｐ＝１在D以右：
静定结构的影响线
A
FRA
1 3

《静定结构影响线》课件

态的结构的总称。
静定结构具有确定的几何形状和确定的承载能力，不会因为受到外力而发生变形或
破坏。
静定结构在受到外力作用时，其内力和反力可以通过静力平衡方程求解，不需要进行复杂
的分析和计算。
02
影响线的计算方法
静力法
静力法是通过在静力平衡状态下，对结构施加单位载荷并计算位移的方法。
静力法计算简单，适用于简单结构，但对于复杂结构，计算过程可能较为繁琐。
连续梁的影响线分析
连续梁的弯矩和剪力影响线比简支梁更为复杂，需要考虑多个支座和跨度的共同作用。
连续梁的影响线分析有助于优化梁的截面尺寸和支座设计，提高结构的承载能力和稳支梁的相互作用。
在连续梁中，弯矩和剪力的最大值可能出现在不同的位置，需要根据具体情况进行分析。
框架结构的影响线分析
框架结构由多个杆件通过节点连接而成，其影响线分析需要考虑杆件之间的相互作用。
在框架结构中，弯矩和剪力的最大值可能出现在不同的节点和杆件上，需要根据具体情况进行分析。
框架结构的弯矩和剪力影响线比简支梁和连续梁更为复杂，需要考虑多维空间的受力分析。
框架结构的影响线分析有助于优化结构的布局和节点设计，提高结构的承载能力和稳定性。
05
结论
影响线在静定结构中的重要性
静定结构影响线是分析结构响应的重要工具，它能够描述结构在不同激励下的变形和内力分布情况。
通过影响线分析，可以确定结构的薄弱环节和关键部位，为结构的优化设计和加固提供依据。
影响线分析有助于评估结构的可靠性和安全性，为工程实践提供重要的参考价值。
未来研究方向
01
静定结构影响线
目录
• 引言 • 影响线的计算方法 • 静定结构影响线的应用 • 静定结构影响线的实例分析 • 结论

作静定结构影响线的三种简单方法

作静定结构影响线的三种简单方法作影响线的基本方法有静力法和机动法，但是对于复杂的静定结构，仅仅运用静力法或机动法求解其内力影响线是不够的，往往不能迅速得到正确结果．我们参考资料归纳了三种简便方法，并借助例题进行阐述．这些方法均建立在静力法、机动法的基础之上，仍然遵循刚体的虚功原理，其处理问题的基本思路可归纳为：首先进行必要的静力计算或分析，考虑是否可以简化处理；再考虑辅以结构等效变形，进行结构简化；最后针对简化的机构运用机动法进行求作，便可迅速而又准确地确定复杂结构的内力影响线．这些方法的优点是既可以避开复杂静力计算、分段讨论，又可以解决机动法不能直接确定复杂静定结构内力影响线的难题。

1、结构等效法有些静定结构形式比较复杂，可以利用刚片法则进行等效，并且在静定结构中，若等效替代静定结构内部某一几何不变部分，则只能改变本部分的受力而不会改变其余部分的反力或内力．我们可以利用静定结构的这一特性并结合刚片组成法则，等效变形较复杂的静定结构，这样可以简化体系、利于快速求作结构内力影响线，这就是所谓的“结构等效法”．有时，复杂静定结构内力影响线无法直接利用机动法进行求解，灵活利用结构等效法可以解决这一难题，比如：不能直接利用机动法求作静定平行弦桁架内力影响线，可通过刚片法则简化并与相应机动简支梁比较，从而将机动法推广到静定平面桁架内力影响线的求作中；或抓住平行弦桁架荷载传递等效于结点荷载这一特点，分别考虑上弦承载及下弦承载的情形，并依据上、下弦杆结点位置确定对应结点荷载分布情况，然后借助结点荷载作用下的主梁某内力影响线求作桁架内力影响线．如图所示，求作图示结构HA的影响线．解：由刚片构造规则不难分析，△ADC及△BEC均可视为由铰接的三角形依次增加二元体形成的几何不变体系，故可以取L型刚片ADC及BEC进行等效替换，从而下部分的桁架可以运用三铰刚架进行等效替换，如下图所示．然后利用三铰刚架的关系式求作HA的影响线即可．2、斜率分析法由机动法作静定结构内力影响线的虚功原理可知：拟求静定结构内力Z的影响线，可以撤去与Z相应的约束并使体系沿着Z的正方向发生虚位移￡z=1，此时结构对应的荷载位移图为所求静定结构内力Z的影响线．也就是说，在竖向单位移动荷载P=1作用下，静定结构内力影响线取结构的竖向位移图；在水平单位移动荷载P=1作用下，静定结构内力影响线取结构的水平位移图；在单位移动力偶M=1作用下，静定结构内力影响线取结构的转角位移图，而当转角位移很小时，有等价关系，所以此时结构内力影响线可取竖向位移图的斜率．影响线竖距的正负号可规定如下：当结构转角位移口与单位移动力偶M=1方向一致时，取负号；反之，取正号．这就是所谓的“斜率法”，此种方法仅适用于求解静定结构在单位移动力偶M=1作用下的内力影响线．如图所示，试求作图示结构在单位移动力偶m=1作用下的Mc、Qc的影响线．解：分别撤去所示静定结构与Mc、Qc相应约束，并令结构分别沿其正方向发生的虚位移为“l”，然后分别作出结构的竖向位移图，如图所示，最后分别取结构竖向位移图的斜率即为所求图示结构Mc、Qc 的影响线，分别如图所示．3、联合分析法静定结构的内力影响线由分段的直线段组成，故可先运用机动法分析静定结构影响线的轮廓特征即影响线有几段及其相互位置关系(铰接或平行)，再利用静力法确定各直线段特征点竖标便可确定所求静定结构的内力影响线，这就是所谓的“联合分析法”。

单位移动力偶作用下静定结构的影响线

单位移动力偶作用下静定结构的影响线
单位移动力偶作用是指在一个结构中，有一个单元（称为“偶作用单元”）的运动带来的影响，即由于偶作用单元的运动而引起的其他部位的变形和应力变化。

对于静定结构来说，单位移动力偶作用下会产生影响线，影响线是指偶作用单元运动对其他部位造成影响的轨迹。

影响线的形状取决于结构的几何形状和材料特性，常见的影响线形状有直线、曲线和圆弧。

举例来说，在一个平板桥中，如果有一个桥面板的运动带来的影响，那么在桥的其他部位就会产生影响线。

假设桥面板的运动方向是向左，那么影响线就是一条向左延伸的直线，其他部位的变形和应力变化都会沿着这条直线传递。

如果桥面板的运动方向是向右上方，那么影响线就是一条向右上方延伸的曲线，其他部位的变形和应力变化也会沿着这条曲线传递。

举例来说，在一个悬臂梁中，如果有一个端部的运动带来的影响，那么在梁的其他部位就会产生影响线。

假设端部的运动方向是向上，那么影响线就是一条向上延伸的直线，其他部位的变形和应力变化都会沿着这条直线传递。

如果端部的运动方向是向右上方，那么影响线就是一条向右上方延伸的圆弧，其他部位的变形和应力变化也会沿着这条圆弧传递。

结构力学-第4章影响线

简要介绍某大桥的工程背景，包括桥梁类型、跨度、设计荷载等。
影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程，包括影响线和包络图的绘制、最不利位置的确定、最大内力的计算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价，包括结构安全性、经济性等方面的评估。同时，可以与其他设计方案进行对比分析，以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图，可以找到结构在地震作用下的最大变形和位移，为结构的刚度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图，可以对建筑结构进行优化设计，如调整结构布置、改变构件截面等，以提高结构的抗震性能和经济效益。
工程案例分析：某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布，对结构进行优化设计，以改善结构的受力性能。
80%
工程实例分析
结合具体工程实例，利用影响线理论进行结构分析和设计，验证理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取基本体系和基本未知量，利用力法方程求解多余未知力，并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线，可以确定移动荷载在桥梁上的最不利位置，从而进行结构分析和设计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图，可以找到桥梁在移动荷载作用下的最大内力，为桥梁的强度设计和稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用

第五章静定结构的影响线

D
3m
A
B
1 MB
C
D
MB影响线
解：3）作 FQB
左的影响线
FP=1
A
4m
B 1m
C
1m 3m
D
3m
A FQB 左 FQB左影响线
C
D
解：4）作 FQB
右的影响线
FP=1
A
4m
B 1m
C
1m 3m
D
3m
A FQB 右 FQB右影响线
C
D
例
用机动法作图示多跨静定梁的MH、FBy、MA的影响线。
x A
1
1
第5章
（2）弯矩影响线
x
A
影响线
RA
l x
l
P=1
C
x RB l
a
b
B
当P=1在C左移动时，
M C RB b x b l
RA
l
RB
0 x a
a
＋
b
ab/l
当P=1在C右移动时，
M C RAa (l x ) a l
a x l
MC影响线
单位移动荷载移到D点时, 产生的C截面的弯矩
(kN.m) (m) 弯矩影响线与弯矩图的比较
荷载位臵截面位臵
M图
横坐标
单位移动荷载位臵截面位臵
影响线弯矩图
变不变
不变变
C点的固定荷载作用下, 产生的D截面的弯矩
x
P=1 C a l b
B
单跨静定梁的影响线特点:
•反力影响线是一条直线； •剪力影响线是两条平行线；
MC
（3）求简支梁剪力的影响线

结构力学：第4章静定结构影响线1

③作MD影响线在DE梁段的基本梁ABCD上竖标为零，在 DE梁上悬臂梁影响线绘制，在铰E处影响线发生拐折，同时注
意到F点影响线竖标为零，由此绘出MD影响线如图。
点击左键，一步步播放。结束播放请点“后退”。
重新播放请点重新播放
4、结点荷载作用下梁的影响线
实际结构的移动荷载有时并不是直接作用在主梁上，而是如下图所示作用在次梁上，再通过横梁将荷载传递到主梁上，这就是间接荷载。
作截面Ⅰ-Ⅰ，分别由左部和右部隔离体的力矩平
衡方程 M5 0 得
FNa
3Fy11 Fy3
FP 1位于结点4以左 FP 1位于结点6以右
并注意到结点4、6间的影响线为线性变化，得
同样作截面Ⅰ-Ⅰ，分别由左部和右部隔离体的力
平衡方程 Fy 0 得
FNb
Fy11 Fy3
FP 1位于结点4以左 FP 1位于结点6以右
移动荷载作用于上或下弦时，影响线是有差异的
作截面Ⅱ-Ⅱ，分别由左部和右部隔离体取 Fy 0
FNc
2Fy11
2Fy3
FP 1位于结点6以左 FP 1位于结点8以右
同理，可作出移动荷载作用于下弦时的各内力
影响线。将会发现当移动荷载作用于上或下弦
时，FNa 、FNc 的影响线不变，但 FNb 的影响线略有变化。
求右图中 M C 的影响线
先将与 M C相应的联系撤除，即在C截面处插入一个铰，并以一对大小等于M C 的力矩取代原有联系中的作用力。如下图所示
然后使结构顺着 M C的正方向发生一虚位移
列虚功方程为
1P MC ( ) 0
1P MC ( ) 0
MC
P
为 M C相应的广义位移

朱慈勉结构力学静定结构的影响线

1 l1 l
l1 l
A x FP 1
C
a
b
BF D d
l1
FRA
l
1 FRA影响线
l2
FRB
FRB影响线 1
l2
l 1 l2
l
1
b
l1
l
l
l2
a
l
l
1
FQC的影响线
例作FRA、FRB、FQC、FQD 的影响线。
解：⑶ 作剪力FQD的影响线：当FP=1在D截面以左时，取D截面右边为隔离体：
⑵当FP=1 在C截面以右移动时，取C截面以左部分为隔离体。
A
C MC
FRA
a
高教M社 C 0, MC FRA a
x FP 1
A
C
a
b
FRA
l
FRB影响线
B x
FRB
1
1
FRA影响线
b
a
ab
l
MC影响线
§4-2 静力法作影响线单跨静定梁的影响线特点: •反力影响线是一条直线； •剪力影响线是两条平行线；
q
(b)平行移动均布荷载
高教社
3）可任意分布均布荷载
图12-1-2
高教社
移动荷载下结构分析的概念
结构在某一确定的恒载或静力荷载作用下，内力图是唯一确定的。但在移动荷载作用下，结构的内力图会随着荷载位置的变化而变化，准确说，每个截面的内力都在变化。
高教社
在移动荷载作用下的结构内力分析，要考虑任意指定截面上的最大或最小内力值，用以做截面设计或验算；还要考虑结构所有截面中的最大或最小内力及它们所在的截面，用以确定结构设计中的最危险控制截面。

静定结构的影响线

静定结构的影响线(总分：100.00，做题时间：90分钟)一、{{B}}选择题{{/B}}(总题数：5，分数：8.00)1.结构某截面某一内力影响线将______而改变。

∙ A.随实际荷载∙ B.不随实际荷载∙ C.因坐标系的不同选择∙ D.随实际荷载数值（分数：1.50）A.B. √C.D.解析：2.单位荷载F P=1在下图所示悬臂梁上移动时，C截面的弯矩影响线在C点的纵标为______。

∙ A.0∙ B.-3m∙ C.-2m∙ D.-1m（分数：1.50）A. √B.C.D.解析：3.下图(b)是下图(a)中哪个截面的剪力影响线______。

∙ A.B截面的∙ B.B左截面的∙ C.B右截面的∙ D.D截面的（分数：1.50）A.B. √C.D.解析：4.分析静定结构某内力量值影响线的基本方法是______。

∙ A.投影法和力矩法∙ B.静定法和超静定法∙ C.机动法和静力法∙ D.积分法和图乘法（分数：1.50）A.B.C. √D.解析：5.机动法作静定结构内力影响线的依据是______。

∙ A.刚体体系的虚力原理∙ B.变形体的虚功原理∙ C.刚体体系的虚位移原理∙ D.变形体的虚位移原理（分数：2.00）A.B.C. √D.解析：二、{{B}}计算分析题{{/B}}(总题数：23，分数：92.00)6.作下图所示伸臂梁截面A的弯矩、剪力影响线。

（分数：4.00）__________________________________________________________________________________________ 正确答案：(用机动法作F QA、M A的影响线，通过去约束代以相应剪力或弯矩，再沿该力的正向给机构以单位虚位移，所得虚位移图即相应的影响线图，具体如下图(a)、(b)所示。

[*])解析：7.求作下图所示多跨静定粱的影响线。

（分数：4.00）__________________________________________________________________________________________ 正确答案：(采用机动法求解，将剪切方向的约束去掉代以相应剪力，注意相应截面改成定向支座后，其截面两侧影响线的斜率一致，具体过程和结果如下图(a)、(b)所示。

第五章静定结构的影响线

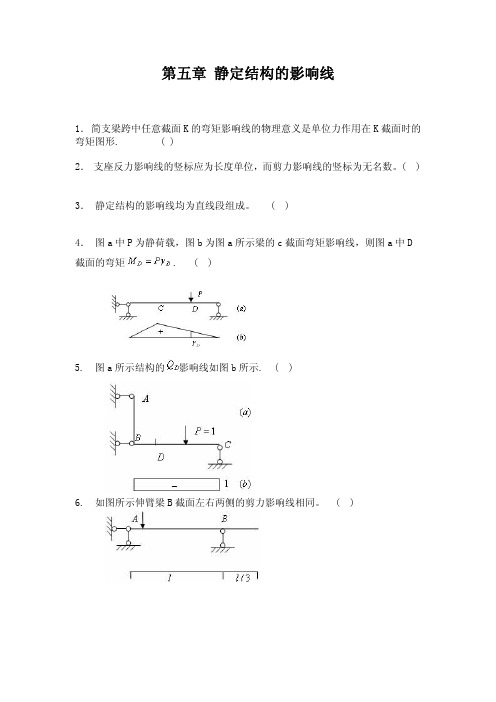
第五章静定结构的影响线1．简支梁跨中任意截面K的弯矩影响线的物理意义是单位力作用在K截面时的弯矩图形. ( )2．支座反力影响线的竖标应为长度单位，而剪力影响线的竖标为无名数。

( ) 3．静定结构的影响线均为直线段组成。

( )4．图a中P为静荷载，图b为图a所示梁的c截面弯矩影响线，则图a中D截面的弯矩. ( )5. 图a所示结构的影响线如图b所示. ( )6. 如图所示伸臂梁B截面左右两侧的剪力影响线相同。

( )7. 多跨静定梁K截面内力影响线图形的非零竖标布满BCDE。

( )8. 图a所示结构的影响线，如图b，竖标的意义是： ( )A.P＝1在B点时，D截面的弯矩值B. P＝1在E时， B截面的弯矩值C. P＝1在B点时，E截面的弯矩值D. P＝1在E点时，D截面的弯矩值.9.图示结构影响线为图中的哪一个？ ( )10.支座反力形状应为图中哪一个？ ( )11.图示多跨静定梁，铰C处剪力影响线，竖标非零的区间. ( )A. ABCDB. BCDC. ABCD. CD12.机动法绘制静定梁内力影响线时，所应用的理论是： ( )A.平衡条件；B.变形条件；C.虚功原理；D.叠加原理。

13.在影响线中，截面B的竖标为： ( )A:L/2 B:L C:0 D:-L/214.简支梁截面K弯矩影响线的竖标表示： ( )A.梁上各截面的弯矩值；B. 梁上任意截面的弯矩值C. 梁上截面K的弯矩值D. 梁上各截面的弯矩最大值15.图b是图a所示梁影响线，表示： ( )A.P=1作用在D点时，之值B. P=1作用在A点时，之值C. P=1作用在A点时，之值D. P=1作用在B点时，之值16.图示结构C截面弯矩影响线C点的纵坐标是： ( )17.静定结构基本部分某截面弯矩影响线在附属部分的影响线竖标为零。

( )18.图示梁B截面弯矩影响线在B点的竖标为： ( )A.0B. L/2C.LD.-L19.图示结构C截面剪力影响线的D点纵坐标等于： ( )20.支座反力影响线的量纲是： ( )A.KNB.KN·mC.无名数D.1/m。

机动法作静定结构内力影响线依据

机动法作静定结构内力影响线依据机动法是研究结构内力影响的一种方法，通过对结构进行静定分析，得到结构的内力分布情况，从而进一步分析结构的变形、刚度和稳定性等性能。

机动法作为一种经典的结构力学分析方法，在工程实践中具有广泛的应用。

机动法的基本思想是假设结构的每个节点都可以自由运动，即每个节点的位移可以独立地变化。

通过对结构进行静定分析，可以得到结构的刚度矩阵和外载荷向量。

然后，通过对结构进行位移控制，使得结构达到平衡状态。

在位移控制的过程中，结构的内力会发生变化，通过求解结构的内力影响线，可以得到结构不同节点处内力的变化情况。

机动法的基本步骤如下：1. 建立结构的静定模型：根据结构的几何形状和材料性质，建立结构的有限元模型。

这个模型是一个静定模型，即结构的节点数等于自由度数，节点之间的位移互相独立。

2. 求解结构的刚度矩阵和外载荷向量：根据结构的几何形状和材料性质，通过有限元方法求解结构的刚度矩阵，同时根据结构的外载荷情况，得到外载荷向量。

3. 位移控制：通过对结构的位移进行控制，使结构达到平衡状态。

在位移控制的过程中，结构的内力会发生变化。

4. 求解内力影响线：通过求解结构的内力影响线，可以得到结构不同节点处内力的变化情况。

内力影响线是指在结构的位移控制过程中，结构不同节点处内力的变化情况。

5. 分析内力影响：通过分析内力影响线，可以得到结构的内力分布情况。

通过比较不同节点处的内力大小，可以判断结构的承载能力和稳定性。

机动法的优点是可以直观地反映结构的内力分布情况，对于分析结构的变形、刚度和稳定性等性能有很大帮助。

同时，机动法的计算过程相对简单，适用于一般结构的力学分析。

然而，机动法也有一些局限性。

首先，机动法只适用于静定结构的力学分析，对于超静定结构和非静定结构无法直接应用。

其次，机动法只能得到结构的内力分布情况，对于结构的变形和位移等情况无法直接得到。

因此，在实际工程中，通常需要结合其他方法进行综合分析。

静定结构的影响线

机动法作静定结构内力影响线依据

10(超)静定结构的影响线解析

作静定结构影响线的三种简单方法

静定结构某一截面某一内力的影响线

第八章 静定结构影响线

第四章 静定结构的影响线10

《静定结构影响线》课件

作静定结构影响线的三种简单方法

单位移动力偶作用下静定结构的影响线

结构力学-第4章影响线

第五章 静定结构的影响线

结构力学：第4章 静定结构影响线1

朱慈勉结构力学 静定结构的影响线

静定结构的影响线

第五章 静定结构的影响线

机动法作静定结构内力影响线依据

第八章静定结构影响线

第四章静定结构的影响线10

第五章静定结构的影响线

结构力学：第4章静定结构影响线1

朱慈勉结构力学静定结构的影响线

第五章静定结构的影响线