孤立导体的电容
大学物理电磁学部分08电容

例:求一半径为R的金属导体球的电容。
解:设孤立导体带电为q。 以无穷远为电势零点。 孤立导体的电势为: U + + + U +q+ + R + ++
q 4 0 R
q C 40 R U
孤立导体的电容正比于导体球的半径。
14
15
16
RB RA
RB RA
B
RA
l
高 斯 面
r
RB
B)通过场强计算两极板间的电势差;
C)由电容器电容的定义式C=Q/U求C。
10
4.电容的串联和并联 1.电容器的串联 U C1
A
C2
C3
特点:
q1 q 2 q q1 q 2 q n
Ci U 等效 B
UA C UB
qi
U U A U B U1 U 2 U n q q q1 q 2 qn 由 U 有 C C1 C 2 Cn C
柱面间的电势差为:
U AB
B
A
E dl
2 0l RA q q 2 0 l 电容 C q RB RB U AB ln ln RA 求电容步骤: 2 0 l R A
A)让两极板带等量异性电荷并求其电场分布;
q
ln
dr Edr 2 r 0 R
1 1 1 1 C C1 C 2 Cn
电容器串联后,等效 电容比每个电容器的 电容都小,但耐压能 力增加了。
11
电容器串联后,等效电容的 倒数是各电容的倒数之和。
2.电容器的并联
q1 C1 q 2 C2
UB
《孤立导体的电容》课件

电容的物理意义
电容是描述电场存储能力的重要物理量 电容的定义与性质 电容的物理意义在电路中的作用 电容的单位和单位换算
电容的单位
法拉(F):国际单位制 中的电容单位
微法拉(uF): 1uF=10^-6F
皮法拉(pF): 1pF=10^-12F
纳法拉(nF): 1nF=10^-9F
03
孤立导体的电容
电容在电源滤波中的应用 电容在振荡电路中的应用 电容在耦合电路中的应用 电容在旁路电路中的应用
电容在电力工程中的应用
用于无功补偿
提高电力系统的稳定性
降低输电线路的损耗
用于谐波治理和滤波
孤立导体电容的特
06
ห้องสมุดไป่ตู้性与影响因素
电容的充放电特性
电容的基本概念:定义、单位、符号等 电容的充放电原理:电场、电荷、电流等 电容的充放电过程:充电、放电、能量转换等 电容的充放电特性:时间常数、充放电电流、电压变化等
电压:电压 升高,电容 器的电容量 会增大
频率:频率 升高,电容 器的电容量 会减小
湿度:湿度 增大,电容 器的电容量 会减小
解决方法: 通过调整温 度、电压、 频率和湿度 等参数来控 制电容器的 电容量
孤立导体电容的发
07
展趋势与展望
电容技术的发展趋势
传统电容技术:介 绍传统电容技术的 原理、应用和发展 历程
测量设备误差:设备精度、 灵敏度等因素导致的误差
测量方法误差:测量方法的 不完善或不合理导致的误差
操作人员误差:操作人员技 能水平、经验等因素对测量
的影响
孤立导体电容的应
05
用
电容在电路中的应用
电容在滤波电路中的应用
电容在耦合电路中的应用
一.孤立导体的电容.ppt

E0
f1
有极分子的极化是由于分子偶极子在外电场的作
用下发生取向的结果
----取向极化
§9-3 静电场中的电介质
三. 电极化强度 1. 电极化强度
第九章 静电场中的导体和介质
无外场时:电介质中任一小体积元V内所有分子
的电偶极矩矢量和为零,即
电介质有极外化场程时度:越电高介,质被p极i越化大,
C U0
r
C0U0
则插入电介质后的电容为
C rC0
U U0 r
:r 电介质的相对介电常数,(相对电容率) Q C0U0
r0 : 电介质的介电常数,(电容率)
由 U U0 及 U Ed
r
可得
E E0
r
在无限大均匀各向同性的电介质中,任意一点的
电场强度,为真空中电场强度的 1 倍。
§9-2 电容 电容器
第九章 静电场中的导体和介质
1.平板电容器
设极板所带电荷为q
E q
VA
VB
BA E0
d
0
S
l Ed
qd
0S
Aq
r
d
S q
B
则
C
q
0S
VA VB d
(真空中 : r 1)
§9-2 电容 电容器
2. 圆柱形电容器
第九章 静电场中的导体和介质
设内外柱面带有电荷分别为+q和-q
HCH4
pe 0
§9-3 静电场中的电介质
第九章 静电场中的导体和介质
有极分子电介质:
无外电场时分子正负 电荷中心不重合,具有固有 电偶极矩,称为有极分子。
H
O pe
H
2. 电介质的极化
高二物理竞赛课件:孤立导体的电容

(2)以上各区域 V 分 布
解(1)由高斯定理: s D dS qi
rR
Da 0
Ea
D
0
rR
Q
D 4r 2
R r R1 R1 r R2
Eb
D 0
Q 40r 2
Ec
D
Q 40r r 2
r R2
Ed
D 0
Q 40r 2
各区域 D、E的方向 均沿半径向外。
Ea 0
Eb
Q 40r 2
Ec
Q 40rr 2
Ed
Q 40r 2
r
(2)以上各区域
V
分布。
Va E dl r Edr
rR Eadr
R1
Ebdr
R2
Ecdr
Ed dr
R
R1
R2
0 Q (1 1 ) Q ( 1 1 ) Q 1
40 R R1 40r R1 R2 40 R2
可以看出a区域是等势体
Vb
Q (1 1 ) Q ( 1 1 ) Q 1 40 r R1 40r R1 R2 40 R2
则筒间最大电压 VM ?
(3)画出 D( r ),E( r ),V ( r )曲线。
r
R2
R1
a
b
r
解:(1)由 s D ds q
R1
r R1 , r R2
a
R1 r a
D0
E D0 0
b
l
D 2rl l arb
D 2r
E D 0 20r
R2
r
r
D
E
D 2rl l
电容器所带的电量与电压成正比: Q = C U
比例系数“C”称为电容器的电容:
孤立导体的电容

4
3 电容器电容的计算
步骤
C
VA VB U
(1)设两极板分别带电Q
(2)求两极板间的电场强度 E常结合对称性 Ga用 us定 s 理
S
均匀电场:
CQ0rS
Ud
UEdlEdlEd
6
例3 球形电容器的电容 解 设内外球带分别带电Q
E
4
Q
π0r2
(R1rR2)
U l E dl
Q R2 dr
4 π 0 r R1 2
+
+
Q (1 1)
+
R2
4π0 R1 R2
+
+
R 1 +
r
+
+
7
U Q ( 1 1)
4π0 R1 R2
特点:非孤立导体,由两极板组成
++++++
+
C C C 电容是表述导体电学性质的物理量1,它与导体是2否带电无关,就象导体的电阻与导体是否通有电流无关一样。
孤立导体带电荷Q与其电势V的比值
U Q /C , U Q /C (1)设两极板分别带电 Q
++++++
1 - - - - - -
12
2
(3)求两极板间的电势差U
U Edl
(4)由C=Q/U求C
5
例1 平行平板电容器(已知如图)
解 设 两极板分别带电Q ,Q/ S
D dS DdS (导体内电场为零)
半径为r的孤立导体球的电容

半径为r的孤立导体球的电容1. 电容的基本概念电容,听起来像是个高大上的词,其实它就是储存电能的“罐子”。
你可以把电容想象成一个大水箱,能装下多少水就代表了它的容量。
电容的单位是法拉(F),这也是一个很重要的概念。
好比你家里的水管,越粗的水管能流过的水就越多,电容也是如此。
更简单地说,电容越大,能储存的电能就越多。
这就让我们聊聊孤立导体球的电容,它可是电学中的明星哦。
2. 孤立导体球的特点2.1 孤立导体球是什么孤立导体球,顾名思义,就是一个完全独立的金属球体。
想象一下,像一个巨大的金属乒乓球,周围没有任何干扰的因素。
这种球的电场是均匀的,简单、明了,给它一个电荷,整个球体都会均匀地“发光”。
就像你给好友一个好消息,他的脸上立刻挂上笑容。
2.2 半径的影响半径r在这里可是个关键角色。
简单说,半径越大,电容越大。
就像你把一个橡皮球吹得越大,它能装下的空气也就越多。
所以,孤立导体球的电容公式可以用 (C = 4pi varepsilon_0 r) 来表示。
这里的 (varepsilon_0) 是真空电容率,像个小助手,帮助我们计算。
这公式里的每一个部分,都有其独特的意义,仿佛在讲述一个动人的故事。
3. 电容的计算3.1 公式解析我们已经提到过电容的公式,接下来就深入挖掘一下。
这个公式中的 (4pi) 看似简单,其实蕴含了圆周的奥秘。
而 (varepsilon_0) 的价值,正如那看不见的水流,时时刻刻在支持着我们的电气世界。
最后,r就是半径,直接影响着电容的大小,像是你家的门口,门越宽,进出的人就越多。
3.2 实际应用说到实际应用,孤立导体球的电容可以在许多地方见到。
比如在无线电发射、接收器中,或者在电池和电容器的设计里,它们都需要考虑电容的大小。
就像你买衣服时会考虑尺码一样,电容的大小也决定了电气元件的性能。
试想一下,一个球形的装置,可以在电流的舞台上翩翩起舞,是多么酷炫的场面啊!4. 结尾思考电容的世界,虽说听起来有点枯燥,但其实它和我们的生活息息相关。
导体的电容

4 0 R
那么它的电容为
C
=
Q U
Q
/
Q
4 0 R
4 0 R
由此可见,电容量是反映导体自身性质的物理量,只与 导体大小和形状有关,与导体是否带有电荷无关。
在国际单位制中,电容的单位为法拉(F),简称法,1F =1C·V–1。在实际应用中,由于法拉的单位太大,因此常用 微法(μF)和皮法(pF)等作为电容的单位,它们之间的换 算关系为
E= Q 2 r 20rrl
场强的方向垂直于轴线而沿径向。
由此可以求出两板间的电势差为
U AB
B
Edl
A
RB Edl
RA
RB Edr RB dr ln RB
RA
RA 20 r r 20 r RA
由电容器电容的定义式,可得圆柱形电容器的电容为
C Q U AB
l
ln RB
20rl
E Q 0 r 0 r S
于是两板间的电压
B
Qd
U AB
Edl Ed
A
0r S
将上式带入电容的定义式(7-37)就可以得到平行板电容器 的电容为
C 0r S
d
上式表明,平行板电容器的电容与极板面积成正比,与
极板间的距离成反比;且其中充满电介质的电容是板间为真空 (εr=1)时的电容的εr倍。
ln RB
20 r RA
RA
由上式可知,圆柱形电容器的电容与圆柱面的长度成正 比,与两圆柱面半径的比值的自然对数成反比;且两极板之 间充满电介质时的电容为板间为真空(εr=1)时的电容的εr 倍。
3.球形电容器
球形电容器是由两个同心的导电球壳组成,如下图所示。 设两球壳半径分别为RA、RB,其间充满相对电容率为εr的电介 质。假设内外球壳带电量为+Q和-Q。
电容学

一、孤立导体的电容: 孤立导体的电容:
孤立导体是指附近无其它带电体或导体,认为地球离它很远。 孤立导体是指附近无其它带电体或导体,认为地球离它很远。 孤立导体球(实为均匀带电球面)的 孤立导体球(实为均匀带电球面) Q Q 电位: 电位: V = , = 4 πε R
4 πε
0 R
1 电容器
电容器——两个带等量 两个带等量异 电容器 号电荷的导体组成的系统 或称相互靠近又彼此绝缘 的导体组所构成的系统。 的导体组所构成的系统。 每个导体称作电极。 每个导体称作电极。
2 电容器的电容
电容器的电容——电容器任一极板所带电量的绝对值与两 电容器任一极板所带电量的绝对值与两 电容器的电容 极板间的电势差之比, 极板间的电势差之比,即
3 圆柱形电容器
圆柱形电容器为内径 RA、外径 RB 组成, 两同轴导体圆柱面 A 和 B组成,且 组成 大得多。 圆柱体的长度 l 比半径 RB大得多。 解:设两柱面带电分别为 +q 和 − q ,则单位长度的带电量为 λ = q / l 确定柱面间的场强, 确定柱面间的场强,作半径为 r、 、 的共轴圆柱 圆柱Gauss面 高为 l 的共轴圆柱Gauss面,容 易求得场强 λ E= 2πε 0 r 两板电势差为
1 平行板电容器
平行板电容器极板面积为 S ,板 求电容器电容。 间距离为 d ,求电容器电容。当S >> d时,可视为理想电容器。 时 可视为理想电容器。 解:设极板带电量为 q
+q
−q
A
B
平行板电容器场强
+q
−q
σ E= ε0
板间电势差
U AB = ∫
B
A
孤立导体的电容

1 1 1 1 CC C 1 C 2 n
注意
1.串联电容个数越多容量越小。
若面积S相同,相当于将极板间距增大。 0S C d 2.可提高电容耐压程度,外加电压由各电 容器分压。
12
2.电容器并联
特点
V V V V 1 2 n q q q q 1 2 n
A
q
E 0
d
d Ed V E d l AB
B
A
B
电容
C
q V AB
S 0S d / 0 d
6
0
C 与 q 无关。
例3:圆柱形电容器
圆柱形电容器由内径 RA、外径 RB 两同轴导体 圆柱面 A 和 B组成,且圆 柱体的长度 l 比半径 RB大 得多,求电容。
第五章 §5-4 电容 电容器
1
一、孤立导体的电容
q 1.孤立导体电容:考虑半径为R的导体球 V 4 0 R 的电势
改写为
q4 0RV
所带的电荷与电势成正比。通常把比例系数C 称为 电容。 定义:
q C V
半径为R的导体球
q C 4 0R V
2
注意:导体电容只与导体的大小、形状有关,与电量、 电势无关。
7 .1 10 (F)
4
3
二、电容器的电容
孤立导体的电容很小,用它作电容器不适 合。用两个导体极板组成的电容器可获得较大 的电容。 q q
q CV AB
这时定义: C
q V AB
q为一个极板带电量的绝对值。
A
B
4
符号:
电容器的电容只与电容器的大小、形状、电介质有 关,而与电量、电压无关。
孤立导体的电容
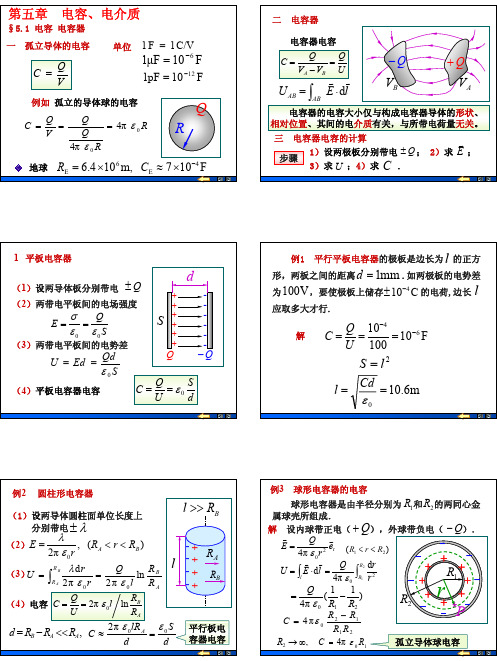
一孤立导体的电容VQ C =例如孤立的导体球的电容RRQ Q VQ C 00π4π4εε===RQ F107m,104.64E 6E −×≈×=C R 地球单位C/V1F 1=F10pF 112−=F10µF 16−=§5.1 电容电容器第五章电容、电介质二电容器电容器电容UQV V Q C B A =−=电容器的电容大小仅与构成电容器导体的形状、相对位置、其间的电介质有关,与所带电荷量无关。
三电容器电容的计算AV B V Q−Q+1)设两极板分别带电;2)求;Q ±E v U C 3)求;4)求.步骤lE U ABAB v v d ⋅=∫dS1 平板电容器+ + + +++Q Q−------SQ E 00εεσ==(2)两带电平板间的电场强度(1)设两导体板分别带电Q±SQd Ed U 0ε==(3)两带电平板间的电势差dS U Q C 0ε==(4)平板电容器电容例1 平行平板电容器的极板是边长为的正方形,两板之间的距离.如两极板的电势差为,要使极板上储存的电荷,边长应取多大才行.l mm 1=dV 100C 104−±l解F101001064−−===U Q C 2l S =m6.100==εCdl A R BRlBR l >>平行板电容器电容例2 圆柱形电容器,A A B R R R d <<−=dSdlR C A 00π2εε=≈ABR Rl U Q C ln π20ε==A B R R R Rl Q r r U B Aln π2π2d 00εελ==∫(3))(,π20B A R r R r E <<=ελ(2)(4)电容++++----(1)设两导体圆柱面单位长度上λ±分别带电1R 2R 例3 球形电容器的电容 球形电容器是由半径分别为 和 的两同心金属球壳所组成.1R 2R 解 设内球带正电( ),外球带负电( ).Q+Q −++++++++−−−−−−−−rr 20π4e r Q E v v ε=)(21R r R <<∫∫=⋅=2120d π4d R R l r r Q l E U εv v )11(π4210R R Q−=ε,2∞→R 10π4R C ε=孤立导体球电容P*21120π4R R R R C −=εR2dλ+λ−E v )(π2π200x d x E E E −+=+=−+ελελxx d x x E U R d R Rd R d )11(π2d 0−+==∫∫−−ελRd R R d ln πln π00ελελ≈−=单位长度的电容RdU C ln π0ελ==解设两金属线的电荷线密度为λ±+E v −E v 例4 两半径为的平行长直导线中心间距为,且, 求单位长度的电容.R d R d >>ox P x x d −三 电容器的串联和并联1 电容器的并联2 电容器的串联∑∑===iiiiC QUQU C 111C 2C +−1C 2C +−QQ Q Q n ====K 21QQ Q Q n =+++K 21UU U U n ====K 21∑∑===iiiiC UQU Q C nU U U U +++=K 21例5如图所示,A 、B 是平行板电容器的两极板,面积为S ,间距为d ,现将此电容器放在一金属盒中,D 1、D 2 是两底面,都与A , B 平行,且间距都为d 。
高二物理竞赛课件:导体的电容电容器

接地后:
Q -Q q=0
q1=q4 q2=-q3
②导体球壳
Q
-Q Q=0
若是内球接地, 则内球电荷通 常不为零.
③任意形状导体
q
q q=0
⒋静电屏蔽及其物理本质
导体静电平衡下场强,电势,电荷分布的计算
•静电平衡的条件: E内 0 V const.
•基本性质方程:
1
③接上,若将球形导体接地, 则Q导=?
V导 V球心 V表面 Vq
Q导 q 0 40R 40r
Q导
q r
R
单位: 法拉 F= C·V-1 1F 106 μ F 1012 pF
若 C = 110 –3 F , 则 R = ? 2. 电容器的电容 通常由形状相同 彼此绝缘 相 距很近的两导体构成电容器。
解:⑴不变.
⑵减小.
-q
V(-q)<V(导体)<V(∞)
+-
+ +
-
[讨论] ①若导体为半径R球体,点电荷q 与球心相
距r,则感应电荷产生的场强?
E感应 Eq 0 E感应 Eq
②若导体是球形的,半径为R,点电荷q 与球 心相距r,则V导=?
q V导 V球 心 V表 面 Vq Vq 4 0r
RA
RB
l
rh
-Q +Q
(3) 球形电容器
4r 2 E Q
0
Q
E 4 0r 2
b
U E dl
Q (1 1)
a
4 0 R1 R2
b
-Q
a
R2 R1
C Q 4 0 R1 R2
U R2 R1
设+Q
一、孤立导体的电容

E
q
RB
RA
40 RA RB C RB RA
孤立导体可认为它与无 限远处的另一导体组成一个 电容器,这个电容器的电容 即为孤立导体的电容。
B
A
RA
RB
上式令 RB→∞, 得导体球的电容
C 40 RA
三.电容器的并联和串联 并联: 各电容器上 的电压相等
U
C1 C2 C3
三、电介质对电场的影响 1. 介质极化对电场的影响 极化电荷激发的电场,使介质内外的 电场分布发生变化。介质内场强减弱。
E0
E'
+ +
E
E 介质中某点的场强,是由外电场 和 0 极化电荷电场 E 叠加而成的,
' ' E 与 E0 的方向相反,且 E E0 ,则 E E0 E E0
B B VA VB A E d l RB dr R RB ln . RA Edr R 20 r 20 RAB A Nhomakorabea 20 r
l
A E
q 20l l C RB RB VA V B ln ln RA 20 RA
§13-5 电容和电容器 一、孤立导体的电容 设孤立导体带电量为q,电势为V, 实验证明 q V , 设 C 为比例系数,则
q CV
q
V
定义电容:
q C V
它表示导体获得单位电势所需电量。 单位: 法拉(F ), 1 F = 1 C/V
电容 C 的大小与导体的几何特征(大 小和形状)有关。
电介质:内部几乎没有可以自由运动 电荷的物体。又称为绝缘体。 H 1. 无极分子电介质:无 H C H 外电场时分子的正负电荷 H 中心重合。 甲烷 CH4
孤立导体的电容C

C 0S d
在极板上电荷不变的情况下,两板间 的电势差与电容成反比
C1 C2 C3
d
CQ U
U C rd U C r (d )
思考:如果将厚度为金属板
插入两极板间, 重新计算. 10/12
同学们再见!
2、电容器的并联
C C1 C2 Cn
n
Ci i 1
q q1 q2 qn U U1 Ui
+q U1-q +q U2 -q
C1
C2
U
+q Un-q Cn
q1 q2
qn
C1 C2
Cn
U
9/12
例题: 平板电容器极板间的距离为d,保持极板上的电荷不变,
设带电为±Q: Q
l
RB RA l
RA
RB
E
由高斯定理: E 2 r h h / 0
E
2 0r
U AB
B E dl
A
B
E
dr
A
hr
U AB
1 RB
RA 2 0
r
dr
2 0
ln
RB RA
Q ln RB
把相对介电常数为r 厚度为 (<d)的玻璃板插入极板间,求无
玻璃板时和插入玻璃板后极板间电势差的比。
r 0
解 看成三个电容器串联
0
0
1 1 1 1 x1 x2 C C1 C2 C3 0S 0 r S 0S
C
0 r S
r (d )
3、电容器电容的计算 C Q Q VA VB U AB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q
计算电容。
VAB
5
例2:平行板电容器极板面积为 S , q q
板间距离为 d ,求电容器电容。 解:设极板带电量为 q
由平行板电容器场强 E
板间电势差
0
A
VAB
B Edl
A
Ed
d 0
电容 C q S 0S VAB d / 0 d
C 与 q 无关。
d
B
6
例3:圆柱形电容器
的电容。
q q
q CVAB
这时定义: C q VAB
AB
q为一个极板带电量的绝对值。
4
符号:
电容器的电容只与电容器的大小、形状、电介质有 关,而与电量、电压无关。
三、电容的计算方法
1.设电容器的带电量为 q。
2.确定极板间的场强。
3.由 VAB
4.由电容定义
B Edl
A
C
计算两板间的电势差。
Cn
11
注意
1 1 1 1
C C1 C2
Cn
1.串联电容个数越多容量越小。
若面积S相同,相当于将极板间距增大。
C 0S
d 2.可提高电容耐压程度,外加电压由各电 容器分压。
12
2.电容器并联 特点
V V1 V2 Vn q q1 q2 qn 由 q CV CV C1V1 C2V2 CnVn
l
Ed S
侧 侧 EdS cos
E 2rl l 0
高 斯 面
RA
r
RB
8
E
2 0r
高
柱面间的电势差为
B
VAB A E dl
斯 面
RB
RA
Edr
RB
RA
2 0r
dr
RA
lr
RB
q ln R B
20l R A
9
电容 C q U AB
q q ln R B
20l R A
20l
1皮法(pF)= 10-6 F = 10-12 F
例1:如果地球当成孤立导体,其电容为多大?(地球 半径为 6.4106 m)
解:C q V
4 0R
4 8.85 10 12 6.4 10 6
7.1104 (F) 3
二、电容器的电容
孤立导体的电容很小,用它作电容器不适
合。用两个导体极板组成的电容器可获得较大
圆柱形电容器由内径
RA、外径 RB 两同轴导体圆 柱面 A 和 B组成,且圆柱体
的长度 l 比半径 RB大得多, 求电容。
l
解:设两柱面带电分别为 +q 和 q ,则单位长度的带电量 为
q/l
R为 r、高为 l 的高斯柱面。
E dS
q
0
侧 上底 下底
ln R B RA
l 越大,C 越大。
RA
l
RB
10
四、电容器串并联 1.电容器串联
q1 C1
C2
Cn
q2 qn
特点: q q1 q2 qn
V1 V2
Vn
V V1 V2 Vn
V
由 V q C
有 q q1 q2 qn
C C1 C2
Cn
1 1 1 1
C C1 C2
q1 C1
q2 C2
qn Cn
C C1 C2 Cn
13
注意
C C1 C2 Cn
1.并联电容个数越多电容越大,若极板间 距 d 相同,电容并联相当面积 S增加。
C 0S
d
14
第五章
§5-4 电容 电容器
1
一、孤立导体的电容
1.孤立导体电容:考虑半径为R的导体球 的电势
V q
4 0R
改写为 q 4 0RV
所带的电荷与电势成正比。通常把比例系数C 称为
电容。
q
定义: C
V 半径为R的导体球 C
q V
4 0R
注意:导体电容只与导体的大小、形状有关,与电量、
电势无关。
2
电容可以存储电能,作为电子元件称为电容器。 单位:法拉,F 1微法(F)=10-6 F
