数字信号处理第一章习题解答【精选】
数字信号处理第一章课后答案

第 1 章 时域离散信号和时域离散系统
n
(7) y(n)= x(m) 令输入为m0
x(n-n0)
输出为
n
y′(n)= =0[DD)]x(m-n0)
m0
nn0
y(n-n0)= x(m)≠y′(n) m0
故系统是时变系统。 由于
n
T[ax1(n)+bx2(n)]=
[ax1(m)+bx2(m)
第 1 章 时域离散信号和时域离散系统
解:
x(n)=δ(n+4)+2δ(n+2)-δ(n+1)+2δ(n)+δ(n-1)
+2δ(n-2)+4δ(n-3)+0.5δ(n-4)+2δ(n-6)
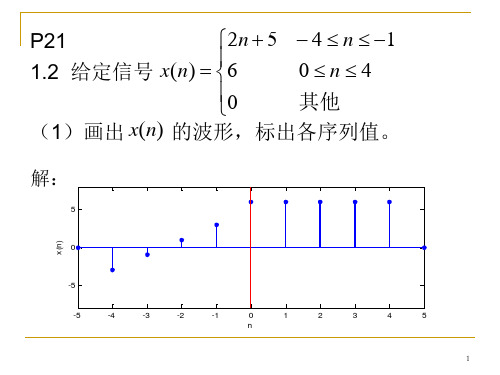
2. 给定信号:
2n+5
-4≤n≤-1
(x(n)= 6 0
0≤n≤4 其它
(1) 画出x(n)序列的波形, 标上各序列值;
(2) y(n)=x(n)+x(n+1)
n n0
(3) y(n)= x(k) k nn0
(4) y(n)=x(n-n0) (5) y(n)=ex(n)
第 1 章 时域离散信号和时域离散系统
解:(1)只要N≥1, 该系统就是因果系统, 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M, 则|y(n)|≤M, (2) 该系统是非因果系统, 因为n时间的输出还和n时间以 后((n+1)时间)的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
第 1 章 时域离散信号和时域离散系统 题2解图(四)
数字信号处理课后答案

k = n0
∑
n
x[ k ]
(B) T {x[n]} =
∑
x[k ]
(C) T {x[ n]} = 0.5
x[ n ]
(D) T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ,输出为 y[n] ,满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ,则系统是(A) (A)线性的 (B)时不变的 (C)因果的 (D)稳定的 解:
(a) T { x[ n ]} = h[ n] + x[ n ], (c) T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ,单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 , n < 0 , 则 y[3] = 0.5 。 解: y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解: (a)
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞
数字信号处理课后习题答案(全)1-7章

第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
第 1 章 时域离散信号和时域离散系统
题4解图(一)
第 1 章 时域离散信号和时域离散系统
题4解图(二)
第 1 章 时域离散信号和时域离散系统
题4解图(三)
第 1 章 时域离散信号和时域离散系统
(4) 很容易证明: x(n)=x1(n)=xe(n)+xo(n)
上面等式说明实序列可以分解成偶对称序列和奇对称序列。 偶对称序列可 以用题中(2)的公式计算, 奇对称序列可以用题中(3)的公式计算。
(2) y(n)=x(n)+x(nN+1)k 0
(3) y(n)= x(k)
(4) y(n)=x(n-nn0)n0
(5) y(n)=ex(n)
k nn0
第 1 章 时域离散信号和时域离散系统
解:(1)只要N≥1, 该系统就是因果系统, 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M, 则|y(n)|≤M, (2) 该系统是非因果系统, 因为n时间的输出还和n时间以 后((n+1)时间)的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
=2x(n)+x(n-1)+ x(n-2)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
数字信号处理习题及解答

只有在如上周期延拓序列中无混叠的点上, 才满足f(n)=fl(n),所以 f(n)=fl(n)=x(n)*y(n) 7≤n≤19
令
数字信号处理习题及解答
第二章Z变换及离散时间系统分析
3 解答
n≥0时, 因为c内无极点,x(n)=0; n≤-1时, c内有极点0 , 但z=0是一个n阶极点, 改为求
圆外极点留数, 圆外极点有z1=0.5, z2=2, 那么
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 3 解答 (2) 收敛域0.5<|z|<2:
数字信号处理习题及解答
第三章信号的傅里叶变换 1 解答
(1) (2) (3)
数字信号处理习题及解答
第三章信号的傅里叶变换 2 试求如下序列的傅里叶变换:
(1) x1(n)=δ(n-3)
(2)
数字信号处理习题及解答
第三章信号的傅里叶变换 2 解答
(1) (2)
数字信号处理习题及解答
第三章信号的傅里叶变换
第一章离散时间信号与离散时间系统
4 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 3 已知
求出对应X(z)的各种可能的序列表达式。
数字信号处理第三版第1章习题答案

第 1 章 时域离散信号和时域离散系统
1.
学习要点
1
信号: 模拟信号、 时域离散信号、 数字信号三者
之间的区别; 常用的时域离散信号; 如何判断信号是周期性的
, 其周期如何计算等。
2
系统: 什么是系统的线性、 时不变性以及因果性
、 稳定性; 线性、 时不变系统输入和输出之
间的关系; 求解线性卷积的图解法(列表法)、 解析法,
第 1 章 时域离散信号和时域离散系统
解线性卷积也可用Z变换法, 以及离散傅里叶变换求解, 这是后面几章的内容。 下面通过例题说明。
设x(n)=R4(n), h(n)=R4(n), 求y(n)=x(n)*h(n)。 该题是两个短序列的线性卷积, 可以用图解法(列表法) 或者解析法求解。 表1.2.1给出了图解法(列表法), 用公式 可表示为
此是非周期序列。
第 1 章 时域离散信号和时域离散系统
4. 对题1图给出的x(n)要求:
(1) 画出x(-n)的波形;
(2) 计算x (n)= [x(n)+x(-n)], 并画出x (n)波形;
e
e
(3) 计算x (n)= o
[x(n)-x(-n)], 并画出x o(n)波形
(4) 令x (n)=x (n)+x (n), 将x (n)与x(n)进行比较, 你能得到
第 1 章 时域离散信号和时域离散系统 图1.3.2
第 1 章 时域离散信号和时域离散系统
[例1.3.5]已知x1(n)=δ(n)+3δ(n-1)+2δ(n-2),x2(n)=u
u(n-3), 试求信号x(n), 它满足x(n)=x1(n)*x2(n), 并画出x( 的波形。
数字信号处理课后习题答案(全)1-7章

第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
第 1 章 时域离散信号和时域离散系统
题8解图(一)
第 1 章 时域离散信号和时域离散系统
(5) 画x3(n)时, 先画x(-n)的波形(即将x(n)的波形以纵轴为中心翻转180°), 然后再右移2位, x3(n)波形如题2解图(四)所示。
第 1 章 时域离散信号和时域离散系统
题2解图(一)
第 1 章 时域离散信号和时域离散系统
题2解图(二)
第 1 章 时域离散信号和时域离散系统
题2解图(三)
分别求出输出y(n)。
(1) h(n)=R4(n), x(n)=R5(n) (2) h(n)=2R4(n), x(n)=δ(n)-δ(n-2) (3) h(n)=0.5nu(n), xn=R5(n)
解: (1) y(n)=x(n)*h(n)=
数字信号处理作业答案(参考版-第一章)

1-2习题1-2图所示为一个理想采样—恢复系统,采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。
解:(1)根据余弦函数傅里叶变换知:)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ,)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。
又根据抽样后频谱公式:∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(,得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以,)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示(2))(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到,)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ,故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理,)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=(3)由题(2)可知,无失真,有失真。
原因是根据采样定理,采样频率满足信号)(1t x a 的采样率,而不满足)(2t x a 的,发生了频谱混叠。
1-3判断下列序列是否为周期序列,对周期序列确定其周期。
(1)()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭(2)()8n j x n eπ⎛⎫- ⎪⎝⎭=(3)()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解:(1)85πω=,5162=ωπ为有理数,是周期序列,.16=N (2)πωπω162,81==,为无理数,是非周期序列; (3)382,43==ωππω,为有理数,是周期序列,8=N 。
(完整word版)数字信号处理习题及答案

==============================绪论==============================1。
A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1。
①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用(n ) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法 乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(—n )的波形图。
②尺度变换:已知x(n)波形,画出x (2n )及x(n/2)波形图.卷积和:①h(n)*求x(n),其他2n 0n 3,h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (—m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4. 如果输入信号为,求下述系统的输出信号。
数字信号处理第一章习题
h1(n) 2h1(n 1) h1(n 2)
h1(n) 表征的系统是因果稳定系统,故存在: n 0, h1(n) 0 h(n) : L 7 当 n 0 时: h3(n) : M 3
h1(n) : N L M 1 5
nn
nn
相加
4
44
2
22
xx1((nn))
x1(n)
0
00
-2
--22
-10 -5
0
5
10
--110 -5
00
55 1100
3
n x(n) xe (n) x3o (n)
nn
2
22
(n)
9
1
1
(n)
1.5 设系统分别用下面的差分方程描述,x(n)和 y(n)分别表示系统输入和输出,判断系统是否 为线性时不变系统。
17
解:
6
4
2
y(n)
0
-2
-6
-4
-2
0
2
4
6
8
10
18
采用解析法,则有:
h(n) 2 (n) (n 1) 0.5 (n 2) x(n) (n 2) (n 1) 2 (n 3)
x(n)* (n) x(n) x(n)* A (n k) Ax(n k) y(n) x(n)*h(n) x(n)*[2 (n) (n 1) 0.5 (n 2)]
(2) y(n) 2x(n) 3
解:
y1(n) 2x1(n) 3
y2 (n) 2x2 (n) 3
非线性系统
T[ax1(n) bx2 (n)] 2ax1(n) 2bx2 (n) 3
数字信号处理课后习题答案(全)1-7章

x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n-k)=Ax(n-k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示,
要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
y(n)=x(n)*h(n)=
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
数字信号处理经典习题(北理工826必备)(附答案)

数字信号处理经典习题(北理工826必备)(附答案)第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前让信号通过一个低通滤波器,是为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称位“抗折叠”滤波器。
在D/A变换之后都要让信号通过一个低通滤波器,是为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故友称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理 计算题:18c 因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T 8π没有影响,故整个系统的截止频率由)(ωj eH 决定,是625Hz 。
(b )采用同样的方法求得kHz T 201=,整个系统的截止频率为Hz Tf c 1250161==二、离散时间信号与系统频域分析 计算题:1( 2(2))(*n x (共轭) 解:DTFT )(**])([)(*)(*ωωωj n n jn jn e X e n x en x n x -∞-∞=∞-∞=-===∑∑2.计算下列各信号的傅里叶变换。
(a )][2n u n- (b )]2[)41(+n u n(c )]24[n -δ (d )nn )21(解:(a )∑∑-∞=--∞-∞==-=2][2)(n nj n nj n ne en u X ωωωωnj e 11)1(==∞( ((X =3 (1))(*n x - (2))](Re[n x (3) )(n nx解: (1))(*])([)(*)(*jw n n jw n jwne X en x en x=-=-∑∑∞-∞=--∞-∞=-(2)∑∑∞-∞=-*-*∞-∞=-+=+=n jw jw jwn n jwne X e X e n xn x en x )]()([21)]()([21)](Re[(3)dw e dX j e n x dw d j dw e n dx j en nx jw n jwnn jwn n jwn)()()(1)(==-=∑∑∑∞-∞=-∞-∞=-∞-∞=- 4.序列)(n x 的傅里叶变换为)(jwe X ,求下列各序列的傅里叶变换。
数字信号处理课后习题答案(全)1-7章

最后结果为 0
n<0或n>7
y(n)= n+1 0≤n≤3 8-n 4≤n≤7
y(n)的波形如题8解图(一)所示。 (2) y(n) =2R4(n)*[δ(n)-δ(n-2)]=2R4(n)-2R4(n-2)
=2[δ(n)+δ(n-1)-δ(n+4)-δ(n+5) y(n)的波形如题8解图(二)所示
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
因此系统是非时变系统。
第 1 章 时域离散信号和时域离散系统
(5) y(n)=x2(n)
令输入为
输出为
x(n-n0)
y′(n)=x2(n-n0) y(n-n0)=x2(n-n0)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=[ax1(n)+bx2(n)]2 ≠aT[x1(n)]+bT[x2(n) =ax21(n)+bx22(n)
第 1 章 时域离散信号和时域离散系统
题4解图(一)
第 1 章 时域离散信号和时域离散系统
题4解图(二)
第 1 章 时域离散信号和时域离散系统
题4解图(三)
第 1 章 时域离散信号和时域离散系统
(4) 很容易证明: x(n)=x1(n)=xe(n)+xo(n)
数字信号处理习题集附答案

第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?2.答:在A/D变化之前为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称为“抗混叠”滤波器。
在D/A变换之后为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故又称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混叠效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b ) 对于kHz T 201=,重复(a )的计算。
解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为 因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T8π没有影响,故整个系统的截止频率由)(ωj e H 决定,是625Hz 。
(b )采用同样的方法求得kHz 201=,整个系统的截止频率为 二、离散时间信号与系统频域分析 计算题:1.设序列)(n x 的傅氏变换为)(ωj e X ,试求下列序列的傅里叶变换。
数字信号处理 第1章习题答案

由于 x2 (n) x1 (n 1) ,而且 y2 (n) y1(n 1) 故当 y(-1)=0时,系统具有移不变性。
(c)设 x3 (n) (n) (n 1) 则 y3 (n) a y3 (n 1) x3 (n) 且 y3 (1) 0
根据 y3 (n) a y3 (n 1) x3 (n) ,当 n ≥ 0 时有
3 ( a ) x( n) A cos( n ) 7 8 (c ) x ( n ) e
j( n ) 6
;
13 (b) x( n) A sin n 3
π π 解 (a) 2 2 14 为有理数 3 π 3 ω
0
7
故 x(n)是周期的,周期 N=14
x(m)h(n m)
x(m) : m n0
h(n m) : n N 1 m n
① 当 n n0时, y(n) 0 ② 当 n0 n n0 N 1 时,
n n
n n y(n) x(m)h(n m) mn0 nm n 0 mn0 mn0 mn0
(b)设 x2 (n) (n 1) ,则 y2 (n) a y2 (n 1) x2 (n) 且 y2 (0) 0
根据 y2 (n) a y2 (n 1) x2 (n) ,当 n > 0 时有
y2 (1) a y2 (0) x2 (1) 1 ,
……
y2 (2) a y2 (1) x2 (2) a
y3 (1) a y3 (0) x3 (1) 1 , y3 (2) a y3 (1) x3 (2) a y3 (3) a y3 (2) x3 (3) a 2 , , y3 (n) a y3 (n 1) x3 (n) a n1
数字信号处理》第三版课后习题答案

数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。
解:2.给定信号:25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n序列;(3)令1()2(2)x n x n=-,试画出1()x n波形;(4)令2()2(2)x n x n=+,试画出2()x n波形;(5)令3()2(2)x n x n=-,试画出3()x n波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)(3)1()x n的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n时,先画x(-n)的波形,然后再右移2位,3()x n波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5.设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。
数字信号处理_第一章_习题

解:
画
一个[- , ]周期频谱图
画
一个[- , ]周期频谱图
解:
解:
解:
习题1-2
解:
习题1-21
解:
讨论系数求解
习题1-21
解:
若
留数法或者线性加权特性求出
若
作业(1-6) 例: 已知抽取器的输入和输出关系为 y[k]=x[Mk]
试判断该离散系统是否为时不变系统?
解:输入序列x[k]产生的输出序列y[k]为 y[k]=T{ x[k]}= x[Mk] y[k-n]=x[M(k-n)] 输入序列x[k-n]产生的输出序列为 T{x[k-n]}= x[Mk-n] 由于 x[Mk-n] y[k-n]故该离散系统是时变系 统。
受频率响
应幅度|H(ej ) | 加 权 影 响 , 而 输 出 的
则为输入相位与相系位统响应相位之和。
解: 系统频响
习题1-25
举例
已知系统函数: 如果输入序列为: 则系统的稳态输出y[k]:
信号离散化过程中频谱分析或者频谱变化规律
采样Ts
? 周期化
作业 1-27
解:
周期为2
解:
周期为2
习题1-12
解:
书14页
习题1-12
解:
书14页
补充(第2章内容)
习题1-12
解:
取一周期主值
解:
1 -
习题1-14
因为X(ej )是偶函数,公式简化为: 若k=0
解: 1
若
-
习题1-14
Hale Waihona Puke 解: 1习题1-14
-
-0.5
0.5
《信号与系统》(第2版)书161
数字信号处理第一章解答

另解上式做Z变换
Y ( Z ) 2Y ( Z ) Z 通解: H ( Z )
1
2Y ( Z ) Z 1 Z
2
X (Z )
1 2Z
k
y [ k ] 2 y [ k 1] 1 y [ k 2 ] k ] x[ 2
h [ k ] (1 k )( 1) u [ k ]
是否 (1) 线性 (2) 因果 (3) 时不变 (4) 稳定
y[ k ] a
l 5
5
x(k l )
a 0
解:
(1)
T {ax1 [ k ] bx2 [ k ]} a+
l 5
5
(ax1[k-l ] bx2 [ k-l ])
5 l 5
aT { x1 [ k ]} bT { x 2 [ k ]} 2a+ (ax1[k-l ] bx2 [ k-l ])
r 2 r 1 0 r1 , 2 1
2
通解: h [ k ] c 1 ( 1) c 2 k ( 1)
k
k
初始条件:
h [ 0 ] 2 h [ 1] h [ 2 ] d [ 0 ] h [ 0 ] 1
y [ k ] 2 y [ k 1] y [ k 2 ] x [ k ]
1 x[ n ] 2x[ n 1] 3 x[ n 2 ] [ n 3] 4x
k 0
{4,11,20,30,20,[ k ] 2 y [ k 1] y [ k 2 ] x [ k ]
解
h [ k ] 2 h [ k 1] h [ k 2 ] d [ k ]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2 (5) y(n) x(n)*h(n) [ (n) (n 3)]*0.8u(n 1)
0.8u(n 1) 0.8u(n 4) {0,0.8,0.8,0.8,0, }
sin( n)
1.4 (5) x(n)
7
n
非周期序列
(7)sin(3 n) cos(15n)
aT [ x1(n)] bT [ x2 (n)]
为线性系统
T[x(n)]g(n)x(n) T[x(nm)]g(n)x(nm)
y(n)T[x(n)]g(n)x(n), y(nm)g(nm)x(nm)T[x(nm)]
为移变系统
1.7 (1) T[x(n)] g(n)x(n) 系统的输出仅取决于n时刻的输入x(n)和g(n),
为因果系统 设 x(n) M ,T[x(n)] g(n)x(n) g(n) x(n)
若 g(n) N ,则系统为稳定系统,否则为不稳定系统
1.7 (5) T[x(n)] nx(n)
T[x1(n)] nx1(n)
T[x2(n)] nx2(n)
T[ax1(n)bx2 (n)]n[ax1(n)bx 2(n)]
x2(n) y2(n) x2(n)
ax1(n) bx2(n) y(n) ax1(n) bx2(n)
ay1(n) by2(n)
为线性系统
T[x(n)]x(n) T[x(nm)]x((nm))x(nm)
y(nm) x((nm)) x(n m)T [ x(n m)]
anx1(n)bnx2 (n)aT [ x1(n)]bT [ x2 (n)]] 系统为线性系统。
T[x(n m)] nx(n m)
y(n)T[x(n)]nx(n), y(n-m)(nm)x(nm)T[x(nm)]
系统为移变系统。
系统n时刻的输出仅取决于n时刻的输入x(n),
为因果系统 设 x(n) M ,T[x(n)] = nx(n) = n x(n)
当n时,T[x(n)] ,为不稳定系统。
1.7 (8) T[x(n)] x(2n)
T[x1(n)] x1(2n)
T[x2(n)] x2(2n)
T[ax1(n)bx2 (n)]ax1(2n)bx 2(2n)]
为移不变系统
1.6 (5) y(n) x(n2)
x1(n)
y1(n)
x (n2 1
)
x2(n) y2(n) x2(n2)
ax1(n) bx2(n) y(n) ax1(n2) bx2(n2)
ay1(n) by2(n)
为线性系统
T[x(n)]x(n2) T[x(nm)]x((nm)2)
a
2
x2 1Biblioteka (n)2abx1(n)
x2
(n)
b2
x2 2
(n)
ay1(n)
by2
(n)
为非线性系统
T[x(n)][x(n)]2 T[x(nm)][x(nm)]2
y(nm)[x(nm)]2 T[x(nm)]2
为移不变系统
1.6 (4) y(n) x(n)
x1(n) y1(n) x1(n)
y(nm)[x(nm)2]2 T[x(nm)]
为移不变系统
1.7 (1) T[x(n)] g(n)x(n)
x1(n) T[x1(n)] g(n)x1(n)
x2(n) T[x2(n)] g(n)x2(n)
ax1(n) bx2(n) T[ax1(n) bx2(n)] g(n)[ax1(n) bx2(n)]
1 3 ,2 15
非周期序列
2 2 1 3
2 2 2 15
1.6 (2) y(n) [x(n)]2
x1(n) y1(n) [x1(n)]2
x2(n) y2(n) [x2(n)]2
ax1(n) bx2(n) y(n) [ax1(n) bx2(n)]2
1.2
(1)
y(n) x(n)*h(n) (n)*R (n) R (n)
5
5
1.2 (2) y(n) x(n)*h(n) R3(n)*R4(n)
R (n)*[ (n) (n 1) (n 2) (n 3)]
3 R3(n) R3(n 1) R3(n 2) R3(n 3) {1,2,3,3,2,1}
为稳定系统。
1.8 (8) h(n) u(4 n)] 当n 0时,h(n) u(4-n)=10
系统为非因果系统。
4
h(n) u(4n) 1
n
n
n
系统为不稳定系统。
aT [ x1(n)]bT [ x2 (n)]] 系统为线性系统。
T[x(n m)] x(2n 2m)
y(n)T[x(n)]x(2n), y(n-m)x(2n2m)T[x(nm)]
系统为移不变系统。
系统的n时刻输出取决于2n时刻的输入x(n),
为非因果系统 设 x(n) M ,T[x(n)] = x(2n) M
