大学物理机械振动和机械波PPT课件

另外一个方法: 能量法
.
22
§4-2 谐振动的能量
以弹簧振子为例
Fkx xAco st() vAsin(t)
E k1 2m v21 2m 2A 2si2(n t)
Ep1 2k2 x1 2k2 A co 2( st) 2 k/m
EEkEp1 2kA 2A（2 振幅的动力学意义）
线性回复力是保守力，作简谐运动的系统机械能守恒
o
A 2cots(π)A2 .
Tt
12
简谐运动的描述和特征
1）物体受线性回复力作用 Fkx平衡位置 x0
2）简谐运动的动力学描述 d2x 2x 0
dt2
3）简谐运动的运动学描述 xA co ts ()
v A si n t ()
4）加速度与位移成正比而方向相反 a 2x
弹簧振子 k m 单摆 g l
F浮
证明：以水面为原点建立坐标OX
x
d2x g x 0
b
dt2 b
mg X
d2x dt2
2
x
0
.
21
解决简谐运动方程问题的一般步骤:
1) 找到振动平衡位置,此时合力为零,选平衡位 置为原点,建立坐标系 2) 设振子离开原点x处,分析受力情况.
3) 应用牛顿定律.
4) 根据初始条件确定A和.
5) 写出振动表达式.
18
讨论
已知 t0,x0,v0求
0Acos
π
2
v 0 Asi n0
sin 0取 π A
x
2
xAcost(π)
o
A
2
.
v
x
o
Tt
T 2
19
例4-1 一轻弹簧,下挂质量为10g 的重物时,伸 长4.9cm.用它和质量80g小球构成弹簧振子. 将小球由平衡位置向下拉1.0cm 后,给向上初 速度v=5.0cm/s.求振动周期及振动表达式.
令 2 mgl
I
d2 2 0
dt2 动力学判据
mcots ()
运动学判据 .
o 转动正向
l
*C
P
（ C点为质心）
11
二 谐振动的速度和加速度
xAcots()
x xt图
A
o
t
T
取 0
A
v A si n t () Av vt图
o
T
t
Acost(π) A
2
a at图
a A 2co t s() A2
.
23
x,v
简谐运动能量图
xt 0
o
t xA co ts
T vt v A si n t
能量
o T T 3T T 42 4
E 1 kA2 2
Ep
1kA2c 2
o2st
t.
Ek
1m2A2sin2t
2
24
推导
能量守恒
简谐振动方程
E1mv21kx2常量 22
d(1mv21kx2)0 dt 2 in t()
dt
d2x 2x 0
dt2
ad2xA2cost ()
d . t2
9
2 单摆 msginmta
mlmdl2m••l
d2t
••
g
s
in
0
l
5时 ,sin令
2
g
l
••
20
mcots ()
.
转动
A
正向
l
Fm
o
mg
10
3 复摆(物理摆)
( 5)
Mmg l mgl I d2
dt2
3）初相位 (t0) 描述质点初始时刻的运动状态.
( 取 [ π π或][0 2 π) ]
.
17
四 常数 A和 的确定
xAcots()
v A si n t ()
初始条件 t0xx0 vv0
A
x0 Acos
x02
v02
2
v0Asin
tan v0 x0
对给定振动系统，周期由系统本身性质
决定，振幅和初相由初.始条件决定.
物理意义.
.
3
四 理解同方向、同频率简谐运动的合 成规律，了解拍的特点.
五 了解阻尼振动、受迫振动和共振的发 生条件及规律.
.
4
本章重点
相位概念的理解及掌握简谐振动的基本规律。 同方向同频率简谐振动的合成。
本章难点
相位概念的理解。
.
5
引言
任一物理量在某一定值附近往复变化均称为 振动.
机械振动 物体围绕一固定位置往复运动. 其运动形式有直线、平面和空间振动. 例如一切发声体、心脏、海浪起伏、地震以
及晶体中原子的振动等.
周期和非周期振动
.
6
简谐振动 最简单、最基本的振动.
简谐振动
合成 分解
复杂振动
谐振子 作简谐振动的物体.
.
7
§4-1 简谐振动
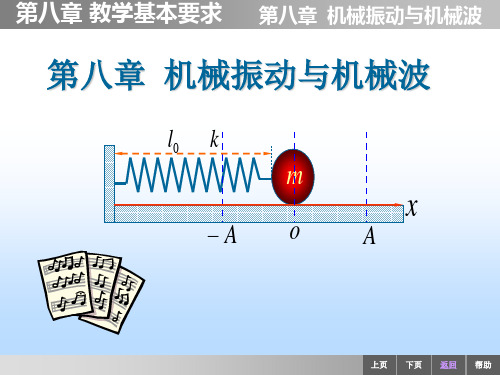
一 简谐振动的特征方程 1 弹簧振子
l0 k
A
平衡位置
m x0 F0
x
oA
.
8
Fm
ox
x
Fk xmaxA co ts ()
令 2 k
m
a2x
积分常数，根据初始条件确定
d2x k x 0
dt2 m
.
25
例4-3 质量为 0.10kg 的物体，以振幅1.0102m
作简谐运动，其最大加速度为 4.0ms2，求：
复摆 . mgl I
13
三 描述简谐振动的物理量(三要素)
1 振幅
A xmax
2 周期、频率
xAcots()
x xt图
A
o
Tt
T
A
2
A co (ts [T)]
周期 T 2π
频率
1
T 2π
圆频率 2π 2π
T.
注意
弹簧振子周期
T 2π m
k
周期和频率仅与振动系 统本身的物理性质有关
14
简谐运动中，x和 v x v xt曲线
第二篇 机械振动和机械波
.
1
.
2
教学基本要求
一 掌握描述简谐运动的各个物理量 （特别是相位）的物理意义及各量间的关系.
二 掌握描述简谐运动的旋转矢量法， 并会用于简谐运动规律的讨论和分析.
三 掌握简谐运动的基本特征，能建立
一维简谐运动的微分方程，能根据给定的初始
条件写出一维简谐运动的运动方程，并理解其
解: 取向下为x轴正向.
5s1
振动方程为 x=0.0141cos(5t+ π/4) (SI)
.
20
例4-2 如图所示，一边长为L的立方体木块浮于静
水中，浸入水中部分的高度为b。今用手将木块压
下去，放手让其开始运动。若忽略水对木块的黏性
阻力，并且水面开阔，不因木块运动而使水面高度
变化，证明木块作谐振动。
月相: 新月, 娥眉月, 上弦月, 满月, 下弦月, 残月等
娥眉月
上弦月
. 满月
下弦月16
3 相位 (位相,周相) t xA co ts ()
1） t (x ,v )存在一一对应的关系;
物理意义：可据以描述物体在任一时刻的运动状态.
2）相位在 0~2π内变化，质点无相同的运动状态；
相差 2nπ(n为整数)质点运动状态全同.（周期性）
之间不存在一一对应的 A
关系.
o
v
T
v T
t
A
2
xAcots ()
v A si n t ()
3 相位 (位相,周相) t
1） t (x ,v ) 存在一一对应的关系;
.
15
3 相位 (位相,周相) t xA co ts ()
1） t (x ,v )存在一一对应的关系;
物理意义：可据以描述物体在任一时刻的运动状态