第三章 空间力系-重心形心
力学第三章空间力系

第三章空间力系二、基本内容1. 基本概念1) 力在空间直角坐标轴的投影(a) 直接投影法:巳知力F 和直角坐标轴夹角a 、丫,则力F 在三个轴上的投 影分别为X = F cos aZ = Feos/(b) 间接投影法(即二次投影法):巳知力F 和夹角八°,则力F 在三个轴上的 投影分别为X = F sin/cos^9Y = F sin/sin 。
Z = F cos/2) 力矩的计算(a) 力对点之矩—、目的和要求能熟练地计算力在空间直角坐标轴上的投影。
熟练掌握力对点之矩与力对轴之矩的计算。
对空间力偶的性质及其作用效应有清晰的理解。
了解空间力系向一点简化的方法,明确空间力系合成的四种结果。
能正确地画出各种常见空间的约束反力。
会应用各种形式的空间力系平衡方程求解简单空间平衡问题。
对平行力系中心和重心应有清晰的概念,能熟练地应用坐标公式求物体 的重心。
1、2、3、4、5、6^ 7、在空间情况下力对点之矩为一个定位矢量,其定义为i j kM0(F) = rx F = x y z = (yZ - zY)i + (zX - xZ)j + (xY - yX)kX Y Zr = xi + yj + zk F = Xi+ Yj + Zk其中尸为力尸作用点的位置矢径(b)力对轴之矩在空间情况下力对轴之矩为一代数量,其大小等于此力在垂直于该轴的平面上的投影对该轴与此平面的交点之矩,其正负号按右手螺旋法则来确定,即M Z(F) = ±F u,h = +2AOAB在直角坐标条下有Mx (乃=yZ-zY M y (F)=zX-xZ M z (F) =xY-yX(c)力矩关系定理力对己知点之矩在通过该点的任意轴上的投影等于同一力对该轴之矩。
在直角坐标系下有Mo(F)^M x(F)i+My(F)j+M2(F)k(d)合力矩定理空间力系的合力对任一点之矩等于力系中各力对同一点之矩的矢量和,即Mo g)二 W, (F)空间力系的合力对任一轴(例如z轴)之矩等于力系中各力对同一轴之矩的代数和,即M z(F R)=ZM z(F)=Z(xY-yX)3)空间力偶及其等效条件(a)力偶矩矢空间力偶对刚体的作用效果决定于三个要素(力偶矩大小、力偶作用面方位及力偶的转向),它可用力偶矩矢肱表示。
工程力学 第三章 空间力系与重心重点

课时授课计划X=cosαcoscos与坐标轴间的夹角不易确定时,可把力上,得到力在三个坐标轴上的投影分别为sinsincos、、=+在坐标轴上的投影和力沿坐标轴的正交分矢量间的关系可表示为=X,=,,,沿向sin=向sincos沿各轴的分力为=-,称为轴向力,对点。
即力矩的大小为h=2的模等于三角形一致。
因此可得=分别为=X=的大小和方向都与矩心,轴的分力(在垂直于不能使静止的门绕表示力对作用线的距离。
因此,力==±=0)==+=zX-xZ对两个分力,其中=Fsin==-(AB+CD)=-F(l+a)cos==-BC=-Flcos==-?=yZ-zY=(l+a)(-Fcos=zX-xZ=0-(-l)(-Fcos=xY-yX=0-(l+a)(Fsin在三个坐标轴上的投影,即=yZ-zY=zX-xz=xY-yX===表示该力对点。
将力投影到通过对==2在轴上的投影,可用=与+=i+、、(4-8),四个力汇交于点=O, sin45°=0=O, cos45°cos30°cos45°cos30°=0=0, cos45°sin30°+oos30°==3.54kN=8.66kN为正值,说明图中所设。
工程力学 第三章 重心和形心

第三章 重心和形心
第十讲 重心和形心
《工程力学》
第十讲
重心和形心
目的要求:掌握平面组合图形形心的计算。
教学重点:分割法和负面积法计算形心。 教学难点:对计算形心公式的理解。
《工程力学》
§3-4 重心和形心
一、重心的概念:
1、重心的有关知识,在工程实践中是很有用的, 必须要加以掌握。 2、重力的概念:重力就是地球对物体的吸引力。 3、物体的重心:物体的重力的合力作用点称为 物体的重心。 无论物体怎样放置,重心总是一个确定点,重心 的位置保持不变。
《工程力学》
方法二(负面积法):
用负面积法求形心。计算简图如图。 A1=80mm×120mm=9600mm2 x1=40mm y1=60mm A2=-108mm×68mm=-7344mm2 x1=12mm+(80-12)mm/2=46mm y1=12mm+(120-12)mm/2=66mm
《工程力学》
《工程力学》
式中V=∑Vi。在均质重力场中,均质物体 的重心、质心和形心的位置重合。
《工程力学》
五、均质等厚薄板的重心(平面组合图形形心)公式:
令式中的∑Ai.xi=A.xc=Sy;
∑Ai.yi=A.yc=Sx 则Sy、Sx分别称为平面图形对y轴和x轴的静矩或截面一 次矩。
《工程力学》
六、物体重心位置的求法 :
1、对称法 凡是具有对称面、对称轴或对称中心的简 单形状的均质物体,其重心一定在它的对称 面、对称轴和对称中心上。对称法求重心的 应用见下图。
《工程力学》
《工程力学》
2、试验法对于形状复杂,不便于利用公式计
算的物体,常用试验法确定其 重心位置,常 用的试验法有悬挂法和称重法。 (1)、悬挂法 利用二力平衡公理,将物体用绳悬挂两次, 重心必定在两次绳延长线的交点上。 悬挂法 确定物体的重心方法见图
空间力系

第三章 空间力系一、空间汇交力系(一)空间汇交力系的合成 1.空间力在坐标轴上的投影 (1)一次投影法如图3-1所示,若已知力F 与三个坐标轴x,y,z 间的夹角分别为θ、β和γ,则力F 在三个坐标轴上的投影分别为⎪⎭⎪⎬⎫===γβθcos cos cos z y x F F F (3.1)图3-1相应的,若已知力F 的三个投影,可以求出力F 的大小和方向,即大小为 222z y x F F F F ++=(3.2)方向 ⎪⎪⎪⎭⎪⎪⎪⎬⎫===F FF F F F z yx γβθcos cos cos(3.3)(2)二次投影法如图3-2所示,若已知力F 与坐标轴Oxy 的仰角γ以及力F 在Oxy 平面上的投影xy F 与x 轴间的夹角ϕ,则力F 在三个坐标轴上的投影分别为γϕλϕγsin sin in cos in F F Fs F Fs F z y x ===,,图3-22.合力投影定理 合力在某轴上的投影,等于各分力在同一坐标轴上投影的代数和。
即∑=+++=xixn x x Rx FF F F F 21 同理 ∑∑==ziRz yi RyF F F F ,3.空间共点力系的合成空间共点力系可以合成为一个合力,该合力的作用线通过力系的公共作用点,合力的大小和方向为()()()222∑∑∑++=zyxR F F F F (3.4)()()()⎪⎪⎪⎭⎪⎪⎪⎬⎫===∑∑∑R z R R yRR xRF F F F F F k F j F i F ,cos ,cos ,cos(3.5)(二)空间汇交力系的平衡 1.空间汇交力系的平衡条件空间汇交力系平衡的充要条件是合力等于零,即()()()0222=++=∑∑∑zyxR F F F F2.空间汇交力系的平衡方程根据平衡条件,得到空间汇交力系的平衡方程为⎪⎪⎭⎪⎪⎬⎫===∑∑∑000y x zFFF(3.6)利用上述三个方程,可以求解3个未知量。
2、空间力系平衡、重心

解:取铰D 脱离体, 为 脱离体, 画受力图如 所示, 图b所示, 各力形成空 间汇交力系。 间汇交力系。
由ΣFx =0, cos60 sin60 60ºsin60º+ cos60 sin60 60ºsin60º= -NADcos60 sin60 + NBDcos60 sin60 =0 NAD=NAD 得 由ΣFy =0, Tcos60 +NCDcos60 -NADcos60 cos60 -NBDcos60 cos60 =0 cos60º+ cos60º- cos60ºcos60 cos60º- cos60ºcos60 cos60º=0 FG+NCD-0.5NAD-0.5NBD=0 得 由ΣFz =0, NADsin60 +NCDsin60 +NBDsin60 ―T sin60 ―FG=0 sin60 60º+ sin60 60º+ sin60 60º― sin60 60º― 866( 866+ 得 0.866(NAD+ NCD+ NBD)-(0.866+1)FG=0 联立求解得 NAD =NBD =31.55kN , NCD=1.55kN。 。
球形铰链
2、向心轴承 、
4、 、 向 心 推 力 轴 承
6、空间固定端 、
例 3 - 3 : 用三角架 ABCD 和绞车提升一重物如图 所示。 为一等边三角形, 所示。设ABC为一等边三角形,各杆及绳索均与水 平面成60 的角。 60º的角 30kN, kN,各杆均为二力 平面成60 的角。已知重物FG=30kN,各杆均为二力 滑轮大小不计。 杆 , 滑轮大小不计 。 试求重物匀速吊起时各杆所 受的力。 受的力。
[例] 已知: RC=100mm, RD=50mm,Px=466N, Py=352N, Pz=1400N。求: 例 平衡时(匀速转动)力Q=?和轴承A , B的约束反力?
《重心和形心》课件

在这份PPT课件中,我们将探讨重心和形心的概念、计算方法以及应用。这 两个概念不仅在物理领域中扮演关键角色,也在各个设计和优化领域中发挥 作用。
什么是重心和形心?
1 重心
物体所受重力的集中点,也是物体平衡的关键点。
2 形心
物体所有小部分形状、质量加权后得到的点,也是物体对应的简化物体的重心。
形心
• 物体质心位移估计 • 物流、仓储布局优化 • 结构设计优化
总结
1 重心和形心的重要
性
重心和形心都是描述物 体重量分布的重要点。
2 计算重心和形心要
考虑的因素
计算重心和形心需要应用
范围
重心和形心的应用涉及 到各个领域的设计和优 化。
如何计算重心和形心?
1 重心
2 形心
若物体均匀,则重心位于物体中心。若物 体不均匀,则可以通过挂钟实验或测量法 计算重心位置。
若物体有规则形状,则可以使用公式计算 形心位置。若物体没有规则形状,则可以 通过分割成若干个规则形状再计算每个形 状的形心位置后加权平均得到。
重心和形心的应用
重心
• 汽车平衡设计 • 物体挂钩位置确定 • 反击点位置确定
工程力学之空间力系和重心

工程力学4.1力在空间坐标轴上的投影4.2力对轴的矩·合力矩定理4.3 空间任意力系的平衡方程4.4 平行力系的中心物体的重心工程中常常存在着很多各力的作用线不在同一平面内的力系,即空间力系,空间力系是最一般的力系。
(a)图为空间汇交力系;(b)图为空间任意力系;在(b)图中去了风力即为空间平行力系。
迎面风力侧面风力b4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:力的三要素:大小、方向、作用点(线)大小:作用点:在物体的哪点就是哪点方向:①由α、β、g 三个方向角确定②由仰角θ与俯角ϕ来确定。
F F=4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:1、一次投影法(直接投影法)由图可知:cos ,cos ,cos x y z F X F F Y F F Z F αβg==⋅==⋅==⋅4.1.2力在空间坐标轴上的投影2、二次投影法(间接投影法)当力与各轴正向夹角不易确定时,可先将投影到xy 面上,然后再投影到x 、y 轴上,即Fsin cos cos cos cos x xy F X F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅sin sin sin cos sin y xy F Y F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅cos sin z F Z F F g θ==⋅=⋅ 4.2 力对轴的矩⋅合力矩定理一、力对轴的矩的概念与计算定义:()()2''z O xy xy m F m F F d OA B ==±⋅=∆的面积由于力和都不能使门转动,所以得出力与轴平行或相交时,力对轴之矩为零。
亦即力与轴共面时,力对轴之矩为零。
y F z F 力对轴的矩是力使刚体绕该轴转动效应的度量,是代数量,其大小等于在垂直于转轴的平面内的分量的大小和它与转轴间垂直距离的乘积,其正负号按右手规则确定,即大拇指方向与轴的正向一致的为正,反之为负。
4.2.2合力矩定理与平面力系情况类同,空间力系的合力矩定理为:12()()()()()z z z z n z i m R m F m F m F m F =+++=∑即:空间力系的合力对某一轴的矩,等于力系中所有各分力对同一轴的矩的代数和。
3章_空间力系与重心(200909)

y R
r1
r2 A1= R2/2 A2= r22/2
2
x
A3= - r12
4r r2 R 4R 2 0 3 2 3 2 yc=yiAi/Ai (R 2 r 2 ) ( r 2 ) 2 1 2
=3.99(cm)
偏心块重心在(0,3.99 cm)处
B、C形成等边三角形。若中线CD上距圆心为a的点M作用铅垂力Q =1500N。求:1、a=200mm时三脚对地面的约束力; 2、使圆桌不 致翻到的最大距离a。 z a P C FC
解:
C
Q A FA D M x B FB
y y a
A D M x
B
以圆桌为研究对象
例题3-1
解:
以圆桌为研究对象
第3章 空间力系的平衡与重心
Equilibrium of space force system & Center of gravity
3.1
绕任意轴变速转动。
空间力系的平衡
Equilibrium of space force system
若物体处于平衡状态,则物体不会沿任意方向变速移动和不会
z
不移
c
悬挂法 2、实验法 称重法 称重法: 笨重,且形状复杂
L A L2 h2
h
W c
FN
W
FN
mA=0
h
确定重心的实验法 悬挂法 所画两条直线的交点即为重心。 称重法:
以连杆为例。首先称出连杆的重量P,测出两孔的距离l。由于连杆 是前后、上下对称的,其重心一定在对称面、对称轴上,只需确定重 心C距孔中心的距离xC 。
若均质,
且薄壳、 板,
重心及截面的几何性质-工程力学-课件-附录
C
形心 x
反之,若图形对某轴静矩为零,该轴一定过形心。 2、平面图形若有对称轴,则形心在对称轴上。 (因为图形关于对称轴的静矩为 0。)
O
5
三、组合图形(组合截面)的静矩与形心
1.组合图形: 由简单图形(矩形、圆形等)组合而成的图形。
2.组合图形的静矩: 组合图形由A1、A2、An组成,其形心分别为(xC1,yC1) (xC2,yC2) (xCn,yCn)。
A A1 A2 An
i 1
n
组合截面的惯性矩等于各个组成部分(简单图形)对同一轴的 惯性矩之和。 对于任意截面,都可以利用积分求惯性矩。但计算繁琐。 由于组合截面由几个简单图形组成,如矩形,圆形。而矩形、 圆形关于自身对称轴的惯性矩已有现成公式,可以在此基础上用平 行移轴定理很方便的求出组合截面的惯性矩。
1
附录:重心及截面的几何性质
z C
§1
C2 C1 ∆W2 Ci ∆Wi W zC yC xC zi xi
重心•形心•静矩
利用合力矩定理: M y (W ) M y ( Wi ) W xC W i x i
∆W1
y
W 若物体在xi、yi、zi处单位体积的重
量为 ,称为重度。 ∆Wi=dVi
xc
x W
i
i
x
yi
xc
对于均质物体 为常量:
V
x dV
V
dV
yc
V
y dV
V
dV
y dV V
zc
V
z dV
V
dV
xc
x dV
第5节 物体的重心

第三章 空间力系
xC =
∑ Gi xi
i =1 n
n
;
∑ Gi
i =1
yC =
∑ Gi yi
i =1 n
n
∑ Gi
i =1
; zC =
∑ Gi zi
i =1 n
n
∑ Gi
i =1
第 5 节 物体的重心
第三章 空间力系
xC = yC = zC =
lim ∑ Gi xi
n→∞ i =1 n
n
G lim ∑ Gi yi
xC = 0mm
半径为 R 的大半圆
A1 = 1 πR 2 = 7200π 2 4 R = 160 mm y1 = 3π π
查表4-1 查表
第 5 节 物体的重心 r1 小半圆
第三章 空间力系
r2 小半圆
n
1 πr 2 = 612 .5π A2 = 2 1 4r1 46.67 y2 = − =− mm 3π π 2 A3 = −πr2 = −225π
第 5 节 物体的重心
第三章 空间力系
匀质、等厚度的薄板、簿壳结构的重心计算公式 匀质、等厚度的薄板、簿壳结构的重心计算公式 的薄板 重心
∫A xdA ; xC =
A
∫A ydA ; yC =
A
∫A zdA zC =
A
对于匀质线段(如等截面匀质细长曲杆、 对于匀质线段(如等截面匀质细长曲杆、细金属 丝等)结构的重心 重心计算公式 丝等)结构的重心计算公式
xC =
∑ Ai xi
i =1
n
A
i =0
9000×15 + 5850×127.5 = = 59.3mm 14850
第三章 空间力系-重心形心

Ai xi xC Ai
Ai yi yC Ai
<2>负面积法: 方法与分割法同,只是除去的面积看作负值。
第三章 空间力系
例1: 已知:Z 形截面,尺寸如图, 求:该截面的形心位置。
解:(1)组合法: 将该截面分割为三部分,
取Oxy直角坐标系,如图
x1 1.5 cm , y1 4.5 cm , A1 3.0 cm2
机械设备中高速旋转的构件,如电机转子、砂轮、飞轮等,都要求
它的重心位于转动轴线上,否则就会使机器产生剧烈的振动,甚至引 起破坏,造成事故。因此,重心与平衡稳定、安全生产有着密切的关
系。另一方面,有时也利用重心的偏移形成振源来制造振动大夯机、
混凝土捣实机等,从而满足了生产上的需要。因此,重心应为有关工 程技术人员所必备的知识之一。
yc
A y ;
A
第三章 空间力系
二、重心的求法:
1、简单几何形状物体的重心(对称法) 若均质物体有对称面,或对称轴,或对称中心,不难看出, 该物体的重心必相应地在这个对称面,或对称轴,或对称中 心上。 简单形状均质物体的重心就是它的几何形状的形心。
第三章 空间力系
2、实验法 如物体的形状复杂或源自量分布不均匀, A第三章 空间力系
上一页 返回目录 下一页
重心和形心的概念
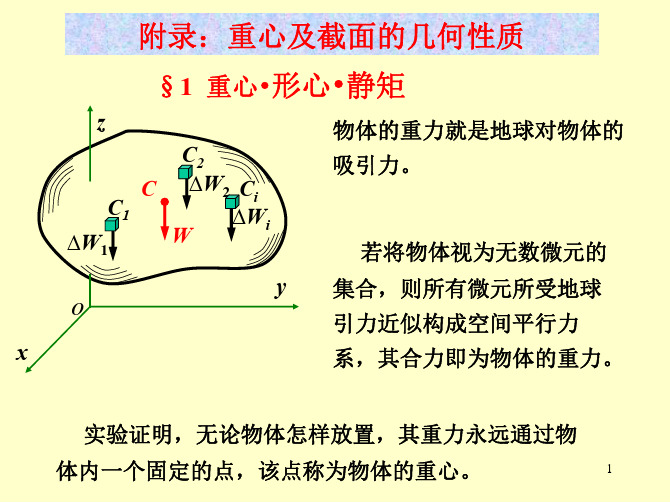
重心 任何物体都可视为由许多微小部分所组成,每一微小部分上都 作用一个指向地球中心的力,这些引力原本应是一空间汇交力系,但 由于地球的半径比所研究物体的尺寸大得多,故可认为这些力为一空 间平行力系(如图)。此力系的合力G为物体的重力,并称重力的作用 点C为物体的重心。 对刚体而言,物体的重心是一个不变的点。 形心 物体几何形状的中心点称为形心。
空间力系与重心

轴上的力和力矩平衡条件。只有当这六个方程同时满足时,空间一般力
系才处于平衡状态。
04
重心位置确定方法
几何法确定重心位置
01
02
03
悬挂法
将物体悬挂于一点,通过 测量悬线的长度和方向, 利用几何关系确定重心位 置。
支撑法
将物体支撑于两点,测量 支撑点的位置和支撑力的 大小,通过几何关系求解 重心位置。
度的基础。
06
重心在工程中应用举例
建筑结构稳定性分析
重心位置与结构稳定性
案例分析
在建筑设计中,通过调整结构布局和 构件尺寸,可以改变结构的重心位置, 从而提高结构的稳定性。
以高层建筑为例,通过优化结构布局 和构件设计,降低重心高度,提高结 构的整体稳定性。
地震作用下的重心影响
地震时,建筑物受到水平地震力的作 用,重心位置的高低直接影响结构的 抗震性能。
THANKS
感谢观看
航空航天领域应用
重心与飞行器稳定性
在航空航天领域,飞行器的重心位置对其稳定性和操控性 具有重要影响。合理设计重心位置可以提高飞行器的稳定 性和操控性。
重心与燃料消耗
飞行器的重心位置不仅影响稳定性和操控性,还影响燃料 消耗。通过优化重心位置可以降低飞行器的燃料消耗。
案例分析
以飞机设计为例,通过精确计算和调整机身、机翼等部件 的质量和布局,实现重心的合理分布,提高飞机的稳定性 和经济性。
力多边形封闭
如果将各力矢量按照一定顺序首 尾相接,可以形成一个封闭的力 多边形,这也是空间汇交力系平 衡的一个必要条件。
空间平行力系平衡条件
各力在任意轴上的投影之和为零
对于空间平行力系,所有力在任意选定的轴上的投影之和必须为零,这是平衡 的一个必要条件。
空间力系3

Fy 0 力
Fz 0
偶 系
空
Mx 0 间
My 0
平 行
Mz 0
力 系
Fx 0 My 0 Mz 0
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第三章 空间力系
例题六 不计重量的正方形薄板,由六根直杆支
第 五 节
持如图所示 .假设这六根杆都可以看作两力杆 ,求
yc
A ydA A
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第三章 空间力系
四、确定物体重心的方法
(1) 利用对称性
第 六 节
重
C
心
C C
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第三章 空间力系
四、确定物体重心的方法
半径为R,顶角为2
的均质圆弧
(2) 积分法
第 六
解:由于对称关系,该圆弧重心必在Ox 轴上,即yC=0。
a
2 2
S3
S4
2 2
S5
S6
0
衡 方 程
㊁ My(F) = 0
a
2 2
S3
S6
0
㊂ Mz(F) = 0
2 2
aS3
S5 0
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
第三章
例题六
第
五
节
S1 = S6 = - P
空
间
任 意
S2 = S3 = 2 P
力
系
的 平
S4= P
衡
方
03-理论力学-第一部分静力学第三章空间力系

X
Y
Z
( yZ zY )i (zX xZ) j (xY yX )k
2 力对轴的矩
力使物体绕某一轴转动效应的度 量,称为力对该轴的矩。
16
力对轴的矩的定 义 M z (F ) MO (Fxy )
力系简化的计算 计算主矢的大小和方向
FRx X , FRy Y , FRz Z
FR FRx2 FRy2 FRz2
cos FRx ,
FR
cos FRy ,
FR
cos FRz
FR
计算主矩的大小和方向
MOx M x (F ) , MOy M y (F ) ,
MOz M z (F )
与 z 轴共面
18
力对轴的矩的解析式
先看对z轴的矩:
M z (F ) MO (Fxy )
M O (Fy ) MO (Fx )
Fy x y Fx
xY yX
类似地,有:
M x (F) yZ zY M y (F ) zX xZ M z (F ) xY yX
Fy
Fx
Fxy
力对轴的矩的 解析表达式
3
§3 - 1 空间汇交力系 本节的主要内容有:
★ 空间力的投影;
★空间汇交力系的合成与平衡。
1 力在直角坐标轴上的投影和力沿直角坐标轴的
分解
(1) ■直接投影法
X F cos
Y F cos
Z F cos
也称为一次投影法
4
■间接投影法
Fx y F sin X Fxy cos F sin cos Y Fxy sin F sin sin
重心与形心

间有如下的关系:
Sx=yCA , Sy=xCA
由上式还可以得到下面的重要结论:若某轴通过平面图形的形 心,则平面图形对该轴的静矩必为零;反之,若平面图形对某轴的 静矩为零,则该轴必通过平面图形的形心。
目录
空间力系\重心和形心
1.5 确定重心和形心位置的方法
1. 利用对称性
图所示,则zC=0, xC和yC分别为
xC
xiAi , A
yC
yi Ai A
或
xdA
yd A
xC
Aห้องสมุดไป่ตู้
A
, yC
A
A
目录
空间力系\重心和形心
若物体为均质等截面细杆(如图)或 曲线,则其形心的坐标公式为
xC
xili , l
yC
yili , l
或
zC
zi li l
xdl
yd l
xC
xiVi , V
yC
yiVi , V
zC
ziVi V
如令各微小部分的体积趋近于零,则有
xdV
yd V
zdV
xC
V
V
,
yC
V
V
,
zC
V
V
由此可见,均质物体的重心位置完全取决于物体的几何形状而
与物体的重量无关。因此,均质物体的重心也称形心。
目录
空间力系\重心和形心
工程实际中常采用薄壳结构,例 如厂房的双曲顶壳、薄壁容器、飞机 机翼等。由于薄壳的厚度相等,并较 其他二个方向的尺寸小得多,若材料 是均质的,可以把它看成是均质曲面 如图所示,则其形心坐标公式为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、实验法
如物体的形状复杂或质量分布不均匀,
A
其重心常由实验来确定。
<1>悬挂法 对于形状复杂的薄平板,求
形心位置时,可将板悬挂于任一点A,根据
B
二力平衡公理,板的重力与绳的张力必在
同一直线上,故形心一定在铅垂的挂绳延
长线AB上;重复施用上述方法,将板挂于
A
D点,可得DE线。显而易见,平板的重心
x2 0.5cm , y2 3.0 cm , A2 4.0 cm2
x3 1.5 cm , y3 0.5 cm , A3 3.0 cm2
xC
Ai xi 3 (1.5) 4 0.5 31.5 0.2 cm
A
343
yC
Ai yi 3 (4.5) 4 3 3 0.5 2.7 cm
xdV
xC
xiVi V
V
V
ydV
yC
yiVi V
V
V
zdV
zC
ziVi V
V
ቤተ መጻሕፍቲ ባይዱ
V
第三章 空间力系
3)物体均质薄板时重心坐标的计算公式(即平面图形 的形心)
xc
A x ; A
yc
A
A
y ;
记Sy=∑xi△Ai= xcA,则Sy称为图形对y 轴的静矩 Sx=∑yi△Ai= ∑yi△Ai= ycA,Sx称为图 形对x轴的静矩
结论 :
若某轴通过图形的形心,则图形对该轴的静矩 必为零;反之,若图形对某轴的静矩为零, 则该轴必通过图形的形心。
第三章 空间力系
二、重心的求法:
1、简单几何形状物体的重心(对称法) 若均质物体有对称面,或对称轴,或对称中心,不难看出,
该物体的重心必相应地在这个对称面,或对称轴,或对称中 心上。 简单形状均质物体的重心就是它的几何形状的形心。
x2=20mm , y2=8mm , A2=16 × 40=640mm2
则有:
xC
xi Ai A1x1 A2x2 14.21mm
Ai
A1 A2
yC
yi Ai A1 y1 A2 y2 25.37mm
Ai
A1 A2
第三章 空间力系
(2)负面积法
将该图形看成是一个大矩形I减去一个小矩
即为AB和DE的交线C。
C
D
B
E
第三章 空间力系
<2>称重法 称出物体的重量G
固定物体,一端支于固 定点A,另一端支于秤上 量出两支点间的水平距离l
读出磅秤上的读数FB
第三章 空间力系
G
h FB l G
3、组合法:(分割法或负面积法)
一般针对均质平板物体而言 <1>分割法:
若物体可以划分为形状简单的几个部分,每个部分的面积 和重心位置都属已知,则整个物体的重心易于求得。
xC
Ai xi Ai
yC
Ai yi Ai
<2>负面积法: 方法与分割法同,只是除去的面积看作负值。
第三章 空间力系
例1: 已知:Z 形截面,尺寸如图, 求:该截面的形心位置。
解:(1)组合法: 将该截面分割为三部分,
A1 A2
取Oxy直角坐标系,如图
A3
x1 1.5cm , y1 4.5cm , A1 3.0 cm2
A
343
第三章 空间力系
例2 试求图示平面图形的形心位置(单位:mm)。
第三章 空间力系
解:该题可用两种方法求解
(1)分割法
如图所示将该图形分解成两个矩形I和II, 它们的形心位置分别为C 1(xl,yl)、
C2 (x2,y2)。其面积分别为A1和A2。得
x1=10mm , y1=10mm , A1=20 × 44=880mm2
形II。它们的形心位置分别为C 1(xl,yl)、 C2 (x2,y2)。其面积分别为A1和A2。根据图 形分析可知,
x1=20mm , y1=30mm , A1=40 × 60=2400mm2
x2=30mm , y2=38mm , A2=20 × 44=880mm2
则有:
xC
xi Ai A1x1 A2x2 14.21mm
第三章 空间力系
1)重心坐标的一般计算公式
如图所示,设物体重力作用点的坐标为G(xc,yc,zc), 得物体的重心坐标公式为
xC
Gi xi Gi
Gi xi G
yC
Gi yi Gi
Gi yi G
zC
Gi zi Gi
Gi zi G
第三章 空间力系
2)物体均质时重心坐标的计算公式 对于均质物体,若用ρ表示其密度,△V表示微体积,则得 物体的重心坐标公式为
第三章 空间力系
上一页 返回目录 下一页
重心和形心的概念
重心 任何物体都可视为由许多微小部分所组成,每一微小部分上都 作用一个指向地球中心的力,这些引力原本应是一空间汇交力系,但 由于地球的半径比所研究物体的尺寸大得多,故可认为这些力为一空 间平行力系(如图)。此力系的合力G为物体的重力,并称重力的作用 点C为物体的重心。 对刚体而言,物体的重心是一个不变的点。 形心 物体几何形状的中心点称为形心。 均质规则的刚体,其重心和形心在同一点上
Ai
A1 A2
yC
yi Ai A1 y1 A2 y2 25.37mm
Ai
A1 A2
第三章 空间力系
§3-5 物体的重心和形心
引入: 重力:由于地球的吸引而使物体受到的力,叫做重力。 方向:总是竖直向下。
第三章 空间力系
当我们用两轮手推车推重物时,只有重物的重心正好与车轮轴线在 同一铅垂面内时,才能比较省力。 起重机用起重物时,吊钩必须位于被吊物体重心的上方,才能使起 吊过程中保持物体的平衡稳定。 机械设备中高速旋转的构件,如电机转子、砂轮、飞轮等,都要求 它的重心位于转动轴线上,否则就会使机器产生剧烈的振动,甚至引 起破坏,造成事故。因此,重心与平衡稳定、安全生产有着密切的关 系。另一方面,有时也利用重心的偏移形成振源来制造振动大夯机、 混凝土捣实机等,从而满足了生产上的需要。因此,重心应为有关工 程技术人员所必备的知识之一。
