矩阵和行列式初步

合集下载

矩阵与行列式算法初步知识点

矩阵与行列式算法初步知识点矩阵与行列式是线性代数的基础概念之一、矩阵可以看作是一个二维数组，具有行和列的属性。

矩阵最常见的应用是线性方程组的求解。

例如，对于一个m×n的矩阵A和一个n×1的向量x，可以通过矩阵乘法Ax=b来求解线性方程组。

行列式是矩阵的一个重要属性，可以用来判断矩阵是否可逆。

一个矩阵的行列式为0表示该矩阵不可逆，否则可逆。

行列式还可以用于求解特征值和特征向量。

特征值和特征向量是矩阵在线性变换下的不变性质，对于很多机器学习和深度学习算法都有重要的应用。

算法是计算机科学中的基础概念，是一种解决问题的方法或步骤。

算法设计的核心目标是解决问题的效率和正确性。

常见的算法设计技巧包括递归、分治、动态规划等。

常见的算法包括排序、图算法等。

排序算法可以将一组数据按照一定的规则进行排序，常见的排序算法有冒泡排序、选择排序、插入排序、快速排序等。

算法用于在一组数据中查找目标元素，常见的算法有线性、二分等。

图算法用于解决图结构相关的问题，常见的图算法有深度优先、广度优先、最短路径算法等。

在实际应用中，矩阵与行列式经常用于数据表示和运算。

例如，在机器学习中，数据通常以矩阵的形式进行表示，通过矩阵运算可以进行特征提取、模型训练等操作。

行列式的性质可以帮助我们优化计算过程，例如通过LU分解来求解线性方程组，可以减少计算量。

在计算机图形学中，矩阵与行列式用于表示和变换物体的位置和形态。

通过矩阵运算可以实现物体的平移、旋转、缩放等操作。

算法的设计与分析是计算机科学中的重要内容。

好的算法可以大大提高程序的执行效率，减少资源的使用。

算法的设计过程包括问题分析、算法设计、编码实现和性能评估等步骤。

在设计算法时，我们要考虑问题的规模、输入数据的特征以及算法的复杂度等因素。

通常，我们希望算法在求解问题时具有较高的时间和空间效率，并且给出符合问题要求的正确结果。

总之，矩阵与行列式、算法初步是计算机科学和线性代数中的重要知识点。

线性代数

第1章矩阵与行列式
>> AB=A*B 运行结果： AB = 6 2 6 1 8 -1 >> D=6*A 运行结果： D= 18 6 12 6 6 12
-2 0 2
6 12 18
第1章矩阵与行列式
>> sym c; >> cA=c*A 运行结果： cA = [ 3*c, c, c] [ 2*c, c, 2*c] [ c, 2*c, 3*c] >> F=A' 运行结果： F= 3 2 1 1 1 2
第1章矩阵与行列式
【矩阵与行列式简介】
在计算机日益发展的今天，线性代数起着越来越重要的作用。线性代数起源于解线性方程组的问题，而利用矩阵来求解线性方程组的Gauss消元法至今仍是十分有效的计算机求解线性方程组的方法。矩阵是数学研究和应用的一个重要工具，利用矩阵的运算及初等变换可以解决求解线性方程组等问题。特殊的矩阵方阵的数字特征之一是方阵的行列式，使用行列式可以描述方阵的一些重要的性质。通过计算行列式可求逆矩阵，n个
第1章矩阵与行列式
>>C=A(2:end,[1,4]) 运行结果： C= 5 8 9 12 13 16 3．>> A=[0 1 2;1 1 4;2 -1 0]; >>E=eye(3); >>B=[A,E] 运行结果： B= 0 1 2 1 1 1 4 0 2 -1 0 0
0 1 0
0 0 1
第1章矩阵与行列式
；
2 x1 4 x 2 x3 x 4 5 （2） x1 2 x2 2 x3 x 4 4 ． x 2x x 2x 1 2 3 4 1

202110715710矩阵和行列式初步(格致中学讲义)

第九章矩阵和行列式初步格致中学第一课时 9.1 矩阵的概念（1）[教学目标]1、了解矩阵的产生背景，并会用矩阵形式表示一些实际问题；2、了解矩阵、行向量、列向量、方矩阵、零矩阵、单位矩阵等概念；3、理解同阶矩阵、相等的矩阵等概念；4、理解线性方程组与系数矩阵及其增广矩阵之间的转化。

[教学重点]1、与矩阵有关的概念；2、线性方程组的系数矩阵及增广矩阵的概念。

[教学难点]学习矩阵的目的。

[教学过程]一、情境设置、引入：引例1：已知向量()1,3OP =，如果把的坐标排成一列，可简记为13⎛⎫⎪⎝⎭；引例2：2008我们可将上表奖牌数简记为：512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭；引例3：将方程组231324244x y mz x y z x y nz ++=⎧⎪-+=⎨⎪+-=⎩中未知数z y x ,,的系数按原来的次序排列，可简记为2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭；若将常数项增加进去，则可简记为：2313242414m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭。

二、概念讲解：1、上述形如13⎛⎫ ⎪⎝⎭、512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭、2313242414m n ⎛⎫⎪- ⎪ ⎪-⎝⎭这样的矩形数表叫做矩阵。

2、在矩阵中，水平方向排列的数组成的向量()12,,n a a a ⋅⋅⋅称为行向量；垂直方向排列的数组成的向量12n b b b ⎛⎫ ⎪ ⎪ ⎪⋅⋅⋅ ⎪⎝⎭称为列向量；由m 个行向量与n 个列向量组成的矩阵称为m n ⨯阶矩阵，m n ⨯阶矩阵可记做m n A ⨯，如矩阵13⎛⎫ ⎪⎝⎭为21⨯阶矩阵，可记做21A ⨯；矩阵512128363836232128⎛⎫⎪⎪⎪⎝⎭为33⨯阶矩阵，可记做33A ⨯。

有时矩阵也可用A 、B 等字母表示。

3、矩阵中的每一个数叫做矩阵的元素，在一个m n ⨯阶矩阵m n A ⨯中的第i （i m ≤）行第j（j n ≤）列数可用字母ij a 表示，如矩阵512128363836232128⎛⎫⎪⎪ ⎪⎝⎭第3行第2个数为3221a =。

沪教版(上海)高二数学上册第9章矩阵和行列式初步复习课件

5 t
,且AB
O,则
3 5 3
t
.
3) 已知
A
2 3
31, f ( x) x2 5 x 3,
则 f (A)
.
4) 若n阶矩阵A满足方程A2 2 A 3E 0,则
A1
.
3 0 0
5) 设A 0 1 0,则An
.
0 0 4
0 0 2
6) 矩阵A 0 5 0的逆矩阵A1 8 0 0
1 0 1
注：对一般的 n 阶方阵 A，我们常常用归纳的方
法求 An 。
例2 解：
0 1 0
设
A
1
0
0 ，求 A2004 2 A2 .
0 0 1
0 1 0 0 1 0
因为
A2
1
0
0 1 0
0
0 0 1 0 0 1
＝
1 0
0 1
00 ，
0 0 1
故 A4 E，从而 A2004 ( A4 )501 E 501 E .
6 分块矩阵
矩阵的分块，主要目的在于简化运算及便于论证。分块矩阵的运算规则与普通矩阵的运算规则类似。
典型例题
一、矩阵的运算二、有关逆矩阵的运算及证明三、矩阵方程及其求解方法
一、矩阵的运算
矩阵运算有其特殊性，若能灵活地运用矩阵的运算性质及运算规律，可极大地提高运算效率。
例1
设α (1，0， 1)T，A ααT，求 An .
故 A(C B)T B. 从而
1 1 0 1 0 0
A B[(C B)T ]1 0 1 1 2 1 0
0 0 1 1 2 1
3 1 0 3 3 1
1 2 1

矩阵和行列式的基本概念

矩阵和行列式的基本概念矩阵和行列式是线性代数中的基本概念，它们在各个领域有着广泛的应用。

本文将介绍矩阵和行列式的基本定义、性质和应用。

1. 矩阵的基本定义矩阵是一个按照行和列排列的矩形数表。

具体而言，一个m行n列的矩阵A可以表示为：A = [a₁₁ a₁₂ a₁₃ …… a₁ₙ][a₂₁ a₂₂ a₂₃ …… a₂ₙ][…… …… …… …… ][aₙ₁ aₙ₂ aₙ₃ …… aₙₙ]其中，aᵢₙ表示矩阵A的第i行第j列的元素。

2. 矩阵的运算2.1 矩阵的加法和减法若A和B是两个相同大小的矩阵，即有相同的行数和列数，则它们的和与差定义为：A +B = [a₁₁ + b₁₁ a₁₂ + b₁₂ a₁₃ + b₁₃ …… a₁ₙ + b₁ₙ][a₂₁ + b₂₁ a₂₂ + b₂₂ a₂₃ + b₂₃ …… a₂ₙ + b₂ₙ] […… …… …… …… ][aₙ₁ + bₙ₁ aₙ₂ + bₙ₂ aₙ₃ + bₙ₃ …… aₙₙ + bₙₙ]A -B = [a₁₁ - b₁₁ a₁₂ - b₁₂ a₁₃ - b₁₃ …… a₁ₙ - b₁ₙ][a₂₁ - b₂₁ a₂₂ - b₂₂ a₂₃ - b₂₃ …… a₂ₙ - b₂ₙ] […… …… …… …… ][aₙ₁ - bₙ₁ aₙ₂ - bₙ₂ aₙ₃ - bₙ₃ …… aₙₙ - bₙₙ]2.2 矩阵的数乘若A是一个矩阵，k是一个数，则kA定义为：kA = [ka₁₁ ka₁₂ ka₁₃ …… ka₁ₙ][ka₂₁ ka₂₂ ka₂₃ …… ka₂ₙ][…… …… …… ][kaₙ₁ kaₙ₂ kaₙ₃ …… kaₙₙ]2.3 矩阵的乘法若A是一个m行n列的矩阵，B是一个n行p列的矩阵，则它们的乘积AB定义为：AB = [c₁₁ c₁₂ c₁₃ …… c₁ₙ][c₂₁ c₂₂ c₂₃ …… c₂ₙ][…… …… …… ][cₙ₁ cₙ₂ cₙ₃ …… cₙₙ]其中，cᵢₙ表示AB的第i行第j列的元素，其计算方式为cᵢₙ =aᵢ₁b₁ₙ + aᵢ₂b₂ₙ + … + aᵢₙbₙₙ。

第一章矩阵与行列式

第一章矩阵与行列式第一节矩阵及其运算一、矩阵的概念人们在从事经济活动、科学研究、社会调查时, 会获得许多重要的数据资料, 将这些数据排成一个矩形的数表111212122212n nm m mn a a a a a a a a a L L M M M L以便于进行储存、运算和分析, 这种矩形的数表就是矩阵.定义1 由m n ⨯个数()1,2,,;1,2,,ij a i m j n ==L L 排成m 行n 列的矩形数表111212122212n n m m mn a a a a a a a a a ⎛⎫⎪ ⎪⎪⎪⎝⎭L L M M M L称为m 行n 列矩阵, 简称为m n ⨯矩阵, 其中ij a 称为矩阵的位于第i 行、第j 列的元素. 通常, 我们用大写字母,,A B L 表示矩阵. 例如, 记111212122212.n n m m mn a a a a a a A a a a ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭L L M M M L其中小括号“()” 也可用方括号“[]”代替. 有时, 矩阵也简记为()ij m nA a ⨯=或()ij A a =. 特别地, 当m n =时, 称A 为n 阶矩阵或n 阶方阵, 其中一阶方阵()a 是一个数, 括号可略去.元素全为实数的矩阵称为实矩阵, 元素全为复数的矩阵称为复矩阵. 本书主要在实数范围内讨论问题.对于由n 个未知量、m 个方程组成的线性方程组：11112211211222221122,,.n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩L L L L L L L L L L L L L (1.1.1) 称矩阵A 11121121222212n n m m mn m a a a b a a a b a a a b ⎛⎫⎪⎪= ⎪⎪⎝⎭LL M M M M L(1.1.2)为线性方程组(1.1.1)的增广矩阵；称矩阵A =111212122212n n m m mn a a a a a a a a a ⎛⎫⎪⎪⎪⎪⎝⎭L L M M M L(1.1.3) 为线性方程组(1.1.1)的系数矩阵；矩阵12m b bB b ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭M (1.1.4)称为线性方程组(1.1.1)的常数项矩阵.显然, 线性方程组(1.1.1)由矩阵(1.1.2)完全地确定.下面介绍一些特殊的矩阵.(1) 零矩阵元素都是零的矩阵称为零矩阵, 记为O . (2) 列矩阵、行矩阵在矩阵A 中, 如果1n =, 则11211m a a A a ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭M , 称这种只有一列的矩阵为列矩阵；同样, 如果1m =, 则()11121n A a a a =L ,称这种只有一行的矩阵为行矩阵.我们也将列矩阵和行矩阵分别称为列向量和行向量. 列向量和行向量统称为向量. 向量的元素称为分量, 有n 个分量的向量称为n 维向量. 矩阵与向量有密切的联系, 矩阵()ij m nA a ⨯=可以看成由n 个m 维列向量12,1,2,,j j mj a a j n a ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭L M 组成, 也可以看成由m 个n 维行向量()12,1,2,,i i in a a a i m =LL 组成.(3) 负矩阵如果矩阵()ij m nA a ⨯=, 则()ij m nA a ⨯-=-称为矩阵A 的负矩阵.(4) 行阶梯形矩阵如果矩阵每一行的第一个非零元素所在的列中, 其下方元素全为零, 则称此矩阵为行阶梯形矩阵. 例如矩阵10234023450056700018A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭, 12102032210003100000B --⎛⎫ ⎪- ⎪= ⎪- ⎪⎝⎭均为行阶梯形矩阵, 而矩阵10232023450056700418C ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 则不是行阶梯形矩阵.(5) 行最简形矩阵如果行阶梯形矩阵中, 非零行的第一个非零元素均为1, 且其所在列的其余元素均为0, 则称此矩阵为行最简形矩阵. 例如, 矩阵1060301205000110000⎛⎫⎪⎪⎪- ⎪⎝⎭是行最简形矩阵.(6) 上(下)三角矩阵 n 阶方阵的左上角到右下角元素的连线称为主对角线, 左下角到右上角元素的连线称为次(副)对角线. 如果方阵的主对角线下(上)方元素全为0, 则称此矩阵为上(下)三角矩阵. 矩阵11121222000n n nn a a a a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭L L M M M L 为上三角矩阵, 矩阵11212212000n n nn a a a a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭LL M M M L 为下三角矩阵.(7) 对角矩阵如果方阵中除主对角线上的元素外, 其余元素全为0, 则称此矩阵为对角矩阵. 例如, 矩阵12000000n λλλ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭L L M M M L 为对角矩阵.(8) 单位矩阵在对角矩阵中, 如果()11,2,,i i n λ≡=L , 即为 100010001⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭L L M M M L, 则称此矩阵为单位矩阵. 单位矩阵一般用E 或I 表示.定义2 如果两个矩阵()ij A a =, ()ij B b =的行数相同、列数也相同, 则称矩阵A 与B 为同型矩阵.定义3 如果两个同型矩阵m n A ⨯, m n B ⨯的对应元素均相等, 即 ()1,2,,;1,2,,ij ij a b i m j n ===L L , 则称矩阵A 与B 相等, 记作A B =.二、矩阵的运算 1. 矩阵的加法定义4 由两个同型矩阵()m n ij m nA a ⨯⨯=, ()m n ij m nB b ⨯⨯=对应元素的和,即ij ij a b +()1,2,,;1,2,,i m j n ==L L 组成的m n ⨯矩阵称为矩阵A 与B 的和,记作A B +, 即111112121121212222221122n n n n m m m m mn mn a b a b a b a b a b a b A B a b a b a b +++⎛⎫ ⎪+++ ⎪+= ⎪ ⎪+++⎝⎭L L M M M L . 由此定义及负矩阵的概念, 我们定义矩阵A 与B 的差为()A B A B -=+-.注只有同型矩阵才能相加(减). 2. 数与矩阵相乘(简称数乘)定义5 数k 乘矩阵A 的每一个元素所得到的矩阵称为数k 与矩阵A 的积, 记作kA , 即111212122212.n n m m mn ka ka ka ka ka ka kA ka ka ka ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭L L M M M L 矩阵的加法和数乘统称为矩阵的线性运算, 其满足如下性质：(1) A B B A +=+； (2) ()()A B C A B C ++=++； (3) ()()A A λμλμ=；(4) ()A A A λμλμ+=+； (5) ()A B A B λλλ+=+； (6) A O A +=； (7) 1A A =；(8) ()A A O +-=.上面的λ, μ都是任意常数.例1 设112034A -⎛⎫= ⎪⎝⎭, 403123B -⎛⎫= ⎪--⎝⎭, 求A B +和23A B -.解14102(3)5110(1)3(2)43117A B +-++---⎛⎫⎛⎫+== ⎪ ⎪+-+-+-⎝⎭⎝⎭；224120923068369A B --⎛⎫⎛⎫-=- ⎪ ⎪--⎝⎭⎝⎭102133121--⎛⎫= ⎪-⎝⎭.3. 矩阵与矩阵相乘(矩阵的乘法)n 个变量12,,,n x x x L 与m 个变量12,,,m y y y L 之间的关系式11111221221122221122,,.n n n nm m m mn n y a x a x a x y a x a x a x y a x a x a x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩L L L L L L L L L L L L (1.1.5) 表示一个从变量12,,,n x x x L 到变量12,,,m y y y L 的线性变换.设有两个线性变换11111221332211222233,.z a y a y a y z a y a y a y =++⎧⎨=++⎩ (1.1.6)和111112222112223311322,,.y b x b x y b x b x y b x b x =+⎧⎪=+⎨⎪=+⎩ (1.1.7) 若要求出从12,x x 到12,z z 的线性变换, 可将(1.1.7)代入(1.1.6), 得 111111221133111112122213322221112221233112112222223322()(),()().z a b a b a b x a b a b a b x z a b a b a b x a b a b a b x =+++++⎧⎨=+++++⎩ (1.1.8) 线性变换(1.1.8)可看作是先作线性变换(1.1.7)、再作线性变换(1.1.6)的结果, 我们称线性变换(1.1.8)为线性变换(1.1.6)与(1.1.7)的乘积, 相应地, 我们将线性变换(1.1.8)所对应的矩阵定义为(1.1.6)与(1.1.7)所对应的矩阵的乘积,即 111211121321222122233132bb a a a b b a a a b b ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭111112211331111212221332211122212331211222222332.a b a b a b a b a b a b a b a b a b a b a b a b ++++⎛⎫= ⎪++++⎝⎭一般地, 我们有：定义6 设有矩阵()ij m sA a ⨯=和()ij s nB b ⨯=, 规定矩阵A 与B 的乘积是一个m n ⨯矩阵()ij m nC c ⨯=, 记为C AB =. 其中11221,1,2,,;1,2,,.ij i j i j is sjsik kj k C a b a b a b a b i m j n ==+++===∑L L L注只有当前一个矩阵的列数等于后一个矩阵的行数时, 两个矩阵才能相乘, 且乘积矩阵C 中的元素ij C 就是A 的第i 行与B 的第j 列的对应元素乘积的和.例2 设201131012A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭, 100221B ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求AB .解AB 201101310201221-⎛⎫⎛⎫ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭2100(1)22002(1)11130121032110110(2)20012(2)1⨯+⨯+-⨯⨯+⨯+-⨯⎛⎫ ⎪=-⨯+⨯+⨯-⨯+⨯+⨯ ⎪ ⎪⨯+⨯+-⨯⨯+⨯+-⨯⎝⎭ 0117.40-⎛⎫ ⎪= ⎪ ⎪-⎝⎭例3 求矩阵1111A -⎛⎫= ⎪-⎝⎭与1111B --⎛⎫= ⎪⎝⎭的乘积AB 及BA .解111122;111122AB ---⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭111100.111100BA ---⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭由以上例题可以看出矩阵乘法与数的乘法有两点显著不同：(1) 矩阵乘法不满足交换律：AB 与BA 未必同时有意义(如例2, BA 没有意义)；即使都有意义也未必相等(如例3). 因此为明确起见, 称AB 为A 左乘B , 或B 右乘A . 只有在一些特殊情况下才有AB BA =, 这时称A 与B 是乘法可交换的. 容易验证数量矩阵aE 与任何同阶方阵A 乘法可交换, 即()().aE A A aE aA ==(2) 矩阵乘法不满足消去律：由AB O =不能得出A O =或B O =(如例3), 即,A O B O ≠≠但AB 有可能为O .有了矩阵相等和乘法的定义, 我们可以把线性方程组(1.1.1)写成矩阵形式：AX B =, 其中A =111212122212n n m m mn a a a a a a a a a ⎛⎫⎪⎪ ⎪⎪⎝⎭L L M M M L, 1122,.n m x b x b X B x b ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭M M若B O =, 则称(1.1.1)为齐次线性方程组；若B O ≠, 则称(1.1.1)为非齐次线性方程组. 也可以把线性变换(1.1.5)写成矩阵形式：Y AX =, 其中12,m y y Y y ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭MA 与X 同上所设.可以证明矩阵的乘法有下列性质： (1) ()()AB C A BC =；(2) ()A B C AB AC +=+；()B C A BA CA +=+； (3) ()()()AB A B A B λλλ==, λ为任意常数； (4) ()().m m n m n m n n aE A aA A aE ⨯⨯⨯==定义7 设A 为n 阶方阵, k 为正整数, 称k 个A 的连乘积为方阵A 的k次幂, 记作k A , 即.k kA AA A =L 14243当,k l 都为正整数时, 由矩阵乘法的性质, 得(1) k l k l A A A +=；(2) ()lk kl A A =.注由于矩阵乘法不满足交换律, 所以, 一般地()kk k AB A B ≠. 例4 设1101A ⎛⎫= ⎪⎝⎭, 求nA (n 为正整数).解1101A ⎛⎫= ⎪⎝⎭；2111112010101A ⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪⎝⎭⎝⎭⎝⎭； 3121113010101A ⎛⎫⎛⎫⎛⎫==⎪⎪ ⎪⎝⎭⎝⎭⎝⎭；一般地, 有101n n A ⎛⎫= ⎪⎝⎭.其正确性可由数学归纳法证得, 证明略.4. 矩阵的转置定义8 把m n ⨯矩阵A 的行与列互换得到的一个n m ⨯矩阵, 称为A 的转置矩阵, 记作T A . 例如, 矩阵120311A ⎛⎫= ⎪-⎝⎭的转置矩阵为1321.01T A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭矩阵的转置也是一种运算, 满足下述运算规律：(1) ()TT A A = ；(2) ()TT T A B A B +=+ ；(3) ()TT A A λλ=, λ为一个数；(4) ()TT T AB B A = .例5 已知201132A -⎛⎫= ⎪⎝⎭, 171423201B -⎛⎫⎪= ⎪ ⎪⎝⎭,求().T AB解法1 因为1712010143423132171310201AB -⎛⎫--⎛⎫⎛⎫ ⎪== ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭,所以()0171413310TAB ⎛⎫ ⎪= ⎪ ⎪-⎝⎭. 解法214221017()72003141313112310T T T AB B A ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪=== ⎪⎪ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭.定义9 设A 为n 阶方阵, 如果满足T A A =, 即 ,,1,2,,.ij ji a a i j n ==L则称A 为对称矩阵. 对称矩阵的特点是：关于主对角线对称的对应元素相等.定义10 设A 为n 阶方阵, 如果满足T A A =-, 即ij ji a a =-, ,1,2,,.i j n =L则称A 为反对称矩阵. 反对称矩阵的特点是：主对角线上的元素全为0, 其余关于主对角线对称的对应元素则互为相反数.习题1-11. 设111210111A ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭, 120124051B -⎛⎫ ⎪=-- ⎪ ⎪⎝⎭, 求23AB A -及T A B .2. 已知两个线性变换113212331232,232,45.x y y x y y y x y y y =+⎧⎪=-++⎨⎪=++⎩ 和 1122133233,2,.y z z y z z y z z =-+⎧⎪=+⎨⎪=-+⎩ 求从1z , 2z , 3z 到1x , 2x , 3x 的线性变换. 3. 计算下列乘积：(1) 401123520-⎛⎫ ⎪- ⎪ ⎪⎝⎭421⎛⎫⎪⎪ ⎪-⎝⎭；(2) ()123321⎛⎫ ⎪ ⎪ ⎪⎝⎭； (3) 321⎛⎫ ⎪⎪ ⎪⎝⎭()123；(4) 121232101110324-⎛⎫⎛⎫⎪⎪-- ⎪⎪ ⎪⎪⎝⎭⎝⎭.4. 设A =1203-⎛⎫ ⎪⎝⎭, B =2032⎛⎫⎪-⎝⎭, 问(1) AB BA =吗?(2) ()2A B +=2A +2AB +2B 吗? (3) ()A B +()A B -=2A 2B -吗? 5. 举反例说明下列命题是错误的： (1) 若2A O =, 则A O =； (2) 若2A A =, 则A O =或A E =； (3) 若AX AY =, 且A O ≠, 则X Y =.6. 设A =1111⎛⎫ ⎪-⎝⎭, 1111B ⎛⎫= ⎪⎝⎭, 求2()AB , 22A B .第二节矩阵的初等变换与初等矩阵一、初等变换的概念中学里, 已经学过用加减消元法解二、三元线性方程组.例1 解三元线性方程组1231231232344,23,226 2.x x x x x x x x x --+=⎧⎪+-=-⎨⎪+-=-⎩ (1.2.1) 解为叙述方便, 方程组的第i 个方程记为(1,2,3)i r i =. i j r r ↔表示对调第i 、第j 个方程, (0)i kr k ≠表示用k 乘第i 个方程的两边, i j r kr +表示第j 个方程的两边乘以k 然后加到第i 个方程上.方程组(1.2.1)12312r r r ↔⨯−−−→12312312323,2344,3 1.x x x x x x x x x +-=-⎧⎪--+=⎨⎪+-=-⎩ (1.2.2)21311232232323,22,2 2.r r r r x x x x x x x +-+-=-⎧⎪−−−→+=-⎨⎪--=⎩ (1.2.3)321232323,22,00.r r x x x x x ++-=-⎧⎪−−−→+=-⎨⎪=⎩(1.2.4)方程组(1.2.4)呈阶梯状(其增广矩阵为行阶梯形矩阵), 称为阶梯形方程组. 方程组(1.2.4)有3个未知量但有效方程只有2个, 因此有1个未知量可以任意取值, 称为自由未知量. 我们不妨取3x 为自由未知量. 先由方程组(1.2.4)中的2r 得：2322x x =--, 再代入(1.2.4)中的1r 得：1351x x =+.方程组(1.2.4)与方程组(1.2.1)是同解的, 由于3x 取值的任意性, 因此方程组(1.2.1)有无穷多组解, 其一般形式(通解)是13233351,22,.x x x x x x =+⎧⎪=--⎨⎪=⎩ 若令3x c =, 即得123x X x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭=5122c c c +⎛⎫ ⎪-- ⎪ ⎪⎝⎭=521c ⎛⎫ ⎪- ⎪ ⎪⎝⎭+120⎛⎫⎪- ⎪ ⎪⎝⎭,其中c 为任意常数.解方程组(1.2.1)的过程中施行了3种变换：(1) 换位变换即互换两个方程的位置；(2) 倍乘变换即用一个非零常数乘某一方程；(3) 倍加变换即把一个方程乘以常数后加到另一个方程上去. 这三种变换统称为线性方程组的初等变换.首先, 我们用换位、倍乘和倍加变换得到的新方程组可以用同类型变换变回原方程组(例如方程组(1.2.2)1232r r r ↔⨯−−−→方程组(1.2.1)), 因此线性方程组的初等变换是同解变换；其次, 可以证明：任何线性方程组都可以用初等变换化为阶梯形方程组, 而阶梯形方程组很容易判定是否有解, 且有解时容易通过自下而上的“回代”得到解.由于线性方程组AX B =和其增广矩阵A 相互唯一地确定, A 的每一行对应AX B =中的一个方程, 因此线性方程组的初等变换就对应着其增广矩阵的相应行变换.定义1 对矩阵施行的下列3种变换统称为矩阵的初等行变换： (1) 换位变换对调矩阵的第i 行和第j 行, 记为i j r r ↔； (2) 倍乘变换用常数0k ≠乘第i 行, 记为i kr ；(3) 倍加变换把第j 行的k 倍加到第i 行上去, 记为i j r kr +.把上述定义中的“行”换成“列”(所有记号只要把""r 换成""c )即为矩阵的初等列变换. 矩阵的初等行变换和初等列变换统称为矩阵的初等变换.回顾例1, 方程组(1.2.1)的初等变换(消元)过程可以用增广矩阵的初等行变换表示如下：234412132262A --⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭12312r r r ↔⨯−−−→121323441131--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭=A 121312r r r r +-−−−→121301220122--⎛⎫ ⎪- ⎪ ⎪--⎝⎭=A 232r r +−−−→121301220000--⎛⎫⎪- ⎪ ⎪⎝⎭=A 3 122r r -−−−→105101220000-⎛⎫⎪- ⎪ ⎪⎝⎭=A 4,A 3是行阶梯形矩阵, A 4是行最简形矩阵, A 4对应的方程组为132351,22,00.x x x x -=⎧⎪+=-⎨⎪=⎩取3x 为自由未知量, 并令3x c =, 即得1235122x c X x c x c +⎛⎫⎛⎫ ⎪ ⎪==--=⎪ ⎪ ⎪⎪⎝⎭⎝⎭521c ⎛⎫ ⎪- ⎪ ⎪⎝⎭+120⎛⎫⎪- ⎪ ⎪⎝⎭, 其中c 为任意常数.利用初等行变换, 把一个矩阵化为行阶梯形矩阵和行最简形矩阵, 是一种很重要的运算. 行阶梯形矩阵不是唯一的, 但其非零行的行数是唯一确定的(第五节将给出证明). 在解线性方程组AX B =时, 将增广矩阵A 化为行阶梯形矩阵, 就可以看出原方程组中是否有矛盾方程, 从而判断AX B =是否有解；在有解时, 进一步地将A 化为行最简形矩阵, 即可写出方程组AX B =的解.例2 将矩阵A =212341352012⎛⎫ ⎪ ⎪ ⎪⎝⎭化为行阶梯形矩阵和行最简形矩阵.解A =212341352012⎛⎫ ⎪⎪ ⎪⎝⎭21312212301110111r r r r --⎛⎫⎪−−−→--- ⎪ ⎪---⎝⎭32212301110000r r -⎛⎫ ⎪−−−→--- ⎪ ⎪⎝⎭(行阶梯形矩阵)1212(1)r r ⨯⨯-−−−→13112201110000⎛⎫ ⎪ ⎪⎪ ⎪ ⎪⎝⎭12121101201110000r r -⎛⎫ ⎪ ⎪−−−→ ⎪ ⎪ ⎪⎝⎭. (行最简形矩阵)例3 求解方程组123423412341234231,41,234,23 6.x x x x x x x x x x x x x x x +++=⎧⎪+-=⎪⎨++-=⎪⎪+--=-⎩解11231011411231423116A ⎛⎫ ⎪-⎪= ⎪- ⎪---⎝⎭31412111231011410114301578r r r r A --⎛⎫ ⎪-⎪−−−→= ⎪- ⎪---⎝⎭3242211231011410000200639r r r r A --⎛⎫ ⎪-⎪−−−→= ⎪ ⎪---⎝⎭34311231011410063900002r r A ↔⎛⎫ ⎪-⎪−−−→= ⎪--- ⎪⎝⎭,矩阵3A 是行阶梯形矩阵, 其对应的方程组为123423434231,41,639,0 2.x x x x x x x x x +++=⎧⎪+-=⎪⎨--=-⎪⎪=⎩ 第四个方程为02=, 这是不可能的, 故原方程组无解.例4 求解方程组1234123412341234231,234,324,23 6.x x x x x x x x x x x x x x x x +++=⎧⎪++-=-⎪⎨---=-⎪⎪+--=-⎩ 解11231123143112423116A ⎛⎫ ⎪-- ⎪= ⎪---- ⎪---⎝⎭ 213141321112310114504711701578r r r r r r A ---⎛⎫ ⎪--⎪−−−→= ⎪---- ⎪---⎝⎭ 3242421123101145003272700633r r r r A +-⎛⎫⎪--⎪−−−→= ⎪---⎪---⎝⎭4323112310114500327270005151r r A -⎛⎫ ⎪-- ⎪−−−→= ⎪--- ⎪⎝⎭1331451()411231011450019900011r r A ⨯-⨯⎛⎫⎪--⎪−−−→= ⎪⎪⎝⎭34241494351120201101001000011r r r r r r A -+--⎛⎫⎪-⎪−−−→= ⎪⎪⎝⎭231312261000101001001000011r r r r r r A ----⎛⎫⎪-⎪−−−→= ⎪⎪⎝⎭,3A 是行阶梯形矩阵, 6A 是行最简形矩阵, 6A 对应的方程组为12341,1,0,1.x x x x =-⎧⎪=-⎪⎨=⎪⎪=⎩故原方程组有唯一解, 即12341101x x x x -⎛⎫⎛⎫⎪ ⎪- ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 二、初等矩阵定义2 将单位矩阵作一次初等变换所得的矩阵称为初等矩阵. 对应于三类初等行、列变换, 有下列三种类型的初等矩阵：(1) 初等换位矩阵对调单位矩阵的第i , j 两行或第i , j 两列而得到的矩阵, 即为11011(,)11011E i j ⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪= ⎪⎪ ⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭O L M O M L O i j ←←第行第行 (2) 初等倍乘矩阵用常数0k ≠乘单位矩阵的第i 行或第i 列而得到的矩阵, 即为11(())11E i k k i ⎛⎫ ⎪⎪ ⎪ ⎪=← ⎪ ⎪ ⎪⎪⎪⎝⎭O O 第行(3) 初等倍加矩阵把单位矩阵的第j 行的k 倍加到第i 行上而得到的矩阵, 即为11(,())11k i E i j k j ⎛⎫ ⎪ ⎪ ⎪← ⎪= ⎪⎪← ⎪⎪⎪⎝⎭O L O M O 第行第行 (,())E i j k 也可看作是把单位矩阵的第i 列的k 倍加到第j 列上而得到的矩阵.下面我们用一个初等矩阵左乘或右乘一个矩阵. 例如111211112121222313233132321222100001010n n n n n n a a a a a a a a a a a a a a a a a a ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭L L L L L L ； 111213111312212223212322123132100001010m m m m m m a a a a a a a a a a a a a a a aa a ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭M M M M M M .由此可见, 用三阶初等换位矩阵(2,3)E 左乘矩阵3n A ⨯, 相当于对矩阵3n A ⨯作一次相应的初等换位行变换(即对调矩阵3n A ⨯的第2,3两行)；用三阶初等换位矩阵(2,3)E 右乘矩阵3m A ⨯, 相当于对矩阵3m A ⨯作一次相应的初等换位列变换(即对调矩阵3m A ⨯的第2,3两列).用初等倍乘矩阵或初等倍加矩阵左乘或右乘一个矩阵, 可得类似的结论.一般地, 有如下定理.定理设A 是一个m n ⨯矩阵, 对A 施行一次初等行变换, 相当于在A 的左边乘一个相应的m 阶初等矩阵；对A 施行一次初等列变换, 相当于在A 的右边乘一个相应的n 阶初等矩阵.由定理可知, 对于同阶初等矩阵, 有(1) (,)(,);E i j E i j E ⋅= (1.2.5) (2) 1(());E i E i k E k ⎛⎫⎛⎫⋅= ⎪ ⎪⎝⎭⎝⎭(1.2.6)(3) (,())(,()).E i j k E i j k E -⋅= (1.2.7)习题1-21. 把下列矩阵化为行阶梯形矩阵及行最简形矩阵：(1) 121131114302-⎛⎫ ⎪---- ⎪ ⎪⎝⎭；(2) 1111532114012211543314⎛⎫⎪⎪⎪⎪⎝⎭.2. 求解下面的方程组(1) 12341234123412343520,2350,7430,415790.x x x x x x x x x x x x x x x x -+-=⎧⎪+-+=⎪⎨-+-+=⎪⎪+-+=⎩(2) 123423412341234231,41,234,236,x x x x x x x x x x x x x x x +++=⎧⎪+-=⎪⎨++-=⎪⎪+--=-⎩(3) 123451234512345321,335432,2244 3.x x x x x x x x x x x x x x x +++-=⎧⎪+++-=⎨⎪+++-=⎩第三节行列式一、n 阶行列式的定义对于二元线性方程组11112212112222,.a x a x b a x a x b +=⎧⎨+=⎩ (1.3.1) 用消元法可得：当112212210a a a a -≠ 时, 存在唯一的解122212*********,b a b a x a a a a -=-211121*********b a b ax a a a a -=-.如果我们将方程组(1.3.1)的系数矩阵11122122a a A a a ⎛⎫= ⎪⎝⎭所对应的二阶行列式定义为1112112212211222a a D A a a a a a a ===-, (1.3.2) 并记1D =112222b a b a , 2D =111212ab a b , 则方程组(1.3.2)的解可写成如下形式11D x D =, 22Dx D=. (1.3.3)同样, 可以用行列式表示三元线性方程组111122133121122223323113223333,,.a x a x a xb a x a x a x b a x a x a x b ++=⎧⎪++=⎨⎪++=⎩ (1.3.4) 的解. 为此定义111213212223112233122331132132313233132231122133112332a a a D a a a a a a a a a a a a a a a a a a a a a a a a ==++--- (1.3.5)为系数矩阵所对应的三阶行列式, 用()1,2,3j D j =分别记用方程组(1.3.4)右端的常数列替换D 中的第j 列所得的三阶行列式, 则当0D ≠时, 方程组(1.3.4)的解可写为11D x D =, 22Dx D =, 33D x D=. (1.3.6)式(1.3.3)和式(1.3.6)分别用二、三阶行列式来表示方程组(1.3.1)、(1.3.4)的解. 这些公式形式简单, 便于记忆, 明显地表示出线性方程组的解与方程组的系数和常数项的关系. 这就启发我们考虑：如果含有n 个未知量、n 个方程的线性方程组有唯一解, 能否给出类似的求解公式？回答是肯定的 . 为此, 必须推广二、三阶行列式.二阶及三阶行列式的定义, 即公式(1.3.2)及(1.3.5), 可以用“对角线法则”来记忆(见下图)：11122122a a a a 111213111221222321223132333132a a a a a a a a a a a a a a a (-) (+) (-) (-) (-) (+) (+) (+)二阶行列式等于主对角线元素的乘积减去副对角线元素的乘积.三阶行列式等于主对角线及与其平行的两条线上各 3 个元素的乘积之和, 减去副对角线及与其平行的两条线上各3 个元素乘积之和.例1 求行列式的值：12(1)34-, 102(2)211313---. 解 (1)1214(2)31034-=⨯--⨯=； (2) 1022113(4)0(6)012313--=-+-+----=--.例2 求解方程211123049x x =. 解方程左端的三阶行列式2223418129256,D x x x x x x =++---=-+由2560x x -+=, 解得2x =或3x =.分析三阶行列式的定义, 我们发现第一, 式(1.3.5)的右端有3!项, 除去带有的正、负号外, 每项都是这个行列式中的每一行和每一列中任取1个且仅取1个元素的积. 如果把元素的第1个下标, 即行标(表示元素所在的行)按照123顺序排列, 则它的任意一项可写成123123j j j a a a , 这里123,,j j j 是1, 2, 3 的一个排列(由１, 2, 3这三个数按某种次序所排成的一个有序数组), 元素的第2个下标, 即列标k j 表示该元素所在的列.第二, 这6项中带有正号的那些项, 列标123,,j j j 形成3个排列： 123, 231, 312；带有负号的那些项的列标也形成3个排列：321, 213, 132.我们感兴趣的是, 这2组排列的区别是什么？为了回答这个问题, 我们给出下面几个定义.定义1 由1,2,,n L 这n 个数按某种次序所排成的一个有序数组12n j j j L 称为一个n 元全排列.显然, n 元全排列的个数为n !定义2 对于n 个不同元素, 若事先规定各元素之间有一个标准次序(例如n 个不同的自然数, 可规定由小到大为标准次序), 于是在这n 个元素的任一排列中, 当某两个元素的先后次序与标准次序不同时, 就说有1个逆序.定义3 一个排列中所有逆序的总数称为这个排列的逆序数, 用τ表示. 定义4 逆序数为奇数的排列称为奇排列, 递序数为偶数的排列称为偶排列.标准排列12n L 的逆序数(12)0n τ=L , 为偶排列. 可以证明：当2n ≥时,n 元全排列中奇、偶排列各占一半, 即各有!2n 个.例3 求排列32514的逆序数, 并指明奇偶性. 解在排列32514中, 3排在首位, 没有逆序；2的前面比2大的数有一个(3), 故有1个逆序； 5是最大数, 没有逆序；1的前面比1 大的数有三个(3, 2, 5), 故有3个逆序；4的前面比4大的数有一个(5), 故有1个逆序, 于是这个排列的逆序数为(32514)1315τ=++=. 从而排列32514是奇排列.现在回过来考察三阶行列式展开式中各项正负号的取法, 因为(123)0τ=, (231)2τ=, (312)2τ=, (321)3τ=, (213)1τ=, (132)1τ=,由此可见：任一项带正号或负号完全由它的行标为标准次序时, 列标形成的排列123j j j 的奇偶性来决定, 即当列标形成的排列为偶排列时, 该项取正号；列标形成的排列为奇排列时, 该项取负号. 因此, 我们有1231231112133!()212223123313233(1)j j j j j j a a a a a a a a a a a a τ=-∑, (1.3.7) 其中3!∑表示对1,2,3的所有排列求和, 共有3!6=项.二阶行列式也可以表示成和式12122!1112()122122(1)j j j j a a a a a a τ=-∑.定义5 设()ij n n A a ⨯=是一个n 阶方阵(2)n ≥, 称121211121!21222()1212(1)n n nn nj j j j j nj n n nna a a a a a a a a a a a τ=-∑L L L L M M M L (1.3.8)为n 阶行列式, 也可称为方阵A 的行列式, 记为A 或det A . 规定一阶行列式a a =(注意不要与绝对值混淆).下面是n 阶行列式的等价定义：121211121!21222()1212(1)n n nn ni i i i i i n n n nna a a a a a a a a a a a τ=-∑L L L L M M M L , (1.3.9)上式右端各项的n 个因子是按列标组成标准次序的.由行列式的定义知, 若行列式的某行(列)的元素都是零, 则此行列式为零.例4 证明对角行列式(对角线以外的元素均为0)(1)1212n nλλλλλλ=L O； (2)1(1)2212(1)n n n nλλλλλλ-=-L N.证明 (1) 由行列式的定义即得.(2) 若记,1i i n i a λ+-=则由行列式的定义可得1122,11nn nn a a a λλλ-=NN12,1112(1)(1)n n n n a a a ττλλλ-=-=-L L , 其中τ为排列(1)21n n -L 的逆序数, 故(1)12(1)2n n n τ-=+++-=L . 例5 证明行列式112122112212000nn n n nna a a D a a a a a a ==L L L M M M L. 证明由于当j i >时, 0ij a =, 故D 中可能不为0的元素i i p a , 其下标应有i p i ≤, 即121,2,,n p p p n ≤≤≤L .在所有排列12n p p p L 中, 能满足上述关系的排列只有一个排列12n L , 其逆序数0τ=, 所以D 中可能不为0的项只有一项1122(1)nn a a a τ-L , 即1122nn D a a a =L . 对角线以下(上)的元素都为零的行列式称为上(下)三角行列式, 它们的值与对角行列式一样, 都等于主对角线上元素的乘积.二、行列式的性质记111212122212n n n n nn a a a a a a A a a a =L L M M M L, 112111222212n n T n n nna a a a a a A a a a =L LM M M L, 行列式T A 称为行列式A 的转置行列式.性质1 行列式与它的转置行列式相等. 例如3421=--3241-=-5.由性质1可知, 行列式对行成立的性质, 对列也成立, 反之亦然. 以下叙述行列式性质时, 只对行叙述.性质2 互换行列式的两行, 行列式变号. 例如3421=--5, 2134--=5-.推论若行列式有两行元素完全相同, 则此行列式为零.性质3 行列式中某一行的所有元素乘同一数k 等于用k 乘原行列式(第i 行乘以k , 记作：i r k ⨯).推论1 行列式中某一行的所有元素的公因子可提到行列式记号外. 由此推论及矩阵的运算, 设A 为n 阶方阵, λ为数, 则n A A λλ=. 例如, 若A 是三阶方阵且2A =, 则322216A =⋅=.推论2 行列式中如果有两行的元素对应成比例, 则此行列式为零. 性质4 若行列式的某一行元素都是两数之和, 例如11121112212n i i i i in inn n nna a a D a a a a a a a a a '''=+++L M M ML MM M L,则行列式D 等于下面的两个行列式之和：111211212n i i in n n nn a a a D a a a a a a =L M M M L M M M L 111211212ni i in n n nna a a a a a a a a '''+L M M M LM M M L. 注行列式的加法与矩阵的加法不同.性质5 把行列式的某一行的各元素乘以同一个数, 然后加到另一行对应的元素上去, 行列式不变.以上性质不难由行列式的定义证得, 以性质4为例, 证明如下. 性质4的证明由(1.3.8)式, 得 1212!()12(1)()n i i n n j j j j j ij ij nj D a a a a a τ'=-+∑L L L 1212!()12(1)n i n n j j j j j ij nj a a a a τ=-∑LL L1212!()12(1)n i n n j j j j j ijnj a a a a τ'+-∑L L L 111211212n i i in n n nn a a a a a a a a a =LM MM LM M M L111211212ni i in n n nna a a a a a a a a '''+L M M M L M M M L. 例6 计算行列式121024*********3D -=---. 解D21314123r r r r r r -++ 1210003202110213-- 23r r ↔ 1210021100320213--- 42r r - 1210021100320022---4323r r + 12100211003210003--10123203=-⨯⨯⨯=-.例7 计算行列式3111131111311111D =. 解这个行列式的特点是各列4个数之和都是6. 将第2, 3, 4行同时加到第一行, 提出公因子6, 然后各行减去第一行, 得D121314r r r r r r +++ 6666131111311111 116r ⨯ 11111311611311111213141r r r rr r --- 1111020064800200002=. 例8 设2113A -⎛⎫= ⎪⎝⎭, 3452B -⎛⎫= ⎪⎝⎭, 求,A ,B AB .解 217,13A -== 342652B -==. 因为21341101352182AB ---⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,所以110182182AB -==.我们注意到：AB A B =. 一般地, 有下列结论：定理1 若A , B 为同阶方阵, 则AB A B =, 从而.AB BA =三、行列式按行(列)展开在三阶行列式的定义式(1.3.5)中, 如果把含111213,,a a a 的项分别合并, 并提出公因子, 则有1112132223212223113233313233a a a aa a a a a a a a a a = 2123123133aa a a a - 2122133132aa a a a +. (1.3.10) 据此, 一个三阶行列式的计算可转化为三个二阶行列式的计算. 自然有一个问题：一个n 阶行列式的计算能否转化为n 个1n -阶行列式的计算, 从而达到降阶的目的？下面讨论这个问题.定义6 在n 阶行列式A 中划去第i 行和第j 列后所剩下的2(1)n -个元素按原来的相对位置所构成的1n -阶行列式称为ij a 在A 中的余子式, 记为ij M , 而称(1)i j ij ij A M +=-为ij a 在A 中的代数余子式, 这里1,i j n ≤≤.例9 在行列式123456789A =中, 求23M , 33M , 23A , 33A . 解 2312678M ==-, 232323(1)6A M +=-=, 3312345M ==-, 333333(1)3A M +=-=-. 利用代数余子式, 式(1.3.10)可以写成111112121313A a A a A a A =++,将上式推广到一般情况, 有下面的结论：定理2 n 阶行列式(2n ≥)等于它的任一行(列)各元素与其代数余子式乘积之和, 即1122i i i i in in A a A a A a A =+++L 1nij ij j a A ==∑, 1,2,,i n =L . (1.3.11)或1122j j j j nj nj A a A a A a A =+++L 1nij ij i a A ==∑, 1,2,,j n =L . (1.3.12)推论行列式的任一行(列)的元素与另一行(列)的元素的代数余子式乘积之和等于零. 即11220i j i j in jn a A a A a A +++=L , (1.3.13) 11220i j i j ni nj a A a A a A +++=L , (1.3.14)其中i j ≠.定理1按行(列)展开计算行列式的方法称为降阶法. 计算行列式时, 将行列式按行(列)展开与行列式的性质结合起来用, 常常能够达到事半功倍的效果.例10 计算行列式 (即本节例6)1210241210213423D -=---.解利用行列式的性质, 将行列式的某行(列)除某个元素外的其余元素化为0, 再按该行(列)展开.D21312c cc c-+1000203212113213---1r 按展开110321(1)211213+⨯--32r r -032211022-1c 按展开21322(1)22+⨯--21020=-⨯=-.例11 证明123213132222123111()()()x x x x x x x x x x x x =---. 证明123222123111x x x x x x 2131c c c c --121312222212131100x x x x x x x x x x ---- 213111212131311(1)()()()()x x x x x x x x x x x x +--=⨯--+-+2131213111()()x x x x x x x x =--++213132()()()x x x x x x =---.上例中的行列式称为三阶范得蒙德行列式. 类似可证n 阶范得蒙德行列式1222212111112111()n n n i j j i nn n n n x x x x x x D x x x x x ≤<≤---==-∏L L L M M M L . 四、克拉默法则下面介绍利用行列式求含有n 个未知量、n 个方程的线性方程组解的公式. 设方程组为11112211211222221122,,.n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩L L L L L L L L L L L L L (1.3.15) 由各方程中的未知量的系数构成的行列式111212122212n nn n nna a a a a a D a a a =L L M M M L(1.3.16) 称为方程组(1.3.15)的系数行列式, 用常数项12,,,n b b b L 替换D 中第j 列的相应元素得行列式记为j D , 即111,111,11212,122,121,1,1j j n j j nj n n j n n j nna ab a a a a b a a D a a b a a -+-+-+=L L L L M M M M M LL. 定理3 (克拉默法则)如果n 元线性方程组(1.3.15)的系数行列式0D ≠, 则方程组有唯一解,1,2,,j j D x j n D ==L .。

高中数学-矩阵与行列式初步(十三)---教师

2 2
，
B
13
42
（1）计算 2A B ； A 3B ；AB；BA。
（2）计算 A2 B2 与 (A B)(A B) ，并判断是否相等。
答案：（1）
7 5
06
；
0 13
144
；
9 10
1146
；
5 7
22
（2）
6 19
286
；
20 16
24 12
，不相等。
点评：① A2 A A
② AB BA
【热身练习】
1、矩阵
1 2
2 3
0 4
的行向量是
1 2
0, 2
3 4
列向量是
12,
32,
0 4
2、方程组
2x 4x
3y 1 y6
0
的系数矩阵是
2 4
31
增广矩阵是
2 4
3 1
16
3、增广矩阵
2 0
1 7
0 1
1 4
对应的方程组是
0 1 4 8
2x y 1 7 y z 4 y 4x 8
答案：当
a
1且a
3时，
x
y
a(a2 2a 7) (a 1)(a 3)
(a 1)2 (a 1)(a 3)
当 a 1或a 3时，方程组无解。
变式
2、
m
为何值时，方程组
mx (m (m 1)x
1) y m 2 (m 2) y m
1
有唯一一组解，且满足
x 0, y 0 ？
gh i
ab
gh
7、 2 a2 b2 a1 b1 3 a1 b1 表示成三阶行列式为 a3 b3 a3 b3 a2 b2

40、矩阵、行列式和算法初步

精锐教育网站：
精锐教育·教务管理部
中小学 1 对 1 课外辅导专家（2）确切性：算法的每一步必须有确切的定义；（3）可行性：算法原则上能够精确地运行，而且人们用笔和纸做有限次即可完成；（4）输入：一个算法有 0 个或多个输入，以刻划运算对象的初始条件。所谓 0 个输入是指算法本身定出了初始条件。（5）输出：一个算法有 1 个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的。
（1）将两人的成绩各阶段成绩用矩形表示；（2）写出行向量、列向量，并指出其实际意义。
算法初步【知识点梳理】
1、算法的概念：由基本运算及规定的运算顺序所构成的完整的解题步骤，或者是按照要求设计好的有限的计算序列，并且这样的步骤或序列能解决一类问题。 2、算法的五个重要特征：（1）有穷性：一个算法必须保证执行有限步后结束；
精锐教育网站：精锐教育·教务管理部
中小学 1 对 1 课外辅导专家 9．计算
cos330 sin 330
sin 270 _______ cos 270
三、解答: 10．已知 A 2 B
1 2 1 0 2 1 ，A B 1 1 ，C 4 1 ，求 2 A B C . 3 1
（2）条件结构分支结构的一般形式
精锐教育网站：
精锐教育·教务管理部
中小学 1 对 1 课外辅导专家
条件是处理
否
是
条件
否
处理 1
处理 2
两种结构的共性： ① 一个入口，一个出口。特别注意：一个判断框可以有两个出口，但一个条件分支结构只有一个出口。 ② 结构中每个部分都有可能被执行，即对每一个框都有从入口进、出口出的路径。以上两点是用来检查流程图是否合理的基本方法（当然，学习循环结构后，循环结构也有此特点）提醒：解决分段函数的求值等问题，一般可采用条件结构来设计算法. （3）循环结构的一般形式在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，反复执行的处理步骤为循环体，显然，循环结构中一定包含条件结构。

高二数学基本概念——第9章_矩阵和行列式初步

第9章矩阵和行列式初步一、矩阵9.1 矩阵的概念矩阵及其相关的概念1、矩形数表叫做矩阵矩阵中的每个数叫做矩阵的元素由个数排成的行列的数表n m ⨯m n ()n j m i a ij ,,2,1;,,2,1 ==mnm m nn a a a a a a a a a212222111211称为矩阵.n m ⨯记作⎪⎪⎪⎪⎪⎭⎫⎝⎛=mn m m n n a a a a a a a a a A212222111211n m ij a ⨯=)(2、矩阵叫做方程组的系数矩阵。

⎪⎪⎭⎫⎝⎛-1321它是2行2列的矩阵，记为22⨯A ，矩阵可简记为An m A ⨯注意: 矩阵的符号，是“（）”，不能是“| |”.列元素。

行第称为矩阵的第其中j i a ij 一般的记为大写字母A 、B 、C 、…等。

等，或者必要时可记为n m ij n m n m a B A ⨯⨯⨯)(,说明：通过对线性方程组的增广矩阵的变换可以得到线性方程组的解，这里所用的矩阵变换有下列三种：（1）互换矩阵的两行（2）把某一行同乘以（除以）一个非零常数（3）某行乘以一个数加到另一行通过上述三种矩阵变换，使线性方程组系数矩阵变成单位矩阵时，其增广矩阵的最后一个列向量给出了方程组的解。

9.2 矩阵的运算矩阵列的矩形表，称为一个行排列成一个个数由n m n m n j m i a n m ij ⨯==⨯),,2,1;,2,1( 111212122212.....................n n m m mn a a a a a a a a a ⎛⎫⎪⎪ ⎪⎪⎪⎝⎭记为列元素。

行第称为矩阵的第其中j i a ij 一般的记为大写字母A 、B 、C 、…等。

,()m n m n ij A B a ⨯⨯必要时可记为等，或者A=。

0m nO O ⨯所有元素均为的矩阵，称为零矩阵，记作或定义1一、复习定义2若两个矩阵A ，B 有相同的行数与相同的列数，并且对应的位置上的元素相等，则称矩阵A 与矩阵B 相等。

线性代数下的行列式和矩阵

线性代数下的行列式和矩阵线性方程组一般有 m 个常数项，n 个未知数，m * n 个系数。

若常数项全为 0 ，则为齐次线性方程组；若未知数全为0 ，则称为零解。

于是我们考虑的问题是：齐次方程组：1.是否存在非零解，以及存在的条件2.通解的结构与性质3.解法非齐次方程组：1.是否有解，以及有解的条件是什么2.有多少解以及对应解数量的条件是什么3.多解的结构与性质4.解法行列式二，三阶行列式行列式的初始作用是解线性方程组！例如：最简单的二元线性方程组\left\{ \begin{aligned} a_{11}x_1 + a_{12}x_2 = b_1 \\ a_{21}x_1 + a_{22}x_2 = b_2 \end{aligned} \right.\Rightarrow 消元 \Rightarrow \left\{ \begin{aligned}x_1 = \frac{b_1a_{22} - b_2a_{12}}{a_{11}a_{22} -a_{12}a_{21}} \\ x_1 = \frac{b_2a_{21} -b_1a_{21}}{a_{11}a_{22} - a_{12}a_{21}} \end{aligned} \right.可以得出结论，答案是由方程的四个系数和常数决定的。

所以记住四个系数作为行列式，指定行列式的值是上式的分母:\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix} = a_{11}a_{22} - a_{12}a_{21}于是有了这么一个行列式之后，我们就可以得到：D = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \ D_1 = \begin{bmatrix} b_1 & a_{12} \\ b_2 & a_{22} \end{bmatrix} \ D_2 = \begin{bmatrix}a_{21} & b_1 \\ a_{21} & b_2 \end{bmatrix} \\Rightarrow \\ x_1 = \frac{D_1}D, x_2 = \frac{D_2}D同理可以推广到三元线性方程组，定义三阶行列式。

第一讲行列式与矩阵

5 r2 r3 0 1 0 0 r2 r4 0 0
11 1 60 5 16 2
1 r3 5 1 r4 2
10
1 0 0 1 0 0 0 0
2 1 11 1 12 8 1 1
1 0 1 c3 c4 10 0 0 0 0 1 1
2
1 0 1
2
0 1 1 11
设变量能用变量线性表示即其中为常数22211211又如在物资调运中某物资有两个产地上海南京三个销售地广州深圳厦门调运方案见下表广州深圳厦门上海172520南京263223销售地产地数量这个调运方案可以简写成一个2行3列的数表233226202517下面给出矩阵的定义定义111122122列矩阵或mn矩阵记作22211211一矩阵概念其中叫做矩阵a的元素ij列的元素矩阵常用大写字母等表示
显然，
T DD
对于n阶行列式，可以用数学归纳法加以证明。
性质二：
互换行列式的两行（列）的位置，行列式仅改变符号。
例如，二阶行列式
a a D 11 12 a a a a 11 22 12 21 交换两行后得到的行列式 a a 21 22
a 21 a 22 a a a a D 21 12 22 11 a a 11 12
a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33
a A a A a A 11 11 12 12 13 13
例4 写出四阶行列式的元素 a 32 的余子式和代数余子式.
2 14 8 1 5 9 12 2 1 6 9 4 7 3 13 11
解
M 32
性质六：行列式的展开与计算
行列式等于它的任一行（列）的各元素与其对应的的代数余子式乘积之和。 a11 a12 a1n

9、高三一轮复习：矩阵、行列式初步

矩阵初步【知识要点】一、矩阵的概念：1、矩阵的定义：由m n ⨯个数排成的m 行、n 列的矩形数表叫做矩阵，即111212122212n n m m mn a a a a a a a a a ⎛⎫⎪ ⎪⎪⎪⎝⎭L L L L L L L，矩阵中的每个数ij a （1i m ≤≤，1j n ≤≤，i 、j ∈N *）叫做矩阵的元素，ij a 表示第i 行第j 列上的元素。

矩阵通常用大写字母表示：()m n ij A a ⨯=（表示m n ⨯阶矩阵），在不混淆的情况下，可简记为A ； 2、矩阵的意义：矩形数表； 3、相关概念：（1）行向量、列向量；（2）方矩阵（方阵）、方矩阵的阶；（3）单位矩阵、零矩阵。

二、矩阵的运算：1、矩阵的相等：若()ij A a =、()ij B b =是两个行数与行数相等、列数与列数相等的矩阵，当且仅当它们对应位置的元素都相等时，即ij ij a b =（i =1，2，…，m ；j =1，2，…，n ），称两矩阵相等，记作A B =；2、矩阵的加减：当两个矩阵A 、B 的行数与列数分别相等时，将它们对应位置上的元素相加ij ij ij c a b =+（相减ij ij ij c a b =-），i =1，2，…，m ；j =1，2，…，n ，所得到的矩阵()ij c 称为矩阵A 、B 的和（差），记作A B +（A B -）；3、矩阵的数乘：设α为任意实数，我们把矩阵()ij A a =的所有元素都与α相乘所得到的矩阵()ij a α叫做矩阵A 与实数α的乘积矩阵，记作A α；4、矩阵的乘法：设矩阵A 是n 行、k 列的矩阵，矩阵B 是k 行、m 列的矩阵，矩阵C 是n 行、m 列的矩阵，如果矩阵C 中第i 行、第j 列的元素ij c 为A 的第i 个行向量与B 的第j 个列向量的数量积（i =1，2，…，m ；j =1，2，…，n ），即1122ij i j i j ik kj c a b a b a b =+++L ，那么矩阵C 叫做矩阵A 和B 的乘积。

第一讲行列与矩阵

第一讲行列式与矩阵一、内容提要（一）n 阶行列式的定义∑-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn j j j njn j j j j j nn n n n n a a a a a a a a a a a a D ΛΛΛΛΛΛΛΛΛ21212211)(212222111211)1(τ（二）行列式的性质1．行列式与它的转置行列式相等，即T D D =； 2．交换行列式的两行（列），行列式变号；3．行列式中某行（列）元素的公因子可提到行列式外面来； 4．行列式中有两行（列）元素相同，则此行列式的值为零；5．行列式中有两行（列）元素对应成比例，则此行列式的值为零； 6．若行列式中某行（列）的元素是两数之和，即nm n n in in i i i i na a ab a b a b a a a a D ΛΛΛΛΛΛΛΛΛ21221111211+++=，则nnn n in i n nnn n in i n a a a b b b a a a a a a a a a a a a D ΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛ21121112112112111211+= 7．将行列式某行（列）的k 倍加到另一行（列）上去，行列式的值不变。

（三）行列式依行（列）展开 1．余子式与代数余子式（1）余子式的定义去掉n 阶行列式D 中元素ij a 所在的第i 行和第j 列元素，剩下的元素按原位置次序所构成的n-1阶行列式称为元素ij a 的余子式，记为ij M（2）代数余子式的定义ij a 的代数余子式的记为ij j i ij ij M A A +-=)1(, 2．n 阶行列式D 依行（列）展开（1）按行展开公式∑=⎩⎨⎧≠==nj kj ij k i ki DA a 10 （2）按列展开公式∑=⎩⎨⎧≠==ni is ij sj sj DA a 10 （四）范德蒙行列式∏≤<≤----==nj i i jn nn n nnx xx x x x x x x x x D 1112112222121)(111ΛΛΛΛΛΛΛ（五）矩阵的概念1．矩阵的定义由m×n 个数),,2,1;,,2,1(n j m i a ij ΛΛ==组成的m 行n 列的矩形数表⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=mn m m n n a a a a a a a a a A ΛΛΛΛΛΛ212222111211 称为m×n 矩阵，记为n m ij a A ⨯=)(2．特殊的矩阵（1）方阵：行数与列数相等的矩阵；（2）上（下）三角阵：主对角线以下（上）的元素全为零的方阵称为上（下）三角阵；（3）对角阵：主对角线以外的元素全为零的方阵；（4）数量矩阵：主对角线上元素相同的对角阵；（5）单位矩阵：主对角线上元素全是1的对角阵，记为E ；（6）零矩阵：元素全为零的矩阵。

高中数学中的行列式与矩阵详尽讲解

高中数学中的行列式与矩阵详尽讲解在高中数学中，行列式与矩阵是两个重要的概念。

它们既有着理论上的意义，也有着实际应用的价值。

本文将详细讲解行列式与矩阵的相关知识。

一、行列式行列式是矩阵的一个重要性质，它可以用来判断矩阵是否可逆。

对于一个n阶方阵A，其行列式记作|A|或det(A)。

行列式的计算方法有很多种，其中最常用的是按照拉普拉斯展开定理进行计算。

拉普拉斯展开定理是指将一个n阶方阵的行列式展开成n个n-1阶方阵的行列式之和。

具体来说，对于一个n阶方阵A，可以选择其中的某一行或某一列，将其元素与对应的代数余子式相乘，再按照正负交错的方式相加，即可得到该行列式的值。

行列式的计算过程需要注意一些规则。

首先，行列式的值与矩阵的行列互换无关，即|A|=|A^T|。

其次，如果矩阵A的某两行（或某两列）互换位置，那么行列式的值将变为原值的相反数，即|A|=-|A'|，其中A'是A互换了两行（或两列）位置后的矩阵。

行列式在线性代数中有着广泛的应用。

例如，行列式可以用来求解线性方程组的解的个数。

当一个n阶方阵的行列式不等于0时，该方阵可逆，对应的线性方程组有唯一解；当行列式等于0时，该方阵不可逆，对应的线性方程组无解或有无穷多解。

二、矩阵矩阵是由一组数按照矩形排列而成的矩形阵列。

矩阵可以表示为m行n列的形式，其中m表示矩阵的行数，n表示矩阵的列数。

矩阵的元素可以是实数或复数。

矩阵的加法和数乘是两个基本的运算。

对于两个相同大小的矩阵A和B，它们的和记作A+B，定义为将对应位置的元素相加得到的新矩阵。

对于一个矩阵A和一个数k，它们的数乘记作kA，定义为将矩阵A的每个元素乘以k得到的新矩阵。

矩阵的乘法是另一个重要的运算。

对于一个m行n列的矩阵A和一个n行p列的矩阵B，它们的乘积记作AB，定义为将矩阵A的每一行与矩阵B的每一列对应元素相乘，并将结果相加得到的新矩阵。

需要注意的是，两个矩阵相乘的前提是第一个矩阵的列数等于第二个矩阵的行数。

2020届上海(沪教版)高考考典——第8章-矩阵和行列式初步教师版

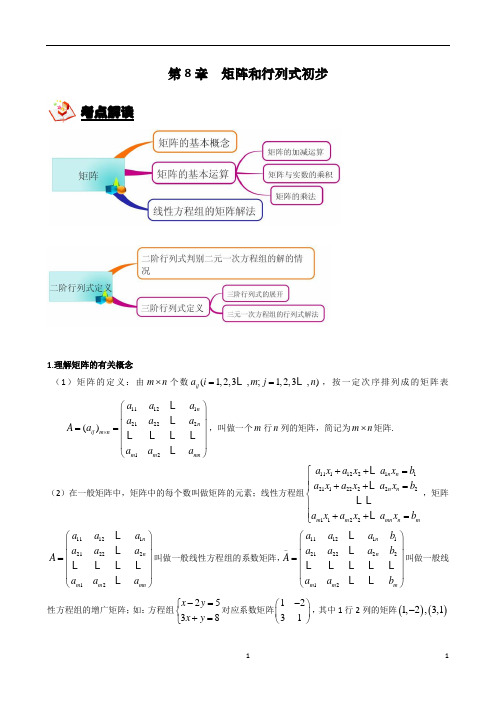
第8章矩阵和行列式初步考点解读1.理解矩阵的有关概念（1）矩阵的定义：由m n⨯个数(1,2,3,;1,2,3,)ija i m j n==L L，按一定次序排列成的矩阵表111212122212()nnij m nm m mna a aa a aA aa a a⨯⎛⎫⎪⎪==⎪⎪⎝⎭LLL L L LL，叫做一个m行n列的矩阵，简记为m n⨯矩阵.（2）在一般矩阵中，矩阵中的每个数叫做矩阵的元素；线性方程组11112211211222221122n nn nm m mn n ma x a x a x ba x a x a x ba x a x a x b++=⎧⎪++=⎪⎨⎪⎪++=⎩LLL LL，矩阵A=111212122212nnm m mna a aa a aa a a⎛⎫⎪⎪⎪⎪⎝⎭LLL L L LL叫做一般线性方程组的系数矩阵，A-=11121121222212nnm m ma a a ba a a ba a b⎛⎫⎪⎪⎪⎪⎝⎭LLL L L L LL L叫做一般线性方程组的增广矩阵；如：方程组2538x yx y-=⎧⎨+=⎩对应系数矩阵1231-⎛⎫⎪⎝⎭，其中1行2列的矩阵()()1,2,3,1-叫做系数矩阵的两个行向量；2行1列的矩阵12,31-⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭叫做系数矩阵的列向量；（3）当矩阵的行数与列数相等时，该矩阵称为方矩阵，简称方阵；我们把主对角线元素为1、其余元素均为零的方矩阵，如1001⎛⎫⎪⎝⎭，叫做单位矩阵.2.矩阵的运算及其性质（1）矩阵的加法，若111212122212()n n ij m nm m mn a a a a a a A a a a a ⨯⎛⎫⎪ ⎪== ⎪⎪⎝⎭L L L L L L L，111212122212()n n ij m n m m mn b b b b b b B b b b b ⨯⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭LL L LL L L，则C A B =+=111112121121212222221122n n n n m m m m mn mna b a b a b a b a b a b a b a b a b +++++++++L LL L L L L.（2）矩阵的加法满足性质: 交换律,结合律.（3）数与矩阵乘法定义：以数k 乘矩阵()ij A a =的每个元素所得的矩阵()ij ka 叫做数k 与矩阵A 相乘的积，记作kA ；（4）设矩阵111211121112212221222122,,a a b b c c A B C a a b b c c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.如果它们元素间的关系可以用下列等式表示：1122(1,2;1,2)ij i j i j c a b a b i j =+==，则C 叫做矩阵A 和矩阵B 的积，记作C =AB（5）矩阵A 的初等变换，指的是对A 实施如下变换：3．行列式的有关概念与性质（1）初中代数中，二元线性方程组111222,a x b y c a x b y c +=⎧⎨+=⎩当12210a b a b -≠时，二元线性方程组有唯一解：1221122112211221c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，为了方便记忆，引入定义a c b d =ad bc -，a c b d 叫做二阶行列式， ad bc -叫做二阶行列式的展开式；设1122a b D a b =，1122x c b D c b =，1122y a c D a c =，则方程组的唯一解可表示为：xy D x D D y D⎧=⎪⎪⎨⎪=⎪⎩. （i ）0D ≠，方程组有唯一解；（ii ）0D =：①x y D D 、中至少有一个不为零，方程组无解； ②0x y D D ==，方程组有无穷多解.（3）三阶行列式的两种展开方法：①按对角线展开.123123123a b c b c a c a b=++321123132a b c b a c a b c---②按一行（或一列）展开.111222333a b ca b ca b c=123231312321213132a b c a b c a b c a b c a b c a b c++---123321322312332()()()a b c b c b a c a c c a b a b=-+-+-(4)把三阶行列式某元素所在的行和列划去，剩下的元素组成的二阶行列式，叫做这个元素的余子式；如果用,i j分别表示某个元素所在的行数和列数，那么这个元素的余子式．补充与提高：行列式运算性质：①把行列式的某一行的所有元素乘以一个数k，等于用k乘以这个行列式；②行列式中某一行所有元素的公因子可以提到行列式记号的外边；③如果行列式中某一行的元素全为0，那么这个行列式的值为0；④交换行列式的任意两行，行列式的绝对值不变，符号相反；⑤如果行列式有两行的对应元素相同，那么这个行列式的值为0；⑥如果行列式有两行的对应元素成比例，那么这个行列式的值为0；⑦如果行列式的某一行的元素都是二项式，那么这个行列式等于把这些二项式各取一项组成相应的行，而其余行不变的两个行列式的和；例如：111222222333a b ca ab bc ca b c'''+++=111222333a b ca b ca b c+111222333a b ca b ca b c'''.注意：红线上三元素的乘积均为正，蓝线上三元素的乘积均为负.乘以(1)i j+-所得的式子，叫做这个元素的代数余子式.（5）三阶行列式D 等于它的任意一行（或列）的所有元素分别和它们的代数余子式的乘积的和.例如：111222333a b c D a b c a b c ==222222a A b B c C ++.(6)三元线性方程组111122223333a x b y c z d a x b y c z d a x b y c z d ++=⎧⎪++=⎨⎪++=⎩，对应系数行列式111222333a b c D a b c a b c =,111222333x d b c D d b c d b c =，111222333y a d c D a d c a d c =，111222333z a b d D a b d a b d =.①当0D ≠时，方程组有唯一解x y z D x D D y D D z D ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩；②当0=0x y D D D =且，时，方程组有无穷多解；③当0x y D D D =且，不全为0时，方程组无解.(7)①三角形的面积公式: △ABC 的三个顶点坐标分别为112233(,),(,),(,)A x y B x y C x y ，则ABC S =△11223311121x y x y x y .②同一平面上A B C 、、三点共线的充要条件为112233111x y x y x y =0.8.1矩阵的概念例题精讲【例1】写出下列线性方程组的系数矩阵和增广矩阵：（1）3560437x y x y ++=⎧⎨=-⎩（2）214625x z y z x y z -=⎧⎪+=⎨⎪-+=⎩一个元素的代数余子式通常用这个元素相应的大写字母并附加相同的下标来表示【参考答案】（1）35356,43437-⎛⎫⎛⎫ ⎪ ⎪---⎝⎭⎝⎭ （2）1021021014,01462112115--⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭8.2矩阵的运算例题精讲【例1】已知矩阵 3 0-2 1A ⎛⎫= ⎪⎝⎭，矩阵-2 1 2 2B ⎛⎫= ⎪⎝⎭，求矩阵X ，使其满足B X A =-32．【参考答案】813320⎛⎫-⎪ ⎪ ⎪-⎝⎭【例2】已知下列矩阵⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=3110146,602413,591732C B A ，计算：（1）A(B+C) (2)(B+C)A (3)BA+CA (4)从（1）（2）（3）的计算结果你能得出什么结论？【参考答案】（1）1198245⎛⎫ ⎪⎝⎭ （2）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭ （3）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭（4）(B+C)A= BA+CA8.3二阶行列式例题精讲【例1】展开并化简下列行列式：（1）3423- （2）245lg 2lg - 【参考答案】（1）17- （2）2lg 24lg5+【例2】判断m 取什么值时，下列关于x,y 的线性方程组（1）有唯一解？（2）无解？（3）有无穷解？⎪⎩⎪⎨⎧=+-+-=--1)1()1(1)5(22y m x m y m x【参考答案】221(5)(1)(2)(3)1(1)m D m m m m m --==++-+-+221(5)2(1)(2)1(1)x m D m m m ---==-+-+11211y D m m -==++（1）1,2,3m ≠--时，方程组有唯一解；（2）13m =-或方程组无解；（3）2m =-方程组有无穷解．8.4三阶行列式例题精讲【例1】按要求计算下列行列式（1）直接化简计算行列式D=412101423--的值；（2）按照第一行展开；（3）按照第一列展开．【参考答案】（1）19D = （2）011110324142421D --=-+（3）01242431214141D ---=-+-【例2】通过对课本知识的学习，我们知道，对于三元一次方程组⎪⎩⎪⎨⎧=++=++=++333322221111dz c y b x a d z c y b x a d z c y b x a ，其中x ，y ，z是未知数，系数)3,2,1(=i c b a i i i 、、不全为零，当系数行列式D=0时，方程组无解或有无穷多解．以下是几位同学在D =0的条件下，类比二元一次方程组的解的情况，对三元一次方程组的解的情况的一些探索结论：结论一：当D=0，且0===z y x D D D 时，方程组有无穷多解结论二：当D=0，且都z y x D D D ,,不为零时，方程组有无穷多解结论三：当D=0，且0===z y x D D D 时，方程组无解．可惜的是这些结论都不正确，下面分别给出了一些反例，现在请你分析一下，这些给出的方程组分别是哪个错误结论的反例，并说出你的理由．（A ）⎪⎩⎪⎨⎧=++=++=++232132032z y x z y x z y x （B ）⎪⎩⎪⎨⎧=+=++=+0420202y x z y x y x （C ）⎪⎩⎪⎨⎧=++=++-=+230212z y x z y x y x【参考答案】（A ）x y z D D D D ====而方程组无解，是结论一的反例．（B ）x y z D D D D ====而方程组无穷多解，是结论三的反例．（C ）0125x y z D D D D ====- 而方程无解，是结论二的反例．过关演练2020年一模汇编——矩阵、行列式一、填空题【宝山2】已知5124=--λλ，则=λ . 【答案】3【解析】由行列式的运算得：524=---)()(λλ，即3=λ【杨浦2】关于x ，y 的方程组2130x y x y -=⎧⎨+=⎩的增广矩阵为【答案】211130-⎛⎫⎪⎝⎭【解析】根据增广矩阵的含义，所以是211130-⎛⎫⎪⎝⎭【长宁，嘉定，金山3】行列式12 31-的值为_______.【答案】7【解析】行列式的化简，12 31-=711--32=⨯⨯）（【浦东4】若关于y x 、的方程组为12x y x y +=⎧⎨-=⎩，则该方程组的增广矩阵为____________．【答案】111112⎛⎫⎪-⎝⎭【解析】矩阵行列式定义【松江6】若关于x y 、的二元一次方程组42mx y m x my m+=+⎧⎨+=⎩无解，则实数m =【答案】2- 【解析】令24401m D m m==-=，2m ∴=±；令22420x m D m m mm+==-=，得0m =或2；令22201y m m D m m m+==--=，得2m =或1-；因为方程组无解，0D ∴=，x D 、y D 不同时为0，2m ∴=-二、选择题【黄浦13】方程2153x x=的解集是（）【A 】{2} 【B 】{2,2}- 【C 】{1,1}- 【D 】{i,i}- 【答案】B【解析】2235,2x x -==±，解集是{2,2}-2020届高三数学一轮复习典型题专项训练6、（2019届嘉定长宁区高三二模）若线性方程组的增广矩阵为2012m n ⎛⎫⎪⎝⎭，则m n +=7、（2019届普陀区高三二模）行列式中第2行第1列元素的代数余子式的值为﹣10，则k＝．8、（2019届徐汇区高三二模）函数cos2sin ()3cos x xf x x-=在区间(0,]2π上的最小值为9、（宝山区2018高三上期末）关于x y ，的二元一次方程组x y x y 341310+=⎧⎨-=⎩1、（2019届黄浦区高三二模）行列式1247的值为 2、（2019届闵行松江区高三二模）若x 、y 的方程组10240x my x y n +-=⎧⎨-+=⎩有无穷多组解，则11m n 的值为3、（2019届浦东新区高三二模）若行列式128012x -=，则x =4、（2019届杨浦区高三二模）函数arcsin 211xx y =-的值域是5、（2019届宝山区高三二模）方程sec 301sin x x=的解集为__________的增广矩阵为（）（A ）3411310-⎛⎫⎪-⎝⎭ （B ）3411310⎛⎫ ⎪--⎝⎭ （C ）3411310⎛⎫⎪-⎝⎭ （D ）3411310⎛⎫ ⎪⎝⎭10、（奉贤区2018高三上期末）关于x 、y 的二元一次方程组的增广矩阵是⎪⎪⎭⎫⎝⎛222111c b a c b a ，则方程组存在唯一解的条件是（）．A ．⎪⎪⎭⎫⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21b b 平行 B ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 C ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫⎝⎛21b b 不平行 D ．⎪⎪⎭⎫ ⎝⎛21b b 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 11、（杨浦区2018高三上期末）已知一个关于x 、y 的二元一次方程组的增广矩阵是112012-⎛⎫⎪⎝⎭，则x y += 12、（虹口区2019届高三一模）若复数sin i 1cos iz θθ-=（i 为虚数单位），则||z 的最大值为 13、（宝山区2019届高三上期末（一模））关于,x y 的二元一次方程组的增广矩阵为12-3015⎛⎫⎪⎝⎭，则x y += ．14、（奉贤区2019届高三上期末（一模））下列以行列式表达的结果中，与sin()αβ-相等的是（）A.sin sin cos cos αβαβ- B.cos sin sin cos βαβα C. sin sin cos cos αβαβ D. cos sin sin cos ααββ-15、（黄浦区2019届高三上期末（一模））已知三阶行列式123456789，元素8的余子式的值与代数余子式的值之和为16、（闵行区2019届高三上期末（一模））方程110322x =-的解为17、（浦东新区2019届高三上期末（一模））不等式2log 1021x >的解为18、（松江区2019届高三上期末（一模））若增广矩阵为1112m m m m +⎛⎫⎪⎝⎭的线性方程组无解，则实数m 的值为19、（徐汇区2019届高三上期末（一模））若数列{}n a 的通项公式为*2()111n na n N n n=∈+，则lim n n a →∞=___________.20、（杨浦区2019届高三上期末（一模））在行列式274434651xx--中，第3行第2列的元素的代数余子式记作()f x ，则1()y f x =+的零点是参考答案：二、行列式1、－12、33、34、14[,]22ππ-+ 5、,3x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭6、37、－148、9、C 10、ｃ 11、－16012、1213、－8 14、C 15、0 16、2log 5x = 17、(4,)+∞ 18、－1 19、－1 20、－1。

矩阵与行列式基础知识-2022年学习资料

怎样求解矩阵方程？-AX=b-因此，有必要了解和学习矩阵和行列-式的相关知识，以便方便的求解矩阵方程。
矩阵的相关概念-相等矩阵-A=4与B=b同型，且-=b,i=1,,7n;j=1,,n-记为A=B.-特殊矩 -零矩阵：如-行矩阵、列矩阵：-6-10--12,-行矩阵、列矩阵也称为向量
对角矩阵：-C1-=diaga11,a22,am）-az称为对角元.-如A-9）=diae2--单位矩阵： =diag1,1,.,1
3.矩阵的数乘-设有一个矩阵A=a,是一个数，那么矩阵-入C11-λ412-入1n-22-M-入am-入m -称为矩阵A与数-的乘积（简称矩阵的数乘，记作入A.-矩阵的线性运算律：加法、数乘。-A+B=B+A-②+B+C=A+B+C-A十O=A-④-A+一A=O-1A=A
4.矩阵的乘法-我们]把矩阵C称为矩阵A与B的乘积，记作C=AB-1.乘法的定义：A=4mxs和B=b,x ,如果AB=C-则矩阵C中每个元素都是A的行，B的列对应元素之积的和。-即-Co=tky ti+aby = aby-i=1,2,L,m;j=1,2,L,n
方程组的矩阵和向量表示形式-aX+a12X3+八+anXn=b-·m个方程n个未知量的线性方程组：-a2x a22x2+A +aanx=b2-M-dmam2X2+anx=b-·向量形式-+X-即xa,+xC&2+∧ xnan=乃-·矩阵形式-即AX=-·若右端向量p=0则-却Ax=0为齐次线性方程组
矩阵与行列式基础知识-介绍
我们常常会碰到一些求解方程的问题：-2X2-3x4=-3x2+4x+7x4=-0-6x2-8x4-能否如一一次方程一样求解？-ax b-X三

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第九章矩阵和行列式初步第一课时 9.1 矩阵的概念（1）[教学目标]1、了解矩阵的产生背景，并会用矩阵形式表示一些实际问题；2、了解矩阵、行向量、列向量、方矩阵、零矩阵、单位矩阵等概念；3、理解同阶矩阵、相等的矩阵等概念；4、理解线性方程组与系数矩阵及其增广矩阵之间的转化。

[教学重点]1、与矩阵有关的概念；2、线性方程组的系数矩阵及增广矩阵的概念。

[教学难点]学习矩阵的目的。

二、概念讲解：1、上述形如13⎛⎫ ⎪⎝⎭、512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭、2313242414m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭这样的矩形数表叫做矩阵。

有时矩阵也可用A 、B 等字母表示。

4、当一个矩阵中所有元素均为0时，我们称这个矩阵为零矩阵。

如000000⎛⎫⎪⎝⎭为一个23⨯阶零矩阵。

5、当一个矩阵的行数与列数相等时，这个矩阵称为方矩阵，简称方阵，一个方阵有n 行（列），可称此方阵为n 阶方阵，如矩阵512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫⎪- ⎪ ⎪-⎝⎭均为三阶方阵。

在一个n 阶方阵中，从左上角到右下角所有元素组成对角线，如果其对角线的元素均为1，其余元素均为零的方阵，叫做单位矩阵。

如矩阵1001⎛⎫ ⎪⎝⎭为2阶单位矩阵，矩阵100010001⎛⎫⎪⎪ ⎪⎝⎭为3阶单位矩阵。

6、如果矩阵A 与矩阵B 的行数和列数分别相等，那么A 与B 叫做同阶矩阵；如果矩阵A 与矩阵B 是同阶矩阵，当且仅当它们对应位置的元素都相等时，那么矩阵A 与矩阵B 叫做相等的矩阵，记为A B =。

7、对于方程组231324244x y mz x y z x y nz ++=⎧⎪-+=⎨⎪+-=⎩中未知数z y x ,,的系数按原来的次序排列所得的矩阵2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭，我们叫做方程组的系数矩阵；而矩阵2313242414m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭叫做方程组的增广矩阵。

三、应用举例：例1、下表是我国第一位奥运会射箭比赛金牌得主张娟娟与对手韩国选手朴成贤在决赛中的（1）将两人的成绩各阶段成绩用矩形表示；（2）写出行向量、列向量，并指出其实际意义。

解：（1）2627292811029262628109⎛⎫⎪⎝⎭（2）有两个行向量，分别为：()126272928110a =，()229262628109a =，它们分别表示两位运动员在决赛各阶段各自成绩；有五个列向量，分别为1234526272928110,,,,29262628109b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=====⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭它们分别表示两位运动员在每一个阶段的成绩。

例2、已知矩阵222,22x x y b a A B x a b y x y ---⎛⎫⎛⎫== ⎪ ⎪++⎝⎭⎝⎭且A B =，求a 、b 的值及矩阵A 。

解：由题意知：22x y x y -=⎧⎨=⎩解得：24x y =-⎧⎨=-⎩，又由222214b a x a b x y -=-=⎧⎨+=+=⎩解得：26a b =⎧⎨=⎩， 22414A ⎛⎫=⎪-⎝⎭例3、写出下列线性方程组的增广矩阵：（1）23146x y x y +=⎧⎨-=⎩；（2）23203250230x y z x y z x y z +-+=⎧⎪-++-=⎨⎪-++=⎩解：（1）231416⎛⎫ ⎪-⎝⎭；（2）123213252113--⎛⎫⎪- ⎪⎪--⎝⎭例4、已知线性方程组的增广矩阵，写出其对应的方程组：（1）235124-⎛⎫ ⎪-⎝⎭ （2）210203213023-⎛⎫⎪- ⎪ ⎪-⎝⎭ 解：（1）23524x y x y +=-⎧⎨-+=⎩ （2）22321323x y y z x z -=⎧⎪-=⎨⎪+=-⎩例5、已知矩阵sin cos 0sin cos 1ααββ+⎛⎫⎪+⎝⎭为单位向量，且,,2παβπ⎡⎫∈⎪⎢⎣⎭，求()sin αβ-的值。

解：由单位向量定义可知：sin cos 1sin cos 0ααββ+=⎧⎨+=⎩，,,2παβπ⎡⎫∈⎪⎢⎣⎭，234παπβ⎧=⎪⎪∴⎨⎪=⎪⎩()sin sin 42παβ⎛⎫∴-=-=- ⎪⎝⎭。

四、课堂练习：1、请根据游戏“剪刀、石头、布”的游戏规则，作出一个3阶方阵（胜用1表示，输用1- 表示，相同则为0）。

解：011101110-⎛⎫ ⎪- ⎪ ⎪-⎝⎭2、奥运会足球比赛中国队所在C 组小组赛单循环比赛结果如下：中国平新西兰1∶1 巴西胜比利时1∶0 中国负比利时0∶2巴西胜新西兰5∶0 中国负巴西0∶3 比利时胜新西兰0∶1（1）试用一个4阶方阵表示这4个队之间的净胜球数；（以中国、巴西、比利时、新西兰为顺序排列）（2）若胜一场可得3分，平一场得1分，负一场得0分，试写出一个4阶方阵表示各队的得分情况；（排列顺序与（1）相同）（3）若最后的名次的排定按如下规则：先看积分，同积分看净胜球，试根据（1）、（2）两个矩阵确定各队名次。

解：（1）0320301521010510--⎛⎫⎪⎪⎪-⎪--⎝⎭（2）0001303330031000⎛⎫⎪⎪⎪⎪⎝⎭（3）名次为巴西、比利时、中国、新西兰。

五、小结：本课学习了矩阵及与矩阵相关的一些概念。

六、作业：习题册P45习题9.1A组1、2；P46 习题9.1B组1。

第二课时 9.1 矩阵的概念（2）格致中学王国伟[教学目标]1、掌握矩阵的三种基本变换；2、掌握运用矩阵基本变换求线性方程组的解。

[教学重点]运用矩阵基本变换求线性方程组的解。

[教学难点]如何利用系数矩阵判断线性方程组是否有解。

[教学过程]一、复习引入：根据下列增广矩阵，写出其对应的线性方程组，并分析这些增广矩阵所对应线性方程组解的关系，从中你能得到哪些启发？（1）213322-⎛⎫⎪-⎝⎭（2）322213-⎛⎫⎪-⎝⎭（3）1312222133⎛⎫-⎪⎪⎪- ⎪⎝⎭（4）1312211366⎛⎫-⎪⎪⎪⎪⎝⎭（5）10811366⎛⎫⎪⎪⎪⎝⎭（6）1080113⎛⎫⎪⎝⎭解：这些方程组为23322x yx y-=⎧⎨-+=⎩；32223x yx y-+=⎧⎨-=⎩；13222233x yx y⎧-=⎪⎪⎨⎪-+=⎪⎩；132211366x yy⎧-=⎪⎪⎨⎪=⎪⎩；811366x y =⎧⎪⎨=⎪⎩；813x y =⎧⎨=⎩。

这些增广矩阵所对应的线性方程组的解都是相同的。

二、新课讲解：通过上面练习，我们可以发现以下三个有关线性方程组的增广矩阵的基本变换：（1）互换矩阵的两行；（2）把某一行同乘（除）以一个非零的数；（3）某一行乘以一个数加到另一行。

显然，通过以上三个基本变换，可将线性方程组的系数矩阵变成单位矩阵，这时增广矩阵的最后一个列向量给出了方程组的解。

三、应用举例：例1、已知每公斤五角硬币价值132元，每公斤一元硬币价值165元，现有总重量为两公斤的硬币，总数共计462个，问其中一元与五角的硬币分别有多少个？（来自网上“新鸡兔同笼问题”）解：设一元硬币有x 个，五角硬币有y 个，则根据题意可得：4620.52165132x y x y+=⎧⎪⎨+=⎪⎩ 则该方程组的增广矩阵为11462112165264A ⎛⎫⎪= ⎪ ⎪⎝⎭，设①、②分别表示矩阵A 的第1、2行，对矩阵A 进行下列变换：11462112165264⎛⎫ ⎪ ⎪ ⎪⎝⎭ 11462116658⎛⎫ ⎪ ⎪--- ⎪⎝⎭ 1146231320405⎛⎫⎪⎪ ⎪⎝⎭1146201352⎛⎫ ⎪⎝⎭ 1011001352⎛⎫⎪⎝⎭由最后一个矩阵可知：110352x y =⎧⎨=⎩答：一元硬币有110个，五角硬币有352个。

例2、用矩阵变换的方法解三元一次方程组4357245238x y z x y z x y z +-=⎧⎪++=⎨⎪--=⎩的解。

解：此方程对应的增广矩阵为：431572145238-⎛⎫ ⎪⎪ ⎪--⎝⎭②()33⨯-①不变 ①15⨯加到② ①不变 ②403⨯①不变 ②(1)⨯-加到① ②不变设此矩阵第1、2、3行分别为①、②、③，对此矩阵进行下列变换：431572145238-⎛⎫ ⎪ ⎪ ⎪--⎝⎭ 115097214264020⎛⎫ ⎪ ⎪ ⎪⎝⎭115097214131052⎛⎫ ⎪⎪ ⎪ ⎪⎪⎝⎭ 43001626016131052⎛⎫-- ⎪⎪-- ⎪ ⎪ ⎪⎝⎭ 32100436016131052⎛⎫ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭ 32100436600143701043⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪⎪ ⎪⎝⎭32100437010436600143⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎪- ⎪⎝⎭， ∴此方程组的解为32437436643x y z ⎧=⎪⎪⎪=⎨⎪⎪=-⎪⎩说明：1、利用矩阵基本变换，将矩阵的每一个行向量所对应的方程只有一个变量；2、在变换过程中，实际为加减消元的过程，此过程中应根据数字的特点，运用适当的程序进行化简运算。

例3、运用矩阵变换方法解方程组：322ax y x y b+=⎧⎨-=⎩（a 、b 为常数）解：此方程组对应的增广矩阵为：3221a b ⎛⎫⎪-⎝⎭，设①、②分别表示此矩阵的第1、2行，对此矩阵进行下列变换：3221a b ⎛⎫⎪-⎝⎭ 602321a b b ++⎛⎫⎪-⎝⎭ⅰ）当60a +≠，即6a ≠-时，以上矩阵可作如下变换：2310621b a b +⎛⎫ ⎪+ ⎪ ⎪-⎝⎭231064016b a ab a +⎛⎫ ⎪+⎪- ⎪- ⎪+⎝⎭ ②加到① ②3⨯加到③ ②不变 ③(2)⨯-加到② ③(5)⨯-加到① ③不变③14⨯①、②不变①2()43⨯-②、③不变①6⨯加到②①13()2⨯-加到③ ①不变交换②、③ ①不变②3⨯加到① ①不变 ①16a ⨯+ ②不变①(2)⨯-加到② ①不变231064016b a ab a +⎛⎫ ⎪+⎪-⎪ ⎪+⎝⎭，∴此时方程有唯一解23646b x a ab y a +⎧=⎪⎪+⎨-⎪=⎪+⎩； ⅱ）当60a +=即6a =-时，若230b +≠即23b ≠-时，方程组无解； ⅲ）当60a +=即6a =-时且23b =-时，方程组有无穷多解，它们均符合6320x y -+=。