流体力学第五章孔口管嘴出流与管路水力计算

合集下载

第五章孔口、管嘴及有压管路

c 1
2
v
1
2 gH 0 n 2 gH 0
Q vA n A 2 gH 0 n A 2 gH 0
其中ζ 为管嘴的局部阻力系数，取0.5；则
流速系数流量系数
n
1 1 0.82＜孔口 0.97 ~ 0.98 1 0.5
n n 0.82 ＞孔口 0.60 ~ 0.62
图1：Q1
Q2；图2：Q1
Q2。（填>、< 或＝）
第五章有压管流
问题：水位恒定的上、下游水箱，如图，箱内水深为
H 和h。三个直径相等的薄壁孔口1,2,3位于隔板上的
不同位置，均为完全收缩。问：三孔口的流量是否相等？为什么？若下游水箱无水，情况又如何？
答案
1=2，3不等；三孔不等
第五章有压管流
v孔口孔口 2 gH孔口孔口 0.97 1 vn n 0.82 n 2 gHn
2.流量比较
Q孔口孔口 A孔口 2 gH孔口孔口 0.62 1 Qn n 0.82 n An 2 gHn
第五章有压管流
【例】为使水流均匀地进入混凝沉淀池，通常在进口处建一道穿孔墙如图，通过穿孔墙流量为125L/s，设若干个15cmⅹ15cm的孔口，按规范要求通过孔口断面平均流速在0.08~1.0m/s，试计算需若干孔口？
容器放空（即H2＝0）时间 t0
2 A0 H1
2 A0 H1 2V A g A 2 gH1 Qmax
结论：在变水头情况下，等横截面的柱形容器放空（或充满）所需的时间
等于在起始水头H1下按恒定情况流出液体所需时间的两倍。
第五章有压管流
第二节、管嘴岀流

流体力学水力学第五章

7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算（Q、d、H）有压流：水沿管道满管流动的水力现象。特点：水流充满管道过水断面，管道内不存在自由水面，管壁上各点承受的压强一般不等于大气压强。
短管：局部水头损失和速度水头在总水头损失中占有相当的比重，计算时不能忽略的管道. （一般局部损失和速度水头大于沿程损失的5% ~ 10%）。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数： c 0 1 0
1 1 流速系数： c 0 1 0
实验得： 0.97 ~ 0.98 1 推求： 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3：如图所示圆形有压涵管，管长50m, 上下游水位差3m 沿程阻力系数为0.03，局部阻力系数：进口 1＝0.5。第一个转弯 2＝0.71，第二个转弯 3＝0.65，出口
4＝1.0，要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g

v

v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g

v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g

流体力学第5章孔口管嘴出流与管路水力计算

5.2.3 其他类型管嘴出流
对于其他类型的管嘴出流，其流速、流量的计算公式与圆柱形管嘴公式形式相似。但流速系数及流量系数各不相同，下面是几种常用的管嘴。
1. 流线形管嘴如图 5.4(a)所示，流速系数ϕ = μ = 0.97 ，适用于水头损失小，流量大，出口断面上速度分布均匀的情况。
2. 扩大圆锥形管嘴如图 5.4(b)所示，当θ = 5°～7°时，μ＝ϕ＝0.42～0.50 。适合于将部分动能恢复为压能的情况，如引射器的扩压管。
流体力学
收缩产生的局部损失和断面 C―C 与 B―B 间水流扩大所产生的局部损失，相当于一般锐缘
管道进口的局部损失，可表示为 hw
=ζ
VB 2 2g
。将
hw 代入上式可得到：
H0
=
(α
+ζ
) VB2 2g
其中， H 0
=
H
+
α
AV
2 A
2g
，则可解得：
V=
1 α + ζ 2gH 0
=ϕ
2gH 0
(5-8)
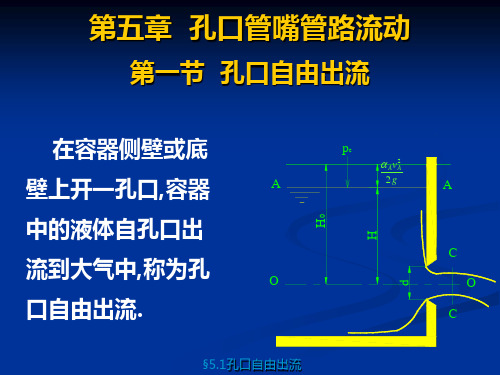
1. 自由出流流体经孔口流入大气的出流称为自由出流。薄壁孔口的自由出流如图 5.1 所示。孔口出流经过容器壁的锐缘后，变成具有自由面周界的流股。当孔口内的容器边缘不是锐缘状时，出流状态会与边缘形状有关。
图 5.1 薄壁孔口自由出流
由于质点惯性的作用，当水流绕过孔口边缘时，流线不能成直角地突然改变方向，只能以圆滑曲线逐渐弯曲，流出孔口后会继续弯曲并向中心收敛，直至离孔口约 0.5d 处。流
5.3.1 短管计算
1. 自由出流
流体经管路流入大气，称为自由出流 ( 图 5.5) 。设断面 A ― A 的总水头为

工程流体力学课件5孔口、管嘴出流及有压管流

H
0v02 2g
v2 2g
hw
忽略管嘴沿程损失，且令
H0
H
0v02
2g
则管嘴出口速度
v 1
2gH0 n 2gH0
Q vA n A 2gH0 n A 2gH0
其中ζ为管嘴的局部阻力系数，取0.5；则
流速系数流量系数
n
1
1 0.82 ＜孔口 0.97 ~ 0.98 1 0.5
说明管嘴过流能力更强
l1, l2 ,1, 2 , n, 1, 2 , 3
求泄流量Q，画出水头线
3
Rd 4
R, n
C
1 n
1
R6
8g C2
1, 3 H
1
2 l1
2
l2
v
1
2gH
1
l d
1
2
1
出口断面由A缩小为A2
出口流速
v2
管内流速
v2
A2 A
3
新增出口局部损失 3
v2
2gH
13
(
l d
1
2
)
A2 A
2
= =
H+h 0
h
v2
l v2
v2
( )
2g
d 2g
2g
1
用3-3断面作下游断面
O1
H
v
23
h O 出口水头损失
按突扩计算 23
( z1
p1
1v12
2g
) (z3
p3 )
3v32
2g
h f 12
h j12 h j23
= = = = =
H+h

第五章管道11

分类:根据短管出流的形式不同，可将其分为自由出流和淹没出流两种。
测压管水头线的定性分析
1
V0≈0
p g
O 1
H
V2 2g
V02 2g
V0≠0
V2 2g
1
V0≠0
1
V2
2
2g
V下≈0
2
1
V0≠0
1
V2
2
2g
V下≠0
2
自由出流
自由出流——短管中的液体经出口流入大气，水股四周受大气压作用。
H
pa
g
av02
2g
0
pa
g
av22
2g
hw , v2
0
H0
H
av02
2g
,
v
1
l d
2gH0 ,
Q
v
A
c
d
4
2
2gH0 .
c
1
,
l d
自由出流与淹没出流的异同点
相同点：
流量计算公式的形式以及流量系数的数值均相同
不同点：
两者的作用水头在计量时有所不同，自由出流时是指上游水池液面至下游出口中心的高度，而淹没出流时则指得是上下游水位差。
d 100 ~ 400mm, 经济流速v =0.6~1.0m/s； d速4v00mm，经济流 =1.0~1.4m/s。
假设：将这种沿程均匀泄流看成是连续的
dhf S0QM2 dx
QM=Q+qx
H
hf
S0l
Q
2
Qql
1 q2l 2 3
近似
H S0lQc2 Qc Q 0.55ql
Qｃ－计算流量

流体力学孔口管嘴出流与管路水力计算

流体力学孔口管嘴出流与管路水力计算流体力学是研究流体运动和力学性质的物理学科。

在水力学中，孔口管嘴出流和管路水力计算是流体力学的一个重要应用。

1.孔口管嘴出流孔口管嘴出流是指在一定压力差下，流体从孔口或管嘴中流出的现象。

它是一种自由射流，不受管道限制，流速和流量可以自由变化。

对于理想流体来说，根据贝努利定律和连续性方程，可以得出孔口管嘴出流速度的计算公式：v = √(2gh)其中，v为出流速度，g为重力加速度，h为液面距离孔口或管嘴的高度差。

可以看出，出流速度与液面高度差成正比，与重力加速度的平方根成正比。

对于真实流体来说，考虑到粘性和摩擦等因素，出流速度会稍有减小。

此时，可以使用液体流量系数进行修正。

液体流量系数是指实际流量与理论流量之比，一般使用实验数据来确定。

根据实验结果，可以通过乘以液体流量系数来修正出流速度的计算。

管路水力计算是指在给定管道材料、管径和流体性质的条件下，计算流体在管路中的流动状态、压力损失以及流量等参数。

管路水力计算是实际工程中常见的问题，它可以帮助我们了解管道的输送性能和节能问题。

管道中的流体运动受到多个因素的影响，包括管道长度、管道粗糙度、流速、流量等。

在水力学计算中，一般常用的公式有达西公式和罗斯诺-魏谢巴赫公式。

达西公式可以用来计算管道中流体的摩阻损失，它的计算公式为：ΔP=λ(L/D)(v^2/2g)其中，ΔP为管道中的压力损失，L为管道长度，D为管道直径，v为流速，g为重力加速度，λ为摩阻系数，也称为达西摩阻系数。

罗斯诺-魏谢巴赫公式则可以用来计算管路中流体的水力损失，它的计算公式为：ΔP=ρ(h_f+h_m)其中，ΔP为管路中的总压力损失，ρ为流体密度，h_f为摩阻压力损失，也称为莫阿P（Moody）摩阻，h_m为各种表面或局部的附加压力损失。

除了达西公式和罗斯诺-魏谢巴赫公式，还有一些经验公式和图表可以用来计算管路的压力损失和流量。

这些公式和图表都是根据实验数据和经验总结得出的，可以帮助工程师在实际应用中进行快速计算。

流体力学第五章

确定流态确定流态
确定 β 、或 λ m 确定 β 、或 λ m
Δ pp Δ
第五章压力管路的水力计算
•
第二类问题：已知： Δp ，Δz ，d，L，μ，γ，求：Q 分析：
Q Q
vv
Re =
？？
vd ν
h h ff
确定流态确定流态
？
Δ pp Δ
确定 β 、或 λ m 确定 β 、或 λ m
管路特性曲线是管路能量平衡（能量供给 =能量消耗）的直观反映。对于给定管路，其特性曲线一定。如：对于长管无泵和有泵两种情况，管路特性曲线如下图：
hf
H H0 hf z2-z1 Q Q
H0
•
管路特性曲线对于确定泵的工况以及自由泄流工况有重要应用价值。第五章压力管路的水力计算
§5.2 长管的水力计算
说明：
– 紊流流态——混合摩擦区（大庆设计院推荐公式）：
Q1.877ν 0.123 L h f = 0.0802 A d 4.877
其中：A = 10( 0.127 lg ε − 0.627 ) , ε = 即：β＝ 0.0802A，m＝0.123 – 紊流流态——水力粗糙区：
∆ ∆ = r 2d
3. 给定管路流量 Q，在已建成的长输管线 AB段改设串联变径管可以延长管路的输送距离。
设变径管后
hfO -A fO-A H
未设变径管前
hfO -B fO-B
hf
O
A
B
C
串联变径管后，主管 AB段d（↑），v （↓），hf （↓），即：hfO -B fO-B <hf。则：作用水头 H仍有部分能量剩余，可供给管中水流继续前进一段距离至C点。第五章压力管路的水力计算

第五章孔口、管嘴出流和有压管路

(2)管嘴长度l=(3～4)d。
5.2.4 其他形式管嘴

工程上为了增加孔口的泄水能力或为了增加(减少)出口的速度，常采用不同的管嘴形式

(1)圆锥形扩张管嘴（θ=5～7° ） (2)圆锥形收敛管嘴（较大的出口流速） (3)流线形管嘴（阻力系数最小）
孔口、管嘴的水力特性
5.3 有压管路恒定流计算
1
从 1→2 建立伯努利方程，有
v2 H 0 00 n 2g 2g 2g
l (3 ~ 4)d
0v0 2
v 2
H
c
0 d
2
0
1 v n
2 gH0 n 2 gH0
c
2
n 0.5
式中：
1 n n
1
n 为管咀流速系数， n 0.82
pc

0.75H 0

对圆柱形外管嘴：
α=1， ε=0.64， φ=0.82
5.2.3 圆柱形外管嘴的正常工作条件

收缩断面的真空是有限制的，如长江中下游地区，当真空度达7米水柱以上时，由于液体在低于饱和蒸汽压时会发生汽化。圆柱形外管嘴的正常工作条件是： (1)作用水头H0≤9米；

5.2 管嘴出流
一、圆柱形外伸管嘴的恒定出流

计算特点: 出流特点:
hf 0
在C-C断面形成收缩，然后再扩大，逐步充满整个断面。 1
l (3 ~ 4)d
H
c
0 d
2
0
c
2
1

在孔口接一段长l=(3～4)d的短管，液流经过短管并充满出口断面流出的水力现象成为管嘴出流。根据实际需要管嘴可设计成： 1）圆柱形：内管嘴和外管嘴 2）非圆柱形：扩张管嘴和收缩管嘴。

工程流体力学第5章管路管嘴

以0-0作为基准面，写出1-1和2-2断面的总流伯努利方程 2 2 p a 1 v1 pa 2 v2 H 0 hl 2g 2g 上式中， v1

0
因为是长管，忽略局部阻力
2 2
2v h r 和速度水头，则 hl h f ，故 2g H hf （5.1）
5.1.2 长管的水力计算

对于一般输水管道，常取y =1/6，即曼宁公式 1 1 c R6 （5.5） n 管壁的粗糙系数值随管壁材料、内壁加工情况以及铺设方法的不同而异。一般工程初步估算时可采用表5.1数值。

5.1.2 长管的水力计算
序号 1 壁面种类及状况安装及联接良好的新制清洁铸铁管及钢管；精刨木板
5.1.1 短管的水力计算
水泵的吸水管、虹吸管、液压传动系统的输油管等，都属于短管，它们的局部阻力在水力计算时不能忽略。短管的水力计算没有什么特殊的原则，主要是如何运用前一章的公式和图表。
[例题5.1] 水泵管路如图5.1所示，铸铁管直径d=150mm，管长 l=180m ，管路上装有吸水网（无底阀）一个，全开截止阀一个，管半径与曲率半径之比为 r/R=0.5 的弯头三个，高程h=100m，流量 Q=225m3/h，水温为20℃。试求水泵的输出功率。
5.2.2 并联管路
根据连续性方程，有 Q Q1 Q2 Q3 （5.11）根据式（5.10）和式（5.11）可以解决并联管路水力计算的各种问题。强调：虽然各并联管路的水头损失相等，但这只说明各管段上单位重量的液体机械能损失相等。由于并联各管段的流量并不相等，所以各管段上全部液体重量的总机械能损失并不相等，流量大的管段，其总机械能损失也大。

流体力学泵与风机-第5章

vC 1
§5.2
孔口淹没出流
1 2
2 gH0
1 2 H
O
v1
H1
C
vC
H2
O
C 1 2
流量： Qv
C
AC vCA A 2gH0 A 2gH0
收缩系数 AC / A 流速系数流量系数
1
1 2

1 1 1
淹没出流和自由出流比较（1）计算公式一样，各项系数值相同，但要注意，流速系数含义不同；自由出流淹没出流

p a pC

0.75H 0
A
H
A
C
B
表明在收缩断面的真空度是作用 O 水头的75%，管嘴的作用相当于将孔口自由出流的作用水头增大了75%，从而管嘴流量大为增加。
d
C
vC l
B
O
4、圆柱外管嘴的正常工作条件
由公式
作用水头H0越大，收缩断面真空度也越大。当收缩断面真空度超过7m水柱时，空气将会从管嘴出口断面被“吸入”，使收缩断面真空被破坏，管嘴不能保持满管出流。
第二类问题的计算步骤（例题4-8，习题4-12）（2）已知hf 、 l、 d 、、 K/d ，求Q；
假设
由hf计算 v 、Re
= New
由Re、 K/d查莫迪图得New
N
校核 New
Y
由v 、 d计算 Q
初始可假设为粗糙区数值
第三类问题的计算步骤（习题4-7）（3）已知hf 、 Q 、l 、、 K，求d。 hf Q l K/d 计算与 d的函数曲线假设求d、v
阻力平方区， SH，Sp是常数
(1)SH,Sp综合反映了管路的沿程阻力和局部阻力情况,称为管路阻抗 (2)简单管路中，总阻力损失与体积流量平方成正比(阻力平方区)

第五章孔口管嘴出流及管路计算

hw 2 s2
1 s2
hw 3 s3
1 s3
Q1 Q2
s2
Q2 ; s1 Q3
s3
Q3 ; s1 Q1
s3 s1
或者：
Q1 : Q2 : Q3 1 s1 : 1 s2 : 1 s3
流量分配规律
第四节流体通过缝隙液流动一、平行平板缝隙图示为在两块平行平板所形成的缝隙间充满了液体，缝隙高度为h，缝隙宽度和长度为b和l，且一般恒有b＞＞h和l＞＞h。
QA QB QC Q0 Q
管路水力计算
2.阻力损失关系：串联管路系统的总水头损失（压头）损失等于各管段水头损失之和。
hw hw A hwB hwC
2 2 2 hw S A Q A S B QB S C QC
第三节
三、并联管路计算
由不同直径或粗糙度的简单管道连接在一起的管道叫做串联管道 1.流量关系：
管路水力计算
列1-1及2-2断面伯努利方程：
2 pa v12 p a v2 H 0 hw g 2 g g 2 g 2 v2 H hw 2g v2 l 对于短管： hw h f h j d 2g l 8 hw 2 4 Q 2 hw SQ2 d gd
第二节
1、管嘴出流流量
管嘴出流
以管嘴中心线为基准线，列1-1及b-b断面伯努利方程：
αV V2 H ζ 2g 2g 2g
2 1 1
α V2
令
1
H0 H
1v12
2g
管嘴出口速度为
V
αζ
2 gH0 n 2 gH0
管嘴流量 Q VA n A 2gH 0 un A 2gH 0

第5章孔口、管嘴出流和有压管路 121页PPT文档

（1）虹吸管的水力计算
虹吸管是一种压力输水管道，顶部弯曲且其高程高于上游供水水面。在虹吸管内造成真空，使水流则能通过虹吸管最高处引向其他处。
虹吸管的优点在于能跨越高地，减少挖方。虹吸管长度一般不长，故按照短管计算。
1 pa
1
虹吸管顶部 zs
2z
2
虹吸管顶部的真空的理论值不能大于最大真空值（10mH2O）。
孔口、管嘴的水力特性
§5.3 简单短管中的恒定有压流
简单管道的水力计算可分为自由出流和淹没出流两种情况。
1.自由出流
管道出口水流流入大气，水股四周都受大气压强的作用，称为自由出流管道。
图5－1中，列断面1－1、2－2的能量方
程z1p 12 1 g1 2z2p 22 2 g2 2hw 12
小孔口：H/d>10
1)小孔口的自由出流
pc=pa=0
hw
hj
0
v22 2g
H
0v02
2g
( c

0
)
vc2 2g
vc
1 c 0
2gH0 2gH0
Q vc Ac A 2gH0 A 2gH0

薄壁小孔口自由出流的基本公式
薄壁小孔口出流的各项系数
当虹吸管内压强接近该温度下的汽化压强时，液体将产生汽化，破坏水流连续性，可能产生空蚀破坏，故一般虹吸管中的真空值7～8mH2O。
例有一渠道用两根直径为1.0m的混凝土虹吸管来跨越山丘，渠道上游水位为▽1＝100.0m，下游水位为▽2 ＝99.0m，虹吸管长度l1 = 8m l2= 15m；l3 = 15m，中间有60°的折弯两个，每个弯头的局部水头损失系数为 0.365，若进口局部水头损失系数为0.5；出口局部水头损失系数为1.0。试确定：

《流体力学》第五章孔口管嘴管路流动

2g
A
C O
C
(C
1)
vc2 2g

(ZA
ZC )
pA

pC

Av
2 A
2g
令
H0

(Z A
ZC )
pA

pC
AvA2
2g
§5.1孔口自由出流
1
则有
vc

c 1
2gH0
H0

(Z A
ZC )
pA

pC
AvA2
2g
H0称为作用水头,是促使
力系数是不变的。
§5.4 简单管路
SH、Sp对已给定的管路是一个定数，它综合反映了管路上的沿程和局部阻力情况，称为管路阻抗。
H SHQ2
p SpQ2
简单管路中，总阻力损失与体积流量平方成正比。
§5.4 简单管路
例5-5：某矿渣混凝土板风道，断面积为1m*1.2m, 长为50m，局部阻力系数Σζ=2.5，流量为14m3/s, 空气温度为20℃，求压强损失。

2v22
2g
1
vc2 2g
2
vc2 2g
令 H0 (H1 ζH12:局)液部体p阻1 经力p孔2系口数处1v的122g1 2v22
1
H1 H
H2
2
2
H0 (1 2 ) 2vcg2突ζ然2:液扩体大在的收局缩部断阻面力之系后数 C
C
§5.2 孔口淹没出流
1
c 1
2gH0
Q A 2gH0 A 2gH0
出流
H0

5.孔口、管嘴出流和有压管流

2
v2 n 2 gH0
2
A2 1 2 1 1 A c
2 2 2 a c pv p a pc a c 1 v2 1 2 2 a 1 2 a 1 n H 0 g g 2 g
A.Q1=Q2；
B.Q1>Q2；
C.Q1<Q2； D.关系不定。
四、应用
1.虹吸管的水力计算（略）
管道轴线的一部分高出无压的上游供水水面，
这样的管道称为虹吸管。因为虹吸管输水，具有能
跨越高地，减少挖方，以及便于自动操作等优点，在工程中广为应用。
虹吸现象
流速 v 2 gH0
1 l1 l2 d 1 2
3、分析：
水击现象只发生在液体中，因气体的压缩性很大，而液体的较小，故当液体的受压急剧升高时就会产生水击；管壁具有足够的刚性才可能产生水击；如果液体是不可压缩的，管壁是完全刚性的，则水击压强可达到无限大。
二、水击的传播过程以较简单的阀门突然关闭为例 1、分析：
与自由出流一致
结论 1、流量公式：
Q A 2 gH 0
2、自由式与淹没式对比： 1> 公式形式相同； 2> φ、μ基本相同，但 H0不同； 3> 自由出流与孔口的淹没深度有关，
淹没出流与上、下游水位差有关。
z H v0 v0 v2
自由式： H0 = H + v02 2g
淹没式： v02 2g v22 2g
2F
A
H H' 2g
解得
H ' 2.44
一昼夜的漏水量
V ( H H ' ) F 8.16m3

第五章孔口管嘴出流及管路计算

由边界条件，
y 0 ,u 0 ;和 y h ,u u 0 ,C1

u0 h

h
2
dp dx
C2 0
在缝隙流中压力沿运动方向的变化率是一常数，有 dp p2p1 -p
dx l
l
速度表达式
u y hypu0 y
2l
h
流量表达式
q 0 h u d y b b 0 (2 1 lh y p u h 0 )y y 1 b b 3 l2 Δ d h p b 2 u 0 h
根管子串联在一起的管道系统叫简单管道。 1.管路计算有三类计算问题：
1）已知管路布置及流量Q，确定管径d和进行水头损失计算。
2）已知流量Q和作用压头H，确定管径d。
3）已知直径d和作用压头H，确定流量Q。
第三节管路水力计算
2、管路计算中常用术语 1）长管和短管（速度水头与局部水头损失小于
沿程损失的5%按短管计算） 2）标准管径 3）经济流速
1.平行平板缝隙（压差和剪切共同作用）
平行六面体在x方向的受力平衡方程式为
p d y ( d ) d x ( p d p ) d d y x
整理后得,
d dp dy dx
而 du dy
因此有
d 2u 1 dp
dy 2 dx
积分后得 u21ddxpy2C1yC2
用 d 代替b
偏心环缝隙流量
用 dbrd代替b
rh3d hrd
dq p 1u 2l
2
u0
h h 0 ec o h s(1 c o )s
e/ ——偏心率
qd0 3h Δ p11.52 1u2l

流体力学例题及思考题-第五章

第五章压力管路的水力计算主要内容长管水力计算短管水力计算串并联管路和分支管路孔口和管嘴出流基本概念：1、压力管路：在一定压差下，液流充满全管的流动管路。

（管路中的压强可以大于大气压，也可以小于大气压）注：输送气体的管路都是压力管路。

2、分类：按管路的结构特点，分为简单管路：等径无分支复杂管路：串联、并联、分支按能量比例大小，分为长管：和沿程水头损失相比，流速水头和局部水头损失可以忽略的流动管路。

短管：流速水头和局部水头损失不能忽略的流动管路。

第一节管路的特性曲线一、定义：水头损失与流量的关系曲线称为管路的特性曲线。

二、特性曲线（1）把225222284212QQdgLdQgdLgVdLhwαπλπλλ==⎪⎭⎫⎝⎛==（2）把上式绘成曲线得图。

第二节长管的水力计算一、简单长管1、定义：由许多管径相同的管子组成的长输管路，且沿程损失较大、局部损失较小，计算时可忽略局部损失和流速水头。

2、计算公式：简单长管一般计算涉及公式2211A V A V = （3） fh p z p z +++γγ2211＝（4）g VD L h f 22λ= （5）说明：有时为了计算方便，h f 的计算采用如下形式：mmmf dLQh --=52νβ（6）其中，β因为g VD L h f 22λ= 且所以（7）a. 层流时，Re 64=λ 代入（7）式得：15112415.415.4--==dLQdL Q h f νν即：β＝ 4.15，m ＝1 b. 水力光滑区，25.0Re3164.0=λ代入（7）式得：25.0525.025.0175.425.075.10246.00246.0--==dLQdLQh f νν即：β＝ 0.0246，m ＝1c. 由大庆设计院推得经验公式，在混合区：877.4123.0877.10802.0dLQAh f ν=即：β＝ 0.0802A ，m ＝0.123其中，()0627.0lg 127.0,10r A ∆==-εεd. 粗糙区5225220826.082dL Q Q dg L gVd L h f λπλλ===即：β＝ 0.0826λ，m ＝03、简单长管的三类计算问题（1）第一类：已知：输送流体的性质 μ，γ管道尺寸 d ，L ，Δ 地形 Δz流量 Q ，，求：h f ，Δp ，i解：Q →V确定流态 → β， m ，λ → h f → 伯努利方程求Δp（2）第二类：已知：μ，γ，d ，L ，Δ，Δz ，Δp 求：Q解：Q 未知→流态也未知→ β， m ，λ 无法确定 → 试算法或绘图法A. 试算法a 、先假设一流态，取β， m 值，算出Q ’f pz h ∆+∆=γb 、Q ’ →m ’ ，校核流态如由 Q ’ →Re ’ 和假设一致， Q ’ 即为所求Q c 、如由 Q ’ →定出的流态和假设不一致，重复a 。

流体力学第五章孔口管嘴出流与管路水力计算

Q VB AB A 2gH0 A 2gH0
H0 作用总水头
流速系数流量系数
相对压强： pC
g
0.75 H 0
真空值：
pV
g
0.75 H 0
§5-3 简单管路
简单管路：管径不变、没有分叉的管路。
复杂管路：由两根或两根以上简单管路组合而成的管道系统。
短管：局部损失和流速水头之和大于总水头的5%。
Q1
H hf CD
AB
Q2
C
D
Q3
三、管网
(a)分枝状管网
(b)环状管网
（1）任一结点处，流出结点的流量与流入结点的流量应相等：
Qi 0
（2）任一环路中，由某一结点沿不同方向到另一个结点的能量损失应相等：
hf 0
•
感
感谢阅
谢阅
读
读
l
d
一、小孔口自由出流
对截面A-A和收缩断面C-C列总流能量方程
zA
pA
g
AVA2
2g
zC
pC
g
CVC2
2g
hm
O
H0
( C
) VC2 2g
A
Av
2 A
2g
H
H0
d vA
A
C
O
vC C
1
VC C
2gH0 2gH0
Q VC AC A 2gH0 A 2gH0
H0 作用总水头
长管：作用水头的95%以上用于沿程水头损失，可以略去局部损失及出口速度水头
取断面A-A和B-B，列总流能量方程
zA
pA
g
AVA2
2g
zB

流体力学第五章孔口管嘴出流与管路水力计算

第五章孔口、管嘴及有压管路

流体力学 水力学 第五章

流体力学 第5章孔口管嘴出流与管路水力计算

工程流体力学课件5孔口、管嘴出流及有压管流

第五章 管道11

流体力学孔口管嘴出流与管路水力计算

流体力学第五章

第五章 孔口、管嘴出流和有压管路

工程流体力学 第5章 管路管嘴

流体力学泵与风机-第5章

第五章 孔口管嘴出流及管路计算

第5章 孔口、管嘴出流和有压管路 121页PPT文档

《流体力学》第五章孔口管嘴管路流动

5.孔口、管嘴出流和有压管流

第五章孔口管嘴出流及管路计算

流体力学例题及思考题-第五章

流体力学第五章孔口管嘴出流与管路水力计算

流体力学水力学第五章

流体力学第5章孔口管嘴出流与管路水力计算

第五章管道11

第五章孔口、管嘴出流和有压管路

工程流体力学第5章管路管嘴

第五章孔口管嘴出流及管路计算

第5章孔口、管嘴出流和有压管路 121页PPT文档