第5章 受弯构件梁
合集下载
第五章 梁(受弯构件)
l1
1）梁的侧向抗弯刚度EIy、抗扭刚度GIt、翘曲刚度EIw 2）梁受压翼缘的自由长度l1 3）荷载类型
4）荷载作用位置
第 28 页
5.3.2 梁整体稳定的保证
提高梁的整体稳定承载力的关键是，增强梁受压翼 缘的抗侧移及扭转刚度。
规范规定，符合下列情况之一时，可不计算梁的整体 稳定性。 （1）有刚性铺板密铺在梁的受压翼缘上并与其连接牢固， 能阻止梁受压翼缘的侧向位移时 （2）工字形截面简支梁受压翼缘的自由长度l1与其宽度之 b1比不超过规定数值（P112，表5.2）
b f
稳定系数 y1 y2
Mx f bW1x
x
W1x —受压纤维确定的毛截面模量
Ix W1x y1
第 33 页
附录3 稳定系数的计算
附3.1 轧制H型钢或焊接等截面工字形简支梁
2 t 4320 Ah 235 y 1 b b 2 1 b fy y W1x 4.4h
1、梁的抗弯强度
y a)
a
σ<fy
b)
c) σ=fy
σ=fy
塑性 弹性
d)
σ=fy
x
εy
全部塑性
塑性
M<My
M=My
My<M<Mp
a
M=Mp
图5.6 各荷载阶段梁截面上的的正应力分布
弹性阶段构件边缘 纤维最大应力为：
Mx Wn x
（5.1）
Wnx —截面绕 x 轴的净截面模量
第 13 页
当最大应力达到屈服点fy时，是梁弹性工作的极限状态， 其弹性极限弯矩（屈服弯矩）My
次梁的整体稳定不满足 ，需另选截面： ' 0.68 设选工字钢范围 I 45 ~ I 63，查得 b 0.73 0.6，则 b 所需截面抵抗矩为： Mx 182.25 ×106 1246cm3 Wx ' b f 0.68 ×215
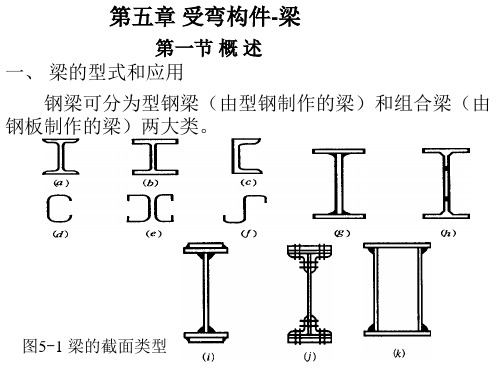
1）梁的侧向抗弯刚度EIy、抗扭刚度GIt、翘曲刚度EIw 2）梁受压翼缘的自由长度l1 3）荷载类型
4）荷载作用位置
第 28 页
5.3.2 梁整体稳定的保证
提高梁的整体稳定承载力的关键是，增强梁受压翼 缘的抗侧移及扭转刚度。
规范规定，符合下列情况之一时，可不计算梁的整体 稳定性。 （1）有刚性铺板密铺在梁的受压翼缘上并与其连接牢固， 能阻止梁受压翼缘的侧向位移时 （2）工字形截面简支梁受压翼缘的自由长度l1与其宽度之 b1比不超过规定数值（P112，表5.2）
b f
稳定系数 y1 y2
Mx f bW1x
x
W1x —受压纤维确定的毛截面模量
Ix W1x y1
第 33 页
附录3 稳定系数的计算
附3.1 轧制H型钢或焊接等截面工字形简支梁
2 t 4320 Ah 235 y 1 b b 2 1 b fy y W1x 4.4h
1、梁的抗弯强度
y a)
a
σ<fy
b)
c) σ=fy
σ=fy
塑性 弹性
d)
σ=fy
x
εy
全部塑性
塑性
M<My
M=My
My<M<Mp
a
M=Mp
图5.6 各荷载阶段梁截面上的的正应力分布
弹性阶段构件边缘 纤维最大应力为：
Mx Wn x
（5.1）
Wnx —截面绕 x 轴的净截面模量
第 13 页
当最大应力达到屈服点fy时，是梁弹性工作的极限状态， 其弹性极限弯矩（屈服弯矩）My
次梁的整体稳定不满足 ，需另选截面： ' 0.68 设选工字钢范围 I 45 ~ I 63，查得 b 0.73 0.6，则 b 所需截面抵抗矩为： Mx 182.25 ×106 1246cm3 Wx ' b f 0.68 ×215
第五章 受弯构件正截面承载力答案
5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢，就算喜欢也是偷偷摸摸的。
”6.方茴说：“我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。
8.这些孩子都很活泼与好动，即便吃饭时也都不太老实，不少人抱着陶碗从自家出来，凑到了一起。
9.石村周围草木丰茂，猛兽众多，可守着大山，村人的食物相对来说却算不上丰盛，只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
1.“噢，居然有土龙肉，给我一块！”2.老人们都笑了，自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂，数落着自己的孩子，拎着骨棒与阔剑也快步向自家中走去。
第五章 钢筋混凝土受弯构件正截面承载力计算一、填空题：1、钢筋混凝土受弯构件，随配筋率的变化，可能出现 少筋、 超筋 和 适筋 等三种沿正截面的破坏形态。
2、受弯构件梁的最小配筋率应取 %2.0m i n =ρ 和 y t f f /45min =ρ 较大者。
3、钢筋混凝土矩形截面梁截面受弯承载力复核时，混凝土相对受压区高度b ξξ ，说明 该梁为超筋梁 。
4．受弯构件min ρρ≥是为了____防止产生少筋破坏_______________；max ρρ≤是为了___防止产生超筋破坏_。
5．第一种T 形截面梁的适用条件及第二种T 形截面梁的试用条件中，不必验算的条件分别是____b ξξ≤___及__min ρρ≥_______。
6．T 形截面连续梁，跨中按 T 形 截面，而支座边按 矩形 截面计算。
7、混凝土受弯构件的受力过程可分三个阶段，承载力计算以Ⅲa 阶段为依据，抗裂计算以Ⅰa 阶段为依据，变形和裂缝计算以Ⅱ阶段为依据。
8、对钢筋混凝土双筋梁进行截面设计时，如s A 与 's A 都未知，计算时引入的补充条件为 b ξξ=。
第五章 受弯构件——梁
σcr =Mcr/Wnx=10.17×105Ah/(λy2Wnx)√1+(λyt1/4.4h)2
(N/mm2)
四、梁的整体稳定性验算公式
σ max =Mx/Wx≤σcr/γR =(σcr/ fy) ( fy/γR)=φb* f
得 Mx/（υb Wx）≤f
式中，φb＝σcr/ fy 称为梁的整体稳定系数。
有两种情况，规范规定不允许截面有塑性发展，
而是采用弹性设计： （1）对于直接承受动力荷载且需计算疲劳强度的梁， 考虑塑性发展会使钢材硬化，促使疲劳断裂提早出 现。应取γx =γy = 1.0 。
（2）当梁的受压翼缘自由外伸宽度与厚度之比 b1/t＞13√235/fy但不超过15√235/fy 时，塑性发展
第五章 受弯构件 — 梁
§5-1 梁的类型和应用
一、梁：实腹式受弯构件，承受横向荷载。
梁的截面内力：弯矩和剪力。 二、梁的类型 （1）型钢梁：热轧型钢梁、冷弯薄壁型钢梁 （2）组合梁: 实腹式梁 格构式梁——又称为桁架
三、梁格类型
梁格：由纵横交错的主梁和次梁组成的平面承重
体系。 梁格按主次梁的排列方式分为三种类型： （1）单向梁格（简式梁格）：只有主梁，适用于柱 距较小的情况。 （2）双向梁格（普通式梁格）：有主梁和一个方向 的次梁，次梁支撑在主梁上。是最常用的梁格类型。 （3）复式梁格（复杂梁格）：在主梁间设纵向次梁， 纵向次梁间再设横向次梁的梁格。梁格构造复杂，传 力层次多，只在必要时才采用。
当符合下列情况之一时，梁的整体稳定有保证， 可不必验算梁的整体稳定性。 （1）有刚性铺板（各种钢筋混凝土板和钢板）密铺 在梁的受压翼缘上，且与其牢固连接，能阻止梁的 受压翼缘的侧向位移时； （2）H型钢或工字形截面简支梁受压翼缘的自由 长度L1与其宽度b1之比 不超过157表5.3所规定的数值时； （3）箱形截面简支梁，当截面高度h与两腹板间距bo 之比满足h/bo≤6 , 且L1/bo≤95(235/fy)时，不必计算 梁的整体稳定性。
5章受弯构件概述
1.梁整体稳定的概念 绕强轴单向受弯的构件，当弯矩增大到某一数值时，
构件可能突然产生在弯矩作用平面外的侧移和扭转，构 件由平面内弯曲状态变为弯扭状态，这就是整体失稳。
2.梁丧失整体稳定的现象：
产生侧向弯曲并伴随着扭转——出平面弯扭屈 曲； 有两个位移u，v和一个转角。
3.梁丧失整体稳定的原因：
不同形式的截面形状系数见P117表5.1。
（3）按有限塑性发展强度准则，限制截面塑性区在截 面高度两侧一定范围（<0.15h）内发展，采用有限截 面塑性发展系数x或y（P118表5.2）。
设计计算公式为：
MxxMex
2. 双向弯曲时的抗弯强度：
（1）按边缘屈服准则，要求截面边缘一点的最大弯曲应力 满足：
一、截面强度破坏
梁在纯弯矩作用下
截面的正应力： 1）弹性阶段 2）弹塑性阶段 3）塑性阶段（塑性铰形成并转动） 4）强化阶段
二、整体失稳
绕强轴单向受弯的构件，当弯矩增大到某一数值时，构 件可能突然产生在弯矩作用平面外的侧移和扭转，构件由 平面内弯曲状态变为弯扭状态，称整体失稳。
x a)
M
z
M
d)
令 h/2l2(EIy/GIt)
1 2
——整体稳定屈曲系数
M crx l EI yGIt
荷载形式不同、作用的位置不同，整体稳定 屈曲系数也不同。如P 124 表5.5
四、影响临界弯矩的主要因素：
1．截面的侧向抗弯刚度EIy、抗扭刚度GIt、翘曲刚度EI； 2．构件的侧向支承点间距； 3．截面的不对称程度，受压翼缘加强，By大， Mcrx大。 4．荷载种类，纯弯曲时， Mcrx最小。 5．支承对位移的约束程度大， Mcrx也大。 6．荷载作用的位置，在下翼缘时有利，a值大。
构件可能突然产生在弯矩作用平面外的侧移和扭转，构 件由平面内弯曲状态变为弯扭状态，这就是整体失稳。
2.梁丧失整体稳定的现象：
产生侧向弯曲并伴随着扭转——出平面弯扭屈 曲； 有两个位移u，v和一个转角。
3.梁丧失整体稳定的原因：
不同形式的截面形状系数见P117表5.1。
（3）按有限塑性发展强度准则，限制截面塑性区在截 面高度两侧一定范围（<0.15h）内发展，采用有限截 面塑性发展系数x或y（P118表5.2）。
设计计算公式为：
MxxMex
2. 双向弯曲时的抗弯强度：
（1）按边缘屈服准则，要求截面边缘一点的最大弯曲应力 满足：
一、截面强度破坏
梁在纯弯矩作用下
截面的正应力： 1）弹性阶段 2）弹塑性阶段 3）塑性阶段（塑性铰形成并转动） 4）强化阶段
二、整体失稳
绕强轴单向受弯的构件，当弯矩增大到某一数值时，构 件可能突然产生在弯矩作用平面外的侧移和扭转，构件由 平面内弯曲状态变为弯扭状态，称整体失稳。
x a)
M
z
M
d)
令 h/2l2(EIy/GIt)
1 2
——整体稳定屈曲系数
M crx l EI yGIt
荷载形式不同、作用的位置不同，整体稳定 屈曲系数也不同。如P 124 表5.5
四、影响临界弯矩的主要因素：
1．截面的侧向抗弯刚度EIy、抗扭刚度GIt、翘曲刚度EI； 2．构件的侧向支承点间距； 3．截面的不对称程度，受压翼缘加强，By大， Mcrx大。 4．荷载种类，纯弯曲时， Mcrx最小。 5．支承对位移的约束程度大， Mcrx也大。 6．荷载作用的位置，在下翼缘时有利，a值大。
第五章 受弯构件——梁
第五章 受弯构件 — 梁
§5-1 梁的类型和应用
一、梁：实腹式受弯构件，承受横向荷载。
梁的截面内力：弯矩和剪力。 二、梁的类型 （1）型钢梁：热轧型钢梁、冷弯薄壁型钢梁 （2）组合梁: 实腹式梁 格构式梁——又称为桁架
三、梁格类型
梁格：由纵横交错的主梁和次梁组成的平面承重
体系。 梁格按主次梁的排列方式分为三种类型： （1）单向梁格（简式梁格）：只有主梁，适用于柱 距较小的情况。 （2）双向梁格（普通式梁格）：有主梁和一个方向 的次梁，次梁支撑在主梁上。是最常用的梁格类型。 （3）复式梁格（复杂梁格）：在主梁间设纵向次梁， 纵向次梁间再设横向次梁的梁格。梁格构造复杂，传 力层次多，只在必要时才采用。
取最大弹塑性弯矩 Mx max =γx Me ， （1.0≤γx＜γF）
则梁的弹塑性工作弯矩
Mx≤Mx max=γxMe=γxWnx fy
即
Mx/(γxWnx) ≤ fy
梁的抗弯强度计算公式：
（1）单向弯曲时
Mx/(γxWnx)≤f
(2)双向弯曲时
Mx/(γxWnx)+My/(γyWny)≤f
式中γx、γy----截面塑性发展系数。 按142(董218)页表5－1取用。
对翼缘局部稳定不利，应取γx=1.0。
二、梁的抗剪强度
根据《材料力学》的剪力流理论，以截面的
最大剪应力不超过剪切屈服点为设计准则。
梁的抗剪强度计算公式：
截面中性轴处
Hale Waihona Puke τ＝VSx / (Ixtw) ≤ fv
三、梁的腹板局部压应力强度
梁在承受固定集中荷载处无加劲肋， 或承受移动 集中荷载（如轮压）作用时， 腹板边缘在压力作用点处压应力最大， 向两边逐渐减小。
§5-1 梁的类型和应用
一、梁：实腹式受弯构件，承受横向荷载。
梁的截面内力：弯矩和剪力。 二、梁的类型 （1）型钢梁：热轧型钢梁、冷弯薄壁型钢梁 （2）组合梁: 实腹式梁 格构式梁——又称为桁架
三、梁格类型
梁格：由纵横交错的主梁和次梁组成的平面承重
体系。 梁格按主次梁的排列方式分为三种类型： （1）单向梁格（简式梁格）：只有主梁，适用于柱 距较小的情况。 （2）双向梁格（普通式梁格）：有主梁和一个方向 的次梁，次梁支撑在主梁上。是最常用的梁格类型。 （3）复式梁格（复杂梁格）：在主梁间设纵向次梁， 纵向次梁间再设横向次梁的梁格。梁格构造复杂，传 力层次多，只在必要时才采用。
取最大弹塑性弯矩 Mx max =γx Me ， （1.0≤γx＜γF）
则梁的弹塑性工作弯矩
Mx≤Mx max=γxMe=γxWnx fy
即
Mx/(γxWnx) ≤ fy
梁的抗弯强度计算公式：
（1）单向弯曲时
Mx/(γxWnx)≤f
(2)双向弯曲时
Mx/(γxWnx)+My/(γyWny)≤f
式中γx、γy----截面塑性发展系数。 按142(董218)页表5－1取用。
对翼缘局部稳定不利，应取γx=1.0。
二、梁的抗剪强度
根据《材料力学》的剪力流理论，以截面的
最大剪应力不超过剪切屈服点为设计准则。
梁的抗剪强度计算公式：
截面中性轴处
Hale Waihona Puke τ＝VSx / (Ixtw) ≤ fv
三、梁的腹板局部压应力强度
梁在承受固定集中荷载处无加劲肋， 或承受移动 集中荷载（如轮压）作用时， 腹板边缘在压力作用点处压应力最大， 向两边逐渐减小。
混凝土结构设计原理-05章-受弯构件的斜截面承载力
第5章 受弯构件的斜截面承载力
第5章 受弯构件的斜截面承载力
主要内容
● ● ● ●
重点
斜裂缝、剪跨比及斜截面受剪破坏形态 简支梁斜截面受剪机理 斜截面受剪承载力计算公式及设计计算 保证斜截面受剪承载力的构造措施
● 斜裂缝、剪跨比及斜截面受剪破坏形态 ● 简支梁斜截面受剪机理 ● 斜截面受剪承载力的设计计算 ● 保证斜截面受剪承载力的构造措施
图形。 材料抵抗弯矩图：按实际配置的受力钢筋计算的各个
正截面受弯承载力 Mu 所绘制的图形。
5.5 保证斜截面受弯承载力的构造措施
第5章 受弯构件的斜截面承载力
对承受均布荷载的单筋矩形截面简支梁：
Mu
As
fsd (h0
fsd As ) 2 fcdb
每根纵筋所承担的
M ui可近似按钢筋面积分配， M ui
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
公式的适用范围 ■ 截面的最小尺寸（上限值） 为防止斜压破坏，要求：
0Vd (0.51 103 ) fcu,k bh0
否则，应加大截面尺寸或提高混凝土强度等级。 ■ 构造配箍条件（下限值）
0Vd (0.5 103 ) 2 f tdbh0
而略有降低。 T形截面梁的受剪承载力高于矩形截面梁。
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
2. 斜截面受剪承载力计算公式
由于抗剪机理和影响因素的复杂性，目前各国规范的斜
截面受剪承载力计算公式均为半理论半经验的实用公式。
《公路桥规》中的斜截面受剪承载力计算公式以剪压破
坏为建立依据，假定梁的斜截面受剪承载力Vu由剪压区混凝 土的抗剪能力Vc、与斜裂缝相交的箍筋的抗剪能力Vsv 和与斜 裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成。
第5章 受弯构件的斜截面承载力
主要内容
● ● ● ●
重点
斜裂缝、剪跨比及斜截面受剪破坏形态 简支梁斜截面受剪机理 斜截面受剪承载力计算公式及设计计算 保证斜截面受剪承载力的构造措施
● 斜裂缝、剪跨比及斜截面受剪破坏形态 ● 简支梁斜截面受剪机理 ● 斜截面受剪承载力的设计计算 ● 保证斜截面受剪承载力的构造措施
图形。 材料抵抗弯矩图：按实际配置的受力钢筋计算的各个
正截面受弯承载力 Mu 所绘制的图形。
5.5 保证斜截面受弯承载力的构造措施
第5章 受弯构件的斜截面承载力
对承受均布荷载的单筋矩形截面简支梁：
Mu
As
fsd (h0
fsd As ) 2 fcdb
每根纵筋所承担的
M ui可近似按钢筋面积分配， M ui
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
公式的适用范围 ■ 截面的最小尺寸（上限值） 为防止斜压破坏，要求：
0Vd (0.51 103 ) fcu,k bh0
否则，应加大截面尺寸或提高混凝土强度等级。 ■ 构造配箍条件（下限值）
0Vd (0.5 103 ) 2 f tdbh0
而略有降低。 T形截面梁的受剪承载力高于矩形截面梁。
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
2. 斜截面受剪承载力计算公式
由于抗剪机理和影响因素的复杂性，目前各国规范的斜
截面受剪承载力计算公式均为半理论半经验的实用公式。
《公路桥规》中的斜截面受剪承载力计算公式以剪压破
坏为建立依据，假定梁的斜截面受剪承载力Vu由剪压区混凝 土的抗剪能力Vc、与斜裂缝相交的箍筋的抗剪能力Vsv 和与斜 裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成。
第五章-钢结构受弯构件
根据主梁和次梁的排列情况，梁格可分为三
种类型：
(1)单向梁格
只有主梁，适用于
楼盖或平台结构的
横向尺寸较小或面板
跨度较大的情况。
(2)双向梁格
有主梁及一个方向的次梁，次梁由主梁支承， 是最为常用的梁格类型。
(3)复式梁格
在主梁间设纵向次梁，纵向次梁间再设横向
次梁。荷载传递层次多，梁格构造复杂，故应用 较少，只适用于荷载重和主梁间距很大的情况
v5q kl35•q kl2• lM kl v
l 38 E x4 I48 8 E x I1E 0 x Il 对变截面简支梁：
v l1M E 0 klx I12 3I5 xI xIx1 v l
5.4 梁的整体稳定承载力
5.3.1 梁整体稳定的概念 为了提高抗弯强度，节省钢材，钢梁截面一
时，应取 x =1.0。 钢材牌号所指屈服点 f y ,
即不分钢材厚度一律取为；Q235钢，235；Q345 钢，345；Q390钢，390；Q420钢，420。
②直接承受动力荷载且需要计算疲劳的梁，
例如重级工作制吊车梁，塑性深入截面将使钢材
发生硬化，促使疲劳断裂提前出现，因此按式
(6.4)和式(6.5)计算时，取 x = y =1.0，
等)，应按下式验算该处的折算应力：
2c 2c 3 21f
M xh0
W nx h
1 —验算折算应力的强度设计值增大系数。
当
与
异号时，取
c
1
=1.2；当
与同
号或 =0时，取 c =1.1。 1
当其异号时，其塑性变形能力比其同号时大，
因此前者的值大于后者。
5.2.2 梁的刚度
对等截面简支梁：
混凝土结构及砌体结构-第五章受弯构件斜截面承载力计算
Asv 1.75 V Vcs f t bh0 f yv h0 1.0 s
注意：
1.5 3
17
2.公式的适用范围 （1）、上限值－－最小截面尺寸和最大配箍率：
hw 当 4 时，V 0.25 c f cbh0 b hw 当 6 时，V 0.2 c f c bh0 b hw 当4 6 时，按线性内插法取用 b
250 300 350 500
150 200
24
3.弯起钢筋的要求
1.画出弯矩图和正截面受弯承载力图； 2.根据各根钢筋面积大小按比例分配受弯承载力图，
弯起的钢筋画在外面； 3.找出要弯起钢筋的充分利用点和不需要点； 4.从充分利用点向外延伸0.5h0，作为弯起点，并 找出弯起钢筋与中和轴的交点。如该点在不需要点 的外面，可以，否则再向外延伸； 5.验算是否满足斜截面受剪承载力要求和其它构造 要求。
las≥15d（光面）
37
（2）中间支座直线锚固：
0.7la ≥l a
l ≥0.a7la
38
（3）中间支座的弯折锚固：
≥0.4la ≥0.4la
15d
39
（4）节点或支座范围外的搭接：
ll
40
5.4.5
箍筋的构造要求
单肢箍n=1
双肢箍n=2
四肢箍n=4
41
梁受扭或承受动荷载时，不得使用开口箍筋
45
46
19
－斜截面上弯起钢筋与构件纵向轴线的夹角。
2. 斜截面承载力计算步骤
⑴ 确定计算截面及其剪力设计值； ⑵ 验算截面尺寸是否足够； ⑶ 验算是否可以按构造配筋；
⑷ 当不能按构造配箍筋时，计算腹筋用量；
⑸ 验算箍筋间距、直径和最小配箍率是否 满足要求。
钢结构第五章受弯构件
螺栓连接
适用于可拆卸的结构和临时性连接，具有施工方便、质量易于保证等优 点；但用钢量较大，且需要定期紧固。
03
铆钉连接
适用于承受动力荷载的结构，具有传力可靠、韧性和塑性好等优点；但
铆接工艺复杂、劳动强度高、用钢量也较大。
节点类型及其适用范围
刚接节点
能传递弯矩和剪力，适用 于固定支座和连续梁等需 要传递弯矩的结构。
03
受弯构件截面设计与优化
截面形状选择原则
01
02
03
符合受力要求
根据受弯构件所受荷载类 型、大小及分布情况，选 择能够有效承受弯矩和剪 力的截面形状。
便于加工制作
考虑现有加工设备和技术 水平，选择易于加工成型 的截面形状。
经济性
在满足受力要求和加工制 作的前提下，尽量选择材 料用量少、成本低的截面 形状。
连接固定
采用合适的连接方式将构件与基础或相邻构 件连接固定，确保稳定性和安全性。
验收标准和方法
验收标准
构件的尺寸偏差、形位公差、表面质量等应符合相关标准和 设计要求。
验收方法
采用测量工具对构件的尺寸、形位等进行测量，目视检查表 面质量，查阅相关质量证明文件等。对于不合格的构件，应 及时进行整改或返工处理，直至符合要求为止。
节点法
对于超静定结构，通过选取节点建立平衡方程，进 而求解内力的方法。
力矩分配法
适用于连续梁和无侧移刚架等结构，通过力矩分配 系数求解内力的方法。
剪力、弯矩图绘制
80%
剪力图的绘制
根据截面法或节点法求得的剪力 值，在构件上按比例绘制剪力图 。
100%
弯矩图的绘制
根据截面法或节点法求得的弯矩 值，在构件上按比例绘制弯矩图 。
适用于可拆卸的结构和临时性连接，具有施工方便、质量易于保证等优 点；但用钢量较大，且需要定期紧固。
03
铆钉连接
适用于承受动力荷载的结构，具有传力可靠、韧性和塑性好等优点；但
铆接工艺复杂、劳动强度高、用钢量也较大。
节点类型及其适用范围
刚接节点
能传递弯矩和剪力，适用 于固定支座和连续梁等需 要传递弯矩的结构。
03
受弯构件截面设计与优化
截面形状选择原则
01
02
03
符合受力要求
根据受弯构件所受荷载类 型、大小及分布情况，选 择能够有效承受弯矩和剪 力的截面形状。
便于加工制作
考虑现有加工设备和技术 水平，选择易于加工成型 的截面形状。
经济性
在满足受力要求和加工制 作的前提下，尽量选择材 料用量少、成本低的截面 形状。
连接固定
采用合适的连接方式将构件与基础或相邻构 件连接固定，确保稳定性和安全性。
验收标准和方法
验收标准
构件的尺寸偏差、形位公差、表面质量等应符合相关标准和 设计要求。
验收方法
采用测量工具对构件的尺寸、形位等进行测量，目视检查表 面质量，查阅相关质量证明文件等。对于不合格的构件，应 及时进行整改或返工处理，直至符合要求为止。
节点法
对于超静定结构，通过选取节点建立平衡方程，进 而求解内力的方法。
力矩分配法
适用于连续梁和无侧移刚架等结构，通过力矩分配 系数求解内力的方法。
剪力、弯矩图绘制
80%
剪力图的绘制
根据截面法或节点法求得的剪力 值，在构件上按比例绘制剪力图 。
100%
弯矩图的绘制
根据截面法或节点法求得的弯矩 值，在构件上按比例绘制弯矩图 。
[建筑土木]第5章梁的斜截面受剪承载力
![[建筑土木]第5章梁的斜截面受剪承载力](https://img.taocdn.com/s3/m/a3272fd90408763231126edb6f1aff00bed570f6.png)
第五章受弯构件的斜截面承载力受弯构件斜截面受力与破坏分析腹筋：箍筋、弯筋无腹筋梁：仅设置纵筋的梁或不配箍筋和弯起钢筋；弯剪型斜裂缝：由梁底的弯曲裂缝发展而成；腹剪型斜裂缝：当梁的腹板很薄或集中荷载至支座距离很小时，斜裂缝可能首先在梁腹部出现。
斜裂缝的类型：腹剪斜裂缝和弯剪斜裂缝。
腹剪斜裂缝弯剪斜裂缝2、无腹筋梁受力及破坏分析n AB面上的混凝土切应力合力Vcn开裂面BC两侧凹凸不平产生的骨料咬合力Van穿越裂缝间的纵筋在斜裂缝处的销栓力Vdn随着荷载的增大，近支座处的一条斜裂缝发展较快，成为导致构件破坏的临界斜裂缝。
临界斜裂缝出现后，梁的受力如一拉杆拱，荷载通过斜裂缝上部的砼拱体传至支座，纵筋相当于拉杆，纵筋与砼拱体的共同工作完全取决于支座处的锚固。
破坏时纵向钢筋的拉应力往往低于屈服强度。
3、有腹筋梁的受力及破坏分析5.1.2、影响斜截面受力性能的主要因素1、剪跨比和跨高比2、腹筋的数量3、混凝土强度等级4、纵筋配筋率5、其他因素1、剪跨比和跨高比剪跨比λ为集中荷载到临近支座的距离a 与梁截面有效高度h 0的比值，即λ＝a / h 0 。
某截面的广义剪跨比为该截面上弯矩M 与剪力和截面有效高度乘积的比值，即λ＝M / （Vh 0）。
剪跨比反映了梁中正应力与剪应力的比值!!2、腹筋的数量腹筋的数量增多时，斜截面的承载力增大。
3、混凝土强度等级斜截面的承载力随混凝土强度等级的提高而增大。
斜截面破坏是因混凝土到达极限强度而发生的，故斜截面受剪承载力随混凝土的强度等级的提高而提高。
4、纵筋配筋率纵向钢筋配筋率越大，斜截面的承载力增大。
试验表明，梁的受剪承载力随纵向钢筋配筋率ρ的提高而增大。
这主要是纵向受拉钢筋约束了斜裂缝长度的延伸，从而增大了剪压区面积的作用。
5、其他因素截面形状、预应力，梁的连续性受压翼缘的存在对提高斜截面的承载力有一定的作用。
因此T形截面梁与矩形截面梁相比，前者的斜截面承载力一般要高10%~30%。
第五章受弯构件的弯扭失稳
R 材料分项系数； b cr f y 稳定系数。
（2）稳定系数的计算
任意横向荷载作用下：
A、轧制H型钢或焊接等截面工字形简支梁
2 y t1 4320 Ah 235 b b b 2 1 4.4h f yW x y 式中 b 等效临界弯矩系数；
力用下式表达：
式中:
M x N e0 N 1 N p M (1 N ) e N Ex
N、Mx—轴心压力和沿构件全长均布的弯矩; e0—各种初始缺陷的等效偏心距； Np—无弯矩作用时，全截面屈服的极限承载 力， Np =Afy； Me—无轴心力作用时，弹性阶段的最大弯矩, Me=W1xfy
L
代入
（d）式中，得：
2 2 2 z M 0 EI w GI t C sin L L L EI y
(e )
上式使任何 z 值都成立，则方括号中的数值必 为零，即：
2 2 M2 EI w GI t 0 L L EI y
N x A
mx M x
N W1x (1 x ) N Ex
f
( 6 8)
上式适用于计算冷弯薄壁型钢压弯构件和格构式压 弯构件绕虚轴弯曲的面内稳定。
2、最大强度准则 （或极限承载力准则）：
以图4-36中B点为计算依据，考虑部分截
面的塑性开展。在N和M作用下，求极限承载
N 计算段轴心压力设计值 ；
N N Ex 1.1，N Ex EA x Ex 1.1 抗力分项系数 R的均值；
此公式适用于双 轴对称截面
第五章梁(受弯构件)
选定高度：hmin≤h≤hmax；h≈he，并认为h0≈he
3、确定腹板厚度（假定剪力全部由腹板承受），则有：
max
VS I xtw
1.2 V h0tw
fV
或按经验公式： tw h0 3.5
tw
1.2
V h0 fV
3、确定翼缘宽度 确定了腹板厚度后，可按抗弯要求确定翼缘板面积Af，已
工字型截面为例：
V1
ctw
T
lztw
tw
T
lz
( T1 2 0.7hf
)2
(
f
V1 2 0.7hf
)2
f
w f
1
hf
1.4
f
w f
T12
( V1
f
)2
第六章 拉弯与压弯构建
第一节 概述 第二节 拉弯与压弯构件的强度与刚度 第三节 实腹式压弯构件的整体稳定 第四节 实腹式压弯构件的局部稳定 第五节 实腹式压弯构件的截面设计 第六节 格构式压弯构件
根据验算结果调整截面，再进行验算，直至满足。
二、组合梁的截面设计
1、根据受力情况确定所需的截面抵抗矩
WT
M max
x f
2、截面高度的确定
最小高度：hmin由梁刚度确定；
最大高度：hmax由建筑设计要求确定；
经济高度：he由最小耗钢量确定；
he 25 WT2 2WT0.4
he 23 W T 30mm
W
2I h
2
twh03
h 12
2
Af
h0 2
t
2
WT
Af
WT h0
h0tw 6
有了Af ，只要选定b、t中的其一，就可以确定另一值。 4、截面验算
受弯构件-梁
β 1—验算折算应力的强度设计值增大系数。当σ 与σ c异 号时，取β 1=1.2；当σ 与σ c同号时或σ c=0,β 1=1.1。
五、 梁的刚度
v≤[v]
v—由荷载标准值产生的最大挠度； [v]—梁的容许挠度值，规范规定的[v]见表5-2。
对受多个集中荷载的梁（如吊车梁、楼盖主梁等）， 其挠度的精确计算比较复杂，但与最大弯矩相同时的均布 荷载作用下的挠度接近。因此，实践上用近似公式验算梁 的挠度： 对等截面简支梁：
一、 剪力流和剪切中心来自•第三节 梁的扭转
梁的弯曲剪应力
截面全部剪应力的总合力等于竖向剪力 V，水平合力则 互相抵消平衡。 薄壁截面单位长度上的剪力q=τ t（N/mm）,将剪力 q=τ t按其方向用箭头线画在薄壁截面中轴线上时，将成 为自下向上或自上向下的连续射线，故q =τ t称为薄壁构 • 件竖向（或水平）弯曲产生的剪力流。 双轴对称截面[如工字形截面]，如果横向荷载作用于 形心轴上时，则梁只产生弯曲，不会扭转。对于槽形、T 形、L形等非双轴对称截面，当横向荷载作用在非对称轴 的形心轴上时，梁除产生弯曲外，还伴随有扭转。 槽形截面梁当横向荷载V不通过截面的某一特定点S时， 梁将产生弯曲并同时有扭转变形，其外扭矩为Ve，若荷载 逐渐平行地向腹板一侧移动，外扭矩和扭转变形就逐渐减 小；直到荷载移到通过S点时，梁将只产生平面弯曲而不 产生扭转，亦即S点正是梁弯曲产生的剪力流的合力作用 线通过点。因此S点称为截面的剪切中心。
S1nx、S2nx—分别为中和轴以上、以下净截面对中和轴x的 面积矩；
W pnx =S lnx + S 2nx—净截面对x轴的塑性模量。
•
梁受弯时各阶段正应力的分布情况
塑性铰弯矩Mxｐ与弹性最大弯矩Mxe之比为： M xp W pnx F M xe Wnx γ F 称为截面形状系数,取决于截面的几何形状而与材料 的性质无关，。
钢结构第5章 受 弯构件
有较大的σ和τ作用时，都应按下式验算折算应力：
eq2c 2c3 21f
式中：σ ﹑τ ﹑σc—腹板计算高度h0 边缘同一点上同时产生的正应力﹑剪应力和局部压应力，σ和σc 以拉应力为正，压应力为负。
β1 — 计算折算应力的强度设计值增大系数:当σ与σc异号时,取β1=1.2；当σ与σc同号时或σc=0时,取 β1=1.1。
lz a5hy
当集中荷载作用在梁端部时，为
lz a2.5hy
式中a为集中荷载沿梁跨度方向的承压长度,在轮压作用下,可取a=5cm。hy为自梁顶面(或底面)或自吊车 梁轨顶至腹板计算高度边缘的距离。腹板的计算高度h0对于型钢梁为腹板与翼缘相接处两内圆弧起点间的距 离,对于组合梁则为腹板高度。
设钢计结原构 理
第五章 受弯构件
局部压应力验算公式为:
c
F
twlz
f
式中：F—集中荷载; ψ—系数,对于重级工作制吊车梁取ψ=1.35,其它梁 ψ =1.0。
设钢计结原构 理
第五章 受弯构件
5.2.2.4 复杂应力作用下强度 在组合梁腹板的计算高度处，当同时有较大的正应力σ、较大的剪应力τ和局部压应力σc作用，或同时
作用在
上翼缘 下翼缘
1.15 1.40
1.75
对 称截面、
上翼缘加
1.20 1.40
强及下翼 缘加强的 界面
10
侧向支承点间无横向荷载
1.75-1.05(M1/M2)+0.3 (M1/M2)2 但≤2.3
注：1、l1、t1和b1分别是受压翼缘的自由长度、厚度和宽度； 2、 M1和M2一梁的端弯矩，使梁发生单曲率时二者取同号，产生双曲率时取异号，| M1 |≥| M2 |； 3、项次3、4、7指少数几个集中荷载位于跨中附近，梁的弯矩图接近等腰三角形的情况；其他情况的
eq2c 2c3 21f
式中：σ ﹑τ ﹑σc—腹板计算高度h0 边缘同一点上同时产生的正应力﹑剪应力和局部压应力，σ和σc 以拉应力为正，压应力为负。
β1 — 计算折算应力的强度设计值增大系数:当σ与σc异号时,取β1=1.2；当σ与σc同号时或σc=0时,取 β1=1.1。
lz a5hy
当集中荷载作用在梁端部时，为
lz a2.5hy
式中a为集中荷载沿梁跨度方向的承压长度,在轮压作用下,可取a=5cm。hy为自梁顶面(或底面)或自吊车 梁轨顶至腹板计算高度边缘的距离。腹板的计算高度h0对于型钢梁为腹板与翼缘相接处两内圆弧起点间的距 离,对于组合梁则为腹板高度。
设钢计结原构 理
第五章 受弯构件
局部压应力验算公式为:
c
F
twlz
f
式中：F—集中荷载; ψ—系数,对于重级工作制吊车梁取ψ=1.35,其它梁 ψ =1.0。
设钢计结原构 理
第五章 受弯构件
5.2.2.4 复杂应力作用下强度 在组合梁腹板的计算高度处，当同时有较大的正应力σ、较大的剪应力τ和局部压应力σc作用，或同时
作用在
上翼缘 下翼缘
1.15 1.40
1.75
对 称截面、
上翼缘加
1.20 1.40
强及下翼 缘加强的 界面
10
侧向支承点间无横向荷载
1.75-1.05(M1/M2)+0.3 (M1/M2)2 但≤2.3
注：1、l1、t1和b1分别是受压翼缘的自由长度、厚度和宽度； 2、 M1和M2一梁的端弯矩，使梁发生单曲率时二者取同号，产生双曲率时取异号，| M1 |≥| M2 |； 3、项次3、4、7指少数几个集中荷载位于跨中附近，梁的弯矩图接近等腰三角形的情况；其他情况的
第5章受弯构件-梁
进行验算，主要需验算组合梁中的翼缘和腹板局部稳定
§5.4 型钢梁的设计
型钢梁受力计算的基本要求
型钢梁的设计计算方法
型钢梁的设计实例
一、型钢梁受力计算的基本要求
强度、刚度、整体稳定
正应力 剪应力 局部压应力
二、型钢梁的设计计算方法
经验
内力计算 Mmax 1、初选截面 确定净截面模量
选பைடு நூலகம்钢材 品种 f
My Mx f xWxn yWyn
截面塑性发展 系数（1，η）
注： 当梁受压翼缘的自由外伸宽度与其厚度之比大于 13
235 / f y 且不超过15 235 / f y 时，γ ＝1.0； x
需要计算疲劳的梁，宜取γx=γy＝1.0
2.抗剪强度 梁同时承受弯矩和剪力共同作用。工字形和槽形截面梁腹板上 的剪应力分布如图所示。 截面上的最大剪应力发生在腹板中和轴处。在主平面受弯的实 腹构件，其抗剪强度应按下式计算：
或
Mx f bW x
常截面焊接工字形钢梁b的简化公式：
y t1 2 4320 Ah 235 b b 2 [ 1 ( ) b ] 4.4h fy y Wx
当为双向受弯时，梁整体稳定性计算公式为
My Mx f bWx yW y
上式是按照弹性工作阶段导出的。可取比例极限fp=0.6fy，当 cr>0.6 fy时，即b>0.6时，梁已进入了弹塑性工作阶段应采用 b’来代替公式中的b值。
假定集中荷载从作用处以 1：2.5(hy高度范围)和1：1(hR高度范 围)扩散，均匀分布于腹板计算高度边缘。梁的局部承压强度可 按下式计算：
c
F
t wl z
f
第5章 受弯构件——钢梁1-4
5.4 钢梁的整体稳定 三、保证梁的整体稳定性的措施
5.4 钢梁的整体稳定 四、 整体稳定公式： 单向弯曲时
Mx f bWx
两个主平面受 弯的H型钢或工 字形截面构件
My Mx f bWx yWy
4. 对动力荷载标准值不乘动力系数。
挠度υ ≤[υ]
My Mx f xWnx yWny
VS fv It w
强度
c
2
F
tw lz
2 c
f
2
c 3 1 f
刚度
挠度υ ≤[υ]
如何保证梁的稳定性 措施？？
稳定性
5.4 钢梁的整体稳定
5.2 钢梁的强度 三、局部承压强度
c
F
tw lz
f
式中：F──集中荷载，对动力荷载应考虑 动力系数； Ψ──集中荷载增大系数： 对重级工作制吊车 对其他荷载 Ψ=1.35 Ψ=1.0
5.2 钢梁的强度 lz──集中荷载在腹板计算高度边缘的假定分
布长度， 跨中按下式计算： 梁端按： lz a 2.5hy a ──集中荷载沿梁跨度方向的支承长度，对 钢轨(吊车梁)上的轮压可取为50mm;
5.4 钢梁的整体稳定
二、梁整体稳定的计算方法
1、梁整体稳定的计算公式
M x cr cr f y b f Wx R f y R
Wx, Wy──按受压纤维确定的对x轴和对y轴毛截 面抵抗矩； b──梁整体稳定系数。
5.4 钢梁的整体稳定 二、梁整体稳定的计算方法 2、整体稳定系数计算公式： （1）等截面焊接工字形（轧制H型钢）简支梁
tw──腹板厚度；
fv──钢材的抗剪强度设计值。
第五章 受弯构件-公式整理
y x x
235 b 235 13 15 fy t fy
时， x
t
1 .0
y
需要计算疲劳强度的梁:
x y 1 .0
（二）抗剪强度
x x
t max
Vmax
Mmax
V S max I t w f v
(5 6)
（三）局部压应力 当梁的翼缘受有沿腹板平面作用的固定集中荷载 且荷载处又未设置支承加劲肋时，或有移动的集中荷 载时，应验算腹板高度边缘的局部承压强度。
b 235 13 强度计算考虑截面塑性发展时： t fy
强度计算不考虑截面塑性发展（γx=1.0）时：
b 235 15 t fy
对于箱形截面受压翼缘在两腹板（或腹板与纵向加 劲肋）间的无支承宽度b0与其厚度的比值应满足：
b0 235 40 t fy
b t
b t
b0 t h0 t
( 2) h0 235 80 ，按计算配置横向加劲 肋，其中： tw fy
h0 235 当 170 （ 受压翼缘扭转受约束） tw fy 时, h0 235 当 150 （受压翼缘扭转未受约 束） tw fy 或计算需要
应在弯曲受压较大区格，加配纵向加劲肋。
l1 / b 1 钢号 Q235 Q345 条件 跨中受压翼缘有侧向支 荷载作用在 荷载作用在 承点的梁,不论荷载作用 在何处 上翼缘 下翼缘 13.0 10.5 20.0 16.5 16.0 13.0
跨中无侧向支承点的梁
Q390
Q420
10.0
9.5
15.5
15.0
12.5
12.0
3）对于箱形截面简支梁，其截面尺寸满足：
235 b 235 13 15 fy t fy
时， x
t
1 .0
y
需要计算疲劳强度的梁:
x y 1 .0
（二）抗剪强度
x x
t max
Vmax
Mmax
V S max I t w f v
(5 6)
（三）局部压应力 当梁的翼缘受有沿腹板平面作用的固定集中荷载 且荷载处又未设置支承加劲肋时，或有移动的集中荷 载时，应验算腹板高度边缘的局部承压强度。
b 235 13 强度计算考虑截面塑性发展时： t fy
强度计算不考虑截面塑性发展（γx=1.0）时：
b 235 15 t fy
对于箱形截面受压翼缘在两腹板（或腹板与纵向加 劲肋）间的无支承宽度b0与其厚度的比值应满足：
b0 235 40 t fy
b t
b t
b0 t h0 t
( 2) h0 235 80 ，按计算配置横向加劲 肋，其中： tw fy
h0 235 当 170 （ 受压翼缘扭转受约束） tw fy 时, h0 235 当 150 （受压翼缘扭转未受约 束） tw fy 或计算需要
应在弯曲受压较大区格，加配纵向加劲肋。
l1 / b 1 钢号 Q235 Q345 条件 跨中受压翼缘有侧向支 荷载作用在 荷载作用在 承点的梁,不论荷载作用 在何处 上翼缘 下翼缘 13.0 10.5 20.0 16.5 16.0 13.0
跨中无侧向支承点的梁
Q390
Q420
10.0
9.5
15.5
15.0
12.5
12.0
3）对于箱形截面简支梁，其截面尺寸满足：
第5章 受弯构件
第5章 受弯构件教学提示：本章着重讲述了受弯构件的可能破坏形式和影响因素；受弯构件的强度和变形；单向和双向受弯构件的整体稳定；受弯及受扭构件的强度和整体稳定；受弯构件的局部稳定。
教学要求： 本章让学生了解受弯构件的种类及应用；掌握梁的拼接和连接主要方法和要求；掌握受弯构件整体稳定和局部稳定的计算原理（难点）；掌握梁的计算方法；5.1受弯构件的可能破坏形式和影响因素只受弯矩作用或受弯矩与剪力共同作用的构件称为受弯构件，俗称梁。
实际工程中，以受弯受剪为主但同时作用着很小的轴力的构件，也常称为受弯构件。
根据使用情况，它可能只在一个主平面内受弯，称为单向受弯构件，也可能在两个主平面内同时受弯，称为双向受弯构件。
钢梁最常用于工作平台梁、楼盖梁、墙梁、擅条和吊车梁等。
受弯构件有两个正交的形心主轴，如图5.1所示的x 轴与y 轴。
其中绕x 轴的惯性矩、截面模量最大，称x 轴为强轴，相对的另一轴（y 轴）则为弱轴。
对于工字形、箱形及T 形截面，其外侧平行于弯曲轴的板称为翼缘、垂直于弯曲轴的板则称为腹板。
x y x y x y x y x y xyx x x xx x y y yy y y图5.1受弯构件的强轴和弱轴按梁的支承情况可将梁分为简支梁、连续梁、悬臂梁等。
按梁在结构中的作用不同可将梁分为主梁与次梁。
按截面是否沿构件轴线方向变化可将梁分为等截面梁与变截面梁。
改变梁的截面会增加一些制作成本，但可达到节省材料的目的。
钢梁按制作方法的不同分为型钢梁和焊接组合梁。
型钢梁又分为热轧型钢梁和冷弯薄壁型钢梁两种。
目前常用的热轧型钢有普通工字钢、槽钢、热轧H型钢等（如图5.2(a)~(c)）。
冷弯薄壁型钢梁截面种类较多，但在我国目前常用的有C形槽钢（图5.2（d））和Z形钢（图5.2 （e））。
冷弯薄壁型钢是通过冷轧加工成形的，板壁都很薄，截面尺寸较小。
在梁跨较小、承受荷载不大的情况下采用比较经济，例如屋面檩条和墙梁。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
梁与柱的半刚性连接
抵抗弯矩？
半刚性和刚性节点的差异体现在什么变量上？
§5.1.2 受弯构件的主要失效形式
1 强度破坏：
a 屈服：塑性区的深入，弹性核变小，塑性铰 材料断裂 b 疲劳 2 失稳：
a 整体失稳：弯曲平面外的弯扭变形 b 局部失稳：翼缘失稳：受压 腹板失稳：不均匀受压、受剪 3 过大变形
折算应力（Mises应力）
sz + c c + 3
2 2
2
应力分量的符号：拉为正、压为负
工程计算公式 sz 1 f d
1 1 弹性准则 1 1 允许局部塑性发展
§5.2.6 复合应力与折算应力
在式中将强度设计值乘以增大系数1，是考虑到折算应力最大值 只在局部区域，同时几种应力在同一处都达到最大值，且材料强度又 同时为最小值的概率较小，故将设计强度适当提高。当和c异号时 比同号时要提早进入屈服，而此时塑性变形能力高，危险性相对较小 故取 1 =1.2。 和c同号时屈服延迟，脆性倾向增加，故取1 =1.1 。
§5.2.4 抗剪强度
1.剪力中心
在构件截面上有一特殊点S，当外力产生的剪力作用在该 点时构件只产生线位移，不产生扭转，这一点S称为构件的剪 力中心。也称弯曲中心，若外力不通过剪力中心，梁在弯曲的 同时还会发生扭转，由于扭转是绕剪力中心取矩进行的，故S 点又称为扭转中心。剪力中心的位置近与截面的形状和尺寸有 关，而与外荷载无关。
Mt
tds t ds
t
其中周边积分 d s 恰好是截面壁厚中线所围成面积的2倍。 即： M 2At 任一点处的剪应力为：
Mt 2 At
闭口截面的抗扭能力要比开口截面的抗扭能力大的多。
5.3.2 开口薄壁的约束扭转
特点：由于支座的阻碍 或其它原因，受扭构件的截 面不能完全自由地翘曲（翘 曲受到约束）。
M z GI t EI ω （4.3.8）
I为截面翘曲扭转常数，又称扇性惯性矩。量纲为（L）6。
常用开口薄壁截面的扇性惯性矩Iω值
双轴对称工字形截面
h I I1 2 4
2
I yh2
I1——一个翼缘截面对y轴的惯性矩。
§5.4 受弯构件整体失稳的弯扭 平衡方程及其临界弯矩
刚度
梁的局部屈曲
§5.2 受弯构件的强度与刚度
§5.2.1 截面应力分布与强度准
材料假定：理想弹塑性 变形假定：平截面假定 截面应力分布与强度准则
受压区
fy
Vmax Mmax
2 y
2 y 2 fy
y
2 y
2
1 y 1 y 1 y 1 f y 1 f y 1 f y
弯矩 构件内力 弯矩+剪力 弯矩+剪力，附加很小的轴力
§5.1.1 受弯构件的类型与截面
受弯构件：弯矩和剪力→梁 弯曲变形：单向受弯与双向受弯
边界约束：简支、固定、自由，连续多跨
传力路径：板→次梁→主梁→柱→基础 截面形式：实腹式→型钢截面、焊接组合截面 空腹式→中空、格构式（桁架） 沿长度变化：等截面与变截面
My1 I n ——弯曲正应力 c——局部压应力
、c c拉应力为正， 压应力为负。 VS1 I nx tw ——剪应力 x
y
y1 1 σ
τ
σc
图4.2.5 、 、c的共同作用
§5.2.7 受弯构件的刚度
梁必须有一定的刚度才能保证正常使用和观感。梁的刚度可用 标准荷载作用下的挠度进行衡量。梁的刚度可按下式验算：
开口截面 自由扭转 剪应力分布
按弹性分析：开口薄壁构件自由扭转时，截面上只有剪应力。 剪应力分布在壁厚范围内组成一个封闭的剪力流；剪应力的方向 与壁厚中心线平行，大小沿壁厚直线变化，中心线处为零，壁内、 外边缘处为最大t 。t的大小与构件扭转角的变化率 成正比。 此剪力流形成抵抗外扭矩的合力矩GIt 。
板件边缘的最大剪应力t与Mt的关系为： k的取值： 槽钢：k=1.12 M tt T形钢： k=1.15 t I字钢： k=1.20 It 角钢： k=1.00
闭口薄壁构件自由扭转时，截面上的剪应力分布 与开口截面完全不同，在扭矩作用下其截面内部将形 成沿各板件中线方向闭合形剪力流。截面壁厚两侧剪 应力方向相同，剪应力可视为沿厚度均匀分布，方向 与截面中线垂直。沿构件截面任意处t为常数。
2 剪力中心S位置的规律 双对称轴截面和点对称截面（如Z形截面），S与截 面形心重和； 单对称轴截面，S在对称轴上； 由矩形薄板中线相交于一点组成的截面，每个薄板中 的剪力通过该点，S在多板件的交汇点处。 常用开口薄壁截面的剪力中心S位置
§5.2.4 抗剪强度
截面剪应力
Vy S x I xt 采用毛截面的 几何参数 对工字形和槽形截面
Pl 3 M xl 2 48EIx 12EIx
式中， Ix——跨中毛截面惯性矩 Mx——跨中截面弯矩
§5.3 梁的扭转
5.3.1 自由扭转
截面不受任何约束，能够自由产生翘曲变形的扭转。
z
y
M
x A
C
B D
M
z
特点：轴向位移不受约束，截面可自由翘曲变形；各截面翘曲 变形相同，纵向纤维保持直线且长度不变，构件单位长度的扭 转角处处相等；截面上只有剪应力，纵向正应力为零。
转动+滑动
蜂窝梁
异种材料组 合的优势和 劣势？
高强T型钢组合梁
异种钢组合梁
预应力梁钢索布置
预应力梁截面形式
试思考钢梁布置预应力索的作用？提高抗力？减少变形？
次梁与主梁的平接
梁支撑在柱的铰接连接
试思考铰接连接的特点体现在哪里？
Hale Waihona Puke 梁支撑在柱侧的铰接连接抵抗弯矩呢？
梁与柱的刚性连接
工厂焊接
试思考分析三种节点在受力和制造上的异同点？
l
z
F
a
tw
支承加劲肋设置与计算
→局部承压由加劲肋承受 支撑加劲肋计算： 加劲肋和附近腹板的强度和稳定 构造规定参考有关规范
F
z
15tw 15tw
z
腹板边缘处的局部承强度的计算公式为：
c
F
tw lz
f
（4.2.7）
式中： F—集中荷载，动力荷载作用时需考虑动力系数 —集中荷载放大系数（考虑吊车轮压分配不均匀），重级工作制吊车 梁=1.35，其它梁=1.0； tw—腹板厚度 lz—集中荷载在腹板计算高度上边缘的假定分布长度，可按下式计算： lz = a+5hy +2hR 跨中集中荷载： 梁端支座反力： lz = a+2.5hy +b a—集中荷载沿梁长方向的实际支承长度。对于钢轨上轮压取a=50mm； hy—自梁顶面至腹板计算高度上边缘的距离。 hR—轨道的高度，对梁顶无轨道的梁hR=0。 b—梁端到支座板外边缘的距离，按实际取，但不得大于2.5hy
即要保证局 部承压处的局部 压应力不超过材 料的屈服强度。
腹板的计算高度h0
ho
t1
t1
b 1）轧制型钢，两内孤起点间距; 2）焊接组合截面，为腹板高度;
b
3）铆接（或高强螺栓连接）时为铆钉（或高强螺栓）间最 近距离。
§5.2.6 复合应力与折算应力
复合应力
同一点上同时出现2个及 以上应力分量 某些截面上的某些点
≤[]
——标准荷载下梁的最大挠度
[]——受弯构件的挠度限值，按附P384表2.1规定采用。 一般说来，梁的最大挠度可用材料力学、结构力学方法计算。
均布荷载下等 截面简支梁 集中荷载下等 截面简支梁
5ql 4 5 M xl 2 M xl 2 384EIx 48 EIx 10EIx
截面塑性发展系数
截面形状系数：
M xp Wpnx F M xe Wnx
取决于截面的几何形状 而与材料的性质无关
请推导证明！
b
▲
当翼缘外伸宽度b与其厚度t之比为：
235 b 235 13 15 fy t fy
Y X X
t
Y
时，塑性发展对翼缘局部稳定会有不利影响，应取x ＝1.0。 ▲ 对于需要计算疲劳的梁，因为有塑性区深入的截面，塑性 区钢材易发生硬化，促使疲劳断裂提前发生，同时，塑性变形 累计将产生不可恢复的残余挠度，因此宜取 x= y =1.0。
开口薄壁构件自由扭转时，作用在构件上的自由扭矩为：
M t GIt 式中： Mt ——截面上的扭矩； Mt GIt——截面扭转刚度； G ——材料剪切模量； It——截面扭转常数，也称抗扭惯性矩，量纲为（L）4； ——截面的扭转角 ——杆件单位长度扭转角，或称扭转率； k I t bi ti3 bi、ti—— 第 i个矩形条的长度、厚度； 3 k ——型钢修正系数。
梁的截面
实腹式 空腹式 组合梁
变截面
梁的布置
a 简单梁格，特点：只有主梁，无次梁 b 普通梁格，特点：同时包含主梁及一级次梁 c 复杂梁格，特点：同时包含主梁及多级次梁
§5.1 主次梁的连接
梁的平接
梁的拼接
（a）组合梁的工厂拼接
（b）采用高强螺栓工地拼接
（c）组合梁的工地拼接
梁的支座
转动
M x, M y Mx + My f d Wxn Wyn
Mx + My f d Wpxn Wpyn 主轴公式 对任意形心轴：
有限塑性发展准则 M x + M y f d xWxn yWyn 的工程计算公式
梁设计时只是有限制地利用截面的塑性，塑性发展深度取a≤h/8～h/4。
▲
受拉区
1 y
1
边缘屈服准则