第8讲-B样条曲线曲面-NURBS曲线曲面
B样条曲线与曲面

四、B 样条曲线与曲面Bezier 曲线具有很多优越性,但有二点不足:1)特征多边形顶点数决定了它的阶次数,当n 较大时,不仅计算量增大,稳定性降低,且控制顶点对曲线的形状控制减弱;2)不具有局部性,即修改一控制点对曲线产生全局性影响。
1972年Gordon 等用B 样条基代替Bernstein 基函数,从而改进上述缺点。
B样条曲线的数学表达式为:∑=+⋅=nk n k ki n i u N Pu P 0,,)()(在上式中,0 ≤ u ≤ 1; i= 0, 1, 2, …, m 所以可以看出:B样条曲线是分段定义的。
如果给定 m+n+1 个顶点 Pi ( i=0, 1, 2,…, m+n),则可定义 m+1 段 n 次的参数曲线。
在以上表达式中:N k,n (u) 为 n 次B 样条基函数,也称B样条分段混合函数。
其表达式为:∑-=+--+⋅⋅-=kn j nj n j n k j k n u C n u N 01,)()1(!1)(式中:0 ≤ u ≤1k = 0, 1, 2, …, n1.均匀B 样条曲线1一次均匀B 样条曲线的矩阵表示空间n+1个顶点i P (i = 0,1,…,n )定义n 段一次(k =0,1,n=1)均匀B 样条曲线,即每相邻两个点可构造一曲线段P i (u ),其定义表达为:[]10 ;,...,1 0111 1)(1≤≤=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=-u n i u u P i i i P P=(1-u )P i -1 + u P i= N 0,1(u )P i -1 + N 1,1(u )P i第i 段曲线端点位置矢量:i i i i P P P P ==-)1(,)0(1,且一次均匀B 样条曲线就是控制多边形。
2 二次均匀B 样条曲线的空间n+1个顶点的位置矢量i P (i=0,1,…,n )定义n -1段二次(k =0,1,2, n=2)均匀B 样条曲线,每相邻三个点可构造一曲线段P i (u )(i=1,…,n -1),其定义表达为:[]10 ;1,...,1 011022121 121)(112≤≤-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=+-u n i u u u P i i i i P P P= !21(1 - 2 u + u 2)P i -1 + !21(1 + 2 u - 2u 2)P i + !21u 2 P i +1= N 0,2(u )P i -1 + N 1,2(u )P i + N 2,2(u )P i +1端点位置矢量:)(5.0)0(1i i i P P P +=-,)(5.0)1(1++=i i i P P P ,即曲线的起点和终点分别位于控制多边形P i-1P i 和P i P i+1的中点。
贝塞尔曲线B样条NURBS样条学习总结

Bezier曲线、B样条曲线和NURBS曲线0.概述1. 贝塞尔曲线(Bezier Curve):贝塞尔曲线由一组控制点和控制点上的权重组成。
贝塞尔曲线的阶数由控制点的数量决定,阶数为n的贝塞尔曲线需要n+1个控制点。
贝塞尔曲线具有局部控制的特性,即曲线上的一段由相邻的几个控制点决定,不受其他控制点的影响。
贝塞尔曲线的计算相对简单,但在变形过程中可能会出现形状扭曲的问题。
2. B样条(B-Spline): B样条曲线是一种基于分段多项式的曲线表示方法。
与贝塞尔曲线不同,B样条曲线的每个控制点都有一个关联的基函数。
这些基函数决定了曲线上每一点的形状。
B样条曲线的阶数可以是任意的,较高阶的B样条曲线能够更灵活地描述复杂的曲线形状。
B样条曲线具有良好的局部控制性和平滑性,可以很好地避免贝塞尔曲线的形状扭曲问题。
3. NURBS曲线(Non-Uniform Rational B-Spline Curve):NURBS曲线是对B样条曲线的扩展,它引入了有理权重的概念。
NURBS曲线的每个控制点都有一个关联的权重,这些权重可以调节曲线上各个点的影响程度。
NURBS曲线能够表示更复杂的曲线形状,如圆弧和椭圆等。
总的来说Bezier曲线中的每个控制点都会影响整个曲线的形状,而B样条中的控制点只会影响整个曲线的一部分,显然B样条提供了更多的灵活性;Bezier和B样条都是多项式参数曲线,不能表示一些基本的曲线,比如圆,所以引入了NURBS,即非均匀有理B样条来解决这个问题;贝塞尔曲线适用于简单的曲线形状设计,B样条曲线具有更好的局部控制和平滑性,适用于复杂曲线的建模而NURBS曲线在B样条的基础上引入了有理权重,可以更准确地描述各种曲线形状Bezier曲线是B样条的一个特例,而B样条又是NURBS的一个特例1.Bezier曲线1.1 贝塞尔曲线的历史:贝塞尔曲线于 1962 年,由法国工程师皮埃尔·贝济埃(PierreBézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计,贝塞尔曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥算法开发,以稳定数值的方法求出贝塞尔曲线。
B样条曲线专题知识省公共课一等奖全国赛课获奖课件

/10/10
第10页10
B-样条曲线定义
t n 1个控制点 Pi
n i0
及参数节点向量Tn,k
nk
i i0 (ti ti1)
确定如下的k阶(k 1次)B样条曲线:
n
P(t) Pi Ni,k (t),t [tk1, tn1] 共n-k+2段 i0
B-样条曲线示例
/10/10
第11页11
1阶B-样条基函数
其它
Ni,k (t)在区间ti ,tik 上有定义,称后者为前者的支撑区间。
/10/10
第20页20
3阶B-样条基函数图形
Ni,3 (t)
Ni,3 (t)的图形
/10/10
第21页21
3阶B样条曲线示例
/10/10
t2
T=[t0,t1,…,tn+1,tn+2,tn+3]
tn1
第22页22
知其然,知其所以然…
此时:Tn,4 {0,1,..., n 4}
1 t [i ,i 1)
Ni,1(t) 0
其它
根据如下的基函数递推公式计算Ni,4 (t):
Ni,k
(t)
t k
i 1
N i ,k 1 (t )
i
k
k 1
t
N i 1,k 1 (t ),i
0,1,..., n
/10/10
第33页33
三次均匀B样条曲线(3)
• 顶点数
• 定义区间
• 段数
/10/10
第24页 24
B-样条基函数性质
• 局部性 • 权性 • 连续性
/10/10
第25页25
B-样条基函数局部性
8.7NURBS曲线

八、NURBS曲线(面)1、NURBS曲线(面)的提出Bezier曲线(面)B样条曲线(面)B样条方法在表示与设计自由型曲线、曲面形状时显示了强大的威力,然而在表示与设计初等曲线、曲面时时却遇到了麻烦B样条曲线(面)和Bezier曲线(面)不能精确表示出抛物线以外的二次曲线(面)。
如圆弧、圆而在工程应用特别是在工业设计当中,都用到图纸。
而表示图纸的元素就是直线、圆弧和一些标注信息NURBS(Non-Uniform Rational B-Splines)——非均匀有理B样条方法,主要是为了找到与描述自由型曲线曲面的B样条方法既相统一,又能精确表示二次曲线曲面(圆弧、抛物线、椭圆等)的数学方法NURBS一种最一般最有代表性的表示方法。
既为标准解析形状(即前面提到的初等曲线曲面),又为自由型曲线曲面的精确表示与设计提供了一个公共的数学形式NURBS广泛应用在各种3D造型系统中,如3DMAX,Maya等非均匀——Non-Uniform:指节点向量的值与间距可以为任意值。
这样我们可以在不同区间上得到不同的混合函数形状,为自由控制曲线形状提供了更大自由有理——Rational:是指每个NURBS物体都可以用有理多项式形式表达式来定义Some years ago a few researchers joked about NURBS, saying that the acronym really stands for NOBODY Understands Rational B-Splines2、NURBS曲线的定义NURBS(Non-Uniform Rational B-Splines)——非均匀有理B样条的缩写有理(Rational)函数是两个多项式之比。
因此,有理B 样条可描述为:∑∑∑=====n i k i i n i k i i n i k i i i u R P u B u B P u P 0,0,0,)()()()(ωω∑==n j k j j k i i k i u B u B u R 0,,,)()()(ωω:i ω是控制顶点的权因子。
B样条曲线曲面和NURBS曲线曲1

B 样条曲线曲面和NURBS 曲线曲面(学习笔记和上机练习)非均匀有理B 样条,通常简称为NURBS(Non-Uniform Rational B-Splines)。
NURBS 是非有理B 样条、有理以及非有理B ézier 曲线曲面的推广。
一、要对B 样条曲线曲面和NURBS 曲线曲面有所了解应先了解B 样条基函数 B 样条基函数的定义和性质令{}m u u u U ,...,,10=是一个实数列,即i u ≤1+i u ,i=0,1,…,m-1。
其中,i u 称为节点,U 称为节点矢量,用)(,u N p i 表示第i 个p 次(p +1阶)B 样条基函数,其定义为⎩⎨⎧=,0,1)(0,u N i 若i u ≤u <1+i u 值为1,其他值为0 )()()(1,11111,,u N u u u u u N u u u u u N p i i p i p i p i i p i ip i -++++++-+--+--= (2)由(2)式可知:(1))(0,u N i 是一个阶梯函数,它在半开区间),[1+∈i i u u u 外都为零; (2)当p >0时,)(,u N p i 是两个p -1次基函数的线性组合;(3)计算一组基函数时需要事先指定节点矢量U 和次数p ; (4)(2)式中可能出现0/0,我们规定0/0=0;(5))(,u N p i 是定义在整个实数轴上的分段多项式函数,只在区间][,0m u u 上有意义; (6)半开区间),[1+i i u u 称为第i 个节点区间,长度可以为零,因相邻节点可以相同; B 样条基函数的一些重要性质:1 如果),[1++∉p i i u u u ,则)(,u N p i =0。
2 对于所有的p i ,和u ,有)(,u N p i ≥0.3 对于任意的节点区间),[1+i i u u ,当),[1+∈i i u u u 时,∑-==ipi j pj u N1)(,。
B样条曲线曲面

第二章三维形态基本建模方法第一节形体的空间定位及表示方法一、空间、物体和结构我们每天的生活发生在三维环境中,而且充满着三维物体,我们总是看到、感到三维。
当设计实体模型时,我们通常认为许多事情理所当然。
但在用计算机对三维场景模型化时,那么我们不得不熟悉大量的计算机软件工具,这些工具可用于模型化物体和环境。
在描述三维场景的三维模型化软件中使用的许多基本约定是基于各种行业中使用的传统约定。
例如,建筑师为了用一个简明的方法表达他们设计的空间,使用各种涉及测量、构图和定序的约定。
即使简单的矩形房间设计也要测量多次,以便于房间的所有构件放在被设计放置的地方。
此外,为了准确地按照设计师的图纸来建造,泥瓦工需要进行测量。
多年来泥瓦工和建筑师已形成约定,如何测量空间、建造物体、在结构中安装,它们的约定是精确、简洁的。
我们用类似的约定来描述用一个计算机程序模拟的三维空间中物体的尺寸、位置和次序。
让我们从定义空间或场景的边界开始三维空间的定义,最简单的方法是想象我们是在一个大立方体内工作。
可以将这个立方体当作我们的空间或环境。
在这个立方体中的物体是可见的,在其外部的物体是不可见的。
在这个空间中的主参考点称为主空间原点。
这个原点通常位于这个空间的中心。
根据模型需要和方案,该点也可放在或重新放在其他点上。
所有三维空间都有3个基本的维:宽度、高度和深度。
表达三维空间中这些维的普遍方法是使用箭头或轴。
通常用字母X表示标记三维空间宽度的轴;用Y表示标记三维空间高度的轴;用Z表示标记三维空间深度的轴。
这三个轴交叉的空间点就是主坐标原点。
直角坐标系可以用来定义三维空间中特定的位置,精确定位三维空间中物体的点。
René Descartes是一位18世纪法国的哲学家和数学家,他正式使用标记为X、Y、Z的3个轴表示三维空间中维的思想。
他推导出的坐标系称为笛卡尔坐标系,在该系统中每个轴被分成许多测量单位。
原理上,这些单位是抽象的值,它可表示不同的测量单位和维刻度。
B样条曲线曲面和NURBS曲线曲面C语言算法源程序
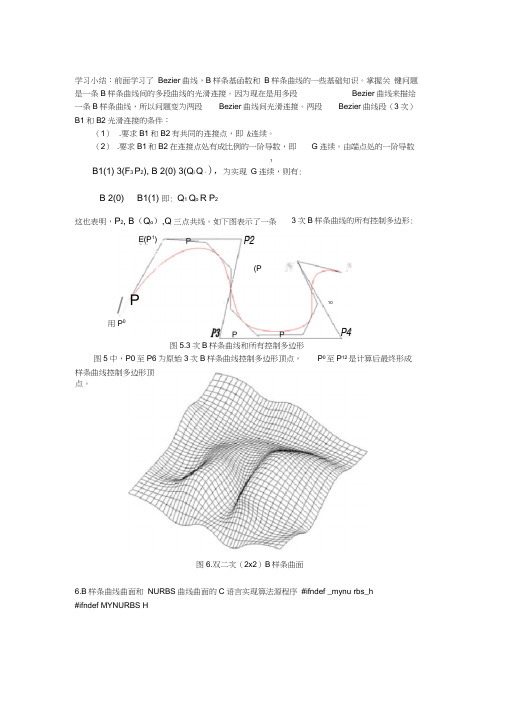
图6.双二次(2x2)B 样条曲面6.B 样条曲线曲面和 NURBS 曲线曲面的C 语言实现算法源程序 #ifndef _mynu rbs_h#ifndef MYNURBS H学习小结:前面学习了 Bezier 曲线,B 样条基函数和 B 样条曲线的一些基础知识。
掌握关 键问题是一条B 样条曲线间的多段曲线的光滑连接。
因为现在是用多段 Bezier 曲线来描绘 一条B 样条曲线,所以问题变为两段 Bezier 曲线间光滑连接。
两段 Bezier 曲线段(3次) B1和B2光滑连接的条件: (1) .要求B1和B2有共同的连接点,即 &连续。
(2) .要求B1和B2在连接点处有成比例的一阶导数,即 G 连续。
由端点处的一阶导数 1 B1(1) 3(F 3 P 2), B 2(0) 3(Q i Q 。
),为实现 G 连续,则有: B 2(0) B1(1) 即: Q 1 Q o R P 2 这也表明,P 2, B (Q o ),Q 三点共线。
如下图表示了一条 3次B 样条曲线的所有控制多边形: E(P 1) P2 (P/ P 用P 0 10 P4 图5.3次B 样条曲线和所有控制多边形图5中,P0至P6为原始3次B 样条曲线控制多边形顶点, P 0至P 12是计算后最终形成样条曲线控制多边形顶点。
#include "gl\gl.h"#include "math.h"//* ************* B样条基函数计算部分************** // 确定参数u 所在的节点区间下标//n=m-p-1//m 为节点矢量U[] 的最大下标//p 为B 样条函数次数int FindSource(int n,int p,float u,float U[]){int low,high,mid;if(u==U[n+1])// 特殊情况return n;// 进行二分搜索low=p;high=n+1;mid=(int)(low+high)/2; while(u<U[mid]||u>U[mid]){if(u<U[mid]) high=mid; else low=mid;mid=(int)(low+high)/2;if(u>=U[mid]&&u<U[mid+1])// 找到u 所在的节点区间的下标break; // 退出二分搜索}return mid; // 返回区间下标}// 计算所有非零B 样条基函数并返回其值//i 为参数u 所在的节点区间下标void BasisFunction(int i,int p,float u,float U[],float N[]){int j,di,dp,k;float tul,tur,left,right;float tmpN[50][50];for(k=0;k<=p;k++){dp=0;for(di=i+p-k;di>=i-k;di--){if(u>=U[di]&&u<U[di+1])tmpN[di][0]=1;elsetmpN[di][0]=0;dp+=1;for(j=1;j<dp;j++){tul=U[di+j]-U[di];tur=U[di+j+1]-U[di+1];if(tul!=0)left=(u-U[di])/tul;elseleft=0;if(tur!=0)right=(U[di+j+1]-u)/tur;elseright=0;tmpN[di][j]=left*tmpN[di][j-1]+right*tmpN[di+1][j-1];}}N[i-k]=tmpN[i-k][p];}}// ----------------------------------------------------------------------// 计算基函数的1 阶导数并保存在NP[] 中//i 为参数u 所在的节点区间下标//p 为B 样条函数次数P>2void DerBasisFunc(int i,int p,float u,float U[],float NP[]){int j,di,dp,k;float tul,tur,left,right,saved,dl,dr;float tmpN[50][50];for(k=0;k<=p;k++){dp=0;for(di=i+p-k;di>=i-k;di--){if(u>=U[di]&&u<U[di+1])tmpN[di][0]=1;elsetmpN[di][0]=0;dp+=1;for(j=1;j<dp;j++){tul=U[di+j]-U[di]; tur=U[di+j+1]-U[di+1]; if(tul!=0) left=(u-U[di])/tul,dl=1/tul;elseleft=0,dl=0;if(tur!=0)right=(U[di+j+1]-u)/tur,dr=1/tur;else right=0,dr=0;tmpN[di][j]=(left*tmpN[di][j-1]+right*tmpN[di+1][j-1]); saved=p*(dl*tmpN[di][j-1]-dr*tmpN[di+1][j-1])/(p+p-1);}}NP[i-k]=saved;}}//*-*-*-*-*-*-*-*-*-*-*-*-*-* Bezier 曲线曲面部*****************// 计算参数u 的p 次基函数值并存在BC[] 中void BernsteinFunc(int p,double t,float BC[]){for(int i=0;i<=p;i++){if(i==0) BC[0]=(float)pow(1-t,p);if(i==p)BC[p]=(float)pow(t,p);if(i>0&&i<p) BC[i]=p*(float)pow(t,i)*(float)pow(1-t,p-i);}}// 获取p 次Bezier 曲线上的lines 个点的值void BezierPoint(int p,float px[],float py[],float pz[],int lines,float tmp[][3]){float BC[20];int i,j;for(j=0;j<=lines;j++){double t=j/(float)lines;BernsteinFunc(p,t,BC); tmp[j][0]=tmp[j][1]=tmp[j][2]=0;for(i=0;i<p+1;i++){tmp[j][0]+=BC[i]*px[i];tmp[j][1]+=BC[i]*py[i];tmp[j][2]+=BC[i]*pz[i];}}}// 获取p 次有理Bezier 曲线上的lines 个点的值void NBezierPoint(int p,float px[],float py[],float pz[],float lines,float tmp[][4])pw[],int {float x,y,z,w,BC[20];int i,j;for(j=0;j<=lines;j++){double t=j/(float)lines;BernsteinFunc(p,t,BC);x=y=z=w=0;for(i=0;i<p+1;i++){x+=BC[i]*px[i]*pw[i];y+=BC[i]*py[i]*pw[i];z+=BC[i]*pz[i]*pw[i];w+=BC[i]*pw[i];}tmp[j][0]=x/w;tmp[j][1]=y/w;tmp[j][2]=z/w;tmp[j][3]=w;}}// --------------------------------------------------------------------------- // 绘制p 次的Bezier 曲线void Bezier(int p,float px[],float py[],float pz[],int lines){float pt[100][3];int j;BezierPoint(p,px,py,pz,lines,pt); for(j=1;j<=lines;j++){glBegin(GL_LINES);glVertex3f(pt[j-1][0],pt[j-1][1],pt[j-1][2]); glVertex3f(pt[j][0],pt[j][1],pt[j][2]);glEnd();}}// ---------------------------------------------------------------------------// 绘制p 次的有理Bezier 曲线void NBezier(int p,float px[],float py[],float pz[],float w[],int lines){float pt[100][4];int j;NBezierPoint(p,px,py,pz,w,lines,pt); for(j=1;j<=lines;j++){glBegin(GL_LINES); glVertex3f(pt[j-1][0],pt[j-1][1],pt[j-1][2]); glVertex3f(pt[j][0],pt[j][1],pt[j][2]);glEnd();}}// ---------------------------------------------------------------------------//计算双p次Bezier曲面上所有的点并保存在Pt[][][] 中//u 和v 分别为曲面(u,v) 方向上的网格数void BezierFacePoint(int p,int u,int v,float px[][4],float pz[][4],float pt[161][161][3])py[][4],float {float urx[11][161],ury[11][161],urz[11][161];float tx[11],ty[11],tz[11],tmp[161][3];int i,j,k;for(j=0;j<p+1;j++){for(i=0;i<p+1;i++){tx[i]=px[i][j];ty[i]=py[i][j];tz[i]=pz[i][j];}BezierPoint(p,tx,ty,tz,v,tmp); for(k=0;k<=v;k++){urx[j][k]=tmp[k][0];ury[j][k]=tmp[k][1];urz[j][k]=tmp[k][2];}}for(i=0;i<=v;i++){for(k=0;k<p+1;k++){tx[k]=urx[k][i];ty[k]=ury[k][i];tz[k]=urz[k][i];}BezierPoint(p,tx,ty,tz,u,tmp);for(j=0;j<=u;j++){pt[i][j][0]=tmp[j][0];pt[i][j][1]=tmp[j][1];pt[i][j][2]=tmp[j][2];}}}// ---------------------------------------------------------------------------// 计算双p 次有理Bezier 曲面上所有的点并保存在Pt[][][] 中//u 和v 分别为曲面(u,v) 方向上的网格数void NuBezierFacePoint(int p,int u,int v,float px[][4],float pz[][4],float w[][4],floatpy[][4],float pt[161][161][3]){float urx[11][161],ury[11][161],urz[11][161],urw[11][161];float tx[11],ty[11],tz[11],tw[11],tmp[161][4];int i,j,k;for(j=0;j<p+1;j++){for(i=0;i<p+1;i++){tx[i]=px[i][j];ty[i]=py[i][j];tz[i]=pz[i][j];tw[i]=w[i][j];}NBezierPoint(p,tx,ty,tz,tw,v,tmp);for(k=0;k<=v;k++)urx[j][k]=tmp[k][0];ury[j][k]=tmp[k][1];urz[j][k]=tmp[k][2];urw[j][k]=tmp[k][3];}}for(i=0;i<=v;i++){for(k=0;k<p+1;k++){tx[k]=urx[k][i];ty[k]=ury[k][i];tz[k]=urz[k][i]; tw[k]=urw[k][i];}NBezierPoint(p,tx,ty,tz,tw,u,tmp);for(j=0;j<=u;j++){pt[i][j][0]=tmp[j][0];pt[i][j][1]=tmp[j][1];pt[i][j][2]=tmp[j][2];} }}// ******** ******* B 样条曲线曲面部**************// 计算样条曲线的1阶导矢( u 所对应的所有点)保存在Der[] 中//n=m-p-1//p 为曲线的次数void BSplineDer(int n,int p,float U[],float P[],float Der[]){float N[100],tmp;int i,j;for(i=p+1;i<=n;i++){DerBasisFunc(i,p,U[i],U,N);tmp=0;for(j=i;j>=i-p;j--) tmp+=N[j]*P[j];Der[i-p]=tmp;// 计算曲线上的点( u 所对应的所有点)保存在Poi[] 中//n=m-p-1//p 为曲线的次数void BSplinePoint(int n,int p,float U[],float P[],float Poi[]){float N[100],tmp;int i,j;for(i=p+1;i<=n;i++){BasisFunction(i,p,U[i],U,N);tmp=0; for(j=i;j>=i-p;j--) tmp+=N[j]*P[j];Poi[i-p]=tmp;}}// 计算3 次样条曲线上的所有控制多边形保存在CP[] 中//m 为节点矢量U[] 的最大下标void B3SplineControlPoint(int m,float U[],float P[],float CP[]){int n,k,i,cp,p;float Poi[100],Der[100],add;p=3; n=m-p-1;BSplinePoint(n,p,U,P,Poi); BSplineDer(n,p,U,P,Der);cp=(n-p)*3+p; for(i=0;i<2;i++){CP[i]=P[i]; CP[cp-i]=P[n-i];}for(i=3;i<cp-1;i+=3){k=(int)i/3; add=Der[k]/p; CP[i]=Poi[k];CP[i-1]=CP[i]-add; CP[i+1]=CP[i]+add;}}// 计算2 次样条曲线上的所有控制多边形保存在CP[] 中//m 为节点矢量U[] 的最大下标void B2SplineControlPoint(int m,float U[],float P[],float CP[]){int n,k,tm,i,cp,p;float Poi[100];p=2;n=m-p-1;BSplinePoint(n,p,U,P,Poi);cp=(n-p)*2+p;for(i=0;i<2;i++)CP[i]=P[i];CP[cp]=P[n];tm=2;for(i=2;i<cp-1;i+=2){k=(int)i/2;CP[i]=Poi[k];CP[i+1]=P[tm];tm++;}}// 绘制3 次B 样条曲线//m 为节点矢量U[] 的最大下标void BSpline3L(int m,float U[],float px[],float py[],float pz[]){float pcx[100],pcy[100],pcz[100],drx[4],dry[4],drz[4];int i,j,tmcp;B3SplineControlPoint(m,U,px,pcx);B3SplineControlPoint(m,U,py,pcy);B3SplineControlPoint(m,U,pz,pcz);/*glColor3f(0.0f,0.0f,0.0f);for(i=1;i<3*m-17;i++){glBegin(GL_LINES); glVertex3f(pcx[i-1],pcy[i-1],pcz[i-1]);glVertex3f(pcx[i],pcy[i],pcz[i]);glEnd();}glColor3f(1.0f,0.0f,0.0f);*/tmcp=m-7;for(i=0;i<=tmcp;i++)for(j=i*3;j<i*3+4;j++){drx[j-i*3]=pcx[j];dry[j-i*3]=pcy[j];drz[j-i*3]=pcz[j];}Bezier(3,drx,dry,drz,20);}}// 绘制2 次B 样条曲线//m 为节点矢量U[] 的最大下标void BSpline2L(int m,float U[],float px[],float py[],float pz[]){float pcx[100],pcy[100],pcz[100],drx[3],dry[3],drz[3];int i,j,tmcp;B2SplineControlPoint(m,U,px,pcx);B2SplineControlPoint(m,U,py,pcy);B2SplineControlPoint(m,U,pz,pcz); tmcp=m-5;for(i=0;i<=tmcp;i++){for(j=i*2;j<i*2+3;j++){drx[j-i*2]=pcx[j];dry[j-i*2]=pcy[j];drz[j-i*2]=pcz[j];}Bezier(2,drx,dry,drz,20);}}// 计算双三次( 3x3)B 样条曲面所有控制多边形顶点,并保存在pt[][][] 中//mu,mv 分别为节点矢量U[],V[] 的最大下标值void BS3FaceControlPoint(int mu,float U[],int mv,float V[],float py[],float pz[],floatpx[],float pt[100][100][3]){int i,j,k,dp;float tmx[50],tmy[50],tmz[50];float tmpx[50][100],tmpy[50][100],tmpz[50][100];float uvx[100][100],uvy[100][100],uvz[100][100];for(i=0;i<mv-3;i++){dp=i*(mu-3);for(j=dp;j<mu-3+dp;j++){tmx[j-dp]=px[j];tmy[j-dp]=py[j];tmz[j-dp]=pz[j];}B3SplineControlPoint(mu,U,tmx,tmpx[i]);B3SplineControlPoint(mu,U,tmy,tmpy[i]);B3SplineControlPoint(mu,U,tmz,tmpz[i]);}for(i=0;i<3*mu-17;i++){for(j=0;j<mv-3;j++){tmx[j]=tmpx[j][i];tmy[j]=tmpy[j][i];tmz[j]=tmpz[j][i];}B3SplineControlPoint(mv,V,tmx,uvx[i]);B3SplineControlPoint(mv,V,tmy,uvy[i]);B3SplineControlPoint(mv,V,tmz,uvz[i]); for(k=0;k<3*mv-17;k++){pt[i][k][0]=uvx[i][k];pt[i][k][1]=uvy[i][k];pt[i][k][2]=uvz[i][k];}}}// 计算双二次( 2x2)B 样条曲面所有控制多边形顶点,并保存在pt[][][] 中//mu,mv 分别为节点矢量U[],V[] 的最大下标值void BS2FaceControlPoint(int mu,float U[],int mv,float V[],float py[],float pz[],floatpx[],float pt[100][100][3]){int i,j,k,dp;float tmx[50],tmy[50],tmz[50];float tmpx[50][100],tmpy[50][100],tmpz[50][100];float uvx[100][100],uvy[100][100],uvz[100][100];for(i=0;i<mv-2;i++){dp=i*(mu-2);for(j=dp;j<mu-2+dp;j++){tmx[j-dp]=px[j];tmy[j-dp]=py[j];tmz[j-dp]=pz[j];}B2SplineControlPoint(mu,U,tmx,tmpx[i]);B2SplineControlPoint(mu,U,tmy,tmpy[i]);B2SplineControlPoint(mu,U,tmz,tmpz[i]);}for(i=0;i<2*mu-7;i++){for(j=0;j<mv-2;j++){tmx[j]=tmpx[j][i];tmy[j]=tmpy[j][i];tmz[j]=tmpz[j][i];}B2SplineControlPoint(mv,V,tmx,uvx[i]);B2SplineControlPoint(mv,V,tmy,uvy[i]);B2SplineControlPoint(mv,V,tmz,uvz[i]); for(k=0;k<2*mv-7;k++){pt[i][k][0]=uvx[i][k];pt[i][k][1]=uvy[i][k];pt[i][k][2]=uvz[i][k];}}}//---------------------------------------------------------------------------- // 设置网格数void SetGridCount(int dt,int tu,int tmk[]){int i,tm;tm=tu%dt;for(i=0;i<dt-1;i++)tmk[i]=(tu-tm)/dt;tmk[dt-1]=tmk[0]+tm;}//----------------------------------------------------------------------------//计算双三次(3x3次)或双二次(2x2次)B样条曲面上所有的点并保存在bs[][][] 中//nu,mv 分别为节点矢量U[],V[] 的最大下标//uk,vk 分别为B 样条曲面(u,v) 方向上的网格数//p 为曲面的次数void BSplineFace(int p,int nu,float U[],int uk,int mv,float V[],int vk,float px[],float py[],float pz[],float bs[161][161][3]){int udk[20],vdk[20],i,j,k,l,hu,sv,du,dv;float tp[100][100][3],td[161][161][3];float tmx[4][4],tmy[4][4],tmz[4][4];du=nu-2*p;dv=mv-2*p;SetGridCount(du,uk,udk);SetGridCount(dv,vk,vdk);if(p==3)BS3FaceControlPoint(nu,U,mv,V,px,py,pz,tp);if(p==2)BS2FaceControlPoint(nu,U,mv,V,px,py,pz,tp);for(i=0;i<dv;i++){for(k=0;k<du;k++){for(j=i*p;j<p+1+i*p;j++) for(l=k*p;l<p+1+k*p;l++) {tmx[j-i*p][l-k*p]=tp[l][j][0];tmy[j-i*p][l-k*p]=tp[l][j][1];tmz[j-i*p][l-k*p]=tp[l][j][2];}BezierFacePoint(p,udk[k],vdk[i],tmx,tmy,tmz,td); for(sv=i*vdk[0];sv<=vdk[i]+i*vdk[0];sv++) for(hu=k*udk[0];hu<=udk[k]+k*udk[0];hu++) {bs[sv][hu][0]=td[sv-i*vdk[0]][hu-k*udk[0]][0];bs[sv][hu][1]=td[sv-i*vdk[0]][hu-k*udk[0]][1];bs[sv][hu][2]=td[sv-i*vdk[0]][hu-k*udk[0]][2];}}}}//-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-* Nurbs 样条曲线曲面部************** // 计算Nurbs 曲线上的点(u 所对应的所有点)保存在Poi[] 中//n=m-p-1//p 为曲线的次数void NurbsPoint(int n,int p,float U[],float P[],float W[],float Poi[]){float N[100],tmp,tmw;int i,j;for(i=p+1;i<=n;i++){BasisFunction(i,p,U[i],U,N); tmp=0;tmw=0;for(j=i;j>=i-p;j--){tmp+=N[j]*P[j]*W[j]; tmw+=N[j]*W[j];}Poi[i-p]=tmp/tmw;}}// 计算Nurbs 曲线的1 阶导矢( u 所对应的所有点)保存在Der[] 中//n=m-p-1 //p 为曲线的次数void NurbsDer(int n,int p,float U[],float P[],float W[],float Der[]){float N[100],CP[100],NW[100],tmp,tw;int i,j;NurbsPoint(n,p,U,P,W,CP);BSplinePoint(n,p,U,W,NW); for(i=p+1;i<=n;i++){DerBasisFunc(i,p,U[i],U,N); tmp=0;tw=0;for(j=i;j>=i-p;j--){tmp+=N[j]*P[j]*W[j]; tw+=N[j]*W[j];}Der[i-p]=(tmp-tw*CP[i-p])/NW[i-p];}}// 计算3 次Nurbs 曲线上的所有控制多边形保存在CP[] 中//m 为节点矢量U[] 的最大下标void Nurbs3ControlPoint(int m,float U[],float P[],float W[],float CP[]){int n,k,i,cp,p;float Poi[100],Der[100],add;p=3;n=m-p-1;NurbsPoint(n,p,U,P,W,Poi);{NurbsDer(n,p,U,P,W,Der); cp=(n-p)*3+p; for(i=0;i<2;i++)CP[i]=P[i];CP[cp-i]=P[n-i];}for(i=3;i<cp-1;i+=3){k=(int)i/3;add=Der[k]/p;CP[i]=Poi[k];CP[i-1]=CP[i]-add;CP[i+1]=CP[i]+add;}}// 计算2 次Nurbs 曲线上的所有控制多边形保存在CP[] 中//m 为节点矢量U[] 的最大下标void Nurbs2ControlPoint(int m,float U[],float P[],float W[],float CP[]){int n,k,tm,i,cp,p;float Poi[100];p=2;n=m-p-1;NurbsPoint(n,p,U,P,W,Poi);cp=(n-p)*2+p;for(i=0;i<2;i++)CP[i]=P[i];CP[cp]=P[n];tm=2;for(i=2;i<cp-1;i+=2){k=(int)i/2;CP[i]=Poi[k];CP[i+1]=P[tm];tm++;// 绘制3 次Nurbs 样条曲线//m 为节点矢量U[] 的最大下标void Nurbs3L(int m,float U[],float px[],float py[],float pz[],float W[]){float pcx[100],pcy[100],pcz[100],drx[4],dry[4],drz[4]; float pcw[100],drw[4];int i,j,tmcp;Nurbs3ControlPoint(m,U,px,W,pcx);Nurbs3ControlPoint(m,U,py,W,pcy);Nurbs3ControlPoint(m,U,pz,W,pcz);B3SplineControlPoint(m,U,W,pcw); tmcp=m-7;for(i=0;i<=tmcp;i++){{for(j=i*3;j<i*3+4;j++)drx[j-i*3]=pcx[j];dry[j-i*3]=pcy[j];drz[j-i*3]=pcz[j]; drw[j-i*3]=pcw[j];}NBezier(3,drx,dry,drz,drw,20);}}// 绘制2 次Nurbs 样条曲线//m 为节点矢量U[] 的最大下标void Nurbs2L(int m,float U[],float px[],float py[],float pz[],float W[]){float pcx[100],pcy[100],pcz[100],drx[3],dry[3],drz[3]; float pcw[100],drw[3];int i,j,tmcp;Nurbs2ControlPoint(m,U,px,W,pcx);Nurbs2ControlPoint(m,U,py,W,pcy);Nurbs2ControlPoint(m,U,pz,W,pcz);B2SplineControlPoint(m,U,W,pcw); tmcp=m-5;for(i=0;i<=tmcp;i++){for(j=i*2;j<i*2+3;j++){drx[j-i*2]=pcx[j];dry[j-i*2]=pcy[j];drz[j-i*2]=pcz[j];drw[j-i*2]=pcw[j];}NBezier(2,drx,dry,drz,drw,20);}}// 计算双三次( 3x3) Nurbs 样条曲面所有控制多边形顶点,并保存在pt[][][] //mu,mv 分别为节点矢量U[],V[] 的最大下标值void Nurbs3FControlPoint(int mu,float U[],int mv,float V[],float py[],float pz[],float W[],float pt[100][100][4]){int i,j,k,dp;float tmx[50],tmy[50],tmz[50],tmw[50];float tmpx[50][100],tmpy[50][100],tmpz[50][100],tmpw[50][100];float uvx[100][100],uvy[100][100],uvz[100][100],uvw[100][100];for(i=0;i<mv-3;i++){dp=i*(mu-3);for(j=dp;j<mu-3+dp;j++){tmx[j-dp]=px[j];tmy[j-dp]=py[j];tmz[j-dp]=pz[j];tmw[j-dp]=W[j];}Nurbs3ControlPoint(mu,U,tmx,tmw,tmpx[i]);Nurbs3ControlPoint(mu,U,tmy,tmw,tmpy[i]);Nurbs3ControlPoint(mu,U,tmz,tmw,tmpz[i]);B3SplineControlPoint(mu,U,tmw,tmpw[i]);}for(i=0;i<3*mu-17;i++){for(j=0;j<mv-3;j++){tmx[j]=tmpx[j][i];tmy[j]=tmpy[j][i];tmz[j]=tmpz[j][i];tmw[j]=tmpw[j][i]; 中px[],float}Nurbs3ControlPoint(mv,V,tmx,tmw,uvx[i]); Nurbs3ControlPoint(mv,V,tmy,tmw,uvy[i]); Nurbs3ControlPoint(mv,V,tmz,tmw,uvz[i]); B3SplineControlPoint(mv,V,tmw,uvw[i]);for(k=0;k<3*mv-17;k++){pt[i][k][0]=uvx[i][k];pt[i][k][1]=uvy[i][k];pt[i][k][2]=uvz[i][k];pt[i][k][3]=uvw[i][k];}}}// 计算双二次( 2x2) Nurbs 样条曲面所有控制多边形顶点,并保存在pt[][][] //mu,mv 分别为节点矢量U[],V[] 的最大下标值void Nurbs2FControlPoint(int mu,float U[],int mv,float V[],float py[],float pz[],float W[],float pt[100][100][4]){int i,j,k,dp;float tmx[50],tmy[50],tmz[50],tmw[50];float tmpx[50][100],tmpy[50][100],tmpz[50][100],tmpw[50][100];float uvx[100][100],uvy[100][100],uvz[100][100],uvw[100][100];for(i=0;i<mv-2;i++){dp=i*(mu-2);for(j=dp;j<mu-2+dp;j++){tmx[j-dp]=px[j];tmy[j-dp]=py[j];tmz[j-dp]=pz[j];tmw[j-dp]=W[j];}Nurbs2ControlPoint(mu,U,tmx,tmw,tmpx[i]);Nurbs2ControlPoint(mu,U,tmy,tmw,tmpy[i]);Nurbs2ControlPoint(mu,U,tmz,tmw,tmpz[i]);B2SplineControlPoint(mu,U,tmw,tmpw[i]);}for(i=0;i<2*mu-7;i++){for(j=0;j<mv-2;j++){tmx[j]=tmpx[j][i];tmy[j]=tmpy[j][i];tmz[j]=tmpz[j][i]; 中px[],floattmw[j]=tmpw[j][i];}Nurbs2ControlPoint(mv,V,tmx,tmw,uvx[i]);Nurbs2ControlPoint(mv,V,tmy,tmw,uvy[i]);Nurbs2ControlPoint(mv,V,tmz,tmw,uvz[i]);B2SplineControlPoint(mv,V,tmw,uvw[i]);for(k=0;k<2*mv-7;k++){pt[i][k][0]=uvx[i][k];pt[i][k][1]=uvy[i][k];pt[i][k][2]=uvz[i][k];pt[i][k][3]=uvw[i][k];}}}//----------------------------------------------------------------------------//计算双三次(3x3次)或双二次(2x2次)Nurbs样条曲面上所有的点并保存在//nu,mv 分别为节点矢量U[],V[] 的最大下标〃uk,vk 分别为B样条曲面(u,v)方向上的网格数//p 为曲面的次数void NurbsFace(int p,int nu,float U[],int uk,int mv,float V[],int vk,float px[],float py[],float pz[],float bs[161][161][3]){int udk[20],vdk[20],i,j,k,l,hu,sv,du,dv;float tp[100][100][4],td[161][161][3];float tmx[4][4],tmy[4][4],tmz[4][4],tmw[4][4];du=nu-2*p;dv=mv-2*p;SetGridCount(du,uk,udk);SetGridCount(dv,vk,vdk);if(p==3)Nurbs3FControlPoint(nu,U,mv,V,px,py,pz,w,tp);if(p==2)Nurbs2FControlPoint(nu,U,mv,V,px,py,pz,w,tp);for(i=0;i<dv;i++){for(k=0;k<du;k++){for(j=i*p;j<p+1+i*p;j++)for(l=k*p;l<p+1+k*p;l++){tmx[j-i*p][l-k*p]=tp[l][j][0];tmy[j-i*p][l-k*p]=tp[l][j][1];tmz[j-i*p][l-k*p]=tp[l][j][2]; bs[][][] 中w[],floattmw[j-i*p][l-k*p]=tp[l][j][3];}NuBezierFacePoint(p,udk[k],vdk[i],tmx,tmy,tmz,tmw,td);for(sv=i*vdk[0];sv<=vdk[i]+i*vdk[0];sv++)for(hu=k*udk[0];hu<=udk[k]+k*udk[0];hu++)bs[sv][hu][0]=td[sv-i*vdk[0]][hu-k*udk[0]][0];bs[sv][hu][1]=td[sv-i*vdk[0]][hu-k*udk[0]][1];bs[sv][hu][2]=td[sv-i*vdk[0]][hu-k*udk[0]][2];}}}} for(j=0;j<=u;j++) //* ************* 绘制曲面部*******************// 计算多边形的外法线返回值 tmN[]void getN(float x[3],float y[3],float z[3],float tmN[3]) { float p1,p2,p3,q1,q2,q3;float nx,ny,nz;p1=x[1]-x[0];p2=y[1]-y[0];p3=z[1]-z[0];q1=x[2]-x[1];q2=y[2]-y[1];q3=z[2]-z[1];nx=p2*q3-q2*p3;ny=q1*p3-p1*q3;nz=p1*q2-p2*q1;tmN[0]=nx;tmN[1]=ny;tmN[2]=nz;} //----------------------------------------------------------------------------// 显示 B 样条曲面//fill 取值为 0 或 1void ShowSurface(int u,int v,float bs[161][161][3],int fill) {int i,j;float x[3],y[3],z[3],tmn[3];for(i=0;i<=v;i++){if(fill!=0){x[0]=bs[i][j][0]; x[1]=bs[i+1][j][0]; x[2]=bs[i+1][j+1][0];y[0]=bs[i][j][1]; y[1]=bs[i+1][j][1]; y[2]=bs[i+1][j+1][1];z[0]=bs[i][j][2];z[1]=bs[i+1][j][2]; z[2]=bs[i+1][j+1][2];getN(x,y,z,tmn); glEnable(GL_NORMALIZE); glBegin(GL_QUADS);glNormal3f(tmn[0],tmn[1],tmn[2]); if(j<u){glVertex3f(bs[i][j][0],bs[i][j][1],bs[i][j][2]);glVertex3f(bs[i][j+1][0],bs[i][j+1][1],bs[i][j+1][2]);}if(i<v){glVertex3f(bs[i+1][j+1][0],bs[i+1][j+1][1],bs[i+1][j+1][2]);glVertex3f(bs[i+1][j][0],bs[i+1][j][1],bs[i+1][j][2]);}glEnd(); glDisable(GL_NORMALIZE);}else{ glBegin(GL_LINES); if(j<u) {glVertex3f(bs[i][j][0],bs[i][j][1],bs[i][j][2]);glVertex3f(bs[i][j+1][0],bs[i][j+1][1],bs[i][j+1][2]); }if(i<v){glVertex3f(bs[i][j][0],bs[i][j][1],bs[i][j][2]);glVertex3f(bs[i+1][j][0],bs[i+1][j][1],bs[i+1][j][2]);} glEnd();}#endif#endif#include 建立库文件“ myNurbs.h ”保存在include 目录下,在文件开始处写上"myNurbs.h" 即可用各函数的功能。
非均匀有理B样条NURBS曲线课件

04 NURBS曲线的应用实例
工业设计中的NURBS曲线应用
汽车设计
在汽车设计中,NURBS曲线被 广泛应用于车身、车轮和座椅等 零部件的轮廓设计,以实现流畅
的曲线和完美的曲面。
航空航天
在航空航天领域,NURBS曲线 用于飞机和航天器的外形设计, 以满足空气动力学和结构强度的
要求。
电子产品
在消费电子产品设计中,NURBS 曲线用于创建具有现代感和时尚 感的外观,如手机、电视和笔记
几何建模
01
在计算几何中,NURBS曲线用于几何建模,以描述复杂的几何
形状和曲面。
计算机图形学
02
在计算机图形学中,NURBS曲线用于渲染和可视化复杂的几何
模型。
机器人学
03
在机器人学中,NURBS曲线用于路径规划和运动控制,以确保
机器人的平滑运动和精确位置。
05 NURBS曲线的优缺点分析
优点分析
本电脑等。
动画制作中的NURBS曲线应用
角色动画
在角色动画中,NURBS曲线用于创建角色的轮廓 和表情,以实现逼真的表情和动作。
场景建模
NURBS曲线用于场景建模,以创建具有复杂几何 形状的背景和道具。
特效制作
在特效制作中,NURBS曲线用于模拟自然现象, 如水流、火焰和烟雾等。
计算几何中的NURBS曲线应用
动画。
02 NURBS曲线的数学表示
参数化
参数化方法
参数化是将几何信息转化 为数学表达的过程,通过 参数化,可以将几何形状 表示为参数值的变化。
参数范围
参数化过程中需要确定参 数的范围,以确保曲线形 状的正确表示。
参数化精度
参数化的精度决定了曲线 表示的准确性和光滑度, 精度越高,曲线表示越精确。
NURBS曲线_作者沙秉辉

• 计算P次基函数的时候需要用到三角形阵如下
例题2.1
• 限制区间闭区间0到1上,2次基函数就是2次伯恩斯坦多项式,所 以节点矢量中相同个数的0和1 此时B样条是贝奇尔的推广。 • 在节点个数不同是才具有一般性 • 如例题2.2
B样条基函数的导数
导数公式不唯一如下两种
• 应用H映射,对于给定的Pi和Wi构造带权控制点,则有定义在四 维空间的B样条曲线如下
计算发现H变换后计算曲线上点容易
• 同理 对C(u)进行H变换得到对应的四维空间有理NURBS曲线
B样条曲面和NURBS曲面
B样条曲面的定义
B样条曲面的一些性质
• • • • • • • • • • 非负性 规范性 局部支撑 可微 由以上得到 插值性 仿射不变 凸包性 局部修改 可微
B样条的计算
第三章B样条曲线曲面
• 定义
• 由控制点组成的多边形成为控制多边形 • 计算曲线上点的步骤
B样条的性质
• 如果n=p,节点矢量中的节点0,1个数相同,则是贝奇尔曲线 • 次数p,控ni制点个数n+1,节点个数m+1满足m=n+p+1 • 端点插值性 • 放射不变。对B样条进行评议 旋转 缩放剪切的变换或者组合变换, 所得到曲线仍然是B样条曲线。 • 强凸形是对B样条曲线的分段线性逼近,通过升阶插入节点修改权 因子可以改进规则是:次数第,B样条曲线靠近控制多边形,全 因子越大,越靠近。
• 由于以上的性质得到NURBS具有一下重要的性质: 端点插值性:即C P 的关系。 仿射不变性:同前 凸包性:同前 可微性:区间节点连续可微同前 局部修改性。改变控制点或者权因子可以改变该部分的曲线形状) (在计算机交互设计中重要)修改效果如下
8.NURBS曲线y
• NURBS曲线的形式(重点)
• NURBS方法的原理 • 权因子的几何意义(重点和难点) • NURBS曲线、二次有理Bé zier曲线和圆锥曲线 • NURBS的应用:IGES标准和G指令
11
透视投影
1
q
y
p
x
透视投影 透视投影特殊化的数学抽象 12
1
O
( px , p y , p ) ( px / p , p y / p )
4
引 入(2)
• NURBS方法使得圆锥曲线曲面和B样条统 一 • IGES规范 • STEP标准
5
讲授提纲
• 引入:为什么需要NURBS曲线 • NURBS曲线的表达式
• 圆锥曲线的NURBS表示
• NURBS的应用:IGES标准
6
NURBS曲线的形式(1)
Di [iVi
表达形式:
i ] [i xi
r (u ) N i ,k (u )Vi
i 0
?
投影
14
[ N i ,k (u )i xi / N i ,k (u )i ,
i 0 i 0 n
n
n
N
i 0
n
i ,k
(u )i yi / N i ,k (u )i ]
i 0
N
i 0
n
i ,k
(u )Vi [ N i ,k (u ) xi , N i ,k (u ) yi ]
23
0 N0,kV0 1 N1,kV1 2 N 2,kV2 0 N3,kV3 4 N 4,kV4 5 N5,kV5 0 N0,k 1 N1,k 2 N 2,k 0 N3,k 4 N 4,k 5 N5,k
B样条曲线曲面省公开课获奖课件市赛课比赛一等奖课件

是由两P0个0 方向u (P20例如
u
P00
和
vu)旳P20 特征
多边形来双决二定次Be,zie这r曲两面和个B样方条向曲面旳特征多
边形构成特征网格。
1.Bezier 曲面
给定了(m+1)(n+1)个空间点列 bi,j (i=0, 1,2,…,n; j=0,1,2,…,m)后,能够定义m n次 Bezier 曲面如下式所示:
法国旳 Bezier 为此提出了一种新旳 参数曲线表达措施,所以称为Bezier 曲线。后来又经过 Gordon、Forrest 和 Riesenfeld等人旳拓广、发展, 提出了B样条曲线。
这两种曲线都因能很好地合用于 外形设计旳特殊要求而取得了广泛旳 应用。
一、Bezier曲线
Bezier曲线旳形状是经过一组多边折
nm
P(u, v)
Bi,n (u) B j,m (v) bi, j
i0 j0
式中:(0 ≤ u,v ≤ 1) ; Bi,n(u) 为 n 次
Bernstein 基函数;连接点列 bi,j 中相
邻两点构成特征网格。
在实际应用中,次数 m 和 n 均不宜 超出 5,不然网格对于曲面旳控制力 将会减弱,这同 Bezier曲线旳情况 是相同旳。其中最主要旳应用是 m=n =3,即双三次 Bezier曲面。 双三次 Bezier曲面旳体现式为:
33
P(u, v)
Bi,3 (u) B j,3 (v) bi, j
i0 j0
U N b N T V T
式中:
U u 3 u 2 u 1 ;V v3 v 2 v 1
1 3 3 1
N
3
6
3
0
B样条

1 Bi ,1 ( t ) = 0
ti Bi,2(t) ti+1 Bi,3(t) ti+1 ti+2 Bi+1,2(t) ti+2 Bi+1,3(t) ti+3 ti+4 ti+3 ti+4
t i <= t < t i +1 其他
1
B i( = , 2 t)
t − ti t −t Bi ,1 (t ) + i + 2 Bi +1,1 (t ) t i +1 − t i t i + 2 − t i +1
(ti , ti + k ) 上不为零,
所以曲线 P (t ) 在区间 (ti , ti +1 ) (k − 1 ≤ i ≤ n)
,
Pi 有关。 上的部分只与控制顶点 Pi −k +1 Pi −k + 2 反过来,如果只变动某一个控制顶点 Pi ( 0 ≤ i ≤ n) 曲线上只有局部形状发生变化,其他部分均 不发生变化。
,…,
P1 P4 P7
P2
P6
P′4 P0 P3
P5 P″4
图8-16 B样条曲线的局部支柱性
(2) 仿射不变性 B样条曲线和Bézier曲线一样,也具有仿射不 变性,即曲线 P (t ) 的形状和位置与坐标系的选择 无关。 (3) 分段参数多项式 P (t )在每一区间 [ti , ti +1 ](k-1≤i≤n)上都是次数不高 于k-1次的参数t的多项式曲线,所以 P (t ) 在 [tk −1 , tn +1 ] 上是关于参数t的分段多项式曲线。 (4)连续性 P (t ) 在L重节点 ti(k≤i≤n)处的连续阶不低于 k-1-L。整条曲线 P (t ) 的连续阶不低于 k − 1 − lmax ,其 中 lmax 表示位于区间 [tk −1 , tn+1 ]内节点的最大重数。
NURBS曲线

• 齐次坐标表示形式说明:NURBS曲线是它的控制顶 点的齐次坐标或带权控制点在高一维空间里所定义 的非有理B样条曲线在ω=1超平面上的投影。 • 不仅包含了明确的几何意义,而且也说明:非 有理B样条曲线的大多数算法都可以推广应用于 NURBS曲线。
NURBS曲线有理分式表示
• 一条k次NURBS曲线可表示为一分段有理多项式矢函数:
n
i Pi Bi,k u
P u
i0 n
i Bi,k u
i0
• 这给出了NURBS的数学定义,也是有理的由来。
• 参数ωi是控制顶点权因子,分别与n+1个控制顶点 Pi(i=0,1,2,…,n)相联系。 • 首末权因子ω0,ωn>0,其余ωi≥0,以防止分母为 零、保留凸包性质及曲线不致于权因子而退化为
• 若移动k次NURBS曲线的一个控制顶点Pi或改变所 联系的权因子将仅仅影响定义在区间[ui,ui+k+1]上那 部分曲线的形状,对NURBS曲线的其它部分不发 生影响。
• 变差减少性质:
• 平面内任一直线与B样条曲线的交点各数不多于该 直线与曲线控制多边形的交点数目。
☆NURBS曲线 ● 有理样条曲线 ● NURBS 曲 线 表
质
● NURBS 形 状 因
子 ☆ 三次曲线比较
有理/非有理样条比较
• 有理样条与非有理样条相比有两个重要的优点: – 有理样条提供了二次曲线的精确表达式; – 非有理样条表达式为多项式,仅能逼近二次曲线。 • 这使图形包能用一个表达式(有理样条)来模拟所 有曲线形状,无需用一个曲线函数库去处理不 同的形状。 – 有理样条对于透视观察变换是不变的。 – 非有理样条关于透视观察变换是可变的。 • 这意味着可对有理曲线上的控制点应用一个透 视观察变换,来得到曲线的正确视图,
计算机图形学第8讲B样条曲线

B样条基底的计算
• 3阶B样条基底
计算机图形学
B样条基底的计算
• 3阶B样条基底
计算机图形学
B样条基底的支撑区间
计算机图形学
B样条基底的支撑区间
计算机图形学
B样条基底的性质
局部支撑性
0
Ni,k
(t)
0
以k=4,n=4为例
t [ti , tik ) otherwise
t0, t1 , t2, t3, t4, t5 , t6, t7, t8
算机图形学
B样条曲线的性质
– 变差缩减性 设平面内 n+1 个控制顶点 构成B样条曲线 P(t) 的 特征多边形。在该平面内的任意一条直线与 P(t) 的交点个数不多于该直线和特征多边形的交点 个数。
– 几何不变性 B样条曲线的形状和位置与坐标系的选择无关。
计算机图形学
B样条曲线的性质
– 仿射不变性
义在区间 [ti ,tik ) 上那部分曲线的形状,对曲线的其
余部分不发生影响。
计算机图形学
B样条曲线的性质
– 连续性 P(t)在r重节点处的连续阶不低于 k-1-r。
– 凸包性
Pk个(t)点在区Pi间k1(,ti ,ti,1P)i,
k 1 i n上的部分位于
的凸包 Ci内,整条曲线
则位于各凸包 Ci 的并集之内。
• 曲线n+1个控制点需要n+1个B样条基Ni,k (t)底需要
n+k+1个节点 t0,t1,, tik
B样条的注意点
• 控制多边形的顶点数=B样条基底函数的个数 • B样条基底函数的个数和阶数k是独立概念 • 控制多边形的顶点个数n不能确定B样条基底阶数k • 需要定义节点矢量T • 设控制多边形顶点数为n+1,B样条基底阶数为k
讲 B样条曲线曲面 NURBS曲线曲面PPT课件

三次Hermite曲线---弗格森 了解内容
a 0 0 0 11 Pk
C
b
1
c 0
d
3
1 0 2
1 1 1
1
Pk
1
0 0
Rk Rk 1
Mh是Hermite矩阵。
。 Gh是Hermite几何矢量
2 2 1 1 Pk
3
0
1
3 0 0
2 1 0
1
0
0
Pk
1
Rk Rk 1
局部性质。 局变差减小性质。 凸包性。 在仿射与透射变换下的不变性。 在曲线定义域内有与有理基函数同样的可微性。
13
第13页/共33页
NURBS曲线---性质
如果某个权因子为零,那么相应控制顶点对曲线没有影响。
若
,则当
时,非有理与有理Bezier曲线和非
有理B样条曲线是NURBS曲线的特殊情况
i
P67-68
8
第8页/共33页
NURBS曲线曲面
NURBS方法的主要优点
既为标准解析形状(初等曲线曲面),又为自由型曲线 曲面的精确表示与设计提供了一个公共的数学形式。
修改控制顶点和权因子,为各种形状设计提供了充分 的灵活性。
具有明显的几何解释和强有力的几何配套技术。 对几何变换和投影变换具有不变性。 非有理B样条、有理与非有理Bezier方法是其特例。
7
第7页/共33页
NURBS曲线曲面
B样条曲线、Bezier曲线都不能精确表示出抛物 线外的二次曲线,B样条曲面、Bezier曲面都 不能精确表示出抛物面外的二次曲面,而只能 给出近似表示。
提出NURBS方法,即非均匀有理B样条方法主要 是为了找到与描述自由型曲线曲面的B样条方 法既相统一、又能精确表示二次曲线弧与二次 曲面的数学方法。
B样条曲线曲面

p02 ?
p12
??M
T B
W
T
?? p2 ?w???
?? p20 p21 p22 ??
。
简记为
S
yz
?u,
w??
UM
B
PM
T B
W
T
2.均匀双三次B样条曲面
? ? 已知曲面的控制点 pij (i, j ? 0,1,2,3,) 参数u,w且 u, w ? 0,1 ,
构造双三次B样条曲面的步骤同上述。
⑴沿w(或u)向构造均匀二次B样条曲线,即有:
? 1 ? 2 1?? p00 ?
? p00 ?
? ? P0 (w) ? w2 w 1 ??? 2
2
0????
p01
? ?
?
WM
B
? ?
p 01
? ?
?? 1 1 0???? p02 ??
?? p02 ??
经转置后
? ? ? ? p0 w ? p00
p 01
? ? ? 1 (t ? 3)3 ? 4(t ? 2)3 ? 6(t ? 1)3 ? 4(t)3 6 1
= 6 (–t3 + 3t2 – 3t + 1)
? F1,3 (t) ?
1 3!
2 j? 0
(? 1)
j
C
j 4
(t
?
3
?
1?
j)3
? ? ?
1 6
C
0 4
(t
?
2) 3
?
C
1 4
(t
?
1) 3
?
? 2t 2 ? 2t ? 1 Pi?1 ?
1 2
t
第7讲-B样条曲线曲面-NURBS曲线曲面

P(u, v)
i0 j0 mn
Pij Ri, p; j,q (u, v)
ij Ni, p (u)N j,q (v) i0 j0
i0 j0
u, v [0,1]
Ri, p; j,q (u, v)
m
ij Ni, p (u)N j,q (v)
n
rs Nr, p (u)Ns,q (v)
r0 s0
19
8
NURBS曲线曲面
B样条曲线、Bezier曲线都不能精确表示出抛物 线外的二次曲线,B样条曲面、Bezier曲面都 不能精确表示出抛物面外的二次曲面,而只能 给出近似表示。
提出NURBS方法,即非均匀有理B样条方法主要 是为了找到与描述自由型曲线曲面的B样条方 法既相统一、又能精确表示二次曲线弧与二次 曲面的数学方法。
n
i Pi Ni,k (t) nP(t) Fra biblioteki0 n
Pi Ri,k (t)
i Ni,k (t) i0
i0
Ri,k (t)
i Ni,k (t)
n
j N j,k (t)
j0
12
NURBS曲线---性质
Ri,k(t)具有k阶B样条基函数类似的性质:
局部支承性:Ri,k(t)=0,t[ti, ti+k]
P67-68
9
NURBS曲线曲面
NURBS方法的主要优点
既为标准解析形状(初等曲线曲面),又为自由型曲线 曲面的精确表示与设计提供了一个公共的数学形式。
修改控制顶点和权因子,为各种形状设计提供了充分 的灵活性。
具有明显的几何解释和强有力的几何配套技术。 对几何变换和投影变换具有不变性。 非有理B样条、有理与非有理Bezier方法是其特例。
3DMAX之NURBS曲线和曲面

3DMAX之NURBS曲线和曲面一、NuRBS曲线作用:可制作圆滑的曲线外形‘Create(创建)‘shape(外形)‘NURBSpoint curve(点曲线)CV curve(控制点曲线):曲线在各控制点连接的多边形内参数:attach(附加):将其它曲线附加到当前曲线中二、NURBS曲面作用:可制作圆滑的面,如汽车外壳,床罩,窗帘丝织物品表面‘create(创建) →‘Geomotry(三维几何体) →‘NurBs surface(NurBs曲面) →‘point surface(点曲面)三、NurBs创建工具箱作用:方便创建曲线或者曲面1、Curves(曲线)工具箱第一个():建立cv curve(控制点曲线)第二个():建立Point curve(点曲面)第三个():连接两个顶点,限定在点曲线面类第四个():复制曲线第五个():连接2个顶点,点曲线,CV曲面都可相连第六个():产生曲线的轮廓线第七个():镜像复制曲线2、surface(曲面)工具箱第一个():建立cv surface(控制点曲面)第二个():建立point surface(点曲面)第三个():复制曲面第四个和第九个():将2个曲线连接成面第五个():复制曲面,不能分开第六个():镜向复制曲面第七个():将曲面拉伸成面第八个():将曲线旋转成面。
智点道CG培训教育学院主要培训建筑表现动画、建筑表现后期、室外设计效果图、影视动画制作、影视特效等。
有兴趣的加建筑表现交流群318796674。
学院配送一线设计师讲师,安排学员个人学习及工作计划,常年来为同行输送数百名CG行业精英人才,就业后薪资待遇丰厚。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
35
第3章 车身曲线曲面的数学模型基础
-------总结 B样条曲线与曲面; 如何理解B样条曲线定义? 与贝齐尔相比的区别? 端点性质?
36
作业
1.说明两条曲线达到C、G连续的条件。 2.分析三次伯恩斯坦基函数对贝齐尔曲线的影响。 3.分析曲线升阶后的意义。 4.如何把一段贝齐尔曲线分成等长的两段?
点P0P2的直线段
P1
双曲线
抛物线
椭圆
P0
P2
图3.1.36 圆锥曲线的 NURBS表示 23
NURBS曲线---修改
常用的方法有修改权因子、控制点和反插节点。 修改权因子
当保持控制顶点和其它权因子不变,减少或增加某权因 子时,曲线被推离或拉向相应顶点。
S* Pi
S
N B
修改权因子
24
NURBS曲线---非均匀有理B样条曲面
⎡ 2 − 2 1 1 ⎤⎡ Pk ⎤
= ⎢⎢− 3
⎢0
⎢ ⎣
1
3 0 0
−2 1 0
−1⎥⎥
0⎥
0
⎥ ⎦
⎢ ⎢
Pk
+1
⎥ ⎥
⎢ ⎢ ⎣
Rk Rk +1
⎥ ⎥ ⎦
=
M
h
⋅
Gh
28
三次Hermite曲线---弗格森
三次Hermite样条曲线的方程为:
p(t) = T ⋅ M h ⋅ Gh
t ∈[0,1]
p(0) = Pk , p(1) = Pk+1 p′(0) = Rk , p′(1) = Rk+1
26
三次Hermite曲线---弗格森
推导:
⎡ax ay az ⎤
p(t) = [t3
t2
t
1]⎢⎢⎢⎢⎢⎣dbcxxx
by cy dy
bz
⎥ ⎥
cz dz
⎥ ⎥ ⎥⎦
⎡a⎤
= [t3
t2
t
1]⎢⎢b
n
∑ 权性:
Ri,k (u) = 1
i=0
可微性:如果分母不为零,在节点区间内是无限次连续可微
的,在节点处 (k-1-r)次连续可导,r是该节点的重复度。
若ωi=0,则Ri,k(t)=0; 若ωi=+∞,则Ri,k(t)=1;
19
NURBS曲线---性质
NURBS曲线与B样条曲线具有类似的几何性质:
v
d23
d13
C2
C1 d22
d32
d12
d33 C3
d42
d34
d44 d43
C4
d21
d31
d11
u
d41
参数v在[0,1] 之间取值vk ,对应于vk曲线C1、C2、C3和C4上可得到 v1k、v2k、v3k和v4k四个点,该四点构成u向的一个特征多边形,定 义一条新的曲线P(u,vk);
d14
,j
≤ v j+1
)分
uv 别是对参数 平面的 u 轴和v 轴的分割,如图所示。称下列张量
积形式的参数曲面为 k × h ( k≤n,h≤m)阶的B样条曲面
nm
∑ ∑ P(u,v) =
Pij Bi,k (u)Bj,h (v)
i=0 j=0
P(u, v)
uk-1≤u≤un+1,vh-1≤v≤vm+1
其 中 Pij 是 空 间 中 给 定 的 (n+1)×(m+1) 个 网 格 点 , 通 常 称 为
有理Bezier曲线和非有理B样条曲线是NURBS曲线的特殊 情况
21
NURBS曲线---性质
取节点向量为 T = [0,0,0,1,1,1] 则NURBS曲线退化为二次
Bezier曲线,且可以证明,这是圆锥曲线弧方程。
P(t)
=
(1− t 2 )ω0P0 + 2t(1− t)ω1P1 + t 2ω2P2 (1− t)2ω0 + 2t(1− t)ω1 + t 2ω2
n
∑ωi Pi Ni,k (t) n
P(t) =
i=0 n
∑ = Pi Ri,k (t)
∑ωi Ni,k (t) i=0
i=0
Ri,k (t) =
ωi Ni,k (t)
n
∑ω j N j,k (t)
j=0
18
NURBS曲线---性质
Ri,k(t)具有k阶B样条基函数类似的性质:
局部支承性:Ri,k(t)=0,t∉[ti, ti+k]
车 身 CAD
山东交通学院 汽车工程系
1
复习:分段三次B-样条曲线
2
B样条曲线的表达式
若给定m+n+1个顶点Pi (i=0,1,2,…,m+n),将多边折 线分成m+1段,每段多边折线称为B特征多边形,构成的第i 段B-样条曲线为n次多项式 (i=0,1,2,…,m) :
n
∑ Pi,n (t) = Pi+k Fk,n (t) k =0
1t
31
三次Hermite曲线---弗格森
特点分析:
1.可以局部调整,因为每个曲线段仅依赖于端点约束。 2 . 基 于 Hermite 样 条 的 变 化 形 式 : Cardinal 样 条 和
Kochanek-Bartels样条 3.Hermite曲线具有几何不变性
32
第3章 车身曲线曲面的数学模型基础
b样条曲面
P23
P03
P33
P02
P12 P22
P32
P11
P21
P01
P31
P10
P20
P00 P30
双三次B样条曲面片
B样条曲面
P23
P03
P33
P02 P01
P12 P22
P32
P11
P21
P31
P00 图3.1.33
P10
P20
P30 双三次B样条曲面片
13
第3章 车身曲线曲面的数学模型基础
z 局部性质。 z 局变差减小性质。 z 凸包性。 z 在仿射与透射变换下的不变性。 z 在曲线定义域内有与有理基函数同样的可微性。
20
NURBS曲线---性质
如果某个权因子为零,那么相应控制顶点对曲线没有影响。
若 ωi → ∞ ,则当 t ∈[ti , ti+k ] P(t) = Pi 时,非有理与
其中,F k , n (t)为n次B样条基函数(德布尔-考克斯递推公式)
3
第3章 车身曲线曲面的数学模型基础
主要讲授内容
CAGD发展; 几何造型技术; 参数曲线和曲面; Bezier 曲线与曲面; B样条曲线与曲面; NURBS曲线与曲面;
4
B样条曲面
给定参数轴u和v的节点矢量
v
C1
C2
C3
V1k
V2k
V3k
u
C4
V4k
与Bézier曲面一样,{Pij}是对曲面 P(u, v) 的大致
形状的勾画,P(u, v) 是对 {Pij } 的逼近。B样条曲
面也具有局部调整性、凸包性、几何不变性等,它的 控制网格也是人机交互的手段,也可以通过某些算法 对其进行计算,这些都与B样条曲线的情况类似。
-------总结 几何造型技术:
线框模型、曲面模型和实体模型三种造 型技术的区别?
33
第3章 车身曲线曲面的数学模型基础
-------总结
参数曲线和曲面; 参数曲线的表示形式?优势? 位置矢量、切矢量、法矢量、曲率和挠率? 曲线间连接的光滑度的度量有两种----C连续与G连续?
34
第3章 车身曲线曲面的数学模型基础
U = [u0 , u1,L, um+ p ]
V = [v0 , v1,L, vn+q ]
p×q阶B样条曲面定义如下
mn
∑ ∑ P(u,v) =
Pij Ni, p (u)N j,q (v)
i=0 j=0
5
{ } u u v 设节点向量
U=
ui
i+=∞−∞,V
=
{v
j
}+∞ j = −∞
(
i ≤ i+1
v
d23
d13
C2
C1 d22
d32
d12
d21 d11
d31 u
d24 d33 C3 d42
d34
d44 d43
C4
d41
9当参数vk在[0,1] 之间取不同值时,P(u,vk)沿箭头方向扫描,即 得到由给定特征网格dij(i=1,2,3,4 j=1,2,3,4)定义的双三次均匀B样 条曲面片P(u,v)。
NURBS曲面的定义
mn
∑ ∑ωij Pij Ni, p (u)N j,q (v) m n
P(u, v) =
i=0 j=0 mn
∑ ∑ =
Pij Ri, p; j,q (u, v)
∑ ∑ωij Ni, p (u)N j,q (v) i=0 j=0
i=0 j=0
u, v ∈[0,1]
Ri, p; j,q (u, v) =
16
NURBS曲线曲面
应用NURBS中还有一些难以解决的问题:
z 比传统的曲线曲面定义方法需要更多的存储空间 z 权因子选择不当会引起畸变 z 对搭接、重叠形状的处理很麻烦。 z 反求曲线曲面上点的参数值的算法,存在数值不稳定问题
17
NURBS曲线---定义
NURBS曲线的定义
