最新多项式除以单项式PPT
合集下载
最新-多项式除以单项式-课件教学讲义PPT

1) 英语字母共26个,每个字母都有大、小写 两种形式;
2) 书写形式有:印刷体和书写体; 3) 读音形式有两种:升调和降调.
字母的读音 英语26个字母按一定的顺序排列起来,就构成 了英语字母表.词典里的词就是按字母表的顺 序排列的.
26个英文字母及发音音标
Consonants are produced by constricting or obstructing the vocal tract at some place to divert, impede, or completely shut off the flow of air in the oral cavity. By contrast, a vowel is produced without such obstruction so no turbulence or a total stopping of the air can be perceived.
2
2
课堂练习
(1)(9x2y6xy2)(3xy);
(2)(3x2yxy21xy)(1xy)。 22
(3)(12a3-8a2-3a)÷4a (4)(6a2b-2ab2-b3)÷(-3b)
继续努力!
(1)(5ax2 15x) 5x
(2)(12m2n15mn2) 6mn
(3)(4a3b3 6a2b3c 2ab5) (2ab2)
= 3x35x2
例题解析
例3 计算:
( 2 ) (2a 3 8 b 2 c a 2 b 3 1a 2 4原式=(2a83b2c)(7a2b)+(a2b3)(7a2b)+(1a42b2)(7a2b)
= (4abc)+( 1 b 2 ) + (2b )
多项式除以单项式PPT教学课件_1

第2课时 多项式除以单项式
复习引入
完成下列各题:
(1)因为(_a+__b_)c=ac+bc,所以(ac+bc)÷c=a_+_b__.
(2)因为(a_b_+__3_a_)b=ab2+3ab,所(ab2+3ab)÷b=_a_b_+_3_a_. (3)由于(_1_-__y_)xy=xy-xy2,所以(xy-xy2)÷xy= _1_-__y_.
首页
由以上解题我们不难得出:
(ac+bc)÷c=a_+_b__=ac÷c __+bcc÷__. (ab2+3ab)÷b=_a_b_+_3_a_=a2b÷b__+3ab÷b __. (xy-xy2)÷xy= 1_-__y__=xy÷x_y__-xy2÷xy___.
合作探究
由此,你能归纳出多项式除以单项式的法则吗? 【归纳】多项式除以单项式,先把这个多项式的每 一项分别除以单项式,再把所得的商相加. 【点拨】多项式除以单项式的运算是转化为单项 式除以单项式来计算的,所以计算中要特别注意每 项的符号.
巩固训练 1.计算(3x2-x)÷(-x)的正确结果是( ) (A)3x (B)3x-1 (C)-3x+1 (D)-3x-1 【解析】选C.(3x2-x)÷(-x) =3x2÷(-x)-x÷(-x)=-3x+1.
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,
则这个多项式为( )
【规范解答】(1)(28a3-14a2+7a)÷7a
=28a3÷7a-14a2÷7a+7a÷7a
特别提醒:不要漏掉(1)
=4a2-2a+1.……………………3分 中的最后一项.
复习引入
完成下列各题:
(1)因为(_a+__b_)c=ac+bc,所以(ac+bc)÷c=a_+_b__.
(2)因为(a_b_+__3_a_)b=ab2+3ab,所(ab2+3ab)÷b=_a_b_+_3_a_. (3)由于(_1_-__y_)xy=xy-xy2,所以(xy-xy2)÷xy= _1_-__y_.
首页
由以上解题我们不难得出:
(ac+bc)÷c=a_+_b__=ac÷c __+bcc÷__. (ab2+3ab)÷b=_a_b_+_3_a_=a2b÷b__+3ab÷b __. (xy-xy2)÷xy= 1_-__y__=xy÷x_y__-xy2÷xy___.
合作探究
由此,你能归纳出多项式除以单项式的法则吗? 【归纳】多项式除以单项式,先把这个多项式的每 一项分别除以单项式,再把所得的商相加. 【点拨】多项式除以单项式的运算是转化为单项 式除以单项式来计算的,所以计算中要特别注意每 项的符号.
巩固训练 1.计算(3x2-x)÷(-x)的正确结果是( ) (A)3x (B)3x-1 (C)-3x+1 (D)-3x-1 【解析】选C.(3x2-x)÷(-x) =3x2÷(-x)-x÷(-x)=-3x+1.
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,
则这个多项式为( )
【规范解答】(1)(28a3-14a2+7a)÷7a
=28a3÷7a-14a2÷7a+7a÷7a
特别提醒:不要漏掉(1)
=4a2-2a+1.……………………3分 中的最后一项.
多项式除以单项式(课件)

m
(ad+bd) ÷d
=(ad+bd)·
1 d
=ad·
1 d
+bd·
1 d
=a+b
除以一个数等于乘以这个数的倒数。 根据多项式乘以单项式法则。
新知讲解
类比有理数的除法
(ma+mb+mc) ÷m=(ma+mb+mc) · 1 =a+b+c. m
(a2b+3ab) ÷a
=(a2b+3ab)·
1 a
=a2b·
新知讲解
【做一做】
小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二
阶段的平均速度为
1 2
v,所用时间为t2.
下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的
路程是相同的,问小明下山用了多长时间?
【解】(12 vt2 + vt1)÷
4v
=
1 8
t2
+
1 4
t1
.
答:小明下山所用时间为
板书设计
1.多项式除以单项式的运算法则: 多项式除以单项式,先把这个多项式的每一项除以这个单项式,再 把所得的商相加. 2.多项式除以单项式的应用
作业布置
课本 P31 练习题 P31 习题1.14
C.3个
D.4个
课堂练习
4.计算:(-2x2y+6x3y4-2xy)÷(-2xy).
解:(-2x2y+6x3y4-2xy)÷(-2xy) =-2x2y÷(-2xy)+6x3y4÷(-2xy)-2xy÷(-2xy) =x-3x2y3+1.
拓展提高
5. 先化简,再求值: [2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2015,y=2014.
(ad+bd) ÷d
=(ad+bd)·
1 d
=ad·
1 d
+bd·
1 d
=a+b
除以一个数等于乘以这个数的倒数。 根据多项式乘以单项式法则。
新知讲解
类比有理数的除法
(ma+mb+mc) ÷m=(ma+mb+mc) · 1 =a+b+c. m
(a2b+3ab) ÷a
=(a2b+3ab)·
1 a
=a2b·
新知讲解
【做一做】
小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二
阶段的平均速度为
1 2
v,所用时间为t2.
下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的
路程是相同的,问小明下山用了多长时间?
【解】(12 vt2 + vt1)÷
4v
=
1 8
t2
+
1 4
t1
.
答:小明下山所用时间为
板书设计
1.多项式除以单项式的运算法则: 多项式除以单项式,先把这个多项式的每一项除以这个单项式,再 把所得的商相加. 2.多项式除以单项式的应用
作业布置
课本 P31 练习题 P31 习题1.14
C.3个
D.4个
课堂练习
4.计算:(-2x2y+6x3y4-2xy)÷(-2xy).
解:(-2x2y+6x3y4-2xy)÷(-2xy) =-2x2y÷(-2xy)+6x3y4÷(-2xy)-2xy÷(-2xy) =x-3x2y3+1.
拓展提高
5. 先化简,再求值: [2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2015,y=2014.
12.4.2多项式除以单项式 课件(共22张PPT).ppt

1 a3b2 2
1 a 4b3 6
0.5a 2b
(7) 2 y 3 7 y 2 2 y 2 y
5
3 3
(8)[(x+y)2-y(2x+y)-8x]÷2x
(9) (a3-3a2b)÷3a2-(3ab2-b2)÷b2
2、化简求值:
(1)已知x=0.5, y=3, 求[4(x2+y)(x2-y)-(2x2-y)2]÷y的值
课后作业
提高练习
1、计算: (1) (14a2b2-21ab2)÷7ab2 (2) (12x3-8x2+16x)÷(-4x) (3) (12a3-6a2+3a)÷3a (4) (6x4-8x3)÷(-2x2) (5) (21x4y3-35x3y2+7x2y2)÷(-7x2y)
(6)
0.25a 2b
你找到了 多项式除以单项式的规律 吗?
多项式除以单项式,先把这个多 项式的每一项分别除以单项式,再 把所得的商相加。
例1 计算:
例题解析
解原式=(28a3b2c) (7a2b)+ (a2b3) (7a2b) + (14a2b2 ) (7a2b)
=(4abc) + ( 1 b2 )+ (2b)
学而不思则罔,思而不探则空。
12.4 整式的除 法——多项式除以单项式
第一课时
回顾 & 思考☞
单项式与单项式相除
1、系数 相除; 2、同底数幂 相除; 3、只在被除式里的幂 不变;
练一练
(1) –12a5b3c÷(–4a2b)= 3a3b2c
(2)(–5a2b)2÷5a3b2 = 5a
(3)4(a+b)7 ÷
1
2 (a+b)3 =
多项式除以单项式PPT教学课件_2

巴尔扎克通过这个形象 写出了资产阶级罪恶的发家 巴尔扎克《欧也妮·葛朗台》 史和金钱关系的罪恶。
结合《欧也妮·葛朗台》归纳现实主 义文学的特点:
2、现实主义文学: 1)背景:
2)特点:
关注社会问题,典型地再现社会风 貌,揭露和批判社会的罪恶。
3)代表作:
国家 英国
作家 狄更斯
法国 巴尔扎克
俄国 列夫.托 尔斯泰
2、现实主义文学:
1)背景: 两次世界大战夺去千百万人的生命,物 质财富遭到惨重损失,给人类的心灵留 下难以愈合的创伤;欧美各国科学技术 与工业生产飞跃发展,不仅没有消除资 本主义的痼疾,反而加剧了人类的生存 危机,人们开始了对丑恶现实的无情批 判。
罗曼·罗兰(1866—1944),法国思想家, 文学家,法国批判现实主义作家、音乐评论家 和社会活动家。长篇小说《约翰·克利斯朵夫》 是其著名的代表作。全书共10卷,以主人公约 翰.克利斯朵夫的生平为主线,描写了主人公 奋斗的一生,从儿时音乐才能的觉醒、到青年 时代对权贵的蔑视和反抗、再到成年后在事业 上的追求和成功、最后达到精神宁静的崇高境 界。《约翰·克利斯朵夫》被高尔基称为“长 篇 叙 事 诗 ” , 被 誉 为 20 世 纪 最 伟 大 的 小 说 。 1915年,又获该年度诺贝尔文学奖。
为:“(他的)伟大之处在于,尽管他
有那些政治与意识形态上的偏见,他依
然用未受污染的眼睛观察所产生的矛盾,
并忠实地描述他们。”据此判断,这一评
论所指的作家是
A.拜伦
B.巴尔扎克
C.薄伽丘
D.莎士比亚
3.18世纪末19世纪初西方某文学流派 “以艺术的方式描摹了这一特定时代人 的激荡、亢奋而敏感、纤弱的心灵世界, 展现了有着强烈个性扩张欲望的自我”。 其创作风格是 A.浪漫主义 B.现实主义 C.古典主义 D.理性主义
结合《欧也妮·葛朗台》归纳现实主 义文学的特点:
2、现实主义文学: 1)背景:
2)特点:
关注社会问题,典型地再现社会风 貌,揭露和批判社会的罪恶。
3)代表作:
国家 英国
作家 狄更斯
法国 巴尔扎克
俄国 列夫.托 尔斯泰
2、现实主义文学:
1)背景: 两次世界大战夺去千百万人的生命,物 质财富遭到惨重损失,给人类的心灵留 下难以愈合的创伤;欧美各国科学技术 与工业生产飞跃发展,不仅没有消除资 本主义的痼疾,反而加剧了人类的生存 危机,人们开始了对丑恶现实的无情批 判。
罗曼·罗兰(1866—1944),法国思想家, 文学家,法国批判现实主义作家、音乐评论家 和社会活动家。长篇小说《约翰·克利斯朵夫》 是其著名的代表作。全书共10卷,以主人公约 翰.克利斯朵夫的生平为主线,描写了主人公 奋斗的一生,从儿时音乐才能的觉醒、到青年 时代对权贵的蔑视和反抗、再到成年后在事业 上的追求和成功、最后达到精神宁静的崇高境 界。《约翰·克利斯朵夫》被高尔基称为“长 篇 叙 事 诗 ” , 被 誉 为 20 世 纪 最 伟 大 的 小 说 。 1915年,又获该年度诺贝尔文学奖。
为:“(他的)伟大之处在于,尽管他
有那些政治与意识形态上的偏见,他依
然用未受污染的眼睛观察所产生的矛盾,
并忠实地描述他们。”据此判断,这一评
论所指的作家是
A.拜伦
B.巴尔扎克
C.薄伽丘
D.莎士比亚
3.18世纪末19世纪初西方某文学流派 “以艺术的方式描摹了这一特定时代人 的激荡、亢奋而敏感、纤弱的心灵世界, 展现了有着强烈个性扩张欲望的自我”。 其创作风格是 A.浪漫主义 B.现实主义 C.古典主义 D.理性主义
多项式除以单项式ppt

,包括如何处理多项式乘以单项式、多项式乘以多项式等问题。
感谢您的观看
THANKS
复杂案例及解析
题目
$(x^{3} + 3x^{2} + 2x + 1) \div (x^{2} + x - 6)$
解答
学生常见错误及纠正方法
错误
在除法运算中,学生可能会将多项式的每一项分别除以 单项式,而不是将整个多项式作为一个整体进行除法运 算。
纠正方法
需要强调多项式除以单项式的概念,让学生明白多项式 是一个整体,需要将整个多项式作为一个整体进行除法 运算。同时,可以多进行练习和讲解,让学生熟悉多项 式除以单项式的运算规则和方法。
下一步学习计划
01
掌握多项式除以单项式的运算规则
通过练习和例题,掌握多项式除以单项式的运算规则,包括如何确定
商和余数,如何处理除数为零的情况等。
02
深入理解除法运算的性质
通过更多的例题和练习,深入理解除法运算的基本性质,包括商和余
数的唯一性、除数不能为零等。
03
进一步拓展数学思维
通过解决更复杂的数学问题,进一步拓展数学思维和解决问题的能力
实际应用中的问题及解决方案
总结词
在实际应用中,多项式除以单项式可能会 遇到除不尽的情况,这时需要注意取舍问 题。
详细描述
在某些情况下,多项式除以单项式的商可 能是无限循环小数或者某些特定形式的小 数,这时需要根据实际应用的需求来确定 如何取舍。例如,在物理、工程等领域中 ,通常会采用保留有效数字的方法来进行 取舍。
多项式除以单项式
2023-10-29
contents
目录
• 多项式除以单项式概述 • 多项式除以单项式的基本步骤 • 多项式除以单项式的注意事项 • 多项式除以单项式的扩展应用 • 多项式除以单项式的练习与案例分析 • 总结与回顾
多项式除以单项式ppt课件
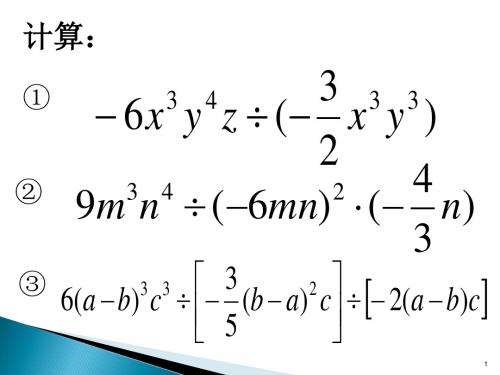
② (15x 2 y 10xy 2 ) 5xy;
③ (8a2b 4ab2 ) 4ab;
④ (4c2d c3d 3) (2c2d ).
12
练习:
(2)计算:
① (16m3 24m2 ) (8m2 );
② (9x3 y2 21xy2 ) 7xy2 ;
③ (25x2 15x3 y 20x4 ) (5x2 ); ④ (4a2 12a2b 7a3b2 ) (4a2 ).
n 平方 加n 除以n 答案
15
n 平方 加n 除以n 答案
16
小结
1.多项式除以单项式的法则是什么? 2.运用该法则应注意什么?
正确地把多项式除以单项式问题转化 为单项式除以单项式问题。计算不可丢 项,分清“约掉”与“消掉”的区别: “约掉”对乘除法则言,不减项;“消 掉”对加减法而言,减项。
9
多项式除以单项式的法则的应用:
10
例4.计算:
[5xy2(x2-3xy)-(-3x2y)3]
÷(2xy)2
=[5x3y2-15x2y3 - (-27x6y3)]
÷4x2y
=[5x3y2-15x2y3+27x6y3)]
÷4x2y
= 5x- 15y + 27 x4y
44
4
11
练习:
(1)计算:
① (6xy 5x) x;
解:原式 28a3 7a 14a2 7a 7a 7a
4a2 2a 1
7
(2)
(36 x4 y3 24 x3 y2 3x2 y2 ) (6x2 y)
8
多项式除以单项式的法则:
例2 化简:
(2x y)2 y( y 4x) 8x 2x
③ (8a2b 4ab2 ) 4ab;
④ (4c2d c3d 3) (2c2d ).
12
练习:
(2)计算:
① (16m3 24m2 ) (8m2 );
② (9x3 y2 21xy2 ) 7xy2 ;
③ (25x2 15x3 y 20x4 ) (5x2 ); ④ (4a2 12a2b 7a3b2 ) (4a2 ).
n 平方 加n 除以n 答案
15
n 平方 加n 除以n 答案
16
小结
1.多项式除以单项式的法则是什么? 2.运用该法则应注意什么?
正确地把多项式除以单项式问题转化 为单项式除以单项式问题。计算不可丢 项,分清“约掉”与“消掉”的区别: “约掉”对乘除法则言,不减项;“消 掉”对加减法而言,减项。
9
多项式除以单项式的法则的应用:
10
例4.计算:
[5xy2(x2-3xy)-(-3x2y)3]
÷(2xy)2
=[5x3y2-15x2y3 - (-27x6y3)]
÷4x2y
=[5x3y2-15x2y3+27x6y3)]
÷4x2y
= 5x- 15y + 27 x4y
44
4
11
练习:
(1)计算:
① (6xy 5x) x;
解:原式 28a3 7a 14a2 7a 7a 7a
4a2 2a 1
7
(2)
(36 x4 y3 24 x3 y2 3x2 y2 ) (6x2 y)
8
多项式除以单项式的法则:
例2 化简:
(2x y)2 y( y 4x) 8x 2x
人教版八年级数学上册《1.7.2多项式除以单项式》优秀课件

3
9
9
6a3b2 18 .
总结
知1-讲
多项式除以单项式实质是转化为单项式除以单项式, 计算时应注意逐项相除,不要漏项,并且要注意符号 的变化,最后的结果通常要按某一字母升幂或降幂的 顺序排列.
知1-练
1 计算(8a2b3-2a3b2+ab)÷ab的结果是( A ) A.8ab2-2a2b+1 B.8ab2-2a2b C.8a2b2-2a2b+1 D.8ab-2a2b+1
第十四章 整式的乘法与因式分解
14.1 整式的乘法
第9课时 整式的乘法——多 项式除以单项式
1 课堂讲解 2 课时流程
多项式除以单项式 整式的混合运算
逐点 导讲练
课堂 小结
作业 提升
复习回顾: 单项式除以单项式的法则是什么?
知识点 1 多项式除以单项式
计算下列各题,说说你的理由 . (1)(ad+bd) ÷d =_________; (2)(a2b+3ab) ÷a =_________; (3) )(xy3-2xy) ÷xy =_________. 如何进行多项式除以单项式的运算?
知2-讲
例3 计算:[(3a+2b)(a+2b)-b(4a+4b)]÷2a . 导引:先算括号内的,再做除法运算. 解:原式=(3a2+8ab+4b2-4ab-4b2)÷2a
=(3a2+4ab)÷2a = 3 a 2b.
2
总结
知2-讲
注意运算顺序,先算括号里面的,再算多项式除以单 项式.
知2-讲
2
2
2
总结
知2-讲
本题运用了整体思想求解.这里不需要具体求出a,b 的值,只需将所得结果进行变形,转化成已知条件便 可得到解决.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单项式与多项式相乘
单项式与多项式相乘 ,就是单用项式 去乘多项式
的每一项,再把所得的积 。 相加
多项式除以单项式
______________________________ ____________________
计算下列各式,并说说你 是怎样计算的?
(1)(am bm)m
(2)(a2 ab)a
(3)(4x2y 2xy2) 2xy
多项式除以单项式
______________________________ ____________________
(am+bm+cm)÷m
=am÷m+bm÷m+cm÷m
多项式除以单项式
多项式除以单项式,
先把这个多项式的每一项
除以这个单项式,再把所
得的商相加。
______________________________ ____________________
2.计算:
(1) (2x2-3x-1)•3x2 = 6x4-9x3-3x2
单项式与多项式相乘 的法则是什么?来自多项式除以单项式______________________________ ____________________
整式的乘除(2)
多项式除以单 项式
______________________________ ____________________
课前练习 1.计算: (1)3a2b3+5a2b3 =8a2b3
(2)3a2b3×5a2b3 =15a4b6
(3)3a2b3 ÷ 5a2b3
=3 5
多项式除以单项式
(4x2y-8x3y3)÷(-2x2y)
多项式除以单项式
______________________________ ____________________
课堂总结
1、多项式除以单项式法则:多 项式除以单项式,先把这个多项 式的每一项除以这个多项式,再 把所得的商相加。
2、应用法则转化多项式除以单 项式为单项式除以单项式。
多项式除以单项式
______________________________ ____________________
例1.计算:
(1)(12a3-8a2-3a)÷4a (2)(6a2b-2ab2-b3)÷(-3b)
多项式除以单项式
______________________________ ____________________
课堂练习
2:化简
2 x y 2 y y 4 x 8 x 2 x
多项式除以单项式
______________________________ ____________________
1.计算: (-8x+6)÷(-4)
(6x2-9x)÷(3x)
(9a3b-12a2b2+8ab3)÷(3ab)
多项式除以单项式
____________________
多项式除以单项式
______________________________ ____________________
3、运算中应注意的问题:
(1)所除的商应写成最简的形式 ;
(2)除式与被除式不能交换;
4、整式混合运算要注意运算顺
序,还要注意运用有关的运算公式
和性质,使运算简便。 ______________________________
