小学数学六年级有关圆的组合图形的面积问题50447

合集下载

圆的组合图形面积及答案#

圆的组合图形面积姓名：【知识与方法】要解决与圆有关的题目，需要注意以下几点：1、熟练掌握有关圆的概念和面试公式：圆的面积= 圆的周长=扇形的面积= 扇形的弧长=（n是圆心角的度数）2、掌握解题技巧和解题方法：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。

例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

数学六年级-圆的组合图形面积计算

辅导讲义案例1：有一个著名的希波克拉蒂月牙问题．如图：以AB为直径作半圆，C是圆弧上一点，（不与A、B重合），以AC、BC为直径分别作半圆，围成两个月牙形（阴影部分）．已知直径AC为6cm，直径BC为8cm，直径AB为10cm．（1）将直径分别为AB、AC、BC所作的半圆面积分别记作S AB、S AC、S BC．分别求出三个半圆的面积。

（2）请你猜测：这两个月牙形（阴影部分）的面积与三角形ABC的面积之间的数量关系，并说明理由。

案例2：归纳总结以下基本图面积计算方法（1）扇形：扇形的面积=扇形中的弧长部分=扇形的周长（2）弓形面积：弓形面积=（3）“弯角”面积：如图：（4）“谷子”面积：如图：例题1：如图，直径AB为3厘米的半圆以A点为圆心逆时针旋转60°，使AB到达AC的位置，求图中的阴影部分的面积。

例题2：如图，三角形ABC是等腰直角三角形，腰AB长为4厘米，求阴影部分的面积？试一试：如图，三角形ABC是直角三角形，AC=20，阴影（1）的面积比阴影（2）的面积小23，求BC的长？例题3：如图，ABCD 是一个正方形，2ED DA AF ===，阴影部分的面积是多少？试一试：下图中，cm DC DB AD 10===，求阴影部分的面积．例题4：如图，ABCD是平行四边形，8cm∠=︒，高4cmCH=，弧BE、DF分DABAB=，30AD=，10cm别以AB、CD为半径，弧DM、BN分别以AD、CB为半径，则阴影部分的面积为多少？(精确到0.01)例题5：如图所示，直角三角形ABC的斜边AB长为10厘米，60ABC∠=︒，此时BC长5厘米．以点B为中心，将ABC∆顺时针旋转120︒，点A、C分别到达点E、D的位置．求AC边扫过的图形即图中阴影部分的面积．试一试：如下图，Rt△CAB中，AB=3，AC=4，将它以A点为中心逆时针旋转60°，得到Rt△EAD，求阴影部分面积是多少？1．有8个半径为1的小圆，用它们圆周的一部分连成一个花瓣图形（如图阴影所示），图中黑点是这些圆的圆心，那么花瓣图形的面积是（）（A）16（B）16π+（C）1162π+（D）162π+2．如图，一只羊被4米长的绳子拴在长为3米，宽为2米的长方形水泥台的一个顶点上，水泥台的周围都是草地，问这头羊能吃到草的草地面积是多少？（结果精确到0.01平方米）3．如图，已知正方形ABCD的边长为5，正方形CEFG的边长为3，求图中阴影部分的面积．（π为3.14）4．如图，ABCD是正方形，边长是8厘米，BE=4厘米，其中圆弧BD的圆心是C点，那么图中阴影部分的面积等于多少平方厘米？5．如图，两个正方形的边长分别是6和5．求图形中阴影部分的面积．6．7．8．如图所示，已知半圆的直径AB=12，BC所对的圆心角∠CAB=30°，并且小阴影面积为3.26，求大阴影的面积.7．如图，正方形的边长为10，那么图中阴影部分的面积是多少？8．如图，矩形的长为4，宽为5，求阴影部分的面积？A BDCA1．如图是以边长为40米的正方形ABCD 的顶点A 为圆心，AB 长为半径的弧与以CD 、BC 为直径的半圆构成的花坛（图中阴影部分）．小杰沿着这个花坛边以相同的速度跑了6圈，用去了8分钟，求（1）花坛（图中阴影部分）面积；（2）小杰平均每分钟跑多少米？2．某同学用所学过的圆与扇形的知识设计了一个问号，如图中阴影部分所示，已知图中的大圆半径为4，两个小圆半径均为2，求图中阴影部分的面积。

圆的组合图形面积及答案

圆的组合图形面积姓名：【常识与办法】要解决与圆有关的标题,须要留意以下几点：1、闇练控制有关圆的概念和面试公式：圆的面积= 圆的周长=扇形的面积= 扇形的弧长=（n是圆心角的度数）2.控制解题技能息争题办法：加减法.朋分重组法.扭转平移法.半数法.抵消法.等积变形法.等量代换法.添帮助线法.例1.求暗影部分的面积.(单位:厘米)解：这是最根本的办法：圆面积减去等腰直角三角形的面积,×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米,求暗影部分的面积.(单位:厘米)解：这也是一种最根本的办法用正方形的面积减去圆的面积.设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7, 所以暗影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中暗影部分的面积.(单位:厘米)解：最根本的办法之一.用四个圆构成一个圆,用正方形的面积减去圆的面积,所以暗影部分的面积：2×2-π＝0.86平方厘米.例4.求暗影部分的面积.(单位:厘米)解：同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求暗影部分的面积.(单位:厘米)解：这是一个用最经常应用的办法解最罕有的题,为便利起见,我们把暗影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米别的：此题还可以算作是1题中暗影部分的8倍.例6.如图：已知小圆半径为2厘米,大圆半径是小圆的3倍,问：空白部分甲比乙的面积多若干厘米？解：两个空白部分面积之差就是两圆面积之差（全加上暗影部分）π-π()=100.48平方厘米（注：这和两个圆是否订交.交的情形若何无关）例7.求暗影部分的面积.(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2,求)正方形面积为：5×5÷2=12.5所以暗影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割.补.增.减变形) 例8.求暗影部分的面积.(单位:厘米)解：右面正方形上部暗影部分的面积,等于左面正方形下部空白部分面积,割补今后为圆,所以暗影部分面积为：π()=3.14平方厘米例9.求暗影部分的面积.(单位:厘米)解：把右面的正方形平移至左边的正方形部分,则暗影部分合成一个长方形,所以暗影部分面积为：2×3=6平方厘米例10.求暗影部分的面积.(单位:厘米)解：同上,平移阁下两部分至中央部分,则合成一个长方形,所以暗影部分面积为2×1=2平方厘米(注: 8.9.10三题是简略割.补或平移)11.例13.求暗影部分的面积.(单位:厘米)解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以暗影部分面积为：8×8÷2=32平方厘米12.例14.求暗影部分的面积.(单位:厘米)解：梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 .13.例16.求暗影部分的面积.(单位:厘米)解：［π＋π－π］=π(116-36)=40π=125.6平方厘米14.例17.图中圆的半径为5厘米,求暗影部分的面积.(单位:厘米) 解：上面的暗影部分以AB为轴翻转后,全部暗影部分成为梯形减去直角三角形,或两个小直角三角形AED.BCD面积和.所以暗影部分面积为：5×5÷2+5×10÷2=37.5平方厘米16.例19.正方形边长为2厘米,求暗影部分的面积.解：右半部分上面部分逆时针,下面部分顺时针扭转到左半部分,构成一个矩形.所以面积为：1×2=2平方厘米17.例25.如图,四个扇形的半径相等,求暗影部分的面积.(单位:厘米)剖析：四个空白部分可以拼成一个以２为半径的圆．所以暗影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π=22-4π=9.44平方厘米18.例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求暗影部分的面积.解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米19.例28.求暗影部分的面积.(单位:厘米)解法一：设AC中点为B,暗影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以暗影面积为:12.5+7.125=19.625平方厘米20.例30.如图,三角形ABC是直角三角形,暗影部分甲比暗影部分乙面积大28平方厘米,AB=40厘米.求BC的长度.解：两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC 长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米21.例33.求暗影部分的面积.(单位:厘米)解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6=4.205平方厘米22.例34.求暗影部分的面积.(单位:厘米)解：两个弓形面积为：π-3×4÷2=π-6 暗影部分为两个半圆面积减去两个弓形面积,成果为π+π-（π-6）=π（4+-）+6=6平方厘米。

新人教版六年级上数学第五单元《含有圆的组合图形的面积》教案板书设计

新人教版六年级上数学第五单元《含有圆的组合图形的面积》教案板书设计本文从网络收集而来，上传到平台为了帮到更多的人，如果您需要使用本文档，请点击下载按钮下载本文档（有偿下载），另外祝您生活愉快，工作顺利，万事如意！新人教版六年级上册数学第五单元《含有圆的组合图形的面积》教案板书设计第4节含有圆的组合图形的面积教学内容：教材第68-69页含有圆的组合图形的面积。

教学目标：1、让学生结合具体情境认识组合图形的特征，掌握计算组合图形的面积的方法，并能准确掌握和计算简单组合图形的面积。

2、通过自主合作，培养学生独立思考、合作探究的意识。

3、让学生在解决实际问题的过程中，进一步体验图形和生活的联系，感受平面图形的学习价值，提高数学学习的举和学习好数学的自信心。

教学重难点：组合图形的认识及面积计算、图形分析。

教具学具准备：多媒体、各种基本图形纸片。

教学设计：⊙创设情境，认识圆环1．师：我们来欣赏一组美丽的图片。

出示圆形花坛、圆形水池外的圆形甬路、奥运五环标志、光盘……2．同学们，你们从图中发现了什么？3．教师拿出环形光盘说明：像这样的图形，我们称它为圆环或环形。

你还知道生活中有哪些环形的物体？它们给我们的生活带来了怎样的变化？4．导入新课：这节课我们一起来探讨环形的知识。

设计意图：从学生掌握的常识和熟悉的事物入手，使其感受到数学就在我们身边，学生从直观上也感受到了环形的特点，为后面学习环形的面积奠定基础。

⊙探索交流，解决问题1．画一画，剪一剪，发现环形特点。

画一画。

让学生在硬纸板上用同一个圆心分别画一个半径为10厘米和5厘米的圆。

剪一剪。

指导学生先剪下所画的大圆，再剪下所画的小圆。

问：剩下的部分是什么图形？师：我们也称它为圆环。

教师手拿学生剪的圆环提问：这个圆环是怎样得到的？生明确：圆环是从外圆中去掉一个内圆得到的。

借助图示认识圆环的各部分名称。

你知道圆环各部分的名称吗？①外圆：又名大圆，它的半径用R表示。

②内圆：又名小圆，它的半径用r表示。

小学数学六年级有关圆的组合图形的面积问题

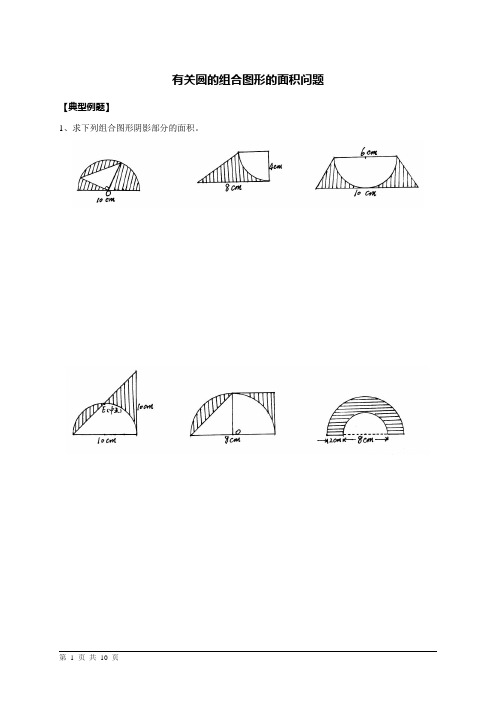
有关圆的组合图形的面积问题【典型例题】1、求下列组合图形阴影部分的面积。

2、①圆的周长是18.84cm，求阴影部分面积。

②长方形的面积和圆的面积相等，已知圆的半径是3cm，求阴影部分的周长和面积。

③求直角三角形中阴影部分的面积。

（单位：分米）④图中阴影①比阴影②面积小48平方厘米，AB=40cm，求BC的长。

⑤一个圆的半径是4cm，求阴影部分面积。

【变式训练】1、求下列各图中阴影部分的面积。

（单位：厘米）2、下图中长方形的长是6厘米，宽是5厘米，求阴影部分的面积。

3、如图长方形的面积是45平方厘米，宽是5厘米，求阴影部分的面积。

4、求下列阴影部分面积和周长5、如右图，阴影部分的面积为2平方厘米，等腰直角三角形的面积为.6、右图中正方形周长是20厘米。

图形的总面积是平方厘米7、如图，半圆S 1的面积是14.13平方厘米，圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?8、右图中4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心. 如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米?9、如图所示，圆的周长是16.4厘米，圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=πS 1S 210、有八个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形(如图). 图中黑点是这些圆的圆心.如果圆周率1416.3=π，那么花瓣图形的面积是平方厘米.11、已知ABCD 是正方形， ED =DA =AF =2厘米，阴影部分的面积是 .12、如图32，大正方形的边长为6厘米，小正方形的边长为4厘米。

求阴影部分的面积。

EDCB AGF。

小学数学六年级有关圆的组合图形的面积问题之欧阳光明创编

*欧阳光明*创编有关圆的组合图形的面积问题欧阳光明（2021.03.07）【典型例题】1、求下列组合图形阴影部分的面积。

2、①圆的周长是18.84cm，求阴影部分面积。

②长方形的面积和圆的面积相等，已知圆的半径是3cm，求阴影部分的周长和面积。

③求直角三角形中阴影部分的面积。

（单位：分米）④图中阴影①比阴影②面积小48平方厘米，AB=40cm，求BC的长。

⑤一个圆的半径是4cm，求阴影部分面积。

【变式训练】1、求下列各图中阴影部分的面积。

（单位：厘米）2、下图中长方形的长是6厘米，宽是5厘米，求阴影部分的面积。

3、如图长方形的面积是45平方厘米，宽是5厘米，求阴影部分的面积。

4、求下列阴影部分面积和周长5、如右图，阴影部分的面积为2积为.6、右图中正方形周长是207、如图，半圆S1的面积是14.13*欧阳光明*创编 2021.03.07 平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?8、右图中4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心. 如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米?9、如图所示，圆的周长是16.4厘米，圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π10、有八个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形(如图). 图中黑点是这些圆的圆心.如果圆周率1416.3=π，那么花瓣图形的面积是平方厘米.11、已知ABCD 是正方形， ED =DA =AF =2厘米，阴影部分的面积是.12、如图32，大正方形的边长为6厘米，小正方形的边长为4厘米。

求阴影部分的面积。

E D C BAGF。

求与圆有关的组合图形的面积ppt课件

说说你知道了哪些数学信息？要解决的问题是什么？
03
任务一
学校阅览室的窗户上面是半圆，下面是正方形（如下图）。窗
户的面积约是多少平方米？（得数保留整数。）
怎样算出这个图形的面积
？小提示先分解，把它变成我们学过
的简单图形，然后再算这些简单
图形的面积的和。
03
任务一
学校阅览室的窗户上面是半圆，下面是正方形（如下图）。窗
板书设计
求与圆有关的组合图形的面积（1）
半圆的面积+正方形的面积=窗户的面积圆环的面积=大圆的面积－小圆的面积 S环=π（R2－r2）
S=ah÷2
S=（a+b）h÷2
S=πr2
02
新知导入
根据这些平面图形，我们能够拼出很多不同形状的图形。
三角形+长方形
三角形+长方形+正方形+圆
02
新知导入
小提示
像这些由几个简单的平面图形组合而成的图形，叫做组合图形。
学习任务一
求与圆有关的组合图形的面积
03
任务一
学校阅览室的窗户上面是半圆，下面是正方形（如下图）。窗户的面积约是多少平方米？（得数保留整数。）
户的面积约是多少平方米？（得数保留整数。）
思考：这个图形可以分解成什么图形
？窗户的面积怎么计算？
03
任务一
学校阅览室的窗户上面是半圆，下面是正方形（如下图）。窗
户的面积约是多少平方米？（得数保留整数。）
半圆
1.2m
正方形
窗户的面积是1个半圆与1个正方形面积的和。
上半部分半圆的直径与正方形的边长有什么关系？
2米 8米
3.14×（102－82） =3.14×36 =113.04（m2）

人教版六年级数学上册第五单元第6课时《圆与正方形组合的面积问题的应用》课件

4．土楼是福建、广东等地区的一种建筑形式，被列入 “世界物质文化名录”，土楼的外围形状有圆形、方形、椭圆形等。圭峰楼和德逊楼是福建省南靖县两座地面是圆环形的土楼，
圭峰楼外直径33 m，内直径14 m；德逊楼外直径 26.4 m，内直径14.4 m。两座土楼的房屋占地面积相差多少？（选题源于教材P73第12题）
6．篮球场上的3 分线是由两条平行线段和一个半圆组成的。请你根据图中的数据计算出3 分线的长度和3 分线内区域的面积。（选题源于教材P73第14题）
半圆的弧长：3.14×6.75＝21.195(m) 3分线的长度：21.195＋2×1.575≈24.35(m) 半圆的面积：(3.14×6.752)÷2＝71.533125(m2) 长方形的面积：6.75×2×1.575＝21.2625(m2) 3分线内区域的面积：71.533125＋21.2625≈92.80(m2) 答：3 分线的长度和3 分线内区域的面积是92.80m2。
3.14×(34÷2)2－3.14×(14÷2)2＝753.6(m2) 3.14×(26÷2)2－3.14×(14÷2)2＝376.8(m2) 753.6－376.8＝376.8(m2)答:占地面积相差376m2。
5．一个圆的周长是62.8 m，半径增加了2 m 后，面积增加了多少？（选题源于教材P73第13题） 62.8÷3.14÷2＝10(m) 10＋2＝12(m) 3.14×122－3.14×102 ＝138.16(m2) 答：面积增加了138.16m2
(2)
4×4－3.14×(4÷2)2 ＝3.44(cm2)
(5×2)2－3.14×52 ＝21.5(m2)
3．解决问题（1）在一块边长为20 cm的正方形铁片中，截取如图

上海2021年六年级数学 4.5 圆的组合图形的面积计算

4.5圆的组合图形的面积计算我们已经学过许多几何图形，例如三角形、长方形、圆、扇形等。

并掌握了它们的面积公式，我们将这些常见的图形称为基本图形．还有一些较为复杂的非基本图形，它们是由一些基本图形组合而成的，现在我们一起来研究如何求组合图形的面积．例1如图，直角梯形的面积是54平方厘米，求阴影部分的面积．解()=r 22S r r +÷梯形=54，解得r =6（厘米），所以2135=54-6360S π⨯⨯阴影=11.61（平方厘米）．例2如图，直径AB 为3厘米的半圆以A 点为圆心逆时针旋转60°，使AB 到达AC 的位置，求图中阴影部分的面积．分析从图中可以看出，，阴影部分面积等于图形总面积减去空白部分面积．将以AC 为直径的半圆称为a ，扇形ABC 称为b ，以AB 为直径的半圆为c ，则阴影部分面积为：a ＋b －c ．因为a 与c 的面积相等，则有：a ＋b －c =b ．所以阴影部分面积等于扇形ABC 的面积．解26013.143=3.1493606⨯⨯⨯⨯=4.71（平方厘米）答：阴影部分的面积是4.71平方厘米．例3如图，正方形的边长是10厘米，那么图中阴影部分的面积是多少平方厘米？解阴影部分面积=半圆面积＋扇形面积－直角三角形面积=2221113.145+ 3.1410-10282⨯⨯⨯⨯⨯=28.5（平方厘米）答：阴影部分的面积是28.5平方厘米．例4如图，∠AOB =90°,C 为AB 弧的中点，已知阴影甲的面积为16平方厘米，求阴影乙的面积．解设OB =2r ，由图得：甲＋丙=21r 2π⨯⨯．乙＋丙=245(2r)360π⨯⨯=21r 2π⨯⨯，即甲＋丙=乙＋丙，所以甲=乙=16（平方厘米）．答：阴影部分面积为15平方厘米．练习4.5（1）1．如图，长方形的宽是8厘米，求阴影部分的面积．2．如图，△ABC 是一个等腰直角三角形，直角边的长度为1米，现在以C 点为圆心，把△ABC 顺时针旋转90°，求AB 边在旋转时所扫过的面积．3．如图，△ABC 是等腰直角三角形，D 是半圆周的中点，BC 是半圆的直径．已知：AB =BC =10,求阴影部分面积．4．已知等腰直角三角形ABC ，D 为斜边中点，AC =BC =2分米，弧DF \弧DH 分别是B 、C 为圆心画的弧，求阴影部分的面积．5．图中，△ABC 是等腰直角三角形，腰AB 长为4厘米，求阴影部分面积．例5如图，正方形的边长为6分米，求阴影部分面积；分析阴影部分面积=正方形面积－两个相同的小扇形的面积（或减去一个圆心角为90°的扇形的面积）．解223.146690360⨯=⨯=7.74（平方分米）．答：阴影部分面积为7.74平方分米．例6图中△ABC 是直角三角形，阴影（1）的面积比阴影（2）的面积小23平方米，求BC 的长度．解设BC 为x 米，由已知[阴影（2）的面积＋空白部分面积]－[阴影（1）的面积＋空白部分面积]=23即21120102322x π⨯⨯-∙=，10x －50π=23，10x =23＋157，10x =180，x =18．答：BC 的长度是18米．例7如图，求阴影部分的面积．解左边正方形中的阴影部分，与右边正方形的空白部分形状相同，所以左右两个正方形的阴影部分恰好拼成一个边长为2的正方形，所以，所求阴影部分面积是：1×2＋2×2=2＋4=6．答：阴影部分的面积是6个平方单位．例8如图，一个大正方形各边都被四等分，分成十六个小正方形，图A 是一个圆，图B 是由三个半圆围成的图形，那么图A 与图B 周长的大小关系是，图A 与图B 面积的大小关系是；解设图A 的半径为r ，图A 的周长是2πr ，图B 的周长是2πr ＋π×2r =4πr ，4πr ＞2πr ，所以图B 的周长大于图A 的周长图A 的面积是2r π，图B 的面积是222(2r)2r r πππ⨯÷-=，22r r ππ=，所以图B 的面积等于图A 的面积．练习4.5（2）1．如图，阴影部分的面积是平方厘米．第1题图第2题图2．如图，阴影部分的周长是厘米，面积是平方厘米．3．如图，等腰Rt △ABC 腰长为10厘米，甲、乙两部分的面积相等，求扇形AEF 所在圆的面积．答案练习4.5（1）1．50.24平方厘米．2．0.6775平方米．3．32.125．4．1平方分米．练习4.5（2）1．5.72．2．16.13；12.185．4.5《圆的组合图形的面积计算》练习练习4.5（1）1．图中，三个同心圆的半径分别为2、6、10，则图中阴影部分占大圆面积的%．2．如图，各圆半径都是3厘米，则阴影部分的面积为平方厘米．3．已知等腰直角三角形ABC，D为斜边中点，且AC=BC=2分米，弧DF、弧DE分别是以B、C为圆心画的弧，弧DE交BC于G，阴影部分的面积是平方分米．4．如图，△ABC是等腰直角三角形，D是半圆周的中点，BC是半圆的直径．已知AB=BC=10，那么阴影部分的面积是多少？5．如图，∠AOB=90°，C为弧AB的中点，已知阴影甲的面积为16平方米，则阴影乙的面积是平方米．练习4.5（2）1．如图，其中四个圆的直径均为4厘米，那么阴影部分的面积为平方厘米．I2．如图，阴影部分的面积是平方厘米．3．如图，AB与CD是两条互相垂直的直径，圆O的半径为15厘米，∠ACB=90°，AEB是以C为圆心，AC为半径的圆弧，则阴影部分的面积为平方厘米．4．如图，阴影部分的面积是．5．如图，等腰Rt△ABC腰长为10厘米，甲、乙两部分的面积相等，则扇形EAF所在圆的面积是平方厘米．6．如图，小正方形的边长4厘米，大正方形边长6厘米，△DBE的面积为3.2平方厘米，求阴影部分的面积？答案练习4.5（1）1．33．提示：可将原图变形为如图形式，这样阴影部分I 的面积占大圆面积的14，即：S I 2110254ππ⨯⨯=，S II =221(62)84πππ⨯⨯-⨯=，所以=33S π阴影，00=100=33S π大圆．2．3.87．提示：因为3个扇形的半径相等，圆心角的和等于三角形内角和为180°，所以可以拼成一个半圆．阴影部分面积=直角三角形－半圆面积，即()()23+33+32-3.1432⨯÷⨯÷=3.87（平方厘米）．3．1．提示：解法一：设AB =2R ，则CD =R ；扇形DBF 的面积=218R π．扇形ECG 的面积=214R π，三角形ABC 的面积=2×2÷2=2．三角形ABC 面积也可以用()2224R R ÷=,可知2=2R ，空白部分面积=112-22+248ππ⎛⎫⨯÷⨯ ⎪⎝⎭=1，所以阴影部分面积为2－1=1（平方分米）；解法二：通过剪拼后如图：阴影部分的面积为边长1分米的正方形，21=1平方分米．4．32.125．提示：如图作出辅助线，则阴影部分的面积为△AED 的面积减去正方形BEDO 的面积再加上圆面积的14．△AED 的面积是：()()110+102102=37.52÷⨯÷⨯，圆面积的14是()21 3.14102=19.6254⨯⨯÷，故阴影部分面积：375-25+19.625=32.125。

圆的组合图形面积及答案

例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

圆的组合图形面积及重点标准答案

圆旳组合图形面积姓名：【知识与措施】要解决与圆有关旳题目，需要注意如下几点：1、纯熟掌握有关圆旳概念和面试公式：圆旳面积= 圆旳周长=扇形旳面积= 扇形旳弧长=（n是圆心角旳度数）2、掌握解题技巧和解题措施：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。

例1.求阴影部分旳面积。

(单位:厘米)解：这是最基本旳措施：圆面积减去等腰直角三角形旳面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分旳面积。

(单位:厘米)解：这也是一种最基本旳措施用正方形旳面积减去圆旳面积。

设圆旳半径为r，由于正方形旳面积为7平方厘米，因此=7，因此阴影部分旳面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分旳面积。

(单位:厘米)解：最基本旳措施之一。

用四个圆构成一种圆，用正方形旳面积减去圆旳面积，因此阴影部分旳面积：2×2-π＝0.86平方厘米。

例4.求阴影部分旳面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分旳面积。

(单位:厘米)解：这是一种用最常用旳措施解最常用旳题，为以便起见，我们把阴影部分旳每一种小部分称为“叶形”，是用两个圆减去一种正方形，π()×2-16=8π-16=9.12平方厘米此外：此题还可以当作是1题中阴影部分旳8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆旳3倍，问：空白部分甲比乙旳面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆与否相交、交旳状况如何无关）例7.求阴影部分旳面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5。

小学数学六年级有关圆的组合图形的面积问题总结.doc

有关圆的组合图形的面积问题2、①圆的周长是18.84cm，求阴影部分面积。

②长方形的面积和圆的面积相等，已知圆的半径是3cm，求阴影部分的周长和面积。

③求直角三角形中阴影部分的面积。

（单位：分米）④图中阴影①比阴影②面积小48平方厘米，AB=40cm，求BC的长。

⑤一个圆的半径是4cm，求阴影部分面积。

【变式训练】1、求下列各图中阴影部分的面积。

（单位：厘米）2、下图中长方形的长是6厘米，宽是5厘米，求阴影部分的面积。

3、如图长方形的面积是45平方厘米，宽是5厘米，求阴影部分的面积。

4、求下列阴影部分面积和周长5、如右图，阴影部分的面积为2平方厘米，等腰直角三角形的面积为.6、右图中正方形周长是20厘米。

图形的总面积是平方厘米.7、如图，半圆S1的面积是14.13平方厘米，圆S2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?S1S28、右图中4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心. 如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米?9、如图所示，圆的周长是16.4厘米，圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π10、有八个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形(如图). 图中黑点是这些圆的圆心.如果圆周率1416.3=π，那么花瓣图形的面积是平方厘米.11、已知ABCD 是正方形， ED =DA =AF =2厘米，阴影部分的面积是 .EDCB AGF12、如图32，大正方形的边长为6厘米，小正方形的边长为4厘米。

求阴影部分的面积。

小学赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所，脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。

科学研究证实,虽然大脑的重量只占人体重量的2%-3%,但大脑消耗的能量却占食物所产生的总能量的20%,它的能量来源靠葡萄糖氧化过程产生。

人教版六年级数学上册第五单元《圆与正方形组合的面积问题的应用》课件

3.14
r
2－
1 2
2r
r
2
=
1.14r
ቤተ መጻሕፍቲ ባይዱ
2
这节课你有什么收获？
1 “外方内圆” 图形中，圆的直径等于正方形的边长。如果圆的半径为r，那么正方形和圆之间部分的面积为0.86r2。
2 “外圆内方”图形中，这个正方形的对角线等于圆的直径。如果圆的半径为r，那么圆和正方形之间部分的面积为1.14r2。
图(1)
下图中正方形的边长是多少呢？
可以把图中的正方形看成两个三角形，它的底和高分别是……
从图(2)可以看出：
图(2)
1 2
2
1
2
=
2
m2
3.14－2＝1.14(m²)
那么我们解答得对不对呢？有什么方法验证吗？
如果两个圆的半径都是r，结果又是怎样的？
左图：(2r)²－3.14×r²＝0.86r²
7．(易错题)如图，大正方形的面积比小正方形的面积多10 cm2。两正方形之间圆的面积是多少？
假设圆的半径为r cm。 (2r)2－2r×r÷2×2＝10 r2＝5 3.14×5＝15.7(cm2) 答：两正方形之间圆的面积是15.7 cm2。
点拨：假设圆的半径为r cm，则大正方形的面积为 4r2 cm2，小正方形的面积为2r×r÷2×2＝2r2(cm2)，由题意可知，4r2－2r2＝10，所以r2＝5，则圆的面积为3.14×5＝15.7(cm2)。
点拨：外圆内方图形中圆和正方形之间部分的面积为1.14r2，其中r＝4 dm，代入求解即可。
提升点 1 “外方内圆”面积计算的应用
5．如图，将一块正方形纸板剪去4个等圆，每个圆的周长均是9.42厘米，这块纸板的剩余面积是多少？