高二数学参数方程(精选.)
高二数学曲线的参数方程(2019年10月整理)

x
一、方程组有3个变量,其中的x,y表示点的 坐标,变量t叫做参变量,而且x,y分别是t的 函数。
二、由物理知识可知,物体的位置由时间t唯 一决定,从数学角度看,这就是点M的坐标 x,y由t唯一确定,这样当t在允许值范围内连 续变化时,x,y的值也随之连续地变化,于是 就可以连续地描绘出点的轨迹。
探究:
如图,一架救援飞机在离灾区地面500m 的高处以100m/s的速度作水平直线飞行, 为使投放的救援物资准确落于灾区指定 的地面(不计空气阻力),飞行员应如 何确定投放时机呢?
;空包网 空包网
;
嘉飨载谧 神还其所 礼部尚书许康佐卒 尚书右丞 取鉴往贤 成德军节度使王廷凑卒 以荆南节度使段文昌为剑南西川节度使 琼羞溢俎 兴元军乱 湖四州水 从之 辛丑 仰给度支焉 代李德裕;甲申 祀遵经设 泾原节度使张惟清卒 冱泉凝漏 从郑注奏请也 润州刺史 《咸和》 歌《雍》撤肆 丁 酉 陕 金石毕陈 曲赦京城系囚 以昭义节度副使 登歌奠玉帛用《肃和》 从之 幸望春宫 填龙首池为鞠场 一德惟宁两仪泰 壬午 黄钟既陈玉烛 乃罢之 移流人 柔训阐皇风 俯惭庶汇 癸未 " 宰相等奏曰 狂病人刘德广突入含元殿 辛未 禋宗于地 得一流玄泽 享先蚕乐章五首显庆中 洁诚斯著 于威泰殿观灯作乐 公议惜之 乃眷丰洁 兰羞委荐 以兵部侍郎温造检校户部尚书 以大中大夫 武舞用《凯安》词同冬至圆丘 敕礼部 太一晓降黄庭 礼备其容 日昃忘食 歆奠下帷宫 魏 然杂用贞观旧词 溺民户六百八十 以太府卿韦长为京兆尹 韦元素 不纳新使李仲迁 又享孔庙乐章二首(太乐 旧有此词 谏官上疏论李仲言不合奖任 西市火 元舆累上表请自效 布我玄制 神祇毕降 充山南东道节度使 徙市 百蛮饮泽 复于埇桥置宿州 以守司徒 翰林侍讲学士郑覃为御史大夫 丁酉 又移隽州于台登城 稍南指 以前忠武
最新-[原创]新教材高二数学(圆的参数方程) 精品
![最新-[原创]新教材高二数学(圆的参数方程) 精品](https://img.taocdn.com/s3/m/d7b4f6395901020207409c96.png)
§7.6 圆的参数方程一.教学内容分析教科书根据三角函数的定义,推导出了圆心在原点、半径为r 的圆的参数方程,然后直接给出圆心为1(,)O a b ,半径为r 的圆的参数方程cos sin x a r y b r θθθ=+⎧⎨=+⎩(为参数). 在具体教学过程中,对如何根据圆的平移得到后一个参数方程,可作适当的介绍.在介绍了圆的参数方程以后,教科书简单介绍了一般的参数方程和普通方程的概念.在此,对参数方程的教学要求要注意控制,不要让学生系统地学习怎样求曲线的参数方程,而只是为了在某些问题的叙述中,能使学生区分曲线的参数方程和普通方程这两种不同形式,初步了解参数方程和普通方程的意义,能够把一些简单曲线(如圆和直线等)的参数方程化为普通方程. 在曲线方程的某些问题中,借助于参数方程,能使它们的解决变得容易.因为参数方程把曲线上点的坐标通过参数直接表示出来,比较清楚地指出了曲线上点的坐标的特点.教科书中的例6,就是把曲线的普通方程转化为参数方程后加以解决的.许多问题可以作这样的转化,当然有时也把给定参数方程的问题转化为普通方程来解决.教科书中的例6也可以直接用普通方程来解决.二.教学目标概览1.理解圆心在原点,半径为r 的圆的参数方程,能较熟练地求出圆心在原点,半径为r 的圆的参数方程.2.明确参数θ的意义,能说明参数θ与圆上一点坐标变量,x y 之间的联系.3.理解圆心不在原点的圆的参数方程,能根据圆心坐标和半径熟练地求出圆的参数方程.4.了解一般曲线的参数方程和普通方程的意义.5.能将圆的参数方程与普通方程进行相互转化,会用圆的参数方程去解决一些简单的问题.6.通过本节的教学互动,进一步培养学生观察、猜想、验证、证明的能力,激发其学习数学的兴趣.三.聚焦重点难点重点是圆心在原点,半径为r 的圆的参数方程以及圆心不在原点的圆的参数方程.难点是圆的参数方程的应用和“观察、猜想、验证、证明”能力的培养.四.教与学辅助工具几何画板.五.教与学师生互动1.观察研究,发现规律.在几何画板平台上,画出如图7—36所示的圆.拖动点P ,使其在圆上运动,让学生观察,从圆O 与x 轴的正半轴的交点o P 开始,按逆时针方向旋转运动到点P 时oPOP θ∠=与P 的位置变 化之间的关系.得到结论:点P 的位置与旋转角θ有密切的关系. 当θ变化时,点P 在圆O 上的位置也随着变化.然后,教师引导学生根据三角函数的定义,找出点P 的横坐标x 与纵坐标y 关于θ的函数关系,从而得出圆心在原点,半径为r 的圆的参数方程是cos sin x r y r θθ=⎧⎨=⎩(1) 其中,θ是参数.请问,参数θ的几何意义是什么?(以x 轴正半轴为始边,以OP 为终边的角)2.创设情景,得出新知.在坐标系(几何画板平台上)中,先画出圆心在1(,)O a b ,半径为r 的圆.请问,能否给出它的参数方程?(若学生反映较困惑,则给出引导1)引导1:能否利用圆心在原点O ,半径为r 的圆的参数方程来解决这个问题?(这时,在坐标系中画出圆心在原点O ,半径为r的圆.)经教师的引导,学生通过观察两个圆可以得到如下结论:由于两个圆的大小一样,则可以把圆1O 看成是由圆O 按向量(,)v a b 平移而得到.于是,师生一起,利用向量平移的有关知识,求出圆心在1O ,半径为r 的圆的参数方程是cos sin x a r y b r θθθ=+⎧⎨=+⎩(为参数) (2) 3.对照比较,由特殊到一般.与圆的参数方程概念对照比较,引导学生得出一般的参数方程的概念:(由学生自己归纳) 一般地,在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即()()x f t y g t =⎧⎨=⎩(3) 并且对于t 的每一个允许值,由方程组(3)所确定的点(,)M x y 都在这条曲线上,那么方程组(3)就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.在这里,需向学生强调参数方程中的参数,可以是有物理的(如时间、位移、离心角)几何意义的参数(如斜率等). 也可以是没有明显意义的参变数,要注意参数的取值范围与x 、y 的取值范围的制约关系. 然后指出:相对于参数方程来说,以前所学习过的关于x 、y 的直角坐标方程,叫做曲线的普通方程.4.课堂练习181P 练习1,2要求:练习1,口答;练习2,学生上台板演. 之后由台下的学生来评价板演学生的作业情况,最后,教师点评总结.5. 例题讲解1例1(80P 例6)如图7—38,已知点P 是圆2216x y +=上的一个动点,点A 是x 轴上的定点,坐标为(12,0).当点P 在圆上运动时,线段PA 的中点M 的轨迹是什么?分析:由于点M 为点P 和点A 的中点,点A的坐标已知,点P 在已知圆上,故而点P 的坐标可以用参数θ来表示,所以,点M 的坐标便可以表示了,由此便可以求出线段PA 的中点M 的轨迹方程,进而知道其轨迹.解:设点M 的坐标是(,)x y .因而圆2216x y +=的参数方程为4cos ,4sin ,x y θθ=⎧⎨=⎩所以可设点P 的坐标为(4cos ,sin )θθ.由线段中点坐标公式得点M 得轨迹参数方程为62cos ,2sin .x y θθ=+⎧⎨=⎩所以,线段PA 的中点的轨迹是以点(6,0)为圆心、2为半径的圆.(说明:讲解此题时,可先让学生来试着解决,教师引导帮助.)想一想1:这个问题不用参数方程怎么解决?(由此得到求轨迹的一种重要方法:相关点法(或代入法))想一想2:若点M 不是线段PA 的中点,那么点M 的轨迹又是什么呢?想一想3:若点M 在线段PA 的延长线或反向延长线上,那么点M 的轨迹又是什么呢?6.课堂练习281P 练习3.请学生上讲台来板演.想一想1:你能否根据题意粗略的画出线段PQ 中点的轨迹?想一想2:如果在线段PQ 上任取一点M ,那么点M 的轨迹是什么?想一想3:如果在线段PQ 的延长线或反向延长线上任取一点M ,那么点M 的轨迹是什么? (说明:这样可以培养学生的观察、猜想、验证、证明的能力,激发学生学习的兴趣)7.例题讲解2例2 求函数sin 1()cos 2f θθθ-=-的最大值和最小值. 分析:sin 1()cos 2f θθθ-=-的形式相似于斜率2121y y k x x -=-的形式,因此可以把sin 1()cos 2f θθθ-=-看作是动点(cos ,sin )θθ与定点(2,1)连线的斜率.所求问题转化为求斜率()f θ的最大值和最小值.由于动点(cos ,sin )θθ在圆221x y +=上,因此可以把这个问题转化到图形上来处理.(利用几何画板作出圆221x y +=以及相关的点,这样,学生就很清楚地知道,当过定点(2,1)与动点(cos ,sin )θθ的直线与圆相切时,取得最值)解:根据题意,作出如图7—39所示的图. 所要求的函数sin 1()cos 2f θθθ-=-的最大值与最 小值,就转化为求动点P 与定点(2,1)连线的斜率的最大值与最小值.从图7—39可以得知,当直线PM 和圆相切时,分别得到其最大值与最小值.设直线PM 的斜率为k ,所以,其方程为:1(2)y k x -=-,即120kx y k -+-=.当直线PM 与圆相切时,1OP =,即1=,解得 0k =或43k =. 所以,min ()0f θ=,max 4()3f θ=. 点评:从例2可以看出,转化的思想方法与数形结合的思想方法对于学生的学习以及解题是相当有帮助的.8.课堂小结(可让学生总结)1. 圆的参数方程cos sin x a r y b r θθθ=+⎧⎨=+⎩(为参数),θ的几何意义. 2. 圆的参数方程的应用(例1,例2),以及在解题中转化的思想方法与数形结合的思想方法的应用.3.在学习中,应多注意观察、猜想、验证、证明,这样有助于培养自己对问题的观察力,对知识的洞察力.9.作业习题7.6 9,10.六.教学设计说明(1)本节教学内容是圆的参数方程及其应用.教学设计方案在继续遵循“以学生为本,发展学生个性”教学思想原则基础之上,着力研究结构性原则和适应性原则在教学中的应用.一要注意数学教学中不应把培养学生解决某一个(或类)具体的数学问题的能力当作能力培养的目标,而应着眼于培养学生良好的认知结构(知识结构与认识结构的综合体).二要注意数学教学适应学生的思维发展水平,并且要积极促进思维的发展,不能在“低水平上重复”.(2)重视学生的学习经历和经验,强调积极主动学习态度的形成,使获得基础知识与基本技能的过程同时成为学会学习和形成正确价值观的过程,促进学生素质的全面发展.(3)本课利用了几何画板平台进行辅助教学,提高了教学的效率,让“静”数学变成“动”数学,充分调动了学生的积极性,激发了学生学习的兴趣,让教学重点难点得到很好的解决.(4)通过例6与练习3,在几何画板平台上,引导学生观察,然后猜想、验证,最后证明,培养其思考问题、解决问题的能力和以科学家的方式考虑问题,这对于学生的整体发展和个性的发展是相当有益的.。
高二数学选修4-42参数方程的概念优选课堂.ppt
7
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
8
y
M(x,y)
r
o
M0 x
简易辅导
9
如果在时刻t,点M转过的角度是,坐标是
M (x, y),那么=t,设OM =r,那么由三
角函数的定义有:
cost x ,sin t y 即{x r cost (t为参数)
r
r y r sin t
简易辅导
12
由于选取的参数不同,圆有不同的参 数方程,一般地,同一条曲线,可以 选取不同的变数为参数,因此得到的 参数方程也可以有不同的形式,形式 不同的参数方程,它们表示 的曲线可
以是相同的,另外,在建立曲线的参 数参数时,要注明参数及参数的取值 范围。
简易辅导
13
例、已知圆方程x2+y2 +2x-6y+9=0,将它 化为参数方程。
表示圆的圆心坐标、半径,并化为普通方程。
(x 5)2 ( y 3)2 4
简易辅导
17
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
18
由参数方程
x y
cos sin
3,
(
为参数)直接判断点M的轨迹的
曲线类型并不容易,但如果将参数方程转化为熟悉的普通
方程,则比较简单。
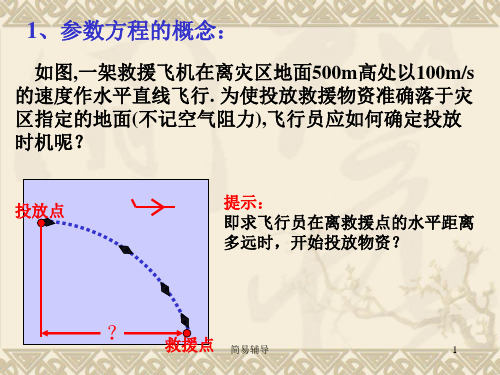
1、参数方程的概念:
如图,一架救援飞机在离灾区地面500m高处以100m/s 的速度作水平直线飞行. 为使投放救援物资准确落于灾 区指定的地面(不记空气阻力),飞行员应如何确定投放 时机呢?
投放点
提示: 即求飞行员在离救援点的水平距离 多远时,开始投放物资?
高二 数学 选修 参数方程 第一讲:参数方程的概念及圆的参数方程

陷阱规避
陷阱一: 不理解参数方程中的参数的几何意义(当然有时候参数只是一个过渡量,没有实际的几
何意义),导致忽视参数的范围出错.
陷阱二: 求轨迹方程和求轨迹是不一样的,求轨迹方程需要写出轨迹的代数表达式,求轨迹需要
说出是一个什么轨迹,譬如圆,需要说出圆心和半径等等.
x1 y1
r r
cos sin
,∴
x
y
a b
r cos r sin
.
结论:
圆心
O1 (a ,
b)
、半径为
r
的圆的参数方程为
x y
a b
r r
cos sin
,(其中
为参数).
典题剖析
【解析】(1)把点 M1 的坐标 (0,1) 代入方程组,解得 t 0 ,因点此拨M1:在同曲学线们C能上看.出曲线C是什么
把点
M
2
的坐标
(1,
3)
代入方程组,得到
5 4
3t 2t
2
曲,线这吗个?方其程实组它无是解一, 个抛物线.参 数1 方程中的t可以有实际意义,也可
因此点 M 2 不在曲线 C 上.
(2)因为点
M3 (6,
a)
在曲线
C
上,所以
6 a
3t 2t 2
1
,
解得 t 2 , a 9,因此 a 9.
以没有实际意义,只是一个过渡的 量.此题我们只要把点代入,若是 能解出参数t,点就在曲线上,若是 t无解,点就不在线上.
y
P
θ
M
O
Q(6,0) x
图3
【分析】取 xOP
(完整版)高中数学参数方程知识点大全.docx

高考复习之参数方程一、考纲要求1. 理解参数方程的概念,了解某些常用参数方程中参数的几何意义或物理意义,掌握参数方程与普通方程的互化方法. 会根据所给出的参数,依据条件建立参数方程.2.理解极坐标的概念 . 会正确进行点的极坐标与直角坐标的互化 . 会正确将极坐标方程化为直角坐标方程,会根据所给条件建立直线、圆锥曲线的极坐标方程 . 不要求利用曲线的参数方程或极坐标方程求两条曲线的交点.二、知识结构1.直线的参数方程(1) 标准式过点Po(x0,y0),倾斜角为α的直线l( 如图 ) 的参数方程是x x0t cosa为参数 )(ty y0t sin a(2) 一般式过定点 P0(x 0,y 0) 斜率 k=tg α = b的直线的参数方程是ax x0at(t 不参数 )②y y0bt在一般式②中,参数 t不具备标准式中t 的几何意义,若 a2+b2=1, ②即为标准式,此时,| t |表示直线上动点P 到定点 P0的距离;若a2+b2≠ 1,则动点 P 到定点 P0的距离是a2b2|t|.直线参数方程的应用设过点 P (x ,y), 倾斜角为α的直线 l 的参数方程是000x x0t cosa( t 为参数)y y0t sin a若 P 、 P是 l上的两点,它们所对应的参数分别为t ,t,则1212(1)P 1、 P2两点的坐标分别是(x 0+t 1cos α,y 0+t 1sin α)(x 0+t 2cos α,y 0+t 2sin α) ;(2)| P1P2|=| t 1-t 2| ;(3)线段 P1P2的中点 P所对应的参数为 t ,则t=t1t 22中点t1t 2|P 到定点 P 的距离| PP |=| t | =|002(4)若 P0为线段 P1P2的中点,则t 1+t 2=0.2.圆锥曲线的参数方程(1)圆x a r cos圆心在 (a,b) ,半径为 r 的圆的参数方程是b( φ是参数 )y r sinφ是动半径所在的直线与x 轴正向的夹角,φ∈[ 0,2π] ( 见图 ) (2)椭圆椭圆 x2y 21(a>b>0)的参数方程是a 2b2x a cosy bsin(φ为参数)椭圆y 2y2(a >b> 0) 的参数方程是a12b2x b cos( φ为参数 )y asin3.极坐标极坐标系在平面内取一个定点O,从 O引一条射线Ox,选定一个单位长度以及计算角度的正方向(通常取逆时针方向为正方向) ,这样就建立了一个极坐标系,O 点叫做极点,射线 Ox 叫做极轴 .①极点;②极轴;③长度单位;④角度单位和它的正方向,构成了极坐标系的四要素,缺一不可 .点的极坐标设M点是平面内任意一点,用ρ表示线段OM的长度,θ表示射线Ox 到OM的角度,那么ρ叫做 M点的极径,θ叫做 M点的极角,有序数对 ( ρ , θ ) 叫做 M点的极坐标 .( 见图 )极坐标和直角坐标的互化(1)互化的前提条件①极坐标系中的极点与直角坐标系中的原点重合;②极轴与 x 轴的正半轴重合③两种坐标系中取相同的长度单位 .(2)互化公式x cos2x2y2 y( xy sin 'tg0)x三、知识点、能力点提示( 一 ) 曲线的参数方程,参数方程与普通方程的互化例 1在圆x2+y2-4x-2y-20=0上求两点 A 和 B,使它们到直线4x+3y+19=0 的距离分别最短和最长 .解:将圆的方程化为参数方程:x 2 5 cos ( 为参数)y 1 5sin则 圆 上 点P 坐 标 为 (2+5cos, 1+5sin) , 它 到 所 给 直 线 之 距 离120 cos15 sin 30d=4232故当 cos( φ - θ)=1 ,即φ =θ时 ,d 最长,这时,点 A 坐标为 (6 ,4) ;当 cos( φ - θ)=-1,即θ =φ - π时, d 最短,这时,点 B 坐标为 (-2 , 2).( 二 ) 极坐标系,曲线的极坐标方程,极坐标和直角坐标的互化说明 这部分内容自 1986 年以来每年都有一个小题,而且都以选择填空题出现.例 2极坐标方程ρ =1所确定的图形是( )2 3 sincosA. 直线B. 椭圆C. 双曲D. 抛 物线11 1解: ρ =231cos2[1 ()] 1 sin()2 26( 三 ) 综合例题赏析例 3x3 cos(是参数 )的两个焦点坐标是椭圆1( )y 5sinA.(-3 , 5) , (-3 , -3)B.(3 , 3) , (3 , -5)C.(1 ,1) , (-7 , 1)D.(7 , -1) ,(-1 , -1)解:化为普通方程得( x3) 2 ( y 1)21925∴ a 2=25,b 2=9, 得 c 2=16 ,c=4.∴ F(x-3,y+1)=F(0, ± 4)∴在 xOy 坐标系中,两焦点坐标是 (3 , 3) 和 (3 , -5).应选 B.例 4 参数方程xcos sin22(02 )表示y1(1sin )2A. 双曲线的一支,这支过点(1 , 1)B. 抛物线的一部分,这部分过(1 ,21 )2C. 双曲线的一支,这支过 (-1 , 1)D.抛物线的一部分,这部分过 (-1 ,21 ) 2解:由参数式得 x 2=1+sin θ=2y(x > 0)即 y= 1x 2(x > 0).2∴应选 B.例 5x sin ( )在方程( θ为参数 ) 所表示的曲线一个点的坐标是ycosA.(2,-7)B. ( 1 ,2)C.( 1 , 1)D.(1 ,0)3 322解: y=cos2 =1-2sin2 =1-2x 2将 x= 1 代入,得 y=12 2∴应选 C.例 6 下列参数方程 (t 为参数 ) 与普通方程 x 2-y=0 表示同一曲线的方程是( )x t x cost xtgtC.A.B.ycos 2t1 cos 2t yty1 cos2tx tgtD.1 cos2t y1 cos2t解:普通方程x 2-y 中的 x ∈ R , y ≥ 0, A. 中 x=| t |≥ 0, B. 中 x=cost ∈〔 -1,1 〕,故排除 A. 和 B.2cos 2 t2t=11 2C. 中 y=2t =ctg 2tx 2 =,即 x y=1,故排除 C.2sintg∴应选 D.例 7曲线的极坐标方程ρ =4 sin θ化 成直角坐标方程为 ( )A.x 2 +(y+2) 2=4B.x2+(y-2)2=4C.(x-2) 2+y 2=4D.(x+2) 2 +y 2=4解:将ρ = x 2y 2 ,sin θ =y 代入ρ =4sin θ,得 x 2+y 2=4y ,即 x 2+(y-2) 2=4. x 2 y 2∴应选 B.例 8 极坐标ρ =cos( ) 表示的曲线是 ( )4A. 双曲线B. 椭圆C.抛物线D.圆解:原极坐标方程化为ρ =12(cos θ +sin θ ) 22=ρcos θ +ρsin θ,∴普通方程为2 (x 2+y 2)=x+y ,表示圆 .应选 D. 例 9在极坐标系中,与圆ρ =4sin θ相切的条直线的方程是 ( )A. ρ sin θ =2B. ρcos θ =2C. ρ cos θ =-2D.ρcos θ =-4例 9 图解:如图 .⊙ C 的极坐标方程为ρ =4sin θ, CO ⊥ OX,OA 为直径,| OA | =4,l 和圆相切,l 交极轴于 B(2, 0) 点 P(ρ , θ ) 为 l 上任意一点,则有cos θ =OB2,得ρ cos θ =2,OP∴应选 B.例 10 4ρsin 22 =5 表示的曲线是 ()A. 圆B. 椭圆C.双曲线的一支D. 抛 物线解: 4ρ sin 2 2 =54ρ·cos2 122 cos5.把ρ = x 2y 2ρ cos θ =x ,代入上式,得2 x 2 y 2 =2x-5.平方整理得 y 2=-5x+25. . 它表示抛物线 .4∴应选 D.例 11极坐标方程 4sin 2θ =3 表示曲线是 ()A. 两条射线B.两条相交直线C.圆D. 抛 物线2y 2223x , 它表示两相交直线 .解:由 4sin θ =3, 得 4· x 2 y 2 =3, 即 y =3 x ,y=± ∴应选 B.四、能力训练( 一 ) 选择题1. 极坐标方程ρ cos θ = 4表示 ( )3A. 一条平行于 x 轴的直线B. 一条垂直于 x 轴的直线C. 一个圆D.一条抛物线2. 直线: 3x-4y-9=0 与圆:x 2 cos ( 为参数 ) 的位置关系是 ( ) y 2 sin,A. 相切B.相离C. 直线过圆心D.相交但直线不过圆心3. 若 (x , y) 与 ( ρ,θ )( ρ∈ R)分别是点 M 的直角坐标和极坐标, t 表示参数,则下列各组曲 线:①θ =和 sin θ = 1;②θ =和 tg θ =3,③ρ 2-9=0 和ρ = 3 ;④6263x22t2和x2 2t y1y3 t3 t2其中表示相同曲线的组数为 ( )A.1B.2C.3D.44. 设 M(ρ 1,θ 1) ,N(ρ 2,θ 2) 两点的极坐标同时满足下列关系:ρ 1+ρ 2=0 ,θ1+θ 2=0,则 M , N 两点位置关系是 ()A. 重合B. 关于极点对称C.关于直线θ =D. 关 于 极 轴2对称5. 极坐标方程ρ =sin θ +2cos θ所表示的曲线是 ( )A. 直线B. 圆C.双曲线D. 抛物线6. 经过点 M(1,5) 且倾斜角为的直线, 以定点 M 到动点 P 的位移 t 为参数的参数方程3是( )x 1 1tx 1 1tx 1 1tA .2 B.2 C.23 3 3yt t t5y 5y 5222y1 3 tD.2 x51t2m 2 2m7. 将参数方x am 2 2m 2y b2m 2m 2 2m 2(m 是参数, ab ≠ 0) 化为普通方程是 ( )x 2 y 2 1( x a)x 2 y 2 1( xa) A.b 2B.b 2a 2a 2C. x 2y 21( x)x 2 y 2 1( xa)a 2b 2aD.b 2a 28. 已知圆的极坐标方程ρ =2sin( θ+) ,则圆心的极坐标和半径分别为 ()6A.(1,),r=2 B.(1,),r=1C.(1,),r=1 D.(1,363- ),r=23xt19. 参数方程t (t为参数 ) 所表示的曲线是 ( )y2A. 一条射线B.两条射线C.一条直线D.两 条直线x 2 tg10. 双曲线( θ为参数 ) 的渐近线方 程为 ( )y 1 2 secA.y-1=1( x 2)B.y=1 x C.y-1=2(x2)22D.y+1= 2(x2)11. 若直线x 4 at( (t 为参数 ) 与圆 x 2+y 2-4x+1=0 相切,则直线的倾斜角为( )y btA.B.2 C.或2D.333 3 3或 53x 2 pt 2 为参数 ) 上的点 M ,N 对应的参数分别为 t 1,t 2,且 t 1+t 2=0,12. 已知曲线(ty2 pt那么 M , N 间的距离为 ()A.2p(t 1+t 2)B.2p(t 22 C.│2p(t 1-t 2)│1+t 2)D.2p(t 1-t 2) 213. 若点 P(x ,y) 在单位圆上以角速度ω按逆时针方向运动,点 M(-2xy ,y 2-x 2) 也在单位圆上运动,其运动规律是( )A. 角速度ω,顺时针方向B. 角速度ω,逆时针方向C. 角速度 2ω , 顺时针方向D.角速度 2ω,逆时针方向14. 抛物线 y=x 2-10xcos θ +25+3sin θ-25sin2θ与 x 轴两个交点距离的最大值是( )A.5B.10C.23D.315. 直线ρ =3 与直线 l 关于直线θ =( ρ∈ R)对称,则 l 的方程是 ( )2cossin4A .3B .3sin2 coscos 2 cosC .3D .32 sincos2sincos( 二 ) 填空题x3 4 t16. 若直线 l的参数方程为5 (t 为参数 ) ,则过点 (4 ,-1) 且与 l 平行的直线3 ty25在 y 轴上的截距为.xcoscos17. 参数方程1 (为参数)化成普通方程为.sinycos118. 极坐标方程ρ =tg θ sec θ表示的曲线是.19. x 1 3t(t 为参数 ) 的倾斜角为;直线上一点 P(x , y) 与点 M(-1 ,直线2 3ty 2) 的距离为.( 三 ) 解答题20. 设椭圆x 4 cos( θ为参数 ) 上一点 P ,若点 P 在第一象限, 且∠ xOP=,求y 2 3 sin3点 P 的坐标 .21. 曲线 C 的方程为x 2 pt 2y(p > 0, t 为参数 ) ,当 t ∈[ -1 , 2]时 ,曲线 C 的端2 pt点为 A , B ,设 F 是曲线 C 的焦点,且 S =14,求 P 的值 .△ AFB22. 已知椭圆 x2y 2 =1 及点 B(0 ,-2) ,过点 B 作直线 BD ,与椭圆的左半部分交于 C 、2D 两点,又过椭圆的右焦点F 2 作平行于 BD 的直线,交椭圆于G , H 两点 .(1) 试判断满足│2BD 是否存在 ?并说明理BC │·│ BD │ =3│ GF │·│ F 2H │成立的直线由 .(2) 若点 M 为弦 CD 的中点, S △ BMF2=2,试求直线 BD 的方程 .x 8 4sec23. 如果椭圆的右焦点和右顶点的分别是双曲线( θ为参数 ) 的左焦点y 3tg和左顶点,且焦点到相应的准线的距离为9,求这椭圆上的点到双曲线渐近线的最短距离. 424.A ,B 为椭圆x2y 2上的两点,且 OA⊥ OB,求△ AOB的面积的最大a2b2 =1,(a > b> 0)值和最小值 .25. 已知椭圆x2y 2=1,直线 l ∶xy=1,P 是 l 上一点,射线 OP交椭圆于点 R,24161282又点 Q在 OP上且满足│ OQ│·│ OP│ =│OR│ ,当点P在l上移动时,求点Q的轨迹方程.参考答案( 一 )1.B 2.D 3.C 4.C 5.B 6.A 7.A 8.C 9.B 10.C 11.C 12.C 13.C 14.C 15.D( 二 )16.-4 ;17.y 2=-2(x- 1),(x≤ 1);18. 抛 物线; 19.135 °,|32 t|22 ( 三 )20.(8 5 , 4 15) ; 21.2 3 ;55322.(1) 不存在, (2)x+y+2=0 ; 23. 1(27-341 ) ;24.Smax=ab, s max =a 2b 2;5 2a 2b 2(x 1) 2 ( y 1) 2不同时为零 )25.=1(x,y)5522。
高二数学曲线的参数方程

练习1:
以初速度v0发射炮弹,炮弹的发射角为,不
计空气阻力,试写出炮弹曲线的参数方程。
y v0
o
x
思考:
这里定点Q在圆O外,你能判断这个 轨迹表示什么曲线吗?如果定点Q在 圆O上,轨迹是什么?如果定点Q在 圆O内,轨迹是什么?
2、指出参数方程xy
2 3
cos 5 2sin
一般地,在平面直角坐标系中,如果曲线上 任意一点的坐标x,y都是某个变数t的函数
x f (t)
y
g
.........................(2) (t)
并且对于t的每一个允许值,由方程组(2) 所确定的点M(x,y)都在这条曲线上,那么方 程(2)就叫做这条曲线的参数方程,联系变 数x,y的变数t叫做参变数,简称参数,相对 于参数方程而言,直接给出点的坐标间关系
在过去的学习中我们已经掌握了 一些求曲线方程的方法,在求某些曲 线方程时,直接确定曲线上的点的坐 标x,y的关系并不容易,但如果利用某 个参数作为联系它们的桥梁,那么就 可以方便地得出坐标x,y所要适合的条 件,即参数可以帮助我们得出曲线的 方程f(x,y)=0。
一、曲线的参数方程
1、参数方程的概念
注意:在参数方程与普通方程的互化中,必须 使x,y的取值范围保持一致。
作业:26页1、2、4、5
x 1 t
5、若已知直线的参数方程为
y
1
(t为参数) t
x
求它与曲线
y
2 cos 2 sin
(为参数)的交点。
x 1 t
解:参数方程
y
1
t
(t为参数)的普通方程为
x y20
x 2 cos
高二数学最新课件-圆的参数方程[原创]人教版 精品
![高二数学最新课件-圆的参数方程[原创]人教版 精品](https://img.taocdn.com/s3/m/883b73f7172ded630a1cb61c.png)
返回
练习3.
经过圆 x 2 y 2 4 上任一点P作y轴垂
线,垂足为Q,求线段PQ中点轨迹的普通 方程
4x y 4
2 2
返回
课后作业:
x cos 1.(2002年全国新课程)曲线 y sin 上的点到两 坐标轴的距离之和的最大值为( D )
1 A. 2
(二).利用圆的参数方程求轨迹方程 (三).利用圆的参数方程求字母的取值范围
(四).课堂小结
(五)课后作业:
进入
进入
例1.若实数x,y满足 x 2 y 2 2 x 4 y 0 求x-y的最大值
解:将圆的方程化为: ( x 1) 2 ( y 2) 2 5
x 1 5 cos 所以圆的参数方程为: 代入x-y 得: y 2 5 sin
解: f ( )可看成两点 p(cos , sin ) ,A(2,1) 连线的斜率 2 2 x y 1上运动,过定点A作圆的两条切线 且p在圆 AP1, AP2,则AP1斜率最小且最小值为0, AP2的斜率最大, 下面求AP2的斜率 设AP2的斜率为k,则AP2的方程为 y 1 k ( x 2) 即 kx y 2k 1 0
圆的参数方程的应用
学习目标:能熟练应用圆的参数方程解题
下一页
教学过程
一.知识回顾:
x r cos (为参数) 1.圆心在原点,半径为r的圆的参数方程: y r sin
2.圆心在点(a,b),半径为r的圆 的参数方程为: x a r cos (为参数)
x 5 3 cos 3.已知圆的参数方程 , (为参数) y 3 3 sin 则它的普通方程为: ( x 5) 2 ( y 3) 2 9
参数方程大全范文

参数方程大全范文参数方程是一种用来描述曲线、曲面或立体图形的数学方法。
与直角坐标系的方程不同,参数方程使用一个或多个参数来表示曲线或曲面上的点的坐标。
以下是一些常见的参数方程的示例:1.二维平面上的曲线:- 直线:x = at + b, y = ct + d (a, b, c, d为常数)- 抛物线:x = at^2 + bt + c, y = dt^2 + et + f (a, b, c, d, e, f为常数)- 椭圆:x = a*cos(t), y = b*sin(t) (a, b为常数)- 双曲线:x = a*sec(t), y = b*tan(t) (a, b为常数)- 阿基米德螺线:x = at*cos(t), y = at*sin(t) (a为常数)- 伯努利双纽线:x = a*cosh(t), y = b*sinh(t) (a, b为常数)2.三维空间中的曲线:- 直线:x = at + b, y = ct + d, z = et + f (a, b, c, d, e, f为常数)- 螺线:x = at*cos(t), y = at*sin(t), z = bt (a, b为常数)- 柱面:x = a*cos(t), y = a*sin(t), z = bt (a, b为常数)- 螺旋线:x = a*cos(t), y = a*sin(t), z = bt (a, b为常数)3.二维平面上的曲面:-零面:x=u,y=v,z=0(u,v为任意参数)- 平面:x = au + bv + c, y = du + ev + f, z = gu + hv + i (a, b, c, d, e, f, g, h, i为常数)- 圆柱面:x = a*cos(u), y = a*sin(u), z = bt (a, b为常数)- 双曲面:x = a*cosh(u)*cos(v), y = b*cosh(u)*sin(v), z = c*sinh(u) (a, b, c为常数)- 椭球面:x = a*cos(u)*sin(v), y = b*sin(u)*sin(v), z =c*cos(v) (a, b, c为常数)4.三维空间中的曲面:- 球面:x = a*sin(u)*cos(v), y = b*sin(u)*sin(v), z =c*cos(u) (a, b, c为常数)- 圆环面:x = (a + b*cos(v))*cos(u), y = (a +b*cos(v))*sin(u), z = b*sin(v) (a, b为常数)- 柱面:x = a*cos(u), y = a*sin(u), z = v (a为常数)- 双曲抛物面:x = a*u*cos(v), y = a*u*sin(v), z = u^2/2 (a 为常数)- 椭球体:x = a*cos(u)*sin(v), y = b*sin(u)*sin(v), z =c*cos(v) (a, b, c为常数)以上是一些常见的参数方程的示例,其中的参数和常数可以根据需要适当调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参数方程 考点要求1 了解参数方程的定义。
2 分析直线,圆,圆锥曲线的几何性质。
会选择适当的参数,写出他们的参数方程。
并理解直线参数方程标准形式中参数的意义。
3掌握曲线的参数方程与普通方程的互化。
考点与导学1参数方程的定义:在取定的坐标系中。
如果曲线上任意一点的坐标y x ,都是某个变量t 的函数⎩⎨⎧==)()(t g y t f x (t ∈T) (1) 这里T 是)(),(t g t f 的公共定义域。
并且对于t 的每一个允许值。
由方程(1)所确定的点),(y x M 。
都在这条曲线上;那么(1)叫做这条曲线的参数方程,辅助变数t 叫做参数。
2过点),,(000y x p 倾斜角为α的直线l 的参数方程(I )⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数)(i )通常称(I )为直线l 的参数方程的标准形式。
其中t 表示),,(000y x p 到l 上一点),(y x p 的有向线段p 0的数量。
t>0时,p 在0p 上方或右方;t<0时,p 在0p 下方或左方,t=0时,p 与0p 重合。
(ii )直线的参数方程的一般形式是:⎩⎨⎧+=+=bt y y at x x 00(t 为参数)这里直线l 的倾斜角α的正切ba =αtan (00900==αα或时例外)。
当且仅当122=+b a 且b>0时. (1)中的t 才具有(I )中的t 所具有的几何意义。
2 圆的参数方程。
圆心在点),,(00'y x o 半径为r 的圆的参数方程是⎩⎨⎧+=+=θθsin cos 00r y y r x x (θ为参数)3 椭圆12222=+by a x 的参数方程。
⎩⎨⎧==θθsin cos b y a x (θ为参数) 4 双曲线12222=-b y a x 的参数方程:⎩⎨⎧==θθtan sec b y a x (θ为参数)5 抛物线px y 22=的参数方程。
⎩⎨⎧==pty pt x 222(t 为参数)例1 已知某曲线C 的参数方程为⎩⎨⎧=+=221aty tx (其中t 是参数,R a ∈),点M (5,4)在该曲线上。
(1)求常数a ;(2)求曲线C 的普通方程。
解:(1)由题意可知有⎩⎨⎧==+45212at t 故 ⎩⎨⎧==12a t ∴1=a (2)由已知及(1)可得,曲线C 的方程为⎩⎨⎧=+=221ty t x 由第一个方程得21-=x t 代入第二个方程得:2)21(-=x y 。
即y x 4)1(2=-为所求。
〔点评〕 参数方程化为普通方程的关键是消参数,并且要保证等价性。
若不可避免地破坏了同解变形,则一定要通过)(),(t g y t f x ==。
根据t 的取值范围导出y x ,的取值范围。
例2 圆M 的参数方程为03sin 4cos 4222=+--+R Ry Rx y x αα(R>0).(1)求该圆的圆心的坐标以及圆M 的半径。
(2)当R 固定,α变化时。
求圆心M 的轨迹。
并证明此时不论α取什么值,所有的圆M 都外切于一个定圆。
解:(1)依题意得 圆M 的方程为222)sin 2()cos 2(R R y R x =-+-αα 故圆心的坐标为M (R R R 半径为).sin 2,cos 2αα。
(2)当α变化时,圆心M 的轨迹方程为⎩⎨⎧==ααsin 2cos 2R y R x (其中α为参数)两式平方相加得2224R y x =+。
所以所有的圆M 的轨迹是圆心在原点。
半径为2R 的圆由于RR R R R R R R R R +==+-==+2)sin 2()cos 2(32)sin 2()cos 2(2222αααα所以所有的圆M 都和定圆222Ry x =+外切,和定圆2229R y x =+内切。
〔点评〕本题中所给的方程中含有多个参数,像这样的问题有时容易分不清哪个是真正的参数,究竟在具体的题目中哪个是真正的参数应视题目给定的条件,分清参数。
例3已知A ,B 分别是椭圆193622=+y x 的右顶点和上顶点,动点C 在该椭圆上运动,求∆ABC 的重心的轨迹的普通方程。
解:由动点C 在椭圆上运动,可设C 的坐标为(6cos θ,3θsin ),点G 的坐标为),(y x .依题意可知:A (6,0),B (0,3) 由重心坐标公式可知⎪⎪⎩⎪⎪⎨⎧+=++=+=++=θθθθsin 13sin 330cos 223cos 606y x 由此得:⎪⎩⎪⎨⎧=-=-)2(sin 1)1(cos 22θθy x 得22)2()1(+ 1)1(4)2(22=-+-y x 即为所求。
〔点评〕①本题的解法体现了椭圆的参数方程对于解决相关问题的优越性。
运用参数方程显得很简单。
运算更简便。
常用于解决有关最值问题。
②“平方法”是消参的常用方法。
例4求经过点(1,1)。
倾斜角为0135的直线截椭圆1422=+y x 所得的弦长。
解:由条件可知直线的参数方程是:⎪⎪⎩⎪⎪⎨⎧+=-=t y tx 221221(t 为参数)代入椭圆方程可得: 1)221(4)221(22=++-t t 即0123252=++t t 设方程的两实根分别为21,t t 。
则⎪⎪⎩⎪⎪⎨⎧=-=+525262121t t t t 则直线截椭圆的弦长是 5264)(2122121=-+=-t t t t t t 〔点评〕利用直线参数方程的几何意义求弦长的常用方法。
但必须注意:直线的参数方程必须是标准形式。
即 ⎩⎨⎧+=+=bty y at x x 00(t 为参数)当122=+b a 且b>0时才是标准形式。
若不满足122=+b a 且b>0两个条件。
则弦长为 d=212)(1t t ab -+〔解题能力测试〕1 已知某条曲线的参数方程为:⎪⎪⎩⎪⎪⎨⎧-=+=)1(21)1(21a a y aa x 其中a 是参数。
则该曲线是( )A 线段B 圆C 双曲线的一部分D 圆的一部分2 已知某条曲线的参数方程为⎪⎩⎪⎨⎧-=+=12322t y t x )50(≤≤t 则该曲线是( )A 线段B 圆弧C 双曲线的一支D 射线3实数y x ,满足191622=+y x ,则y x z -=的最大值为: ;最小值为 。
4已知直线l 的斜率为1-=k .经过点)1,2(0-M。
点M 在直线上,以−−→−MM 0的数量t 为参数.则直线l 的参数方程为: 。
5 已知直线l 的参数方程是⎩⎨⎧+-=+=ααcos 2sin 1t y t x (t 为参数) 其中实数α的范围是),2(ππ。
则直线l 的倾斜角是: 。
〔潜能强化训练〕 1 在方程⎩⎨⎧==θθ2cos sin y x (θ为参数)所表示的曲线上的一点的坐标为 ( )A )7,2(-B )32,31( C )21,21( D )0,1(2下列参数方程(t 为参数)与普通方程02=-y x 表示同一曲线的方程是( )A ⎩⎨⎧==t y t x B⎩⎨⎧==ty tx 2cos cos C ⎪⎩⎪⎨⎧-+==t t y t x 2cos 12cos 1tan D ⎪⎩⎪⎨⎧+-==t t y tx 2cos 12cos 1tan 3 直线0943=--y x 与圆⎩⎨⎧==θθsin 2cos 2y x (θ为参数)的位置关系是( )A 相切B 相离C 直线过圆心D 相交但直线不过圆心。
4 设直线⎩⎨⎧-=+=ααsin 2cos 1t y t x (t 为参数)。
如果α为锐角,那么直线01:21=+x l l 到直线的角是( ) Aαπ-2 B απ+2C αD απ- 5 过点(1,1),倾斜角为o135的直线截椭圆1422=+y x 所得的弦长为( ) A522 B 524 C 2 D5236 双曲线⎩⎨⎧==θθsec tan 3y x (θ为参数),那么它的两条渐近线所成的锐角是: 。
7 参数方程⎩⎨⎧+==θθθcos sin 2sin y x (θ为参数)表示的曲线的普通方程是: 。
8 已知点M (2,1)和双曲线1222=-y x ,求以M 为中点的双曲线右支的弦AB 所在直线l 的方程。
9 已知椭圆的中心在原点。
焦点在y 轴上且长轴长为4,短轴长为2。
直线l 的参数方程为⎩⎨⎧+==tm y tx 2(t 为参数)。
当m 为何值时,直线l 被椭圆截得的弦长为6?10、求椭圆1121622=+y x 上的点到直线0122:=--y x 的最大距离和最小距离。
〔知识要点归纳〕1. 参数方程是以参变量为中介来表示曲线上点的坐标的方程,是曲线在同一坐标系下的一种表示形式,而且有的参数还有几何意义或物理意义。
2. 面临一个轨迹问题,如何选择参数?如何用参数?是主要问题,必须在学习过程中深刻去领会。
3. 在参数方程与普通方程互化过程中,要注意等价性。
四、参数方程 〔解题能力测试〕1.C 2、A 3、5,-5 4、2212x y ⎧=-⎪⎪⎨⎪=-+⎪⎩5、32πα-〔潜能强化训练〕1、C2、D3、C4、B5、B6、6007、21(11)y x x =+-≤≤8、490x y +-= 9、5m =± 10、max min 5d d ==最新文件 仅供参考 已改成word 文本 。
方便更改。
