测量平差课后习题答案PPT
测量平差教案第二章36页PPT
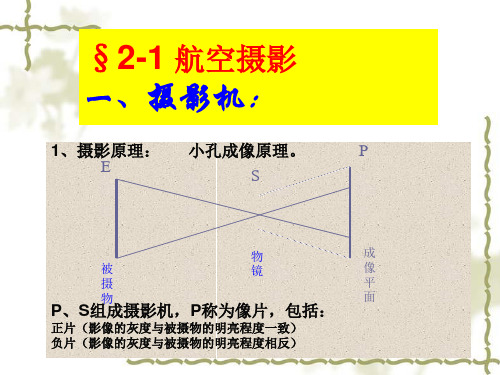
数码航摄仪:
❖ 传统航摄像机使用胶片作为记录信息的载体,通 过对航片进行高精度扫描获取数字影像;
❖ 数码航摄像机使用光敏元件作为成像器件,将光 学信号转换成数字信息,直接获取数字影像。
❖ 第20 届 ISPRS,国际著名公司展出数码航摄像 机。
❖ 数码航摄像机的推出与成功应用,已成为航空摄 影测量的又一个里程碑。
0.015mm 4、各色滤色片齐全,暗合压平质量良好
《航空摄影测量规范》
航摄比例尺与地形图比例尺的关系表
地形图比例尺
1:500 1:2000 1:10000
航摄比例尺
1:4000~ 1:8000 1:8000~ 1:18000 1:20000~ 1:40000
正射影象图比 例尺
1:500
1:2000
§2-2 摄影测量常用坐标系
一、像平面上的直角坐标系: 1、框标坐标系:p-x’y’
选择框标连线的交点 p为原点,框标连线 为x’,y’轴,航线方向为x’轴的正轴。
2、像平面直角坐标系(o-xy): ❖ 像片的像主点o为原点,x、y轴分别平行于
框标坐标系的x’、y’轴。 ❖ 距f,P在称o为-x摄y中影的机坐的标内:方x位0,y元0,素及。摄影机的主
普通摄影机:
为生活娱乐而设计。 镜箱和暗箱连为一体。
量测用摄影机:
为摄影测量目的而设计制造。
航空摄影机、 摄影经纬仪。
❖
量测用摄影机的特点:
物镜具备良好的光学性能(分辨率高、畸变 差小、透光性强);
机械结构稳定 ;具有自动装置和压平装置; 同一台摄影机的像距是固定的已知值; 摄影机像平面的框架上有框标标志; 内方位元素已知; 像幅: 23cm*23cm,18cm*18cm ,13cm*18cm
测量平差课后习题答案 张书毕

4
.解答:
第 1 页/共 44 页
《测量平差》参考答案 Ch1---Ch4
2 1 0 P LL 1 3 1 0 1 2 Q P LL Q Q
LL LL
I
P LL 5 1 0 0 8 2 1 0 1 0 0 1 E 1 3 1 0 1 0 0 1 0 4 0 1 2 0 0 1 0 0 1 1 8 1 4 1 2 1 4 1 4 1 2 1 4 1 8 1 4 5 8
cos L2 sin L1 sin(L1 L2 ) dL dL2 1 cos2(L1 L2 ) cos2(L1 L2 )
所以 S (
cos L2 sin L1 sin(L1 L2 ) 2 2 )2 12 ( ) 2 cos (L1 L2 ) cos2(L1 L2 )
《测量平差》参考答案 Ch1---Ch4
D XL =E X E X L E L T E AL AE L L E L T AE ( L E L )( L E ( L) )
104 m 2
T2 (
Y Y X Y 2 2 )2 )2 X Y = 5.4 X ( Y 2 2 2 2 X Y X Y (X 2 Y 2 )2
1010 m 2
S ST X 9.4 108 m2
1 2 2
ˆ 所以一测回的角度中误差
第 7 页/共 44 页
《测量平差》参考答案 Ch1---Ch4
12
.解答:
解 设路线总长 S 公里,按照测量学上的附合路线计算步骤,则路线闭合差
测量平差第三章习题与答案

测量平差第三章思考题3.1 下列各式中的()1,2,3i L i =均为等精度独立观测值,其中误差为s ,试求X 的中误差: (1)()12312X LL L =++;(2)123L L X L =3.2 已知观测值1L ,2L 的中误差12s s s ==,120s =,设11225,2X L Y L L =+=-,12Z L L =,t X Y =+,试求X ,Y ,Z 和t 的中误差。
的中误差。
3.3 设有观测向量[]12331TL L L L =,其协方差阵为,其协方差阵为40003002L LD éùêú=êúêúëû分别求下列函数的的方差:分别求下列函数的的方差: (1)1133F L L =-; (2)2233F L L =3.4 设有同精度独立观测值向量[]12331TL LLL=的函数为113s i n s i n A BL Y S L =,22A B Y L a =-,式中A B a 和A B S 为无误差的已知值,测角误差1"s =,试求函数的方差12y s 、22y s及其协方差12y y s3.5 在图中△ABC 中测得A A s б,边长b b s ±,c c s ±,试求三角形面积的中误差ss 。
3.6 在水准测量中,设每站观测高差的中误差均为1mm ,今要求从已知点推算待定点的高程中误差不大于5cm ,问可以设多少站?,问可以设多少站? 3.7 有一角度测4个测回,得中误差为0.42〃,问再增加多少个测回其中误差为0.28〃?〃? 3.8 在相同观测条件下,应用水准测量测定了三角点A ,B ,C 之间的高差,设三角形的边长分别为S 1=10km ,S 2=8km ,S 3=4km ,令40km 的高差观测值权威单位权观测,试求各段观测高差之权及单位权中误差。
测量平差-获奖课件

2 X1
D XX
2 X
2
X1
2 X
n
X1
2 X1X 2
2 X2
2 XnX2
2 X1X n
2 X2Xn
2 Xn
若有X旳t个函数:
z1
Z
t1
z2
KX
K0
zt
k11 k12
K
tn
k21
k22
kt1 kt 2
1n
k2n
ktn
k10
K0
k20
t1 kt0
DZZ
1
xe
(
x)2 2 2
dx
2
数学期望旳传播规律:
常数c旳数学期望为E(c)=c
随机变量X乘以常数c,则有 ECX CEX
随机变量X1, X 2,, X之n 和旳数学期望为
EX1 X2 Xn EX1 EX2 EXn
相互独立旳随机变量 X1, X 2,,X 之n 积旳数学期望为:
二、协因数传播律
Y FX F 0 Z KX K 0
由协方差传播律得:
DYY F DXX F T DZZ K DXX K T DYZ F DXX K T
2 0
DYY
F
2 0
DXX
FT
2 0
DZZ
K
2 0
DXX
KT
2 0
DYZ
F
2 0
DXX
KT
即:
QYY F QXX F T QZZ K QXX K T QYZ F QXX K T
例4:设有函数, Z t ,1
F1
t,n
X
n,1
F1
t,r
经典的测量平差ppt

练习(一)填空题1.在图1所示水准路线中,A 、B 为已知点,为求C 点高程,观测了高差1h 、2h ,其观测中误差分别为1σ、2σ。
已知1212σσ=,取单位权中误差02σσ=。
要求平差后P 点高程中误差2C mm σ≤, 则应要求1σ≤ ① 、2σ≤ ② 。
2.已知观测值向量1,13,12,1X Z Y ⎡⎤⎢⎥=⎢⎥⎣⎦的协方差阵310121013ZZD -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,12,12Y Y Y ⎡⎤=⎢⎥⎣⎦,若设权11Y P =,则权阵XX P = ③ ,YY P = ④ ,协因数阵12Y Y Q = ⑤ ,1Y X Q = ⑥ 。
3.已知平差后某待定点P 的坐标的协因数和互协因数为P X Q ˆ、P Y Q ˆ和PP Y X Q ˆˆ,则当 PPY X Q Q ˆˆ=,0ˆˆ<PP Y X Q 时,P 点位差的极大方向值=E ϕ ⑦ ,极小方向值=F ϕ ⑧ 。
二、问答题1.在图2所示三角形中,A 、B 为已知点,C 为待定点,同精度观测了1234,,,L L L L共4个方位角,1S 和2S 为边长观测值,若按条件平差法平差:(1)应列多少个条件方程;(2)试列出全部条件方程(不必线性化)。
2.在上题中,若设BAC ∠、ABC ∠和ACB ∠为 参数1X 、2X 、3X ,(1)应采用何种函数模型平差;图2(2)列出平差所需的全部方程(不必线性化)。
3. 对某控制网进行了两期观测。
由第一期观测值得到的法方程为111111ˆT T B PB X B PL =, 由第二期观测值得到的法方程为222222ˆT T B P B X B P L =。
有人认为将两期观测值一起 平差得到的参数估值为1111222111222ˆ()()T T T T X B PB B P B B PL B P L -=++ 这样作对吗?为什么?三.计算题1.有一长方形如图3所示,421,,,L L L 为独立同 精度观测值,mm L 3.121=,mm L 5.82=,mm L 6.143=,mm L 6.124=。
测量平差习题参考答案

第一章 习题参考答案 1题.略2题.解 (1)222194σσ+(2)2221212219)3(σσL L L +-(3) 222212211212212211211")(cos )sin(sin ")(cos )sin(sin )cos(cos σρσρ⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++++L L L L L L L L L L L L L 3题. 解TT TLL XY LL YL LL XL B A AD D BAD D AD D ===,,4题.解 设路线总长S 公里,按照测量学上的附合路线计算步骤,则路线闭合差B A h H h h H f -++=21由于是路线中点,故()B A h H h h H f v v -++-===21212121 则线路中点高程()()B A B A B A A A H H h h H H h h H h h H h H v h H H ++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=++-=-++-+=-+=2121212121212121ˆ212121111中点设每公里高差观测中误差为0σ,则021)2/(σσσs h h ==按误差传播定律)(16,10425)52/(41)52/(41)2/(41)2/(414141212100212122220202222ˆ21121km S S s s s s h h h h H ≤≤=⋅⨯+⋅⨯=⨯+⨯=+=⎪⎪⎪⎪⎭⎫⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=σσσσσσσ中点5.解 设每个测回的中误差为0σ,需要再增加n 个测回,则)2(2028.0,28.020)1(2042.0,42.0200000+±=±=+±=±=n n σσσσ由上式可解出n.即252023202028.042.020222=-⎪⎭⎫ ⎝⎛⨯=-⨯=n 再增加25个测回6题.解[][][][][][][][][]][][][,100010001...,...)...(2121211212122111⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎢⎣⎡⎥⎦⎤=+++==p p p p p p p p p P p P p P p Q L L L P p P p P p L p L p L p x n n n p xx n n n n p p pL x][][][][][][p p p p p p p p p p p p p p p nnn⋅⋅++⋅⋅+⋅⋅=1 (1)12221117题。
第3讲习题测量平差课件

L4
B
例2:观测四个方向,得等精度 观测值L1~L6,若选参数
ˆ ˆ X X1
L6
L5 C
ˆ X2
ˆ X3
T
ˆ L1
ˆ L2
ˆ L4
Hale Waihona Puke TD按附有限制条件的条件平差法 (1)列出条件方程和限制条件方程; (2)列出法方程,解出参数的平差值; (3)求改正数向量及观测角的平差值。
B 2 4 1 A 5 8 11
若选P1点高程及AP1路线上高差平差值为未知参数
附有限制条件的条件平差: (1)试列出条件方程和未知数间的限制条件;
和
X2
,试按
(2)试求待定点P1及P2的高程平差值及各路线上的高差平差值;
(3)试求P1点平差后高程的中误差。 h1 A
X2 X1
h2 P2
h3
B
P1
A
L1 O
L3 L2
习题课
例1:在如图的单一附合水准路线中,已知A,B点高程为 HA=10.258m,HB=15.127m,P1,P2点为待定点,观测高差及路 线长度为:
m, h1 2 . 154 m, h 1 . 678 2 m, h 3 1 . 031
S1 2
km km km
X1
S2 3
S3 4
P1
3 7
6 12
C
9 10
P2
例3:A、B、C为已知点,P1、P2为待 定点,观测了12个角,若选∠2和∠4 为未知参数X1和X2,按附有限制条件 的条件平差: (1)列出条件方程和限制条件; (2)列法方程。
例4:A为已知点,P1、P2 、P3为待定点,观测了5条 路线的高差,相应的路线长度等长,若P2点平差后 高程值的权,采用什么函数模型较好?并求其权。 P2 2 3
测量平差练习题及答案

计算题1、如图,图中已知A 、B 两点坐标,C 、D 、E 为待定点,观测了所有内角,试用条件平差的方法列出全部条件方程并线性化。
解:观测值个数 n =12,待定点个数t =3,多余观测个数r =n -2t =6① 图形条件4个:)180(0)180(0)180(0)180(0121110121110987987654654321321-++-==-++-++-==-++-++-==-++-++-==-++L L L w w v v v L L L w w v v v L L L w w v v v L L L w w v v v d d c c b b a a② 圆周条件1个:)360(0963963-++-==-++L L L w w v v v e e③ 极条件1个:ρ''--==----++)sin sin sin sin sin sin 1(0cot cot cot cot cot cot 852741774411885522L L L L L L w w v L v L v L v L v L v L f f3、如图所示水准网,A 、B 、C 三点为已知高程点, D 、E 为未知点,各观测高差及路线长度如下表所列。
用间接平差法计算未知点D 、E 的高程平差值及其中误差;C3、解:1)本题n=6,t=2,r=n-t=4;选D 、E 平差值高程为未知参数21ˆˆX X 、 则平差值方程为:1615142322211ˆˆˆˆˆˆˆˆˆˆˆˆˆX H hH X h H X h H X h H X h X X h AA BAB -=-=-=-=-=-=则改正数方程式为:6165154143232221211ˆˆˆˆˆˆˆl xv l x v l x v l x v l x v l x xv --=-=-=-=-=--=取参数近似值 255.24907.2220221011=+==++=h H X h h H X B B 、令C=1,则观测值的权阵:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=10111101P ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=010*********B ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------=+-=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=7551000)()()()()()()(016015014023022020110654321X H h H X h H X h H X h H X h X X h d BX h l l l l l l l C A B A B组法方程0ˆ=-W xN ,并解法方程: ⎪⎪⎭⎫ ⎝⎛--==3114PB B N T⎪⎪⎭⎫ ⎝⎛-==107Pl B W T⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛==-311074113111ˆ1W N x求D 、E 平差值:m x X X H m x X X H D C 258.24ˆˆˆ906.22ˆˆˆ20221011=+===+== 2)求改正数:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=-=664734ˆl xB v 则单位权中误差为:mm r pv v T 36.64162ˆ0±=±=±=σ则平差后D 、E 高程的协因数阵为:⎪⎪⎭⎫⎝⎛==-41131111ˆˆNQ X X 根据协因数与方差的关系,则平差后D 、E 高程的中误差为:mmmm Q mm mm Q E D 84.311229ˆˆ32.322669ˆˆ220110±=±==±=±==σσσσ4、如图,在三角形ABC 中,同精度观测了三个内角:4000601'''︒=L ,5000702'''︒=L ,7000503''''︒=L ,按间接平差法列出误差方程式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
HC
HC'
H
" C
2
H A h1 H B h2 2
h1 h2
S 2
公里
2
2 h1
2 h2
S
2 公里
hC
4
4
10mm S公里 10mm S 16km
5
hC
2
习题
1.5:有一角度测20测回,得中误差 0.42'',问再增加多少测回其中误差为0.28''?
考点:同精度独立观测值的算术平均值的精度
DXY ADLL (BA)T ADLL AT BT
或
Y BX B
O
X L
X O
A
X L
,
DXY O
A
DXX DLX
DXL DLL
BT O
ADLX
ADLL
BT O
ADLX BT
ADLL AT BT
或
Y BX, X IX
DXY ID XX BT DXX BT
而 DXX ADLL AT
dx (L1 3L2 )dL1 3L1dL2
2 x
(L1
3L2) 2m12
9L12m22
x (L1 3L2 ) 2m12 9L12m22
1
习题
(3)对此函数式进行全微分或先取对数再求微分,得:
dx
c os L1
cos(L1 L2 ) cos2 (L1
sin L1 L2 )
sin(L1
x
L
N
1 N
L1
1 N
L2
L
1 N
LN
x
N
N个同精度独立观测值的算术平均值的 中误差=各观测值中误差除以 N
解析:观测值的中误差为:
x
N 0.42''
''
20 0.84 5
' x
N N
''
代入数值后得:0.28'' 0.84 5 20 N
N 25
6
m22
x
cos2 cos4 (L1
L2 L2 )
m12
sin2 L1 sin2 (L1 L2 ) cos4(L1 L2)
m22
2
习题
1.3 已知观测值L及其协方差阵DLL ,组成函数 X AL 和Y BX,A、B为常数阵, 求协方差阵 DXL 、DYL 和 DXY 。
解:(1) X AL, L IL (I为单位阵)
所以 DXY DXX BT ADLL AT BT
4
习题
1.4:若要在两已知高程点间布设一条附合水准路线(如图所示),已知每千米
观测中误差等于5.0mm,欲使平差后路线中点C点高程中误差不大于10mm,
问该路线长度最多可达几千米?
h1
h2
C
B
解析:设A、B间最大距离为Skm
HC' HA h1 HC" HB h2
习题
1.2 已知独立观测值L1、L2的中误差分别为m1、m2,求下列函数的中误差:
(1) x 2L1 3L2
(2)x
L12 2
3L1L2 (3) x
sin L1 cos(L1 L2 )
解:(1)因L1、L2是独立观测值,则
2 x
4m12
9m22
x 4m12 9m22 (2)对此函数式进行全微分,得:
DXL ADLL I T ADLL
(2) Y BX, X ADLL I T BADLL
,
或
Y BX B
O
X L
L IL O
I
X L
DYL B
O
DXX DLX
DXL DLL
O I
BDXX
BDXL
O I
BDXL
BADLL
3
习题
(3) Y BAL, X AL
L2
)
dL1
sin L1 sin(L1 cos2 (L1
L2 L2 )
)
dL2
c os L2 cos2 (L1
L2
)
dL1
sin L1 sin(L1 cos2 (L1
L2 L2 )
)
dL2
2 x
cos2 cos4 (L1
L2 L2 )
m12
sin2 L1 sin2 (L1 L2 ) cos4 (L1 L2 )
