1.4 整式的乘法(第3课时)
14.1.4整式的乘法(第3课时)(课件)-八年级数学上册精品课堂(人教版)

① 将单项式分别乘以多项式的各项,
② 再把所得的积相加.
2.进行单项式与多项式乘法运算时,要注意什么?
① 不能漏乘: 即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
复习引入
计算:1.单项式乘以单项式
(-4ab)·3a2bc;
解:原式=(-4×3)·(a·a2)·(b·b)·c
=-12a3b2c;
=x·x-xy-8xy+8y2
=x2-9xy+8y2;
典例精析
例6 计算:
计算时不能漏乘.
(3) (x+y)(x2-xy+y2).
(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
=x3+y3.
需要注意的几个问题:(1)漏乘;
(2)符号问题;
总体上看,(a+b)(p+q)的结果可以看作由a+b的
每一项乘p+q的每一项,再把所得的积相加而得到的,
即 (a+b)(p+q)=ap+aq+bp+bq
新知探究
(a+b)( p+q)=ap+aq+bp+bq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个
多项式的每一项,再把所得的积相加.
C.(x+2)(x-10)=x2-8x-20
D.(x+y)(x2-xy+y2)=x3+y3
随堂检测
3.计算:
(1)(2x+1)(x+3)
(2)(m+2n)(3n-m)
中学七年级数学下册 1.4 整式的乘法(第3课时)教案 (新版)北师大版 教案

整式的乘法一、教学目标:1.知识与技能:在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算. 2.过程与方法:经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.3.情感与态度:在解决问题的过程中了解数学的价值,发展“用数学”的信心. 二、教学过程: (一)复习回顾教师提出问题,引导学生复习上节课所学的单项式乘多项式 1、如何进行单项式乘多项式的运算?你能举例说明吗?2、计算:(1))()3222n mn m mn -+⋅( (2))2()52(22b a b b a a a ---- 处理问题2时出错,主要是第(2)小题中的符号处理出现错误.通过教师与学生共同订正错误,使学生的认识有了进一步的提高.(二)创设情境引入 活动内容:图1-1是一个长和宽分别为m ,n 的长方形纸片,如果它的长和宽分别增加a ,b ,所得长方形(图1-2)的面积可以怎样表示?学生独立思考后,全班交流,主要产生了四种解法: 方法一:长方形的长为(m+a ),宽为(n+b ),所以面积可以表示为))(b n a m ++(; 方法二:长方形可以看做是由四个小长方形拼成的,四个小长方形的面积分别为mn ,mb ,an ,ab ,所以长方形的面积可以表示为ab an mb mn +++;方法三:长方形可以看做是由上下两个长方形组成的,上面的长方形面积为b (m+a ),下面的长方形面积为n (m+a ),这样长方形的面积就可以表示为n (m+a )+ b (m+a ),根据上节课单项式乘多项式的法则,结果等于ba bm na nm +++方法四:长方形可以看做是由左右两个长方形组成的,左边的长方形面积为m (b+n ),右边的长方形面积为a (b+n ),这样长方形的面积就可以表示为m (b+n )+ a (b+n ),根据上节课单项式乘多项式的法则,结果等于an ab mn mb +++将四种方法的过程板书到黑板上,由于求的是同一个长方形的面积,于是我们得到:))(b n a m ++(=)()(a m b a m n +++=)()(n b a n b m +++=ab an mb mn +++教师引导学生观察这个等式,并启发性的将等式板书为以下形式:))(b n a m ++( =)()(a m b a m n +++或))(b n a m ++(=)()(n b a n b m +++ 或))(b n a m ++(=ab an mb mn +++式子的最左边是两个多项式相乘,最右边是相乘的结果,由此引出新课,多项式与多项式的乘法. (三)探究尝试教师设置三个层层递进的问题:1、 你能说出))(b n a m ++(=)()(a m b a m n +++这一步运算的道理吗?2、结合这个算式))(b n a m ++(=ab an mb mn +++,你能说说如何进行多项式与多项式相乘的运算?3、归纳总结多项式与多项式相乘的运算法则.学生独立思考,顺利完成前两个问题.在教师的启发引导下,学生归纳总结,得到多项式乘多项式的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.实际教学效果:用乘法分配律展开时要做到不重不漏对学生而言是易错点也是难点,教学时可结合问题1、2让学生交流各自方法,进行及时总结.(四)应用新知教师通过例题,引导学生应用多项式乘多项式的法则进行计算.mm n an图1-1 图1-2例3 计算:(1))6.0(1x x --)( (2)))(2(y x y x -+ (3)2)2n m +-( 综合练习:(1))1x 1)(x 2++-x ( (2))2)(1()3)(2(-+-++y x y x 学生总结易错点:1、两个多项式相乘,是把一个多项式的每一项分别与另一个多项式的每一项相乘,再把它们的积相加,要注意不要漏乘;2、进行乘法运算时,要注意确定积中各项的符号;3、两个多项式相乘,他们的积是和的形式,在没合并同类项之前,积的项数应是这两个多项式项数的积,注意检查.(五)变式训练 活动内容: ★1、计算:(1))2)(2n m n m -+( (2))3)(52-+n n ( ★★2、计算:)3)(5()5(1-2+--+x x x x )(★★★3、若,2))((22y nxy x y x y mx -+=-+ 求m ,n 的值.学生喜欢具有挑战性的题目,这样的设置有利于促进他们进行思考.实践证明,教师注重对学生思维能力的培养,在学生的最近发展区内提出较高要求,能够激发学生学习数学的兴趣.(六)总结串联教师引导学生回顾本节课的学习过程,自己总结: 1、本节课学习了哪些知识?2、领悟到哪些解决问题的方法?感触最深的是什么?3、对于本节课的学习还有什么困惑? (七)达标检测计算:(1)))((d cx b ax(2)2)2y x +( (八)课后作业: 1.习题1.82.拓展作业:解方程)4)(1()3(2+-=-+x x x x )(3.预习作业:两项式乘以两项式,结果可能是四项吗?可能是三项吗?可能是两项吗?请你举例说明 三、 教学反思:通过这三课时的学习,应让学生体会:当他们遇到新问题时,可以效仿之前用到的数学思想方法来解决,从而真正掌握数学学习方法,提高数学学习能力。
北师大版数学七年级下册1.4 整式的乘法(第3课时)同步课件

新课引入
图1是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分 别增加a, b,所得长方形(图2)的面积可以怎样表示?
例题讲解
例2.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b), 其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b) =a3-8b3-a3-3a2b+5a2b+15ab2 =-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
=x3-x2y+xy2+x2y-xy2+y3 = x3+y3.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式 (是同类项的要合并).
新知探究
(x + 2)(x + 3)= x2 +___5_x +___6_ (x – 2)(x + 3)= x2 +__1__x +_–__6_ (x + 2)(x – 3)= x2 +_–__1_x +_–__6_ (x – 2)(x – 3)= x2 +_–__5_x +__6__ 观察上面四个等式,你能发现什么规律?
6. 如图7,有正方形卡片A类、B类和长方形卡片C类各若干张, 如果要拼一个长为(a+3b),宽为(2a+b)的大长方形,那么需要 A类、B类和C类卡片的张数分别为( A ) A. 2,3,7 B. 3,7,2 C. 2,5,3 D. 2,5,7
14.1.4整式的乘法(3) 课件(共20张PPT)

课后作业
教材105页习题14.1第5题.
合作探究
你你能能通得过到计多
为了扩大街心花园的绿地面积,把一块原长am,宽算项pm说式的明乘长它以方们多形绿地,
加长了bm,加宽了qm. 你能用几种方法表示扩大后的绿项相地式等面的吗积方??法
Байду номын сангаас
吗?
(a b)(p q) = ap aq bp bq b
p
p
b
q
q
ap aq bp bq
2x2 4x 6 x2 2x 1 x2 2x 5;
实战演练
(2)(2x 3)( x 2) ( x 1)2 ;
解:原式 2 x 2 4 x 3x 6 ( x 2 12 )
2x2 7x 6 x2 1
x2 7 x 7.
( x 1)( x 1)
( x2 2x 1)
合作探究
多项式乘以多项式的法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项
式的每一项,再把所得的积相加. (a b)(p q) = ap aq bp bq
典例精析
例1 计算:(1)(3x+1)(x+2); (2)(x-8y)(x-y);
(3)(x+y)(x2-xy+y2). 解: (1) 原式 =3x·x+2·3x+1·x+1×2
计算时不能漏乘.
小试牛刀
1.计算:
(1)(2x+1)(x+3); =2x2+7x+3;
(2)(m+2n)(3n-m); =-m2+mn+6n2;
(3)(a-1)2;
=a2-2a+1;
1.4整式的乘法第3课时课件初中数学北师大版七年级下册

四、典型例题
例1 计算: (1)(3x+1)(x+2)
(2)(x-8y)(x-y)
解:(1)(3x+1)(x+2)
(2)(x-8y)(x-y)
=3x·x +3x×2+1×x+1×2 =x·x+x·(-y)+(-8y)·x+(-8y)·(-y)
=3x2+6x+x+2Βιβλιοθήκη =x2-xy-8xy+8y2
=3x2+7x+2
经过考古学家的估测,长方形古城的一些建筑之间的距离大致如图.若 城门的宽度忽略不计,你能表示出古城的面积吗?
q p
a
思考:能用几种方法表示 古城的面积?
b
三、概念剖析
方法1:我们可以直接计算出古城的长和宽,再长和宽相乘得出它面积.
(长和宽可任意选取)
q p a
b
古城的长和宽为: (a+b)和(p+q) 古城的面积是: (a+b)(p+q)
(2)通过计算结果,我们发现: (x+a)(x+b)=( x )2+( a+b )x+( ab )
x
a
x x2
ax
实际上该结果我们由右图也可以得到
b bx
ab
四、典型例题
例2.若多项式(x+m)与(x+1)乘积的结果中不含x的一次项,则m值为?
分析:利用多项式与多项式相乘的法则先求出结果,再进行判断.
q p
每部分面积分别是:
a
ap、aq、bp、bq
古城的面积是:
b
ap+aq+bp+bq
2020--2021学年北师大版 七年级数学下册1.4 整式的乘法(第3课时)课件

多项 式× 多项 式
多项式与多项式相乘,先用一个多项 运
算 式的每一项乘另一个多项式的每一项,
法 则
再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
实质上是转化为单项式×多项式的运算
注 意 不要漏乘;正确确定各符号;结果要最简
2.(2019•南京)计算(x+y)(x2﹣xy+y2) 解:(x+y)(x2﹣xy+y2) =x3-x2y+xy2+x2y-xy2+y3, =x3+y3.
基础巩固题
1.计算(x-1)(x-2)的结果为( D ) A.x2+3x-2 B.x2-3x-2 C.x2+3x+2
D.x2-3x+2
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a、b满足 ( C) A.a=b B.a=0 C.a=-b D.b=0
解:原式=a3-8b3-(a2-5ab)(a+3b) =a3-8b3-a3-3a2b+5a2b+15ab2 =-8b3+2a2b+15ab2.
当a=-1,b=1时,
原式=-8+2-15=-21.
变式训练
先化简,再求值
(x-y)(x-2y)- (2x-3y)(x+2y),其中
x=-2,y=
1 2
解:(x-y)(x-2y)- (2x-3y)(x+2y)
解:原式 2x2 4x 6 (x 1)( x 1)
七年级数学下册 1.4整式的乘法(第3课时)教案 (新版)北师大版

辽宁省辽阳市第九中学七年级数学下册 1.4整式的乘法(第3课时)教案 (新版)北师大版一、 学生起点分析:依据新课标制定教学难点:学生在这一章前面几节课中学习了幂的运算,通过前两课时的学习,学生已经掌握了单项式乘单项式、单项式乘多项式的法则,并能正确的进行相关的计算,为本课时单项式乘多项式的学习奠定了充足的知识基础.依据新课标制定教学重点:在前面的运算学习中,学生经历了一些探索活动,初步积累了一些经验,在上一课时探索单项式乘多项式的法则时,学生一方面体会了对同一面积的不同表达和乘法分配律的运用,另一方面也体会了转化思想在解决新问题中的重要作用,这都为本课时的学习积累了活动经验.二、教学任务分析:1.教学目标:在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算.2.知识目标:经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.3.能力目标:在解决问题的过程中了解数学的价值,发展“用数学”的信心.三、 教学设计分析:本节课共设计了七个环节:前置诊断,开辟道路——创设情境,自然引入——设问质疑,探究尝试——目标导向,应用新知——变式训练,巩固提高——总结串联,纳入系统——达标检测,评价矫正.第一环节:前置诊断,开辟道路活动内容:教师提出问题,引导学生复习上节课所学的单项式乘多项式1、如何进行单项式乘多项式的运算?你能举例说明吗?2、计算:(1))()3222n mn m mn -+⋅( (2))2()52(22b a b b a a a ----活动目的:单项式乘以多项式运算是多项式乘以多项式运算的基础,所以帮助学生回忆单项式乘多项式的运算非常重要.课前通过单项式乘多项式的热身活动,帮助学生唤起昨天课堂的记忆,重温探索法则的过程中所积累的活动经验。
在上一课时的学习及课后作业的巩固基础上,学生已经能够熟练应用法则进行计算,所以问题2的设置更突出了知识的综合.实际教学效果:大多数学生能够熟练的说出单项式乘多项式的运算法则,通过练习发现个别学生在处理问题2时出错,主要是第(2)小题中的符号处理出现错误.通过教师与学生共同订正错误,使学生的认识有了进一步的提高.第二环节:创设情境,自然引入活动内容:图1-1是一个长和宽分别为m ,n 的长方形纸片,如果它的长和宽分别增加a ,b ,所得长方形(图1-2)的面积可以怎样表示?学生独立思考后,全班交流,主要产生了四种解法: 方法一:长方形的长为(m+a ),宽为(n+b ),所以面积可以表示为))(b n a m ++(; 方法二:长方形可以看做是由四个小长方形拼成的,四个小长方形的面积分别为mn ,m b ,an ,ab ,所以长方形的面积可以表示为ab an mb mn +++;方法三:长方形可以看做是由上下两个长方形组成的,上面的长方形面积为b (m+a ),下面的长方形面积为n (m+a ),这样长方形的面积就可以表示为n (m+a )+ b (m+a ),根据上节课单项式乘多项式的法则,结果等于ba bm na nm +++方法四:长方形可以看做是由左右两个长方形组成的,左边的长方形面积为m (b+n ),右边的长方形面积为a (b+n ),这样长方形的面积就可以表示为m (b+n )+ a (b+n ),根据上节课单项式乘多项式的法则,结果等于an ab mn mb +++将四种方法的过程板书到黑板上,由于求的是同一个长方形的面积,于是我们得到:))(b n a m ++(=)()(a m b a m n +++=)()(n b a n b m +++=ab an mb mn +++n n 图1-1 图1-2教师引导学生观察这个等式,并启发性的将等式板书为以下形式:))(b n a m ++( =)()(a m b a m n +++或))(b n a m ++(=)()(n b a n b m +++ 或))(b n a m ++(=ab an mb mn +++ 式子的最左边是两个多项式相乘,最右边是相乘的结果,由此引出新课,多项式与多项式的乘法.活动目的:引导学生通过观察、实验、类比、归纳获得数学猜想. 在上一课时中,学生已经有了利用图形面积探究法则的经验,因此用不同方法计算同一图形面积猜想出多项式乘法法则并不困难,顺利引出新课.实际教学效果:由于学生有不同的知识基础和思维习惯,运用不同的方法得出长方形的面积,为进一步合作交流提供了实质性的内容. 实际教学表明,学生能够很快解决这个问题,四种方法在班级都能出现。
人教版14.1.4__整式的乘法_第3课时
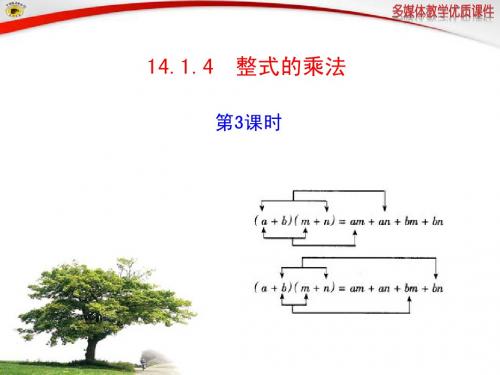
结论:
(a+b)( p+q)=ap+aq+bp+bq
多项式与多项式相乘的法则: 多项式与多项式相乘,先用一个多项式的每一项
乘另一个多项式的每一项,再把所得的积相加.
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
【例题】
【例1】计算 : (1)(3x+1)(x-2); 【解析】(1)(3x+1)(x-2) = (3x)•x+(3x)•(-2)+1•x+1×(-2) = 3x2-6x+x-2 =3x2-5x-2. 注意:1.不要漏乘 2.注意符号 3.结果化为最简形式 (2)(x-8y)(x-y). (2)(x-8y)(x-y) = x2-xy-8xy+8y2 = x2-9xy +8y2.
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
(x+p)(x+q)=x2+(p+q)x+pq
【例2】计算 (1)(x+y)2. (2) (x+y)(x 2y+y2).
(3)(x+y)(2x–y)(3x+2y).
【解析】(1)原式=(x+y)(x+y)
=x2+ xy+ xy+ y2 =x2+ 2xy+ y2. (2)原式=x3y+ xy2+x2y2+y3. (3)原式=(2x2-xy+2xy-y2)(3x+2y )
×
)
1.4整式乘法第三课时课件初中数学

b
n
m
图1-1
n
m
图1-2
a
探究尝试:
1、你能说出 (m a)(n b) n(m a) b(m a) 这一步运算的道理吗?
2、 结合这个算式
(m+a)(n+b)=mn+mb+an+ab
你能说说如何进行多项式与多项式相乘的运算?
(m+b)(n+a)= mn + ma + bn + bn
( x 1)( x 4)
3.预习作业: 两项式乘以两项式,结果可能是四项吗? 可能是三项吗?可能是两项吗?请你举 例说明
1.若 (mx y)(x y) 2 x nxy y ,
2 2
求m,n的值. 2.已知
( x m x n)(x 1)
2
2
的结果中不含 x 项和 x 项,求m,n 的值.
多项式与多项式相乘:
先用一个多项式的每一项 乘另一个多项式的每一项 再把所得的积相加。
在进行多项式乘法运算的过程中运用 了哪些数学思想方法?
运用了整体、转化和数形结合的数学思想。
应用新知:
例1 计算:
(1)
(1 x)(0.6 x)
(2 x y)( x y )
(2) (3)
(2m n)
=2kx2+8x-3kx-12
=2kx2-(3k-8)x-12
=ax2-x-12 所以a=2k,-1=-(3k-8) ∴ k=3, a=6.
多项式乘以多项式的 依据是什么? 如何进行多项式与多项式乘法运算?
运用多项式乘法法则,要有序地逐项相 乘,不要漏乘,并注意项的符号.
1.4整式的乘法(第3课时)教学课件北师大版中学数学七年级(下)

随堂训练
1.下列多项式相乘,结果为x2-4x-12的是( B )
A.(x-4)(x+3)
B.(x-6)(x+2)
C.(x-4)(x-3)
D.(x+6)(x-2)
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b
满足
(C )
A.a=b
B.a=0
C.a=-b
D.b=0
第 一章 整式的乘除
第一章 整式的乘除
1.4
整式的乘法
第3课时 多项式与多项式相乘
学习目标
1.理解并经历探索多项式乘多项式法则的过程, 熟练应用
多项式乘多项式的法则解决问题.(重点)
2.培养独立思考、主动探索的习惯和初步解决问
题的能力.
知识回顾
1.单项式与单项式相乘
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余
=-20.
课堂小结
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘另
一个多项式的每一项,再把所得的积相加.
( + )( + )= + + +
实质:转化为单项式乘多项式的运算
(2) (2 –3)( +4).
解:(1)( +2 )(5 +3 )
= ·5 +·3 +2·5 +2·3
= 5 +3 +10 +6
(2)(2 –3)( +4)
= 2 2+8 –3 –12
=2 2 +5 –12
14.1.4整式的乘法3教案

新课讲授创设情境,感知新知:1.问题:为了扩大绿地面积,要把街心花园的一块长a米,宽m米的长方形绿地增长b米,加宽n米,求扩地以后的面积是多少?2. 提问:用几种方法表示扩大后绿地的面积?不同的表示方法之间有什么关系?3.得出结果:方法一:这块花园现在长(a+b)米,宽(m+n)米,因而面积为(a+b)(m+n)米2.方法二:这块花园现在是由四小块组成,它们的面积分别为:am米2、an米2、bm米2、bn米2,故这块绿地的面积为(am+an+bm+bn)米2.(a+b)(m+n)和(am+an+bm+bn)表示同一块绿地的面积,所以有(a+b)(m+n)=am+an+bm+bn三、学生动手,推导结论:1.引导观察:等式的左边(a+b)(m+n)是两个多项式(a+b)与(m+n)相乘,把(m+n)看成一个整体,那么两个多项式(a+b)与(m+n)相乘的问题就转化为单项式与多项式相乘,这是一个我们已经解决的问题,请同学们试着做一做.2.过程分析:(a+b)(m+n)=a(m+n)+b(m+n)----单×多=am+an+bm+bn ----单×多3.得到结论:多项式与多项式相乘:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.巩固练习:1.先化简,再求值:(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6.2.化简求值:)32)(12()1)(1(3)3)(2(-+--+++-xxxxxx,其中x=54.学生小组合作完成本题。
学生自行总结。
北师大版七年级数学下册课件1.4整式的乘法(第三课时)

= mn+ma + bn+ba
(m+b)(n+a)=m(n+a) + b (n+a) =mn + ma + bn + ba
探究二
归纳:多项式与多项式相乘法则
(m+b)(n+a)=m(n+a) + b (n+a) =mn + ma + bn + ba
1.4 整式的乘法
第3课时
学习目标
1. 通过视察和动手操作用几何方法探究多项式与多项式的乘法运算 法则 .
2. 通过类比和转化用代数方法探究多项式与多项式的乘法运算法则. 3. 利用多项式与多项式的乘法运算法则进行整式的乘法运算.
自主学习
多项式: 几个单项式的和叫做多项式.
项: 每个单项式叫做多项式的项.
(5)(x+2y)(5a+3b) (6) (2x–3)(x+4)
(7)化简:4m(m n) (5m n)(m n)
活动探索
填空: (x 2)( x 3) x2 _5_ x _6_ (x 4)( x 1) x2 (-_3_) x (_-_4) (x 4)( x 2) x2 _2_ x (_-8_) (x 2)( x 3) x2 (_-5_) x _6_
解:原式 2x2 4x 3x 6 (x 1)(x 1)
2x2 7x 6 x2 2x 1
x2 9x 7 x2 5x 5
(x2 2x 1) x2 2x 1
学以致用
计算: (1)(1−x)(0.6−x) (3)(2x + y)(2x−y)
人教版数学八年级上册1.4整式的乘法(第3课时)课件

实质上是转化为单项式×多项式 的运算
不要漏乘;正确确定各符号;结 果要最简
(x-1)2在一般情况下不等于x2-12.
计算:
当堂检查
( 1 ) (x + 5)(x 7)
( 2 ) (x 7 y)(x + 5y)
( 3 ) (2m + 3n)(2m 3n)
3.计算求值: 当堂练习 (4x+3y)(4x-3y)+(2x+y)(3x-5y), 其中x=1,y=-2.
解:原式= 16x2 12xy +12xy 9 y2 + 6x2 10xy + 3xy 5y2
22x2 7xy 14 y2
当x=1,y=-2时, 原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56 =-20.
能力提升
(x + 2)(x + 3) x2 + __5 x + 6__; (x 4)(x +1) x2 + __(-3)x + _(-4_); (x + 4)(x 2) x2 + __2 x + _(-8_) ; (x 2)(x 3) x2 + _(_-5)x + _6 _ .
由于(a+b)(m+n)和(ma+mb+na+nb)表示相同的面积, 故有:
(a+b)(m+n)=ma+ mb+ na + nb
实际上,把(m+n)看成一个整体,有:
(a+b) (m+n) = (m+n)a+(m+n)b = —m—a+—mb—+—na—+n—b
1.4 整式的乘法(第3课时)

注意检查.
合作研学
若(mx+y) (x-y)=2x2+nxy-y2 ,求m,n的值.
检测评学
检测评学
检测评学
2.计算(备用): (1) (2x-1) (x+5)-(x-5)(x+3)
(2) (x-1) (x2+x+1)
检测评学
3.计算(备用): (1) (x+2) (y+3)-(x+1) (y-2)
(2) (-2m+n)2
检测评学
4.(备用):两项式乘以两项式,结果可能是四项吗?可能是 三项吗?可能是两项吗?请你举例说明.
目标导学
1.复习回顾 (1)如何进行单项式乘多项式的运算?你能举例说明 吗?
(2)计算:① (3mn)2·(m2+mn-n2) ② 2a2-a(2a-5b)-b(2a-b)
解:①原式=9m2n2·(m2+mn-n2) =9m2n2·m2+9m2n2·mn-9m2n2·n2 =9m4n2+9m3n3-9m2n4
②原式=2a2-(a·2a-a·5b)-(b·2a-b·b) =2a2-(2a2-5ab)-(2ab-b2) =2a2-2a2+5ab-2ab+b2 =3ab+b2
目标导学
目标导学
小明有四种表示方式:
⑴ (m+a) (n+b)
⑵ mn+mb+an+ab
⑶ n(m+a)+b(m+a) ⑷ m(b+n)+a(b+n)
你认为小明的想法对吗?从中你受到什么启发?
ห้องสมุดไป่ตู้
解:∵求的是同一个长方形的面积 ∴ (m+a) (n+b)=n(m+a)+b(m+a)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即时练习:
先化简,再求值:
2a b2 2a ba b 2a 2ba 2b ,其中
b
2
a
1
2
0
.
2
巩固练习
例 5 已知 a 1,求 a 4a 3 a 1a 3.
即时练习:
已知 a 22 ,求 aa 2 a 2a 2 .
素养考点 3 用多项式乘以多项式法则求字母的值
b
数学 a 七年级(下) 姓名: ____________ c
课堂检测
b
b a
m m
c
面积:(2m+2b+c)(2m+a)
课堂检测
解:(2m+2b+c)(2m+a) = 4m2+2ma+4bm+2ab+2cm+ca.
答:小东应在挂历画上裁下一块 (4m2+2ma+4bm +2ab+2cm+ca)平方厘米的长方形.
2x2 4x 6 ( x2 2x 1)
3x
2x2 4x 6 x2 2x 1 x2 2x 5;
课堂检测
(2)(2 x+3)( x+2) ( x 1)2 ;
解:原式 2x2 +4x+3x 6 (x2 12 )
2x2 +7x 6 x2 1
x2+7x 7.
(x 1)(x 1)
所以-2a+3b=0且-2b+3=0.
不含某一项,可得这一
故a 9 , b 3 .
42
项系数等于零,再列出 方程解答.
巩固练习
变式训练
(1+x)(2x2+ax+1)的结果中x2项的系数为-2,则a 的值为( C )
A.-2
B.1
C.-4
D.以上都不对
巩固练习
要点三:挖掘提升
例 6 已知 x a2 3x2 ax 6 中不含 x 的三次项,求 a 的值。
课堂检测
能力提升题
解方程:(1)(x-3)(x-2)+18=(x+9)(x+1);
(2)(3x+6)(3x-6)=9(x-2)(x+3).
解:(1)去括号,得x2-5x+6+18=x2+10x+9, 移项合并,得15x=15, 解得x=1; (2)去括号,得9x2-36=9x2+9x-54, 移项合并,得9x=18, 解得x=2 .
已知等式(x+a)(x+b)= x2+mx+28,其中a、b、m均为正
考 整数,你认为m可取哪些值?它与a、b的取值有关吗?请
考 你
你写出所有满足题意的m的值.
解:由题意可得a+b=m,ab=28.
因为a,b均为正整数,故可分以下情况讨论:
①a=1,b=28或a=28,b=1,此时m=29;
②a=2,b=14或a=14,b=2,此时m=16;
例3 已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,
求系数a、b的值. 解:(ax2+bx+1)(3x-2) =3ax3-2ax2+3bx2-2bx+3x-2,
方法总结:解决此类问 题首先要利用多项式乘 法法则计算出展开式,
由于积不含x2的项,也不含x的项, 合并同类项后,再根据
素养考点 2 用多项式乘以多项式法则进行化简求值 例2 先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a +3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b) =a3-8b3-a3-3a2b+5a2b+15ab2 =-8b3+2a2b+15ab2.
课堂检测
基础巩固题
1.计算(x-1)(x-2)的结果为( D ) A.x2+3x-2 B.x2-3x-2 C.x2+3x+2
D.x2-3x+2
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a、b满足 ( C) A.a=b B.a=0 C.a=-b D.b=0
3.已知ab=a+b+1,则(a﹣1)(b﹣1)=___2____.
③a=4,b=7或a=7,b=4,此时m=11.
综上所述,m的取值与a,b的取值有关,m的值 为29或16或11.
课堂检测
拓广探索题
小东找来一张挂历画包数学课 本.已知课本长a厘米,宽b厘 米,厚c厘米,小东想将课本封 面与封底的每一边都包进去m 厘米,问小东应在挂历画上裁 下一块多大面积的长方形?
当a=-1,b=1时,
原式=-8+2-15=-21.
巩固练习
变式训练
先化简,再求值
(x-y)(x-2y)- (2x-3y)(x+2y),其中
x=-2,y=
1 2
解:(x-y)(x-2y)- (2x-3y)(x+2y)
=x2-2xy-xy+2y2-(2x2+4xy-3xy-6y2)
=x2-2xy-xy+2y2-2x2-xy+6y2
= -x2-4xy+8y2
当x= -2,y=
1 2
时
原式= -6
巩固练习
例 3 已知 m2 m 2 0 ,求 mm 1 m 1m 2的值.
即时练习:
已知 a2 2a 2 ,求 3a 23a 2 2a4a 1的值.
巩固练习
例 4 先化简,再求值: 5x2x 1 2x 35x 1,其中 x 12
课堂检测
基础巩固题
4.计算m2-(m+1)(m-5)的结果正确的是( B )
A.-4m-5
B.4m+5
C.m2-4m+5
D.m2+4m-5
课堂检测
基础巩固题
5.判别下列解法是否正确,若错,请说出理由. (1) (2x 3)(x 2) (x 1)2; 解:原式 2x2 4x 6 (x 1)( x 1)
3.试一试,计算: 1 a bab 2a
2 2a 13a 5
需要注意的几个问题: 提 示 (1)不要漏乘;
(2)符号问题;
(3)最后结果应化成最简形式.
巩固练习
1.例 1 多项式乘以多项式:
1 m 2nm 2n 2 2n 5n 3
3 x 2y2
4 ax bcx d
巩固练习
即时练习:
1.4 整式的乘法(第3课时)
导入新知
为了把校园建设成为花园式的学校,经研究决定将原有的长为a 米,宽为b米的足球场向宿舍楼方向加长m米,向厕所方向加宽n米, 扩建成为美化校园绿草地.你是学校的小主人,你能帮助学校计算
b
n
知识点 1 多项式乘多项式的法则
如图1是一个长和宽分别为m,n的长方形纸片,如 果它的长和宽分别增加 a,b,所得长方形(图2)的面 积可以怎样表示?
(x2 2x 1)
课堂检测
基础巩固题
6.计算:(1)(x−3y)(x+7y); (2)(2x + 5y)(3x−2y).
解: (1) (x−3y)(x+7y), =x2 + 7xy −3yx − 21y2
= x2 +4xy-21y2;
(2) (2x +5 y)(3x−2y) = 2x•3x −2x• 2y +5 y• 3x − 5y•2y = 6x2 −4xy + 15xy −10y2 = 6x2 +11xy−10y2.
即时练习:
已知 x3 mx n x2 3x 1 中不含 x 的三次项与二次项,求 m,n 的值。
连接中考
1.(2019•台湾)计算(2x-3)(3x+4)的结果,与下列哪一个 式子相同?( D ) A.-7x+4 B.-7x-12 C.6x2-12 D.6x2-x-12
2.(2019•南京)计算(x+y)(x2﹣xy+y2) 解:(x+y)(x2﹣xy+y2) =x3-x2y+xy2+x2y-xy2+y3, =x3+y3.
b
n
n
m
m
a
图1
图2
多项式乘以多项式的运算法则 多项式与多项式相乘,先用一个多项式的每一 项乘另一个多项式的每一项,再把所得的积相加.
2
1
1
2
3
4
(a+b)(m+n)=am+an+bm+bn
34
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
素养考点 1 多项式乘法的法则的运用
1 x ya 2b
3 2x 32x 3 5 2m 13m 2
2 2a 3 3 b 5
2
4 x y2 6 2x 32
巩固练习
例 2 混合运算:
1 x 22 x 1x 3 2 3a 12a 3 6a 5a 4 3 5x x 23x 1 2x 1x 5
4 2x 11 2x 4x2 x3x 13x 1
课堂检测
运
算
法
多项
则
式×
多项
式
注 意
多项式与多项式相乘,先用一个多项 式的每一项乘另一个多项式的每一项, 再把所得的积相加 (a+b)(m+n)=am+an+bm+bn 实质上是转化为单项式×多项式的运算
不要漏乘;正确确定各符号;结果要最简
拓展思考:计算 (1)(x+2)(x+3)=_x_2_+_5_x_+_6___; (2)(x-4)(x+1)=__x_2-_3_x_-_4___; (3)(y+4)(y-2)=__y_2+_2_y_-_8___; (4)(y-5)(y-3)=__y_2_-8_y_+_1_5__.
