利用凯特摆测定重力加速度g值(精)
重力加速度

实 验 报 告 评分13系 07级 姓名龙林爽 日期2008-12-5 No.PB07013075实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验内容: 一、仪器调节调节四个摆锤的位置,并随时倒转摆锤测量各自的周期,当120.1T T ms -<时,可认为两摆动周期近似相等。
二、测量摆动周期12T T 和1、测量凯特摆正、倒摆动10个周期的时间,记录数据如下:1117.306217.3059+17.305817.305717.30595101.73059T T s+++=⨯=误差分析10.000187083s0.000083666s T A A u σσ==∴===类不确定度0.000100.00010.00010.000033333B B B s ss u s C ∆=∆=∆==∆∴===人仪B类不确定度0.950.0001673U s===合成不确定度2217.306017.3063+17.305917.306117.30635101.730612T T s +++=⨯=误差分析10.000178885s0.0000799998s T A A u σσ==∴===类不确定度0.000100.00010.00010.000033333B B B s ss u s C ∆=∆=∆==∆∴===人仪B类不确定度0.950.0001603U s合成不确定度2、测量两刀口间的距离l 和重心与1T 时刀口的距离1h74.153330.74153333l cm m ===误差分析0.00025170.000145319l A A m u mσ==∴===类不确定度0.10.010.1005cm 0.0010050.0010050.033503B B B cm cmm u m C ∆=∆=∆===∆∴===仪估B类不确定度0.950.033501U m合成不确定度43.2143.2543.2343.230.43233h cm m ++===误差分析0.00020.00011547l A A mu mσ==∴===类不确定度0.10.010.1005cm 0.0010050.0010050.033503B B B cm cmm u m C ∆=∆=∆===∆∴===仪估B类不确定度0.950.033508U m==合成不确定度3、计算g 值并计算不确定度由()22222121214222T T T T g l h l π+-=+-得:()()222221212122222121212422242229.7752925121g T T T T l h l g T T T T l h l g m s ππ=+-+-=+-+-= 误差分析2221242g T T lπ=+ 两边取对数得:()2221222212ln ln 4ln2ln ln 4ln ln 2T T g l g T T lππ+=-=-++两边求导得:()()22212221222122222121222221212ln ln 4ln ln 222g T T ld T T dg dl g T T lT T dg dl dT dT g T T T T l π=-+++=++⎛⎫⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭不确定度传递公式为:20.0044571m s g g u u ==()29.775290.0044571(0.95)g m s p ∴=±=思考题:1、凯特摆测量重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:此实验比以往测量重力加速度的实验更加精确,实验设计比较巧妙。
用凯特摆测量重力加速度 (7)

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mgh I T π2=(1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2 (2)代入式(1)得:mgh mh I T G 22+=π (3)对比单摆周期的公式gl T π2= 可得 mhmh I l G 2+=(4),称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
左图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π (5) 22222mgh mh I T G +=π (6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l即为等效摆长。
由式(5)和(6)消去I G ,可得:()22222121214222T T T T a b g l h l π+-=+=+- (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l ,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l 的值,粗略估算T 值。
初中物理凯特摆测量重力加速度

凯特摆测量重力加速度1818年凯特提出的倒摆,经雷普索里德作了改进后,成为当时测量重力加速度g 最精确的方法。
波斯坦大地测量研究所曾用五个凯特摆用了8年时间(1896-1904),测得当地的重力加速度g=(981.274±0.003)cm/s 2,许多地区的g 值都曾以此为根据。
凯特摆测量重力加速度的方法不仅在科学史上有着重要的价值,而且在实验设计上亦有值得学习的技巧。
教学目的:1. 学习凯特摆的实验设计思想和技巧。
2. 掌握一种比较精确的测量重力加速度的方法。
教学重点及难点:1. 复摆的原理2. 凯特摆的结构及原理3. 利用凯特摆测量重力加速度的方法教学内容:一.实验原理图一是复摆的示意图,设一质量为m 的刚体,其重心G 到转轴O的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为mghI T π2= (1) 式中g 为当地的重力加速度。
设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有2mh I I G += (2)代入式(1)得 mgh mh I T G 22+=π (3) 对比单摆周期的公式gl T π2=,可得mh mh I l G 2+= (4)l 称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
复摆的周期我们能测得非常精确,但利用mhmh I l G 2+=来确定l 是很困难的。
因为重心G 的位置不易测定,因而重心G 到悬点O 的距离h 也是难以精确测定的。
同时由于复摆不可能做成理想的、规则的形状,其密度也难绝对均匀,想精确计算I G 也是不可能的。
我们利用复摆上两点的共轭性可以精确求得l 。
在复摆重心G 的两旁,总可找到两点O 和O ’,使得该摆以O 悬点的摆动周期T 1与以O ’为悬点的摆动周期T 2相同,那么可以证明'OO 就是我们要求的等效摆长l 。
图一 复摆示意图 图二 凯特摆摆杆示意图 图二是凯特摆摆杆的示意图,对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
用凯特摆测量重力加速度

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验仪器:凯特摆、光电探头、米尺和VAFN多用数字测试仪。
实验原理:1,复摆。
质量为m的刚体,其重心G到转轴O的距离为h,绕O轴的转动惯量为I。
当摆幅很小时,刚体绕O转动的周期为(1)设复摆绕通过重心G的转动惯量为,当G轴与O轴平行时有:(2)代入(1)得:(3)对比单摆周期公式,可得:(4)l称为复摆的等效摆长,因此只要测出周期和等效摆长便可球的重力加速度。
2,凯特摆。
如左图对凯特摆而言,两刀口间距就是该摆的等效摆长l。
在实验种当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可以使正、倒悬挂时的摆动周期和基本相等,即。
由公式(3):(5)(6)当时,即为等效摆长。
由公式(5)和(6)可得:(7)此式中,l、T1、T2都是可以精确测定的量,而h1则不易测准。
由此可知,a项可以精确求得,而b项则不易精确求得。
但当T1=T2以及|2h1-l| 的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
实验步骤:1,仪器调节调节摆锤A、B、C、D到合适位置,是正,倒悬的摆动周期相等。
2,测量摆动周期测量凯特摆正,倒悬摆动10个周期的时间,等效摆长和转轴O到G的距离,记录如下:的A类不确定度:的B类不确定度:所以的展伸不确定度:同理,的展伸不确定度:同上,同上,将具体的数值代入一步写清楚3,计算重力加速度及其不确定度根据公式(7):所以:g=以下求的合成不确定度。
已知:(8)对(8)式等号两边取对数:等号两边求导并合并同类项:所以的合成不确定度公式为:(9)将上述数据代入(9):所以:注意单位由于,很小可以忽略,所以只合成g和的不确定度。
类似(8)到(9)的过程:所以:最后可得:不确定度取一到两位有效数字思考题:1,凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度设计特点是:减少一些量的测量,提高实验精度。
用凯特摆测量重力加速度实验报告 (7)

用凯特摆测量重力加速度化学物理系04级龚晓李PB042060022005-12-5实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复摆绕通过重心G的转轴的转动惯量为I G 。
当G轴与O轴平行时,有I=I G+mh2∴∴复摆的等效摆长l=( I G+mh2 )/mh2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg 。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg 。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,u A =σ/=0.01764cm,∴ΔA =t P·u A =1.32*0.01764=0.02328cmu B=ΔB /C=0.1/3=0.03333cm∴u L ==0.04066cmT e ==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,u A =σ/=1.129*10¯⁴s∴ΔA =t P·u A =1.14*0.0001129=1.287*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T1 ==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,u A =σ/=0.6570*10¯⁴s∴ΔA =t P·u A =1.14*0.00006570=0.7489*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T2 ==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]}=9.813m/s²∴u g0.68 =g·{l¯²* u L²+[2 T₁/(T₁²+T₂²)]²·u T1²+[2 T₂/(T₁²+T₂²)]²·u T2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴u g0.95 =2* u g0.68 =0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
用凯特摆测量重力加速度 (4)
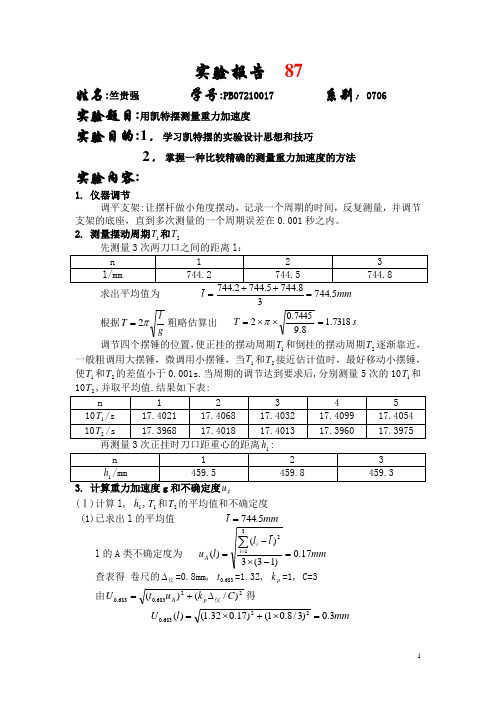
实验报告 87姓名:竺贵强 学号:PB07210017 系别:0706 实验题目:用凯特摆测量重力加速度实验目的:1.学习凯特摆的实验设计思想和技巧2.掌握一种比较精确的测量重力加速度的方法实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动,记录一个周期的时间,反复测量,并调节支架的底座,直到多次测量的一个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=⨯⨯=π 调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,一般粗调用大摆锤,微调用小摆锤,当1T 和2T 接近估计值时,最好移动小摆锤,使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=⨯+⨯=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=⨯+⨯=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5)()(512111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=⨯=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(512222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=⨯=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=⨯+=下面求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-⨯-= (3)比较a 和b 的大小,%15.0%100=⨯ab ,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =⨯= 所以 20.004)m /s 9.708(±=g P=0.683误差分析:1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同5. 在实验过程中,可能会形成不易察觉的锥面摆6. 从数据果看出,测得的十个周期数据并不理想,在调节时,两个周期分别为1.74005和1.74003,但在测量十个周期时周期的偏差比较大,可能是由于等待稳定的时间选的不好,导致周期有偏差改进方法:先测量一个周期,当稳定后,再迅速调到十个周期的档测量(这样能保证摆动已经稳定)。
凯特摆测量重力加速度

凯特摆测量重力加速度1818年凯特提出的倒摆,经雷普索里德作了改进后,成为当时测量重力加速度g 最精确的方法。
波斯坦大地测量研究所曾用五个凯特摆用了8年时间(1896-1904),测得当地的重力加速度g=(981.274±0.003)cm/s 2,许多地区的g 值都曾以此为根据。
凯特摆测量重力加速度的方法不仅在科学史上有着重要的价值,而且在实验设计上亦有值得学习的技巧。
教学目的:1. 学习凯特摆的实验设计思想和技巧。
2. 掌握一种比较精确的测量重力加速度的方法。
教学重点及难点:1. 复摆的原理2. 凯特摆的结构及原理3. 利用凯特摆测量重力加速度的方法教学内容:一.实验原理图一是复摆的示意图,设一质量为m 的刚体,其重心G 到转轴O的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为mghI T π2= (1)式中g 为当地的重力加速度。
设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有2mhI I G += (2)代入式(1)得mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2=,可得mhl G =(4)l 称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
复摆的周期我们能测得非常精确,但利用mhmh I l G 2+=来确定l 是很困难的。
因为重心G 的位置不易测定,因而重心G 到悬点O 的距离h 也是难以精确测定的。
同时由于复摆不可能做成理想的、规则的形状,其密度也难绝对均匀,想精确计算I G 也是不可能的。
我们利用复摆上两点的共轭性可以精确求得l 。
在复摆重心G 的两旁,总可找到两点O 和O ’,使得该摆以O 悬点的摆动周期T 1与以O ’为悬点的摆动周期T 2相同,那么可以证明'OO 就是我们要求的等效摆长l 。
图一 复摆示意图 图二 凯特摆摆杆示意图图二是凯特摆摆杆的示意图,对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
凯特摆实验报告

实验目的:本实验的目的是学习凯特摆的设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
主要实验仪器设备:凯特摆,光电探测器,用数字测试仪。
实验原理:图1复摆示意图图1是复摆示意图,设一质量为m的刚体,其重心G到转轴0的距离为h,绕0轴的转动惯量为I,当摆幅很小时,刚体绕0轴摆动的周期T为:丸II1—(L)式中g为当地的重力加速度.设复摆绕通过重心G的轴的转动惯量为1G,当G轴与0轴平行时,有I=I G+mh⑵代入式(1)得:对比单摆周期的公式称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长I。
在实验中当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T i和T2基本相等。
由公式(3)可得丿G ■+(5)為-21初直妇潜、其中T i和h i为摆绕0轴的摆动周期和O轴到重心G的距离。
当T i〜T2时,h i+h2=l即为等效摆长。
由式(5)和(6)消去I G,可得:I 4,曽十好T^-T^ t I——= ---- + ------ - =宀+0 』、g 21盘绚-。
(?)此式中,l、T i、T2都是可以精确测定的量,而h i则不易测准。
由此可知,a 项可以精确求得,而b项则不易精确求得。
但当T i=T2以及|2h i-l |的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
实验内容:i •正确调节仪器,测量凯特摆的等效摆长l,并利用估算摆动周期T值,以作为调节T i: T2的参考。
2•调节四个摆锤的位置,使T i与T2逐渐靠近,当| T i-T2|三时,测量T i和T2的值。
3•根据上述测量值计算重力加速度g及不确定度目数据记录与处理: 分析讨论:。
用凯特摆测量重力加速度实验报告

用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复。
摆绕通过重心G的转轴的转动惯量为IG当G轴与O轴平行时,有I=I+mh2G∴+mh2 )/mh∴复摆的等效摆长l=( IG2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,uA=σ/=0.01764cm,∴ΔA =tP·uA=1.32*0.01764=0.02328cmu B=ΔB/C=0.1/3=0.03333cm∴uL==0.04066cmTe==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,uA=σ/=1.129*10¯⁴s∴ΔA =tP·uA=1.14*0.0001129=1.287*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT1==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,uA=σ/=0.6570*10¯⁴s∴ΔA =tP·uA=1.14*0.00006570=0.7489*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT2==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]} =9.813m/s²∴ug0.68 =g·{l¯²* uL²+[2 T₁/(T₁²+T₂²)]²·uT1²+[2 T₂/(T₁²+T₂²)]²·uT2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴ug0.95 =2* ug0.68=0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
凯特摆实验报告

实验目的:本实验的目的是学习凯特摆的设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
主要实验仪器设备:凯特摆,光电探测器,用数字测试仪。
实验原理:图1是复摆示意图,设一质量为m的刚体,其重心G到转轴O的距离为h,绕O轴的转动惯量为I,当摆幅很小时,刚体绕O轴摆动的周期T为:式中g为当地的重力加速度.,当G轴与O轴平行时,有设复摆绕通过重心G的轴的转动惯量为IG+mh2(2)I=IG代入式(1)得:对比单摆周期的公式可得称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l。
在实验中当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。
由公式(3)可得其中T1和h1为摆绕O轴的摆动周期和O轴到重心G的距离。
当T1≈T2时,h 1+h2=l即为等效摆长。
由式(5)和(6)消去IG,可得:此式中,l、T1、T2都是可以精确测定的量,而h1则不易测准。
由此可知,a项可以精确求得,而b项则不易精确求得。
但当T1=T2以及|2h1-l| 的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
实验内容:1.正确调节仪器,测量凯特摆的等效摆长l,并利用,粗略估算摆动周期T值,以作为调节T1:T2的参考。
2.调节四个摆锤的位置,使T1与T2逐渐靠近,当| T1-T2|≦时,测量T1和T2的值。
3.根据上述测量值计算重力加速度g及不确定度。
数据记录与处理:分析讨论:。
计算机仿真实验用凯特摆测重力加速度
实验1 计算机仿真实验 用凯特摆测重力加速度一、 实验目的1. 学习凯特摆的实验设计思想和技巧。
2. 掌握一种比较精确的测量重力加速度的方法。
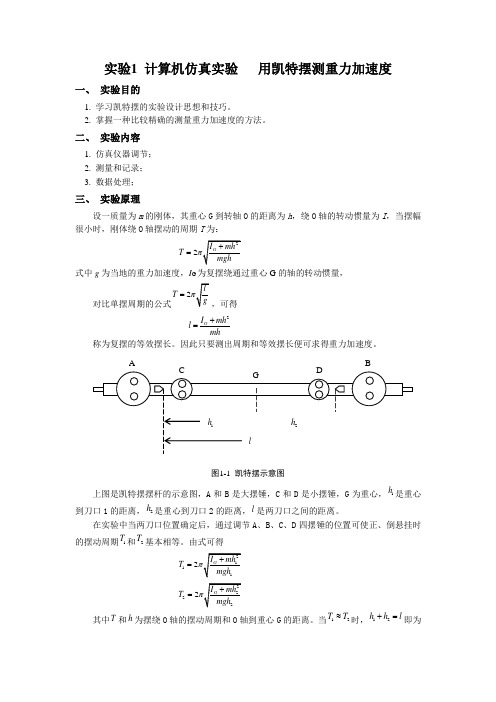
二、 实验内容1. 仿真仪器调节;2. 测量和记录;3. 数据处理;三、 实验原理设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:2T =式中g 为当地的重力加速度,I G 为复摆绕通过重心G 的轴的转动惯量,对比单摆周期的公式2T =,可得2G I mh l mh +=称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
图1-1 凯特摆示意图上图是凯特摆摆杆的示意图,A 和B 是大摆锤,C 和D 是小摆锤,G 为重心,1h 是重心到刀口1的距离,2h 是重心到刀口2的距离,l 是两刀口之间的距离。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期1T 和2T 基本相等。
由式可得12T =22T =其中T 和h 为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当12T T ≈时,12h h l +=即为A B等效摆长。
由上面二式消去G I ,可得:()22222121214222T T T T a b g l h l π+-=+=+-此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,式中第一项a可以精确求得,而第二项b 则不易精确求得。
但当12T T ≈以及12h l-的值较大时,b 项的值相对项是非常小a 的,b 这样项的不精确对测量结果产生的影响就微乎其微了。
四、 实验仪器本实验为仿真实验,在仿真大学物理实验软件平台上进行。
实验中用到的主要仪器有:凯特摆、多用数字测试仪、光电检测探头。
五、 实验数据及处理1. 测量数据:72.620.05cml =± ()120.030.05cmh =± 2. 平均值:()22222121214222T T T T a b g l h l π+-=+=+-224.02410s a -=⨯ 522.910s cm b -=-⨯2981.8cm g =3. 不确定度()1212T T T =+()u T =()222222*********T T T T T g l h l lπ+-=+≈-()()0.7%u g u g gτ==()()2981.80.07%0.7cm s u g g u g τ==⨯=g 4. 实验结果 ()2981.80.7cm g =±六、 实验讨论利用单摆、复摆也能测量重力加速度,但凯特摆设计精妙,利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响,提高了测量重力加速度的精度。
用凯特摆测量重力加速度 (14)
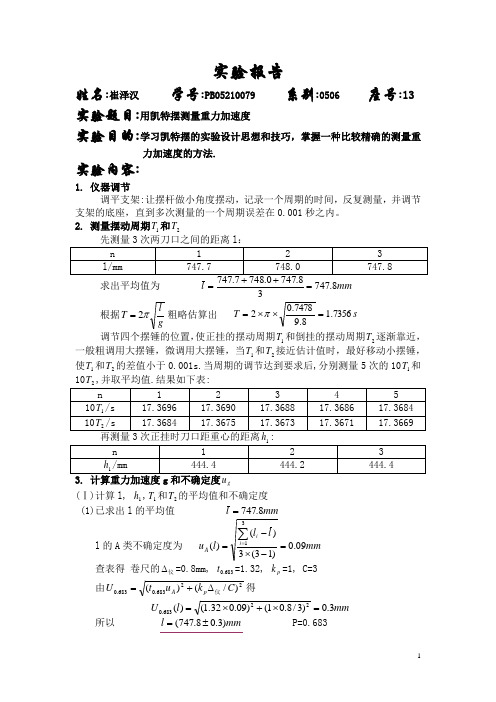
实验报告姓名:崔泽汉 学号:PB05210079 系别:0506 座号:13 实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法.实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动,记录一个周期的时间,反复测量,并调节支架的底座,直到多次测量的一个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 8.7473== 根据gl T π2=粗略估算出 s T 7356.18.97478.02=⨯⨯=π 调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,一般粗调用大摆锤,微调用大摆锤,当1T 和2T 接近估计值时,最好移动小摆锤,使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度(1)已求出l 的平均值 mm l 8.747=l 的A 类不确定度为 mm l l l u i i A 09.0)13(3)()(31=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()09.032.1()(22683.0=⨯+⨯= 所以 mm l )3.08.747(±= P=0.683(2)求出1h 的平均值 mm h 3.44434.4442.4444.4441=++=1h 的A 类不确定度为 mm h h h u i i A 07.0)13(3)()(31111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()07.032.1()(221683.0=⨯+⨯=所以 mm h )3.03.444(1±= P=0.683(3)求出1T 的平均值 s T T i 73689.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00002.0)15(5)()(51111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00002.000002.014.1)(1683.0=⨯=所以 s T )00002.073689.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73674.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00003.0)15(5)()(51222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00003.000003.014.1)(2683.0=⨯=所以 s T )00003.073674.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220339.47478.0273674.173689.1s m a -=⨯+=下面求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl ldT T T T dT T T Tda a 1221222212122211-+++=系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07478.01()00003.073674.173689.173674.12()00002.073674.173689.173689.12(0339.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0016m s =所以 2-10.0016)m 0339.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220018.0)7478.04443.02(273674.173689.1s m b -=-⨯-= (3)比较a 和b 的大小,%04.0%100=⨯ab,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.787m /s 0339.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00016.00339.4787.9)(s m g U =⨯= 所以 20.004)m /s 9.787(±=g P=0.683误差分析:1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同.思考题:1.凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?该实验在设计中避免了一些不易直接或精确测量的量的测量,并在计算过程中利用数学技巧把这些量消去.避免了重心到悬点距离h和复摆转动惯量I的测量.G降低了周期T的测量精度.I;利用复摆的两点共轭性可以精确求得等效摆长l,而不必去测量h和G利用数字测试仪精确测10T,可精确求得周期T.2.结合误差计算,你认为影响凯特摆测g精度的主要因素是什么?将所得到的实验结果与当地的重力加速度的公认值相比较,你能得到什么结论?若有偏差是分析之。
凯特摆测重力加速度的讲义

锤的位置:如本图,小塑料锤向远端移动了 1cm,两个周期值更接近了。所以,进一步远离, 可望它们会更加接近。 + +
+ ×
×
实验内容 参阅课本<<大学物理实验>>第二册 P8,实验 1.1.2 必做要求:当凯特摆调好后 1.测量凯特摆正,倒摆动 10 个周期各 5 次,取平均值 , 2.等效摆长及 h1 各测 3 次 ,求平均值 3.计算 g 值;计算第一项的不确定度 (第二项对结果影响很小,忽略 ). 选作 :研究摆的角幅度(即摆杆的偏转角) 的大小,对实验有无影响?能否进行理论修正 . 增选 :单摆,凯特摆,复摆等都可以测量重力加速度,试通过实验分析他们之间的共同点和不同点.
(7)
此式中,l、T1、T2 都是可以精确测定的量,而 h1 则不易测准。由此可知,a 项可以精确求得, 而 b 项则不易精确求得。但当 T1=T2 以及 |2h1-l| 的值较大时,b 项的值相对 a 项是非常小的,这样 b 项的不精确对测量结果产生的影响就微乎其微了。
学习重点和难点
� � � 学习一种比较精确的测量重力加速度的方法。 学习凯特摆的实验设计思想和技巧。 选定两刀口间的距离,通过调节 A、B、C、D 四摆锤的位置,使得该摆以两个刀口为悬点的摆 动周期基本相心 G 到转轴 O 的距离为 h,绕 O 轴的转动惯量为 I ,当摆幅很小 时,刚体绕 O 轴摆动的周期 T 为:
T = 2π
I mgh
(1)
式中 g 为当地的重力加速度. 设复摆绕通过重心 G 的轴的转动惯量为 IG,当 G 轴与 O 轴平行时,有
I=IG+mh2
T2 基本相等。由公式(3)可得
T1 = 2π
I G + mh12 mgh1
用凯特摆测量重力加速度实验讲义

用凯特摆测量重力加速度实验简介1818年Kater 设计出一种物理摆,他巧妙地利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响,提高了测量重力加速度的精度。
19世纪60年代雷普索里德对此作了改进,成为当时测重力加速度的最精确方法。
波斯坦大地测量所曾同时以五个Kater 摆花了八年时间(1896-1904)测得当地重力加速度的值G = ( 981.274 ± 0.003 ) cm / s 2 。
凯特摆测量重力加速度的方法不仅在科学史上有重要价值,而且在实验设计思想上亦有值得学习的地方。
实验原理设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:2T = 式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2(2)代入式(1)得:2T π=对比单摆周期的公式2T π= 可得2 (4)G I mh l mh+=l 称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
图一是凯特摆摆杆的示意图上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l。
在实验中当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。
由公式(3)可得12Tπ=22T π=其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得:()22222121214 (7)222T T T T a b g h l π+-=+=+- 此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
用凯特摆测量重力加速度(附有详细过程,图片及数据)
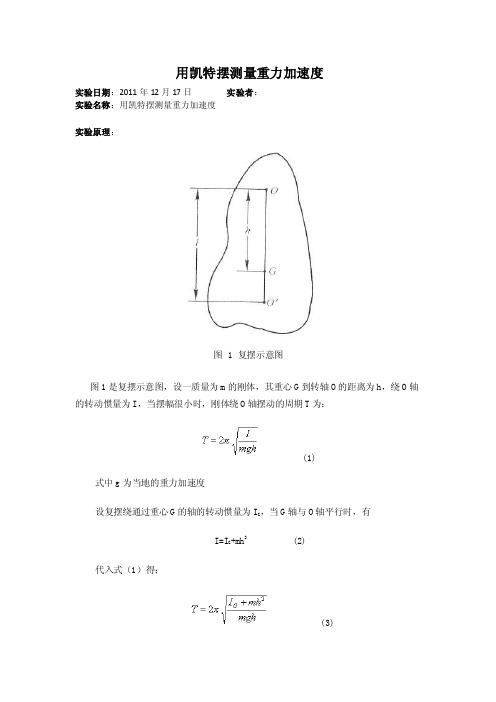
用凯特摆测量重力加速度实验日期:2011年12月17日实验者:实验名称:用凯特摆测量重力加速度实验原理:图1复摆示意图图1是复摆示意图,设一质量为m的刚体,其重心G到转轴O的距离为h,绕O轴的转动惯量为I,当摆幅很小时,刚体绕O轴摆动的周期T为:(1)式中g为当地的重力加速度设复摆绕通过重心G的轴的转动惯量为I G,当G轴与O轴平行时,有I=I G+mh2 (2)代入式(1)得:(3)对比单摆周期的公式,可得(4)称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l。
在实验中当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。
由公式(3)可得(5)(6)其中T1和h1为摆绕O轴的摆动周期和O轴到重心G的距离。
当T1≈T2时,h1+h2=l 即为等效摆长。
由式(5)和(6)消去I G,可得:(7)此式中,l、T1、T2都是可以精确测定的量,而h1则不易测准。
由此可知,a项可以精确求得,而b项则不易精确求得。
但当T1=T2以及 |2h1-l| 的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
一、实验目的:1.学习一种比较精确的测量重力加速度的方法。
2. 学习凯特摆的实验设计思想和技巧。
3. 选定两刀口间的距离,通过调节A、B、C、D四摆锤的位置,使得该摆以两个刀口为悬点的摆动周期基本相等。
二、实验所用仪器及使用方法实验仪器图1:凯特摆测量重力加速度实验仪器包括凯特摆、光电探头和多用数字测试仪。
图2:凯特摆凯特摆的两端共大小4个摆锤,调节摆锤的位置可以改变凯特摆的重心,两端相同的位置各有一个固定刀口。
实验之前需要先调节凯特摆的重心位置,重心调节完成的标志是:使用任何一个刀口时,凯特摆的摆动周期相同。
图3:凯特摆的大摆锤图4:凯特摆的小摆锤图5:固定刀口和V形刀承可将摆杆悬挂到支架上,使摆杆能在铅垂面内自由摆动。
凯特摆测重力加速度的讲义1

用凯特摆测量重力加速度1818年Kater 设计出一种物理摆,他巧妙地利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响,提高了测量重力加速度的精度。
19世纪60年代雷普索里德对此作了改进,成为当时测重力加速度的最精确方法。
波斯坦大地测量所曾同时以五个Kater 摆花了八年时间(1896-1904)测得当地重力加速度的值g= ( 981.274 ± 0.003 ) cm / s 2 。
凯特摆测量重力加速度的方法不仅在科学史上有重要价值,而且在实验设计思想上亦有值得学习的地方。
实验原理设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mghIT π2= (1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2(2)代入式(1)得:mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2= 可得mhmh I l G 2+=(4)称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π(5)22222mgh mh I T G +=π(6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得:()l h T T l T T g --++=12221222122224π (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
複擺
5.移動滑體,改變重心位置,重覆步驟1.、 2.、3.、4.,求g值。 B.曲線法 1.量取O1O2距離L。 2.以O1為懸點,利用測量法之步驟2.並將滑體位置定在10公分, 測出週期T1, 重複三次,逐次移動滑體10公分再測量週期T1 , 至 位置80公分為止。 3.再以O2為懸點,仿步驟2.來量測週期T2。 4.以滑體位置為橫軸,週期T為縱軸,畫出T1 、 T2的曲線並找出 交點所對應的時間T0,帶入式(6) ,求g值。
複擺
一、目的 利用凱特擺測定重力加速度g值。 二.原理 (A)測量法:固定滑體和黑色圓形重物的位置, 找出質心並利用複擺求得重力加速度g值。 凱特(Kater)擺是兩端不對稱的複擺,做小角 度擺動時,運動方程式為τ = Iα (1)
(τ是力矩,I 是轉動慣量,α是角加速度,θ為擺角)
複擺
圖一 複擺結構裝置與示意圖
定值,即使不同交點,T1=T2=T0=T'1= T'2仍存在】
複擺
三、儀器與裝置 儀器:複擺支座、複擺刀口、複擺、水平儀、 平衡支架、光時閘、光電計時器 四、步驟
A.測量法 1.用平衡支架找出複擺重心位置G,量得O1G、O2G距離h1、h2。 2.先以O1為懸點,使其自由擺動,但擺幅不得超過5度,記錄擺 動10次的平均時間,即得擺動週期T1,重覆四次,取平均值。 3.以O2為懸點,重覆步驟2.,求得T2之平均值。 4.將T1、T2、h1、h2帶入式(5),即可求得g值。
複擺
以O1為懸點,轉動θ角時,複擺所受力矩大小為τ =-M g h1sinθ~-M g h1θ (2)其解 為 (A、δ為常數,由初始條件決定, I為複擺
對懸點O1的轉動慣量,且I=Icm+Mh12=M(R2+h12)【Icm為複擺 以質心G點為轉軸的轉動慣量,假設Icm=MR2,R未知且與質量 分佈有關】 )
擺動週期為 同理,若以O2為懸點,則此複擺之週期為
(3) (4)
複擺
由式(3)、式(4)消去R,則得
(5) 由式(5)知,若分別測此複擺懸掛O1 、 O2之 週期T1、T2及兩懸掛點至重心G之距離h1、h2色圓形重物的位置,移動滑 體藉此求得重力加速度g值(不須找出質心!) 此法是在複擺上選定幾個位置,移動滑體至該 處並以O1(O2)懸點,量出週期T1 ( T2 ),將 不同位置的T1、T2繪製成曲線去觀察相交的狀況
【備註:滑體位置的改變只代表質心位置(h1,h2)的變動,由 於未測量質心,因此並不知道(h1,h2)的正確值】
複擺
當曲線有交點則T1=T2=T0,h1+h2=L,R為某定 值!由式(3)、(4)且對本複擺而言, h1 ≠ h2, 可得R2=h1h2 。若交點超過一個,則代表有不同 的R(R´ )及(h1,h2)【(h1´ ,h2´ )】,此時 公式(5)會簡化成, (6) 可由T0的平均值求得重力加速度g值。【備註:g是
複擺
五、注意事項 1.凱特擺須置於複擺刀口的凹槽內,並確實扣 上安全鎖,避免掉落傷人。 2.由於θ大小會影響實驗的精確度,請注意每 次振盪的振幅要保持固定。 3.由於複擺上的黑色圓形重物質量極重,稍一 移動即影響質心位置,甚至導致找不出T=T的 情況,因此未經助教允許,嚴禁移動其位置。
複擺
六、參考資料 1.Michele Rossi, Lorenzo Zaninetti:“The cubic period-distance relation for the Kater reversible pendulum”, Central European Journal of Physics, Vol.3(4), (2005), pp.636-659.
