第六章 光路计算和像差理论
工程光学第6章光线的光路计算及像差理论
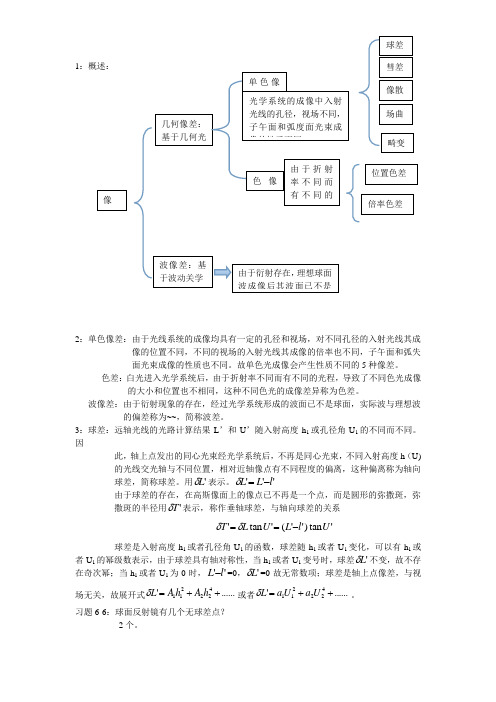
1:概述:2:单色像差:由于光线系统的成像均具有一定的孔径和视场,对不同孔径的入射光线其成 像的位置不同,不同的视场的入射光线其成像的倍率也不同,子午面和弧失 面光束成像的性质也不同。
故单色光成像会产生性质不同的5种像差。
色差:白光进入光学系统后,由于折射率不同而有不同的光程,导致了不同色光成像 的大小和位置也不相同,这种不同色光的成像差异称为色差。
波像差:由于衍射现象的存在,经过光学系统形成的波面已不是球面,实际波与理想波 的偏差称为~~,简称波差。
3:球差:远轴光线的光路计算结果L ’和U ’随入射高度h 1或孔径角U 1的不同而不同。
因此,轴上点发出的同心光束经光学系统后,不再是同心光束,不同入射高度h (U) 的光线交光轴与不同位置,相对近轴像点有不同程度的偏离,这种偏离称为轴向 球差,简称球差。
用'L δ表示。
'''l L L -=δ由于球差的存在,在高斯像面上的像点已不再是一个点,而是圆形的弥撒斑,弥 撒斑的半径用'T δ表示,称作垂轴球差,与轴向球差的关系'tan )''('tan 'U l L U L T -==δδ球差是入射高度h 1或者孔径角U 1的函数,球差随h 1或者U 1变化,可以有h 1或者U 1的幂级数表示,由于球差具有轴对称性,当h 1或者U 1变号时,球差'L δ不变,故不存在奇次幂;当h 1或者U 1为0时,''l L -=0,'L δ=0故无常数项;球差是轴上点像差,与视场无关,故展开式......'422211++=h A h A L δ或者......'422211++=U a U a L δ。
习题6-6:球面反射镜有几个无球差点?2个。
像几何像差:基于几何光波像差:基于波动关学 由于衍射存在,理想球面波成像后其波面已不是单色像色像由于折射率不同而有不同的光学系统的成像中入射光线的孔径,视场不同,子午面和弧度面光束成像的性质不同 球差彗差 像散 场曲 畸变 位置色差 倍率色差。
电子教材-光线的光路计算

工程光学 Engineering Optics
第六章 第二节 光线的光路计算
四、子午面内光线的特殊情况
1.折射平面
I = −U ⎧ ⎪ sin I ' = n sin I / n' 远轴光线 ⎪ ⎨ U ' = −I ' ⎪ ⎪ L' = L tan U / tan U ' ⎩
i = −u ⎧ ⎪ i' = n ⋅ i / n' ⎪ 近轴光线 ⎨ u' = −i' ⎪ ⎪l ' = l ⋅ u / u' = l ⋅ n' / n ⎩
工程光学 Engineering Optics
第六章 第二节 光线的光路计算
第一章回顾 单个折射球面光路计算
BUPT Automation School
北京邮电大学 自动化学院
宋 晴
工程光学 Engineering Optics
第六章 第二节 光线的光路计算
二、子午面内近轴光线的光路计算
1.轴上点近轴光线(细光束)——“第一近轴光线”
解:按照“轴上点远轴光线”公式: 由 (La, Ua) (La’, Ua’) 由 (Lz, Uz) (Lz’, Uz’) 由 (Lb, Ub) (Lb’, Ub’) 由 L L’ 像高: 上光线 ya ' = ( La '− L' ) tan U a ' 主光线 y z ' = ( La '− L' ) tan U z ' 下光线 yb ' = ( Lb '− L' ) tan U b ' 实际像高 BUPT Automation School 北京邮电大学 自动化学院 宋 晴
工程光学第六章光线的光路计算及像差理论

工程光学第六章光线的光路计算及像差理论光线的光路计算及像差理论是工程光学中非常重要的主题。
在实际的光学工程设计中,准确地计算光线的光路和考虑像差对于正确预测和优化光学系统的性能至关重要。
本文将详细介绍光线的光路计算方法和像差理论。
光线的光路计算是指在给定光学系统的参数和输入光线的条件下,确定光线在系统中的传播路径。
光线的传播路径可以通过几何光学的基本定律来计算,如光线的折射、反射和偏折等。
在确定光线的传播路径时,需要考虑光线的入射角、光线的折射率、光学元件的形状和位置等因素。
光线的光路计算可以采用追迹方法或者矢量法进行,具体方法取决于所研究问题的复杂性和准确性要求。
在光线的光路计算过程中,通常需要考虑光线的反射和折射,这需要利用光学元件的表面曲率和入射光线的入射角来计算。
对于球面曲率的光学元件,可以使用球心距离和球心方向来确定入射光线的出射角度。
对于非球面曲率的光学元件,可以通过数值方法来求解光线的光路。
像差是指光线传播过程中光学系统造成的光线聚焦不完美的现象。
像差的存在会导致图像的模糊、畸变和色差等问题。
像差的产生主要源于光学元件的形状和折射性质的不完美。
像差理论可以通过将光线的传播过程分解为一系列的近似操作来描述和计算。
常见的像差包括球差、色差、像散和畸变等。
球差是指在球面镜或球面透镜上,由于光线入射角的不同,导致光线的聚焦位置不一致的现象。
球差的计算可以通过利用轴上点和非轴上点的光线角度来求解。
色差是指由于光的折射性质的不同,导致不同波长的光聚焦位置不一致的现象。
色差的计算可以通过利用不同波长的光的折射率来求解。
像散是指由于光线的折射作用,导致光线聚焦位置随着入射光线离轴距离的变化而变化的现象。
像散的计算可以通过利用非轴上点的入射角度和位置来求解。
畸变是指由于光学元件形状的不对称性,导致图像的形状和位置发生变化的现象。
畸变的计算可以通过利用非球面曲率的光学元件的光路来求解。
总之,光线的光路计算和像差理论对于工程光学的实际应用具有重要意义。
第六章_光线的光路计算及像差理

sin I ( L r )
sin U r
★由折射定律
sin I
n sin I n
★ ΔAEC 及ΔA′EC: U I U I ★ ΔA′EC中,由正弦定律
sin I sin U L r r
U U I I
sin I 像距 L r (1 sin U )
第6章
光线的光路计算及像差理论
概述 光线的光路计算 轴上点的球差 正弦差和彗差 场曲和像散 畸变 色差 像差特征曲线与分析 波像差
本章重点
光学系统像差的基本概念
光学系统像差的种类
初级单色像差
在几何光学中,我们知道一个物点经单折射球面后不能够完 善成像,但若把光线限制在近轴范围内,即 : ,cos 1 sin 则可认为物点成理想的像点,但
L’=150.7065mm L’=147.3711mm L’=141.6813mm
n A O
-240mm
E
n’ C
可以发现:同一物点发出的物方倾斜角 不同的光线过光组后并不能交于一点!
球差的定义和表示方法
1、球差的定义
轴上点发出的同心光束,经光学系统各个折射面折射 后,不同孔经角U的光线交光轴于不同点上,相对于 理想像点的位置有不同的偏离,这就是球面像差,简 称球差。它由孔径引起。 L' L' l '
入瞳
对于有k个面的折射系统,根据过渡公式由初始数据可以 确定像方截距和像方孔径角. 用小l公式进行光路追迹确定像方截距和像方孔径角.
近轴光线的光路计算
1、近轴光线 ★ 近轴条件:
sin i tgi i
sin I ( L r ) sin U r
(工程光学教学课件)第6章 光线的光路计算及像差理论

无像质要求系统:
(1)
有像质要求的一般系统:
(1)、(2)
有像质要求的大视场系统: (1)、(2)、(3)
有像质要求的大视场、大孔径系统:(1)、(2)、(3)、(4)
光线光路的计算主要有三类:
✓子午面内的光线光路计算 ✓沿轴外点主光线的细光束像点的计算 ✓子午面外光线或空间光线的计算
子午面内的光线光路计算
L' )tgU L' )tgU
' a
' z
Yb'
( L'b
L' )tgU
' b
B’b B’z
B’a
Y’b
Y’z Y’a
-U’a
P’ -U’z -U’b
O
A’o
--L’a
--L’b
--L’z --L’
3.折射平面和反射平面的光路计算
远轴光按大L公式进行计算:
sin I L r sin U r
补充:五、光学设计的一般过程和内容 (了解)
(1) 成像要求:基本类型,视场,观测方式,景深,渐晕, 分辨率,仪器尺寸,其它要求等;
(2) 建立理想 基本光组数量,焦距,成像光路,物像共轭距、 系统模型:物像四要素,反射棱镜(用平行平板表示)等;
(3) 构造基本 按最低数量配置透镜,初步确定透镜的材料、 光学系统:形状、孔径、曲率半径等参数,配置必要光阑, 确定反射棱镜的形状和大小,其它器件等;
(4) 光线计算 以理想成像为标准,用光线理论进行实际光线 求 像 差:的光路计算,以确定各类像差;
(5) 像质评价:按照系统像质要求,确定主要和次要像差, 并进行像差评价和分析,研究改善方案;
修正设计:通过对系统各类参数的调整和增加透镜,重复 前面(3)、(4)步骤,逐渐校正像差,最终达到 系统的像质要求。
第六章 光学系统的光路计算和像差理论(2013总第10-11讲)

第六章 光线的光路计算及像差理论
本章内容 像差概述-像差的定义和分类 光线的光路计算
轴上点的球差
正弦差和彗差 场曲和像散 畸变 色差
像差特征曲线与分析
波像差
大纲要求:
⑴掌握像差的定义、种类和消像差的基本原则。 ⑵了解单个折射球面的不晕点(齐明点)的概念和性质, 求解方法。 ⑶掌握七种几何像差的定义、影响因素、性质和消像差方
线成像特性的比较,研究不同视场的物点对应不同孔径和不同色光的像差值。
对两边缘谱线F光(λ =486.1nm)和C光(λ =656.3nm)校正色差。
②普通照相系统:对最灵敏谱线F光校正单色像差;对
两边缘谱线D光和G’光(λ =434.1nm)校正色差。
天 文 照 相 系 统 , 常 用 G’ 光 校 正 单 色 像 差 , 对 h 光 (λ=404.7nm)和F光校正色差。 ③近红外光学系统:对C光校正单色像差;对d光 (λ=587.6nm) 和A’光(λ=768.2nm)校正色差。
五. CIE色度学系统表示颜色的方法
第十节 均匀颜色空间及色差公式
一、(x,y,Y)颜色空间是非均匀颜色空间 二、均匀颜色空间及色差公式
(一)CIE1964均匀颜色空间
(二)CIE1976均匀颜色空间 (三)CIE1976均匀颜色空间
(W *U *V *) ( L * u * v*)
( L * a * b*)
cie色度学系统表示颜色的方法专业文档第十节均匀颜色空间及色差公式一xyy颜色空间是非均匀颜色空间二均匀颜色空间及色差公式vuw一cie1964均匀颜色空间二cie1976均匀颜色空间vulbal三cie1976均匀颜色空间专业文档第六章光线的光路计算及像差理论本章内容?像差概述像差的定义和分类?光线的光路计算?轴上点的球差?正弦差和彗差?场曲和像散?畸变?色差?像差特征曲线与分析?波像差专业文档掌握像差的定义种类和消像差的基本原则
第六章 光线的光路计算及像差理论

下光线tgUb ( y h)
y ( L l )tgU
' z '
' z ' b
y ( L l )tgU
' b ' b '
3.折射平面和反射面的光路计算 折射平面远轴光线的光路计算公式: I U
sin I n sin I
'
n
'
U ' I ' L' LtgU tgU '
' 1 ' 2
' k 1
d k 1
校对公式:h lu l 'u ',J n 'u ' y ' nuy
' 求焦距公式:令1 , u1 , f ' h1 / uk l
轴外点近轴光线光路计算 (第二近轴光线光路计 算):求出理想像高。
初始数据:l z , u z y /(l z l1 ) 像高数据:y (l l )u
1
n
作业
1,2,11,12,17
路计算 2.轴外点沿主光线的细光束光路计算 3.子午面的空间光线光路计算
二、子午面内的光线光路计算: 1.近轴光线光路计算:求出理想像的位置
和大小
近轴光线光路计算
(第一近轴光线光路计算):求出理想像的位置
l r i u r n i' i n' u' u i i' i' l ' r (1 ) u'
第六章 光线的光路计算 及像差理论
实际光学系统与理想系统之间存在差异;实际像和 理想像之间的差异称为像差。
光路计算以及像差理论

光路计算以及像差理论光路计算和像差理论是光学领域中重要的理论和计算方法,用于研究和描述光在光学系统中的传播和成像过程。
本文将详细介绍光路计算和像差理论的基本概念和原理,并进一步分析它们的应用和意义。
光路计算是指通过对光线的追踪和计算,来确定光线在光学系统中的传播路径和成像效果。
光线是一种理论上的模型,用于描述光的传播。
光线在光学系统中的传播路径可以通过光线传播的三个基本规律来描述:一是光线沿直线路径传播,即自由传播定律;二是光线在分界面上发生折射,即折射定律;三是光线在反射面上发生反射,即反射定律。
根据这些规律,可以利用向量法对光线进行计算和分析,确定其传播路径和成像位置。
光路计算主要用于分析和设计光学系统,如透镜组、反射镜、光纤等。
通过对光路的计算,可以确定图像的位置、放大倍率和畸变等参数。
例如,在透镜组中,可以通过光路计算来确定光线在透镜组中的光路和成像位置,进而优化透镜组的设计,并实现清晰准确的成像效果。
光路计算还可以应用于光学传感器和光学通信系统等领域。
在光学传感器中,可以通过光路计算来确定光源到传感器的传输路径和成像效果,从而提高传感器的灵敏度和分辨率。
在光学通信系统中,可以通过光路计算来确定光信号在光纤中的传输路径和衰减情况,从而优化光通信系统的传输性能和距离。
像差理论是描述光学系统成像质量的理论框架。
在光学系统中,由于折射、反射以及光学元件的形状等因素的影响,光线在成像过程中会发生一些畸变和偏差,导致最终成像结果与理想成像有差异,这种差异称为像差。
像差理论主要研究和描述这些差异的产生原因和影响程度。
常见的像差包括球面像差、色差、像散、畸变等。
球面像差是由于透镜的球面形状导致光线在透镜中的聚焦位置发生变化,使得不同位置的物体成像位置不同。
色差是由于光线的折射率随着波长的变化而变化,导致不同波长的光线成像位置发生偏差。
像散是由于光线在透镜中的色散效应导致不同波长的光线在成像后的位置不同。
6光线的光路计算及像

球差是入射高度h1或孔径角U1的函数,球差随h1或U1的变化 规律,可以由h1或U1的幂级数表示。由于球差具有轴对称性, 当h1或U1变号时,球差δL′不变,级数展开时不存在h1或U1 奇次项;当h1或U1为零时,像方截距L′ = l ′,即δL′ = 0, 所 以展开式中没有常数项;球差是轴上点像差,与视场无关, 所以展开式中无y或ω项,所以球差可以表示为:
波动光学:波像差; 波动光学:波像差; 研究像差的目的: 研究像差的目的: 根据光学系统的作用和接收器的特性把影响像质的主要像差校正到 某一公差范围内,使接收器不能察觉,即认为像质是满意的。 某一公差范围内,使接收器不能察觉,即认为像质是满意的。
6.1.2 像差计算的谱线选择
单色像差: 对光能接收器最灵敏的谱线校正单色像差; 单色像差: 对光能接收器最灵敏的谱线校正单色像差; 色差: 对光能接收器所能接收的波段范围两边缘附近的谱线校正色差; 色差: 对光能接收器所能接收的波段范围两边缘附近的谱线校正色差; 匹配: 光源、光学系统材料、接收器的光谱特性; 匹配: 光源、光学系统材料、接收器的光谱特性; 目视光学系统(人眼观察用) 目视光学系统(人眼观察用) 单色像差: 光 接近(555) 单色像差:D光(589.3) e光(546.1) →接近 光 色差: 光 色差:F光(486.1) C光(656.3) 光 普通照相系统(照相底片) 单色像差: 光 普通照相系统(照相底片) 单色像差:F光 色差: 光 色差:D光,G’光(434.1) 光 近红外、 近红外、近紫外光学系统 激光系统: 只校准单色像差(用照明光源),不校准色差, ),不校准色差 激光系统: 只校准单色像差(用照明光源),不校准色差,因单色 光照明。 光照明。
6.1.3 像差成因
6第6章 光线的光路计算及像差理论

作业:完成本例题的光路追迹!
计算举例
一望远物镜的焦距f’=100mm,相对口径D/f’=1/5, 视场角2ω=6°,其结构参数如下:
r/mm 62.5 -43.65 -124.35 d/mm 4.0 2.5 nD 1.51633 1.67270 νD 0.00806 0.015636
试求该物镜的第一、二近轴光线成像特征和远轴光线 成像特征,以及主光线细光束成像特征。
轴上点的球差
球差的定义和表示方法
1、球差的定义
轴上点发出的同心光束,经光学系统各个折射面折射 后,不同孔经角U的光线交光轴于不同点上,相对于 理想像点的位置有不同的偏离,这就是球面像差,简 称球差。它由孔径引起。 L' L' l '
L' 0 球差校正不足 或欠校正
L' 0 球差校正过头 或过校正
Lz1 0.8025
用大L公式进行光线追迹: L' z 3.378 U z ' 259'6' '8 实际像高: ys ' (L'z l ' ) tanU '3 5.2351 实际像高与理想像高差:
y' ys ' y' 0.007
解:
沿主光线细光束计算的初始数据: t1 s1 l1 h1 10 mm
用小l公式分别对y1=0.3Y、0.5Y、0.707Y、0.85Y、Y 进行光路追迹确定像方截距和像方孔径角.
2.远轴光线的光路计算
子午面内的远轴光按大L公式进行计算:
Lr sin U r n sin I ' ' sin I n U' U I I' sin I sin I ' L r r sin U '
工程光学-第6章 光线的光路计算及像差理论

第六章 光线的光路计算及像差理论
前后折射面过渡公式
′ −1 − d k ′ −1 ⎧lk = lk ⎪ ′ −1 ⎨uk = uk ⎪n = n′ k −1 ⎩ k
前后折射面校对公式
⎧h = lu = l ′u′ ⎨ ⎩nuy = n′u′y′ = J
系统焦距
′ = f ′ = h1 / u ′ l1 = ∞, u1 = 0 → lk
(1)无穷远处物体
第六章 光线的光路计算及像差理论
轴外点与轴上点的重要区别 光束相对于主光线失去了对称性
第六章 光线的光路计算及像差理论
(1)无穷远处物体 初始数据
上光线U a = U z , La = Lz + h / tan U z ⎫ ⎪ 主光线U z = ω , Lz ⎬ 下光线U b = U z , Lb = Lz − h / tan U z ⎪ ⎭
第六章 光线的光路计算及像差理论
2、目视光学系统 人眼响应波段:380~760nm 最灵敏波长:555nm 校正单色差:e光λ=546.1nm 校正色差:F光λ=486.1nm和C光λ=656.3nm 选择光学材料 nD , vD = ( nD − 1) / ( nF − nC ) 3、普通照相系统 一般照相乳胶对蓝光较灵敏,具体应根据实际照相底片参数而定 校正单色差:F光λ = 486.1nm 校正色差:D光λ=589.3nm和G′光 λ =434.1nm ′ − nD ) 选择光学材料 nF , vF = ( nF − 1) / ( nG
3、球差是入射高度和孔径角的函数(偶次)
重复轴上点远轴光线计算步骤 可得实际高
第六章 光线的光路计算及像差理论
(2)有限远处物体
初始数据
上光线 tan U a =(y - h)/(Lz - L),La = Lz + h/ tan U a ⎫ ⎪ 主光线 tan U z =y/(Lz - L),Lz ⎬ 下光线tanU b =(y + h)/(Lz - L),Lb = Lz + h/ tan U b ⎪ ⎭
工程光学第六章像差理论重点讲解

校对公式:
h lu lu nuy nuy J
最后可计算出像点位置和系统各基点位置。
焦点位置及焦距计算:l1 , u1 0
f ' h1 / u'k
2、轴外物点近轴光线光路计算(第二近轴光线)
仍用近轴光线光路计算公式和校对公式,所有量均注以下标z.
已知:物方物位、入瞳位置和物高,即 l, lz , uz 。 求解:像方物位、出瞳位置和像高,即 l, lz , uz 。
i
l
r
r
u(当l1
时, u1
0,i1
h1
/
r1)
i' n i
n'
u' u i i'
l' r(1 i' )
u'
l' n'lr
n'l n(l r)
第二节 光线的光路计算
对于有k个面的折射系统,需利用根据过渡公式:
过渡公式:
lk lk1 dk 1 uk uk 1 nk nk 1
对于小视场的光学系统,例如望远物镜和显微物镜等,只 要求校正与孔径有关的像差,所以只需计算上述第一种光线。 对大孔径、大视场的光学系统,如照相物镜等,要求校正所 有像差,所以需要计算上述三种光线。
第二节 光线的光路计算
由已知条件:
光学系统的结构参数(r,d,n)
物体的位置和大小 入瞳的位置和大小
解决问题:
第一节 概述
像差校正:
在实际光学系统中,各种像差是同时存在的,像差 影响光学系统成像的清晰度、相似性和色彩逼真度等 ,就降低了成像质量。故像差的大小反映了光学系统 质量的优劣。
除了平面镜成像以外,没有像差的光学系统是不 存在的。完全消除像、色差是不可能的,针对光学系 统的不同用途,只要把像、色差降低在某范围内,使 光接收器不能分辨,或者说这种差别只要能骗过光接 收器,就可以认为是理想的。
工程光学第六章光线光路计算及像差理论

I
U ; sin I '
n sin I n'
U '
I '; L'
L
tgU
tgU
当角U很小时,用上式计算不够精确,宜把正切改
为余弦
L L tgU
L sinU cosU L ncosU
tgU cosU sinU n cosU
2、 近轴光计算公式:
则
L ' L ' l '
即为轴向球差的大小。 当δL′=0时,称这种光学系统为消球差系统。
大孔径产生的球差
P
P• P•
L l
Lm
Lm l
L L l
L<0 负球差(凸透镜)(出射光束是会聚光束)
L >0 正球差(凹透镜)(出射光束是发散光束)
一、
1、
A
-U1
-Y
-Uz1
-L1
Lz1
入瞳
当物体位于无限远时,l1 时,
uz1 1 为已知。
2、
当U 0时,sin I h
r
轴外点初始数据为
轴外物点发出的主光线及上、下光线的初始数据为 入瞳半径可由下式确定 (Lz L)tgU
差,把像差校正到某一公差范围内,使成像质量达 到技术要求;同时了解各种像差的现象、产生原 因、光束结构、减小像差的措施。
第二节 光线的光路计算
光线光路的计算主要有三类:
子午面内的光线光路计算 轴外点沿主光线的细光束像点的计算 子午面外光线或空间光线的计算
对于小视场的光学系统,例如望远物镜和显微物 镜等,只要求校正与孔径有关的像差,所以只需计 算上述第一种光线。对大孔径、大视场的光学系统, 如照相物镜等,要求校正所有像差,所以需要计算 上述三种光线。
第六章.像差(工程光学)第二讲

k 1
SIII
(6-52)
(1)由像散分布式可知,对单个折射球面而言,没有正弦差
子午场曲:
xt'
lt'
l
'
t
'
sU
' z
x
l
'
弧矢场曲:
xs'
ls'
l'
s'
cosU
' z
x
l'
(6-44)
4、场曲的性质
★ 细光束的场曲与孔径u(或入射高度h)无关,只是视场ω (y)的函数。
★ 视场为零,则场曲为零。
5、场曲的幂级数表达式
x' t(s)
A1 y 2
A2 y4
A3 y6
(6-45)
SIV J 2 (n'n)/nn'r
J 为拉赫不变量
(6-46) (6-47) (6-48) (6-49)
二、像散
1、场曲与像散的关系
图610(b)
★ 图6-10(b)表示细光束子午场曲和弧矢场 曲的像差曲线。随着视场的增大.场曲和像 散迅速增大。这是因为场曲和像散随视场的 平方倍(初级)和四次方倍(高级)增大。
(6-40)
比较式(6-34)和(6-40),得彗差与正弦差的关系为:
OSC' Ks' / y'
(6-41)
彗差是轴外像差之一,它破坏了轴外视场成像的清晰度。
彗差值随视场的增大而增大,故对大视场的光学系统,必须校 正彗差。若光阑通过单折射面的球心,则不产生彗差。
后面将要论述,有些光学系统,不仅不产生彗差,其轴外点的
只能要求其成像光束结构与轴上点成像光束结构相同,也就是 说,轴上点和近轴点有相同的成像缺陷,称为等晕成像。欲满 足等晕成像的要求,光学系统必须满足等晕条件,即
第六章 光路计算和像差理论

是以一定的宽度的光束对具有一定大小 的物体进行成像,由于只有近轴区才具有理想光学系统性质, 故不能成完善像,就存在一定的像差。
6.1 概
3、 像差产生的原因
述
在第一章我们曾讲过近轴光/实际光的光路计算公式。
并且说明这二组公式 最大的区别是对于近 轴光:是用弧度值取 代正弦值而得 到的。即 sin I≈ I。
但实际上这一取代并不是完全精确的,它存在着一定的误差量值, 因为它们仅仅是近似相等,从而导致实际与理想之间存在差异。这 就是像差产生的原因。
计算实例: 课本表8.2
回忆: 第一和第二近轴光分别用来计算 系统的哪些参数?
6.2 光路计算
(二) 实际光线的光路计算
1、轴上点公式(也分有限远及无限远):
Lr sin I sin U r n sin I ' sin I n' U ' U I I ' L' r r sin I ' sin U '
显然实际像与理想像之间存在着沿轴的差异,就把实际像点与理想 像点的偏移为球差,用δL'表示:
2、对于轴外点:
当物位于无限远时,至少要计算三条光线,分别为:上光线a, 主光线z,下光线b,如图:
计算实例:课本表8.4
6.2 光路计算
当物位于有限远时,h为入瞳半高度;为物高。
6.2 光路计算
对于轴外点,我们要计算多少条光线呢?
工程光学 第六章 光线的光路计算及像差理论

第一节 概 述
二、像差计算的谱线选择
1、目视光学系统
目视光学系统的接收器是人的眼晴。只对波长在 380—760nm范围内的波段有响应,其中最灵敏的 波长555nm,
目视光学系统:
➢一般选择靠近此灵敏波长的D光(589.3nm)或e光 (546.1nm)校正单色像差。 因e光比D光更接近于 555nm,故用e光校正单色像差更为合适,
一、正弦差
➢ 正弦差用来表示小视场时宽光束成像的不对称性 。
➢ 垂直于光轴平面内两个相邻点,
➢一个是轴上点, ➢一个是靠近光轴的轴外点,
正弦条件
➢ 其理想成像的条件是:
nsyiU n n 'y'siU n '
一、正弦差 ➢ 当光学系统满足正弦条件时, ✓若轴上点理想成像,则近轴物点也理想成像, ✓即光学系统既无球差也无正弦差, ✓这就是所谓不晕成像。
工程光学 第六章 光线的 光路计算及像差理论
第六章 光线的光路计算及像差理论
第一节 概 述 第二节 光线的光路计算 第三节 轴上点球差 第四节 正弦差和彗差 第五节 场曲和像散 第六节 畸 变 第七节 色 差
第一节 概 述
一、基本概念
(1)近轴光学系统中: ➢根据精确的球面折射公式,导出在动
sina=a,cosa=1时的物像大小和位置,即理想光学 系统的物像关系式。一个物点的理想像仍然是一个 点,从物点发出的所有光线通过光学系统后都会聚 于一点。 ➢近轴光学系统只适用于近轴的小物体以细光束成像 。
➢同一光学介质对不同的色光有不同的折射率 ➢白光进入光学系统后,由于折射率不同而有不同的
光程, ➢这样就导致了不同色光成像的大小和位置也不相同
第一节 概 述
一、基本概念
光路的计算

第四节 正弦差和彗差
上光线:轴外点发出通过某孔径带上边缘的光线称 某孔径带的上光线; 下光线:轴外点发出通过某孔径带下边缘的光线称 某孔径带的下光线
前光线:轴外点发出通过某孔径带前边缘的光线称 某孔径带的前光线 后光线:轴外点发出通过某孔径带后边缘的光线称 某孔径带的后光线
第三节 轴上点的球差
二、单个折射球面的球差分布和不晕点 单个折射面球差分布公式: k 1 L s uk sin U k 1 2nk
niL sin U (sin I sin I )(sin I sin U ) s 1 1 1 cos ( I U ) cos ( I U ) cos ( I I ) 2 2 2
一、基本概念
因此,单色光成像会产生性质不同的五种像差, 即球差、彗差(正弦差)、象散、场曲和畸变,统 称为单色像差。 实际上绝大多数的光学系统都是对白光或复色光 成像的,由于同一光学介质对不同的色光有不同的 折射率,因此,白光进入光学系统后,由于折射率 不同而有不同的光程,这样就导致了不同色光成像 的大小和位置也不相同,这种不同色光的成像差异 称为色差。色差有两种,即位置色差和倍率色差。 以上讨论时基于几何光学的,所以上述七种像差 称为几何像差。
第四节 正弦差和彗差
主光线:某视场点发出的通过入瞳中心过入瞳边缘点 的“近轴”光线; 第二近轴光线:轴外某视场点发出的通过入瞳中心 的“近轴”光线
子午平面:包含物点和光轴的平面称子午平面; 弧矢平面:包含主光线并与子午平面垂直的平面 辅轴:轴外点和球心的连线称为该折射球面的辅轴
第三节 轴上点的球差
一、球差的定义及表示方法 由第二章实际光线得光路计算公式知,物距L为定值 时,像距L′是孔径角U的函数。由轴上一点发出光 线,角U 不同,通过光学系统后有不同的像距L′。 即轴上点发出的同心光束经光学系统后,不再是同 心光束,不同入射高度h(U)的光线交于光轴不同位 置,相对于近轴像点(理想像点)有不同程度的偏 离,这种偏离称为轴向球差,简称球差。用 δ L′ 表示: δ L′=L′- l′
光学设计与cad ppt第六章 光线光路计算及像差理论

垂直球差
U m
••
T
•
T
U
L
TL tanU
球差的特点:
球差是入射高度h1或孔径角U1的函数 球差具有对称性 球差与视场角无关
球差可以展开为h或U的多项式:
L ' A 1h 1 2A 2h 1 4A 3h 1 6
或 L ' a 1 U 1 2a 2 U 1 4a 3 1 6
初级球差 二级球差 三级球差 ‥‥‥
成像位置和大小也不同)有 两种:
➢位置色差(轴向色差) ➢倍率色差(垂轴色差)
场曲
畸变
基于物理光学: 波象差(实际波面与理想球面波
的偏差)
光线光路的计算主要有三类:
✓子午面内的光线光路计算 ✓轴外点沿主光线的细光束像点的计算 ✓子午面外光线或空间光线的计算
对于小视场的光学系统,例如望远物镜和显微物 镜等,只要求校正与孔径有关的像差,所以只需计 算上述第一种光线。对大孔径、大视场的光学系统, 如照相物镜等,要求校正所有像差,所以需要计算 上述三种光线。
第六章 光线的光路计算 及像差理论
教学要求:
内容:实际光学系统中的单色像差,复色差 球差、慧差(正弦差)、像散、场曲、畸变、 产生的原因及矫正方法,光线光路的 计算方法
要求:掌握光线光路的计算方法、各种像差的 概念。掌握像差产生的原因及矫正方法
重点:掌握像差产生的原因及矫正方法。
难点:正弦差(慧差)
故轴上物点发出的光束,经光学系统后不 能相交于一点,而成弥散的圆形像斑的现象。 称为球面像差。
P
P•
P•
L m
Ll
L m l
其中: l 近轴光线束与光轴交点距离(理想像距);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光路计算分类:
6.3
轴上点的球差
一、分类:可在沿轴方向和垂轴方向来度量分别称为轴 向球差和垂轴球差。 (1)轴向球差又称为纵向球差,它是沿光轴方向度量 的球差,用符号δ L’ 表示。 (2)垂轴球差是过近轴光线像点A’的垂轴平面内度 量的球差。用符号δT’ 表示。 它表示由轴向球差引起的弥散圆的半径。
L ' A1
h h A 2 h h m m
2 4
例题1
所以刚才求最大剩余球差的过程可以描述如下: 2 h 只考虑二级的高级球差,所以有: L '初 A hm
对边缘光校正球差,即h hm, Lm ' 0时, 上式应有A1 A2。 h 2 h 4 这时候有 L ' A2 h h m m 为求极大值,将上式对h求导,并令导数为0,即 代回到 Lm ' 0时的级数展开式,有 L0.707 ' A2 4 h d L ' 0, 求得h m 0.707hm dh 2
n sin I n' n' sin I sin I ' n sin I '
n Lr n n' sin U L r n' r n n ' L ' r n n' sin U ' L ' r n r n'
物点位置Байду номын сангаас
像点位置
这对共轭点都在球心的同一侧,所以实物成虚像,或者是虚物成实像。 二者的简单关系: n ' L ' nL
光学系统中对某一给定孔径的光线达到δ L’ =0的系 统称为消球差系统。
单透镜的球差与焦距、相对孔 径、透镜的形状及折射率有关。
对于给定孔径焦距和折射率的 透镜,通过改变其形状可使球 差达到最小(透镜弯曲)。
h/hmax
0.85 0.7 0.5 0.3 0.2
δL’
13
2016/7/19
0
球差
2016/7/19
三、球差的级数展开
球差是半孔径角U或光线入射高度h的函数。将其按级数展 开,并且考虑到它的轴对称性,有:
L ' A1h2 A2 h4 A3h6 ...... L ' a1U 2 a2U 4 a3U 6 ......
其中的第一项称为初级球差,第二项为二级球差,第三项三级 球差,以此类推......注意,除了第一项初级球差,后面的球差 统称“高级球差”!
第六章 光线的光路计算及像差理论
6.1 概 述 6.2 光路计算 6.3 轴上点的球差 6.4 彗差及正弦差 6.5 像散及场曲 6.6 畸 变 6.7 色 差 6.8 波像差
6.1
概
述
实际光学系统都有一定大小的相对孔径和视 场,远远超出近轴区所限定的范围。 与近轴区成像相比必然在成像位置和像的 大小方面存在一定的差异,被称为像差。 指在光学系统中由透镜材料的特性或折射 (或反射)表面的几何形状引起实际像与理想 像的偏差。
4
A2 yhm K 'S 0.707 4
为全孔径二级彗差的(-1/4)
3、 彗差的分布式
3 K 'T 2 n 'k u ' k 1 K 'S 2n 'k u 'k iz 其中 S II i
S
1
k
II
初级子午彗差 初级弧矢彗差 初级彗差分布系数, 也叫第二塞德和数。
14
球差影响图像清晰度
2016/7/19
15
注意:所谓的消球差一般只是能使某一孔径带的球差为 0,而不能使各个孔径带全部为0,一般对边缘光孔径 校正球差,而此时一般在0.707口径有最大的剩余球差, 大小约为边缘光高级球差的-1/4。 当边缘口径的球差不为0时,如果存在负球差称为“校 正不足”,如果存在正球差,称为“校正过度”。
这些圆斑相互叠加的结果就形成了带 有彗星形状的光斑。
光斑的头部(尖端)较亮,至尾部亮度 逐渐减弱,称为彗星像差,简称彗差。
C E A B
2016/7/19
By’ Ay’ F
O
D
27
说 明
1)彗差是一有符号数,当交点BT’位于主光线之下
为“-”,当交点BT’位于主光线之上为“+”;
彗星像斑的尖端指向视场中心的称为正彗差; 彗星像斑的尖端指向视场边缘的称为负彗差。
2)彗差是轴外像差之一,其危害是使物面上的轴外
点成像为彗星状的弥散斑,破坏了轴外视场的成像清 晰度,且随孔径及视场的变化而变化,所以彗差属于 轴外像差。
3)由于彗差没有对称轴只能垂直度量,所以它是 垂轴像差的一种。
2016/7/19 28
入 瞳
像 面
2016/7/19
29
2016/7/19
30
式中第一项为初级彗差;后二项为二级彗差(孔径项,视场项),对于不同 光学系统:
小孔径小视场,彗差主要由第一项表示;(望远镜)
大孔径小视场,彗差主要由第一、二项表示;(显微镜) 小孔径大视场,彗差主要由第一、三项表示;(照相物镜)
大孔径大视场,彗差主要由第一、二、三项表示。(特殊照相物镜)
同样当边缘彗差校正为零时,在0.707处有最大的剩余彗差:
-Umax
A -U
△y’
h hmax
A’
L’
2016/7/19
δL’ l’
10
对于单透镜来说,U越大则球差值越大。 单透镜自身不能校正球差。
入瞳 像面
a
Yb’ Ya’ YZ’
Z b
2016/7/19
11
单正透镜会产生负值球差;单负透镜会产生正值球差。
如果将正负透镜组合起来,能否使球差得到校正? 这种组合光组被称为消球差光组。
2016/7/19
31
彗差
2016/7/19
32
6
2.5
1
2016/7/19
33
2、 彗差的级数展开(以弧矢为例)
由于彗差既与孔径相关又与视场相关,所以其展开式中明 显的含有相关的量:
2 4 3 2 KS ' A yh A yh A y h ...... 1 2 3
性和色彩逼真度等,降低了成像质量。
2016/7/19
3
6.1
概
述
3、 像差产生的原因 在第一章我们曾讲过近轴光/实际光的光路计算公式。
lr i r u n i ' i n' u ' u i i ' l ' r (1 i ' ) u'
6.1
概
述
二、像差谱线的选择――主要取决于接收器的光谱特性 进行像差校正时,只能校正某一波长的单色像差, 对于不同的接收器件像差谱线的选择有很大的区别。
1、目视光学系统:一般选择D光或e光校正单色像差, 对F , C光校正色差。 2、普通照相系统(胶片):一般对F光校正单色像差, 对D, G '校正色差。 3、近红外光学系统:一般对C光校正单色像差,对d, A '校正色差。 4、对特殊光学系统(激光):只对使用波长校正单色 像差。
四、 球差分布公式
由于光学系统是由多个光组构成,而每一个折射面都将对 整个系统的球差有所贡献,而整个系统的球差值就是各个 折射面产生的球差传递到系统像空间后相加而成的,故称 每个折射面对系统总球差的贡献量值叫球差分布。 所谓的球差分布式是指构成系统的每个面对球差的贡献。 其形式为: k 1 L' S一 其中S-为每个面上的球差分布系数 2n'k U 'k sin U 'k 1
若在近轴区内, k 1 l ' S 2 I 2n ' k U ' k 1
其中
S I luni (i i ')(i ' u ) lu h
其中SI称为初级球差分布系数,也叫第一塞德尔(Seidel)和数。
五、 单个折射面的三对无球差点(如何消球差?)
1、三对齐明点(不晕点): 1)当L=0时,即物位于顶点处,此时 L'= 0 ,即物、像位于 顶点处; 2)当sinI −sinI’=0时,此时有:I=I’=0,即相当于入射光线 与球面法线相重合,此时物点与像点均位于曲率中心(折射 面球心)处; 3)当sinI’-sinU=0,或I’=U。此时:
δT’= δL’ tanU’
球差是轴上点唯一的单色像差。
2016/7/19
7
2016/7/19
8
2016/7/19
9
二、球差与孔径之间的关系 对应孔径角Umax入射光线的高度hmax被称为全孔径(边 光球差);对应孔径角U入射光线的高度h 若h/hmax=0.7,则称为0.7孔径或0.7带光(带光球差)
2、 齐明点处的放大率
在顶点处
1)
=1
nL ' n = n'L n' n ' n 2 n r nL ' n n ' = n ' n n'L n ' n' r n
2)在球心处
3)在不晕点处
例题2
6.3
彗差及正弦差
一、 彗差(KT’、KS’)
(1)子午平面:由轴外物点和光轴所确定的平面,子午平面 内的光束称子午光束。 (2)弧矢平面:过主光线且与子午平面垂直的平面,弧矢平 面内的光束称弧矢光束。
6.2 光路计算
