Mathematica数学实验——简单数理统计
MATH5微分方程与数理统计

假设检验
❖ 1.总体数学期望的假设检验 <<Statistics`HypothesisTests` MeanTest[data,μ,KnownVariance->var]已知方差var,由数
据表data检验总体数学期望μ,求出P值(基于正态分布)
MeanTest[data, μ]由数据表data检验总体数学期望μ,求出P值
求x,y的相关系数
n
n
n
(xix)y (iy) (xix)2 (yiy)2
i 1
i 1
i 1
常用的分布计算
❖ 1.离散分布
<<Statistics`DiscreteDistributions`
BernoulliDistribution[p]
Bernoulli分布
BinomialDistribution[n,p]
<<Statistics`ContinuousDistributions`
NormalDistribution[μ,σ]
正态分布
UniformDistribution[min,max]
均匀分布
ExponentialDistribution[λ]
指数分布
StudentTDistribution[n]
t分布
mean求总体数学期望的置信区间(基于正态分布)
❖ StudentTCI[mean,se,dof] 用于方差未知,由样本平均值
mean求总体数学期望的置信区间(基于t分布),其中se= s ,而
dof是自由度(等于n-1)
n
❖ 例:铅的相对密度测量值服从正态分布,测量16次算出平均 值x=2.705,S=0.029。试求铅的相对密度的置信区间。
基于Mathematica的数学实验教学研究

提 高 学 生 学 习数 学 的 积 改
关 键 词 : 学 实验 ; 数 实践 ; 现 ; 新 ; ah m t a 发 创 M te ai c
学 的心理 障碍 , 强学 生学 习数 学 的兴趣 , 增 而且 还 可 以提高 学生 提 出问题 、 索问题 、 决 问题 的 能力 . 探 解
1 对 数 学 实 验 的 认 识
1 1 数 学 实验 是一 种新 的数 学课 程模 式 . 数 学 教学 中 的数学 实验 是从 给定 的实 际 问题 出发 , 利用 计算 机 系统作 为实 验工具 , 以数学 理论作 为 实验
第2 1卷 第 3期
2 2年 9 月 01
河 南 教 育 学 院 学报 ( 自然 科 学 版 )
Ju n l fHe a n tueo d c t n ( aua ce c io o ra n nI s tt fE u ai o i o N trl in eEdt n) S i
还 可 以解 决复 杂 的符号 运算 . 包含 了数 学多 方 向 的新 方 法和新 技 术 , 广泛 应用 于各 个学科 . 它 并
,
、
1 、
’ /
,
、
1 、n +1
/
借助于Mtmt , 将数学的抽 aeac 可以 h i a 象问 题具体化, 我们以数 a= +, , = 1 ) , = 列 I }b (+, c 1 I t t i
中 图分 类 号 : 4 . G6 2 0 文献 标 识 码 : A 文 章 编 号 :0 7—0 3 2 1 0 10 8 4( 0 2) 3—0 5 0 5—0 3
#Mathematica基础数学实验1

课程教学的基本要求
1. 掌握mathematica软件的基本使用方法; 2. 掌握高等数学中求极限, 导数, 微分, 复杂问题的 极值, 泰勒多项式(级数)的方法; 3. 掌握高掌握函数和解析几何图形的描绘; 5. 掌握线性代数中行列式计算, 矩阵的运算, 线性方 程组的求解, 特征值与特征向量的计算等问题; 6. 介绍线性规划问题的计算方法; 7. 掌握概率论中常见分布及其数字特征的计算; 8. 掌握数理统计中区间估计, 假设检验, 线性回归分 析问题的理论和计算问题.
实验九 矩阵的运算 实验十 矩阵的特征值与特征向量二次型的正交变换 实验十一 数学规划模型的计算 实验十二 概率论中常用计算 实验十三 区间估计与假设检验 实验十四 回归分析简介
注意: 需要观看程序, 请安装软件包mathematica5.0 版本.
实验一 了解Mathematica软件包 实验二 一元函数图形 实验三 求极限, 导数, 微分方法, 简单程序的编制 实验四 空间几何图形的描绘 实验五 微分学应用 实验六 积分计算 实验七 级数与近似函数 实验八 微分方程的解
讲授 与
实验
1/1
1.5/0.5
*
1/1
1/1
1.5/0.5
*
2/0 讲授 *
15.5/14.5
教学参考书:
1.《高等数学实验》: 章栋恩等主编, 高教出版社 2.《mathematica5.0在大学数学中的应用》丁大正 编,高教出版社 3.《数学实验室》: 白峰杉等译, 高教, Springer出版 社 4.《数学的原理与实践》: 申大维等译, 高教, Springer出版社 5.《Mathematica全书》: 赫孝良等译, 西安交大出 版社
欢迎同学们选修
mathematica 数学实验报告

数学实验报告实验一数学与统计学院信息与计算科学(1)班郝玉霞201171020107数学实验一一、实验名:微积分基础二、实验目的:学习使用Mathematica的一些基本功能来验证或观察得出微积分学的几个基本理论。
三、实验环境:学校机房,工具:计算机,软件:Mathematica。
四、实验的基本理论和方法:利用Mathematica作图来验证高中数学知识与大学数学内容。
五、实验的内容和步骤及结果内容一、验证定积分dttsx⎰=11与自然对数xb ln=是相等的。
步骤1、作积分dttsx⎰=11的图象;语句:S[x_]:=NIntegrate[1/t,{t,1,x}]Plot[S[x],{x,0.1,10}]实验结果如下:21图1dttsx⎰=11的图象步骤2、作自然对数xb ln=的图象语句:Plot[Log[x],{x,0.1,10}] 实验结果如下:2 1图2xb ln=的图象步骤3、在同一坐标系下作以上两函数的图象语句:Plot[{Log[x],S[x]},{x,0.1,10}] 实验结果如下:21图3dttsx⎰=11和xb ln=的图象内容二、观察级数与无穷乘积的一些基本规律。
(1)在同一坐标系里作出函数xy sin=和它的Taylor展开式的前几项构成的多项式函数3!3xxy-=,!5!353xxxy+-=,⋅⋅⋅的图象,观察这些多项式函数的图象向xy sin=的图像逼近的情况。
语句1:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,2]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:64242图4x y sin =和它的二阶Taylor 展开式的图象语句2:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,3]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,1,1]}] 实验结果如下:642321图5x y sin =和它的三阶Taylor 展开式的图象语句3:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,4]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,1,0]}] 实验结果如下:642321图6x y sin =和它的四阶Taylor 展开式的图象语句4:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,5]},{x,-2Pi,2Pi},PlotStyle->{RGB[1,0,0]}] 实验结果如下:642321图7x y sin =和它的五阶Taylor 展开式的图象语句5:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}] Plot[{Sin[x],s[x,2],s[x,3],s[x,4],s[x,5] },{x,-2Pi,2Pi}] 实验结果如下: 6422图8xy sin=和它的二、三、四、五阶Taylor展开式的图象(2)分别取n=10,20,100,画出函数xkkynk)12sin(1211--=∑=在区间[-3π,3π]上的图像,当n→∞时,这个函数趋向于什么函数?语句1:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,10],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}]实验结果如下:6420.5图9 n=10时,xkkynk)12sin(1211--=∑=的图像语句2:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,20],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:6420.5图10 n=20时,xk k y nk )12sin(1211--=∑=的图像语句3:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,100],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:6420.5图11 n=100时,xk k y nk )12sin(1211--=∑=的图像(3)分别取5,15,100,,在同一坐标系里作出函数x x f sin )(=与∏=-⋅=nk k x x x p 1222)1()(π在区间[-2π,2π]上的图像。
mathematica实验报告5张西西

mathematica实验报告5张西西Mathematica是一款强大的数学软件,可以进行各种数值计算和符号计算。
在本次实验中,我使用Mathematica进行了一些数值计算的实验,并总结了实验结果。
首先,我使用Mathematica计算了一元函数的数值积分。
通过使用内置的函数NIntegrate,我计算了函数f(x) = x^2在区间[0, 1]上的数值积分。
结果显示,该函数在该区间上的数值积分为1/3接下来,我进行了一元方程的数值求解实验。
我使用内置函数NSolve,求解了方程x^2 - 2x + 1 = 0。
结果显示,方程的解为x = 1然后,我进行了一些线性代数的实验。
首先,我使用内置函数LinearSolve,求解了线性方程组Ax = b,其中A是一个2x2的矩阵,b是一个长度为2的向量。
结果显示,方程组的解为x = {1, 2}。
接着,我使用内置函数Eigenvalues和Eigenvectors,计算了一个2x2的矩阵的特征值和特征向量。
结果显示,该矩阵的特征值为{-1, 2},特征向量为{{1, 2}, {1, -1}}。
最后,我进行了一些常微分方程的数值解实验。
我使用内置函数NDSolve,求解了一阶常微分方程dy/dx = y,初始条件为y(0) = 1、结果显示,该方程的数值解为y = Exp[x]。
综上所述,通过本次实验,我使用Mathematica进行了一些数值计算的实验,包括数值积分、方程求解、线性代数和常微分方程的数值解。
Mathematica的强大功能和简洁的语法使得这些实验变得简单而又高效。
我相信在未来的学习和工作中,Mathematica将会成为我不可或缺的工具。
Mathematica数学实验报告 实验三

数学实验报告实验三学院:数学与统计学院班级:信息与计算科学(1)班姓名:郝玉霞学号:201171020107实验三一、实验名:最佳分数近似值二、实验目的:研究怎样用分数近似值去给定的无理数作最佳逼近。
“最佳”就是既要误差小,又要分母小。
我们首先需要对“最佳”定出具体而明确的标准,还要寻找一个求最佳分数近似值的简单易行的算法。
三、实验环境:学校机房,Mathematica 软件。
四、实验的基本理论和方法:1、根据高中数学及大学数学中所学内容,经过分析研究,得出基本结论,利用Mathematica 来进行验证,并寻找一个求最佳分数近似值的简单易行的算法。
2、计算圆周率π“连分数展开”方法,并且利用特定的函数来展开其他数。
五、实验的内容和步骤实验步骤: 1、计算对数值对给定的正实数b ,N 且b ≠1,要求对数值a=N b log ,也就是求实数a 使a b =N ,如果能找到整数p ,q 使q pN b≈,则N b qp ≈,N b log qp≈,以lg2为例:由102=1024≈1000=310可得lg2≈103=0.3,再要提高精确度,就要找出更大的q 使q2更接近10的某个幂q10,也就是使p q32更接近于1。
练习题1:让q 依次取遍1到10000的所有的正整数,对每一个q ,按如下的递推法则求出一个正整数p=p(q)使实数p qq 102)(=λ最接近于1:q=1时,p(1)=0,λ(1)=01102=2.设已对q 求出p(q)和λ(q),计算2λ(q),如果2λ(q)<10,则取p(q+1)=p(q),λ(q+1)=2λ(q),如果2λ(q )≥10,则取p(q+1)=p(q)+1,λ(q+1)=10)(2q λ. 如果λ(q)比以前所有的λ(i)(11-≤≤q i )都更接近1,即|λ(q)-1|<|λ(i)-1|对所有3、Mathematica 中常用的展开数与多项式的函数的使用;的1≤i ≤q-1成立,就取qp都是最佳逼近lg2的的分数近似值,它们可以展开成小数近似值。
Mathematica实验报告

Mathematica 实验报告【实验名称】利用MA THEMA TICA 作图、运算及编程.【实验目的】1。
掌握用MA THEMATICA 作二维图形,熟练作图函数Plot 、ParametricPlot 等应用,对图形中曲线能做简单的修饰.2。
掌握用MATHEMA TICA 做三维图形,对于一些二元函数能做出其等高线图等,熟练函数Plot3D ,ParametricPlot 的用法。
3、掌握用MA THEMATICA 进行微积分基本运算:求极限、导数、积分等。
【实验原理】1.二维绘图命令:二维曲线作图:Plot[fx,{x ,xmin,xmax}],二维参数方程作图:ParametricPlot[{fx ,fy},{t ,tmin ,tmax}]2.三维绘图命令:三维作图plot3D [f,{x ,xmin ,xmax},{y,ymin ,ymax}],三维参数方程作图:ParameticaPlot3D[{fx,fy ,fz },{t ,tmin,tmax }]【实验内容】(含基本步骤、主要程序清单及异常情况记录等)1。
作出函数)sin(22y x z +=π的图形. 步骤: z=Sin [Pi Sqrt[x^2+y^2]];Plot3D [z ,{x,-1,1},{y,—1,1},PlotPoints →30,Lighting →True]2。
椭球面()⎪⎪⎩⎪⎪⎨⎧=∈⎪⎭⎫ ⎝⎛-∈==u z v u v u y v u x R R R R R R sin ,,,2,0,2,2,sin cos cos cos 332121πππ自行给定,作图. 步骤:ParametricPlot3D [{4Cos[u ]Cos[v],3Cos [u]Sin[v],2Sin[u]},{u ,—Pi/2,Pi/2},{v,0,2Pi}]3.做出极坐标描绘的图形:)cos 1(4θ+=r步骤:r [t_]:=4(1+Cos[t ]);ParametricPlot [{r [t ]Cos[t],r [t ]Sin [t]},{t,0,2Pi}]【实验结果】结果1:结果2:结果3:【总结与思考】MATHEMATICA作图的常见错误:General::spell1: Possible spelling error,因为在MATHEMATICA中作图函数大小写有区别.由于拼写间要有空格,易导致错误。
mathematica实验报告

mathematica实验报告Mathematica 实验报告一、实验目的本实验旨在深入了解和掌握 Mathematica 软件的基本功能和操作方法,通过实际的案例和问题解决,提升运用 Mathematica 进行数学计算、数据分析、图形绘制以及编程的能力。
二、实验环境操作系统:Windows 10Mathematica 版本:121三、实验内容与步骤(一)数学计算1、基本运算在 Mathematica 中,直接输入数学表达式进行计算,例如:计算 2+ 3 4 的结果,输入`2 + 3 4` ,得到结果 14。
2、函数计算使用内置函数进行复杂的数学运算,如计算正弦函数`SinPi / 6`的值,结果为 05。
(二)数据分析1、数据导入通过`Import` 函数导入外部数据文件,如 CSV 格式的数据文件。
假设我们有一个名为`datacsv` 的文件,包含两列数据`x` 和`y` ,使用`data = Import"datacsv"`即可将数据导入。
2、数据处理对导入的数据进行处理,如计算平均值、方差等统计量。
可以使用`Meandata` 计算平均值,`Variancedata` 计算方差。
(三)图形绘制1、二维图形绘制简单的函数图形,如`PlotSinx, {x, 0, 2 Pi}`绘制正弦函数在`0` 到`2 Pi` 区间的图形。
2、三维图形绘制三维图形,如`Plot3Dx^2 + y^2, {x, -2, 2},{y, -2, 2}`绘制一个抛物面。
(四)编程实践1、定义函数使用`Function` 关键字定义自己的函数,例如定义一个计算阶乘的函数`factorialn_ := Ifn == 0, 1, n factorialn 1` 。
2、循环结构使用`For` 循环和`While` 循环实现重复操作,例如使用`For`循环计算 1 到 10 的和,`sum = 0; Fori = 1, i <= 10, i++, sum += i; sum` 。
Mathematica数学实验[4]
![Mathematica数学实验[4]](https://img.taocdn.com/s3/m/48f870ff0242a8956bece4d9.png)
14
求极限
【实验目的】 (1)通过本实验深刻理解极限概念; (2)学习并掌握利用Mathematica求极限的基本方法。 【预备知识】 (1)极限、左极限、右极限的概念; (2)本实验所用Mathematica有关命令: x→ ● Limit[expr, x->x0] 求表达式在x0 时的极限 ● Limit[expr,x->x0,Direction -> 1] 求左极限 ● Limit[expr,x->x0,Direction ->-1] 求右极限
13
【实验内容与要求】 (1)计算 546 × 54564
46545 45676
(2)对于方程 x 4-2 x 3-4 x 2 + 3 = 0 试用Solve []和Nsolve[]分别对 它进行求解,并比较得到的结果,体会代数解即精确解与数值 解的差别。 (3)先观察函数 f ( x) = sin x − cos x 的图形,然后选择一个 初始点求解,并且根据图形确定在某个区间中搜索它的零点。
【实验内容与要求】
x +1 x 2 + 3x + 5
(1)求出被积函数F(x)= 的原函数和导函数,并画 出被积函数、原函数和导函数的图形,试分辨出哪一条曲线属于 哪个函数。 (2)对函数sinx在0点展开10阶和20阶,并以图形方式对比 展开的结果和sinx的差别,并分析阶数高的展式对于原来函数的 逼近程度是否优于阶数低的展式。
2
Mathematica 的编程 Mathematica可以有两种常用的工作方式: 一种是直接交互的指令行操作方式; 另一种是批处理方式。 为了更好的利用Mathematica,需要掌握基本的程序设计技 巧。Mathematica可以把很多命令放在自己定义的函数里, 也可以自己编写更加复杂的程序,下面着重介绍函数的定义和 编写程序的几个结构。
数理统计实验

§13.6概率统计实验[学习目标]1. 会用Mathematica 求概率、均值与方差;2. 能进行常用分布的计算;3. 会用Mathematica 进行期望和方差的区间估计;4. 会用Mathematica 进行回归分析。
概率统计是最需要使用计算机的领域,过去依靠计算器进行统计计算,由于计算机的普及得以升级换代。
本节介绍Mathematica 自带的统计程序包,其中有实现常用统计计算的各种外部函数。
一、 样本的数字特征1. 一元的情况Mathematica 的内部没有数理统计方面的功能,但是带有功能强大的数理统计外部程序,由多个程序文件组成。
它们在标准扩展程序包集的Statistic 程序包子集中,位于目录D :\Mathematica\4.0\AddOns\StandardPackages\Statistics下。
通过查看Help ,可以找到包含所需外部函数的程序文件名。
在程序文件DescriptiveStatistics.m 中,含有实现一元数理统计基本计算的函数,常用的有:SampleRange[data] 求表data 中数据的极差(最大数减最小数)。
Median[data] 求中值。
Mean[data] 求平均值∑=ni i x n 11。
Variance[data] 求方差(无偏估计)∑=--ni i x x n 12)(11。
StandardDeviation[data] 求标准差(无偏估计)∑=--ni i x x n 12)(11。
VarianceMLE[data] 求方差∑=-ni i x x n 12)(1。
StandardDeviationMLE[data] 求标准差∑=-ni i x x n 12)(1。
实际上程序文件中的函数很多,这里只列出了最常用的函数,其它计算函数可以通过Help 浏览。
例1 给出一组样本值:6.5,3.8,6.6,5.7,6.0,6.4,5.3,计算样本个数、最大值、最小值、均值、方差、标准差等。
Mathematica实验报告
实验名称Mathematica综合实验实验目的和要求:通过本次综合实验,进一步熟练掌握Mathematica系统中进行程序设计的基本方法,熟练运用各种综合性语句,完成Mathematica绘图、计算和编程等常用操作,进一步熟练掌握其功能和语法。
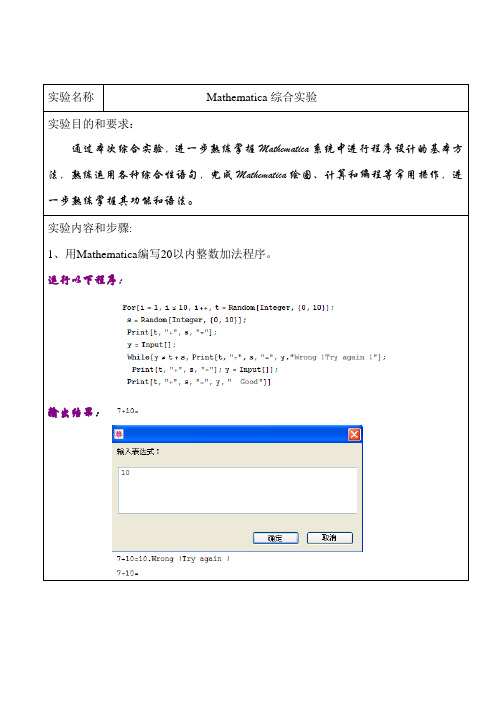
实验内容和步骤:1、用Mathematica编写20以内整数加法程序。
运行以下程序:输出结果:2、编写程序,列出9*9的乘法表来。
输入程序:9*9乘法表3、编写程序,输入两个正整数,用“辗转相除法”求它们的最大公约数。
辗转相除法:(1) 以大数m作被除数,小数n做除数,相除后余数为r。
(2) 若r ≠ 0,则m ← n,n ← r,继续相除得到新的r。
若仍有r ≠ 0,则重复此过程,直到r = 0为止。
(3) 最后的n就是最大公约数。
Mathematica代码如下:运行结果4、统计一个班级某次考试个分数段的人数。
输入程序:运行结果:5、编写程序用切线法求方程的解。
Mathematica语句和运行结果如下:6、编写Mathematica程序显示二维码图像。
输入程序:二维码图像7、用0~8这九个数字,组成一个二位数和一个三位数相乘使他们的积恰好是四位数.数字不能重复。
即□□×□□□=□□□□输入以下Mathematica程序:输出结果:8、用Mathematica编写程序绘制一个围棋棋盘.输入以下程序:围棋棋牌9、假设新开辟的国家公园里没有兔子和狐狸,现引进兔子和狐狸个50只,n 个月后兔子和狐狸的数量分别记为n R 和n F ,假定有⎩⎨⎧+=-=++nn n n n n F R F F R R 6.02.02.01.111Mathematica 程序如下:运行结果如下:注释:在一段时间内,兔子和狐狸的数量均会减少,但最终均会趋于一个稳定值。
10、有一个木工、一个电工和一个油漆工,三人协商合作装修他们的房子,并达成如下协议:a.每人总共工作10天(包括给自己家干活);b.每人日工资根据市场价确定在60 80 元之间;c.每人的总支出与每人的总收入相等。
Mathematica基础数学实验13

置信区间: {73.5243,126.476}, 即[73.5243,126.476].
此时的自由度dof极大可能不是整数, 如果查表, 则只好取一个近似整数, 否则无表可查.
例2 研究A,B两种机床生产的某种零件的尺寸. 抽 取A生产的18支, 测得方差为:0.34mm2; 抽取B生产的 13支, 测得方差为:0.29mm2. 两机床的生产相互独立, 但它们的均值, 方差均未知, 求两总体的方差比的置信 度为0.9的置信区间. FRatioCI[0.34/0.29,17,12,ConfidenceLevel->0.9]
2 s1
m
ห้องสมุดไป่ตู้
2 s2
n
, dof
n m
2 s1
2 2 1 s2 s1 m 1 m n 1 n
1
2
2
.
当数据量较大(m,n50)时, 依④和⑤作出的区间估计偏差不大.
4)单总体方差的区间估计 给出具体数据data时: VarianceCI[data, 选项] 5)两总体方差比的区间估计 给出具体数据data1, data2时: VarianceRatioCI[data1,data2, 选项]. 6) 给出概括数据时: 2统计量: ChiSquareCI[variance,dof, 选项]; F统计量: FRatioCI[ratio,mundof,fendof, 选项]. dof=m-1, mundof=m-1, fendof=n-1. 4),5),6)三者仅有选项: ConfidenceLevel->0.95.
3. 假设检验:
在以上假设检验中总是给出P(概率)值, 依据所给 显著水平比较作出判断.
第十章 Mathematica 数学实验

第十章Mathematica数学实验在学习了一系列的数学知识以后,如果我们能学会如何用计算机处理各类数学问题,则无疑使我们的数学应用能力有一个质的飞跃.用计算机处理各类数学问题,必须要有理想的数学软件. 在众多的数学软件中,Mathematica 以它的功能强大、应用面广、易学易用等优点得到了各国科研人员和工程技术人员的高度认同.Mathematica是由美国科学家Stephen Wolfram主持的一个科研小组开发的. 它的语法规则简单,操作语言与人们的日常语言非常相近. 在功能方面,除数值计算外,强大的符号运算功能和制图功能使得它一直享有盛名。
由于Mathematica能给出问题的解析符号解,从而使得用户能用该软件方便地处理微积分、微分方程、线性代数和规划优化等各类问题. 现在,Mathematica软件已在工程、科研、教学等各个领域被广泛使用。
在大学生的数学建模活动中,Mathematica也是非常得力的工具.本章将通过与本书配套的22个精编的数学实验问题,介绍Mathematica的各种基本命令以及相应的需要注意问题。
对于每个实验问题,书中都列出了供参考的求解命令及其计算结果.初学Mathematica,建议不妨先将本书中的各个问题的求解命令一一模仿输入,看看能否在计算机上顺利通过,能否得到正确的计算结果;遇有问题时再查阅本书中的“实验须知”及“说明”栏等处的文字,或直接向指导老师请教. 及早开展人机对话是迅速掌握Mathematica的捷径。
预期学会本章基本内容只需4至6学时.Mathematica系统从1.2版开始,经过多次升级换代,目前最新的版本为5.1版本. 各种版本都未见有中文版本。
本书将依照Mathematica英文5.1 版介绍Mathematica的语句.这些语句绝大多数也适用于Mathematica较为早期的版本.§10-1Mathematica实验一基本运算、函数与作图一实验内容四则运算、基本初等函数的求值、代数式的化简、函数的作图.二实验目的能熟练地使用Mathematica进行四则运算;并能熟练地对初等函数进行求值计算和作图操作;会用“Simplify”语句对函数或代数式进行化简;了解分段函数的定义和作图命令;了解三维作图的命令.三实验须知1.Mathematica的启动:在Windows环境下,点击“开始—程序—Mathematica 5.1—Mathematica 5.1”,即可启动Mathematica,此时计算机的屏幕将出现如图10-1的窗口。
“概率论与数理统计”中的几个数学实验

I[ :r3 ; n2 == O 】
n OБайду номын сангаас0 =l 0 0;
( 输入初始数据与模拟次数 )
I[] D [ = a l[ad m Itgr l 6 }{lr ;b a/ no; n3: oa T beR o [ ee, , 51d ,}b =a/ in = a n n { 3 , {l U s【:t eghb lr1 1i ,} s]IL n t[b<,, ,, n】 . [ 0 {l e= al[ [,,,1 c T be si(1 ] s ]i n ; ( 编 程 计算 } ) I[] p .ls n4: :Pu@@c / : c/ N ( 要求 概率 的近似值 )
关键词概率论与数理统计数学实验mathematica高校理科研究487科技信息in7quantileaa1095用另外一种方式计算上005分out7196751in8randomaa11生成一个参数为11服从的分布的随机数out8136576in9sss1tablerandomaa1110000生成10000个参数为11服从的分布的随机数in10gaphics加载图形包in11histogramsss1绘制直方图graphics例2student氏t分布in1clearnn16清除变量的赋值in2aa2studenttdistributionn产生一个服从参数为16的t分布的随机变量in3f2xevaluatepdfaa2x定义其概率密度函数in4plotf2xx66绘制概率密度函数的图形out4graphicsin5plotg2xx66绘制分布函数的图形out5graphicsin6findrootg2x095x13计算上005分位点out6x174588in7f2xdx验证上005分位点out700500003in8quantileaa2095用另外一种方式计算上005分out8174588in9randomaa2生成一个参数为16服从的t分布的随机数out9139094in10sss2tablerandomaa210000生成10000个参数为16服从的t分布的随机数in11graphics加载图形包in12histogramsss2绘制直方图out12gsphics例3f分布in1clearnmn16m19清除变量赋值输入参数值in2aa3fratiodistributionnm生成服从f1619分布的随机变量in3f3xevaluatepdfaa3x定义其概率密度函数in4plotf3xx09绘制概率密度函数的图形out4graphicsin5g3xevaluatecdfaa3xin6plotg3xx09绘制分布函数的图形out6graphicsin7findrootg3x095x9计算上005分位点out7x298897in8f3xdx验证上005分位点out800451076in9quantileaa3095用另外一种方式计算上005分位out9298897in10randomaa3生成一个服从f1619分布的随机数out10109471in11tablerandomaa310生成10个服从f161
mathematica 实验报告

Mathematica实验报告引言Mathematica是一款功能强大的数学软件,广泛应用于数学、科学和工程等领域。
本实验报告旨在介绍Mathematica软件的使用方法,并通过一系列实例演示其在数学问题求解中的应用。
实验步骤步骤一:安装和启动Mathematica首先,我们需要下载并安装Mathematica软件。
根据操作系统的不同,可以从官方网站或其他可靠来源获取安装文件。
安装完成后,双击启动Mathematica软件。
步骤二:创建新的NotebookMathematica使用Notebook作为工作环境,可以将其类比为一个电子文档。
在Mathematica启动后,点击“File”菜单,选择“New”并选择“Notebook”,即可创建一个新的Notebook。
步骤三:编写代码在Notebook中,我们可以编写Mathematica代码。
Mathematica的代码由一系列的函数、变量和运算符组成。
以下是一个简单的示例代码,用于计算平方根:a = 9;Sqrt[a]在上述代码中,我们首先定义了变量a的值为9,然后使用Sqrt函数计算变量a的平方根。
要执行代码,可以按下“Shift” + “Enter”键,Mathematica将输出计算结果。
步骤四:编辑和运行代码在Mathematica中,可以随时编辑和运行代码。
例如,我们可以更改变量a的值,并重新计算平方根。
只需修改代码为:a = 16;Sqrt[a]然后再次按下“Shift” + “Enter”键,Mathematica将根据新的变量a的值重新计算平方根。
步骤五:绘制图表Mathematica还提供了强大的绘图功能,可以可视化数据和函数。
以下是一个简单的示例代码,用于绘制正弦函数的图表:Plot[Sin[x], {x, 0, 2Pi}]在上述代码中,我们使用Plot函数绘制了正弦函数在0到2π范围内的图表。
执行代码后,Mathematica将显示出相应的图表。
Mathematica4.0使用方法(数学实验课讲义)

Mathematica4.0使用方法数学实验课教材首钢工学院Mathematica数学实验Mathematica 是一个交互式的计算系统.这里说的交互是指:在使用Mathematica 系统的时候,计算是在使用者(用户)和Mathematica 互相交换、转递信息数据的过程中完成的.用户通过输入设备(一般指计算机键盘)给系统发出计算的指令(命令),Mathematica 完成给定的计算工作后把计算结果告诉用户(一般通过计算机显示器).Mathematica 是一个集成化的计算机软件系统.它的主要功能包括三个方面:符号演算、数值计算和图形绘制.例如,它可以完成多项式的各种计算(四则运算、展开、因式分解);可以求多项式方程、有理式方程和超越方程的精确解和近似解;做数值的或一般表达式的向量和矩阵的各种计算;求一般函数表达式的极限、导函数、积分、幂级数展开,求解微分方程等等.根据教学大纲的要求及学校的课时安排(共12课时,内含2课时考试),我们将Mathematica数学软件的学习缩编成下面的四个实验,以期在短时间内使同学们掌握该软件的基本使用方法,学会用它解决高等数学中的一些常见问题.目录第一篇微积分 (1)实验一……………………………………………………实验二……………………………………………………实验三……………………………………………………实验四……………………………………………………第二篇线性代数……………………………………………………实验一……………………………………………………实验二……………………………………………………第三篇概率统计……………………………………………………第四篇复数与积分变换……………………………………………附录Mathematiac一部分函数及意义……………………第一篇微积分实验一一、实验目的1.学习在Windows下Mathematica 4.0软件的启动与退出,并熟悉其界面;2.建立文件与保存文件;3.学习用基本运算符号和模板进行加、减、乘、除、乘方、开方等常用的算术运算;4.学习表示计算结果的近似结果;5.会用符号或模板进行常见函数的输入及多项式的变换;6.会给变量赋值.二、内容与步骤1.Mathematica 4.0的启动与退出启动计算机,屏幕上显示Windows界面,单击“开始”进入主菜单,将鼠标移向“程序”,找到包含Mathematica 4.0的程序组,单击可执行程序Mathematica 4.0就进入了该系统,此时系统已进入交互状态,在等待用户输入命令.当软件使用完毕后,需要退出Mathematica系统时,只须单击工作窗口右上方的“File”菜单中选用命令“Exit”,或者按“Alt+F4”键均可退出系统,回到操作系统状态.例如:输入2+3后,按Enter+Shift组合键或右边小键盘上的Enter键运行,屏幕上就显示出In[1]:=2+3Out[1]=5其中In[1]:= 表示第一个输入,Out[1] = 表示第一个输出,它们是在运行后由系统自动显示的,用户不必输入.注意:若直接按左边的Enter键,只是在输入的组合命令中起换行的作用.2.建立文件与保存文件在工作窗口做好的某些内容,如果想要保留以供今后多次使用,通常是建立一个文件,将做好的内容保存在文件中.单击File/ Save as,在文件名N一栏内键入一个文件名,然后左击保存S.3.算术运算与模板的使用a):输入基本运算符号加+减-乘*(或用一个空格表示相乘)除/幂乘yx^优先运算:用圆括号,并可重复多次使用.b):模板的调出与运用方法一:在Mathematica 3.0以上版本的输入中,可以使用工具按钮输入各种运算,其步骤如下:①单击菜单栏中的文件File选项;②在下拉菜单中选择调色板Palettes选项;③在下一级菜单中单击基本计算BasicaCalculations选项,将会另外出现一个工具窗口;④在其窗口中单击计算与数值Arithmetic and Numbers选项前的符号“”,使其符号变成“▽”,将出现加、减、乘、除、乘方、开方等工具按钮;⑤单击需要的按钮,在原Notebook窗口中将会出现相应输入格式,将光标移到标有“□”的位置上,输入数值或表达式,就可以完成输入格式.方法二:在第③步,在下一级菜单中单击基本计算BasicInput 选项,出现一个常用的含有多种运算的模板(加、减可以直接从键盘输入+、-号) 4. 近似与精确 a ) 命令输入:N[表达式,n] 精确到n 位有效数字;N[表达式] 近似值按计算机默认的数位(6位)处理; [表达式]// N 同上;% 表示最近一次计算机运行后的输出结果;注意:1)当输出结果是610以下的数字,近似值按计算机默认的6位有效数字处理;610及610以上的近似值计算机按科学计数法处理.2)N[表达式,n] 表示精确到n 位有效数字(注:当n=1~16时,结果都按计算机默认的6位处理). b) 模板调出:与上述算术运算模板调出的方法一相同. 例1 1)输入: N310,结果显示:0.0141592653589792)输入:N ,结果显示: 3.1(按计算机默认的6位处理) 3)输入:N %, 表示对当前结果取18位有效数字近似 4)输入:4566000.66777777777777结果显示:4.5665.Mathematica中的常数、数学函数与常见的多项式变换a)直接从键盘输入(在英文状态下)Mathematica的常数:Pi 表示πE 表示eDegree (π/180)表示度I 表示虚数iInfinity 表示无穷大∞Mathematica中常用的数学函数:幂函数Sqrt[x] (求平方根) ;指数函数Exp[x] (以e为底的指数函数);对数函数Log[x] (以e为底的对数函数);Log[a,x] (以a为底的对数函数);三角函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x];反三角函数ArcSin[x],ArcCos [x],……;双曲函数Sinh[x],Cosh[x],Tanh[x],Coth[x],……;反双曲函数ArcSinh[x],…….Mathematica中常见的多项式变换:Factor[表达式] 将表达式分解因式Expand[表达式] 将表达式展开成多项式和的形式Simplify[表达式] 将表达式化简成最简形式Apart[表达式] 将表达式分解为部分分式之和函数表达式的运算规则有:1).它们都以大写字母开头,后面用小写字母.当函数名可以分成几段时,每一个段的头一个字母用大写,后面的字母用小写.例如,ArcSin[x].2).函数的名字是一个字符串,其中不能有空格.3).函数的自变量表用方括号括起来,不能用圆括号.4).多元函数的自变量之间用逗号分隔.b)模板介绍在Mathematica3.0以上版本的输入中,可以使用工具按钮输入各种函数,其步骤如下:①击菜单栏中的文件File选项;②在下拉菜单中选择调色板Palettes选项;③在下一级菜单中单击基本计算BasicaCalculations选项,将会另外出现一个工具窗口;在其窗口中单击三角与指数函数Trigonometric and Exponential Finctions选项前的符号“”,使其符号变成“▽”并列出子选项的清单;在此清单中单击三角Trigonometric选项前的符号“”,使其符号变成“▽”,将会出现一些三角函数和反三角函数工具按钮;单击需要的按钮,在原Notebook窗口中将会出现相应三角函数或反三角函数输入格式,将光标移到标有“□”的位置上,输入数值或表达式,就可以完成输入格式;在此清单中单击指数与对数Exponential and Logarithmic选项前的符号“”,使其符号变成“▽”,将会出现一些指数与对数函数工具按钮;单击需要的按钮,在原Notebook窗口中将会出现相应指数或对数函数输入格式,将光标移到标有“□”的位置上,输入数值或表达式,就可以完成输入格式;在此清单中单击双曲函数Hyperbolic选项前的符号“”,使其符号变成“▽”,将会出现一些双曲函数和反双曲函数工具按钮;单击需要的按钮,在原Notebook窗口中将会出现相应双曲函数和反双曲函数输入格式,将光标移到标有“□”的位置上,输入数值或表达式,就可以完成输入格式. 在其窗口中单击计算与数值Algebra 选项前的符号“”,使其符号变成“▽”,将出现Polynomial Manipulation ,Simplifyication 等工具按钮进行相关选择即可完成多项式的变换; 例2In[13]:=Log[2,3.256] Out[13]:=1.7031 例3:已知1 ,1232221-=-+=x p x x p ,计算2121 ,p p p p ⨯+,21p p ÷并将2121 ,p p p p ⨯+的结果分解因式、展开多项式,将21p p ÷的结果分解为部分分式 输入:p1 3x^22 结果显示: 12xp2 x^1P122x p11x212xp1Factor p11x1x21Expand p1p212x 4x 22x3Apart p 136. 变量赋值:命令格式:x= a 将值a 赋给变量xu=v=a 将值a 赋给变量u 、v (给多个变量赋值)f[x]/. x->a 变量x 赋值为a (求函数f[x]在x=a 时的值) u := 延迟赋值,按Shift+Enter 键没有结果输出,待给变量赋值运行后才有结果u= 直接赋值,按Shift+Enter 键后有结果输出 u=. 清除变量u 的值Clear[x] 清除变量x 的值,多用作清除函数注意:应随时将以后不再使用的变量的值清除掉,以免影响后面某些计算结果的正确性.习题一1. 计算1)62456log 3e -+并保留15位有效数字.2) sin(30)+tan(6π)并精确到小数点后7位.3)7lg 21arctan 1arcsin ++2. 给变量赋值并计算1) 若x=6,y=e,z=x+3y ,计算3z-5y 2+6(x-7)52)x=3,y=5π,计算(lgx )⨯arcos(2y)- 9并保留18位有效数字.3.设p1=2x-1, p2=3x-7, 求 p1×p2, 并展开它,再分解因式,最后将 1/(p1×p2)分解为部分分式. 练习过程及答案N 34Log 2,566,316.8.1.0z x 3y . x 6,y3z 5y 26 x 75. x 6,y ,z 665 23 69.000000000000000000.33490675722196522x 1 3x 12x 73Expandy9.实 验 二一、实验目的1、学习使用自定义函数,会求函数值;2、学习用绘图语句作函数图形;3、学习用解方程的语句解方程、方程组;4、会建立表,进行表的基本运算. 二、内容与步骤 1、自定义函数:一般函数: f[x_]= 表达式 定义的规则x 可以被替代 f[x_]:= 表达式 延迟赋值 f[x_]=. 清除f[x_]的定义Clear[f] 清除所有以f 为函数名的函数定义 分段函数:Which[条件1,表达式1,条件2,表达式2,…条件n ,表达式n]Which 语句是表示分段函数的常用语句. 例1:定义函数:x x x x f cos )(2++=,并求f (2)的值输入命令:显示输出: 4.9输入显示结果注意:f[2.]表示求自变量为2时函数的近似值;f[2]表示为精确值..10.例2:定义函数....0()0.. 0....0x x g x x x x >⎧⎪==⎨⎪-<⎩并求:)0(),3(),1(g g g -的值 输入命令g x_: Which x 0,x,x 0,0,x0,(将分段函数自定义成一个函数)显示结果 1 输入显示结果 3 输入显示结果 0注意:中括号内的等号要输成双等号 2.作图:1)基本作图命令格式(a )只规定自变量范围的作图命令:Plot[f(x),{x,x1,x2}](b) 不仅规定自变量范围,还规定因变量范围的作图命令Plot[f(x),{x,x1,x2},PlotRange->{y1,y2}](c) 不仅规定自变量范围,还可以加标注(函数名称,坐标轴) Plot[f(x),{x,x1,x2},PlotLabel->“表达式 ”,AxesLabel ->{“x ”,“y ”}11.2)观察函数图形的叠加情况设)...(),(21x f y x f y==,若在一个坐标系里观察这几个函数图像命令格式为:Plot[{ )(),(21x f x f },{x,x1,x2}]注意:不要将“ )(),(21x f x f ”写成“ )(),(21x f y x f y ==”例3:做出y=sinx 在[-4π4π]之间的图像Plot S in x , x ,4Pi,4例4:做出y=tanx 在[0,4π],y ∈[-5,5]之间的图像PlotT an x , x ,0,4 ,PlotRange 5,.12.例5:做出y=sinx,sin2x,sin3x 在[0,2π]内的标出坐标轴的且用三种不同颜色标示的图像.3) 分段函数的作图先利用条件语句Which 自定义分段函数,然后用Plot 语句画出分段函数的图形格式步骤:首先输入 f [x _]:= Which[条件1,表达式1,条件2,表达式2,…条件n ,表达式n]再输入 Plot[f(x),{x,x1,x2}] 例6 作出....0()0.. 0....0x x g x x x x >⎧⎪==⎨⎪-<⎩的图像g x _ : Which x 0,x,x 0,0,x0, Plot g x , x ,2,13 .4)参数方程作图使用 ParametricPlot 函数可以画参数形式的图形,格式如下: ParametricPlot[{x(t),y(t)},{t ,a ,b},可选项]ParametricPlot[{{x1(t),y1(t),{x2(t),y2(t)},...},{t ,a ,b},可选项]例7 画出圆的参数方程的⎩⎨⎧==ty tx sin cos ,0<t <2π曲线图形解 In[5]:=ParametricPlot[{Sin[t],Cos[t]},{t ,0,2Pi},AspectRatio ->Automatic] Out[5]:=AspectRatio :指定作图的纵横比例.系统默认值约0.618:1.可以为 AspectRatio 指定任何一个其他数值.如果希望系统按实际情况作图即纵横比例为1:1,则需要将这个可选项设置为Automatic . 5)二元函数的图像命令格式:首先定义二元函数: z[x_,y_]:=表达式 然后作图Plot3D[z[x,y],{x,x1,x2},{y,y1,y2}].14.例8 做出222y x z +=的图像输入: 输出:上述命令大多可以通过模板调出 ① 左击菜单栏中的文件File 选项; ②在下拉菜单中选择调色板Palettes 选项;③在下一级菜单中单击基本计算BasicaCalculations 选项,将会另外出现一个工具窗口;④ 在其窗口中单击图形Graphics 选项前的符号“”,使其符号变成“▽”并列出子选项的清单进行选择3.解方程: 1)解方程命令格式:Solve[f(x)= =0,x] 2) 解方程组命令格式:Solve[{f (x)= =0,g (y)= =0,…},{x,y,…}]15.上述命令可以通过模板调出 ①左击菜单栏中的文件File 选项; ②在下拉菜单中选择调色板Palettes 选项;③在下一级菜单中单击基本计算BasicaCalculations 选项,将会另外出现一个工具窗口;④在其窗口中单击图形Algebra 选项前的符号“”,使其符号变成“▽”并列出Solving Equations 选项的清单进行选择 例9 求方程063523=++-x x x 的根. 解: 输入Solve x 35x 23x 60 输出:例10 求方程组⎩⎨⎧=+=-ny x m y x 2的根 解: 输入Solvex 2y m,x y n , x ,输出:例11求解方程b x x =++-11 解: 输入输出:4.表的操作 1)表的生成.16.一维表:{a,b,c…}二维表(表中表):{{一维表1},{一维表2},{一维表n}…} 如:一维表{1,2,3},二维表{{1,2},{5,2},{6}}2)表中元素的提取一维表b 的第i 个元素: b[[i]] 或Part[[b,i]] 二维表b 的第i 个分表:b[[i]] 或Part[[b,i]] 二维表b 的第i 个分表中的第j 个元素: b[[i,j]] 如:b={{1,2},{5,2},{6}} b[[2]]-----显示 {5,2} b[[2,1]]----- -显示53)表的运算设b1,b2表示结构完全相同的两个表,表b1,b2的和、差、积、商等于对应元素的相应运算(分母不为零)b1={{1,2},{5,2},{6}},b2={{3,1},{0,2},{2}} b1+ b2={{4,3},{5,4},{8}}习题21. 解方程组⎪⎩⎪⎨⎧=+=342y x x y 2.f(x)=2x 2+5x-8, 求f (1) f (3)f( 2)作出图像3.作出⎪⎪⎩⎪⎪⎨⎧>-≤≤-<=2 (22)0........20................sin )(32x x x x x x x x f 的图像,并求f(0.3)17.4.作出y=cosx,cos2x,cos3x 在[0,2π],标出坐标轴并带有三种不同颜色的图像 答案:Solvey 2 4x,x y 3 , x ,yx 1,y 2 , x 9,y 6f x _2x^25x 85x 2fPlot f x , x ,5,5Graphicsg 0.0.79895Plot g x , x ,5,5GraphicsPlot C os x ,Cos 2x ,Cos 3x , x ,0,2Pi ,AxesLabel "x","y" PlotStyle R GBColor 1,0,1 ,RGBColor 0,1,0 ,RGBColor 0,0,1GraphicsSurfaceGraphics实 验 三一、 实验目的1.学习用软件计算极限,判断函数的连续性;2.学习用软件计算一元函数的导数、多元函数的偏导数;3.学习用软件计算隐函数、参数式函数的导数及函数的微分、全微分; 4.学习用软件计算微分方程的解; 5.导数的简单应用. 二、 内容与步骤 1. 极限、连续:1)求一元函数的极限的命令格式是:Limit[f[x],x ->x 0] 表示求函数x →x 0 的极限;Limit[f[x],x ->x 0,Direction ->1] 表示求函数x →x 0-的极限(左极限); Limit[f[x],x ->x 0,Direction ->-1] 表示求函数x →x 0+的极限(右极限).2)若x 趋于无穷,即 x → ∞,则格式为Limit[f[x],x → ∞] x 趋于负无穷或正无穷格式为:Limit[f[x],x → - ∞] , Limit[f[x],x → + ∞]3)注:->∞ 也可由File → Palettes → BasicInput 中的符号输入 例1 求下列函数的极限:(1)443lim 24---→x x x x输入: Limit[4 ,4432→---x x x x ]输出:5 (2)xxx 3arctan lim+∞→输入:Limit[ArcTan[x]3x,x→+∞]输出:0 (3)x x x 2)4751(lim -+∞→ 输入:Limit[x x 2)4751(-+,x→∞] 输出:例2 求 x x e --→133lim 及x x e +-→133lim输入:Limit[,x→3,Direction→1]Limit[,x→3,Direction→-1] (e 为BasicInput 符号栏中的 )输出:0 输出:∞还有一些函数没有极限,此时系统会进行相应的处理,返回一些特殊的结果.例3 求当x →0时,y =sinx1的极限. 解:输入:Limit[Sin[1/x],x→0]输出:Interval[{-1,1}]上面这个例子表示当x →0时,函数sin x1在-1与1之间无穷震荡,所以没有确定的极限.例4 判定函数⎪⎩⎪⎨⎧≤+>=02302sin )(x x x xxx f 在 x=0点是否连续.解:输入:Limit[Sin[2x]x,x →0,Direction→-1] 右极限 输出:2输入: Limit[3x +2, x →0, Direction→1]] 左极限 输出:2输入:3x+2/.x→0 计算函数值 输出:2∴ 函数在x =0这一点连续. 2. 导数、偏导数1)一阶导数)(x f '的命令格式为: D[f ,x] (f 为函数表达式,x 为自变量) 2)n 阶导数)()(x f n 的命令格式为: D[f,{x,n}] (n 为导数的阶数) 3)用BasicInput 工具栏输入: (函数表达式变量∂ 此时的函数表达式可以是一元或多元函数,变量可有一个或多个,使用灵活.如输入: x x 3(求一元函数x 3对x 的一阶导数) 输出:8x输入: x,x x 3(求一元函数x 3对x 的二阶导数) 输出:输入: x x 3y 4x (求二元函数x 3y 4对x 的一阶偏导数)输出:3x 2y 8输入: y x 3y 4x (求二元函数x 3y 4对y 的一阶偏导数)输出:x 38输入: x,x x 3y 4x (求二元函数x 3y 4对x 的二阶偏导数)输出:6x y输入:x,y x 3y 4x (求二元函数x 3y 4先对x 后对y 的二阶偏导数)输出:3x 21输入: y,y x 3y 4x(求二元函数x 3y 4对y 的二阶偏导数)输出:例1 求下列显函数的导数:(1)3532x x y += (2)x e x y 2= (3)12ln +=x x y 解:(1)输入: D[2 x 5+3 x 3,x]输出: 9x 2+10x 4(2)输入:x x输出:2 xx(3)输入:x Log x2x输出:例2 求函数22ln ),(y x y x f +=的偏导数x f ∂∂,y f∂∂,y x f ∂∂∂2解: 输入:输出:x输入: 输出:x输入:输出:例3 求函数5-202Q Q R =,当Q=15和Q=20时的()20)15(R R ''及 解:求函数在一点x 0处的导数值,只需在输入表达式后面再继续输入“/.x→x 0”即可.方法一:输入:D[Q ,5Q -Q 202]/.Q →15 输出:14 (即 (15)14R '=)输入:D[Q ,5Q -Q 202]/.Q →20 输出:12. (即 (20)12R '=)方法二:(函数表达式)变量∂/.x->a输入:输出:输入:输出:12例4 求函数f (x )=sin ax cos bx 的一阶导数dx df ,并求ba x dxdf+=1.解: 输入:x S in a x Cos b x.x a输出:例5 求下列函数的高阶导数:(1)5x y = 求:y ''' (2)x xe y 3= 求:y '' (3)xx xy cos sin sin += 求:y ''解:(1)输入:D[x ^5,{x ,3}]输出:60x 2(2)输入:D[x Exp[3 x],{x ,2}]输出:6 3x9输入:Simplify[D[Sin[x]/(Sin[x]+Cos[x]),{x,2}]] 输出:Cos[x]-Sin[x]Cos[x]+Sin[x]-22()()3. ㈠求隐函数的导数由方程F (x , y )=0 确定的函数)(x f y =,称为隐函数.方法:1)自定义一个导函数G[x_]对F (x ,y )求导,但必须将变量y 输入成y[x],即y 是x 的函数.2)用Solve 函数将y [x]'解出即可.即先求导再解方程.例6 求由方程12222=+by a x 所确定的隐函数的导数.解:方法一输入:D[2222x y[x]+a b-1,x ](先自定义一个导函数G[x],这里表达式中的y 应写成y[x])输出:22b [x]2y[x]y'a 2x + 输入:Solve[G[x]==0,y'[x]](用解方程Solve 命令,从导函数的方程G[x ]=0 中解出y'[x],这里方程必须使用双等号“==” )输出:{{y'[x] → -y[x]a xb 22}}方法二:利用工具栏与解方程语句:输入:输出:例7 已知方程0=-y xe xy 确定一个y 是x 的函数)(x f ,求 )(x f '. 解: 输入:Solve x xx y xy x0,y'输出:例8.设函数满足方程sin x x y ye +=0,求 ()y x '. 解:输入:Solve x x Sin y xy xx 0,y'输出:㈡ 求函数的微分、全微分求函数的微分dy ,其形式为Dt[f(x)].输出的表达式中所含的Dt[x],这里可以视为dx .求函数f (x, y )的全微分dz , 其形式为 Dt[f[x ,y]] 例9 求y =sin2x 的微分dy . 解: 输入:Dt[Sin[2x]]输出:2 Cos[2 x] Dt[x]例10 求函数x e x x y 23ln +=的微分dy . 解: 输入:Dt[x ∧ 3 Log[x]+Exp[2 x]]输出:2 e 2 x Dt[x]+x 2Dt[x]+3x 2Dt[x]Log[x] 再化简一下输入:Simplify[%]输出:Dt[x](2 e 2 x +x 2+3x 2 Log[x]) 即 dx x x x e dy x )ln 32(222++= 例11 求函数u xy z =23的全微分. 解: 输入:Dt[x y^2 z^3]输出:y 2 z 3 Dt[x] + 2 x y z 3 Dt[y] + 3 x y 2 z 2 Dt[z] ㈢ 参数式函数的求导形如 ⎩⎨⎧==)()(t x t y ψϕ 的函数为参数式函数,其导数 t t x x y y ''='. 其输入方式为:例12.设 ⎪⎩⎪⎨⎧==ta y ta x 33sin cos ,求 dx dy解: 输入: 输出:Ta例13.求椭圆⎩⎨⎧==tb y t a x sin cos 在 4π=t 处的导数解: 输入:输出:4.用 Mathematica 解微分方程其格式为: DSolve[微分方程,y[x],x] 注意要将y 输入成y[x] 例14 解微分方程 ()()y x y x '+=1解: 输入:DSolve[y'[x]+y[x]==1,y[x],x]输出:{{y[x]->1+xE C[1]}} 例15 求微分方程(x 2+y 2)dx -xydy =0的通解.解: 输入:DSolve[(x^2+y[x]^2)Dt[x]-x y[x] Dt[y[x]]==0,y[x],x]输出:{{y[x]->-Sqrt[x 2 (C[1]+2 Log[x])]},y[x]-> Sqrt[x 2 (C[1]+2 Log[x])]}}例16 求微分方程 ()x y xy '''+=212满足初始条件10==x y ,3'0==x y 的特解. 解: 输入:DSolve[{(x^2+1)y''[x]==2x y'[x], y[0]==1, y'[0]==3}, y[x],x]输出:{{y[x]-> 1+3 x +x 3}}5.导数的简单应用 (1)求函数的单调区间例17 求函数123+-=x x y 的单调区间解:函数的单调区间需要用到一阶导函数的图像、一阶导函数为零的驻点.输入:f x _ : x 32(建立函数) Plotf x ,f' x, x ,3,3 ,PlotStyle G rayLevel 0.01 ,Dashing0.01(画函数与导函数图像,其中虚线为导函数图像)输出:输入:Solve f ' x(求函数的驻点) 输出:观察图像,两个驻点将定义域分成三个区间,可看出函数在 ),32,(--∞),32(+∞内为增函数,在)32,32(-内为减函数.(2)求函数的极值例18 求函数21xxy +=的极值 解: 输入:g x _ : 1 Plotg x ,g' x, x ,3,3 ,PlotStyle G rayLevel 0.01 ,Dashing0.01输出:输入:Solve g ' x输出: x 1 , x(从图中可看出两驻点分别是极小值点和极大值点)输入: g输出:2(3)求极值的近似值 例19 求函数)2(cos 25)2(sin 222xx x y +=位于),0(π内的极值的近似值. 解:输入:Plot f x , x ,0,输出:观察图形,函数约在x=0.8、x=2.3处有极大值,在x=1.6处有极小值,可用命令FindMinimum 直接求极值的近似值,其格式为:FindMinimum[f[x],{x ,x 0}],求以x 0为初始点的局部极小值.FindMinimum 只可求极小值的近似值,欲求极大值的近似值,须将函数换成相反函数.输入: FindMinimum f x , x ,1 输出:1.94461, x 1.623即同时得到极小值1.94461和极小值点1.62391 输入:FindMinimum f x , x ,0输出: 3.73233,x 0.8641输入: FindMinimum f x , x ,2输出:2.95708,x 2.244即函数-y 的两个极小值和两个极小值点,从而得到函数y 的两个极大值和极大值点.(4)最大、最小值的应用例20 要制造一个容积为2,上端为半球形,下端为圆柱的粮仓,问:当圆柱的高和底半径为何值时,粮仓的表面积最小? 解: 设粮仓的表面积为S ,圆柱的高为h>0, 底半径为r>0.由题意,粮仓的容积2=323421 r h r ππ⋅+,则 )31 1(2 322223r r r r h -=-=πππ ∴粮仓的表面积S=⋅r 2π)31 1(22r r -π+324 42122r r r ππ+=⋅. 输入: FindMinimum[4/r+2πr 2/3,{r,10}] 输出:{6.09295,{r →0.984745}}.(5)微分方程的应用例21 一质量为m 千克的物体从高处下落,所受空气阻力与速度成正比,设物体开始下落时(t=0)的速度为零,求物体下落速度与时间的函数关系v (t). 解:设物体所受空气阻力为f ,由题得 kv f =(k 为比例系数),下落时所受重力为mg ,根据牛顿第二定律有 v m ma kv mg f mg '==-=- 输入:DSolvem v' t m g k v t ,v 0 0 ,v t输出: 输入:Simplif输出:习题3 (每小题中括号内为该题答案)1. 求导数:(1)tan )2xy =[(2)1124=y (3)sin cos cos x y y y -+=220 求 .y '(4)cos()sin ,y xy x =223求 .y ' 326s i n [3x ]c o s [3x ]+y s i n [x y ][]2ycos[xy]-xy sin[xy](5),6x e y x ⋅= 求 )1()5(y [4051e] (6)x y z cos = , 求 y x z z '' , [y Si ,Co](7)xy e z =,求 y x z z '' , [,](8)求 y e z x cos sin = 的二阶偏导数 [SinxCos x2Cos ySin xCos y Si,SinxCos x Si,Sin xCo] (9) 求函数 ⎪⎩⎪⎨⎧==-tt ey tex 的导数[(10)求函数 ⎩⎨⎧-=-=)cos 1()sin (t a y t t a x 的导数[2.求微分及全微分:(1)674335+-+=x x x y [7Dt x 12x 2Dt x 15x 4D] (2)32cot(ln )=x y ex[(3)xxx y ++=1sin ln [(4)y e z x sin = [ xCos y Dt yxDt x Si] (5))cos(y x x z += [Cos x y Dt x x Dt x Dt ySinx] 3.解微分方程 (1)求微分方程yxdx dy -=的通解. [(2)求微分方程0)1(22=++dy x dx xy 的通解.[(3)求微分方程x yx y dx dy tan +=的通解. [{y xx ArcSin x}] (4)求微分方程x x x y dxdysin 2cot =-的通解.[y x x 2Sin x C 1 Sin] (5)求微分方程42x y y x =+'满足初始条件61)1(=y 的特解. [ y x]4.求下列极限 (1)1lim1-+→x xx [∞](2)11lim31++-→x x x [31 ] (3)121lim +-∞→⎪⎭⎫⎝⎛+x x x x [ 2e ](4)判断函数 ⎪⎩⎪⎨⎧>≤-=0,0,1)(2x x x x x f 在 0=x 处是否连续? [ 不连续 ]实 验 四一、 实验目的1、 学习用软件计算不定积分;2、 学习用软件计算定积分、二重积分和广义积分;3、 定积分的简单应用,求平面面积和旋转体体积. 二、 内容与步骤 1.不定积分输入格式: BasicInput 符号栏中的符号注意:输出结果均不带积分常数. 例1 求下列不定积分 ⎰dx x5解:输入:x输出:6x 62. 定积分输入格式: BasicInput 符号栏中的符号例2 求下列定积分 ⎰-212 1dx x x解:输入:输出:3 例3 计算广义积分⎰+∞∞-+dx x 211解:输入:输出:例4 计算由抛物线2x y =和直线x y =所围成的平面图形的面积及该图形绕x 轴旋转一周所得的旋转体体积(表示出必要的步骤)解:(1)求交点输入:Solvey x,y x^2 , x ,输出: y 0,x 0 , y 1,x(2)作图 输入:Plotx ,x^2 , x ,2,输出:GraphClea Clea(3)定积分求面积输入:1 x x^2输出:6(4)定积分求体积输入:1x 2x输出:13.二重积分用Mathematica 计算二重积分的命令格式是:输入方法:先输入一元定积分符号,在中间积分变量的位置再输入一次定积分符号,作为累次积分的第一次积分.括号内为第一次积分,括号外为第二次积分. 例5 计算⎰⎰+1212x xxydy dx解: 输入:012xx 21x y输出:121 例6 计算⎰⎰+=Ddxdy y x I )(22, 其中D 由2 ,21,===y x y x y 围成解:①画平面区域图输入:输出:② Y - 型区域输入: 02y2yx 2y 2输出:3习题4(每小题中括号内为该题答案)求下列积分:(1)⎰-dx x x x)11(2[x+x](2)⎰+dx xsin 11[x 2Sin[]2x x Cos[]+Sin[]22] (3)⎰+dx x x 3)cos (sin [1(-9Cos[x]-Cos[3x]+9Sin[x]-Sin[3x])6](4)2ln(sin )sin x dx x⎰[ -x-Cot[x]-Cot[x] Log[Sin[x]]] (5)⎰xdx x arctan 2 [(6)21sin 1cos x xdx x++⎰ [(7)⎰--1145dx xx [6](8)⎰∞--02dx xex [](9)[2](10) 计算由曲线282yx =-和x 轴所围成的平面图形的面积及该图形绕x 轴旋转一周所得的旋转体体积(表示出必要的步骤)[3,(11)计算由曲线21yx =-和22y x =+所围成的平面图形的面积及该图形绕x 轴旋转一周所得的旋转体体积(表示出必要的步骤) 过程: Solvey x 21,y 2x 2 , x ,y 0,x 1 , y 8,xPlotx 21,2x 2 , x ,2,Graph132x 2 x 213132x 2 ^2 x 21 ^2(12)计算二重积分3y Ded σ-⎰⎰,其中D 由20,1,x y y x ===围成过程:①画平面区域图② Y - 型区域1y 2 y3第二篇 线性代数实验 一一、实验目的6.掌握Mathmatica 中矩阵的输入方法; 7.学习用Mathmatica 软件计算行列式;8.学习用Mathmatica 软件进行矩阵的基本运算; 9.学习用Mathmatica 求逆矩阵及矩阵的秩.二、内容与步骤1.Mathmatica 中矩阵的输入方法 (1)按表的格式输入: (一般方法)}}{},{},{{1212222111211mn ,m ,m n ,,n ,,a a a a a a a a a A ,生成m 行n 列的矩阵(2)菜单输入:(适用于大矩阵) a)打开主菜单Input 项;b)单击Create Table/Matrix 项,输入行数及列数,填数即可。
综合数学实验报告(mathematica)

综合数学实验报告(mathematica)数学综合实验报告学院:数学与统计学院专业:数学与应用数学姓名:##########学号:##########班级:##########综合实验实验一:观察数列极限一、实验目的利用数形结合的方法观察数列的极限,可以从点图上看出数列的收敛性,以及近似地观察出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
通过此实验对数列极限概念的理解形象化、具体化。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用的函数及函数调用的方法;2、对Fabonacci数列、调和级数以及3n+1问题规律的掌握。
四、实验内容及步骤设为实数列,为定数.若对任给的正数,总存在正整数,使得当时有,则称数列收敛于定数称为数列的极限,并记作或。
下面,我们以求为例进行实验,程序编写及运行如下:程序运行结果如下:五、实验结果和结果分析由运行结果和图像可知,发现在时,函数值无限靠近2.7左右。
实验二:函数图像绘制一、实验目的通过函数图形来认识函数,运用函数的图形来观察和分析函数的有关性态,建立数形结合的思想。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用绘图函数Plot在绘制一元函数时的方法;2、函数迭代法的基本理论以及在Mathematica中的使用。
四、实验内容及步骤1、求的所有根(先画图再求解)。
2、求方程与的根。
3、求下列各题的解。
(1);(2),求;(3)(精确到17位有效数字);(4);(5)将在处展开(最高次幂为8);(6),求。
4、作sinx的n阶Taylor展开(n=10,30,60)并比较图像5、已知函数,作出并比较当分别取-1,0,1,2,3时的图形,并从图形上观察极值点、驻点、单调区间、凹凸区间以及渐近线。
在mathematica中输入下面语句:Do[Plot[1/(x^2+2x+c),{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]],{c,-1,3}]程序运行结果如下:实验结果和结果分析观察图可得:第一幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间为,渐近线为水平,垂直, .第二幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间.第三幅图:没有极值点,没有驻点,单调增区间为,单调减区间为,凸区间为、.第四、五幅图:极大值点为,驻点为,单调区间为增,减,凸区间为、.实验三:泰勒公式与函数逼近一、实验目的利用Mathematica计算函数的各阶泰勒多项式,并通过绘制曲线图形,根据图形观察泰勒展开的误差,进一步掌握泰勒展开与函数逼近的思想,并对泰勒公式与原函数作出比较。
Mathcad2001-数学运算-数理统计与数据处理

求平均值: mean(data)=-0.17 求中值: median(data)=-0.022 求标准偏差:SD(data)=0.883 求方差: SD(data)=0.779
(2)统计分布函数
Mathcad2001提供十几种统计分布函数, 其中每一个又包括四个函数:统计分布 密度函数、累积分布密度函数、逆统计 分布函数以及统计分布的随机点列生成 函数,这四个函数的首字母依次是:d、 p、q和r。因此,每个函数的名称是首字 母+分布类型的名称,如F分布的四个函 数名称依次是:dF、pF、qF和rF。下面 我们仅列出一些统计分布密度函数:
首先使用两个向量输入表中的数据:
相关系数 corr(X,Y)=-0.9998
截距
b:=intercept(X,Y)
b=6.58302
A:= eb0
A=722.72014
斜率
b:=slope(X,Y)
b=-0.08393
求x=25时y的值 x:=25
y:= b0+ b1x y=4.48472
求y=980时x的值 y:=980 x:= y b0
intercept(vx,vy) : 给 出 一 组 数 据 点 的 拟 合直线的截距。
其中vx和vy均为实值向量,vx中的元素值 对应于x的值,vy中的元素值对应于样本值y, 且vx必须为升序,vy中的元素个数应与vx中的 一致。
例1:进行下表所列数据的线性回归
X 10 15 20 25 30 Y 1003 1005 1010 1011 1014
ksmooth(vx,vy,b):得到一个m维向量, 该向量由用高斯内核(Gaussian kernel) 进行平滑处理,以得到vy中元素的加权 平均。常用于数据点的间距相对恒定时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教师指导实验6
实验名称:简单数理统计
一、问题:求样本数据的特征数字值;绘制样本的频率分布条形图和直方图。
二、实验目的:
学会使用Mathematica求求样本数据的极差、中位数、均值、方差及标准差;绘制样本的频率分布直方图并作简单的修饰。
三、预备知识:本实验所用的Mathematica命令提示
1、SampleRange[data] 求样本数据data的极差(最大数减最小数);
Median[data] 求样本数据data的中位数;
Mean[data] 求样本数据data的均值;
2、VarianceMLE[data] 求样本数据data的方差;
StandardVarianceMLE[data] 求样本数据data的标准差;
3、BarChart[data1, data2,…] 分别绘制样本数据data1,data2,…的条形图
图形修饰选项:
BarSpacing 设置两条形的总宽度,设置值是实际宽度相对于区间宽度的比值;
BarGroupSpacing 设置相邻条形的宽度,设置值是条形的实际宽度相对于条形的总宽度的比值;
BarStyle 条形风格设置;BarEdgeStyle 条形边界风格设置;
BarLabels 条形标签设置,PlotLabel 图形名称设置,
4、Histogram[data] 绘制样本数据data的频率分布直方图
图形修饰选项:
Ticks设置标记相对于条形的位置;
HistogramScale 设置条形高度为频率密度,使条形的面积和为所设置的值。
四、实验的内容和要求:
1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;
2、对以上数据绘制样本频率分布直方图;
3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
五、操作提示
1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;
In[1]:=<<Statistics`DescriptiveStatistics`
In[2]:=data=Table[Random[Integer,{1,20}],{60}];
In[3]:=SampleRange[data]
Out[3]= 19
In[4]:= Median[data] Out[4]= 11
In[5]:=Mean[data]
Out[5]=221 20
In[6]:=VarianceMLE[data]
Out[6]=44017 1200
In[7]:=StandarDevarianceMLE[data]
Out[7]=
2、对以上数据绘制样本频率分布直方图;
In[8]:=<<Graphics`Graphics`
In[9]:=Histogram[data]
Out[9]= -Graphics-
In[10]:=Histogram[data,Ticks->IntervalCenters, HistogramScale->1]
Out[10]= -Graphics-
In[11]:=Histogram[data,Ticks->IntervalBoundaries,
HistogramScale->2]
Out[11]= -Graphics-
3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
BarChart[{1,3,4,5,3.5,3},{3,2,5,3}]
In[12]:=
In[13]:=BarChart[{1, 3, 4, 5, 3.5, 3}, {3, 2, 5, 3},
BarSpacing -> 0.7, BarGroupSpacing -> 0.5,
BarStyle -> {BGBColor[1,0,0], BGBColor[0,1,0.2]},
BarEdgeStyle->{{Dashing[{.01}],BGBColor[0,0,1]},
GrayLevel[0]},
BarLabels ->{"Apr","May","Jun","Jul","Aug","Sep"},
PlotLabel -> "Projected and Current Profit,Tourist Season",
DefaultFont -> {"Helvetica", 11}]
Out[13]= -Graphics-
学生实验6
实验名称:简单数理统计
一、问题:求样本数据的特征数字值;绘制样本的频率分布条形图和直方图。
二、实验目的:
学会使用Mathematica求求样本数据的极差、中位数、均值、方差及标准差;绘制样本的频率分布直方图并作简单的修饰。
三、实验的内容和要求:
1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;
2、对以上数据绘制样本频率分布直方图;
3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
五、操作提示
1、取50个在1到20的随机整数,求这组数的极差、中位数、均值、方差及标准差;
In[1]:=<<Statistics`DescriptiveStatistics`
In[2]:=data=Table[Random[Integer,{1,20}],{60}];
In[3]:=SampleRange[data]
Out[3]= 19
In[4]:= Median[data]
Out[4]= 11
In[5]:=Mean[data]
Out[5]=221 20
In[6]:=VarianceMLE[data]
Out[6]=44017 1200
In[7]:=StandarDevarianceMLE[data]
Out[7]=
2、对以上数据绘制样本频率分布直方图;
In[8]:=<<Graphics`Graphics`
In[9]:=Histogram[data]
Out[9]= -Graphics-
In[10]:=Histogram[data,Ticks->IntervalCenters,
HistogramScale->1]
Out[10]= -Graphics-
In[11]:=Histogram[data,Ticks->IntervalBoundaries, HistogramScale->2]
Out[11]= -Graphics-
3、data1={1, 3, 4, 5, 3.5, 3}, data2={3, 2, 5, 3},在同一图表中绘制data1和data2的条形图,并作一定的修饰。
In[12]:=BarChart[{1,3,4,5,3.5,3},{3,2,5,3}]
Out[12]= -Graphics-
In[13]:=BarChart[{1, 3, 4, 5, 3.5, 3}, {3, 2, 5, 3},
BarSpacing -> 0.7, BarGroupSpacing -> 0.5,
BarStyle -> {BGBColor[1,0,0], BGBColor[0,1,0.2]},
BarEdgeStyle->{{Dashing[{.01}],BGBColor[0,0,1]},
GrayLevel[0]},
BarLabels ->{"Apr","May","Jun","Jul","Aug","Sep"},
PlotLabel -> "Projected and Current Profit,Tourist Season",
DefaultFont -> {"Helvetica", 11}]
Out[13]= -Graph。
