2.5热力学第二定律公式的导出
热力学第二定律

热机在最理想的情况下,也不能把所吸收的热全部
转化为功,而有一个限度(极限)。η<1(η≠1)
2、卡诺循环
(1)设想由四个可逆步骤构成。 (汽箱中物质的量为1m膨胀:曲线AB段
从高温热源T2吸 热Q2, 作功W1;
ΔU=0 Q2 = -W1=RT2ln(V2/V1)
结论:热传递的自发过程具有不可逆性。
(2)热功转化的方向性: ① 功可以完全变为热,而不引起其他变化 —自发过程(经验所得);
② 热不可能完全变为功,而不引起其他变化
—非自发过程(经验所得)。
例1 重物推动活塞,活塞带动涡轮转动,活塞和涡轮与
水摩擦生热,功完全变为热;逆过程不可能自动实现。 即热完全变为功而不产生任何影响是不可能的。
2、克劳修斯不等式和熵增原理
(1)不等式:
掌握
卡诺定理
δQ1 / T1 +δQ2 / T2 ≤ 0
熵导出中推广了可逆情况,即∑(δQr / T)= 0 或 ∮(δQr / T)= 0 对任何不可逆过程可同样推广,即 ∑(δQ / T )< 0 或 ∮(δQ / T)< 0
综合得: ∑(δQ / T )≤ 0
(2)证明:见P55
在两个热源之间有卡诺热机R 和任意热机I 设ηI> ηR 则有:W/ > W 据能量守恒定律有:|QI /|< Q1| 从W/中取出W对热机R作功驱 动其反转,从低温热源取出Q1 转入到高温热源
结果是:高温热源没有任何变化;低温热源损失了 |Q1|- | Q1/|热;环境得到W/ –W功。
(见P52 图2.2 卡诺循环 ) ↑
↓
D(T1、V4、P4 )a,r←C(T1、V3、P3 )T,r
(3)结果分析:
第三章 热力学第二定律

第三章热力学第二定律热力学第一定律过程的能量守恒热力学第二定律过程的方向和限度§3.1 热力学第二定律(1)过程的方向和限度自发过程:体系在没有外力作用下自动发生的变化过程,其有方向和限度。
例如:水位差、温度差、压力差等引起的变化过程。
自发过程,有做功能力方向:始态终态反自发过程,需消耗外力平衡状态限度:始态终态无做功能力自发过程的共同特征:不可逆性(2)热力学第二定律的表达式经典表述:人们不能制造一种机器(第二类永动机),这种机器能循环不断地工作,它仅仅从单一热源吸取热量均变为功,而没有任何其它变化。
一般表述:第二类永动机不能实现。
§3.2 卡诺循环1824年,法国工程师卡诺(Carnot)使一个理想热机在两个热源之间,通过一个特殊的可逆循环完成了热→功转换,给出了热机效率表达式。
这个循环称卡诺循环。
(1)卡诺循环过程设热源温度T1 > T2,工作物质为理想气体。
卡诺循环1. 恒温可逆膨胀(A → B ):0U 1=∆ 12111V V lnnRT W Q == 2. 绝热可逆膨胀(B → C ):0q =, )T T (nC U W 21V 22-=∆-=3. 恒温可逆压缩(C → D ):0U 3=∆, 342322V V lnnRT W q Q ==-= 4. 绝热可逆压缩(D → A ):0q =, )T T (nC U W 12V 44-=∆-=整个循环过程的总功为:34212112V 34221V 1214321V Vln nRT V V lnnRT )T T (nC V Vln nRT )T T (nC V V ln nRT W W W W W +=-++-+=+++= 热机循环一周有:0U =∆, W q Q Q Q Q 2121=-=+=热机效率:1213421211V V ln nRT V Vln nRT V V lnnRT Q W+==η对于绝热可逆膨胀:k12312V V T T -⎪⎪⎭⎫ ⎝⎛=对于绝热可逆压缩: k14121V V T T-⎪⎪⎭⎫ ⎝⎛=比较得:1423V V V V =或 4312V V V V = 则: 121121Q Q Q T T T +=-=η η— 卡诺热机效率(2) 卡诺定理卡诺定理:一切工作于高温热源T 1与低温热源T 2之间的热机效率,以可逆热机的效率为最大。
热力学第二定律

第二章热力学第二定律2.1 自发变化的共同特征自发变化某种变化有自动发生的趋势,一旦发生就无需借助外力,可以自动进行,这种变化称为自发变化。
自发变化的共同特征—不可逆性任何自发变化的逆过程是不能自动进行的。
例如:(1)焦耳热功当量中功自动转变成热;(2)气体向真空膨胀(3)热量从高温物体传入低温物体;(4)浓度不等的溶液混合均匀;(5)锌片与硫酸铜的置换反应等,它们的逆过程都不能自动进行。
当借助外力,体系恢复原状后,会给环境留下不可磨灭的影响。
2.2热力学第二定律(T h e S e c o n d L a w o f T h e r m o d y n a m i c s)克劳修斯(Clausius)的说法:“不可能把热从低温物体传到高温物体,而不引起其它变化。
”开尔文(Kelvin)的说法:“不可能从单一热源取出热使之完全变为功,而不发生其它的变化。
” 后来被奥斯特瓦德(Ostward)表述为:“第二类永动机是不可能造成的”。
第二类永动机:从单一热源吸热使之完全变为功而不留下任何影响。
2.3卡诺循环与卡诺定理2.3.1卡诺循环(C a r n o t c y c l e)1824 年,法国工程师N.L.S.Carnot (1796~1832)设计了一个循环,以理想气体为工作物质,从高温T h热源吸收Q h的热量,一部分通过理想热机用来对外做功W,另一部分Q c的热量放给低温热源T c。
这种循环称为卡诺循环.1mol 理想气体的卡诺循环在pV图上可以分为四步:过程1:等温T h 可逆膨胀由 p 1V 1到p 2V 2(AB)10U ∆= 21h 1lnV W nRT V =- h 1Q W =- 所作功如AB 曲线下的面积所示。
过程2:绝热可逆膨胀由 p 2V 2T h 到p 3V 3T c (BC)20Q = ch 22,m d T V T W U C T =∆=⎰所作功如BC 曲线下的面积所示。
2.5-2.6热力学第二定律 第三定律 演示文稿

T
2.5.3 克劳修斯提出熵的概念
• 对于不可逆过程,克劳修斯写道:“在一循 环过程中所有变换的代数和只能是正数。即 N>0。他将这种变换称为”非补偿的“变换。 • 虽然在上式中,等价值N是不严格的(因为 没有采用绝对温标),但N这个函数已经具 备了熵的基本特性。 • 1865年,克劳修斯发表《热的动力理论的基 本议程的几种方便形式》,他明确用T表示绝 对温标,提出用S表示Q/T,认为S是只与状 态有关的量,并且建议将其命名 为”Entropie( 熵)“。
2.5.2 W.汤姆生研究热力学第二定律
开尔文在1852年发表的“关于自然界中机械 能耗散的普遍趋向”一文中,把克劳修斯的 公理说成是:一台不借助任何外界作用的自 动机器,把热从一个物体传到另一个温度比 他高的物体,这是不可能的。今天把他说成: 热不能自动地有低温物体转移到高温物体上 去。这就是称之为热力学第二定律的克劳修 斯表述。
2.6.1
气体的液化与低温的获得 --液化工作的改进
• 1883年,波兰物理学家乌罗布列夫斯基(S。 Wroblewski,1845-1888)和化学家奥耳舍夫斯 基(K.Olszewski,1846-1915)合作,将以上 两种方法综合运用,并作了两点改进:
– 一是将液化的氧用一小玻璃管收集; – 二是将小玻璃管置于盛有液态乙烯的低温槽中 (温度保持在-130℃),这样他们就第一次收 集到了液氧。
p 完 全 液 体 48.1℃ 完全汽化 C (临界点) 31.3℃ B c D b 汽液平衡区 V
2.6.1 气体的液化与低温的获得 --氧的液化 • 1877年,几乎同时由两位物理学家分别用不同的方 法实现了氧的液化。
– 法国人盖勒德(Louis Paul Cailletet,1832-1913)将纯净的 氧压缩到300大气压,再把装有压缩氧气的玻璃管置于二 氧化硫蒸气(-29℃)中,然后令压强突降,这时在管 壁上观察到了薄雾状的液氧。 – 瑞士人毕克特(Paous-Pierre Pictet,1846-1929)从日内 瓦打电报给法国科学院:“在320大气压和140冷度(即 -140℃)下联合使用硫酸和碳酸液化氧取得成功。”他 用真空泵抽去液体表面的蒸气,液体失去了速度最快的 分子而降温,然后用降温后的液体包围第二种液体,再 用真空泵抽去第二种液体表面的蒸气,它的温度必然低 于第一种液体,如此一级一级联下去,终于达到了氧的 临界温度。
热力学第二定律

3. 我们可根据“第二类永动机不可能造成”这一结论 来判断一指定过程的方向。 例如在任意一个过程中,令系统的状态先由A变 到B,再让它逆向进行,假若再由B变到A时将能构成 第二类永动机,则可断言,该系统由A变到B的过程是 自发的,而由B自动变到A是不可能的。 这样的判断方法太抽象,在考虑能否构成第二类 永动机时需要繁杂的手续和特殊的技巧,并且不能指 出过程进行的限度。在第二定律中最好能找到像热力 学第一定律中的内能U和焓H那样的热力学函数,只要 计算此函数的变化值,就可判断过程的方向和限度.
然而,随着对更多的反应进行研究,发现有 不少吸热反应仍能自动进行。例如: 高温下的水煤气反应: C(s) +H2O(g)→CO(g)+H2(g) 事实说明,热力学第一定律只有告诉人们一 化学反应的能量效应,但不能告诉人们在一 定条件下指定化学反应能否自动发生,以及 进行到什么程度为止,亦即不能解决化学变 化的方向、限度问题。
(2) 热由高温物体传向低温物体
设有高温热源T2及低温热源T1。其热容均为无 限大,现有Q2的热从高温热源T2传向低温热 源T1 。 环 境
Q=W
T2
Q’=Q2+W
Q2
W
机器
Q2 T1 T 1
(3) 镉放入氯化铅溶液变成氯化镉溶液和铅 Cd (s)+PbCl2(aq)=CdCl2(aq)+pb(s)
决定自发过程的方向和限度的因素是什么?
上述各类不同的过程有着不同的决定因素: 决定热传导方向及限度的因素是温度T; 决定气体流动方向及限度的因素是压力p; 决定电流方向及限度的因素是电压V。 决定化学反应方向和限度的因素是什么呢? 需要找出决定一切自发过程变化方向及限度的共 同因素,这个共同因素既能判断一切自发过程的方向 和限度,也能用来判断化学过程的方向及限度。这个 共同因素究竟是什么?这就是热力学第二定律所要解 决的中心课题。
2第二章 热力学第二定律

/ S 2 定压
/ 1
/
三、理想气体PVT均变化过程的熵变
理想气体发生(T1V1---T2V2)状态变化:
V2 S nR ln nCv , mLn T 2 T1 V1
理想气体发生(T1P1-----T2P2)状态变化:
p1 S nR ln nCP , mLn T 2 T1 p2
13
第三节 熵的概念—熵与熵增原理
一、可逆循环过程与可逆过程的热温商: 对于一任意可逆循环过程:
p
a
2
QR Q R T T 0
再将循环分成途径a(12)和b(21), 有
1 QR 0 1 2 T a T b 2 QR
1
b
第二类永动机:从单一热源吸热使之完全变为功而不留 下任何影响的机器。
7
第二节 卡诺循环与卡诺定理 蒸气机发展史上研究热机效率的初衷, 只是寻求解决 热功转化的方向和限度问题。 热不能完全转化成功,如何在理论上求热功转化的 最大效率?
1824年Carnot N L S 提出热机效率有一个极限; Clausius R J E和Kelvin L 分别于1850年和1851年得出了热力学 第二定律.
4
第一节 自发过程的共同特征-不可逆性 • 要使环境也恢复原状,则取决于在不引起其他变化 的条件下,环境得到的热能否全部转变为功。
• 自发过程的不可逆性本质: • 功和热转化的不可逆性-----功可以全部转变为热, 但在不引起其他变化条件下,热不能全部转变为功。 要使热全部转变为功,必然引起其他变化(即一定 有一部分热传给温度较低的热源。 所以实际可能发 生的过程都必然是不可逆的.)
二、不可逆循环过程与不可逆过程的热温商
物理化学02章_热力学第二定律02

S体系
Qr Qsurr Qsys Q Δ S环 = = = Tsurr Tsurr Tsurr T
Δ S 总 =Δ S 体 + Δ S 环 ≥ 0
上一讲回顾
(1) 熵变的计算: 可逆过程,直接计算过程的热温商 不可逆过程,设计可逆过程计算。 (2) 等温过程,变温过程及相变过程熵变的计算 (3) 利用熵变判断过程的方向
a)恒 T 可逆 b)恒 T 不可逆 V2 V2 V2 Δ S 总 = nRTLn +(-nRLn ) Δ S 总 = nRTLn + 0 V1 V1 V1
= 0
V2 = nRTLn > 0 V1
等温过程的熵变
例: 1mol理想气体在等温下通过:(1)可逆膨胀,(2)真 空膨胀,体积增加到10倍,分别求其熵变。 解:(1)可逆膨胀
简化:
V2 P2 等 T:Δ S= nRLn =- nRLn V1 P1 T2 等 P:Δ S= CP Ln T1
T2 等 V:Δ S= CV Ln T1
变温过程的熵变
1. 先等温后等容 2. 先等温后等压 3. 先等压后等容
T2 nCV ,m dT V2 S nR ln( ) T1 V1 T T2 nC p ,m dT p1 S nR ln( ) T1 p2 T V2 p2 S nC p ,m ln( ) nCV ,m ln( ) V1 p1
S T
T2
1
nCV ,m dT T
(2) 物质的量一定的等压变温过程
S T
T2
1
nC p ,m dT T
等 P 过程:
W`=0, QP = dH = CPdT = QR
QR QP C P dT dS = = = T T T CP S )P 或 ( T T
2.5热力学第二定律公式的导出

代表着某个性质的改变量。我们把这种状态性质称为熵,
用S表示,其改变量S
S
SB
SA
B A
Qr
T
;
dS
Qr
T
熵是全微分
二、热力学第二定律
Q ir
(QT1 QT 2 QT 2
) ir
T2 T1 T2
;
QT 1 T1
QT 2 T2
ir
0
即
第五节 热力学第二定律 公式的导出
p
V
一、熵的引出
根据热力学第一定律和卡诺循环
dU 0 W ( Q1 Q2 )
-W Q2 Q1 T2 T1
Q2
Q2
T2
即 Q1 = - T1
Q2
T2
定义: Q 热温商
T
Q1 + Q2 = 0 T1 T2
结论:卡诺循环中,过程的热温商之和等于零。
方法:将与系统密切相关的环境包括在一起, 构成一个孤立系统。
S孤立= S系统S环境 0
“>” 号为自发过程 “=” 号为可逆过程 “<” 号为不可能发生的过程
S孤立 0
等号表示可逆过程,不等号表示不可逆过程。 孤立系统排除了环境对系统以任何方式的干扰,因此,孤立系 统中的不可逆过程必然是自发过程。
熵增加原理可表述为:孤立系统中自发过程的方向总是朝 着熵值增大的方向进行,直到在该条件下系统熵值达到最 大为止,此时孤立系统达平衡态。
三、熵增加原理
应用:熵增加原理用于孤立系统,可判别过程的方 向和限度。
T
结合 dS Qr 可逆过程
第三章热力学第二定律主要公式及其适用条件

第三章热力学第二定律主要公式及使用条件1. 热机效率〃=-W/Q =(e1+e2)/e1二⑺一“”刁式中0和。
2分别为工质在循环过程中从高温热源厂吸收的热量和向低温热源乃放出的热。
W为在循环过程中热机中的工质对环境所作的功。
此式适用于在任意两个不同温度的热源之间一切可逆循环过程。
2.卡诺定理的重要结论Q\ 6 +Q2 /Ty v =0,可逆循环<0,不可逆循环任意可逆循环的热温商之和为零,不可逆循环的热温商之和必小于零。
3. 矯的定义dS = bQJT4.克劳修斯不等式(=8e/r,可逆dS[>dQ/T,不可逆5. 爛判据A5iso=AS sys + AS amb(>0,不可逆(=0,击遗式中iso, sys和amb分别代表隔离系统、系统和环境。
在隔离系统中,不可逆过程即自发过程。
可逆,即系统内部及系统与环境之间皆处于平衡态。
在隔离系统中,一切自动进行的过程,都是向爛增大的方向进行,这称之为爛增原理。
此式只适用于隔离系统。
6. 环境的熾变△Samb = Oamb/^mb =~Qsy7-癇变计算的主要公式di/ + /?dV _ f—Vd”T Ji 7对于封闭系统,一切刃v=o的可逆过程的朋计•算式,皆可山上式导出(1)△S = nC V m ln(7;/7])+ H/?\n(V2 /V,)△S = nC p m \n(T2 IT x) + nR ln(p1 / p2)△S = /iC V m ln(p2//?,) + nC p m ln(V2 / %)上式只适用于封闭系统、理想气体、G m为常数,只有〃"卩变化的一切过程(2)AS T=nR \n(V2 / V, )=/?/? ln(p / p2)此式使用于n—定、理想气体、恒温过程或始末态温度相等的过程。
(3)AS=/?C pm ln(7;/7])此式使用于"一定、-口为常数、任意物质的恒压过程或始末态压力相等的过程。
第三章 热力学第二定律
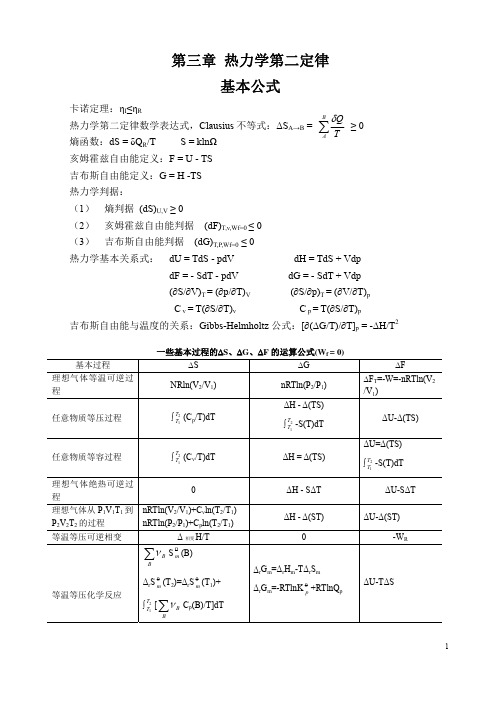
第三章热力学第二定律基本公式卡诺定理:ηI≤ηR热力学第二定律数学表达式,Clausius不等式:ΔS A→B = ∑BATQδ≥ 0熵函数:dS = δQ R/T S = klnΩ亥姆霍兹自由能定义:F = U - TS吉布斯自由能定义:G = H -TS热力学判据:(1) 熵判据 (dS)U,V≥ 0(2) 亥姆霍兹自由能判据(dF)T,v,Wf=0 ≤ 0(3) 吉布斯自由能判据(dG)T,P,Wf=0≤ 0热力学基本关系式:dU = TdS - pdV dH = TdS + VdpdF = - SdT - pdV dG = - SdT + Vdp(∂S/∂V)T = (∂p/∂T)V(∂S/∂p)T = (∂V/∂T)pC v = T(∂S/∂T)v C p = T(∂S/∂T)p吉布斯自由能与温度的关系:Gibbs-Helmholtz公式:[∂(ΔG/T)/∂T]p = -ΔH/T2一些基本过程的ΔS、ΔG、ΔF的运算公式(W例题例1 一个理想卡诺热机在温差为100K的两个热源之间工作,若热机效率为25%,计算T1、T2和功,已知每一循环中T1热源吸热1000J,假定所作的功W以摩擦热的形式完全消失在T2热源上,求该热机每一循环后熵变和环境的熵变。
解:卡诺热机效率η = (T2 - T1)/T225% =100K/T2, T2=400K, T1 = 300K热机效率定义:η = W/Q2η = W/(Q1+ W), 25% =W/(1000J + W), W =333.3JQ2 = W/η = 333.3J/25% = 1333JΔS体 =0(热机循环一周回到原态)由题意知,热机对环境所作的功完全以摩擦热的形式释放在T2热源上。
故T2热源得到了W的热量。
放出了Q2的热量。
ΔS环 =Q环,1/T1 + Q环,2/T2 = Q1/T1 + (Q2+W)/T2=1000J/300K + (-1333+333.3)J/400K =0.83J.K -1例2 有一绝热体系,中间隔板为导热壁,右边容积为左边容积的2倍,已知气体的C V,m = 28.03 J.mol-1,试求:1mol O2 273K 2mol N2 298K(a)不抽掉隔板达平衡后的ΔS ;(b) 抽去隔板达平衡后的ΔS。
第三章 热力学第二定律

IR
WIR QIR
(Q1)IR (Q2 )IR (Q1 ) IR
T1 T2 T1
1 (Q2 )IR 1 T2
(Q1 ) IR
T1
(Q1)IR (Q2 )IR 0 用(b)中相同(T的1)环方法(,T2 )对环 任意的变温不可逆循环,也可
以用无限个微小过程代替,得到
任意不可逆循环热温商之和小于零。
BQI
A
T环
不可逆 可逆
,或
dS QI TSU
不可逆 可逆
• 若系统经绝热过程 QI 0
有
S绝 0
不可逆 ,或
可逆
dS绝 0
不可逆 可逆
• 若在隔离系统中发生的过程 QI 0
不可逆
S隔 0 可逆 ,或
不可逆
dS隔 0 可逆
此二式就是熵增加原理的数学表达式。它表示:在绝
热或隔离系统中进行不可逆过程(实际可发生的过
低温物体(T(不2)可逆)
由上分析看见:无论是功→热的转化,还是 传热过程都 有明确的方向。这些实际发生的过 程都不能简单逆转,其共性——都是不可逆的
9
3.2 熵,熵增原理···················
1. 卡诺定理
(i)工作于两个一定温度间的所有卡诺循环都有相同 的
效率
R
T1 T2 T1
若V1 V2
S
CV
为常数
,m
nCV ,m
ln
T2
T1
由此二式可知,当T2>T1,ΔS>0,即定压(或定容) 下,S高温>S低温。
21
(3)系统经绝热可逆过程 (QR )S 0 , (QR )S 0
S
QR
T
0
热力学基本公式的导出关系概念图(新)
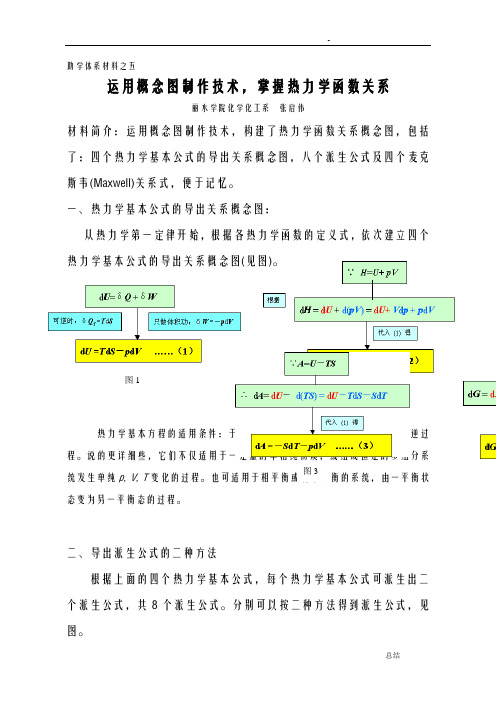
图1助学体系材料之五运用概念图制作技术,掌握热力学函数关系丽水学院化学化工系 张启伟材料简介:运用概念图制作技术,构建了热力学函数关系概念图,包括了:四个热力学基本公式的导出关系概念图,八个派生公式及四个麦克斯韦(Maxwell)关系式,便于记忆。
一、热力学基本公式的导出关系概念图:从热力学第一定律开始,根据各热力学函数的定义式,依次建立四个热力学基本公式的导出关系概念图(见图)。
热力学基本方程的适用条件:于封闭的热力学平衡系统所进行的一切可逆过程。
说的更详细些,它们不仅适用于一定量的单相纯物质,或组成恒定的多组分系统发生单纯p , V, T 变化的过程。
也可适用于相平衡或化学平衡的系统,由一平衡状态变为另一平衡态的过程。
二、导出派生公式的二种方法根据上面的四个热力学基本公式,每个热力学基本公式可派生出二个派生公式,共8个派生公式。
分别可以按二种方法得到派生公式,见图。
图2图3派生公式汇总表如下:等熵(∂U /∂V )S =-p 2d H = T d S + V d p等压 (∂H /∂S )p =T 等熵 (∂H /∂p )S =V 3 d A =-S d T -p d V等容 (∂A /∂T )V =-S 等温 (∂A /∂V )T =-p 4d G =-S d T + V d p等压 (∂G /∂T )p =-S 等温(∂G /∂p )T =V注:同色偏微分的相同关系。
归纳为四组:T = (∂U /∂S )V = (∂H /∂S )p ;p =-(∂U /∂V )S =-(∂A /∂V )T V = (∂H /∂p )S = (∂G /∂p )T S =-(∂A /∂T )V =-(∂G /∂T )p在学习过程中,一是要注意不同偏微分的相互替代关系;二是要注意难测或难得的偏微分可用一个简单的状态函数取代的关系。
三、麦克斯韦(Maxwell)关系式导出关系概念图同样以四个热力学基本公式为基础,每个基本公式可导出一个Maxwell 关系式。
第三章热力学第二定律

第三章热力学第二定律第三章 热力学第二定律(一)主要公式及其适用条件1、热机效率1211211/)(/)(/T T T Q Q Q Q W -=+=-=η式中:Q 1及Q 2分别为工质在循环过程中从高温热源T 1所吸收的热量和向低温热源T 2所放出的热量,W 为在循环过程中热机对环境所作的功。
此式适用于在两个不同温度的热源之间所进行的一切可逆循环。
2、卡诺定理的重要结论⎩⎨⎧<=+不可逆循环可逆循环,0,0//2211T Q T Q不论是何种工作物质以及在循环过程中发生何种变化,在指定的高、低温热源之间,一切要逆循环的热温商之和必等于零,一切不可逆循环的热温商之和必小于零。
3、熵的定义式TQ dS /d r def = 式中:r d Q 为可逆热,T 为可逆传热r d Q 时系统的温度。
此式适用于一切可逆过程熵变的计算。
4、克劳修斯不等式⎰⎩⎨⎧≥∆21)/d (可逆过程不可逆过程T Q S上式表明,可逆过程热温商的总和等于熵变,而不可逆过程热温商的总和必小于过程的熵变。
5、熵判据∆S (隔) = ∆S (系统) + ∆S (环境)⎩⎨⎧=>系统处于平衡态可逆过程能自动进行不可逆,,0,,0 此式适用于隔离系统。
只有隔离系统的总熵变才可人微言轻过程自动进行与平衡的判据。
在隔离系统一切可能自动进行的过程必然是向着熵增大的方向进行,绝不可能发生∆S (隔)<0的过程,这又被称为熵增原理。
6、熵变计算的主要公式⎰⎰⎰-=+==∆212121r d d d d d T p V H T V p U T Q S对于封闭系统,一切可逆过程的熵变计算式,皆可由上式导出。
(1)∆S = nC V ,m ln(T 2/T 1) + nR ln(V 2/V 1)= nC p,m ln(T 2/T 1) + nR ln(p 2/p 1)= nC V ,m ln(p 2/p 1) + nC p,m ln(V 2/V 1)上式适用于封闭系统、理想气体、C V ,m =常数、只有pVT 变化的一切过程。
热力学第二定律-物理化学-课件-03

说明: 1.各种说法一定是等效的。若克氏说法不成 立,则开氏说法也一定不成立(证明见书48页); 2.要理解整个说法的完整性切不可断章取义。如 不能误解为热不能转变为功,因为热机就是一种把 热转变为功的装置;也不能认为热不能完全转变为 功,因为在状态发生变化时,热是可以完全转变为 功的(如理想气体恒温膨胀即是一例) 3.热二律与热一律同样都是建立在无数客观事实基础 上的客观规律。至今还没有发现违背热二律的事实。
平衡
20
(2)真空膨胀 熵是状态函数,始终态相同,系统熵变也相同, 所以:
S sy 19.14 J K
1
S su
Q pra Tex
0
Sis Ssy Ssu 19.14 J K 1 0
自发过程
21
恒容变温
QV= dU = nCV,mdT
S
4
自发过程的定义
没有环境的影响下而能自动发生的过程 自发过程的特点 有方向的,有限度的,是不可逆过程。 要正确理解自发过程具有单向性(不可逆)的含义: 并不是其不能反向进行,环境对系统做功,可以使 系统复原,如利用水泵引水上山;利用空调机,可 以把热量从低温物体传到高温物体,但是一定在环 境中留下痕迹。 5
22
PVT均变化的ΔS的计算-理想气体
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
恒容 SV
S
( p ',V1 , T2 )
恒温 ST
T2 V2 S SV ST nCV ,m ln nR ln T1 V1
23
( p1 ,V1 , T1 ) ( p2 , V2 , T2 )
V2 p2 Qr Wr nRT ln nRT ln V1 p1 Qr V2 p2 S nR ln nR ln T V1 p1
热力学第二定律.

S f
2 dQ 1T
系统熵的变化量与熵流之差定义为熵产,用“Sg”表示
Sg S2 S1 S f
(S2 S1) S f Sg
熵流是由于系统与外界的发生热交换而引起的,其取 值可正可负可为零,而熵产是过程不可逆性的度量, 可逆过程熵产为零,不可逆过程熵产大于零,任何过 程的熵产不可能小于零。
• (2)若把此热机当制冷机使用,同样由克劳修斯积分 判断
Q Q1 Q2 2000 800 0.585 kJ / K 0
T T1 T2 973 303
工质经过任意不可逆循环,克劳修斯积分必小于零, 因此循环不能进行。
• 若使制冷循环能从冷源吸热800kJ,假设至少 耗功Wmin,根据孤立系统熵增原理有△Siso=0:
因为工质恢复到原来状态,所以工质熵变
△SE=0
对热源而言,由于热源放热,所以
SH
Q1 T1
2000 973
2.055 kJ / K
• 对冷源而言,冷源吸热
S L
Q2 T2
800 303
2.64 k J
/K
代入得:
Siso (2.055) 2.64 0 0.585 kJ / K 0
2 Q
1T
对于微元过程:
ds
(
dq T
) re v
或 dS
dQ
( T
) re v
mds
由于熵是状态参数,所以不论过程是否可逆,熵 变只由初终状态决定。
可逆与不可逆的情况
S2
S1
2 1
Q
T
my热力学 热力学第二定律

热力学第二定律一.熵及其物理意义1864年德国物理学家克劳修斯(Clausus)在《热之唯动论》中,首次提出熵(Entropy)的概 念:如果物体的热力学温度为T ,物体从外界吸收的热量为ΔQ ,则ΔQ /T 就是物体的熵增ΔS .ΔS=ΔQ /T 的必要条件是吸热过程为可逆的平衡过程(这一条件只具有理论意义).熵的精确定义即热力学含义为:T dQ T dQ dS dS dS irr rev g f //+=+=,式中f S 为熵流,g S 为熵产;rev dQ 为可逆过程中热源传给工质的微元热量;irr dQ 是实际过程产生的微元耗散能(摩擦生热等);T 是工质或热源的瞬时绝对温度。
克劳休斯关于熵的概念显然是指熵流f S 。
熵的宏观意义是系统能量分布均匀性的一种量度,可以表示物体所处状态是否稳定及系统变化的方向.能量分布越均匀,熵越大,反之,则熵越小.当熵最大时,系统能量分布完全均匀而达到热平衡状态,即无温度势差,也无压力势差.在该状态下,即使系统的温度再高,也不能作功,能量无法输出,连卡诺循环都没有了。
影响系统非作功能变化的因素有:随同热量或质量迁移的非作功能以及系统内不可逆因素引起的有效能退化成的非作功能.前者使系统的非作功能可增可减,而后者总使系统的非作功能增加.当闭口系进行可逆过程时,影响系统非作功能变化的因素就只有传热,所以进行可逆过程的闭口系非作功能变化ωdA 应等于随热量迁移的非作功能q dA ω,即 ωdA =q dA ω (1)根据卡诺定理,热量的非作功能为q dA ω=re Q TT 0 (2) 由式(1)、(2)得 ωdA =re Q T T 0 或ωda =re q TT 0 (3) 式中,下标“ re ”表示可逆过程,T 为系统的温度,0T 为环境温度,令dS =T Q re 或ds =Tq re (4) 式中S 为熵,s 为比墒.上式即熵的定义式。
将式(4)代式(3),得ωdA =dS T 0 或 ωda =ds T 0 (5)由于 )(ωωa A 是态函数,故S(s)也是状态函数.这是熵的重要性质.既然熵是状态函数,必有0=⎰T Q re 或 0=⎰T q re上式由克劳修斯根据卡诺定理首先导得,称为克劳修斯积分式.传统的熵定义式就是根据该积分式定义的.式(5)表明:系统熵变化是系统非作功能变化的量度,此即熵的宏观物理意义.二.熵的本质热力学是一种以物理学为基础的宏观唯象理论,它的基本定律描述了宏观世界的统一和普适规律.热力学第一定律是研究能量平衡的守恒定律,能量在转换过程中没有丝毫的增减.热力学第二定律则揭示了能量转换过程中质量不守恒的一般规律,它的核心是熵.一切实际热力过程必然伴随有熵产0=g S 产生,这从本质上说明了实际过程的方向性和不可逆性.统计力学中也大量涉及熵,信息论研究的中心概念也是熵.构成熵理论的方法不断深入和发展,不仅在热力学、生物学及化学领域是这样,在信息论、决策论及社会学中也是如此。
热力学第二定律数学式的导出

作者: 曹庆林
作者机构: 合肥工业大学化工系
出版物刊名: 化工高等教育
页码: 55-51页
主题词: 热力学第二定律 数学式 不可逆过程 自发过程 任意循环过程 热库 物理意义 数学表达式 熵函数 发展进程
摘要: 目前一般教材中在介绍热力学第二定律时,通常是先从大量的事实归纳出Clausius说法,Kelvin说法,进而证明Carnot定律,再推广到任意循环过程,从而导出熵函数和第二定律的数学表达式。
这种传统的方法虽然符合历史上热力学的发展进程,但叙述冗长,耗了较多学时仍形象不清。
因此一些文献介绍了其它方法,如Caratheodry方法、公理化推导法等。
但这些方法需要较多的数学手段,显得更为抽象,使初学者更难理解,所以在普通教材中也不宜采用。
本文介绍一种方法,简明易懂,化时较少。
它直接从熵函数的物理意义入手,假设一个热库作为参考系用来标定熵变,即可得到热力学第二定律的数学式。
热力学第二定律公式

热机效率:11Q WQ W =-=η (3-1) 热机效率:1211Q Q Q Q W +=-=η (3-2) 卡诺可逆热机效率:1211211T T T Q Q Q Q W -=+=-=η(3-3) 卡诺循环的热温商之和等于零:02211=+T Q T Q (3-4) 任意的可逆循环:0=⎪⎪⎭⎫⎝⎛∑ri i iT Q δ (3-5) 任意的可逆循环:0=⎪⎪⎭⎫ ⎝⎛⎰riiTQ δ (3-6) 熵的定义式:r T Q dS ⎪⎭⎫⎝⎛=δ(3-7) 熵的定义式:rBA T Q S ⎰⎪⎭⎫ ⎝⎛=∆δ(3-8) 不可逆热机的热温商之和小于零:02211<⎪⎪⎭⎫⎝⎛+r i T Q T Q (3-9)任意不可逆循环过程:0<⎪⎪⎭⎫⎝⎛∑i iriiT Q δ (3-10) 任意不可逆循环过程:irBA B A T Q S ∑⎪⎭⎫⎝⎛〉∆→δ (3-11) 克劳修斯不等式:⎪⎪⎭⎫⎝⎛=>≥∆∑→可逆不可逆B AB A T Q S δ(3-12)熵增加原理:⎪⎪⎭⎫⎝⎛=>≥∆可逆不可逆绝热0S (3-13)平衡的熵判据:⎪⎪⎭⎫⎝⎛=>≥∆平衡自发隔离0S (3-14)su sys S S S ∆+∆=∆隔离 (3-15)环境熵变的计算:sur BA su su T Q S ,⎰⎪⎪⎭⎫⎝⎛=∆δ (3-16)环境熵变的计算:sususu T Q S =∆(3-17)环境熵变的计算:susu T QS -=∆(3-18) 系统熵变的计算:rr BA T T Q T Q S ⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛=∆⎰δ (3-19)(等温可逆过程) 系统熵变的计算:2112ln ln p pnRT V V nRT Q == (3-20) (理想气体等温可逆过程) 系统熵变的计算:⎰⎰=⎪⎭⎫⎝⎛=∆21,T T m p rBA p T dT C n T Q S δ (3-21) (等压过程)系统熵变的计算:12,lnT T nC S m p p =∆ (3-22) (等压过程) 系统熵变的计算:⎰⎰=⎪⎭⎫⎝⎛=∆21,T T m V rBA V T dT C n T Q S δ (3-23) (等容过程)系统熵变的计算:12,lnT T nC S m V V =∆ (3-24) (等容过程) 系统熵变的计算:)ln ln (B B A A mix y R n y R n S +-=∆(3-25)(理想气体混合过程) 系统熵变的计算:THn S m βαβα∆=∆ (3-26) (可逆相变化过程)能斯特热定理:0lim 0=∆→S T r (3-27)热力学第三定律:0)0(*=K S 完美晶体,(3-28) 规定摩尔熵:rT K m T Q n n T B S T B S ⎰⎪⎭⎫ ⎝⎛==01),(),(δ (3-29) 化学反应熵变的计算:∑=∆Bm B m r T B S T S ),,()(相态θθν (3-30)化学反应熵变的计算:⎰∑+∆=∆21)()()(,12T T Bm p Bm r m r TdT B C T S T S νθθ (3-31)玻尔兹曼公式:Ω=ln k S (3-32)克劳修斯不等式:⎪⎪⎭⎫⎝⎛=>≥∆可逆不可逆T Q S (3-33) (等温) W S T U ≤∆-∆ (3-34) (等温)W TS U ≤-∆)( (3-35) (等温)亥姆霍兹函数定义式:TS U A -= (3-36)⎪⎪⎭⎫⎝⎛=<≤∆可逆不可逆W A T (3-37) (等温)⎪⎪⎭⎫ ⎝⎛=<≤∆可逆不可逆',W A VT (3-38) (等温、等容)亥姆霍兹函数判据:⎪⎪⎭⎫⎝⎛=<≤∆平衡自发0,V T A (3-39)(等温、等容且没有非体积功) 亥姆霍兹函数变的计算:S T U A T ∆-∆=∆ (3-40) (等温) 亥姆霍兹函数变的计算:r T W A =∆ (3-41) (等温可逆过程)亥姆霍兹函数变的计算:⎰-=∆21V VT pdV A (3-42) (等温可逆且不作非体积功)亥姆霍兹函数变的计算:1221ln lnp pnRT V V nRT A T ==∆ (3-43) (理想气体,等温且不作非体积功)亥姆霍兹函数变的计算:V p A ∆-=∆βα (3-44) (可逆相变化过程,等温等压) 亥姆霍兹函数变的计算:nRT A gl -=∆ (3-45) (可逆相变化过程,等温等压) 亥姆霍兹函数变的计算:nRT A g s -=∆ (3-46) (可逆相变化过程,等温等压) 吉布斯函数的导出:')(W TS pV U ≤-+∆ (3-47) (等温等压)吉布斯函数定义式:pV A TS H TS pV U G +=-=-+=(3-48) 吉布斯函数的导出:⎪⎪⎭⎫ ⎝⎛=<≤∆可逆不可逆',W G p T (3-49) (等温等压)吉布斯函数判据:⎪⎪⎭⎫ ⎝⎛=<≤∆可逆不可逆0,pT G (3-50) (等温等压且没有非体积功) 吉布斯函数判据:⎪⎪⎭⎫ ⎝⎛=<≤∆平衡自发0,p T G (3-51) (等温等压且没有非体积功) 吉布斯函数变的计算:S T H G T ∆-∆=∆(3-52) (等温) 吉布斯函数变的计算:⎰=∆21p p T Vdp G (3-53)(等温且不作非体积功可逆过程) 吉布斯函数变的计算:⎰=∆21p p T Vdp G (3-53)(等温且不作非体积功可逆过程)吉布斯函数变的计算:2112ln ln V VnRT p p nRT G T ==∆(3-54) (等温且不作非体积功可逆,理想气体)吉布斯函数变的计算:0=∆G βα (3-55) (可逆相变化过程)吉布斯函数变的计算:B B A A mix y RT n y RT n G ln ln +=∆(3-56)(理想气体混合过程)纯物质两相平衡条件:),(),(βαB G B G m m *=*(3-72)(一定温度、压力)克拉贝龙方程:*∆*∆=m m V T H dT dp (3-73) 克拉贝龙方程:*∆*∆=m m H V T dp dT (3-74) 克劳修斯-克拉贝龙方程:{}2ln RT H dT p d m vap *∆= (3-75) (凝聚相体积忽略不计) 克劳修斯-克拉贝龙方程不定积分:{}B TR H p m vap +⋅*∆-=1ln (3-76)克劳修斯-克拉贝龙方程定积分:⎪⎪⎭⎫ ⎝⎛-*∆-=121211ln T T R H p p m vap (3-77) 克劳修斯-克拉贝龙方程定积分:()211212ln T RT T T H p p m vap -*∆= (3-78)特鲁特规则:1188/--⋅⋅≈*∆=**∆K molJ S T H m vap b m vap (3-79)对于固气平衡:{}2ln RTH dT p d m sub *∆= (3-80)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
δ Qr
A
∴∫ = −∫ T α T β A B
此式说明
B
δ Qr
δ Qr
δ Qr 即∫ = ∫ T α A T β A
B B
δ Qr
δQ r ∫ T 的积分值仅取决于始终 态 ( A, B )而与过程 (α,β)无关, 代表着某个性质的改变 量。我们把这种状态性 质称为熵, 用S表示,其改变量 ∆S
∆S孤立= ∆S系统+∆ 环境 ≥ 0 +∆S
“>” 号为自发过程 “=” 号为可逆过程 “<” 号为不可能发生的过程
B
∆S = S B − S A = ∫
A
δ Qr
T
; dS =
δ Qr
T
( 熵是全微分 )
二、热力学第二定律
QT 1 + QT 2 T2 − T1 Qηir = ( )< ; ir QT 2 T2 QT 1 QT 2 ∴ + <0 T2 ir T1 δ Qir δ Qr 即∑ 又Q ∑ <0 T T δ Qr ∴∆S = ∑ T δ Qir > ∑ T
结论:卡诺循环中 过程的热温商之和等于零。 结论:卡诺循环中,过程的热温商之和等于零。 循环
一、熵的引出
• 1.可逆过程热温商 ——熵(entropy)的引出
QT1 + QT 2 T 2 − T1 Qη = = T2 QT 2 QT1 QT 2 ∴ + = 0; T1 T2 or ∑ Qi = 0 (可逆过程 Ti
T δQ dS ≥ T
( 可逆过程 )
对于孤立体系 δ Q = 0, 则有 dS隔离 ≥ 0 或 ∆S = ∆S 体系 + ∆S 环境 ≥ 0
三、熵增加原理
对于孤立体系, 所以Clausius 对于孤立体系,δQ = 0 ,所以Clausius 不等式为 孤立体系
∆S孤立 ≥ 0
等号表示可逆过程,不等号表示不可逆过程。 等号表示可逆过程,不等号表示不可逆过程。 孤立系统排除了环境对系统以任何方式的干扰,因此, 孤立系统排除了环境对系统以任何方式的干扰,因此,孤立 排除了环境对系统以任何方式的干扰 系统中的不可逆过程必然是自发过程 不可逆过程必然是自发过程。 系统中的不可逆过程必然是自发过程。
)
Q 称为某热源的热温商。 T
一、熵的引出
表示沿封闭曲线环积分 ; ∫ Qi δQr 极限条件下 ∑ T = 0 → ∫ T = 0;该封闭曲线由无数个小卡诺 i 循环组成( 如图2 − 5所示)
一、熵的引出
B
A
β(可逆过程)
B A
α(不可逆) β(可逆过程)
=0
r——可逆过程( reversible process) 可逆过程( 可逆过程 ) ir——不可逆过程 (irreversible process) 不可逆过程 )
二、热力学第二定律
则 dS > 结合
δ Qir
T dS =
( 不可逆过程 )
δ Qr
不可逆过程 > 得 可逆过程 = (热力学第二定律数学表达式 − 克劳修斯不等式 )
δQr dS = T 第五节 热力学第二定律 公式的导出
p
V
一、熵的引出
根据热力学第一定律和卡诺循环
dU = 0 − W = ( Q1 − Q2 )
-W Q2 + Q1 T2 − T1 η= = = Q2 Q2 T2
即
Q1 T1 =Q2 T2
Q1 Q2 + =0 T1 T2
Q 定义: 定义: T
热温商
α(可逆过程)
图2—6 可逆循环 不可逆
一、熵的引出
证明:上式是状态性质的积分 ( 从图2-6,并可推广到图2-7 ) δ Qr Q ∫ T = ∫ T + ∫ T = 0 A B α β
B A
δ Qr
熵增加原理可表述为: 熵增加原理可表述为:孤立系统中自发过程的方向总是朝 可表述为 着熵值增大的方向进行, 着熵值增大的方向进行,直到在该条件下系统熵值达到最 大为止,此时孤立系统达平衡态。 大为止,此时孤立系统达平衡态。
三、熵增加原理
应用:熵增加原理用于孤立系统, 应用:熵增加原理用于孤立系统,可判别过程的方 向和限度。 向和限度。 方法:将与系统密切相关的环境包括在一起, 方法:将与系统密切相关的环境包括在一起, 构成一个孤立系统。 构成一个孤立系统。
