生存分析与Cox回归[研究材料]

合集下载

ALL患者生存分析应用参数与COX回归模型对比研究的开题报告

ALL患者生存分析应用参数与COX回归模型对比研究的开题报告题目：ALL患者生存分析应用参数与COX回归模型对比研究摘要：急性淋巴细胞白血病（ALL）是一种常见的恶性肿瘤，患者的生存预后对治疗效果有重要影响。

本研究旨在比较不同模型在ALL患者生存分析中的应用效果，探讨最佳的生存分析模型选取方法。

通过收集ALL患者的临床资料，对生存相关因素进行分析，采用参数法和Cox回归模型进行生存分析，并比较两种模型的优劣。

关键词：ALL，生存分析，参数法，Cox回归模型一、研究背景和意义急性淋巴细胞白血病（ALL）是一种恶性肿瘤，患者生存预后对治疗效果有重要影响。

生存分析方法是对患者生存情况进行研究的一种有效手段。

目前常用的生存分析方法主要包括参数法和Cox回归模型。

参数法是通过估计患者生存分布函数或者生存率函数来进行预测，而Cox回归模型则是通过建立合适的比例风险模型来预测患者的生存情况。

对于ALL患者生存分析，不同的模型可能会导致不同的结果，如何选择最合适的生存分析模型具有重要意义。

因此，本研究旨在比较不同模型在ALL患者生存分析中的应用效果，探讨最佳的生存分析模型选取方法。

二、研究内容和方法1.研究内容本研究将收集ALL患者的临床资料，通过分析未经治疗的患者生存情况来探究影响患者生存的相关因素。

主要研究内容包括：（1）分析不同年龄段患者的生存情况；（2）分析患者性别、白细胞计数、血小板计数和病情等级对生存情况的影响；（3）比较参数法和Cox回归模型在ALL患者生存分析中的应用效果；（4）探究最佳的生存分析模型选取方法。

2.研究方法本研究采用回溯性队列研究方法，收集全部入院的ALL患者的病例资料，在去除不符合研究条件的患者后，纳入样本进行统计分析。

采用参数法和Cox回归模型进行生存分析，并比较两种模型的优劣。

三、研究预期成果本研究旨在探讨ALL患者生存分析的最佳模型选取方法和影响患者生存的相关因素。

通过比较参数法和Cox回归模型在ALL患者生存分析中的应用效果，期望得到以下预期成果：（1）明确ALL患者生存分析中各生存分析方法的应用价值；（2）识别患者生存的主要影响因素，并提出预防和治疗的策略；（3）为ALL患者的临床治疗和预后评估提供科学依据。

生存分析与Cox回归解析

生存分析与Cox回归
流行病与卫生统计学教研室曹明芹
生存分析与Cox回归
生存资料概述
生存分析的基本概念生存资料的统计描述生存曲线的比较 Cox回归
2018/10/24
生存分析与Cox回归
2
一、生存资料概述
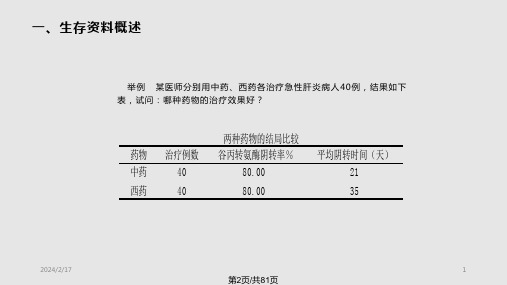
举例某医师分别用中药、西药各治疗急性肝炎病人 40例，结果如下表，试问：哪种药物的治疗效果好？
2018/10/24
生存分析与Cox回归
4
一、生存资料概述
医学随访研究一般有两种
所有研究对象同时进入研究(观察起始时间相同)
例如，队列研究、动物的随访观察
被研究对象逐个进入研究(观察起始时间不同)
例如，临床随访研究
由于受经费和时间的限制，最终观察时间不能无限延长
2018/10/24
生存分析与Cox回归
2018/10/24
生存分析与Cox回归
19
3. 生存资料的数据形式
10年间346例大肠癌患者手术后的生存时间患者编号性别年龄（岁） dtime 结局生存时间（月） 1 1 32 10 1 11 2 2 48 12 0 10 3 2 26 6 1 37 4 1 55 3 0 25 5 2 58 8 0 9 … … … … … …
② 可用于时间未分组的资料，也可用于时间分组资料
③ 各组间生存时间的比较根据各组生存曲线的高低及中位生存时间判断 ④ 需满足生存资料的基本要求，且各样本生存曲线不能交叉 ⑤ 生存曲线若出现交叉，则提示可能存在混杂因素，应采用分层
对数秩检验或Cox比例风险回归模型进行分析
2018/10/24
生存分析与Cox回归
1. 基本概念
完全数据提供了观察对象确切的生存时间，是生存分

Cox回归模型【生存分析】

Cox回归模型【⽣存分析】参考：《复杂数据统计⽅法——基于R的应⽤》吴喜之在⽣存分析中，研究的主要对象是寿命超过某⼀时间的概率。

还可以描述其他⼀些事情发⽣的概率，例如产品的失效、出狱犯⼈第⼀次犯罪、失业⼈员第⼀次找到⼯作、青少年第⼀次吸毒等等。

⽣存函数S(t)：S(t)=P(T>t)=1-P(T<=t),t>0T:表⽰寿命的随机变量t:特定时间综合⽣存函数图：⽤到包survival案例：⼝腔癌数据实验分成两组：TX=1：仅放疗TX=2：放疗+化疗#读取数据u=read.csv("pharynx1.csv")#因⼦化定性变量x=1:11(x=x[-c(5,11)]) #去掉第五个和第11个（定性变量的下标）for(i in x) u[,i]=factor(u[,i]) #把定性变量从数值型转换成因⼦型#回归分析a=lm(TIME~.,data=u)summary(a)R2和调整R2不⾼，结果不理想。

同时正态性条件不满⾜，所以检验得到的p-值也没有多⼤意义。

对TIME做指数变换，Box-Cox变换是统计建模中常⽤的⼀种数据变换，⽤于连续的响应变量不满⾜正态分布的情况。

MASS包中的boxcox()函数可以寻找λ。

#BOX-COX变换library(MASS)b=boxcox(TIME~.,data=u)I=which(b$y==max(b$y)) #which⽤于找到值在数组中的位置使对数似然最⼤的λ位置b$x[I]尝试⽤TIME的0.4次⽅作为因变量来拟合数据a=lm(TIME^0.4~INST+SEX+TX+AGE+COND+T.STAGE+N.STAGE+STATYS,data=u)b=step(a)summary(b)anova(b)shapiro.test(b$res)拟合并不好。

生存分析的cox回归模型案例spss

一、生存分析基本概念1、事件（Event）指研究中规定的生存研究的终点，在研究开始之前就已经制定好。

根据研究性质的不同，事件可以是患者的死亡、疾病的复发、仪器的故障，也可以是下岗工人的再就业等等。

2、生存时间(Survival time)指从某一起点到事件发生所经过的时间。

生存是一个广义的概念，不仅仅指医学中的存活，也可以是机器出故障前的正常运行时间，或者下岗工人再就业前的待业时间等等。

有的时候甚至不是通用意义上的时间，比如汽车在出故障前的行驶里程，也可以作为生存时间来考虑。

3、删失（Sensoring）指由于所关心的事件没有被观测到或者无法观测到，以至于生存时间无法记录的情况。

常由两种情况导致：（1）失访；（2）在研究终止时，所关心的事件还未发生。

4、生存函数（Survival distribution function）又叫累积生存率，表达式为S（t）=P(T>t),其中T为生存时间，该函数的意义是生存时间大于时间点t的概率。

t=0时S(t)=1，随着t的增加S(t)递减（严格的说是不增），1-S(t)为累积分布函数，表示生存时间T不超过t的概率。

二、生存分析的方法1、生存分析的主要目的是估计生存函数，常用的方法有Kaplan-Meier法和寿命表法。

对于分组数据，在不考虑其他混杂因素的情况下，可以用这两种方法对生存函数进行组间比较。

2、如果考虑其他影响生存时间分布的因素，可以使用Cox回归模型（也叫比例风险模型），利用数学模型拟合生存分布与影响因子之间的关系，评价影响因子对生存函数分布的影响程度。

这里的前体是影响因素的作用不随时间改变，如果不满足这个条件，则应使用含有时间依存协变量的Cox回归模型。

下面用一个例子来说明SPSS中Cox回归模型的操作方法。

例题要研究胰腺癌术中放疗对患者生存时间的影响，收集了下面所示的数据：操作步骤：SPSS变量视图菜单选择：点击进入Cox主对话框，如下，将time选入“时间”框，将代表删失的censor 变量选入“状态”框，其余分析变量选入“协变量”框。

生存分析及COX回归

第十二章生存分析及COX回归在临床医学中, 对病人治疗效果的考查. 一方面可以看治疗结局的好坏，另一方面还可以通过治疗时间的长短来衡量。

例如某种疾病治愈的时间, 某癌症病人手术后的存活时间等, 把这类与时间有关的资料统称为生存资料。

生存资料一般通过随访收集，从某标准时刻(发病、手术或出院等)开始，按某种相等或不等时间间隔，对观察对象定期观察预定项目所得的资料，它的结局是死亡，治愈、复发、阳性等。

但在临床上，往往由于各种原因：(1)因迁移原因失去联系；(2)死于其他原因而造成失访；(3)预定终止结果迟迟不发生，致使在一定时期内，一部分病例得不到确切的生存期，但它们提供了其生存期长于观察期的信息，这种数据称为删失数据，也称截尾数据或终检值(censored data)，包含终检值的数据即为不完全数据。

处理这类数据的统计分析方法称为生存分析。

它包括三个方面的内容1）生存过程的描述，主要是生存率的估计；2）生存过程的比较；3）影响因素的分析。

§12.1 生存率的估计生存率估计常用的有两种方法乘积极限法和寿命表法。

1乘积极限法又称Kaplan-Meier 法适用于小样本资料。

基本思想：将生存时间由小到大依次排列，在每个死亡点上，计算其期初人数、死亡人数、死亡概率、生存概率和生存率。

CHISS实现：点击重复测量→生存分析→乘积极限法应用举例：例12-1某疗法治疗白血病后的存活月数为： 2+,13,7+,11+,6,1,11,3,17,7。

试估计其生存率。

带“＋”为存活终检值。

解步骤：1 进入数据模块此数据库已建立在CHISS\data文件夹中，文件名为：a9_0生存分析.DBF。

打开数据库点击数据→文件→打开数据库表找到文件名为：a9_0生存分析.DBF →确认2 进入统计模块进行统计计算点击重复测量→生存分析→乘积极限法时间变量： time 终检值指标：censor→确认3 进入结果模块查看结果点击结果乘积限估计法生存分析, 数据来自文件: C:\CHISS\Data\a9_0生存分析.DBF数据过滤条件：━━━━━━━━━━━━━━━━━━━秩观察死亡观察生存率次时间序号数生存率标准误(i) t(i) (j) n(i) S(j) Ss(j)───────────────────0 0 0 10 1.0000 ...1, 1 1 10 0.9000 0.09492, 2+ ... 9 ... ...3, 3 2 8 0.7875 0.13404, 6 3 7 0.6750 0.15515, 7 4 6 0.5625 0.16516, 7+ ... 5 ... ...7, 11 5 4 0.4219 0.17378, 11+ ... 3 ... ...9, 13 6 2 0.2109 0.172610, 17 7 1 0.0000 ...━━━━━━━━━━━━━━━━━━━注：删失数据为1。

【统计学】生存分析和COX回归

H 对风险函数作图。横、纵坐标分别为t，H(t)。只适用于寿命表法
小样本资料的乘积极限法 (Kaplan-Meier法）
例14-4 某医师对11例脑瘤患者用甲法治疗，另9例脑瘤患者用乙法治疗试估计两法的生存率，并比较两种疗法的生存率有无差别。
甲法组：5 7* 13 13 23 30 30* 38 42 42 45*
乙法组：1 3 3 7 10 15 15 23 30
2020/11/19 Thursday
10
data ex14_1; do group='A','B'; input n; do i=1 to n; input t ; if t<0 then censor=0; else censor=1; t=abs(t); output; end; end; cards;
Stratum 1: group = A
Product-Limit Survival Estimates
t Survival 生存时间生存率
数据为删失数据、截尾数据、终检数据(censored data)
2020/11/19 Thursday
。
1
❖生存率(survival rate) 又称累积生存概率，即个体活过时点t 的概率,用S(t)表示。
❖
如果没有删失数据，生存率可以直接估计。
S (t )
t时刻存活的观察例数期初总观察例数
如果有删失数据，则要分时段估计每个时段的生存概率pi(i=1,2,…,t)，然后根据概率乘法原理估计累积生存概率。
[ freq <变量名>；] /*指定频数变量名 */
PROC过程[选项]
1.method=方法 /*指定估计生存率所用的方法：*/

生存分析cox回归和sas应用总结课件

最大似然法
最大似然法
参数检验 F-test t-test
参数解释回归系数b
似然比检验 Wald检验 score检验
优势比OR
似然比检验 Wald检验 score检验
RR
样本含量至少变量数旳10倍
应用
原因分析预测预报 Y
至少变量数旳20倍
原因分析预测、鉴别P(Y＝1)
非截尾例数至少变量数旳10倍
SELECTION=自变量筛选措施 FORWARD/F: 按要求旳P值SLE从无到有依次选择变量进入模型 BACKWARD/B: 按要求旳P值SLS从具有全部变量旳模型开始，依次剔除变量
STEPWISE/S:按SLE旳原则依次选入变量，同步对模型中既有旳变量按SLS旳原则剔除不明显旳变量 SCORE 采用最优子集选择法
模型检验，无效假设为β=0
Covariates Covariates Model Chi-Square
Without
With
106.176
83.260 22.916 with 2 DF (p=0.0001)似然比检验
.
.
29.715 with 2 DF (p=0.0001)比分检验
.
.
13.863 with 2 DF (p=0.0010) Wald检验
成百分比风险模型检验：（（最大似然法迭代）（似然比
模型参数旳检验：似然比、比分检验和Wald检验
PHREG过程旳语法格式如下： PROC PRREG [过程选项]; MODEL <生存时间变量*截尾指示变量(数值)>=<自变量名> /[模型选项]; STRATA <分层变量名列>; FREQ <变量名列>; BY <分组变量名列>; RUN;

生存分析-cox回归与sas应用总结x

生存分析的应用场景
01
02
03
医学研究
在临床试验和流行病学研究中，生存分析用于评估患者的生存时间，探究疾病进展和治疗效果。
生物学研究
在生物学和生物医学研究中，生存分析用于研究生物体的寿命、疾病发生和种群动态。
经济学研究
在经济学领域，生存分析用于研究企业的寿命、市场退出和产业动态等。
比例风险假设
Cox回归模型要求满足比例风险假设，即风险函数的比例不随时间变化。
数据完整性
数据需要完整，包括每个观察对象的结局和生存时间。
独立性
自变量之间需要满足独立性条件，避免多重共线性问题。
Cox回归模型在生存分析中的重要性
广泛应用
Cox回归模型是生存分析中最常用的方法之一，适用于多种生物医学和工程领域。
• 多模态数据融合：未来的研究可以探索如何将不同来源和类型的数据进行融合，以提高生存分析的精度和预测能力。例如，可以将基因组学、影像学等多模态数据与临床数据相结合，以更全面地了解疾病进展和预后。
• 个性化治疗：随着精准医学的发展，未来的研究可以关注如何利用生存分析的方法来评估个性化治疗的效果，为患者提供更精准的治疗方案。
PHREG过程用于执行 Cox比例风险回归模型，用于分析生存时间数据并评估协变量的影响。
LIFETEST过程可用于估计生存函数、计算生存时间的中位数和进行生
存比较等。
使用SAS进行Cox回归的步骤与示例
导入数据
01 使用SAS的数据导入功能将数
据加载到适当的SAS数据集中。
数据清理和预处理
未来研究方向与展望
• 改进模型：针对Cox回归的限制，未来研究可以探索改进的模型和方法，以提高生存分析的准确性和适用性。例如，可以考虑使用半参数模型、混合效应模型等其他方法来处理生存数据。

生存分析与Cox回归解析

例如，比较两种不同治疗措施治疗恶性肿瘤患者的生存曲线，可了解哪种治疗措施较优，从而为临床决策提供依据。常用方法有对数秩检验。
2024/2/17
20
第21页/共81页
4. 生存分析的基本内容
• ③ 生存过程的影响因素分析
例如，为了改善鼻咽癌患者的预后，应先了解可能影响患者预后的因素，如年龄、病程、病情、术前健康状况、有无淋巴结转移、术后有无感染、辅助治疗措施、营养状况等，通过随访收集患者术后的生存时间和上述因素的资料，然后采用多因素生存分析方法确定影响患者预后的主要因素，从而为在手术前后进行预防或干预提供参考依据。
2024/2/17
50
第51页/共81页
对数秩检验(log-rank)注意事项
① 属于单因素分析方法，适用于两组及多组间的比较
② 可用于时间未分组的资料，也可用于时间分组资料
③ 各组间生存时间的比较根据各组生存曲线的高低及中位生存时间判断
④ 需满足生存资料的基本要求，且各样本生存曲线不能交叉
⑤ 生存曲线若出现交叉，则提示可能存在混杂因素，应采用分层对数秩检验或Cox比例风险回归模型进行分析
2024/2/17
44
第45页/共81页
第46页/共81页
三、生存曲线比较 (单因素分析)
2024/2/17
46
第47页/共81页
பைடு நூலகம்
三、生存曲线比较 (单因素分析)
2024/2/17
47
第48页/共81页
第49页/共81页
第50页/共81页
生存资料分析的基本要求 • 样本应由随机抽样得到，要保证一定的样本含量 • 死亡例数不宜太少 • 截尾例数不宜太多 • 生存时间应尽可能精确

生存分析和COX回归课件

生存时间是指个体从某一事件（如疾病诊断）到另一事件（如死亡）的时间距离；事件指的是影响生存时间的具体情况。
3 分类时间的定义
根据具体的研究目标和数据特点，可以定义不同类型的分类时间，如生存时间、复发时间等。
生存分析的基本方法
Kaplan-Meier曲线
基于观察数据构建生存函数曲线，估计不同因素对生存概率的影响。
Cox比例风险模型
1 原理
通过建立风险函数，考虑多个协变量对生存时间的影响，估计各个因素的风险比例。
ห้องสมุดไป่ตู้
2 假设条件
比例风险假设和协变量的线性关系假设，合理解释变量的选择和模型的适用性。
3 参数估计
使用最大似然法进行参数估计，得到各个因素的估计值和显著性检验。
4 预测和解释
根据模型的系数，预测不同情况下的生存时间，并解释各个因素对生存时间的影响。
生存分析和COX回归ppt 课件
本课件介绍了生存分析和COX回归的基本概念、方法和应用。通过生动的图表和案例分析，帮助学习者掌握生存分析和COX回归在实际数据分析中的应用技巧。
什么是生存分析
1 概念和应用场景
探索个体从某一事件（如疾病诊断）发生到另一事件（如死亡）的时间分布和影响因素。
2 生存时间和事件
实际数据分析中的应用
1
数据清洗和变量筛选
2
对数据中的缺失值和异常值进行处理，
选择合适的变量进行建模。
3
结果解释和可视化
4
利用图表和统计指标解释模型的结果，可视化生存曲线和因素的影响。
生存分析和COX回归的分析流程
从数据清洗和变量筛选到模型建立和检验，系统讲解实际数据分析的步骤和技巧。

COX回归分析解析

变量xj暴露水平时的风险率与非暴露水平时的风险率之比称为风险比hr (hazard ratio)
hr= eβi
hr风险比相对危险度RR
（5）Cox回归模型的检验
▪ 对Cox模型的检验采用似然比检验。
▪ 假设为H0：所有的βi 为0 ，
▪
H1：至少有一个 βi 不为0 。
▪
将值分Ho和别记H1条为件
（x1,x2,…)------ok
1、数据结构
设含有p个变量x1, x2,…,xp及时间T和结局C的 n个观察对象. 其数据结构见表3。
表3 COX模型数据结构
实验对象 t CLeabharlann 1t1 12
t2 0
3
t3 0
… ……
n
tn 1
X1 X2
a11 a12 a21 a22 a31 a32
……
an1 an2
另一部分病人由于失访、意外事故、或到观察结束时仍存活等原因，无法知道确切的生存时间，它提
供了不完全的信息，称为不完全数据（截尾数据、
删失数据:censor data）。
▪ 始点
终点
▪ 始点
终点
▪ 生存分析 (survival analysis) ：生存时间一般是通过随访收集。不完全数据提供了部分信息。须要用专门的方法进行统计处理，这类统计方法起源于对寿命资料的统计分析，故称为生存分析。
▪ 表2 Logistic回归模型的数据结构
实验对象 y
X1
X2
1
y1 a11 a12
2
y2 a21 a22
3
y3 a31 a32
X3 …. XP
a13 … a1p a23 … a2p a33 … a3p

生存分析和COX回归

生存分析和COX回归生存分析是一种统计分析方法，用于研究人们在不同时间点发生一些特定事件（如死亡、疾病复发、结婚等）的概率。

COX回归（也称为比例风险模型）是生存分析中最常用的一种方法，它允许我们在考虑其他协变量（如年龄、性别、治疗方式等）的影响下，评估不同因素对事件发生时间的影响。

生存分析主要关注两个重要的概念，一个是生存函数，另一个是危险函数。

生存函数（Survival Function）描述了在给定时间t内，一些个体没有经历特定事件（如死亡）的概率。

危险函数（Hazard Function）描述了在给定时间t内，一些个体经历特定事件的概率，它是事件发生概率与未经历事件的个体数量之比，还可以理解为在一段时间内每个时刻发生事件的速率。

COX回归是一种用于分析比例风险的方法，它使用半参数模型，不需对基础风险函数做出任何具体的假设，因此非常灵活。

COX回归的基本原理是将危险函数分解为一个基础风险函数和一个与协变量相关的相对风险函数的乘积。

这种分解形式使得我们可以在不对基础风险函数做出假设的情况下，通过估计相对风险函数来评估协变量对风险的影响。

COX回归有以下几个主要的优点：1.它可以同时考虑多个协变量对生存时间的影响，且不需要对基础风险函数做出具体的假设。

这使得COX回归适用于各种不同的生存分析场景。

2.COX回归可以通过估计相对风险函数的参数，提供有关各个协变量的相对风险比较。

这有助于研究者了解哪些因素对事件发生时间具有重要的影响。

3.COX回归可以对不完整的数据进行分析，即使在存在丢失观测值的情况下，也能给出合理的结果。

4.COX回归是一种非参数方法，不需要假设数据的分布性质，因此具有很高的灵活性。

使用COX回归进行生存分析的步骤通常包括以下几个：1.收集生存数据，包括事件发生时间（如死亡时间）和相关协变量（如年龄、性别等）。

3.进行参数估计，通常使用最大似然估计法来估计相对风险函数的参数。

通过最大似然估计，可以得到与协变量相关的风险比较。

生存分析Cox回归

wangbingshun@
生存时间的非正态分布
40 30
20
10
0 0 5 10 15 20 25 time (Month) 30 35 40 45
102名黑色素瘤患者的生存时间分布示意图(右偏、非负)
wangbingshun@
方案
生存分析是一种既考虑事件结局，又考虑出现结局时间（即生存时间）的统计分析方法充分利用研究中所得到的信息，能够更加准确地评价及比较随访资料
wangbingshun@
0.75
0.50
0.25
0.00 0 5 10 15 20 25 30 analysis time 35 40 45
－－生存时间－－
特点3 非正态数据
错误的做法：错误2（统计推断）：采用常规 t 检验或方差分析进行组间比较。（应采用log-rank检验比
生存时间：
基准时点→期待结局
之间所持续的时间。
试验组
合格的研究对象对照组伴随因素混杂因素出现结果尚未出现结果失访、脱落
随访研究(follow-up study)示意图
wangbingshun@
－－生存时间－－基准时点癌症确诊治疗开始接触铅尘治疗开始缓解开始
wangbingshun@
－－生存时间－－
如何评价两组间的比较： A: 3 6 8 10 22 26 30＋30＋ B: 6 7 11 20 30＋30＋30＋30＋ •以30天为界的分类结果：死亡生存 A 6 2 B 4 4
wangbingshun@
特点2 截尾数据
FinalDate 2001-1-8 2002-10-25 2002-12-31 2001-8-22 2001-11-22 … …

生存分析和COX回归

•
例22.1 用某中药加化疗(中药组)和化疗(对照组)两种疗法治疗白血病后, 随访记录各患者的生存时间,不带 "+"号者表示已死亡,即完全数据,带"+" 号者表示尚存活, 即截尾数据,试作生存分析。时间单位为月。 • 中药组 10,2+,12+,13,18,6+,19+,26,9+,8+,6+,43+,9,4,31,24
• 对照组 2+,13,7+,11+,6,1,11,3,17,7
资料中药组积限法计算生存率
───────────────────────────────────── 时间状态期初人数死亡人数条件生存率累积生 di ∑di/ni(ni-di)累积生存 ti si ni di (ni-di)/ni 存率^S(ti)ni(ni-di) 率标准误 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨=⑥√⑧ ───────────────────────────────────── 2 活 4 死 15 1 0.9333 0.9333 0.004762 0.004762 0.0644 6 活 6 活 8 活 9 死 11 1 0.9090 0.8485 0.009091 0.013853 0.0999 9 活 10 死 9 1 0.8889 0.7542 0.013889 0.027742 0.1256 12 活 13 死 7 1 0.8571 0.6465 0.023810 0.051551 0.1468 18 死 6 1 0.8333 0.5387 0.033333 0.084885 0.1570 19 活 24 死 4 1 0.7500 0.4040 0.083333 0.168218 0.1657 26 死 3 1 0.6667 0.2694 0.166667 0.334885 0.1559 31 死 2 1 0.5000 0.1347 0.500000 0.834885 0.1231 43 活 ─────────────────────────────────────

生存分析首医大研究生2010

大肠癌患者的随访记录
编号性别年龄 … 手术日期随访终止日期随访结局生存时间(天)
1 男 45 …1991.05.20 1995.06.04 死亡 1476
2 男 50 …1992.01.12 1998.08.25 死亡 2417
3 女 36 …1991.10.24 1994.03.18 失访
/2
如果间隔时期很短，即 t 0 时，死亡概率/t 为t时刻的瞬时死亡概率，或称为风险函数（hazard function, h(t)），其意义为刚刚活过t时刻的个体在t时刻死亡的概率。
生存概率(survival probability)
表示在某单位时段开始时存活的个体到该时段结束时仍存活的可能性大小,记为p。年生存概率计算公式为：
▪ 预测： Cox回归模型预测生存率。
截尾数据的处理
因为不太好处理截尾数据，很多临床研究工作者常常将失访或中止等原因造成的截尾数据在分析时抛弃。截尾数据提供的信息虽然是不完全的，但也很有价值，不应随便删掉它。
例在对资料进行描述时： 5名癌症患者存活时间（月） 6 10 14 20 20 n=5 平均生存时间,
• 观察起点和终点（年、月、日）
•
生存时间
•
生存结局
▪ 样本含量：非截尾例数至少是可能影响因素的10倍。
▪ （二）搜集资料 ▪ 可能的影响因素： ▪ 从病历获得。 ▪ 生存时间及结局：
• 短期可观察到的结局可从病历获得；
• 长期结局一般不能从病历直接获得，通过信访、电话等得到。
生存资料基本要求
预测：具有不同因素水平的个体生存预测，如根据脑瘤病人的年龄、性别、病程、肿瘤分期、治疗方案等预测该病人t年（月）生存率。