西南交大信号与系统第二版课后答案
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
[信号与系统][第二版][奥本海姆][课后答案][英文][文字版]
![[信号与系统][第二版][奥本海姆][课后答案][英文][文字版]](https://img.taocdn.com/s3/m/bb82272210661ed9ad51f3c4.png)
(b) The signal x[n] is shifted by 4 to the left. The shifted signal will be zero for n<-6. And n>0.
(c) The signal x[n] is flipped signal will be zero for n<-1 and n>2.
2
E =
2
2
dt
=
dt = ,
x (t) P = lim 1 T T 2T T
2
2
dt lim
1
T dt lim1 1
T 2T T
T
x (c)
(t) =cos(t). Therefore,
2
E
=
x3(t)
2
dt
=
Signals & Systems
(Second Edition)
—Learning Instructions
(Exercises Answers)
Department of Computer Engineering 2005.12
Contents
Chapter 1 ······················································· 2 Chapter 2 ······················································· 17 Chapter 3 ······················································· 35 Chapter 4 ······················································· 62 Chapter 5 ······················································· 83 Chapter 6 ······················································· 109 Chapter 7 ······················································· 119 Chapter 8 ······················································· 132 Chapter 9 ······················································· 140 Chapter 10 ·······················································160
信号与系统第二版课后答案

则有
相加得
即
可见
即满足可加性,齐次性是显然的。故系统为线性的。
1-8若有线性时不变系统的方程为
若在非零f(t)作用下其响应 ,试求方程
的响应。
解因为f(t) ,由线性关系,则
由线性系统的微分特性,有
故响应
第2章习题解析
2-1如图2-1所示系统,试以uC(t)为输出列出其微分方程。
2-10对图示信号,求f1(t) *f2(t)。
题2-10图
解(a)先借用阶跃信号表示f1(t)和f2(t),即
f1(t)= 2(t)2(t1)
f2(t)=(t)(t2)
故
f1(t) *f2(t) = [2(t)2(t1)] * [(t)(t2)]
因为
(t) *(t)= =t(t)
故有
f1(t) *f2(t) = 2t(t)2(t1)(t1)2(t2)(t2)+ 2(t3)(t3)
解因方程的特征根=3,故有
当h(t) =(t)时,则冲激响应
阶跃响应
2-9试求下列卷积。
(a)(t+ 3 ) *(t5 )
(b)(t) * 2
(c)tet(t)*(t)
解(a)按定义
(t+ 3 ) *(t5 )=
考虑到<3时,(+ 3 )= 0;>t5时,(t5 )= 0,故
(t+ 3 ) *(t5 )=
试证明:
(1)
(2)利用(1)的结果,证明阶跃响应
证(1)因为
y(t)=f(t)h(t)
由微分性质,有
y(t)=f(t)h(t)
再由积分性质,有
(2)因为
信号与系统_第二版_奥本海默 _课后答案[1-10章]
![信号与系统_第二版_奥本海默 _课后答案[1-10章]](https://img.taocdn.com/s3/m/6ff45c8f83c4bb4cf6ecd112.png)
学霸助手[]-课后答案|期末试卷|复习提纲
学霸h助us手 Contents baz Chapter 1 ······················································· 2 xue Chapter 2 ······················································· 17
e 5 = 5 j0 ,
e -2 = 2 ,jp
e -3 j = 3
-
j
p 2
e 1
2
-
j
3 2
=
, -
j
p 2
e 1+ j =
2
, j
p 4
( ) 1- j e 2 =2
-
j
p 2
ep
j(1- j) = 4 ,
e 1+
1-
j j
=
p 4
e 2 + j 2 = -1p2
1+ j 3
ò e 1.3.
(a)
xue学ba霸zh助usS手hoiug.ncoaml(Sseco&nd EdSitioyn)stems
—Learning Instructions
xu(eEbxe学arzc霸hisue助sshA手onus.wceorms)
Department
of
Computer 2005.12
Enginexeurein学bga霸zh助us手
=¥
E¥
0
-4tdt
=
1 4
,
P ¥ =0, because
E¥ < ¥
手 om ò (b)
x e , 2(t) = j(2t+p4 )
西南交大2012-2013(2)信号与系统A期末考试试卷B答案
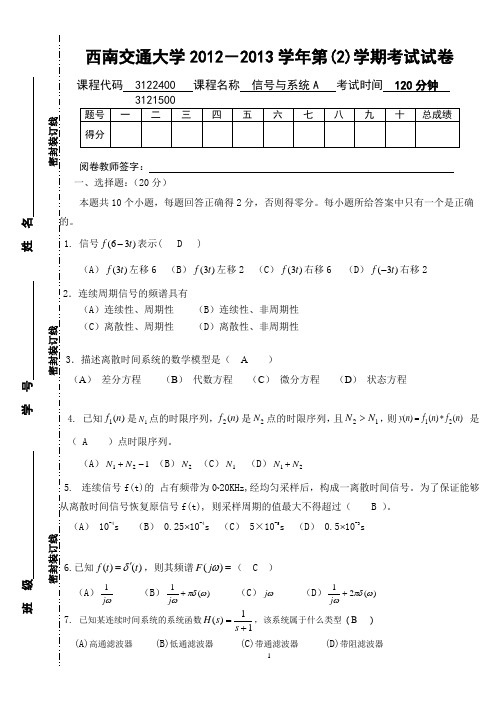
西南交通大学2012-2013学年第(2)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1. 信号(63)f t -表示( D )(A )(3)f t 左移6 (B )(3)f t 左移2 (C )(3)f t 右移6 (D )(3)f t -右移2 2.连续周期信号的频谱具有(A )连续性、周期性 (B )连续性、非周期性 (C )离散性、周期性 (D )离散性、非周期性3.描述离散时间系统的数学模型是( A )(A ) 差分方程 (B ) 代数方程 (C ) 微分方程 (D ) 状态方程4. 已知)(1n f 是1N 点的时限序列,)(2n f 是2N 点的时限序列,且12N N >,则)()()(21n f n f n y *= 是( A )点时限序列。
(A )121-+N N (B )2N (C )1N (D )21N N +5. 连续信号f(t)的 占有频带为0~20KHz,经均匀采样后,构成一离散时间信号。
为了保证能够从离散时间信号恢复原信号f(t), 则采样周期的值最大不得超过( B )。
(A ) 10-4s (B ) 0.25⨯10-4s (C ) 5×10-5s (D ) 0.5⨯10-3s6.已知()()f t t δ'=,则其频谱()F j ω=( C ) (A )ωj 1 (B ))(1ωπδω+j (C )ωj (D ))(21ωπδω+j 7. 已知某连续时间系统的系统函数11)(+=s s H ,该系统属于什么类型 ( B ) (A)高通滤波器 (B)低通滤波器 (C)带通滤波器 (D)带阻滤波器班 级 学 号 姓 名密封装订线 密封装订线 密封装订线8.下列各式中正确的是 ( C )(A ))()2(t t δδ= (B ))(2)2(t t δδ=;(C ))(21)2(t t δδ= (D ))2(21)(2t t δδ=9.若离散时间系统是稳定因果的,则它的系统函数的极点( C ) (A ) 全部落于单位圆外 (B )全部落于单位圆上 (C ) 全部落于单位圆内 (D ) 上述三种情况都不对 10. 已知)()()(t h t x t y *=,则(3)(4)x t h t -*-=( C )。
信号与系统第二版课后答案_西安交大_奥本海姆(汉语)

第一章1.3 解:(a). 2401lim(),04Tt T TE x t dt e dt P ∞-∞∞→∞-====⎰⎰(b) dt t x TP T TT ⎰-∞→∞=2)(21lim121lim ==⎰-∞→dt T TTT∞===⎰⎰∞∞--∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞--∞∞→∞→∞--===∞+===⎰⎰⎰⎰(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→-=∞→∞∑∑N N n x N P N Nn n N N N n N 34)21()(lim202===∑∑-∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=-=-===++∑∑ (f) ∑-=∞→∞=+=NNn N n x N P 21)(121lim 2∑-=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的; c) 00007,,22mN N ωωππ=== d). 010;N = e). 非周期的; 1.12 解:∑∞=--3)1(k k n δ对于4n ≥时,为1即4≥n 时,x(n)为0,其余n 值时,x(n)为1易有:)3()(+-=n u n x , 01,3;M n =-=- 1.15 解:(a)]3[21]2[][][222-+-==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+-, 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=-+-+-+-,1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =-+-+- 其中][n x 为系统输入。
西南交通大学(2)《信号与系统A》期末考试试卷

西南交通大学2009-2010学年第(2)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟题号 一 二 三 四 五 六 七 八 九 十 总成绩 得分阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1. 若 ()f t 是已录制声音的磁带,则下列表述错误的是( ) (A )()f t −表示将磁带倒转播放产生的信号 (B )(2)f t 表示将磁带以二倍速度加快播放 (C )()2tf 表示原磁带放音速度降低一半播放(D )(2)f t 将磁带的音量放大一倍播放2.连续周期信号的频谱具有(A )连续性、周期性 (B )连续性、非周期性 (C )离散性、周期性 (D )离散性、非周期性3.周期矩形脉冲的谱线间隔与( ) (A )脉冲幅度有关 (B )脉冲宽度有关 (C )脉冲周期有关(D )周期和脉冲宽度有关4. 已知)(1n f 是1N 点的时限序列,)(2n f 是2N 点的时限序列,且12N N >,则)()()(21n f n f n y ∗= 是( )点时限序列。
(A )121−+N N (B )2N (C )1N (D )21N N +5. 若对f (t )进行理想取样,其奈奎斯特取样频率为f s ,则对)231(−t f 进行取样,其奈奎斯特取样频率为( )。
11班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6. 周期信号f(t)如题图所示,其直流分量等于( )(A )0 (B )4 (C )2(D )67. 理想不失真传输系统的传输函数H (j ω)是 ( )。
(A )0j tKe ω− (B )0t j Ke ω−(C )0t j Ke ω−[]()()c c u u ωωωω+−−(D )00j t Keω− (00,,,c t k ωω为常数)8.已知)()(ωj F t f ↔,则信号)5()()(−=t t f t y δ的频谱函数 )(ωj Y 为( )。
信号与线性系统第二版答案

信号与线性系统第二版答案【篇一:7月份自考信号与线性系统习题答案】f(k)?cos(3?5k)为周期序列,其周期为( c )a. 2 b. 5 c. 10d. 122. 题2图所示f(t)的数学表达式为(b )图题2a.f(t)?10sin(?t)[?(t)??(t?1)] b. f(t)?10sin(?t)[?(t)??(t?1)] c.f(t)?10sin(?t)[?(t)??(t?2)] d. f(t)?10sin(?t)[?(t)??(t?2)] 3.已知f(t)? ??sin(?t)t??(t)dt,其值是( a )a.? b. 2? c. 3?d. 4?4.冲激函数?(t)的拉普拉斯变换为( a )a. 1 b. 2 c. 3 d. 45.为了使信号无失真传输,系统的频率响应函数应为(d )a. h(jw)?ejwtdb. h(jw)?e?jwtdc. h(jw)?kejwtdd. h(jw)?ke?jwtd6.已知序列f(k)?()?(k),其z变换为(b )1k3a.zz?13b.zz?13zz?14d.zz?147.离散因果系统的充分必要条件是( a)a.h(k)?0,k?0 b. h(k)?0,k?0c. h(k)?0,k?0 d. h(k)?0,k?0 8.已知f(t)的傅里叶变换为f(jw),则f(t?3)的傅里叶变换为( c )a.f(jw)e b. f(jw)ekjwj2wc. f(jw)ej3wd. f(jw)ej4w9.已知f(k)???(k),h(k)??(k?2),则f(k)?h(k)的值为(b ) a.? k?1?(k?1) b. ?k?2?(k?2) c. ?k?3?(k?3) d. ?k?4?(k?4)10.连续时间系统的零输入响应的“零”是指( a)a. 激励为零b. 系统的初始状态为零c. 系统的冲激响应为零d. 系统的阶跃响应为零 ?11. 已知序列f(k)?ej3k为周期序列,其周期为( c )a. 2 b. 4 c. 6 d. 812. 题2图所示f(t)的数学表达式为(a)ta.f(t)??(t?1)??(t?1)b.f(t)??(t?1)??(t?1) c.f(t)??(t)??(t?1)f(t)??(t)??(t?1)13.已知f1(t)??(t?1),f2(t)??(t?2),则 f1(t)?f2(t)的值是(d )a.?(t) b. ?(t?1) c. ?(t?2)d. ?(t?3)14.已知f(j?)?j?,则其对应的原函数为( b ) a.?(t) b. ?(t) c. ?(t) d. ?15.连续因果系统的充分必要条件是( b )a. h(t)?0,t?0 b. h(t)?0,t?0 c. h(t)?0,t?0 d. h(t)?0,t?0 16.单位阶跃序列?(k)的z变换为( d )a.zz?1,z?1 b. zz?1,z?1 c. zz?1,z?1 d. zz?1,z?1 17.已知系统函数h(s)?1s,则其单位冲激响应h(t)为(a )a.?(t) b. t?(t) c. 2t?(t) d. 3t?(t)18.已知f(t)的拉普拉斯变换为f(s),则f(5t)的拉普拉斯变换为(c)a.f(s) b. 1s1s53f(5) c. 5f(5) d. 1s7f(5) 19.已知f(k)??k?2?(k?2),h(k)??(k?2),则f(k)?h(k)的值为( d )a.?k?1?(k?1)b. ?k?2?(k?2) c. ?k?3?(k?3) d. ?k?4?(k?4)20.已知f(t)的傅里叶变换为f(j?),则f(jt)的傅里叶变换为( c )d.a. ?f(??)b. ?f(?)c. 2?f(??)d. 2?f(?)21. 下列微分或差分方程所描述的系统是时变系统的是(b)a. y(t)?2y(t)?f(t)?2f(t)b. y(t)?sinty(t)?f(t)c. y(t)?[y(t)]?f(t)d.y(k)?y(k?1)y(k?2)?f(k)22. 已知f1(t)?t?(t),f2(t)??(t),则f1(t)?f2(t)的值是( c)a.0.1t?(t) b. 0.3t?(t) c. 0.5t?(t)d. 0.7t?(t)23.符号函数sgn(t)的频谱函数为( b )22222a.1234b.c.d. j?j?j?j?24.连续系统是稳定系统的充分必要条件是( a ) a.???h(t)?mb.????h(t)?mc.????h(t)dt?md.????h(t)dt?m25.已知函数f(t)的象函数f(s)?(s?6),则原函数f(t)的初值为(s?2)(s?5)(b )a. 0b. 1 c. 2 d. 3 26.已知系统函数h(s)??t?t3,则该系统的单位冲激响应为( c) s?1?t?ta.e?(t) b.2e?(t) c.3e?(t) d. 4e?(t) 27.已知f(k)??kk?1?(k?1),h(k)??(k?2),则f(k)?h(k)的值为( d )k?1a.??(k) b.??(k?1) c.?k?2?(k?2) d. ?k?3?(k?3)28. 系统的零输入响应是指( c )a.系统无激励信号b. 系统的初始状态为零c. 系统的激励为零,仅由系统的初始状态引起的响应d. 系统的初始状态为零,仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中( b )a.只有正弦项 b.只有余弦项c. 只有偶次谐波 d. 只有奇次谐波 30. 已知信号f(t)的波形,则f()的波形为(b )a.将f(t)以原点为基准,沿横轴压缩到原来的c. 将f(t)以原点为基准,沿横轴压缩到原来的t21214b. 将f(t)以原点为基准,沿横轴展宽到原来的2倍d. 将f(t)以原点为基准,沿横轴展宽到原来的4倍简答题.。
信号与系统课后答案(PDF)
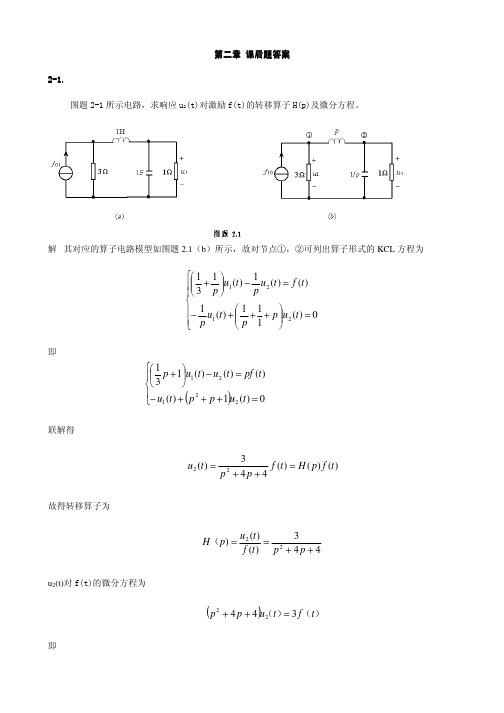
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
信号与系统课后答案(西南交大)

y x (t ) = 3e −2 t − 2 e−3 t t ≥ 0 y f ( t ) = te−2 t − e−2 t + e −3 t t ≥ 0
自由响应 2 e−2 t − e −3 t 强迫响应 te−2 t 稳态响应 0
暂态响应 te−2 t + 2e −2 t − e− 3t t ≥ 0
2.19 y f ( t ) =
2.22① t 3 u( t ) ④(
②∞
③( t−
1 2
1 1 −2 t + e )u( t ) 4 4
sin t + cost 1 −t − e )u( t ) ⑤ eu (t − 3) + e t − 2 u( 3 − t ) ⑥ cos(ωt + 45° ) 2 2 1 − cosπt cosπt − 1 1 1 2.23① u( t ) + u( t − 2) ② t 2 u( t ) − ( t − 1)2 u( t − 1) π π 2 2
3.6 f (t ) =
1 − j 3 ω0 t 3 − j 2 ω 0 t 3 1 e + e + e − jω 0 t + 1 + e jω 0 t + e j 2 ω0 t + e j 3 ω 0t 2 2 2 2
3.7 f (t ) = cos( 4ω0 t + 20°) + 2 cos( 2ω0 t + 30 °) + 3 cos(ω 0 t + 10° ) + 2
p2 + p +1 2.3 H ( p ) = 3 p + 2 p2 + 3p + 2 p2 + 3 p + 2 2.4 H ( p ) = 2p2 +3p +2
《信号与系统》第二版课后答案_(郑君里)_高等教育出版社

5t −∞
e2
(τ
)
dτ
= c1r1 (t ) + c2r2 (t )
∫ ∫ ∫ ( ) ( ) ( ) ( ) ( ) 时变:输入 e t − t0
,输出
5t
e
−∞
τ
− t0
τ −t0 = x
dτ =
e 5t −t0
−∞
x
dx ≠
e 5(t−t0 )
−∞
x
dx = r
t − t0
非因果: t
= 1时,
解题过程: (1)方法一:
f (t)
1
f (t − 2)
1
→
-2
-1
f (3t − 2)
0
1
→
1
2
f (−3t − 2)
1
→
3
2/3 1
-1 -2/3
方法二:
f (t)
f (3t )
1
1
→
→
-2
-1
f (3t − 2)
0
1
-2/3
→
1/3
f (−3t − 2)
2/3 1 方法三:
-1 -2/3
1
f (t)
(2) r (t ) = e(t )u (t )
线性:设 r1 (t ) = e1 (t )u (t ) 、 r2 (t ) = e2 (t )u (t ) , 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) = c1r1 (t ) + c2r2 (t )
6
时变:输入 e (t − t0 ) ,输出 e (t − t0 )u (t ) ≠ e (t − t0 )u (t − t0 ) = r (t − t0 ) 因果: r (t ) 仅与此时刻 e (t ) 有关 (3) r (t ) = sin ⎡⎣e(t )⎤⎦ u (t ) 非线性:设 r1 (t ) = sin ⎡⎣e1 (t )⎤⎦ u (t ) 、 r2 (t ) = sin ⎡⎣e2 (t )⎤⎦ u (t ) , 则 sin ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) ≠ sin ⎡⎣c1e1 (t )⎤⎦ u (t ) + sin ⎡⎣c2e2 (t )⎤⎦ u (t ) 时变:输入 e (t − t0 ) ,输出 sin ⎡⎣e (t − t0 )⎤⎦ u (t ) ≠ sin ⎡⎣e(t − t0 )⎤⎦ u (t − t0 ) = r (t − t0 ) 因果: r (t ) 仅与此时刻 e (t ) 有关 (4) r (t ) = e (1− t ) 线性:设 r1 (t ) = e1 (1− t ) 、 r2 (t ) = e2 (1− t ) ,则 c1e1 (1− t ) + c2e2 (1− t ) = c1r1 (t ) + c2r2 (t ) 时变:设 e1 (t ) = u (t ) − u (t −1.5) ,则 r1 (t ) = u (t + 0.5) − u (t ) e2 (t ) = e1 (t − 0.5) = u (t − 0.5) − u (t − 2) ,则 r2 (t ) = u (t +1) − u (t − 0.5) ≠ r1 (t − 0.5) 非因果:取 t = 0 ,则 r (0) = e (1) ,即 t = 0 时刻输出与 t = 1时刻输入有关。 (5) r (t ) = e(2t ) 线性:设 r1 (t ) = e1 (2t ) 、 r2 (t ) = e2 (2t ) ,则 c1e1 (2t ) + c2e2 (2t ) = c1r1 (t ) + c2r2 (t ) 时变:设 e1 (t ) = u (t ) − u (t − 2) ,则 r1 (t ) = u (t ) − u (t −1) e2 (t ) = e1 (t − 2) = u (t − 2) − u (t − 4) ,则 r2 (t ) = u (t −1) − u (t − 2) ≠ r1 (t − 2) 非因果:取 t = 1,则 r (1) = e (2) ,即 t = 1时刻输出与 t = 2 时刻输入有关。 (6) r (t ) = e2 (t ) 非线性:设 r1 (t ) = e12 (t ) 、 r2 (t ) = e22 (t ) , 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦2 = c12e12 (t ) + c22e22 (t ) + 2c1c2e1 (t ) e2 (t ) ≠ c1r1 (t ) + c2r2 (t ) 时不变:输入 e (t − t0 ) ,输出 e2 (t − t0 ) = r (t − t0 ) 因果: r (t ) 仅与此时刻 e (t ) 有关
信号与系统第二版课后习题解答(6-7-9)奥本海姆

Chap 66.1 Consider a continuous-time LTI system with frequency response()()|()|H j H j H j e ωωω=and real impulse response h(t). Suppose that we apply an input 00()cos()x t t ωφ=+ to this system .The resulting output can be shown to be of the form0()()y t Ax t t =-Where A is a nonnegative real number representing anamplitude-scaling factor and 0t is a time delay.(a)Express A in terms of |()|H j ω.(b)Express 0t in terms of0()H j ω Solution:(a) For 0()()y t Ax t t =-So 0()()jt Y j AX j eωωω-= 0()()()j t Y j H j Ae X j ωωωω-== So |()|A H j ω=(b) for 0()H j t ωω=- So 0()H j t ωω=-6.3 Consider the following frequency response for a causal and stable LTI system:1()1j H j j ωωω-=+ (a) Show that |()|H j A ω=,and determine the values of A. (b)Determine which of the following statements is true about ()τω,the group delay of the system.(Note()(())/d H j d τωωω=-,where ()H j ωis expressed in aform that does not contain any discontinuities.)1.()0 0for τωω=>2.()0 0for τωω>>3 ()0 0for τωω<>Solution:(a) for |()|1H j ω== So A=1(b) for )(2)()()1()1()(ωωωωωωarctg arctg arctg j j j H -=--=+∠--∠=∠ 212)()(ωωωωτ+=∠-=d j H d So ()0 0for τωω>>6.5 Consider a continuous-time ideal bandpass filter whose frequency response is⎩⎨⎧≤≤=elsewherej H c c,03||,1)(ωωωω (a) If h(t) is the impulse response of this filter, determine a functiong(t) such that)(sin )(t g t t t h c πω=(b) As c ω is increased, dose the impulse response of the filter get more concentrated or less concentrated about the origin?Solution(a) Method 1. Let1()()()()()()2h t x t g t H j X j G j ωωωπ=↔=* They are shown in the figures,where1,sin ()(){0,c c ctx t X j t ωωωωωωπ<=↔=> So we can get()2cos(2)()2[(2)(2)]c c c g t t G j ωωπδωωδωω=↔=-++Method 2. Using the inverse FT definition,it is obtained331(){}2c c c cj t j t h t e d e d ωωωωωωωωπ--=+⎰⎰ 11{sin 3sin }{sin }{2cos 2}c c c c t t t t t tωωωωππ=-= (b) more concentrated.Chap 77.1 A real-valued signal x(t) is know to be uniquely determined by its samples when the sampling frequency is10,000s ωπ=.For what values ofω is ()X j ω guaranteed to be zero? Solution:According to the sampling theorem 2s M w w > That is 110000500022M s w w ππ<== So if 5000M w w π>=,0)(=jw X7.2 A continuous-time signal x(t) is obtained at the output of an ideal lowpass filter with cutoff frequency 1,000c ωπ=.If impulse-train sampling is performed on x(t), which of the following sampling periods would guarantee that x(t) can be recovered from its sampled version using an appropriate lowpass filter?(a) 30.510T -=⨯(b) 3210T -=⨯(c) 410T -= Solution: π1000==c M w wFrom the sampling theorem,∴π20002=>M s w w ,that is 3102000222-==<πππM s w T ∴the conditions (a) and (c) are satisfied with the sampling theorem,(b) is not satisfied.7.3 The frequency which, under the sampling theorem, must be exceeded by the sampling frequency is called the Nyquist rate. Determine the Nyquist rate corresponding to each of the following signals:(a)()1cos(2,000)sin(4,000)x t t t ππ=++ (b)sin(4,000)()t x t tππ=(c) 2sin(4,000)()()t x t t ππ= Solution: (a) )4000sin()2000cos(1)(t t t x ππ++=max(0,2000,4000)4000M w πππ==∴ the Nyquist rate is 28000s M w w π>= (b) sin(4000)()t x t tππ= 4000M w π=∴ the Nyquist rate is 28000s M w w π>= (c) 2sin(4000)()t x t t ππ⎛⎫= ⎪⎝⎭ 2sin(4000)()t x tt ππ⎛⎫= ⎪⎝⎭221(1cos(8000))2t t ππ=- ∴8000M w π=∴the Nyquist rate is 216000s M w w π>=7.4 Let x(t) be a signal with Nyquist rate 0ω. Determine the Nyquist rate for each of the following signals:(a)()(1)x t x t +- (b)()dx t dt(c)2()x t(d)0()cos x t t ωSolution:(a) we let 1()()(1)y t x t x t =+-So 1()()()(1)()j j Y j X j e X j e X j ωωωωωω--=+=+ So the Nyquist rate of signal (a) is 0ω.(b) we let 2()()dx t y t dt= So 2()()Y j j X j ωωω=So the Nyquist rate of signal (b) is0ω. (c) we let 23()()y t x t = So 31()()*()2Y j X j X j ωωωπ= So the Nyquist rate of signal (c) is 20ω.(d) we let 40()()cos y t x t t ω=For 000cos [()()]FT t ωπδωωδωω→-++ So 4001()((()(())2Y j X j X j ωωωωω=-++ So the Nyquist rate of signal (d) is 03ω7.9 Consider the signal 2sin 50()()t x t tππ= Which we wish to sample with a sampling frequency of 150s ωπ= to obtain a signal g(t) with Fourier transform ()G j ω.Determine the maximum value of 0ω for which it is guaranteed that0()75() ||G j X j for ωωωω=≤Where ()X j ω is the Fourier transform of x(t).Solution: 2sin(50)()t x t t ππ⎛⎫= ⎪⎝⎭))100cos(1(2122t t ππ-= ∴100M w π=But π150=s wthe figure about before-sampling and after-sampling of )(jw H isWe can see that only when π500≤w , the before-sampling and after-sampling of )(jw H have the same figure.So if 0..)..(75)(w w for jw X jw G ≤=The maximum value of 0w is π50.Chap 99.2 Consider the signal 5()(1)t x t e u t -=- and denote its Laplace transform by X(s).(a)Using eq.(9.3),evaluate X(s) and specify its region of convergence. (b)Determine the values of the finite numbers A and 0t such that the Laplace transform G(s) of 50()()t g t Ae u t t -=-- has the same algebraic form as X(s).what is the region of convergencecorresponding to G(s)?Solution:(a). According to eq.(9.3), we will getdt e t x s X st -∞∞-⎰=)()(dt e t u e st t --∞∞--=⎰)1(5dt e t s )5(1+-∞⎰=)5()5()5()5()5(1)5(+=+--=+-=+-+-∞+-s e s e s e s s t s ROC:Re{s}>-5 (b). )()(05t t u Ae t g t --=-−→←LT 0)5(5)(t s e s A s G ++-=, Re{s}<-5 ∴ If )()(s X s G =then it ’s obviously that A=-1, 10-=t , Re{s}<-5.9.5 For each of the following algebraic expressions for the Laplace transform of a signal, determine the number of zeros located in the finite s-plane and the number of zeros located at infinity: (a)1113s s +++ (b) 211s s +- (c) 3211s s s -++ Solution :(a).1, 1)3)(1(423111+++=+++s s s s s ∴ it has a zero in the finite s-plane, that is 2-=sAnd because the order of the denominator exceeds the order of the numerator by 1∴ X(s) has 1 zero at infinity.(b). 0, 111)1)(1(1112-=-++=-+s s s s s s ∴ it has no zero in the finite s-plane.And because the order of the denominator exceeds the order of the numerator by 1∴ X(s) has 1 zero at infinity.(c). 1, 011)1)(1(112223-=++++-=++-s s s s s s s s s ∴ it has a zero in the finite s-plane, that is 1=sAnd because the order of the denominator equals to the order of the numerator∴ X(s) has no zero at infinity.9.7 How many signals have a Laplace transform that may be expressed as 2(1)(2)(3)(1)s s s s s -++++ in its region of convergence?Solution:There are 4 poles in the expression, but only 3 of them have different real part.∴ The s-plane will be divided into 4 strips which parallel to the jw-axis and have no cut-across.∴ There are 4 signals having the same Laplace transform expression.9.8 Let x(t) be a signal that has a rational Laplace transform with exactly two poles located at s=-1 and s=-3. If2()() ()t g t e x t and G j ω=[ the Fourier transform of g(t)]converges, determine whether x(t) is left sided, right sided, or two sided.Solution:)()(2t x e t g t =∴)2()(-=s X s G ROC: R(x)+Re{2}And x(t) have three possible ROC strips:),1(),1,3(),3,(+∞-----∞∴g(t) have three possible ROC strips: ),1(),1,1(),1,(+∞---∞ IF jw s s G jw G ==|)()(Then the ROC of )(s G is (-1,1)∴)(t x is two sides. 9.9 Given that1(),{}Re{}sat e u t Re s a s a -↔>-+ Determine the inverse Laplace transform of22(2)(),Re{}3712s X s s s s +=>-++ Solution: It is obtained from the partial-fractional expansion:22(2)2(2)42()712(4)(3)43s s X s s s s s s s ++-===+++++++,Re{}3s >-We can get the inverse Laplace transform from given formula and linear property.43()4()2()t t x t e u t e u t --=-9.10 Using geometric evaluation of the magnitude of the Fourier transform from the corresponding pole-zero plot ,determine, for each of the following Laplace transforms, whether the magnitude of the corresponding Fourier transform is approximately lowpass, highpass, or bandpass. (a): 1}Re{,.........)3)(1(1)(1->++=s s s s H (b): 221(),{}12s H s e s s s =ℜ>-++(c): 232(),{}121s H s e s s s =ℜ>-++ Solution:(a). 1}Re{,.........)3)(1(1)(1->++=s s s s H It ’s lowpass.(b).21}Re{,.........1)(22->++=s s s s s H It ’s bandpass.(c). 1}Re{., (1)2)(223->++=s s s s s H It ’s highpass.9.13 Let ()()()g t x t x t α=+- ,Where ()()t x t e u t β-=. Andthe Laplace transform of g(t) is 2(),1{}11s G s e s s =-<ℜ<-. Determine the values of the constantsαand βSolution: ()()()g t x t x t α=+-,and ()()t x t e u t β-=The Laplace transform : ()()()G s X s X s α=+- and()1X s s β=+,Re{}1s >- From the scale property of Laplace transform, ()1X s s β-=-+,Re{}1s < So 2(1)(1)()()()111s G s X s X s s s s βαββαβαα--+=+-=+=+-+-,1Re{}1s -<< From given 2()1s G s s =-,1Re{}1s -<< We can determine : 11,2αβ=-=。
信号与系统第二版课后习题解答(3-4)

信号与系统第二版课后习题解答(3-4)Chap 33.1 A continuous-time periodic signal x(t) is real value and has a fundamental period T=8. The nonzero Fourier series coefficients for x(t) arej a a a a 4,2*3311====--.Express x(t) in the form)cos()(0k k k k t A t x φω+=∑∞=Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑3.2 A discrete-time periodic signal x[n] is real valued and has afundamental period N=5.The nonzero Fourier series coefficients for x[n] are10=a ,4/2πj e a --=,4/2πj e a =,3/*442πj ea a ==- Express x[n] in the form)sin(][10k k k k n A A n x φω++=∑∞=Solution:for, 10=a , 4/2πj ea --=, 4/2πj ea =, 3/42πj ea --=,3/42πj e a =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=nj j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++=)358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n n3.3 For the continuous-time periodic signal)35sin(4)32cos(2)(t t t x ππ++=Determine the fundamental frequency 0ω and the Fourier series coefficients k a such thattjk k kea t x 0)(ω∑∞-∞==.Solution: forthe period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6, i.e. 3/6/20ππ==w )35sin(4)32cos(2)(t t t x ππ++=)5sin(4)2cos(21200t t ωω++=0000225512()2()2j t j t j t j t e e j e e ωωωω--=++--then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Let 1()x t be a continuous-time periodic signal with fundamental frequency 1ω and Fourier coefficients k a . Given that211()(1)(1)x t x t x t =-+-How is the fundamental frequency 2ω of 2()x t related to?Also, find a relationship between the Fourier series coefficients k b of 2()x t and the coefficients k a You may use the properties listed in Table 3.1. Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x ,that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw t k TT b x t e dt x t x t e dt T --==-+-?? 111111(1)(1)jkw t jkw t TTx t e dt x t e dt T T --=-+-??111)(jkw k k jkw k jkw k e a a e a e a -----+=+=3.8 Suppose given the following information about a signal x(t): 1. x(t) is real and odd.2. x(t) is periodic with period T=2 and has Fourier coefficients k a .3. 0=k a for 1||>k .4 1|)(|21202=?dt t x .Specify two different signals that satisfy these conditions. Solution:0()j kt k k x t a e ω∞=-∞=∑while: )(t x is real and odd, then k a is purely imaginary andodd ,00=a , k k a a --=,.2=T , then 02/2ωππ==and 0=k a for 1>k so0()j kt k k x t a e ω∞=-∞=∑00011j t j t a a e a e ωω--=++)sin(2)(11t a e ea t j tj πππ=-=-for12)(2121212120220==++=-?a a a a dt t x ∴ j a 2/21±=∴ )sin(2)(t t x π±=3.13 Consider a continuous-time LTI system whose frequency response is∞∞--==ωωωω)4sin()()(dt e t h j H t jIf the input to this system is a periodic signal<≤-<≤=84,140,1)(t t t x With period T=8,determine the corresponding system output y(t). Solution:Fundamental period 8T =.02/8/4ωππ==0()j kt k k x t a e ω∞=-∞=∑∴ 00()()jk t k k y t a H jk e ωω∞=-∞=∑0004, 0sin(4)()0, 0k k H jk k k ωωω=?==?≠? ∴ 000()()4jkw t k k y t a H jk e a ω∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=另:x(t)为实奇信号,则a k 为纯虚奇函数,也可以得到a 0为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1口 7 -, 刀、歹L
2.25
CD CD
f(t) = IOcosl 11(1) 证明: J(t)关8(1-1。) =f(t-1。)
@ f(t) = e-''u(t) (?) f(t)
状态响应可以表示力
2.26
已知线性时不变系统的输入力f(t)'系统的阶跃响应力g(t)'试证明系统的零 汕) = Lf'(,!)g(t-,!)d儿 2.27 2.28 2.29 用MATLAB求题2.7的全响 应。 用MATLAB求题2. 9的零输入响应。 (此式称为杜阿美尔积分)
=
心Yx (/)=7e-'-5e-2'(t汃0)
(2)yx (1)=6e-'-(4+5/)e-3'(t;>O) CZ) /,(1)= te-'11(1) 3 @i,(1) = -e-2'sin(21)11(1) 2
2.11 2.12
CD /,(1)�(-2e-'+2e-")的)+ 0(1)
心yx (t)�ze-" -2e-" (1;;, O) I 5 8 3 y(t) � - 3 e- '+ 2e-" + 6
第1章信号与系统概述
习题1
心f(t)=cost+2 sin(2 兀t) @ f(t)=e _,, srn(2 亢I) (J) f(k)=sm(2忒) 心f(t)=cos( 兀 I) @ 1.2 1.1 判断 下列信号是否是周期信号。若是周期信号,则确定信号周期。 @ f(t)= costu(t) CZ) f(t)= sin(3 兀t)+cos(2 兀t) @八I)= sin'[
2
@y x (t)飞e-2『 cos( 2.9 2.10
三)
(r>O)
@yx (t)=(l+t)e-'(t>O) @y,(t) = 丘os(
(1>0)
三)
(t>O)
@y,(t)=2 0e-' - (17+10r)e-" (r习0) +O.se-2'(1;;,0) @y,(t)=l.5 -2e-' 心/,(1)= (0.Se-'+ 0.5e- 3') 11(1) ©h(t)
j (I)
、
@ f( t)=u(t)r(2-t) 1.5
© 八I)=2r(t)-3r(t-l)+r(l-2)
@ f(t)=r(3t)u(2-t)
@ f(/)=11(1)11( 1- 1)
试写出题1.5图所示各信号的函数式。
/(, �f(,
b ,
(a) f(t)
J(k)
(b)
厂
(C) j (k)
、
-II
题2.4图
。
IH IH IH
IH
+
+
,,
IQ
+
f(t)
3Q
IQ
J(r)
题2.5图 2.7 已知系统的微分方程为
题2.6图
业+3竺+2y(t)业+4/(1)
输入信号f(I)=e-2'11(1), 初始条件力y(O)=0 , y'(O)=0 , 试用微分方程经典解法求系统的全响应。 2.8 已知系统的微分方程和初始条件如下, 求系统的零输入响应。 (D y'(t)+4y'(t)+3y(t)=f'(t)+2f(t), y(O_)=O, y'(0_)=2 @ y'(t)+2y'(t)+y(t)=f(t), y,(O_)=l, 义(O_)=0 @ y'(t)+9y(t)=f(t), y(O_)=l, y'(0_)=3 @ y'(t)+4y'(t)+8y(t)=3f(t), y(O_)=l, y'(O_)=O @ y"(t)+5y"(t)+8y'(t)+4y(t)=f(t), y(0_)=3, y'(0_)=4, y'(0_)=-8 已知系统的传输算子和初始条件如下, 求系统的零输入响应。 d户 dt dt
三)
和 @ f(/)=e
®f(k)= sm(2k) CZ) f(t)= 11( 1) @ f(t)=2e-' @ f(t)=e心
判断下列信号是能撞信号还是功率信号,并计算其总能箭或平均功率。 @ f(t)= cos(rrt)+sm(2 兀I) CZ) f(t)= cos(t-1)11(/)
sin( 亢t) -1归1 几) ={ 0 其他
CD y'(t)+4y'(t)+3y(t)= f'(t)+2/(t) @ y'(t)+4y'(t)+8y(t)=3f(t) @ y (/)+5y"(t)+8y'(t)+4y(f)=f(t)
m
已知系统的传输算子H(p)如下, 求系统的单位冲激响应h(t)。 p(p+3) p+I p+4 也H(p)= (g) H(p)= @ H(p)= 2 1 (p+l)(p+2) (p+l)(p+3) p(p +3p+2) 2.12 已知系统的微分方程为 2.11 y"(t)+ Sy'(t) +6y(t) = f'(t)+ f(t) 初始条件力y(O_)=O, y'(0_)=2, 求在下列输入信号作用下的零输入响应、零状态响应和全响应。
* 11(1-1。) =f 勹 f(r) dr
2.30
用MATLAB绘出题2.22的卷积积分。
用MATLAB绘出题2.10的单位冲激响应h(t)。
习题2参考答案
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 (DH(p)= 心y"(r)+3y'(r)+ 2y'(r)= f'(r)+4f(r) p'+p+I H(p) = p'+2矿+3p+2 H(p)= H(p) = H(p) = y(t)
2.9
p(p+3) , Yx (O_)=2, 义(O_)=3 (p+l)(p+2) p+I 2, 义(O+ )= I , y; (O+ )=0 (g) H(p)= 2 , Yx (0 十 )= (p+l)(p+3) (D H(p)= @ H(p)= 2.10 p+4 , y(O_)=O, y'(O_)=I, y'(O_)=O 1 p(p +3p+2) 已知系统的微分方程如下, 求系统的单位冲激响应h(t)。 @ y'(t)+2y'(t)+ y(t) 二 f(t) @ y'(t)+9y(t)=f(t)
求题2.4图所示电路中II J.t f(t)的传输算子H(p)。 1n IH
!J._____
p+4 3p+l ®H(p)= p(p'+ 3p+2) p(p'+4p+8) 求题2.3图所示电路中陌it f(I)的传输算子H(p)。
,,
。
IH
,,
F l 2 _
+
IF f(t)
IH
f(I)
U
。
题2.3图 2.5 2.6 求题2.5图所示电路中;, 对f(t)的传输算子H(p)。 求题2.6图所示电路中 ll J.t f(t)的传输算子H(p)。
-siu(3 1)11(1) 3
I
@ h(t) = (e-'-te-2' -e-2『) 11(1)
@些 2
2
@-1
®0
®4
@)线性系统 句线性系统 @)时变系统
@线性系统 @非线性系统 @时变系统 @非时变系统
1.12 心线性,时变,因果系统 @线性,时变,非因果系统 @线性,非时变,因果系统 @线性,非时变,非因果系统 1.13 y(r)=-2e-2'+sil山 (1 ;;,,Q)
一
1.14心y,(r)= -6e-" + Se ' (r江)
=
p +2p+ I 3 1 p +4p +5p+2
1
@H(p)=
(2)y"(r) +4y'(r)+Sy'(t)= 3f'(r)+ f(r)
p+I p +5p+6
(Dyx (r)=e-•-e-"
-2e-" -2 re-2'(1;;,, 0) 2e-'
p +3p+2 2p 2 +3p+ 2 3p 1 p +4p+4 p(p+3) p(p '+2矿+2p+3)
输入信号与初始条件如下, 求系统的全响应。 (D f(t)=u(t), y(O_)=O, y'(O_)=O, y'(O_)=O @ f(t)=e-3'11(t), y(O_)=O, y'(O_)=O, y"(O_)=O 3p+I 2.2 0 巳知传输算子为H(p)= '输入信号f(t)= u(t) , 初始条件为y(O_)= 0, p(p+ l)' y'(O_) = 0, y"(O_)= 0, 求系统的全响应。 I 2.21 已知传输算子力H(p)= '输入信号f(t)=e''u(-t), 求系统的零状态响应。 p+l
