沪科版九年级数学上册第22章相似形练习题

合集下载

沪科版九年级数学上册试题第22章《相似形》单元测试卷(含答案详解)

第22章《相似形》单元测试卷一、单选题（本大题共10小题，每小题3分，共30分）1．两千多年前，古希腊数学家欧多克索斯发现了黄金分割，即：如图，点P 是线段AB 上一点（AP ＞BP ），若满足，则称点P 是AB 的黄金分割点．黄金分割在日常生活中处处可见，例如：主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长20米，主持人从舞台一侧进入，设他至少走x 米时恰好站在舞台的黄金分割点上，则x 满足的方程是（）A ．（20﹣x ）2＝20xB ．x 2＝20（20﹣x ）C ．x （20﹣x ）＝202D ．以上都不对2．如图，点D ，E ，F 分别在的边上，，，，点M 是的中点，连接并延长交于点N ，则的值是（）A ．B ．C ．D ．3．将含有的三角板按如图所示放置，点在直线上，其中，分别过点，作直线的平行线，，点到直线，的距离分别为，，则的值为（）BP APAP AB=ABC V 13AD BD =DE BC ∥EF AB ∥EF BM AC ENAC32029161730︒ABC A DE 15BAD ∠=︒B C DE FG HIB DE HI 1h 2h 12h hA ．1 BCD4．如图，点D 是△ABC 中AB 边上靠近A 点的四等分点，即4AD ＝AB ，连接CD ，F 是AC 上一点，连接BF 与CD 交于点E ，点E 恰好是CD 的中点，若S △ABC ＝8，则四边形ADEF 的面积是（）A ．4B ．C ．2D ．5．如图，在边长为的小正方形组成的网格中，建立平面直角坐标系，的三个顶点均在格点（网格线的交点）上．以原点为位似中心，画使它与的相似比为，则点的对应点的坐标是（）A ．B ．C ．或D ．或6．如图，已知、，与相交于点，作于点，点是的中点，于点，交于点，若，，则值为（）11-1181171ABC V O 111A B C △ABC V 2B 1B ()42，()42--，()42，()42--，()42，()42，-AB BC ⊥DC BC ⊥AC BD O OM BC ⊥M E BD EF BC ⊥G AC F 4AB =6CD =OM EF -A．B ．C ．D ．7．如图，在平面直角坐标系中，为原点，为平面内一动点，，连接，点是线段上的一点，且满足．当线段取最大值时，点的坐标是（）A ．B ．C ．D ．8．如图，四边形是矩形，平分，，、的延长线交于点，连接，连接交于点．下列结论错误的是（）A ．图中共有三个等腰直角三角形B ．C ．D ．9．如图，在平面直角坐标系中，点，点B 是线段上任意一点，在射线上取一点C ，使，在射线上取一点D ，使．所在直线的关系式为，点F 、G分别为线段的中点，则的最小值是（）751253525O OA OB ==C 32BC =AC M AC :1:2CM MA =OM M36,55⎛⎫ ⎪⎝⎭612,55⎛⎫ ⎪⎝⎭ABCD CE BCD ∠AE CE ⊥EA CB F DE BD CE G DGC EBC∠=∠AB AD CG CE⋅=⋅∽CDG CEBV V ()E OE OA OB BC =BC BD BE =OA 12y x =OC DE 、FGABC ．D ．4．810．如图所示，正方形由四个全等的直角三角形和一个小正方形组成，且内接于正方形，连接，．已知正方形与正方形面积之比为，若，则（）A BCD ．二、填空题（本大题共8小题，每小题4分，共32分）11．已知，且，则．12．在中，M ，N 分别是BC ，AC 边上一点，连接AM ，BN 交于点P ，若，，则．13．正方形中，E ，F 分别是，上的点，连结交对角线于点G ，若恰好平分，，则的值为．ABCD FGHI DE BE CE>ABCD FGHI 59DE CH ∥BECE=32::3:5:7a b c =10a b c -+=a b c ++=ABC V :2:3BM CM =:1:4AN CN =:AP MP =ABCD AD DC EF BD BE AEF ∠413DG GB =DE AE14．宽与长的比等于黄金比的矩形称为黄金矩形．古希腊很多矩形建筑中宽与长的比都等于黄金比，如图，矩形ABCD 为黄金矩形，AB ＜AD ，以AB 为边在矩形ABCD 内部作正方形ABEF ，若AD ＝1，则DF ＝．15．如图，矩形的两条对角线相交于点O ，，垂足为E ，F 是的中点，连接交于点P，那么．16．如图，中，，，，若正方形的顶点在上，顶点、都在上，射线交边于点，则长为．17．如图：等腰直角三角形中，E 为边上一点，．将沿着翻折得到线段，连接，若．ABCD AC BD ，OE AB ⊥OC EF OB OPPB=ABC V 90ACB ∠=︒2BC =4AC =DEFC D AB F G AC AF BC H CH ABC BC 3BE CE =AB AE AD CD AB =CD =18．如图，在矩形中，，，点在直线上，从点出发向右运动，速度为每秒，点在直线上，从点出发向右运动，速度为每秒，相交于点，则的最小值为．三、解答题19．（8分）如图，，于点D ，M 是的中点，交于点P ，．若，求的长．ABCD 5cm AB =6cm BC =E AD A 0.5cm F BC B 2cm BE AF 、G BG CG +cm AB AC =AD BC ⊥AD CM AB DN CP ∥6cm AB =PN20．（8分）如图，四边形ABCD 中，AB=AC=AD ，AC 平分∠BAD ，点P 是AC 延长线上一点，且PD ⊥AD ．（1）证明：∠BDC=∠PDC ；（2）若AC 与BD 相交于点E ，AB=1，CE ：CP=2：3，求AE 的长．21．（10分）如图，在斜坡的顶部有一铁塔AB ，B 是CD 的中点，CD 是水平的，在阳光的照射下，塔影DE 留在坡面上.若铁塔底座宽CD=12m ，塔影长 m ，小明和小华的身高都是1.6m ，同一时刻小明站在点E 处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m 和1m ，求塔高AB．18DE22．（10分）如图1，在，，，D 为上一点，连接，分别过点A 、B 作于点N ，于点M ．（1）求证：；（2）若点D 满足，求的长；（3）如图2，若点E 为中点，连接，求证：．图1 图2Rt ABC △90ACB ∠=︒1AC BC ==AB CD AN CD ⊥BM CD ⊥ACN CBM V V ≌21BDAD =∶∶DM AB EM 45EMN ∠=︒23．（10分）如图，在正方形中，点是对角线上一点，的延长线交于点，交的延长线于点，连接．（1）求证：；（2）求证：；（3）若的长．ABCD G BD CG AB E DA F AG CG AG =2AB BE DF =⋅GE =GC =EF24．（12分）如图，在平面直角坐标系中，点A 在轴的正半轴上，点在轴的负半轴上，点在轴的正半轴上，且，线段、的长是一元二次方程的两个根，且.（1）求点A 、点的坐标；（2）求点的坐标；（3）若直线过点A 交线段于点，且，求点坐标；（4）在平面内是否存在一点，使得以为直角顶点的与相似，若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由.x B x C y 90ACB ∠=︒OB OA 213360x x -+=OB OA <B C l BC D :1:2ABD ADC S S =△△D P P APC △ABC V P答案一、单选题1．A【分析】点P 是AB 的黄金分割点，且PB ＜PA ，PB ＝x ，则PA ＝20−x ，则，即可求解．解：由题意知，点P 是AB 的黄金分割点，且PB ＜PA ，PB ＝x ，则PA ＝20−x ，∴，∴（20−x ）2＝20x ，故选：A ．2．A【分析】过点F 作交AC 于点G,可证．同理，可得，，；由,得，于是；设，则，，，从而得．解：过点F 作交AC 于点G,∴∴．BP AP AP AB=BP AP AP AB =FG BN ∥EN GN =13AE AD EC DB ==3EC AE =13AE BF EC FC ==FG BN ∥13BF NG FC GC ==3GC NG =EN NG a ==3=GC a 5EC a =203AC a =320EN AC =FG BN ∥1EN EM GN FM==EN GN =∵，∴．∴．∵，∴．∵,∴．∴．设，则，∴∴．∴．∴．∴．故选：A3．B【分析】设交于点，由，得三角形BCM 为等腰直角三角形，再由含30度角直角三角形三边长比及等腰直角三角形的边长比，设BC 为x ，可得MA 为，再由平行线分线段成比例求解．解：设交于点，∵，，DE BC ∥13AE AD EC DB ==3EC AE =EF AB ∥13AE BF EC FC ==FG BN ∥13BF NG FC GC ==3GC NG =EN NG a ==3=GC a 5EC EN NG GC a=++=35EC AE a ==53AE a =520+533AC AE EC a a a =+==320203EN a AC a ==CE FG M 45DAC BAD CAB ∠=∠+∠=︒MA x =-CE FG M 30CAB ∠=︒15BAD ∠=︒∴，∵，∴，三角形为等腰直角三角形，在Rt △ABC 中，设长为，则，∵，∴，∴，∵，∴，故选：B ．4．D【分析】过D 点作DG∥EF ，连接AE ，，GF ＝FC ，再计算△ADE 和△AEF 的面积即可．解：过D 点作DG ∥EF ，连接AE ，∵点E 恰好是CD 的中点，4AD ＝AB ，∴，GF ＝FC ，设AG ＝k ，则AF ＝4k ，GF ＝3k ，FC ＝3k ，∴，∵，S △ABC ＝8，∴，∴，∵，∴，∴＝．45DAC BAD CAB ∠=∠+∠=︒//FG DE 45CMB DAC ∠=∠=︒BCM BC x CM BC x ==30CAB ∠=︒CA ==MA x =-////HI FG DE 121h MA h CM ===14AG AD AF AB ==14AG AD AF AB ==43AF FC =14ACD ABC S AD S AB ∆∆==124ACD ABC S S ∆∆==112ADE AEC ACD S S S ∆∆∆===43AEFCEF S AF S CF ∆∆==4477AEF AEC S S ∆∆==417ADE AEF ADEF S S S ∆∆=+=+四边形117故选：D ．5．C【分析】直接利用位似图形的性质画出三角形顶点的对应点，再顺次连接即可画出图形，根据点的位置写出坐标即可．解：如图所示，当和在原点同侧时，∵与的相似比为2，，∴，即；如图所示，当和在原点两侧时，∵与的相似比为2，，∴，即；综上所述，或，故选C．1B ABC V 111A B C △111A B C △ABC V ()2,1B ()122,12B ⨯⨯()142B ，ABC V 111A B C △111A B C △ABC V ()2,1B ()122,12B -⨯-⨯()142B --，()142B --，()142B ，6．A【分析】证明，，，，求出，求出，，得出即可得出答案．解：、，，∴，，，∴，，∴，，∴，，∴，点是的中点，，，，∴，，∴，∴，故选：．7．DCOM CAB △∽△BOM BDC V V ∽OM CM AB BC =OM BM DC BC =125OM =132EG CD ==122FG AB ==1EF EG FG =-=AB BC ⊥ DC BC ⊥OM BC ⊥OM AB CD ∥∥COM CAB ∴V V ∽BOM BDC V V ∽OM CM AB BC =OM BM DC BC =4OM CM BC =6OM BM BC=125OM =EF BC ⊥ EG AB CD ∥∥ E BD BE DE ∴=BG CG ∴=CF AF ∴=132EG CD ==122FG AB ==1EF EG FG =-=75OM EF -=A【分析】由题意可得点在以点为圆心，为半径的上，在轴的负半轴上取点，连接，分别过、作，，垂足为、，先证，得，从而当取得最大值时，取得最大值，结合图形可知当，，三点共线，且点在线段上时，取得最大值，然后分别证，，利用相似三角形的性质即可求解．解：∵点为平面内一动点，，∴点在以点为圆心，为半径的上，在轴的负半轴上取点，连接，分别过、作，，垂足为、，∵∴∴，∵，∴，∵，∴，∴，∴当取得最大值时，取得最大值，结合图形可知当，，三点共线，且点在线段上时，取得最大值，C B 32OB x 0D ⎛⎫ ⎪ ⎪⎝⎭BD C M CF OA ⊥ME OA ⊥F E OAM DAC V V ∽23OM OA CD AD ==CD OM D B C B DC CD BDO CDF V V ∽AEM AFC V V ∽C 32BC =C B 32OB x 0D ⎛⎫ ⎪ ⎪⎝⎭BD C M CF OA ⊥ME OA ⊥F E OA OB ==AD OD OA =+=23OA AD =:1:2CM MA =23OA CM AD AC==OAM DAC ∠∠=OAM DAC V V ∽23OM OA CD AD ==CD OM D B C B DC CD∵∴，∴，∵，∴，∵轴轴，，∴，∵，∴，∴，解得同理可得，，∴，解得∴∴当线段取最大值时，点的坐标是，故选D ．8．A【分析】根据矩形的性质以及角平分线的性质得，是等腰直角三角形，，是等腰直角三角形，由证明，可得，，则，是等腰直角三角形，由，可得，由三角形外角的性质可得，证明，列比例式并结合等量代换可得．OAOB ==OD =BD =152==9CD BC BD =+=23OM CD =6OM =y x ⊥CF OA ⊥90DOB DFC ∠∠==︒BDO CDF ∠∠=BDO CDF V V ∽OB BD CF CD =1529=CF =AEM AFC V V ∽23ME AM CF AC ==23=ME =OE ===OM M 45DCE BCE ∠=∠=︒CEF △45F DCE ∠=∠=︒ABF △SAS (SAS)≌EBF EDC V V FEB CED ∠=∠BE ED =90FEB CEB CEB CED ∠+∠=∠+∠=︒BED V EBF EDC △≌△FEB CED ∠=∠DGC EBC ∠=∠∽CDG CEB V V AB AD CG CE ⋅=⋅解：如图：四边形是矩形，，，，平分，，，，是等腰直角三角形，，，是等腰直角三角形，，，，，，，，是等腰直角三角形，是等腰直角三角形，故A 错误；，，，，故B 正确；，，故D正确；ABCD AB CD ∴=90ABC BCD ADC ∠=∠=∠=︒90ABF ∴∠=︒CE BCD ∠45DCE BCE ∴∠=∠=︒AE CE ⊥ 90FEC ∴∠=︒CEF ∴V EF CE ∴=45F ∠=︒ABF ∴V BF AB CD ∴==45F DCE ∠=∠=︒ (SAS)≌EBF EDC ∴V △FEB CED ∴∠=∠BE ED =90FEB CEB CEB CED ∴∠+∠=∠+∠=︒BE ED = BED ∴V DCH V 45EBD ∴∠=︒45DGC GCB CBG CBG ∠=∠+∠=︒+∠ 45EBC EBD CBG CBG ∠=∠+∠=︒+∠DGC EBC ∴∠=∠DCG ECB ∠=∠ ∽CDG CEB ∴V V，，，，，故C 正确．故选：A ．9．A【分析】如图所示，连接，设射线交射线于H ，过点H 作于M ，连接，先根据三线合一定理得到，，进而证明四边形是矩形，得到，，故当点B 与点M 重合时，最小，即最小，最小值为，设，则，求出，利用相似三角形的性质求出（舍去），则的最小值为．解：如图所示，连接，设射线交射线于H ，过点H 作于M ，连接，∵，，点F 、G 分别为线段的中点，∴，，∵，∴，即，∴四边形是矩形，∴，，∴当最小时，最小，∴当点B 与点M 重合时，最小，即最小，最小值为，∵点H 在直线上，∴可设，∴，∵，CD CG CE CB∴=CD AB = BC AD =AB CG CE AD∴=AB AD CG CE ∴⋅=⋅BF BG ，ED OA HM OE ⊥BH BF OC BG DE ⊥，⊥OBF CBF DBG EBG ==∠∠，∠∠BFHG FG BH =90OHE ∠=︒BH FG HM ()2H m m ，2OM m HM m ==，OE =OMH HME △∽△m =0m =FG BF BG ，ED OA HM OE ⊥BH OB BC =BD BE =OC DE 、BF OC BG DE ⊥，⊥OBF CBF DBG EBG ==∠∠，∠∠180OBF CBF DBG EBG +++=︒∠∠∠∠90CBF DBG +=︒∠∠90FBG ∠=︒BFHG FG BH =90OHE ∠=︒BH FG BH FG HM 12y x =()2H m m ，2OM m HM m ==，()E∴∵，∴，又∵，∴，∴，∴∴（舍去），经检验，∴，故选A ．10．A【分析】设，，则，根据正方形与正方形面积之比为，得到，求出，作交于点M ，作交于点P ，证明出，设，则然后利用相似三角形的性质得到，然后解方程求解即可．解：由题意可得，∴设，，则，∵，∴，OE =90MEH HOE MHO MOH +=︒=+∠∠∠∠MHO MEH =∠OMH HME =∠∠OMH HME △∽△OM HM HM ME=2m m =m =0m =m =FG CI DH a ==CH b =IH a b =+ABCD FGHI 59()22259a b a b +=+2BI CH a ==BM GH ⊥GH NE BM ⊥BM BPE ENC ∽V V CN m =IN BP a m ==+a m a a m +=BIC CHD ≌V V CI DH a ==CH b =IH a b =+90H ∠=︒22222CD CH DH a b =+=+∵正方形与正方形面积之比为，∴，即，∴整理得，∴，解得或（舍去），∴，∴，如图所示，作交于点M ，作交于点P ，由题意可得，，∵，∴四边形，是矩形，∴，，∴，∴设，则，∵，∴，∵，∴，∴，又∵，∴，ABCD FGHI 592259CD IH =()22259a b a b +=+222520a ab b -+=25220a a b b ⎛⎫-+= ⎪⎝⎭12a b =2a b=2b a =2BI CH a ==BM GH ⊥GH NE BM ⊥BM AGD DHC ≌V V ED CH ∥BINP ENHD 2PN BI a ==EN DH a ==PE PN EN a =-=CN m =IN BP a m ==+BE CE ⊥90BEP CEN ∠+∠=︒BP PN ⊥90BEP PBE ∠+∠=︒CEN PBE ∠=∠90BPE ENC ∠=∠=︒BPE ENC ∽V V∴，即，∴整理得，∴，∴解得，∴故选：A ．二、填空题11．30【分析】设，，，根据得到，求得，从而得出，，，代入进行计算即可．解：，设，，，，，解得：，，，，，故答案为：30．12．【分析】过点M 作，交于点Q ，根据平行线分线段成比例可得，设，求出，即可求解．解：过点M 作，交于点Q ，BP PE BE EN CN CE ==a m a a m+=220a am m -+=210a a m m ⎛⎫-+= ⎪⎝⎭a m =BE CE =3a k =5b k =7c k =10a b c -+=35710k k k -+=2k =6a =10b =14c =::3:5:7a b c = ∴3a k =5b k =7c k =10a b c -+= 35710k k k ∴-+=2k =6a ∴=10b =14c =6101430a b c ∴++=++=5:8MQ BN ∥AC 23BM NQ CM CQ ==2,3NQ k CQ k ==54k AN =MQ BN ∥AC∵，∴，设，∴，∵，∴，则，∵，∴，故答案为：．13．或4【分析】延长交于R ，作于T ，不妨设，，，可证得是等腰三角形，可推出，进而表示出，然后解，从而求出x 的值，进而可得结果．解：如图，延长交于R ，作于T ，，不妨设，，则，设，MQ BN ∥23BM NQ CM CQ ==2,3NQ k CQ k ==5CN NQ CQ k =+=:1:4AN CN =154AN k =54k AN =MQ PN ∥55428kAP AN MP NQ k ===5:812EF BC GT DE ⊥4DG =13GB =4DE x =REB V 413EG DE DG RG BR BG ===EG DEG △EF BC GT DE ⊥ 413DG GB =∴4DG =13GB =17BD =4DE x =四边形是正方形，，，，，，恰好平分，，，，，在中，，由勾股定理得，解得，，当，当，综上所述，或4，故答案为：或4．14【分析】先根据黄金矩形求出AB ，再利用正方形的性质求出AF ，然后进行计算即可解答．解：∵矩形ABCD 为黄金矩形，AB ＜AD ，ABCD ∴BC AD ∥AD ==∴EBC AEB ∠=∠4AE AD DE x =-=413EG DE DG RG BR BG ===∴13BR x = BE AEF ∠∴AEB FEB ∠=∠∴EBC FEB ∠=∠∴13ER BR x ==∴4521717EG ER x ==Rt EGT V GT DT DG ===4ET DE DT x =-=-((22252417x x ⎛⎫+-= ⎪⎝⎭1x =2x =∴4DE x ==DE =AE ==∴4DE AE=DE =AE ==∴12DE AE =12DE AE =12∴∴∵四边形ABEF 是正方形，∴∴DF=AD -AF=15．【分析】根据矩形性质得到，利用三角形的三线合一得，过O 作交于点Q ，则有，，计算即可．解：∵是矩形，∴，∵F 是的中点，∴，又∵，∴，过O 作交于点Q ，∴，，∴，故答案为：．16．AB AD =AB AD ==1=13OA OB OC ==AE EB =OQ AB P EF OQF AEF V V ∽OQP BEP V V ∽ABCD OA OB OC ==OC 1122OF OC OA ==OA OB =OE AB⊥AE EB =OQ AB P EF OQF AEF V V ∽OQP BEP V V ∽13OP OQ OQ OF PB BE AE AF ====1343【分析】证明，，由相似三角形的性质得出，，设，可得，，从而可得出答案．解：∵四边形为正方形，，∴，，∴，， ∴，，设， ∴，， ∴， ∴， ∴．故答案为．17．2【分析】如图，作，使，连接，，交于，过作于，可得，，可得，求解，，可得，由对折可得：，，，证明，可得，再证明，可得，有，，求解，可得，从而可得答案．解：∵等腰直角三角形，∴，如图，作，使，连接，，交于，过作于，△∽△ADG ABC AEF AHC V V ∽DG AG BC AC=EF AF CH AC =DG EF x ==24x AG =4x AG x CH +=DGFE 90ACB ∠=︒DG EF BC ∥∥DG EF =△∽△ADG ABC AEF AHC V V ∽DG AG BC AC=EF AF CH AC =DG EF x ==24xAG =4x AG x CH +=2AG x =24x x x CH +=43CH =43AH AE ⊥AH AE =DE EH CH DE K A AF BC ⊥F BAE CAH ∠=∠BC ==12AF CF BC ===()SAS BAE CAH ≌△△454590BCH ∠=︒+︒=︒BE CH ==CE EF ==AH AE ===52EH ==AB AD ==BAE DAE ∠=∠DE BE =45ADE ABE ∠=∠=︒()SAS AEC AHD V V ≌90ECH EDH ∠=∠=︒()Rt Rt HL HEC EHD V V ≌HED CHE ∠=∠CH DE ==EK HK =CK DK =EK HK ==CK DK ===HKE CKD V V ∽ABC AB =AB AC ==BC =AH AE ⊥AH AE =DE EH CH DE K A AF BC ⊥F∵等腰直角三角形，∴，，∴，∴，∴，，∴，∵，∴，，∴∴，由对折可得：，，，∵，∴，∴，∵，，∴，∴，∴，∴，∵，，∴，ABC 90BAC EAH ∠=︒=∠AB AC ==45B ACB ∠=∠=︒BAE CAH ∠=∠BC ==12AF CF BC ===()SAS BAE CAH ≌△△BE CH =45B ACH ∠=∠=︒454590BCH ∠=︒+︒=︒3BE CE =BE CH ==CE EF ==AH AE ===52EH =AB AD ==BAE DAE ∠=∠DE BE ==45ADE ABE ∠=∠=︒90BAC EAH ∠=∠=︒90BAE EAC DAE DAH ∠+∠=︒=∠+∠EAC DAH ∠=∠AE AH =AB AC AD ==()SAS AEC AHD V V ≌45ACE AHD ∠=∠=︒CE HD ==454590EDH ∠=︒+︒=︒90ECH EDH ∠=∠=︒EH EH =CE DH =()Rt Rt HL HEC EHD V V ≌∴，，∴，，由勾股定理可得：，∴，∴，∴，∴，，∴，∴，∴，故答案为：218．10【分析】过点作直线，分别交、于点，过点作直线，分别交、于点，易知四边形、、为矩形，证明，由相似三角形的性质可得；设两点运动时间为，则，，易得，；作点关于直线的对称点，由轴对称的性质可得，故当三点共线时，的值最小，即取最小值，此时，在中，由勾股定理求得的值，即可获得答案．解：如下图，过点作直线，分别交、于点，过点作直线，分别交、于点，HED CHE ∠=∠CH DE ==EK HK =CK DK =222EK CE CK =+222EK EK ⎫=-+⎪⎪⎭EK HK ==CK DK ===45DK CK EK HK ===HKE DKC ∠=∠HKE CKD V V ∽45CD CK HE HK ==4452552CD EH ==⨯=G MN BC ⊥AD BC M N 、G PQ CD ∥AB DC P Q 、ABNM PBNG GNCQ GAE GFB V V ∽AE GM BF GN =E F 、t 0.5AE t =2BF t =1cm GM =4cm GN =C PQ K CG KG =B G K 、、BG KG +BG CG +Rt BCK △BK G MN BC ⊥AD BC M N 、G PQ CD ∥AB DC P Q 、易知四边形、、为矩形，，∵四边形为矩形，∴，∴，，∴，∴，设两点运动时间为，则，，则有，即，∵，∴，，∵四边形为矩形，∴，作点关于直线的对称点，如图，则，，由轴对称的性质可得，当三点共线时，的值最小，即取最小值，此时，在中，，∴的最小值为．故答案为：10．三、解答题19．ABNM PBNG GNCQ 5cm MN AB ==ABCD AD BC ∥AB DC∥GAE GFB ∠=∠GEA GBF ∠=∠GAE GFB VV ∽AEGM BF GN=E F 、t 0.5AE t =2BF t =0.5124GM t GN t ==4GN GM =5cm MN =1cm GM =4cm GN =GNCQ 4cm QC GN ==C PQ K 4cm QK QC ==8cm KC QK QC =+=CG KG =B G K 、、BG KG +BG CG +Rt BCK △10cm BK ===BG CG +10cm解：∵，，∴，又∵，∴，∴，∵点M 是线段的中点，，∴，∴，∴，∵，∴．20．解：（1）证明：∵AB=AD ，AC 平分∠BAD ，∴AC ⊥BD ，∴∠ACD+∠BDC=90°，∵AC=AD ，∴∠ACD=∠ADC ，∴∠ADC+∠BDC=90°，∵PD ⊥AD ，∴∠ADC+∠PDC=90°，∴∠BDC=∠PDC ；（2）解：过点C 作CM ⊥PD 于点M ，AB AC =AD BC ⊥BD DC =DN CM ∥1BN BD PN DC==BN NP =AD DN CM ∥1AP AM PN MD==AP PN =13PN AB =6cm AB =()1162cm 33PN AB ==⨯=∵∠BDC=∠PDC ，∴CE=CM ，∵∠CMP=∠ADP=90°，∠P=∠P ，∴△CPM ∽△APD ，∴=，设CM=CE=x ，∵CE ：CP=2：3，∴PC=x ，∵AB=AD=AC=1，∴=，解得：x=，故AE=1-=．21．解：如图，过点D 作，交AE 于点F ，过点F 作，垂足为点G.由题意得，，∴，∵，，∴，∴，答：塔高AB 为24m.CM AD PC PA32x 13x 23x 12+131323DF CD ⊥FG AB ⊥1.62DF DE =18 1.6214.4(m)DF =⨯÷=16m 2GF BD CD === 1.61AG GF =1.669.6(m)AG =⨯=14.49.624(m)AB =+=22．解：（1）证明：∵，，∴，，又∵，∴，∴∵，∴；（2）解：∵，，∴，∴，设，则，由（1）知，，∵，∴，∴，∴，∴，∴；（3）解：延长，相交于点H，AN CD ⊥BM CD ⊥90ANC ∠=︒90BMC ∠=︒90ACB ∠=︒90ACN BCM BCN CBM ∠+∠=∠+∠=︒ACN CBM∠=∠AC BC =()ACN CBM ASA V V ≌AND BMD ∠=∠ADN BDM ∠=∠AND BMD V V ∽12AN DN AD BM DM DB ===AN x =2BM x =AN CM x ==2BM CN x ==222AN CN AC +=()22221x x +=x =CM =CN =MN 2233DM MN ===ME AN∵E 为的中点，∴∵，，∴，∴，，∴，∴，又∵，∴，又∴，∴，∴．23．解：（1）证明：∵是正方形的对角线，∴，，在和中，，∴，∴；（2）证明：∵四边形是正方形，∴，，，AB AE BE=90ANM ∠=︒90BMN ∠=︒AN BM ∥HAE MBE ∠=∠AHE BME ∠=∠()AAS AHE BME V V ≌AH BM =BM CN =CN AH =CM AN=MN HN =45HMN ∠=︒45EMB ∠=︒BD ABCD 45C D B A D B ∠=∠=︒DC DA =CDG V ADG △DC DA CDG ADG DG DG =⎧⎪∠=∠⎨⎪=⎩()SAS CDG ADG ≌△△CG AG =ABCD 90CBE FDC ∠=∠=︒CB CD AB ==CB DF ∥∴，∴，∴，即，∴；（3）解：∵∴，∵四边形是正方形，∴，，，∴，∴，，∴，∴，设，则，∴，∵，∴，，∴，∴，∴，∴的长为24．（1）解：∵，∴．∴．∵点A 在轴的正半轴上，点在轴的负半轴上，BCE DFC ∠=∠BCE DFC ∽△△CB FD BE DC =AB FD BE AB=2AB BE DF =⋅GE =GC =CE CG GE =+=ABCD CD AB ∥CD AB =CB AD ∥BE CD ∥EBG CDG ∠=∠BEG DCG ∠=∠BEG DCG ∽△△BE GE DC GC ==BE =6CD x =(66AE AB BE CD BE x x =-=-==AF CB ∥FAE CBE ∠=∠AFE BCE ∠=∠AFE BCE △∽△EF AE EC BE==EF =EF 213360x x -+=(4)(9)0x x --=124,9x x ==x B x∴A 点坐标为，B 点坐标为，（2）∵A 点坐标为，B 点坐标为，∴，设点C 的坐标为，则，∵，，∴，∴，∴，∴，∴，解得，经检验，是方程的解且符合题意，∴点C 的坐标是；（3）过点D 作轴于点E ，轴于点F ，如图，则，∴，，∵，∴．∴；，∵，，∴；，()9,0()4,0-()9,0()4,0-9,4OA OB ==()0,t ()0t >OC t =90ACB ∠=︒90AOC COB ∠=∠=︒90OCB ACO OCB OBC ∠+∠=∠+∠=︒ACO OBC ∠=∠ACO CBO V V ∽OC AO OB OC=94tt =6t =6t =()0,6DE x ⊥DF y ⊥DE OC ∥DF OB∥BED BOC V V ∽CDF CBO V V ∽:1:2ABD ADC S S =△△:1:2BD DC =13DE BD OC BC ==23DF CD BO BC ==4OB =6OC =2DE =243DF =解得．∴．（4）解：存在，求解过程如下：设，由题意可得：，，当时，，即，，解得，或，即点坐标为或，当时，，即，，解得或，即点坐标为或，综上可知，满足条件的P 点为：或或或83DF =8,23D ⎛⎫- ⎪⎝⎭(,)P x y 13AB OB OA =+=BC ===AC ===AP =CP =APC ACB △∽△AP AC PC AC AB CB ==29AC AP AB===6AC CB CP AB ⨯===00x y =⎧⎨=⎩721310813x y ⎧=⎪⎪⎨⎪=⎪⎩P (0,0)72108,1313⎛⎫⎪⎝⎭APC BCA △∽△AP AC PC BC AB AC ==6AC BC AP AB ⨯===29AC CP AB===96x y =⎧⎨=⎩45133013x y ⎧=⎪⎪⎨⎪=-⎪⎩P ()9,64530,1313⎛⎫- ⎪⎝⎭(0,0)72108,1313⎛⎫ ⎪⎝⎭()9,64530,1313⎛⎫- ⎪⎝⎭。

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、已知△ABC和△A′B′C′是位似图形．△A′B′C′的面积为6cm2，周长是△ABC的一半．AB＝8cm，则AB边上高等于（）A.3 cmB.6 cmC.9cmD.12cm2、如图，点D，E分别为△ABC边AB，AC上的一点，且DE∥BC，S△ADE ＝4，S四边形DBCE＝5，则△ADE与△ABC相似比为（）A.5：9B.4：9C.16：81D.2：33、如图所示的4个三角形中，相似三角形有（）A.1对B.2对C.3对D.4对4、如图，已知△ADE与△ABC的相似比为1：2，则△ADE与△ABC的面积比为（）．A.1：2B.1：4C.2：1D.4：15、如图所示的三个矩形中，其中相似形是（）A.甲与乙B.乙与丙C.甲与丙D.以上都不对6、如图，AB是⊙O的直径，OD垂直弦AC于点E，且交⊙O于点D，过点D作⊙O的切线与BA的延长线相交于点F，下列结论不一定正确的是（）A.∠CDB=∠BFDB.△BAC∽△OFDC.DF∥ACD.OD=BC7、若非零实数x ， y满足，则等于（）A.3：4B.4：3C.2：3D.3：28、如图，为了测量某棵树的高度，小明用长为2m的竹竿作测量工具，移动竹竿，使竹竿顶端、树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距6m,与树相距15m，则树的高度为( )A.4mB.5mC.7mD.9m9、点是线段的黄金分割点，且，则的长为（）A. B. C. 或D. 或10、相似三角形的概念是（）A.对应角相等、对应边成比例的两个三角形B.两角分别相等的两个三角形C.三边对应成比例的两个三角形D.两边对应成比例且夹角相等的两个三角形11、如图．巳知直线a∥b∥c，直线m交直线a，b，c于点A,B，C，直线n交直线a，b，c于点D，E，F，若再,DE=2,则EF的长是( )A.6B.5C.4D.312、已知点C在线段AB上，且点C是线段AB的黄金分割点（AC＞BC），则下列结论正确的是（）A.AB 2=AC•BCB.BC 2=AC•BCC.AC= BCD.BC= AB13、如果两个相似三角形对应边之比是，那么它们的对应中线之比是（）A.1:3B.1:4C.1:6D.1:914、如图所示，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O.若S△DOE ：S△COA＝4：25，则S△BDE与S△CDE的比是( )A.1：2B.1：3C.2：3D.2：515、如图，在△ABC中，DE∥BC分别交AB，AC于点D，E，若＝，则下列说法不正确的是（）A. ＝B. ＝C. ＝D.＝二、填空题(共10题，共计30分)16、如图，直线l1∥l2∥l3，直线AC和DF被l1，l2，l3所截，AB＝5，BC＝6，EF＝4，则DE的长为________．17、一个铝质的三角形框架的三边长分别为24 cm，30 cm，36 cm，要做一个与它相似的铝质三角形的框架，现有长27 cm，45 cm的两根铝材，要求以其中的一根为边，从另一根上截下两段(允许有余材)，则截法有________种．18、如图，△ABD与△AEC都是等边三角形，AB≠AC．下列结论中，正确的是________．①BE＝CD；②∠BOD＝60º；③△BOD∽△COE．19、如图：平行四边形ABCD中，E为AB中点，，连E、F交AC于G，则AG：GC=________；20、已知如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足是D，写出图中的一组相似三角形________．21、如图，点在的边上，请你添加一个条件，使得∽,这个条件可以是 ________.22、如图，在△ABC中，AB＝BC＝2 ，AE⊥BC，垂足为点E，延长AE至点D，使AD＝AB，连接CD、BD，若∠ACD＝90°，则BD的长为________．23、如图，在矩形ABCD中，AB＝3，AD＝7，点E是AD边上的一点，连接BE，将BE绕点E顺时针旋转90°至B′E，连接B′D，当△B′ED是直角三角形时，线段AE的长为________.24、如图，在△ABC中，∠C=90°，AB=5，BC=3，D是AB的中点，点E在边AC 上，将△ADE沿DE翻折，使点A落在点A'处，当A'E⊥AC时，A'B=________．25、在矩形ABCD中，∠B的角平分线BE与AD交于点E，∠BED的角平分线EF 与DC交于点F，若AB=9，DF=2FC，则BC=________．（结果保留根号）三、解答题(共5题，共计25分)26、如果，且x＋y＋z＝18，求x，y，z的值．27、在矩形中，已知，在边上取点，使，连结，过点作，与边或其延长线交于点．猜想：如图①，当点在边上时，写出线段与的大小关系。

沪科版九年级上册数学第22章相似形含答案(真题汇编)

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，已知△ABC中，P是边AC上的一点，连接BP，以下条件不能判定△ABP∽△ACB的是（）A.∠ABP=∠CB.∠APB=∠ABCC. =D. =2、如图，一块含有30°的直角三角板的直角顶点和坐标原点重合，30°角的顶点在反比例函数的图象上，顶点B在反比例函数的图象上，则k的值为（）A.-4B.4C.-6D.63、在下列命题中：①三点确定一个圆；②同弧或等弧所对圆周角相等；③所有直角三角形都相似；④所有菱形都相似；其中正确的命题个数是（）A.0B.1C.2D.34、如图，在△ABC中，DE∥BC，若，则等于( )A. B. C. D.5、如下图，以某点为位似中心，将△AOB进行位似变换得到△CDE，记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为（）A. B. C. D.6、如图，已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点)，要使ΔABC∽ΔPBD，则点P的位置应落在A.点上B.点上C.点上D.点上7、如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC，BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为（）A.5B.4C.3D.28、如图，以某点为位似中心，将△AOB进行位似变换得到△CDE，记△AOB与△CDE对应边的比为k，则位似中心的坐标和k的值分别为（）A.(0，0)，2B.（2，2）,C.(2，2)，2D.(2，2)，39、如图，等腰直角△ABC的直角边长为3，P为斜边BC上一点，且BP=1，D为AC上一点，且∠APD=45°，则CD的长为A. B. C. D.10、已知与相似，且相似比为，则与的周长比为（）A. B. C. D.11、在相同时刻的物高与影长成比例，如果高为1.5m的测杆的影长为2.5m，那么影长为30m的旗杆是（）A.20mB.16mC.18mD.15m12、下列说法正确的是（）A.对角线互相平分的四边形是矩形B.平行四边形是轴对称图形C.位似三角形是相似三角形D.可以选用同一种正五边形图形镶嵌地面13、如图，，分别是两条中线，连结，则的比值是（）A. B. C. D.14、下列判断中，正确的是（）A.相似图形一定是位似图形B.位似图形一定是相似图形C.全等的图形一定是位似图形D.位似图形一定是全等图形15、已知A，B两地的实际距离AB=5km，画在图上的距离为CD=2cm，则该图的比例尺为（）A.2：5B.1：250000C.250000：1D.1：2500二、填空题(共10题，共计30分)16、如图，正方形纸片ABCD的边长为12，E,F分别是边AD,BC上的点，将正方形纸片沿EF折叠，使得点A落在CD边上的点处，此时点落在点处.已知折痕EF＝13，则AE的长等于________.17、如图，在中，，，垂足为，，则的长为________.18、如图，在一块直角三角板ABC中，∠C=90°，∠A=30°，BC=1，将另一个含30°角的AEDF的30°角的顶点D放在AB边上，E，F分别在AC，BC上，当点D在AB边上移动时，DE始终与AB垂直，若△CEF与△DEF相似，则AD=________．19、如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，则△ABC 与△DEF的面积之比为________ ．20、如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O 为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C 的坐标为________ ．21、函数y＝kx，y＝，y＝的图象如图所示，下列判断正确的有________.（填序号）①k，a，b都是正数；②函数y＝与y＝的图象会出现四个交点；③A，D两点关于原点对称；④若B是OA的中点，则a＝4b.22、如图，在△ABC中，AB＝4，AC＝3，D是AB边上的一点.若△ABC∽△ACD，则AD的长为________.23、已知△ABC与△DEF相似且面积的比为4:9，则△ABC与△DEF的周长比为________ .24、如图，在中，，，，，分别为、上的点，沿直线将折叠，使点B恰好落在上的处，当恰好为直角三角形时，BE的长为________．25、阳光下，高为4m的旗杆在地面上的影长为7m，此时测得一建筑物在地面上的影长为21m，则建筑物的高度为________．三、解答题(共5题，共计25分)26、若a：b=1：2，求（a+b）：a的值．27、“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E，南门点F 分别是AB、AD的中点，EG⊥AB，FH⊥AD，EG＝15里，HG经过点A，问FH多少里？28、已知a：b：c=2：3：4，且2a+3b﹣2c=10，求a﹣2b+3c的值．29、如图，直线l1∥l2∥l3，直线AC依次交l1， l2， l3于A，B，C三点，直线DF依次交l1， l2， l3于D，E，F三点，若，DE＝2，求EF的长.30、在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．参考答案一、单选题(共15题，共计45分)1、D2、C3、B4、C6、B7、D8、C9、C10、B11、C12、C13、B14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、28、30、。

(真题汇编)沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；② ；③△PMN为等边三角形；④当∠ABC=45°时，BN= PC．其中正确的个数是（）A.1个B.2个C.3个D.4个2、下列条件中，能判定两个等腰三角形相似的是（）A.都含有一个30°的内角B.都含有一个45°的内角C.都含有一个60°的内角D.都含有一个80°的内角3、若，且，则的值是（）A.4B.2C.20D.144、如图，在正方形中，点分别是边上的两点，且分别交于.下列结论：① ；② 平分；③ ；④ ．其中正确的结论是（）A.②③④B.①④C.①②③D.①②③④5、如图，在中，于点，若，则的值为（）A. B. C. D.6、如图，⊙O半径为5，PC切⊙O于点C，PO交⊙O于点A，PA=4，则PC的长为（）A.6B.C.D.7、如图，若DC∥FE∥AB，则有（）A. B. C. D.8、如图，△ABC和△A1B1C1是以点O为位似中心的位似三角形，若C1为OC的中点，AB＝4，则A1B1的长为( )A.1B.2C.4D.89、△ABC与△DEF满足下列条件，其中能使△ABC∽△DEF的是( )A.AB＝1，BC＝1.5，AC＝2，DE＝8，EF＝12，DF＝16B.AB＝，BC＝，AC＝，DE＝，EF＝3，DF＝3 C.AB＝3，BC＝4，AC＝6，DE ＝6，EF＝8，DF＝16 D.AB＝3，BC＝4，AC＝5，DE＝，EF＝2，DF＝10、如图，在△ABC中，∠BAC=90°，D，E为BC上两点，过点D，E分别作AC，AB的垂线，两垂线交于点M，垂足分别为G，F，若∠AED=∠BAD，AB=AC=2，则下列说法中不正确的是（）A.△CAE∽△BDAB.C.BD•CE=4D.BE= BF11、如果点D、E分别在△ABC中的边AB和AC上，那么不能判定DE∥BC的比例式是（）A. AD：DB＝AE：ECB. DE：BC＝AD：ABC. BD：AB ＝CE：ACD. AB：AC＝AD：AE12、已知，那么下列式子中一定成立的是（）A.x+y=5B.2x=3yC.D.13、如图，点G是△ABC的重心，下列结论：① ；② ；③△EDG∽△CGB；④ ．其中正确的个数有（）A.1个B.2个C.3个D.4个14、如图，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现他身后影子的顶部刚好接触到路灯AC的底部，当他向前再步行20 m到达Q点时，发现他身前影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5 m，两个路灯的高度都是9 m，则两路灯这间的距离是( )A.24mB.25mC.28mD.30m15、如图，在平行四边形中，为的中点，为上一点，交于点，，则的长为（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，△ABC与△DEF是位似图形，位似比为2：3，已知AB=4，则DE的长为________．17、如图，⊙O是△ABC的外接圆，已知AD平分∠BAC交⊙O于点D，交BC于点E，若BD=6，AE=5，AB=7，则AC=________.18、如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为________m．19、如果，那么k的值为________.20、在综合实践课上，小明同学设计了如图测河塘宽AB的方案：在河塘外选一点O，连结AO，BO，测得AO=18m，BO=21m，延长AO，BO分别到D，C两点，使OC=6m，OD=7m，又测得CD=5m，则河塘宽AB=________m．21、在中，，点在直线上，，点为边的中点，连接，射线交于点，则的值为________.22、如图，任两个竖直或水平相邻的点都相距个单位长度．已知线段交线段于点，则线段的长是________．23、如图，直角三角形ABC中，∠ACB=90°，AB=10，BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F，现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A1；AD的中点E的对应点记为E1，若△E1FA1∽△E1BF，则AD=________．24、如图，△ABC与△A′B′C′是位似图形，且顶点都在格点上，则位似中心的坐标是________．25、△ABC中，D、E分别在AB、AC上，DE∥BC，AD=1，BD=3，则△ADE与△ABC的面积之比为________．三、解答题(共5题，共计25分)26、已知：，求的值.27、如图，已知等腰中，AB=AC=2，点D在边BC的反向延长线上，且DB=3，点E在边BC的延长线上，且∠EAC=∠D，求线段CE的长28、求证：相似三角形对应高的比等于相似比．(请根据题意画出图形，写出已知，求证并证明)29、如图，在网格图中的△ABC与△DEF是否成位似图形？说明理由．如果是，同时指出它们的位似中心．30、在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB=2m，它的影子BC=1.6m，木竿PQ落在地面上的影子PM=1.2m，落在墙上的影子MN=0.8m，求木竿PQ的长度．参考答案一、单选题(共15题，共计45分)1、D2、C3、A4、D5、B6、D7、D8、D9、A10、B11、B12、D13、C14、D15、B二、填空题(共10题，共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、29、30、。

沪科版九年级上册数学第22章相似形含答案

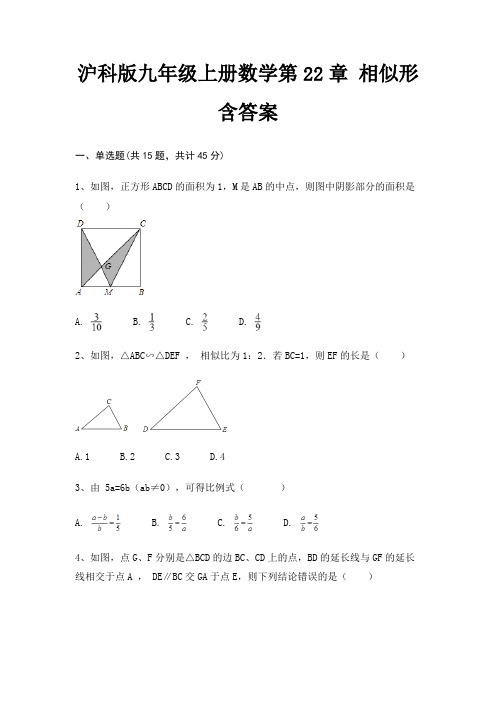
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，正方形ABCD的面积为1，M是AB的中点，则图中阴影部分的面积是（）A. B. C. D.2、如图，△ABC∽△DEF ，相似比为1：2．若BC=1，则EF的长是（）A.1B.2C.3D.43、由 5a=6b（ab≠0），可得比例式（）A. B. C. D.4、如图，点G、F分别是△BCD的边BC、CD上的点，BD的延长线与GF的延长线相交于点A ， DE∥BC交GA于点E，则下列结论错误的是（）A. B. C. D.5、如图，□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF:FC 等于（）A.3:2B.3:1C.1:1D.1:26、已知=，那么下列等式中，不一定正确的是（）A.2a=5bB. =C.a+b=7D. =7、如图，△ABC内接于⊙O，AD⊥BC于点D，AD=2cm，AB=4cm，AC=3cm，则⊙O 的直径是( )A.2cmB.4cmC.6cmD.8cm8、如图，在中，于点，若，则的值为（）A. B. C. D.9、如图，直线l1∥l2∥l3，直线AC分别交l1， l2， l3于点A ， B ，C；直线DF分别交l1， l2， l3于点D ， E ， F ． AC与DF相交于点H ，且AH=2，HB=1，BC=5，则的值为（）.A. B.2 C. D.10、已知x：y=3：2，则下列各式中不正确的是（）A. B. C. D.11、下列各组图形中一定相似的有（）A.两个矩形B.两个等腰梯形C.两个等腰三角形D.两个等边三角形12、如图，△ABC中，D是边AC上的一点，且∠DBC=∠A，BC=， AC=3，则CD的长是 ( )A.1B.C.2D.13、雨后初晴，一学生在运动场上玩耍，从他前面2米远一块小积水处，他看到旗杆顶端的倒影，如果旗杆底端到积水处的距离为40米，该生的眼部高度是1.5米，那么旗杆的高度是（）A.30米B.40米C.25米D.35米14、已知，那么的值为（）A. B. C. D.15、如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB，若AB=3BD。

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，AB∥GH∥CD，点H在BC上，AC与BD交于点G，AB＝2，CD＝3，则GH长为（）A.1B.1.2C.2D.2.52、如图，已知直线l∥m∥n，直线a分别与l，m，n交于点A，B，C，过点B 作直线b交直线l，n于点D，E，若AB=2，BC=1，BD=3，则BE的长为（）A.4B.2C.D.3、下列命题中不成立的是（）A.矩形的对角线相等B.三边对应相等的两个三角形全等C.两个相似三角形面积的比等于其相似比的平方D.一组对边平行，另一组对边相等的四边形一定是平行四边形4、如图，△ABC中，D、E分别为边AB、AC上的点，且DE∥BC，下列判断错误的是（）A. =B. =C. =D. =5、如图，△ABC， AB=12，AC=15，D为AB上一点，且AD= AB ，在AC上取一点E，使以A，D，E为顶点的三角形与ABC相似，则AE等于（）A. B.10 C. 或10 D.以上答案都不对6、如图，已知，，那么下列结论中，正确的是（）A. B. C. D.7、如图；在△ABC中，∠CAB=Rt∠，以△ABC的各边为边作三个正方形，点E 落在FH上，点J落在ED的延长线上，若图中两块阴影部分面积的差是30，则AB的长是（）A. B. C.8 D.8、如图，在△ABC中，已知∠ADE=∠B，则下列等式成立的是（）A. =B. =C. =D. =9、如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A.1：16B.1：4C.1：6D.1：210、在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2012个正方形的面积为（）A.5×2010B.5×2010C.5×2012D.5×402211、两相似三角形对应高长的比为3：4，则对应中线长的比为（）A.3：4B.9：16C. ：2D.4：312、如图，在ABC中，AD平分∠BAC，AE:AC=AF:AB=1:3，那么AG:GD的值为（）A.1：2B.1：3C.2：5D.3：513、如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射到桌面后在地面上形成（圆形）的示意图. 已知桌面直径为1.2米，桌面离地面1米. 若灯泡离地面3米，则地面上阴影部分的面积（）A.0.36π米2B.0.81π米2C.2π米2D.3.24π米214、某一时刻，身高1.6m 的小明在阳光下的影长是0.4m．同一时刻同一地点，测得某旗杆的影长是5m，则该旗杆的高度是（）A.1.25mB.10mC.20mD.8m15、如图所示，长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下矩形与原矩形相似，那么剩下矩形的面积是（）A.28cm 2B.27cm 2C.21cm 2D.20cm 2二、填空题(共10题，共计30分)16、如图，点A，点B分别在y轴x轴上，OA=OB，点E为AB的中点，连接并延长OE交反比例函数（x>0）的图象于点C，过点C作CD⊥x轴于点D，点D关于直线AB的对称点恰好在反比例函数图象上，则=________.17、如图，在正方形ABCD中，点E为AD的中点，连接EC，过点E作EF⊥EC，交AB于点F，则tan∠ECF=________.18、在上午的某一时刻身高1.7米的小刚在地面上的影长为3.4米，同时一棵树在地面上的影子长12米，则树的高度为________米.19、将一副三角板按图叠放，则△AOB与△DOC的面积之比等于________20、如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B、C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=，则线段CE的最大值为________ ．21、如图，在△ABC中，DE∥BC，AH⊥BC于点H，与DE交于点G．若，则=________．22、已知，则=________23、若，则=________．24、如图，在矩形ABCD中，AB＝4，BC＝，M为BC边中点，E为AD边上的一动点，过点A作BE的垂线，垂足为F，连接FM，则FM的最小值为________.在线段FM上取点G，使GM＝FM，将线段GM绕点M顺时针旋转60°得到NM，连接GN，CN，则CN的最小值为________.25、在△ABC中，D，E分别在边AB，AC上，且DE∥BC，过点A作平行于BC的直线分别交CD和BE的延长线于点M，N，若DE=2，BC=6，则MN=________．三、解答题(共5题，共计25分)26、已知x：y：z=2：3：4，求的值．27、已知：如图，四边形ABCD是平行四边形，F是AB上一点，连接DF并延长交CB的延长线于E.求证：AD：AF＝CE：AB28、在△ABC中，M是AB上一点，若过M的直线所截得的三角形与原三角形相似，试说明满足条件的直线有几条，画出相应的图形加以说明．29、网格中每个小正方形的边长都是1.(1)将图1中画一个格点三角形DEF，使得△DEF≌△ABC(2)将图2中画一个格点三角形MNL，使得△MNL∽△ABC,且相似比为2:1(3)将图3中画一个格点三角形OPQ，使得△OPQ∽△ABC，且相似比为:130、如图，要测量河岸相对的两点A、B的距离，先从点B出发与AB成90°角方向，向前走50m到C处立一根标杆，然后方向不变继续朝前走10m到D处，在D处转90°沿DE方向再走17m，这时A、C、E在同一直线上．问A、B间的距离约为多少？参考答案一、单选题(共15题，共计45分)1、B2、D3、D4、B5、C6、A7、A8、B9、D10、D11、A12、A13、B14、C15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、27、29、30、。

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，AD是的一条角平分线，点E在AD上.若，，则与的面积比为（）A.1:5B.5:1C.3:20D.20:32、如图，Rt△ABC中，AB⊥AC，AB=3，AC=4，P是BC边上一点，作PE⊥AB于E，PD⊥AC于D，设BP=x，则PD+PE=（）A. B. C. D.3、下列两个图形一定相似的是）A.任意两个矩形B.任意两个等腰三角形C.任意两个正方形D.任意两个菱形4、如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）A. B. C. D.5、如图，△ABC 与△A′B′C′是位似图形，点O 是位似中心，若OA=2AA′，S △ABC =8，则S △A′B′C′=（）A.18B.12C.32D.166、如图，Rt△ABC 中，∠BAC=90°，AD⊥BC 于点D ，若BD ：CD=3：2，则= （）A. B. C. D.7、如图，中，，则下列等式中不成立的是（）A.B.C.D.8、已知△ABC∽△DEF，且相似比为2：3，则△ABC 与△DEF 的对应高之比为（）A.2：3B.3：2C.4：9D.9：4 9、如图所示，不能判定△ABC∽△DAC 的条件是（）A.∠B=∠DACB.∠BAC=∠ADCC.AD 2=BD•BCD.AC 2=DC•BC10、如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD=60°，BP=1，CD=，则△ABC的边长是（）A.3B.4C.5D.611、已知：，下列式子中错误的是（）A. B. C. D.12、如图△ABC∽△ACD，则下列式子中不成立的是（）A. ＝B. ＝C.AC 2＝AD•ABD. ＝13、按100分制60分及格来算，满分是150分的及格分是（）A.60分B.72分C.90分D.105分14、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=12，AD=4，BC=9，点P是AB上一动点．若△PAD与△PBC是相似三角形，则满足条件的点P的个数有（）A.1个B.2个C.3个D.4个15、如图所示，E为□ABCD的边AD上的一点，且AE∶ED＝3∶2，CE交BD于F，则BF∶FD （）A.3∶5B.5∶3C.2∶5D.5∶2二、填空题(共10题，共计30分)16、如图是的中线，是上一点，且，的延长线交于点，若，则________．17、在同一时刻,太阳光下身高1.6m的小强的影长是1.2m,学校旗杆的影长是15m,则旗杆高为________ m18、如图，已知顶点，以原点为位似中心，把缩小到原来的，则与点对应的点的坐标是________．19、如图，已知△ABC中，D为边AC上一点，P为边AB上一点，AB=12，AC=8，AD=6，当AP的长度为________时，△ADP和△ABC相似.20、如图，在方格纸中，以每个小方格的边长为单位1，△ABC和△EPD的顶点均在格点上，请你提供一个符合条件的点P，使△ABC与以E，P，D为顶点的三角形相似，则点P所在的格点坐标可以是________21、如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的是________ .22、如图，内接于，于点D，，若的半径，则的长为________.23、如图，某风景区在建设规划过程中，需要测量两岸码头A、B之间的距离．设计人员在O点设桩，取OA、OB的三等分点C、D，测得CD=25m，则AB=________ ．24、如图，A的坐标是（0，2），点C是x轴上的一个动点，点B与点O在直线AC两侧，∠BAC＝∠OAC，BC⊥AC，点B的坐标为（x，y），y与x的函数关系式为________.25、如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为________．三、解答题(共5题，共计25分)26、已知a、b、c满足，且，分别求出a、b、c 的值.27、如图：已知等边三角形ABC，D为AC边上的一动点，CD=nDA，连线段BD，M为线段BD上一点，∠AMD=60°，AM交BC于E．（1）若n=1，则= ．= ；（2）若n=2，求证：BM=6DM；（3）当n= 时，M为BD中点．（直接写结果，不要求证明）28、已知：如图，Rt△ABC中，∠ACB=90°，P是边AB上一点，AD⊥CP，BE⊥CP，垂足分别为D、E，已知AB=3， BC=3， BE=5．求DE的长．29、如图，小明在地面上放置一个平面镜来测量铁塔的高度，镜子与铁塔的距离米，镜子与小明的距离米时，小明刚好从镜子中看到铁塔顶端．已知小华的眼睛距地面的高度CD=1.6米，求铁塔的高度．（根据光的反射原理，）30、如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E。

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、在平面直角坐标系中，，，若把线段扩大倍得线段，若，则的坐标可以是（）A. B. C. D.2、若a、b、c、d是成比例线段，其中a=5cm，b=2.5cm，c=10cm，则线段d的长为（）A.2cmB.4cmC.5cmD.6cm3、如图，菱形ABCD中，点M，N在AC上，ME⊥AD， NF⊥AB. 若NF = NM = 2，ME = 3，则AN =（）A.3B.4C.5D.64、如图，将△ABC的三边分别扩大一倍得到△A1B1C1（顶点均在格点上），若它们是以P点为位似中心的位似图形，则P点的坐标是（）A.（-3，-3）B.（-4，-4）C.（-4，-3）D.（-3，-4）5、如图，Rt△ABC中，∠ACB=90°，CD为斜边上的高，AC=2，AD=1，则BC的长是（）A.4B.3C.D.6、如图，在平面直角坐标系中有一个四边形ABCD，现将四边形ABCD各顶点的横坐标和纵坐标都乘2，得到四边形A1B1C1D1，则四边形A1B1C1D1的面积与四边形ABCD的面积之比为（）A.2：1B.3：1C.4：1D.5：17、如图所示，在正方形ABCD中，E是BC的中点，F是CD上的一点，AE⊥EF，下列结论：①∠BAE＝30°；②CE2＝AB CF；③CF＝FD；④△ABE∽△AEF.其中正确的有（）A.1个B.2个C.3个D.4个8、如图，在平面直角坐标系中，动点A、B分别在x轴上和函数y=x的图象上，AB＝4，CB⊥AB，BC＝2，则OC的最大值为（）A.2 ＋2B.2 ＋4C.2D.2 ＋29、一个油桶高0.8m，桶内有油，一根长lm的木棒从桶盖小口插入桶内，一端到达桶底，另一端恰好在小口处，抽出木棒量得浸油部分长0.8m，则油桶内的油的高度是（）A.0.8mB.0.64mC.1mD.0.7m10、如图，□ABCD中，EF∥AB，DE∶EA = 2∶3，EF = 4，则CD的长为（）A. B.8 C.10 D.1611、将一副三角板如图叠放，交点为O则△AOB与△COD面积之比是（）.A. B. C. D.12、若一个图形的面积为2，那么将它与成中心对称的图形放大为原来的两倍后的图形面积为（）A.8B.6C.4D.213、有以下命题：．①如果线段d是线段a、b、c的第四比例项，则有②如果点C是线段AB的中点，那么AC是AB、BC的比例中项③如果点C是线段AB的黄金分割点，且AC>BC，那么AC是AB、BC的比例中项④如果点C是线段AB的黄金分割点，且AC>BC，且AB=2，则AC= -1其中正确的有( )A.1个B.2个C.3个D.4个14、如图，一次函数的图象与x轴，y轴交于A，B两点，与反比例函数的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接．有下列四个结论：①与的面积相等；②；③；④．其中正确的结论是（）A.1个B.2个C.3个D.4个15、如图，在△ABC中，DE∥BC ，则下列比例式中，不成立的是（）.A. B. C. D.二、填空题(共10题，共计30分)16、如图，在△ABC中，D，E两点分别在边AB，AC上，AB=8cm，AC=6cm，AD=3cm，要使△ADE与△ABC相似，则线段AE的长为________17、如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是________．18、高6m的旗杆在水平地面上的影子长4m，同一时刻附近有一建筑物的影子长20米，则该建筑物的高为________19、在如图所示方格纸中，已知△DEF是由△ABC经相似变换所得的像，那么△DEF的每条边都扩大到原来的________ 倍．20、如图所示，△ABC中，DE∥BC，AE：EB=2：3，若△AED的面积是4m2，则四边形DEBC的面积为________21、如图，在平行四边形ABCD中，AB=3，AD=4 ，AF交BC于E，交DC的延长线于F，且CF=1，则CE的长为________．22、如图，在△ABC中，AD是BC上的高，且BC＝9，AD＝3，矩形EFGH的顶点F、G在边BC上，顶点E、H分别在边AB和AC上，如果设边EF的长为x（0＜x ＜3），矩形EFGH的面积为y，那么y关于x的函数解析式是________.23、如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝2，GD＝1，DF＝5，那么的值等于________.24、如图，四边形ABCD与四边形EFGH的对应边平行，AD是△PHE的中位线，若四边形ABCD的面积4，则四边形EFGH面积是________．25、如图，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于点E， cos B＝，则＝________．三、解答题(共5题，共计25分)26、如图，某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上，已知此人的眼睛到地面的距离AB=1.6m，标杆FC=2.2m，且BC=1m，CD=5m，标杆FC、ED垂直于地面．求电视塔的高ED．27、如图，在△ABC中，EF∥BC且EF= BC=2cm，△AEF的周长为10cm，求梯形BCFE的周长．=2，四边形A′28、如图，四边形ABCD和四边形A′B′C′D′位似，位似比k1B′C′D′和四边形A″B″C″D″位似，位似比k=1．四边形A″B″C″D″和2四边形ABCD是位似图形吗？位似比是多少？29、如图△ABC中，D、E是AB、AC上点，AB=7.8，AD=3，AC=6，AE=3.9，试判断△ADE与△ABC是否会相似．30、如图，△ABC中，点D在AB上，∠ACD=∠ABC，若AD=2，AB=6，求AC的长．参考答案一、单选题(共15题，共计45分)1、C2、C3、B4、C5、D6、C7、C8、A9、B10、C11、B12、A13、C14、D15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、28、30、。

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD 于点E、F，连接BD、DP,，BD与CF相交于点给出下列结论:①BE=2AE；②△DFP∽△BPA:③：④DP2=PH.PC其中正确的是（）A.①②③④B.①③④C.②③D.①②④2、如图，△ABC是一张锐角三角形的纸片，AD是边BC上的高，已知BC=20cm，AD=15cm，从这张纸片上剪一下一个矩形，使矩形的一边在BC上，另两个顶点分别在AB、AC上。

则下列结论不正确的是（）A.当△AHG的面积等于矩形面积时，HE的长为5cmB.当HE的长为6cm 时，剪下的矩形的边HG是HE的2倍C.当矩形的边HG是HE的2倍时，矩形面积最大D.当矩形的面积最大时，HG的长是10cm3、如图，DE∥BC，则下列不成立的是（）A. B. C. D.4、如图，∠1＝∠2，则下列各式中，不能说明△ABC∽△ADE的是( )A.∠D＝∠BB.∠E＝∠CC.D.5、如图，在直角三角形ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，则x的值为（）A.5B.6C.7D.86、在△ABC中，点D、E分别在AB、AC上，如果AD=2，BD=3，那么由下列条件能够判定DE∥BC的是（）A. =B. =C. =D. =7、如图，平面直角坐标系中，，反比例函数的图象分别与线段交于点，连接.若点关于的对称点恰好在上，则（）A. B. C. D.8、如图，在△ABC中，两条中线BE，CD相交于点O，则S△DOE ：S△COB等于（）A.1：2B.1：3C.1：4D.2：39、△ABC∽△A′B′C′，且∠A=68°，则∠A′=（）.A.22°B.44°C.68°D.80°10、如果两个相似多边形的相似比为1：5，则它们的面积比为（）A.1：25B.1：5C.1：2.5D.1：11、若△ABC∽△A′B′C′，AB=2，BC=3，A′B′=1，则B′C′等于( )A.1.5B.3C.2D.112、如图，已知AB∥CD，AD与BC相交于点O，AO：DO=1：2，那么下列式子正确的是（）A.BO：BC=1：2B.CD：AB=2：1C.CO：BC=1：2 D.AD：DO=3：113、若，则的值是（）A. B. C. D.14、下列关于相似的说法：①所有的等腰直角三角形一定相似；②所有的菱形一定相似；③所有的全等三角形一定相似；④所有的有一个角为60°的等腰梯形一定相似．其中说法正确的有( )A.1个B.4个C.3个D.2个15、在□ABCD中，是上一点，交于点，若，，则的长为（）A.4B.5C.6D.7二、填空题(共10题，共计30分)16、如图，在矩形ABCD中，AB＝4，AD＝3，以点C为圆心作⊙C与直线BD相切，点P是⊙C上一个动点，连接AP交BD于点T，则的最大值是________.17、已知等腰直角△ABC，∠C=90°，AC=2，D为边AC上一动点，连结BD，在射线BD上取一点E使BE•BD=AB2.若点D由A运动到C，则点E运动的路径长为________.18、如图所示是一块含30°角的直角三角板，直角顶点位于坐标原点，斜边轴，顶点在函数的图像上，顶点在的图像上，，则________19、如图，小“鱼”与大“鱼”是位似图形，已知小“鱼”上一个“顶点”的坐标为（a，b），那么大“鱼”上对应“顶点”的坐标为________．20、如图，和都是等边三角形，且点A、C、E在同一直线上，与、分别交于点F、M，与交于点N．下列结论正确的是________（写出所有正确结论的序号）．①；②；③；④21、如图：平行四边形ABCD中，E为AB中点，，连E、F交AC于G，则AG：GC=________；22、已知点是线段的黄金分割点，，且，则等于________ .23、在Rt△ABC纸片上剪出9个如图所示的正方形，点E，F落在AB边上，每个正方形的边长为1，则Rt△ABC的面积为________。

九年级数学上册第22章相似形单元测试卷(沪科版 2024年秋)

九年级数学上册第22章相似形单元测试卷（沪科版2024年秋）一、选择题(本大题共10小题，每小题4分，满分40分)题序12345678910答案1.已知2x ＝3y (y ≠0)，则下面结论成立的是()A.x y ＝32B.x 3＝2yC.x y ＝23D.x 2＝y 32．下列四组线段中，成比例的是()A ．a ＝1，b ＝2，c ＝3，d ＝4B ．a ＝3，b ＝6，c ＝9，d ＝18C ．a ＝1，b ＝3，c ＝2，d ＝8D ．a ＝1，b ＝2，c ＝4，d ＝63．如图，在△ABC 中，DE ∥BC ，AD ＝2，BD ＝3，AC ＝10，则AE 的长为()A ．3B ．4C ．5D ．6(第3题)(第5题)4．已知线段AB ＝2，点P 是线段AB 的黄金分割点(AP ＞BP )，则线段AP 的长为()A.5＋1B.5－1C.5＋12D.5－125．如图，下列条件中不能判定△ACD ∽△ABC 的是()A ．∠ADC ＝∠ACB B.AB BC ＝AC CDC ．∠ACD ＝∠BD ．AC 2＝AD ·AB6．如图，在△ABC 中，AB ∥DE ，若AE CE ＝23，则△ECD 与△ACB 的面积之比为()A.35B.925C.45D.1625(第6题)(第7题)7．如图，小明在A 时测得某树的影长为3m ，B 时测得该树的影长为2m ，若两次日照的光线互相垂直，则树的高度为()A ．±6mB.6mC ．6mD.5m8．若一个三角形能够分成两个与原三角形都相似的三角形，就把这样的三角形称为和谐三角形，则下列选项中属于和谐三角形的是()A ．等边三角形B ．等腰三角形C ．直角三角形D ．等腰三角形或直角三角形9．如图，在△ABC 中，∠ABC ＝90°，以点A 为圆心，AB 长为半径作弧交AC 于点D ，连接BD ，再分别以点B ，D 为圆心，大于12BD 的长为半径作弧，两弧交于点P ，作射线AP 交BC 于点E ，连接DE ，则下列结论正确的是()A ．DE 垂直平分ACB ．△ABE ∽△CBAC ．BD 2＝BC ·BED ．CE ·AB ＝BE ·CA(第9题)(第10题)10.如图，在正方形ABCD 中，F 为AB 上一点，E 是BC 延长线上一点，且AF ＝EC ，连接EF ，DE ，DF ，M 是EF 的中点，连接MC ，设EF 与BD 和DC 分别相交于点G 和N ，下列结论：①△FGD ∽△BGE ；②若BF ＝4，则CE ＝22；③∠CME ＝∠CDE ；④DG 2＝GN ·GE ，其中正确的是()A ．①②③B ．①③④C ．②③④D ．①②④二、填空题(本大题共4小题，每小题5分，满分20分)11．已知△ABC ∽△A ′B ′C ′，AD 和A ′D ′是它们的对应中线，若AD ＝8，A ′D ′＝6，则△ABC 与△A ′B ′C ′的周长比是________．12．如图，在平面直角坐标系中，矩形OABC 的顶点坐标分别是O (0，0)，C (6，0)，B (6，4)，A (0，4)，已知矩形OA ′B ′C ′与矩形OABC 位似，位似中心是原点O ，且矩形OA ′B ′C ′的面积等于矩形OABC 面积的14，则点B ′的坐标是____________．(第12题)(第13题)13．如图，线段AB ，CD 的端点都在正方形网格的格点上，它们相交于点M .若每个小正方形的边长都是1，则MCMD的值是________．14.如图，在矩形ABCD 中，AB ＝4，点E 为边AD 上一点，AE ＝3，F 为BE 的中点．(第14题)(1)EF ＝________；(2)若CF ⊥BE ，CE ，DF 相交于点O ，则OCCE＝________．三、(本大题共2小题，每小题8分，满分16分)15．已知x ＋y x＝32.(1)求yx 的值；(2)求x －y x ＋y的值．16．如图，直线l 1∥l 2∥l 3，AC 分别交l 1，l 2，l 3于点A ，B ，C ，DF 分别交l 1，l 2，l 3于点D ，E ，F ，AC 与DF 交于点O .已知DE ＝3，EF ＝6，AB ＝4.(第16题)(1)求AC的长；(2)若OE：OF＝1：3，求OB：AB.四、(本大题共2小题，每小题8分，满分16分)17.如图，在平面直角坐标系中，每个小正方形的边长都是1个单位，△ABC的顶点都在格点上．(第17题)(1)以原点O为位似中心，在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1；(2)△A1B1C1的面积为______．18．如图，在△ABC中，AB＝AC，∠A＝36°，BD为∠ABC的平分线．求证：AD2＝AC·DC.(第18题)五、(本大题共2小题，每小题10分，满分20分)19．某校同学参与“项目式学习”综合实践活动，小明所在的数学活动小组利用所学知识测量旗杆EF的高度．如图，他在距离旗杆40m的D处立下一根3m 高的竖直标杆CD，然后调整自己的位置，当他与标杆的距离BD为4m时，他的眼睛、标杆顶端和旗杆顶端在同一直线上，若小明的眼睛离地面的高度AB为1.6m，求旗杆EF的高度．(第19题)20．如图，将等边三角形ABC折叠，使点A落在BC边上的点D处(不与B，C 重合)，折痕为EF.(1)求证：△BDE∽△CFD；(2)若BD＝6，DC＝2，求BE的长(第20题)六、(本题满分12分)21．如图，在矩形ABCD中，E是CD边的中点，且BE⊥AC于点F，连接DF.求证：(1)AD＝DF；(2)DF2＝BE·BF.(第21题)七、(本题满分12分)22．阅读下列材料，并完成相应的任务．规定：在一个三角形中，若一个内角是另一个内角度数的n 倍，则称三角形为“n 倍角三角形”．当n ＝1时，称为“1倍角三角形”，显然等腰三角形是“1倍角三角形”；当n ＝2时，称为“2倍角三角形”．小康通过探索后发现，“2倍角三角形”的三边有如下关系：在△ABC 中，∠BAC ，∠B ，∠C 所对的边分别为a ，b ，c ，若∠BAC ＝2∠B ，则a 2－b 2＝bc .下面是小康的两种探索证明过程：证法1：如图①，作∠BAC 的平分线AD ，则∠BAD ＝∠CAD ＝12∠BAC .∵∠BAC ＝2∠B ，∴∠BAD ＝∠CAD ＝∠B .∴AD ＝BD .∵∠ACD ＝∠BCA ，∴△ACD ∽△BCA ，∴AC BC ＝DC AC ＝AD AB.设DC ＝x ，则AD ＝BD ＝a －x .(第22题)∴b a ＝x b ＝a －x c ，∴b 2＝ax ，a 2－ax ＝bc ，∴a 2－b 2＝bc .证法2：如图②，延长CA 到点D ，使得AD ＝AB ＝c ，连接BD ，∴∠ABD ＝∠D .……任务：(1)上述材料中的证法1是通过作辅助线，构造出________三角形来加以证明的(填“全等”或“相似”)；(2)请补全证法2剩余的部分．八、(本题满分14分)23．如图，在△ABC中，∠BAC＝90°，AB＝AC，D为BC的中点，F，E是AC 上两点，连接BE，DF交于△ABC内一点G，且∠EGF＝45°.(1)求证：∠FDC＝∠AEB；(2)若AE＝3CE＝6，求BG的长；(3)连接AG，求证：∠EAG＝∠ABE.(第23题)答案一、1.A 2.B 3.B4.B5.B6.B7.B8.C9．D 点拨：由题意得AB ＝AD ，AP 平分∠BAC ，∴∠EAB ＝∠EAD .在△ABE 与△ADE ＝AE ，EAB ＝∠EAD ，＝AD ，∴△ABE ≌△ADE ，∴BE ＝ED ，∠ADE ＝∠ABC ＝90°.∴∠EDC ＝90°＝∠ABC .又∵∠C ＝∠C ，∴△EDC ∽△ABC ，∴CE CA ＝EDAB，∴CE ·AB ＝ED ·CA .∵ED ＝BE ，∴CE ·AB ＝BE ·CA .A ，B ，C 选项无法证明．故选D.10．B 二、11.4：312.(3，2)或(－3，－2)13.12714.(1)52(2)3239三、15.解：由x ＋y x＝32可得，x ＝2y .(1)y x ＝y 2y ＝12.(2)x －y x ＋y ＝2y －y 2y ＋y ＝13.16．解：(1)∵l 1∥l 2∥l 3，∴DE ∶DF ＝AB ∶AC ，即3∶(3＋6)＝4∶AC ，解得AC ＝12.(2)∵l 2∥l 3，∴OB ∶OC ＝OE ∶OF ＝1∶3，∴OC ＝3OB .∵AB ＝4，AC ＝12，∴BC ＝8，即OC ＋OB ＝8，∴4OB ＝8，∴OB ＝2，∴OB ∶AB ＝2∶4＝1∶2.四、17.解：(1)如图，△A 1B 1C 1即为所求．(第17题)(2)1418．证明：∵∠A＝36°，AB＝AC，∴∠ABC＝∠C＝72°.∵BD为∠ABC的平分线，∴∠ABD＝∠DBC＝36°，∴∠ABD＝∠A，∠BDC＝∠A＋∠ABD＝72°，∴BD＝AD，∠C＝∠BDC，∴BC＝BD＝AD.∵∠DBC＝36°＝∠A，∠C＝∠C，∴△BCD∽△ACB.∴BCAC＝CDCB，∴ADAC＝CDAD，∴AD2＝AC·DC.五、19.解：过点A作AH⊥EF，交CD于点G，交EF于点H.由题意易得HF＝DG＝AB＝1.6m，AG＝BD＝4m，HG＝FD＝40m，∴CG＝CD－DG＝3－1.6＝1.4(m)．易知CD∥EF，∴△AGC∽△AHE，∴AGAH＝CGEH，∴44＋40＝1.4EH，∴EH＝15.4m，∴EF＝EH＋HF＝15.4＋1.6＝17(m)．答：旗杆EF的高度为17m.20．(1)证明：∵△ABC是等边三角形，∴∠B＝∠C＝∠A＝60°.由折叠的性质可得∠EDF＝∠A＝60°.∵∠FDB＝∠C＋∠DFC＝∠EDF＋∠EDB，∴∠EDB＝∠DFC，∵∠B＝∠C，∴△BDE∽△CFD.(2)解：∵BD＝6，DC＝2，∴BC＝BD＋DC＝8.∵△ABC是等边三角形，∴AB＝AC＝BC＝8.由折叠的性质可知AE＝ED，AF＝FD，∴△BDE 的周长为BD ＋DE ＋BE ＝BD ＋AE ＋BE ＝BD ＋AB ＝6＋8＝14，△CFD 的周长为CD ＋DF ＋FC ＝CD ＋AF ＋FC ＝CD ＋AC ＝2＋8＝10.∵△BDE ∽△CFD ，∴BE CD ＝1410＝75.∵DC ＝2，∴BE 2＝75，∴BE ＝2.8.六、21.证明：(1)过点D 作DG ∥BE 交AB 于点G ，交AC 于点H ，如图所示．(第21题)∵四边形ABCD 为矩形，∴AB ∥CD ，AB ＝CD ，∴四边形BEDG 为平行四边形，∴DE ＝BG .∵点E 为CD 的中点，∴DE ＝12CD ，∴易得BG ＝AG .∵DG ∥BE ，∴AH HF ＝AG GB＝1，∴点H 为AF 的中点．∵BE ⊥AC ，∴∠AFB ＝90°.∵DG ∥BE ，∴∠DHF ＝∠AFB ＝90°，∴DH 垂直平分AF ，∴AD ＝DF .(2)∵四边形ABCD 为矩形，∴AD ＝BC ，∠BCE ＝90°.∵AD ＝DF ，∴DF ＝BC .∵BE ⊥AC ，∴∠BFC ＝90°，∴∠BFC ＝∠BCE .∵∠CBF ＝∠EBC ，∴△BCF ∽△BEC ，∴BC BE ＝BF BC，∴BC 2＝BE ·BF ，∴DF 2＝BE ·BF .七、22.解：(1)相似(2)补全证法2剩余的部分如下：∴∠BAC ＝∠ABD ＋∠D ＝2∠D .又∵∠BAC ＝2∠ABC ，∴∠ABC ＝∠D .又∵∠ACB ＝∠BCD ，∴△ACB ∽△BCD ，∴AC BC ＝BC DC，∴BC 2＝AC ·DC ，∴a2＝b(b＋c)，∴a2－b2＝bc.八、23.(1)证明：∵∠BAC＝90°，AB＝AC，∴∠C＝45°.∵∠BGD＝∠EGF＝45°，∴∠C＝∠BGD.∵∠FDC＝∠EBC＋∠BGD，∠AEB＝∠EBC＋∠C，∴∠FDC＝∠AEB.(2)解：∵AE＝3CE＝6，∴CE＝2，∴AB＝AC＝8.∵∠BAC＝90°，∴BE＝AB2＋AE2＝10，BC＝AB2＋AC2＝8 2.∵D为BC的中点，∴BD＝4 2.∵∠BGD＝∠C，∠DBG＝∠EBC，∴△BGD∽△BCE，∴BGBC＝BDBE，即BG82＝4210，∴BG＝325.(3)证明：连接AD.∵AB＝AC，D为BC的中点，∴AD⊥BC，∴∠ADB＝∠CAB＝90°.∵∠ABD＝∠CBA，∴△ABD∽△CBA，∴ABBC＝BDAB，∴AB2＝BD·BC.由(2)知BGBC＝BDBE，∴BG·BE＝BD·BC，∴AB2＝BG·BE，∴ABBE＝BGAB.∵∠ABG＝∠EBA，∴△ABG∽△EBA，∴∠AGB＝∠BAE＝90°，∴∠EAG＋∠BAG＝∠BAG＋∠ABE＝90°，∴∠EAG＝∠ABE.。

沪科版九年级上册数学第22章相似形含答案(黄金题型)

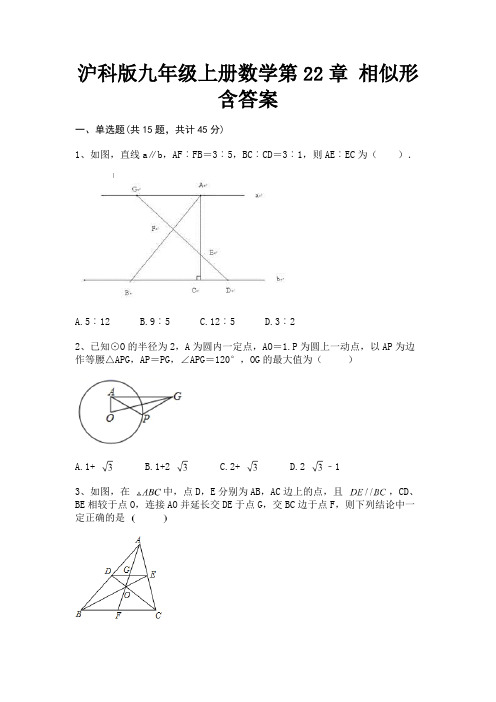
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题，共计45分)1、如图，直线a∥b，AF︰FB＝3︰5，BC︰CD＝3︰1，则AE︰EC为（）．A.5︰12B.9︰5C.12︰5D.3︰22、已知⊙O的半径为2，A为圆内一定点，AO＝1.P为圆上一动点，以AP为边作等腰△APG，AP＝PG，∠APG＝120°，OG的最大值为（）A.1+B.1+2C.2+D.2 ﹣13、如图，在中，点D，E分别为AB，AC边上的点，且，CD、BE相较于点O，连接AO并延长交DE于点G，交BC边于点F，则下列结论中一定正确的是A. B. C. D.4、如图，在矩形ABCD中，E，F分别是AD，BC的中点，AF与BE相交于点M，CE与DF相交于点N，QM⊥BE，QN⊥EC相交于点Q，PM⊥AF，PN⊥DF相交于点P，若2BC=3AB，记△ABM和△CDN的面积和为S，则四边形MQNP的面积为（）A. S  B. SC. SD. S5、下列两个图形：①两个等腰三角形；②两个直角三角形；③两个正方形；④两个矩形；⑤两个菱形；⑥两个正五边形．其中一定相似的有（）A.2组B.3组C.4组D.5组6、如图，E，F是平行四边形ABCD对角线BD上的两点，DE=EF=BF，连接CE并延长交AD于点G，连接CF并延长交AB于点H，连接CH，设△CDG的面积为S 1，△CHG的面积为S2，则S1与S2的关系正确的是（）A. B. C. D.7、如果x：y＝2：3，那么下列各式不成立的是（）A. B. C. D.8、如图，已知，那么添加下列一个条件后，仍然无法判定的是（）A. B. C. D.9、如图，直线 l1∥l2∥l3，直线 AC 分别交 l1， l2， l3于点 A，B，C；直线 DF 分别交 l1， l2， l3于点 D,E，F，AC 与 DF 相交于点 G，且AG=2，GB=1，BC=5,则的值是（）A. B.2 C. D.10、已知两个相似三角形的相似比为1：4，则它们的周长比为（）A.1：4B.4：1C.1：2D.1：1611、如图所示，下列条件中能单独判断△ABC∽△ACD的个数是（）个．①∠ABC＝∠ACD；②∠ADC＝∠ACB；③ ＝；④AC2＝AD•ABA.1B.2C.3D.412、如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，如果AC=3，AB=6，那么AD的值为（）A. B. C. D.313、美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．如图，某女士身高165cm，下半身长x与身高l的比值是0.60，为尽可能达到好的效果，她应穿的高跟鞋的高度大约为（）A.4cmB.6cmC.8cmD.10cm14、如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是（）A. B.1 C. D.215、如图，在矩形ABCD中，E是CD边的中点，且BE⊥AC于点F，连接DF，则下列结论错误的是（）A.△ADC∽△CFBB.AD＝DFC. ＝D. ＝二、填空题(共10题，共计30分)16、已知，则=________．17、正方形DEFG是的内接正方形，AM⊥BC于M，交DG于H，若AM=4cmcm，BC长6cm, 则正方形DEFG的边长是________cm。

沪科版九年级数学上册第22章 相似形 练习题

沪科版九年级数学上册试题 第22章《相似形》单元测试卷(含答案详解)

沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章 相似形含答案(真题汇编)

(真题汇编)沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章 相似形 含答案

九年级数学上册 第22章 相似形 单元测试卷(沪科版 2024年秋)

沪科版九年级上册数学第22章 相似形含答案(黄金题型)

沪科版九年级数学上册第22章相似形练习题

沪科版九年级数学上册试题第22章《相似形》单元测试卷(含答案详解)

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案(真题汇编)

(真题汇编)沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案

沪科版九年级上册数学第22章相似形含答案

九年级数学上册第22章相似形单元测试卷(沪科版 2024年秋)

沪科版九年级上册数学第22章相似形含答案(黄金题型)