2021版高考物理一轮复习专题突破(四)天体的相遇问题学案
2021版高考物理一轮复习第四章曲线运动万有引力与航天4第四节万有引力与航天学案
第四节 万有引力与航天【基础梳理】提示:椭圆 一个焦点 面积 半长轴 公转周期 质量m 1和m 2的乘积 它们之间距离r 的二次方G m 1m 2r2 质量分布均匀GM RgR【自我诊断】1.判一判(1)所有物体之间都存在万有引力.( )(2)地面上的物体所受地球的引力方向一定指向地心.( ) (3)两物体间的距离趋近于零时,万有引力趋近于无穷大.( ) (4)第一宇宙速度的大小与地球质量有关.( )(5)同步卫星可以定点在北京市的正上方.( )(6)同步卫星的运行速度一定小于地球第一宇宙速度.( ) 提示:(1)√ (2)√ (3)× (4)√ (5)× (6)√ 2.做一做(1)近年来,人类发射了多枚火星探测器,对火星进行科学探究,为将来人类登上火星、开发和利用火星资源奠定了坚实的基础.如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该探测器运动的周期为T ,则火星的平均密度ρ的表达式为(k 是一个常数)( )A .ρ=kTB .ρ=kTC .ρ=kT 2D .ρ=kT2提示:选D.由万有引力定律知G Mm r 2=m 4π2T 2r ,联立M =ρ·43πR 3 和r =R ,解得ρ=3πGT 2,3πG为一常数,设为k ,故D 正确.(2)(2020·安徽安庆二模)2019年1月3日10时26分,嫦娥四号探测器成功着陆在月球背面南极艾特肯盆地的预选着陆区.存在“月球背面”是因为月球绕地球公转的同时又有自转,使得月球在绕地球公转的过程中始终以同一面朝向地球.根据所学物理知识,判断下列说法中正确的是( )A .月球绕地球公转的周期等于地球自转的周期B .月球绕地球公转的周期等于月球自转的周期C .月球绕地球公转的线速度大于地球的第一宇宙速度D .月球绕地球公转的角速度大于地球同步卫星绕地球运动的角速度提示:选B.由题意知,月球绕地球一周的过程中,其正面始终正对地球,据此可知,月球公转一周的时间内恰好自转一周,故形成人们始终看不到月球背面的原因是月球绕地球的公转周期与其自转周期相同,故A 错误,B 正确;根据万有引力提供向心力得线速度为v =GM r,地球的第一宇宙速度是绕地球做圆周运动的最大环绕速度,所以月球绕地球公转的线速度小于地球的第一宇宙速度,故C 错误;根据万有引力提供向心力得角速度为ω=GM r 3,月球绕地球公转的半径大于地球同步卫星绕地球运动的半径,所以月球绕地球公转的角速度小于地球同步卫星绕地球运动的角速度,故D 错误.开普勒行星运动定律与万有引力定律[学生用书P78]【知识提炼】1.地球表面的重力与万有引力地面上的物体所受地球的吸引力产生两个效果,其中一个分力提供了物体绕地轴做圆周运动的向心力,另一个分力等于重力.(1)在两极,向心力等于零,重力等于万有引力;(2)除两极外,物体的重力都比万有引力小;(3)在赤道处,物体的万有引力分解为两个分力F 向和mg 刚好在一条直线上,则有F =F 向+mg ,所以mg =F -F 向=GMm R 2-mRω2自.2.星体表面上的重力加速度(1)设在地球表面附近的重力加速度为g (不考虑地球自转),由mg =GmM R 2,得g =GM R 2.(2)设在地球上空距离地心r =R +h 处的重力加速度为g ′,由mg ′=GMm (R +h )2,得g ′=GM(R +h )2所以gg ′=(R +h )2R 2.3.求天体质量和密度常用的估算方法使用方法 已知量 利用公式 表达式 备注质量的计算利用运行天体r、TGMmr2=mr4π2T2M=4π2r3GT2只能得到中心天体的质量r、v GMmr2=mv2r M=rv2Gv、TGMmr2=mv2rT=2πrvM=v3T2πG利用天体表面重力加速度g、R mg=GMmR2M=gR2G密度的计算利用运行天体r、T、RGMmr2=mr4π2T2M=43ρπR3ρ=3πr3GT2R3当r=R时ρ=3πGT2利用近地卫星只需测出其运行周期利用天体表面重力加速度g、Rmg=GMmR2M=43ρπR3ρ=3g4πGR(2019·高考全国卷Ⅱ)2019年1月,我国嫦娥四号探测器成功在月球背面软着陆,在探测器“奔向”月球的过程中,用h表示探测器与地球表面的距离,F表示它所受的地球引力,能够描述F随h变化关系的图象是( )[解析] 在嫦娥四号探测器“奔向”月球的过程中,根据万有引力定律,可知随着h的增大,探测器所受的地球引力逐渐减小但并不是均匀减小的,故能够描述F 随h 变化关系的图象是D.[答案] D【迁移题组】迁移1 开普勒定律在椭圆轨道上的应用1.(多选)(2017·高考全国卷Ⅱ)如图,海王星绕太阳沿椭圆轨道运动,P 为近日点,Q 为远日点,M 、N 为轨道短轴的两个端点,运行的周期为T 0.若只考虑海王星和太阳之间的相互作用,则海王星在从P 经M 、Q 到N 的运动过程中( )A .从P 到M 所用的时间等于T 04B .从Q 到N 阶段,机械能逐渐变大C .从P 到Q 阶段,速率逐渐变小D .从M 到N 阶段,万有引力对它先做负功后做正功解析:选CD.在海王星从P 到Q 的运动过程中,由于引力与速度的夹角大于90°,因此引力做负功,根据动能定理可知,速率越来越小,C 正确;海王星从P 到M 的时间小于从M 到Q 的时间,因此从P 到M 的时间小于T 04,A 错误;由于海王星运动过程中只受到太阳引力作用,引力做功不改变海王星的机械能,即从Q 到N 的运动过程中海王星的机械能守恒,B 错误;从M 到Q 的运动过程中引力与速度的夹角大于90°,因此引力做负功,从Q 到N 的过程中,引力与速度的夹角小于90°,因此引力做正功,即海王星从M 到N 的过程中万有引力先做负功后做正功,D 正确.迁移2 星球附近重力加速度的求解2.科幻大片《星际穿越》是基于知名理论物理学家基普·索恩的黑洞理论,加入人物和相关情节改编而成的.电影中的黑洞花费三十名研究人员将近一年的时间,用数千台计算机精确模拟才得以实现,让我们看到了迄今最真实的黑洞模样.若某黑洞的半径R 约为45 km ,质量M 和半径R 的关系满足M R =c 22G (其中c =3×108 m/s ,G 为引力常量),则该黑洞表面的重力加速度大约为( )A .108 m/s 2B .1010 m/s 2C .1012 m/s 2D .1014 m/s 2解析:选C.黑洞实际为一天体,天体表面的物体受到的重力近似等于物体与该天体之间的万有引力,设黑洞表面的重力加速度为g ,对黑洞表面的某一质量为m 的物体,有GMm R 2=mg ,又有M R=c 22G,联立解得g =c 22R,代入数据得重力加速度约为1012 m/s 2,故C 正确.迁移3 天体质量和密度的计算3.(2018·高考全国卷Ⅱ)2018年2月,我国500 m 口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T =5.19 ms ,假设星体为质量均匀分布的球体,已知引力常量为 6.67×10-11 N ·m 2/kg 2.以周期T 稳定自转的星体的密度最小值约为( )A .5×109 kg/m 3B .5×1012 kg/m 3C .5×1015 kg/m 3D .5×1018 kg/m 3解析:选C.毫秒脉冲星稳定自转时由万有引力提供其表面物体做圆周运动的向心力,根据G Mm R 2=m 4π2R T 2,M =ρ·43πR 3,得ρ=3πGT2,代入数据解得ρ≈5×1015 kg/m 3,C 正确.计算中心天体的质量、密度时的两点区别(1)天体半径和卫星的轨道半径通常把天体看成一个球体,天体的半径指的是球体的半径.卫星的轨道半径指的是卫星围绕天体做圆周运动的圆的半径.卫星的轨道半径大于或等于天体的半径.(2)自转周期和公转周期自转周期是指天体绕自身某轴线运动一周所用的时间,公转周期是指卫星绕中心天体做圆周运动一周所用的时间.自转周期与公转周期一般不相等.卫星运行规律及特点[学生用书P79]【知识提炼】1.卫星的轨道(1)赤道轨道:卫星的轨道在赤道平面内,同步卫星就是其中的一种.(2)极地轨道:卫星的轨道过南北两极,即在垂直于赤道的平面内,如极地气象卫星.(3)其他轨道:除以上两种轨道外的卫星轨道,且轨道平面一定通过地球的球心. 2.地球同步卫星的特点:六个“一定”3.卫星的各物理量随轨道半径变化的规律4.解决天体圆周运动问题的两条思路(1)在中心天体表面或附近而又不考虑中心天体自转影响时,万有引力等于重力,即G MmR2=mg ,整理得GM =gR 2,称为黄金代换.(g 表示天体表面的重力加速度)(2)天体运动的向心力来源于天体之间的万有引力,即G Mm r 2=m v 2r =mrω2=m 4π2rT2=ma n . 【典题例析】(2019·高考全国卷Ⅲ)金星、地球和火星绕太阳的公转均可视为匀速圆周运动,它们的向心加速度大小分别为a 金、a 地、a 火,它们沿轨道运行的速率分别为v 金、v 地、v 火.已知它们的轨道半径R 金<R地<R 火,由此可以判定()A .a 金>a 地>a 火B .a 火>a 地>a 金C .v 地>v 火>v 金D .v 火>v 地>v 金[解析] 金星、地球和火星绕太阳公转时万有引力提供向心力,则有G Mm R 2=ma ,解得a =G MR 2,结合题中R 金<R 地<R 火,可得a 金>a 地>a 火,A 正确,B 错误;同理,有G Mm R 2=m v 2R,解得v =GM R,再结合题中R 金<R 地<R 火,可得v 金>v 地>v 火,C 、D 均错误.[答案] A【迁移题组】迁移1 卫星运行参量的比较1.地球赤道上有一物体随地球的自转,所受的向心力为F 1,向心加速度为a 1,线速度为v 1,角速度为ω1;绕地球表面附近做圆周运动的人造卫星(高度忽略),所受的向心力为F 2,向心加速度为a 2,线速度为v 2,角速度为ω2;地球的同步卫星所受的向心力为F 3,向心加速度为a 3,线速度为v 3,角速度为ω3;地球表面的重力加速度为g ,第一宇宙速度为v ,假设三者质量相等,则( )A .F 1=F 2>F 3B .a 1=a 2=g >a 3C .v 1=v 2=v >v 3D .ω1=ω3<ω2解析:选D.地球同步卫星的运动周期与地球自转周期相同,角速度相同,即ω1=ω3,根据关系式v =ωr 和a =ω2r 可知,v 1<v 3,a 1<a 3;人造卫星和地球同步卫星都围绕地球转动,它们受到的地球的引力提供向心力,即G Mm r 2=mω2r =mv 2r=ma 可得v =GMr ,a =G Mr2,ω=GM r 3,可见,轨道半径大的线速度、向心加速度和角速度均小,即v 2>v 3,a 2>a 3,ω2>ω3;绕地球表面附近做圆周运动的人造卫星(高度忽略)的线速度就是第一宇宙速度,即v 2=v ,其向心加速度等于重力加速度,即a 2=g ;所以v =v 2>v 3>v 1,g =a 2>a 3>a 1,ω2>ω3=ω1,又因为F =ma ,所以F 2>F 3>F 1.由以上分析可见,A 、B 、C 错误,D 正确.迁移2 同步卫星的运行特点2.(多选)(2020·甘肃兰州理一诊)中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,是继美国全球定位系统(GPS)、俄罗斯格洛纳斯卫星导航系统、欧洲伽利略卫星导航系统之后第四个成熟的卫星导航系统.2018年12月27日北斗三号基本系统完成建设,即日起提供全球服务.在北斗卫星导航系统中,有5颗地球静止轨道卫星,它们就好像静止在地球上空的某一点.对于这5颗静止轨道卫星,下列说法正确的是( )A .它们均位于赤道正上方B .它们的周期小于近地卫星的周期C .它们离地面的高度都相同D .它们必须同时正常工作才能实现全球通讯解析:选AC.所有地球静止轨道卫星的位置均位于赤道正上方,故A 正确;地球静止轨道卫星的轨道半径大于近地卫星的轨道半径,据开普勒第三定律知,地球静止轨道卫星的周期大于近地卫星的周期,故B 错误;根据G Mmr 2=m ⎝ ⎛⎭⎪⎫2πT 2r 知,地球静止轨道卫星的轨道半径相同,离地面的高度相同,故C 正确;同步卫星离地高度较高,有三颗地球静止轨道卫星工作就可能实现全球通讯,故D 错误.迁移3 宇宙速度问题3.(2020·广西高三上学期跨市联合调研)天文兴趣小组查找资料得知:某天体的质量为地球质量的a 倍,其半径为地球半径的b 倍,表面无大气层,地球的第一宇宙速度为v .则该天体的第一宇宙速度为( )A .vabB .vb aC.abvD.b av解析:选A.设地球质量为M ,半径为r ,某天体的质量是地球质量的a 倍,其半径是地球半径的b 倍,卫星沿地球表面做匀速圆周运动的速度为v ,则由万有引力提供向心力得:G Mm r 2=m v 2r,解得地球的第一宇宙速度v =GM r,同理得该天体的第一宇宙速度v 天体=G ·aM br=va b,A 正确.双星及多星模型[学生用书P80]【知识提炼】1.模型特征(1)多星系统的条件①各星彼此相距较近.②各星绕同一圆心做匀速圆周运动.(2)多星系统的结构类型双星模型三星模型结构图向心力由两星之间的万有引力提供,故两星的向心力大小相等运行所需向心力都由其余行星对其万有引力的合力提供运动参量两星转动方向相同,周期、角速度相等—【跟进题组】1.(多选)(2018·高考全国卷Ⅰ)2017年,人类第一次直接探测到来自双中子星合并的引力波.根据科学家们复原的过程,在两颗中子星合并前约100 s 时,它们相距约400 km ,绕二者连线上的某点每秒转动12圈.将两颗中子星都看做是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )A .质量之积B .质量之和C .速率之和D .各自的自转角速度解析:选BC.由题意可知,合并前两中子星绕连线上某点每秒转动12圈,则两中子星的周期相等,且均为T =112 s ,两中子星的角速度均为ω=2πT,两中子星构成了双星模型,假设两中子星的质量分别为m 1、m 2,轨道半径分别为r 1、r 2,速率分别为v 1、v 2,则有:G m 1m 2L 2=m 1ω2r 1、Gm 1m 2L 2=m 2ω2r 2,又r 1+r 2=L =400 km ,解得m 1+m 2=ω2L 3G,A 错误,B 正确;又由v 1=ωr 1、v 2=ωr 2,则v 1+v 2=ω(r 1+r 2)=ωL ,C 正确;由题中的条件不能求解两中子星自转的角速度,D 错误.2.(多选)2017年三名美国科学家获本年度诺贝尔物理学奖,用以表彰他们在引力波研究方面的贡献.人类首次发现了引力波来源于距地球之外13亿光年的两个黑洞(质量分别为26个和39个太阳质量)互相绕转最后合并的过程.设两个黑洞A 、B 绕其连线上的O 点做匀速圆周运动,如图所示.黑洞A 的轨道半径大于黑洞B 的轨道半径,两个黑洞的总质量为M ,两个黑洞间的距离为L ,其运动周期为T ,则( )A .黑洞A 的质量一定大于黑洞B 的质量B .黑洞A 的线速度一定大于黑洞B 的线速度C .两个黑洞间的距离L 一定,M 越大,T 越大D .两个黑洞的总质量M 一定,L 越大,T 越大解析:选BD.设两个黑洞质量分别为m A 、m B ,轨道半径分别为R A 、R B ,角速度为ω,由万有引力定律可知:Gm A m BL 2=m A ω2R A ,Gm A m BL 2=m B ω2R B ,R A +R B =L ,得m A m B =R B R A,黑洞A 的质量小于黑洞B 的质量,A 错误;v A =ωR A ,v B =ωR B ,B 正确;又由M =m A +m B 得GM =ω2L 3,又因为T =2πω,故T =2πL 3GM,C 错误,D 正确.卫星的变轨问题[学生用书P81]【知识提炼】1.卫星发射及变轨过程概述人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图所示.(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.(2)在A 点点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅱ. (3)在B 点(远地点)再次点火加速进入圆形轨道Ⅲ. 2.卫星变轨的实质两类变轨离心运动近心运动示意图变轨起因卫星速度突然增大卫星速度突然减小万有引力与向心力的大小关系GMmr2<mv2r GMmr2>mv2r变轨结果转变为椭圆轨道运动或在较大半径圆轨道上运动转变为椭圆轨道运动或在较小半径圆轨道上运动新圆轨道上运动的速率比原轨道的小,周期比原轨道的大新圆轨道上运动的速率比原轨道的大,周期比原轨道的小动能减小、势能增大、机械能增大动能增大、势能减小、机械能减小【典题例析】如图所示,1、3轨道均是卫星绕地球做圆周运动的轨道示意图,1轨道的半径为R,2轨道是一颗卫星绕地球做椭圆运动的轨道示意图,3轨道与2轨道相切于B点,O点为地球球心,AB为椭圆的长轴,三轨道和地心都在同一平面内.已知在1、2两轨道上运动的卫星的周期相等,引力常量为G,地球质量为M,三颗卫星的质量相等,则下列说法正确的是( )A.卫星在3轨道上的机械能小于在2轨道上的机械能B.若卫星在1轨道上的速率为v1,卫星在2轨道A点的速率为v A,则v1<v AC.若卫星在1、3轨道上的加速度大小分别为a1、a3,卫星在2轨道A点的加速度大小为a A,则a A <a1<a3D.若OA=0.4R,则卫星在2轨道B点的速率v B>5GM8R[解析] 2、3轨道在B点相切,卫星在3轨道相对于2轨道是做离心运动的,卫星在3轨道上的线速度大于在2轨道上B点的线速度,因卫星质量相同,所以卫星在3轨道上的机械能大于在2轨道上的机械能,A错误;以OA为半径作一个圆轨道4与2轨道相切于A点,则v4<v A,又因v1<v4,所以v1<v A,B正确;加速度是万有引力产生的,只需要比较卫星到地心的高度即可,应是a A>a1>a3,C错误;由开普勒第三定律可知,2轨道的半长轴为R ,OB =1.6R ,3轨道上的线速度v 3=5GM8R,又因v B <v 3,所以v B <5GM8R,D 错误. [答案] B【迁移题组】迁移1 卫星变轨过程中运动参量的变化分析1.(2020·江南十校联考)据外媒综合报道,英国著名物理学家史蒂芬·霍金在2018年3月14日去世,享年76岁.这位伟大的物理学家,向人类揭示了宇宙和黑洞的奥秘.高中生对黑洞的了解为光速是在星球(黑洞)上的第二宇宙速度.对于普通星球,如地球,光速仍远远大于其宇宙速度.现对发射地球同步卫星的过程进行分析,卫星首先进入椭圆轨道Ⅰ,P 点是轨道Ⅰ上的近地点,然后在Q 点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ,则( )A .卫星在同步轨道Ⅱ上的运行速度大于第一宇宙速度7.9 km/sB .该卫星的发射速度必定大于第二宇宙速度11.2 km/sC .在轨道Ⅰ上,卫星在P 点的速度大于第一宇宙速度7.9 km/sD .在轨道Ⅰ上,卫星在Q 点的速度大于第一宇宙速度7.9 km/s解析:选C.第一宇宙速度是卫星在近地轨道的线速度,根据G Mm r 2=m v 2r可知v =GM r,故轨道半径越大,线速度越小,所以同步卫星的运行速度小于第一宇宙速度,A 错误;该卫星为地球的卫星,所以发射速度小于第二宇宙速度,B 错误;P 点为近地轨道上的一点,但要从近地轨道变轨到Ⅰ轨道,则需要在P 点加速,所以在轨道Ⅰ上卫星在P 点的速度大于第一宇宙速度,C 正确;在Q 点要从轨道Ⅰ变轨到轨道Ⅱ,则需要在Q 点加速,即轨道Ⅱ上经过Q 点的速度大于轨道Ⅰ上经过Q 点的速度,而轨道Ⅱ上的速度小于第一宇宙速度,故在轨道Ⅰ上经过Q 点时的速度小于第一宇宙速度,D 错误.迁移2 卫星的追及、相遇问题2.(2020·江西重点中学联考)小型登月器连接在航天站上,一起绕月球做匀速圆周运动,其轨道半径为月球半径的3倍,某时刻,航天站使登月器减速分离,登月器沿如图所示的椭圆轨道登月,在月球表面逗留一段时间完成科考工作后,经快速启动仍沿原椭圆轨道返回,当第一次回到分离点时恰与航天站对接,登月器的快速启动时间可以忽略不计,整个过程中航天站保持原轨道绕月运行.已知月球表面的重力加速度为g,月球半径为R,不考虑月球自转的影响,则登月器可以在月球上停留的最短时间约为( )A.10π5Rg-6π3Rg B.6π3Rg-4π2RgC.10π5Rg-2πRg D.6π3Rg-2πRg解析:选B.当登月器和航天站在半径为3R的轨道上绕月球做匀速圆周运动时,应用牛顿第二定律有GMm r2=m4π2rT2,r=3R,则有T=2πr3GM=6π3R3GM.在月球表面的物体所受重力近似等于万有引力,可得GM=gR2,所以T=6π3Rg①,登月器在椭圆轨道上运行的周期用T1表示,航天站在圆轨道上运行的周期用T2表示,对登月器和航天站依据开普勒第三定律有T2(3R)3=T21(2R)3=T22(3R)3②,为使登月器仍沿原椭圆轨道回到分离点与航天站实现对接,登月器可以在月球表面停留的时间t应满足t=nT2-T1(其中n=1、2、3、…)③,联立①②③式得t=6πn 3Rg-4π2Rg(其中n=1、2、3、…),当n=1时,登月器可以在月球上停留的时间最短,即t min=6π3Rg-4π2Rg.[学生用书P82]卫星运动规律分析【对点训练】1.(2019·高考天津卷)2018年12月8日,肩负着亿万中华儿女探月飞天梦想的嫦娥四号探测器成功发射,“实现人类航天器首次在月球背面巡视探测,率先在月背刻上了中国足迹”.已知月球的质量为M、半径为R,探测器的质量为m,引力常量为G,嫦娥四号探测器围绕月球做半径为r的匀速圆周运动时,探测器的( )A.周期为4π2r3GM B.动能为GMm2RC.角速度为Gmr3D.向心加速度为GMR2解析:选A.嫦娥四号探测器环绕月球做匀速圆周运动时,万有引力提供其做匀速圆周运动的向心力,有GMmr2=mω2r=mv2r=m4π2T2r=ma,解得ω=GMr3、v=GMr、T=4π2r3GM、a=GMr2,则嫦娥四号探测器的动能为E k=12mv2=GMm2r,由以上可知A正确,B、C、D错误.2.(2019·高考江苏卷)1970年成功发射的“东方红一号”是我国第一颗人造地球卫星,该卫星至今仍沿椭圆轨道绕地球运动.如图所示,设卫星在近地点、远地点的速度分别为v1、v2,近地点到地心的距离为r ,地球质量为M ,引力常量为G .则( )A .v 1>v 2,v 1=GM r B .v 1>v 2,v 1>GM rC .v 1<v 2,v 1=GM rD .v 1<v 2,v 1>GM r解析:选B.“东方红一号”环绕地球在椭圆轨道上运行的过程中,只有万有引力做功,机械能守恒,其由近地点向远地点运动时,万有引力做负功,引力势能增加,动能减小,因此v 1>v 2;又“东方红一号”离开近地点开始做离心运动,则由离心运动的条件可知G Mm r 2<m v 21r,解得v 1>GM r,B 正确,A 、C 、D 错误.[学生用书P323(单独成册)] (建议用时:40分钟)一、单项选择题1.(2018·高考全国卷Ⅲ)为了探测引力波,“天琴计划”预计发射地球卫星P ,其轨道半径约为地球半径的16倍;另一地球卫星Q 的轨道半径约为地球半径的4倍.P 与Q 的周期之比约为( )A .2∶1B .4∶1C .8∶1D .16∶1解析:选C.由开普勒第三定律得r 3T 2=k ,故T PT Q=⎝ ⎛⎭⎪⎫R P R Q 3=⎝ ⎛⎭⎪⎫1643=81,C 正确. 2.(2020·山东聊城一模)嫦娥四号探测器平稳落月,全国人民为之振奋.已知嫦娥四号探测器在地球上受到的重力为G 1,在月球上受到月球的引力为G 2,地球的半径为R 1,月球的半径为R 2,地球表面处的重力加速为g .则下列说法正确的是( )A .月球表面处的重力加速度为G 1G 2gB .月球与地球的质量之比为G 1R 22G 2R 21C .若嫦娥四号在月球表面附近做匀速圆周运动,周期为2πR 2G 1gG 2D .月球与地球的第一宇宙速度之比为G 1R 2G 2 R 1解析:选C.嫦娥四号绕月球表面飞行时受到月球的引力为G 2,由G 2=mg ′,解得月球表面的重力加速度为:g ′=G 2m =G 2G 1g ,故A 错误;嫦娥四号的质量为:m =G 1g ,根据万有引力等于重力得:G M 地mR 21=mg ,解得地球质量为:M 地=gR 21G ,月球对飞船的引力为:G 2=G M 月m R 22,解得月球的质量为:M 月=G 2R 22Gm=G 2R 22g GG 1,则月球与地球质量之比为:M 月M 地=G 2R 22G 1R 21,故B 错误;根据G 2=m4π2T 2R 2得探测器沿月球表面轨道上做匀速圆周运动的周期为:T =2πR 2G 1gG 2,故C 正确;根据G MmR 2=mg 得第一宇宙速度为:v =gR ,则月球与地球的第一宇宙速度之比为v 月v 地=g ′R 2gR 1=G 2R 2G 1R 1,故D 错误.3.(2017·高考全国卷Ⅲ)2017年4月,我国成功发射的天舟一号货运飞船与天宫二号空间实验室完成了首次交会对接,对接形成的组合体仍沿天宫二号原来的轨道(可视为圆轨道)运行.与天宫二号单独运行时相比,组合体运行的( )A .周期变大B .速率变大C .动能变大D .向心加速度变大解析:选C.组合体比天宫二号质量大,轨道半径R 不变,根据GMm R 2=m v 2R,可得v =GM R,可知与天宫二号单独运行时相比,组合体运行的速率不变,B 错误;又T =2πRv,则周期T 不变,A 错误;质量变大、速率不变,动能变大,C 正确;向心加速度a =GM R 2,不变,D 错误.4.(2020·北京顺义二模)2019年1月3日10时26分,“嫦娥四号”探测器成功在月球背面着陆,标志着我国探月航天工程达到了一个新高度.已知地球和月球的半径之比为4∶1,表面重力加速度之比约为6∶1.则地球和月球相比较,下列说法中最接近实际的是( )A .地球的密度与月球的密度之比为3∶2B .地球的质量与月球的质量之比为64∶1C .地球的第一宇宙速度与月球的第一宇宙速度之比为8∶1D .苹果在地球表面受到的引力与它在月球表面受到的引力之比为60∶1解析:选A.由G Mm R 2=mg 得M =R 2g G ,则M 地M 月=4212×61=961,B 错误;由M =R 2g G 、V =43πR 3、ρ=MV 得:ρ=3g4πRG ,则ρ地ρ月=61×14=32,A 正确;由G Mm R 2=m v 21R 和G Mm R 2=mg 得v 1=gR ,则v 1地v 1月=61×41=261,C 错误;由F =G Mm R 2得F 苹地F 苹月=M 地M 月×R 2月R 2地=961×1242=61,D 错误.5.土星最大的卫星叫“泰坦”(如图),每16天绕土星一周,其公转轨道半径约为1.2×106 km ,已知引力常量G =6.67×10-11 N ·m 2/kg 2,则土星的质量约为( )A .5×1017 kgB .5×1026 kgC .7×1033 kgD .4×1036 kg解析:选B.卫星绕土星运动,土星的引力提供卫星做圆周运动的向心力,设土星质量为M :GMm R 2=m4π2T 2R ,解得M =4π2R 3GT2,代入数据计算可得:M ≈5×1026 kg ,故B 正确,A 、C 、D 错误. 6.(2020·江苏淮安质检)科学家预测银河系中所有行星的数量大概在2~3万亿之间.目前在银河系。
高考一轮复习 专题4 天体运动的“两类热点”问题

专题四 天体运动的“两类热点”问题考点突破热点一 赤道上的物体、同步卫星和近地卫星师生共研1.同步卫星和近地卫星比较二者都是由万有引力提供向心力⎝ ⎛⎭⎪⎫GMm r 2=mv2r =m ω2r ,是轨道半径不同的两个地球卫星,应根据卫星运行参量的变化规律比较各物理量.2.同步卫星和赤道上的物体比较二者的角速度相同,即周期相等,半径不同,由此比较其他物理量.注意:赤道上的物体由万有引力和支持力的合力提供向心力,G Mm r 2=m v2r 不适用,不能按照卫星运行参量的变化规律判断.3.近地卫星和赤道上的物体比较先将近地卫星和赤道上物体分别与同步卫星比较,然后再对比二者的各物理量.例1 [2021·广州一模]如图所示,A 是地球的同步卫星,B 是地球的近地卫星,C 是地面上的物体,A 、B 、C 质量相等,均在赤道平面上绕地心做匀速圆周运动.设A 、B 、C 做圆周运动的向心加速度为a A 、a B 、a C ,周期分别为T A 、T B 、T C ,A 、B 、C 做圆周运动的动能分别为E kA 、E kB 、E kC .下列关系式正确的是( )A .aB =aC >a A B .a B >a A >a C C .T A =T B <T CD .E kA <E kB =E kC练1 国务院批复,自2016年起将4月24日设立为“中国航天日”.1970年4月24日我国首次成功发射的人造卫星东方红一号,目前仍然在椭圆轨道上运行,其轨道近地点高度约为440 km ,远地点高度约为2 060 km ;1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km 的地球同步轨道上.设东方红一号在远地点的加速度为a 1,东方红二号的加速度为a 2,固定在地球赤道上的物体随地球自转的加速度为a 3,则a 1、a 2、a 3的大小关系为( )A .a 2>a 1>a 3B .a 3>a 2>a 1C .a 3>a 1>a 2D .a 1>a 2>a 3练2 (多选)如图所示,同步卫星与地心的距离为r ,运行速率为v 1,向心加速度为a 1;地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是( )A.a1a2=rRB.a1a2=⎝⎛⎭⎪⎫Rr2 C.v1v2=rRD.v1v2=Rr题后反思赤道上的物体(A)、近地卫星(B)和地球同步卫星(C)之间常见的运动学物理量比较如下:半径r A<r B<r C周期T A=T C>T B角速度ωA=ωC<ωB线速度v A<v C<v B向心加速度a A<a C<a B热点二卫星(航天器)的变轨及对接问题多维探究题型1|卫星变轨问题1.卫星变轨的实质两类变轨离心运动近心运动变轨起因卫星速度突然增大卫星速度突然减小受力分析G<m G>m变轨结果变为椭圆轨道运动或在较大半径圆轨道上运动变为椭圆轨道运动或在较小半径圆轨道上运动2.人造卫星的发射过程,如图所示.(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅱ.(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.例2 近年来,我国的航天事业飞速发展,“嫦娥奔月”掀起高潮.“嫦娥四号”进行人类历史上的第一次月球背面登陆.若“嫦娥四号”在月球附近轨道上运行的示意图如图所示,“嫦娥四号”先在圆轨道上做圆周运动,运动到A点时变轨为椭圆轨道,B点是近月点,则下列有关“嫦娥四号”的说法正确的是( ) A.“嫦娥四号”的发射速度应大于地球的第二宇宙速度B.“嫦娥四号”要想从圆轨道进入椭圆轨道必须在A点加速C.“嫦娥四号”在椭圆轨道上运行的周期比圆轨道上运行的周期要长D.“嫦娥四号”运行至B点时的速率大于月球的第一宇宙速度题型2|卫星的对接问题在低轨道运行的卫星,加速后可以与高轨道的卫星对接.同一轨道的卫星,不论加速或减速都不能对接.例3 [2021·南宁一模]我国是少数几个掌握飞船对接技术的国家之一,为了实现神舟飞船与天宫号空间站顺利对接,具体操作应为( )A.飞船与空间站在同一轨道上且沿相反方向做圆周运动接触后对接B.空间站在前、飞船在后且两者沿同一方向在同一轨道做圆周运动,在合适的位置飞船加速追上空间站后对接C.空间站在高轨道,飞船在低轨道且两者同向飞行,在合适的位置飞船加速追上空间站后对接D.飞船在前、空间站在后且两者在同一轨道同向飞行,在合适的位置飞船减速然后与空间站对接题型3|变轨前、后各物理量的变化规律4 2020年10月6日,诺贝尔物理学奖的一半颁给了给出黑洞形成理论证明的罗杰·彭罗斯,引起世界轰动.黑洞是近代引力理论所预言的宇宙中的一种特殊天体,在黑洞引力范围内,任何物体都不能脱离它的束缚,甚至连光也不能射出,欧洲航天局由卫星观察发现银河系中心存在一个超大型黑洞,假设银河系中心仅存一个黑洞,太阳系绕银河系中心做匀速圆周运动,则根据下列哪组数据可以估算出该黑洞的质量(引力常量为已知)( )A.太阳系的质量和太阳系绕该黑洞公转的周期B.太阳系的质量和太阳系到该黑洞的距离C.太阳系的运行速度和该黑洞的半径D.太阳系绕该黑洞公转的周期和轨道的半径题后反思航天器变轨的问题“四个判断”(1)判断速度①在两轨道切点处,外轨道的速度大于内轨道的速度.②在同一椭圆轨道上,越靠近椭圆焦点速度越大.③对于两个圆轨道,半径越大速度越小.(2)判断加速度①根据a =,判断航天器的加速度.②公式a =对椭圆不适用,不要盲目套用.(3)判断机械能①在同一轨道上,航天器的机械能守恒.②在不同轨道上,轨道半径越大,机械能一定越大.(4)判断周期:根据开普勒第三定律,行星轨道的半长轴(半径)越大周期越长.题型4|卫星的追及相遇问题行星A和B围绕恒星O做匀速圆周运动,周期分别为T A和T B.设t=0时刻,A、B和O三者共线,则三者再次共线所需要的最少时间t满足以下条件:情境图若A、B公转方向相同若A、B公转方向相反t0=0时,A、B在O同侧(A、B再次在O同侧)⎝⎛⎭⎪⎫2πT B-2πT At=2πtT B-tT A=1(A、B再次在O同侧)⎝⎛⎭⎪⎫2πT A+2πT Bt=2πtT A+tT B=1t0=0时,A、B在O异侧⎝⎛⎭⎪⎫2πT B-2πT At=πtT B-tT A=12⎝⎛⎭⎪⎫2πT A+2πT Bt=πtT A+tT B=12例5 火星冲日现象即火星、地球和太阳刚好在一条直线上,如图所示.已知火星轨道半径为地球轨道半径的1.5倍,地球和火星绕太阳运行的轨道都视为圆且两行星的公转方向相同,则( ) A.火星与地球绕太阳运行的线速度大小之比为2:3B.火星与地球绕太阳运行的加速度大小之比为4:9C.火星与地球的公转周期之比为:D.2021年10月13日前有可能再次发生火星冲日现象练3 [2021·湖南怀化一模]随着嫦娥奔月梦想的实现,我国不断刷新深空探测的“中国高度”.“嫦娥”卫星整个飞行过程可分为三个轨道段:绕地飞行调相轨道段、地月转移轨道段、绕月飞行轨道段.我们用如图所示的模型来简化描绘“嫦娥”卫星飞行过程,假设调相轨道和绕月轨道的半长轴分别为a、b,公转周期分别为T1、T2.关于“嫦娥”卫星的飞行过程,下列说法正确的是( )A.=B.“嫦娥”卫星在地月转移轨道上运行的速度应大于11.2 km/sC.从调相轨道切入到地月转移轨道时,卫星在P点必须减速D.从地月转移轨道切入到绕月轨道时,卫星在Q点必须减速练4 [2021·成都七中二诊](多选)2020年3月9日我国成功发射第54颗北斗导航卫星,意味着北斗全球组网仅差一步之遥.人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图所示,在发射地球同步卫星的过程中,卫星从近地圆轨道Ⅰ的A点先变轨到椭圆轨道Ⅱ,然后在B点变轨进入地球同步轨道Ⅲ,则( )A.卫星在同步轨道Ⅲ上的运行速度小于7.9 km/sB.卫星在轨道Ⅱ稳定运行时,经过A点时的速率比过B点时小C.若卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行的周期分别为T1、T2、T3,则T1<T2<T3D.现欲将卫星由轨道Ⅱ变轨进入轨道Ⅲ,则需在B点通过点火减速来实现思维拓展卫星通信中的“阴影区”问题在卫星的通信、观测星体问题中,由于另一个星体的遮挡出现“阴影区”,解决此类问题的基本方法是:(1)建立几何模型:通过构建平面几何画图,找出被星体挡的“阴影区”.(2)建立几何关系:关键是找出两个星体转动角度之间的几何关系.例1 [2020·福州二模]有一颗绕地球做匀速圆周运动的卫星,其运行周期是地球近地卫星的2倍,卫星圆形轨道平面与地球赤道平面重合,卫星上有太阳能收集板可以把光能转化为电能,已知地球表面重力加速度为g,地球半径为R,忽略地球公转,此时太阳处于赤道平面上,近似认为太阳光是平行光,则卫星绕地球一周,太阳能收集板的工作时间为( )A. B. C. D.例2 侦察卫星对国家有极高的战略意义,尤其是极地侦察卫星.极地侦察卫星在通过地球两极的圆轨道上运行,由于与地球自转方向垂直,所以理论上可以观察到地球上任何一处.假如它的运行轨道距地面高度为h,要使卫星在一天的时间内将地面上赤道各处在日照条件的情况下全都拍摄下来,在卫星通过赤道上空时,卫星上的摄像机至少应拍摄地面上赤道圆周的弧长是多少?(设地球半径为R,地面处的重力加速度为g,地球自转的周期为T)专题四天体运动的“两类热点”问题考点突破例1 解析:C与A的角速度相同,根据a=ω2r,可知a C<a A;根据卫星的加速度a=,可知a A<a B;所以a C<a A<a B,故A项错误,B项正确;对卫星A、B,由开普勒第三定律=k,知T A>T B,卫星A是地球的同步卫星,则T A=T C,所以T A=T C>T B,故C项错误;对于卫得A、B,由v=分析知v A<v B.由于卫星A、C角速度相等,由v=ωr分析知v C<v A,所以v C<v A<v B,卫星的动能为:E k=mv2可得:E kC<E kA<E kB,故D项错误.答案:B练1 解析:由于东方红二号卫星是同步卫星,则其角速度和赤道上的物体角速度相等,根据a=ω2r,r2>r3,则a2>a3;由万有引力定律和牛顿第二定律得,G=ma,由题目中数据可以得出,r1<r2,则;综合以上分析有,a1>a2>a3,选项D正确.答案:D练2 解析:对于卫星,其共同特点是由万有引力提供向心力,有G=m,故=.对于同步卫星和地球赤道上的物体,其共同特点是角速度相等,有a=ω2r,故=.答案:AD例2 解析:“嫦娥四号”的发射速度应大于地球的第一宇宙速度7.9 km/s,小于地球的第二宇宙速度11.2 km/s,故A错误;“嫦娥四号”要想从圆轨道变轨到椭圆轨道,必须在A点进行减速,故B错误;由开普勒第三定律知=,由题图可知,圆轨道的半径r大于椭圆轨道的半长轴a,故“嫦娥四号”在圆轨道上运行的周期T1大于在椭圆轨道上运行的周期T2,所以C错误;“嫦娥四号”要想实现软着陆,运行至B点时必须减速才能变为环月轨道,故在B点时的速率大于在环月轨道上运行的最大速率,即大于月球的第一宇宙速度,故D正确.答案:D例3 解析:飞船在轨道上高速运动,如果在同一轨道上沿相反方向运动,则最终会撞击而不是成功对接,故A项错误;两者在同一轨道上,飞船加速后做离心运动,则飞船的轨道抬升,故不能采取同一轨道加速对接,故B项错误;飞船在低轨道加速做离心运动,在合适的位置,飞船追上空间站实现对接,故C项正确;两者在同一轨道飞行时,飞船突然减速做近心运动,飞船的轨道高度要降低,故不可能与同一轨道的空间站实现对接,故D项错误.答案:C例4 解析:太阳系绕银河系中心的黑洞做匀速圆周运动,万有引力提供向心力,则有G=mr=m=mω2r=mωv,分析可知,要计算黑洞的质量M,需知道太阳系的公转周期T与轨道半径r,或者线速度v与轨道半径r,或者轨道半径r与角速度ω,或者角速度ω、线速度v与轨道半径r,选项A、B、C 错误,D正确.答案:D例5 解析:火星和地球绕太阳做圆周运动,万有引力提供向心力,有G=m=ma=m r,得v=,a=,T=2π.由v=可知v∝,则火星与地球的公转线速度大小之比为,选项A错误;由a=可知a∝,则火星与地球的向心加速度大小之比为4∶9,选项B正确;由T=2π可知T∝,则火星与地球公转周期之比为3∶2,选项C错误;再次相距最近时,地球比火星多转动一周,则据此有t=2π,其中T火∶T地=3∶2,解得t≈2.2年,故下一次发生火星冲日现象的时间为2022年10月13日前后,选项D错误.答案:B练3 解析:根据开普勒第三定律,调相轨道与绕月轨道的中心天体分别对应地球和月球,故它们轨道半长轴的三次方与周期的二次方比值不相等,故A错误;11.2 km/s是第二宇宙速度,是地球上发射脱离地球束缚的卫星的最小发射速度,由于嫦娥卫星没有脱离地球束缚,故其速度小于11.2 km/s,故B错误;从调相轨道切入到地月转移轨道时,卫星的轨道将持续增大,故卫星需要在P点做离心运动,故在P 点需要加速,故C错误;从地月转移轨道切入到绕月轨道时,卫星相对月球而言,轨道半径减小,需要在Q点开始做近心运动,故卫星需在Q点减速,故D正确.答案:D练4 解析:卫星绕地球做匀速圆周运动,万有引力提供向心力,有=,得v=.可知卫星运动半径r越大,运行速度v越小,所以卫星绕近地轨道运行时速度最大,即地球的最大的环绕速度(7.9 km/s),则卫星在同步轨道Ⅲ上的运行速度小于7.9 km/s,选项A正确.卫星在轨道Ⅱ上从A向B运动过程中,万有引力对卫星做负功,动能逐渐减小,速率也逐渐减小,所以卫星在轨道Ⅱ上过A点的速率比卫星在轨道Ⅱ上过B点的速率大,选项B错误.设卫星在轨道Ⅰ上运行的轨道半径为r1、轨道Ⅱ的半长轴为r2、在轨道Ⅲ上运行的轨道半径为r3.根据图中几何关系可知r1<r2<r3,又由开普勒第三定律有=k,可得T1<T2<T3,选项C正确.卫星在B点要进入Ⅲ必须加速做离心运动,所以卫星在B点通过点火加速可实现由轨道Ⅱ进入轨道Ⅲ,选项D错误.答案:AC思维拓展典例1 解析:地球近地卫星做匀速圆周运动,根据牛顿第二定律:mg=mR T=2π,此卫星运行周期是地球近地卫星的2倍,所以该卫星运行周期T′=4π,由=m′r,=m′g,得r=2R.如图,当卫星在阴影区时不能接受阳光,据几何关系:∠AOB=∠COD=,卫星绕地球一周,太阳能收集板工作时间为:t=T′=.答案:C典例2 解析:设卫星运行周期为T1,则有G=(h+R)物体处于地面上时有G=m0g解得T1=在一天内卫星绕地球转过的圈数为,即在一天中有次经过赤道上空,所以每次摄像机拍摄的赤道弧长为s==T1,将T1代入,可得s=.答案:。
步步高高考物理一轮复习(新课标)配套导学案:学案4运动图象 追及相遇问题.DOC

学案4 运动图象追及相遇问题一、概念规律题组1.如图1所示为甲、乙两物体的x-t图象,则()图1A.甲、乙两物体都做匀速直线运动B.若甲、乙两物体在同一直线上运动,则一定会相遇C.t1时刻甲、乙相遇D.t2时刻甲、乙相遇答案ABC2.某物体沿一直线运动,其v-t图象如图2所示,则下列说法中正确的是()图2A.第2 s内和第3 s内速度方向相反B.第2 s内和第3 s内速度方向相同C.第2 s末速度方向发生变化D.第5 s内速度方向与第1 s内方向相同答案B3.如图3所示为某质点运动的速度—时间图象,下列有关该质点运动情况的判断正确的是()图3A.0~t1时间内加速度为正,质点做加速运动B.t1~t2时间内加速度为负,质点做减速运动C.t2~t3时间内加速度为负,质点做减速运动D.t3~t4时间内加速度为正,质点做加速运动答案AB解析由图象可知,在0~t1时间内加速度为正,速度也为正,加速度方向与速度方向相同,故质点做加速运动;在t1~t2时间内加速度为负,速度为正,加速度方向与速度方向相反,故质点做减速运动;在t2~t3时间内加速度为负,速度也为负,加速度方向与速度方向相同,故质点做加速运动;在t3~t4时间内加速度为正,速度为负,加速度方向与速度方向相反,质点做减速运动.4.如图4所示为一物体做匀变速直线运动的图象.由图象作出的下列判断中正确的是()图4A.物体始终沿正方向运动B.物体先沿负方向运动,在t=2 s后沿正方向运动C.在t=2 s前物体位于出发点负方向上,t=2 s后位于出发点正方向上D.在t=2 s时,物体距出发点最远答案BD解析物体的运动方向即为速度方向.由图象知,在t=2 s前,速度为负,物体沿负方向运动,2 s后速度为正,物体沿正方向运动,A是错的,B是正确的.物体的位置由起点及运动的位移决定.取起点为原点则位置由位移决定.在v-t图象中,位移数值是图象与坐标轴所围的面积.由图象可知t<2 s时物体的位移为负,t=2 s时绝对值最大.t=2 s后,位移为负位移与正位移的代数和,绝对值减小,所以t=2 s时位移绝对值最大即物体离出发点最远,所以D正确,C错,所以选B、D.二、思想方法题组5.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图象中(如图5所示),直线a、b分别描述了甲、乙两车在0~20 s的运动情况.关于两车之间的位置关系,下列说法中正确的是()图5A.在0~10 s内两车逐渐靠近B.在10~20 s内两车逐渐远离C.在5~15 s内两车的位移相等D.在t=10 s时两车在公路上相遇答案C解析由题图知乙做匀减速直线运动,初速度v乙=10 m/s,加速度大小a乙=0.5 m/s2;甲做匀速直线运动,速度v甲=5 m/s.当t=10 s时v甲=v乙,甲、乙两车距离最大,所以0~10 s内两车之间的距离越来越大;10~20 s内两车之间的距离越来越小,t=20 s时,两车距离为零,再次相遇,故A、B、D错误;在5~15 s时间内,两图线与时间轴围成的面积相等,因而两车位移相等,故C正确.6.一辆警车在平直的公路上以40 m/s的速度巡逻,突然接到报警,在前方不远处有歹徒抢劫,该警车要尽快赶到出事地点且到达出事地点时的速度也为40 m/s,有三种行进方式:a为一直匀速直线运动;b为先减速再加速;c为先加速再减速,则()A.a种方式先到达B.b种方式先到达C.c种方式先到达D.条件不足,无法确定答案C解析作出v-t图象如右图所示,从出发点到出事地点位移一定,根据v-t图象的意义,图线与坐标轴所围的面积相等,则只能t c<t a<t b,所以c种方式先到达.思维提升1.x-t图象和v-t图象都只能反映直线运动的规律,而不能反映曲线运动的规律.2.x-t图象和v-t图象是用图线直观地反映位移或速度随时间变化的工具.图线上每一点表示某一时刻的位移或速度随时间的推移,也可反映其变化情况,而正负表示了位移或速度的方向.3.利用图象解决问题要做到“六看”,即看轴、看线、看斜率、看面积、看截距、看拐点.4.解决追及相遇问题要注意“一个条件”和“两个关系”,即两者速度相等;时间关系和位移关系.一、运动图象的分析与运用运动学图象主要有x-t图象和v-t图象,运用运动学图象解题可总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面积”,五看“截距”,六看“特殊点”.1.一看“轴”:先要看清两轴所代表的物理量,即图象是描述哪两个物理量之间的关系.2.二看“线”:图象表示研究对象的变化过程和规律.在v-t图象和x-t图象中倾斜的直线分别表示物体的速度和位移随时间变化的运动情况.3.三看“斜率”:斜率表示纵、横坐标轴上两个物理量的比值,常用一个重要的物理量与之对应,用于定量计算对应物理量的大小和定性分析变化的快慢.x-t图象中斜率表示运动物体的速度的大小和方向.v-t图象中斜率表示运动物体的加速度的大小和方向.4.四看“面积”:即图象和坐标轴所围的面积,也往往代表一个物理量,这要看两物理量的乘积有无意义.如v和t的乘积vt=x,有意义,所以v-t图与横轴所围“面积”表示位移,x-t图象与横轴所围面积无意义.5.五看“截距”:截距一般表示物理过程的初始情况,如t=0时的位移或速度.6.六看“特殊点”:如交点、拐点(转折点)等.如x-t图象的交点表示两质点相遇,但v-t图象的交点只表示速度相等.【例1】(2010·广东·17)图6是某质点运动的速度-时间图象,由图象得到的正确结果是()图6A.0~1 s内的平均速度是2 m/sB.0~2 s内的位移大小是3 mC.0~1 s内的加速度大于2~4 s内的加速度D.0~1 s内的运动方向与2~4 s内的运动方向相反答案BC解析 由题图可以看出:0~1 s 内质点做初速度为零、末速度为2 m /s 的匀加速直线运动;1~2 s 内质点以2 m /s 的速度做匀速直线运动;2~4 s 内质点做初速度为2 m /s ,末速度为0的匀减速直线运动,故0~1 s 内质点的平均速度为v =0+22m /s =1 m /s ,选项A 错误;0~2 s 内图象与时间轴所围的面积在数值上等于位移的大小,x 2=(1+2)×22m =3 m ,选项B 正确;0~1 s 内质点的加速度a 1=2-01 m /s 2=2 m /s 2,2~4 s 内质点的加速度a 2=0-22m /s =-1 m /s 2,选项C 正确;因0~4 s 内图线都在时间轴的上方,故速度一直沿正方向,选项D 错误.[规范思维] 运动的v -t 图象是高考的热点.(1)v -t 图象中,图线向上倾斜表示物体做加速运动,向下倾斜表示物体做减速运动.(2)v -t 图象中,图线与横轴所围成的“面积”在数值上等于物体的位移,在t 轴下方的“面积”表示位移为负.[针对训练1] (2010·天津·3)质点做直线运动的v -t 图象如图7所示,规定向右为正方向,则该质点在前8 s 内平均速度的大小和方向分别为( )图7A .0.25 m /s 向右B .0.25 m /s 向左C .1 m /s 向右D .1 m /s 向左答案 B 解析 在v -t 图象 ,图线与横轴所围面积代表位移,0~3 s 内,x 1=3 m ,向右;3~8 s 内,x 2=-5 m ,负号表示向左,则0~8 s 内质点运动的位移x =x 1+x 2=-2 m ,向左,v =x t=-0.25 m /s ,向左,选项B 正确. 【例2】 (2010·全国Ⅰ·24)汽车由静止开始在平直的公路上行驶,0~60 s 内汽车的加速度随时间变化的图线如图8所示.图8(1)画出汽车在0~60 s 内的v -t 图线;(2)求在这60 s 内汽车行驶的路程.答案 (1)见解析图 (2)900 m 解析 (1)0~10 s 内,汽车做初速度为0的匀加速直线运动,10 s 末速度v 1=a 1t 1=2×10 m /s =20 m /s10~40 s 内,汽车做匀速直线运动,40~60 s 内,汽车做匀减速直线运动.60 s 末的速度v 2=v 1+a 2t 2=20 m /s -1×20 m /s =0.v -t 图线如右图所示.(2)x =12v 1t 1+v 1t +12(v 1+v 2)t 2=12×20×10 m +20×30 m +12×(20+0)×20 m =900 m . [规范思维] 要掌握v -t 图象的斜率表示a ,这也是a -t 图象与v -t 图象的联系点.本题由a -t 图象画v -t 图象,由v -t 图象求路程,设计新颖、环环相扣.【例3】 某质点在东西方向上做直线运动,其位移-时间图象如图9所示(规定向东为正方向).试根据图象:图9 (1)描述质点运动情况;(2)求出质点在0~4 s 、0~8 s 、2~4 s 三段时间内的位移和路程.(3)求出质点在0~4 s 、4~8 s 内的速度.答案 (1)见解析 (2)见解析 (3)2 m /s ,方向向东;4 m /s ,方向向西解析 (1)从图象知:质点从t =0开始由原点出发向东做匀速直线运动,持续运动4 s ,4 s 末开始向西做匀速直线运动,又经过2 s ,即6 s 末回到原出发点,然后又继续向西做匀速直线运动直到8 s 末.(2)在0~4 s 内位移大小是8 m ,方向向东,路程是8 m .在0~8 s 内的位移为-8 m ,负号表示位移的方向向西,说明质点在8 s 末时刻处于原出发点西8 m 的位置上,此段时间内路程为24 m .在2~4 s 内,质点发生的位移是4 m ,方向向东,路程也是4 m .(3)在0~4 s 内质点的速度为v 1=x 1t 1=84m /s =2 m /s ,方向向东; 在4~8 s 内质点的速度为v 2=x 2t 2=-8-84m /s =-4 m /s ,方向向西. [规范思维] x -t 图象不同于v -t 图象,x -t 图象中,图线向上倾斜表示物体沿正方向运动,向下倾斜表示物体沿负方向运动,图线的斜率表示物体的速度.[针对训练2] (2010·潍坊二检)一遥控玩具小车在平直路上运动的位移-时间图象如图10所示,则( )图10A .15 s 末汽车的位移为300 mB .20 s 末汽车的速度为-1 m /sC .前10 s 内汽车的速度为3 m /sD .前25 s 内汽车做单方向直线运动答案 BC解析 由位移-时间图象可知:前10 s 内汽车做匀速直线运动,速度为3 m /s ,加速度为0,所以C 正确;10 s ~15 s 汽车处于静止状态,汽车相对于出发点的位移为30 m ,所以A 错误;15 s ~25 s 汽车向反方向做匀速直线运动,速度为-1 m /s ,所以D 错误,B 正确.二、追及相遇问题讨论追及、相遇问题的实质,就是分析两物体在相同时间内能否到达相同的空间位置.1.分析追及问题的方法技巧可概括为“一个临界条件”、“两个等量关系”.(1)一个临界条件——速度相等.它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断问题的切入点(2)两个等量关系:时间关系和位移关系,通过画草图找出两物体的位移关系是解题的突破口.2.能否追上的判断方法物体B 追赶物体A :开始时,两个物体相距x 0.若v A =v B 时,x A +x 0<x B ,则能追上;若v A =v B 时,x A +x 0=x B ,则恰好不相撞;若v A =v B 时,x A +x 0>x B ,则不能追上.3.若被追赶的物体做匀减速直线运动,一定要注意判断追上前该物体是否已经停止运动.【例4】 汽车以25 m /s 的速度匀速直线行驶,在它后面有一辆摩托车,当两车相距1 000 m 时,摩托车从静止起动做匀加速运动追赶汽车,摩托车的最大速度可达30 m /s ,若使摩托车在4 min 时刚好追上汽车.求:(1)摩托车做匀加速运动的加速度a.(2)摩托车追上汽车前两车相距最大距离x.答案 (1)2.25 m /s 2 (2)1 138 m解析 (1)设汽车位移为x 1,摩托车位移为x 2摩托车的加速度为a ,摩托车达到最大速度所用时间为t ,则30 m /s =atx 1=25×240 m =6 000 mx 2=3022a +30(240-30a) 恰好追上的条件为x 2=x 1+1 000 m解得a =94m /s 2=2.25 m /s 2 (2)摩托车与汽车速度相等时两车相距最远设此时刻为T ,最大距离为x max由运动学公式得25 m /s =aT解得T =1009s 所以x max =1 000+25T -aT 22=10 2509m =1 138 m[规范思维] (1)要抓住追上的等量关系x 2=x 1+x 0;(2)要抓住追上前的临界条件:速度相等.(3)解追及相遇问题除题中所述解析法外,还有图象法、数学极值法等.本题同学们可试着用图象法求解.[针对训练3] (2009·海南·8)甲乙两车在一平直道路上同向运动,其v -t 图像如图11所示,图中△OPQ 和△OQT 面积分别是x 1和x 2(x 1<x 2).初始时,甲车在乙车前方x 0处( )图11A .若x 0=x 1+x 2,两车不会相遇B .若x 0<x 1,两车相遇2次C .若x 0=x 1,两车相遇1次D .若x 0=x 2,两车相遇1次答案 ABC 解析 若乙车追上甲车时,甲、乙两车速度相同,即此时t =T ,则x 0=x 1,此后甲车速度大于乙车速度,全程甲、乙仅相遇一次;若甲、乙两车速度相同时,x 0<x 1,则此时乙车已在甲车的前面,以后甲还会追上乙,全程中甲、乙相遇2次;若甲、乙两车速度相同时,x 0>x 1,则此时甲车仍在乙车的前面,以后乙车不可能追上甲车了,全程中甲、乙都不会相遇,综上所述,选项A 、B 、C 对,D 错.【基础演练】1.(2010·山东淄博期中)如图12所示为一质点做直线运动的速度-时间图象,下列说法正确的是( )图12A .整个过程中,CE 段的加速度最大B .整个过程中,BC 段的加速度最大C .整个过程中,D 点所表示的状态离出发点最远D .BC 段所通过的路程是34 m答案 ACD 解析 在速度-时间图象中,斜率代表加速度,CE 段的斜率最大,故该段的加速度最大,故选项A 正确;在D 点,运动方向发生改变,故D 点所表示的状态离出发点最远,选项C 正确;在速度-时间图象中,图象与横轴所围的面积表示位移大小,故x BC =(5+12)×42m =34 m ,BC 段为单向直线运动,路程与位移相等,选项D 正确.2. 某人骑自行车在平直道路上行进,图13中的实线记录了自行车开始一段时间内的v -t 图象.某同学为了简化计算,用虚线作近似处理,下列说法正确的是( )图13A .在t 1时刻,虚线反映的加速度比实际的大B .在0~t 1时间内,由虚线计算出的平均速度比实际的大C .在t 1~t 2时间内,由虚线计算出的位移比实际的大D .在t 3~t 4时间内,虚线反映的是匀速直线运动答案 BD解析 如右图所示,t 1时刻,实线上A 点的切线为AB ,实际加速度的大小即为AB 的斜率,由图可知虚线反映的加速度小于实际加速度,故选项A 错误;在v -t 图象中,位移等于所对应图线与坐标轴所包围的面积,0~t 1时间内,虚线所对应的位移大于实线所对应的位移,由v =x t知,由虚线计算出的平均速度比实际的大,故选项B 正确;在t 1~t 2时间内,由虚线计算出的位移比实际的小,故选项C 错误;t 3~t 4时间内虚线为平行于时间轴的直线,此线反映的运动为匀速直线运动,故选项D 正确.3.(2011·温州模拟)如图14所示为在同一直线上运动的A 、B 两质点的x -t 图象,由图可知( )图14 A .t =0时,A 在B 的前面B .B 在t 2时刻追上A ,并在此后跑在A 的前面C .B 开始运动的速度比A 小,t 2时刻后才大于A 的速度D .A 运动的速度始终比B 大答案 AB解析 t =0时,A 质点在x 1处,而B 质点在原点处,故A 正确;由题图可知,0~t 1时间内,A 质点运动的速度比B 大,但t 1以后A 质点静止不动,速度为零,故C 、D 均错误;t 2时刻A 、B 两质点到达同一位置,之后B 质点继续向前运动,跑到A 质点的前面,故B 正确.4.(2011·潍坊模拟)如图15所示,汽车以10 m /s 的速度匀速驶向路口,当行驶至距路口停车线20 m 处时,绿灯还有3 s 熄灭.而该汽车在绿灯熄灭时刚好停在停车线处,则汽车运动的速度(v)-时间(t)图象可能是( )图15答案BC解析清楚地理解v-t图象中“面积”的物理意义是解本题的关键,A、D中的v-t图象中“面积”不等于20 m;B中v-t图象的“面积”可能等于20 m;C中v-t图象的“面积”正好等于20 m.B、C项正确,A、D项错误.5.t=0时,甲乙两汽车从相距70 km的两地开始相向行驶,它们的v-t图象如图16所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是()图16A.在第1小时末,乙车改变运动方向B.在第2小时末,甲乙两车相距10 kmC.在前4小时内,乙车运动加速度的大小总比甲车的大D.在第4小时末,甲乙两车相遇答案BC解析速度-时间图象在t轴以下的均为反方向运动,故2 h末乙车改变运动方向,A错;2 h末从图象围成的面积可知乙车运动位移大小为30 km,甲车位移为30 km,相向运动,此时两车相距70 km-30 km-30 km=10 km,B对;从图象的斜率看,斜率大加速度大,故乙车加速度在4 h内一直比甲车加速度大,C对;4 h末,甲车运动位移为120 km,乙车运动位移为30 km,两车原来相距70 km,故此时两车还相距20 km,D错.6.一物体由静止开始沿直线运动,其加速度随时间的变化规律如图17所示,取开始运动的方向为正方向,则物体运动的v-t图象正确的是()图17答案 C 解析 本题考查加速度在v -t 图象中的表示.在0~1 s 内,a =1 m /s 2,物体从静止开始做正向匀加速运动,速度图象是一条直线,1 s 末速度v 1=at =1 m /s .在1 s ~2 s 内,a 2=-1 m /s 2,物体将仍沿正方向运动,但要减速,2 s 末时速度v 2=v 1+a 2t =0,2 s ~3 s 内重复0~1 s 内运动情况,3 s ~4 s 内重复1 s ~2 s 内运动情况,故选C 项.7. (2011·陕西宝鸡调研)某跳伞运动训练研究所,让一名跳伞运动员从悬停在高空的直升机中跳下,研究人员利用运动员随身携带的仪器记录下了他的运动情况,通过分析数据,定性画出了运动员从跳离飞机到落地的过程中在空中沿竖直方向运动的v -t 图象如图18所示,规定向下的方向为正方向,则对运动员的运动,下列说法正确的是( )图18A .0~15 s 末都做加速度逐渐减小的加速运动B .0~10 s 末做自由落体运动,15 s 末开始做匀速直线运动C .10 s 末打开降落伞,以后做匀减速运动至15 s 末D .10 s 末~15 s 末加速度方向竖直向上,加速度的大小在逐渐减小答案 D解析 在v -t 图象中,图线的斜率代表加速度,从图象可以看出,0~10 s 内,加速度方向向下,图线的斜率越来越小,故不是自由落体运动,是变加速直线运动,10 s 末速度达到最大值;10 s 末打开降落伞,加速度方向向上,物体做加速度逐渐减小的减速运动,15 s 末加速度为零,速度达到稳定值,以后将做匀速直线运动.故选项D 正确.【能力提升】8.甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m /s 的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的.为了确定乙起跑的时机,需在接力区前适当的位置标记.在某次练习中,甲在接力区前x 0=13.5 m 处作了标记,并以v =9 m /s 的速度跑到此标记时向乙发出起跑口令.乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒.已知接力区的长度为L =20 m .求:(1)此次练习中乙在接棒前的加速度a.(2)在完成交接棒时乙离接力区末端的距离.答案 (1)3 m /s 2 (2)6.5 m解析 (1)在甲发出口令后,甲、乙达到共同速度所用时间为t =v a① 设在这段时间内甲、乙的位移分别为x 1和x 2,则------精品文档!值得拥有!------------珍贵文档!值得收藏!------ x 2=12at 2② x 1=vt ③x 1=x 2+x 0④联立①②③④式解得a =v 22x 0=3 m /s 2. (2)在这段时间内,乙在接力区的位移为x 2=v 22a=13.5 m 完成交接棒时,乙离接力区末端的距离为L -x 2=6.5 m .9.(2011·江苏海安模拟)一辆值勤的警车停在公路边,当警员发现从他旁边以v =10 m /s 的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5 s 后警车发动起来,并以2.5 m /s 2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km /h 以内.问:(1)警车在追赶货车的过程中,两车间的最大距离是多少?(2)判定警车在加速阶段能否追上货车.(要求通过计算说明)(3)警车发动后要多长时间才能追上货车?答案 (1)75 m (2)不能 (3)12 s解析 (1)警车在追赶货车的过程中,当两车速度相等时,它们的距离最大,设警车发动后经过t 1时间两车的速度相等.则t 1=102.5s =4 s x 货=(5.5+4)×10 m =95 mx 警=12at 21=12×2.5×42 m =20 m ;所以两车间的最大距离Δx =x 货-x 警=75 m . (2)v m =90 km /h =25 m /s ,当警车刚达到最大速度时,运动时间t 2=252.5s =10 s x 货′=(5.5+10)×10 m =155 mx 警′=12at 22=12×2.5×102 m =125 m 因为x 货′>x 警′,故此时警车尚未赶上货车.(3)警车刚达到最大速度时两车距离Δx ′=x 货′-x 警′=30 m ,警车达到最大速度后做匀速运动,设再经过Δt 时间后追赶上货车.则Δt =Δx ′v m -v=2 s 所以警车发动后要经过t =t 2+Δt =12 s 才能追上货车.易错点评1.要注意区分x -t 图象与v -t 图象的不同意义.2.要注意把图象与实际的运动情境相结合.3.比较位移相等的不同运动形式的时间长短问题用v -t 图象方便.4.用图象解决追及相遇问题简洁直观,便于理解分析.。
高考物理一轮复习 1.5追及与相遇问题学案

高考物理一轮复习 1.5追及与相遇问题学案基础知识归纳1.追及和相遇问题当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题.2.追及问题的两类情况(1)速度大者减速(如匀减速直线运动)追速度小者(如匀速运动):①当两者速度相等时,若两者位移之差仍小于初始时的距离,则永远追不上,此时两者间有最小距离.②若两者位移之差等于初始时的距离,且两者速度相等时,则恰能追上,也是两者相遇时避免碰撞的临界条件.③若两者位移之差等于初始时的距离时,追者速度仍大于被追者的速度,则被追者还有一次追上追者的机会,其间速度相等时两者间距离有一个极大值.(2)速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):①当两者速度相等时有最大距离.②若两者位移之差等于初始时的距离时,则追上.3.相遇问题的常见情况(1)同向运动的两物体追及即相遇.(2)相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇.重点难点突破一、追及和相遇问题的常见情形1.速度小者追速度大者常见的几种情况:类型图象说明匀加速追匀速①t=t0以前,后面物体与前面物体间距离增大②t=t0时,两物体相距最远为x0+匀速追匀减速Δx③t=t0以后,后面物体与前面物体间距离减小④能追及且只能相遇一次注:x0为开始时两物体间的距离匀加速追匀减速2.速度大者追速度小者常见的情形:类型图象说明匀减速追匀速开始追及时,后面物体与前面物体间距离在减小,当两物体速度相等时,即t =t 0时刻: ①若Δx =x 0,则恰能追及,两物体只能相遇一次,这也是避免相撞的临界条件 ②若Δx <x 0,则不能追及,此时两物体间最小距离为x 0-Δx ③若Δx >x 0,则相遇两次,设t 1时刻Δx 1=x 0两物体第一次相遇,则t 2时刻两物体第二次相遇 注:x 0是开始时两物体间的距离匀速追匀加速匀减速追匀加速二、追及、相遇问题的求解方法分析追及与相遇问题大致有两种方法,即数学方法和物理方法,具体为: 方法1:利用临界条件求解.寻找问题中隐含的临界条件,例如速度小者加速追赶速度大者,在两物体速度相等时有最大距离;速度大者减速追赶速度小者,在两物体速度相等时有最小距离.方法2:利用函数方程求解.利用不等式求解,思路有二:其一是先求出在任意时刻t 两物体间的距离y =f (t ),若对任何t ,均存在y =f (t )>0,则这两个物体永远不能相遇;若存在某个时刻t ,使得y =f (t )≤0,则这两个物体可能相遇.其二是设在t 时刻两物体相遇,然后根据几何关系列出关于t 的方程f (t )=0,若方程f (t )=0无正实数解,则说明这两物体不可能相遇;若方程f (t )=0存在正实数解,则说明这两个物体可能相遇.方法3:利用图象求解.若用位移图象求解,分别作出两个物体的位移图象,如果两个物体的位移图象相交,则说明两物体相遇;若用速度图象求解,则注意比较速度图线与t 轴包围的面积.方法4:利用相对运动求解.用相对运动的知识求解追及或相遇问题时,要注意将两个物体对地的物理量(速度、加速度和位移)转化为相对的物理量.在追及问题中,常把被追及物体作为参考系,这样追赶物体相对被追物体的各物理量即可表示为:s 相对=s 后-s 前=s 0,v 相对= v 后-v 前,a 相对=a 后-a 前,且上式中各物理量(矢量)的符号都应以统一的正方向进行确定.三、分析追及、相遇问题的思路和应注意的问题1.解“追及”、“相遇”问题的思路(1)根据对两物体运动过程的分析,画出物体的运动示意图.(2)根据两物体的运动性质,分别列出两物体的位移方程.注意要将两物体运动时间的关系反映在方程中.(3)由运动示意图找出两物体位移间的关联方程.(4)联立方程求解.2.分析“追及”、“相遇”问题应注意的几点(1)分析“追及”、“相遇”问题时,一定要抓住“一个条件,两个关系”:“一个条件”是两物体的速度满足的临界条件,如两物体距离最大、最小、恰好追上或恰好追不上等.“两个关系”是时间关系和位移关系.其中通过画草图找到两物体位移之间的数量关系,是解题的突破口.因此,在学习中一定要养成画草图分析问题的良好习惯,因为正确的草图对帮助我们理解题意、启迪思维大有裨益.(2)若被追赶的物体做匀减速运动,一定要注意追上该物体前是否停止运动.(3)仔细审题,注意抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”、“恰好”、“最多”、“至少”等,往往对应一个临界状态,要满足相应的临界条件.1.运动中的追及和相遇问题【例1】在一条平直的公路上,乙车以10 m/s 的速度匀速行驶,甲车在乙车的后面做初速度为15 m/s ,加速度大小为0.5 m/s 2的匀减速运动,则两车初始距离L 满足什么条件时可以使(1)两车不相遇;(2)两车只相遇一次;(3)两车能相遇两次(设两车相遇时互不影响各自的运动).【解析】设两车速度相等经历的时间为t ,则甲车恰能追上乙车时,应有v 甲t -22t a 甲=v 乙t +L其中t =甲乙甲a v v ,解得L =25 m 若L >25 m ,则两车等速时也未追及,以后间距会逐渐增大,即两车不相遇.若L =25 m ,则两车等速时恰好追及,两车只相遇一次,以后间距会逐渐增大.若L <25 m ,则两车等速时,甲车已运动至乙车前面,以后还能再次相遇,即能相遇两次.【思维提升】对于追及和相遇问题的处理,要通过两质点的速度进行比较分析,找到隐含条件(即速度相同时,两质点间距离最大或最小),再结合两个运动的时间关系、位移关系建立相应方程求解.【拓展1】两辆游戏赛车a 、b 在两条平行的直车道上行驶.t =0时两车都在同一计时处,此时比赛开始.它们在四次比赛中的v-t 图象如图所示.哪些图对应的比赛中,有一辆赛车追上另一辆 ( AC )【解析】由v-t 图象的特点可知,图线与t 轴所围成面积的大小,即为物体位移的大小.观察4个图象,只有A 、C 选项中,a 、b 所围面积的大小有相等的时刻,故A 、C 正确.2.追及、相遇问题的求解【例2】在水平轨道上有两列火车A 和B 相距s ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同.要使两车不相撞,求A 车的初速度v 0应满足什么条件?【解析】解法一:(物理分析法)A 、B 车的运动过程(如图所示)利用位移公式、速度公式求解.对A 车有s A =v 0t +21×(-2a )×t 2 v A =v 0+(-2a )×t 对B 车有s B =21at 2,v B =at 两车有s =s A -s B追上时,两车不相撞的临界条件是v A =v B 联立以上各式解得v 0=as 6故要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤as 6解法二:(极值法)利用判别式求解,由解法一可知s A =s +s B ,即v 0t +21×(-2a )×t 2=s +21at 2 整理得3at 2-2v 0t +2s =0这是一个关于时间t 的一元二次方程,当根的判别式Δ=(2v 0)2-4×3a ×2s <0时,t 无实数解,即两车不相撞,所以要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤as 6 解法三:(图象法)利用速度—时间图象求解,先作A 、B 两车的速度—时间图象,其图象如图所示,设经过t 时间两车刚好不相撞,则对A 车有v A =v =v 0-2at对B 车有v B =v =at以上两式联立解得t =av 30 经t 时间两车发生的位移之差,即为原来两车间的距离s ,它可用图中的阴影面积表示,由图象可知 s =21v 0•t =21v 0•a v a v v 63212000=• 所以要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤as 6【思维提升】三种解法中,解法一注重对运动过程的分析,抓住两车间距有极值时速度应相等这一关键条件来求解;解法二中由位移关系得到一元二次方程,然后利用根的判别式来确定方程中各系数间的关系,这也是中学物理中常用的数学方法;解法三通过图象不仅将两物体运动情况直观、形象地表示出来,也可以将位移情况显示,从而快速解答.【拓展2】从地面上以初速度2v 0竖直上抛物体A ,相隔Δt 时间后再以初速度v 0竖直上抛物体B .要使A 、B 在空中相遇,Δt 应满足什么条件?【解析】A 、B 两物体都做竖直上抛运动,由s =v 0t -21gt 2作出它们的s-t 图象,如图所示.显然,两图线的交点表示A 、B 相遇(s A =s B ).由图象可看出Δt 满足关系式g v t g v 004<<2∆时,A 、B 在空中相遇. 3.分析追及、相遇问题的思路【例3】现检测汽车A 的制动性能:以标准速度20 m/s 在平直公路上行驶时,制动后40 s 停下来.若A 在平直公路上以20 m/s 的速度行驶时发现前方180 m 处有一货车B 以6 m/s 的速度同向匀速行驶,司机立即制动,能否发生撞车事故?【错解】设汽车A 制动后40 s 的位移为x 1,货车B 在这段时间内的位移为x 2.据a =tv v 0-得车的加速度a =-0.5 m/s 2 又x 1=v 0t +21at 2得 x 1=20×40 m+21×(-0.5)×402 m =400 m x 2=v 2t =6×40 m=240 m两车位移差为400 m -240 m =160 m因为两车刚开始相距180 m>160 m所以两车不相撞.【错因】这是典型的追及问题.关键是要弄清不相撞的条件.汽车A 与货车B 同速时,两车位移差和初始时刻两车距离关系是判断两车能否相撞的依据.当两车同速时,两车位移差大于初始时刻的距离时,两车相撞;小于、等于时,则不相撞.而错解中的判据条件错误导致错解.【正解】如图,汽车A 以v 0=20 m/s 的初速度做匀减速直线运动经40 s 停下来.据加速度公式可求出a =-0.5 m/s 2.当A 车减为与B 车同速时,是A 车逼近B 车距离最多的时刻,这时若能超过B 车则相撞,反之则不能相撞.据v 2-20v =2ax 可求出A 车减为与B 车同速时的位移x 1=5.02364002202⨯-=-a vv m =364 m此时间t 内B 车的位移为x 2,则t =5.06200-=-a vv s =28 sx 2=v 2t =6×28 m=168 mΔx =364 m -168 m =196 m>180 m所以两车相撞.【思维提升】分析追及问题应把两物体的位置关系图(如解析中图)画好.通过此图理解物理情景.本题也可以借助图象帮助理解,如图所示,阴影区是A 车比B 车多通过的最大距离,这段距离若能大于两车初始时刻的距离则两车必相撞.小于、等于则不相撞.从图中也可以看出A 车速度成为零时,不是A 车比B 车多走距离最大的时刻,因此不能作为临界条件分析.。
高三物理复习学案追及和相遇问题

高三物理一轮复习学案--追击和相遇问题【学习目标】1、进一步理解掌握匀变速直线运动的规律2、掌握追及及相遇问题的特点;能熟练解决追及及相遇问题【自主学习】两物体在同一直线上追及、相遇或避免碰撞问题中的条件是:两物体能否同时到达空间某位置。
因此应分别对两物体研究,列出位移方程,然后利用时间关系、速度关系、位移关系而解出。
追及问题1、追及问题中两者速度大小与两者距离变化的关系。
甲物体追赶前方的乙物体,若甲的速度大于乙的速度,则两者之间的距离 。
若甲的速度小于乙的速度,则两者之间的距离 。
若一段时间内两者速度相等,则两者之间的距离 。
2、追及问题的特征及处理方法:“追及”主要条件是:两个物体在追赶过程中处在同一位置,常见的情形有三种:初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙,一定能追上,追上前有最大距离的条件:两物体速度 ,即v v =乙甲。
⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙,存在一个能否追上的问题。
判断方法是:假定速度相等,从位置关系判断。
①若甲乙速度相等时,甲的位置在乙的后方,则 ,此时两者之间的距离 。
②若甲乙速度相等时,甲的位置在乙的前方,则 。
③若甲乙速度相等时,甲乙处于同一位置,则 ,为临界状态。
解决问题时要注意二者是否同时出发,是否从同一地点出发。
⑶ 匀减速运动的物体追赶同向的匀速运动的物体时,情形跟⑵类似。
3、分析追及问题的注意点:⑴ 要抓住一个条件,两个关系:一个条件是两物体的速度满足的临界条件,如两物体距离最大、最小,恰好追上或恰好追不上等。
两个关系是时间关系和位移关系,通过画草图找两物体的位移关系是解题的突破口。
⑵若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已经停止运动。
⑶仔细审题,充分挖掘题目中的隐含条件,同时注意v t -图象的应用。
二、相遇⑴ 同向运动的两物体的相遇问题即追及问题,分析同上。
⑵ 相向运动的物体,当各自发生的位移绝对值的和等于开始时两物体间的距离时即相遇。
物理-人教版-一轮复习-20版:专题突破 天体运动中的“三大难点”(创新设计).doc
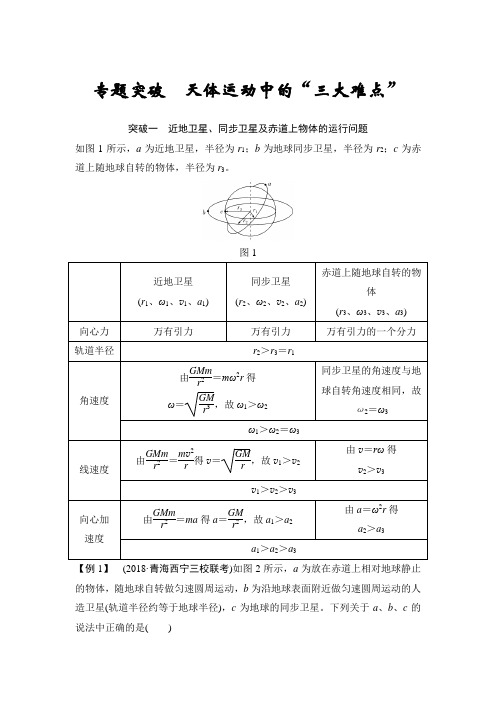
专题突破天体运动中的“三大难点”突破一近地卫星、同步卫星及赤道上物体的运行问题如图1所示,a为近地卫星,半径为r1;b为地球同步卫星,半径为r2;c为赤道上随地球自转的物体,半径为r3。
图1近地卫星(r1、ω1、v1、a1)同步卫星(r2、ω2、v2、a2)赤道上随地球自转的物体(r3、ω3、v3、a3)向心力万有引力万有引力万有引力的一个分力轨道半径r2>r3=r1角速度由GMmr2=mω2r得ω=GMr3,故ω1>ω2同步卫星的角速度与地球自转角速度相同,故ω2=ω3ω1>ω2=ω3线速度由GMmr2=m v2r得v=GMr,故v1>v2由v=rω得v2>v3v1>v2>v3向心加速度由GMmr2=ma得a=GMr2,故a1>a2由a=ω2r得a2>a3a1>a2>a3【例1】(2018·青海西宁三校联考)如图2所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径约等于地球半径),c为地球的同步卫星。
下列关于a、b、c的说法中正确的是()图2A .b 卫星转动线速度大于7.9 km/sB .a 、b 、c 做匀速圆周运动的向心加速度大小关系为a a >a b >a cC .a 、b 、c 做匀速圆周运动的周期关系为T c >T b >T aD .在b 、c 中,b 的速度大解析 b 为沿地球表面附近做匀速圆周运动的人造卫星,根据万有引力定律有G Mm R 2=m v 2R ,解得v =GMR ,代入数据得v =7.9 km/s ,故A 错误;地球赤道上的物体与同步卫星具有相同的角速度,所以ωa =ωc ,根据a =rω2知,c 的向心加速度大于a 的向心加速度,根据a =GM r 2得b 的向心加速度大于c 的向心加速度,即a b >a c >a a ,故B 错误;卫星c 为同步卫星,所以T a =T c ,根据T =2πr 3GM得c 的周期大于b 的周期,即T a =T c >T b ,故C 错误;在b 、c 中,根据v =GM r ,可知b 的速度比c 的速度大,故D 正确。
高三总复习专题追击相遇问题导学案

年级:高三学科:物理班级:学生姓名:制作人:不知名编号:2023-29专题强化课(一)追及、相遇问题
学习目标:理解追及和相遇的临界,并学会应用
预学案
1.追及相遇问题中的一个条件和两个关系
(1)一个条件:即两者速度相等,它往往是物体间能够追上、追不上或两者距离最大、最
小的临界条件,也是分析判断的切入点.
(2)两个关系:即时间关系和位移关系,这两个关系可通过画出运动示意图得到.
2. 追及、相遇问题常见情景
速度大者追速度小者
探究案
探究一:总复习大本12页角度1 典例6
探究二:总复习大本12页角度2 典例7
多维训练:13页1,2
检测案
1. 甲、乙两辆汽车从同一地点同时出发,沿同一方向行驶,它们运动的x
-t图像如图所示。
t
下列判断正确的是()
A.在4 s以前,乙车的速度比甲车的大
B.在4 s以后,乙车的加速度比甲车的大
C.在4 s时,甲、乙两车相距最远
D.在前4 s内,甲、乙两车的平均速度大小相等
2.a、b两物体同时从同一地点开始做匀变速直线运动,二者运动的v-t图象如图所示,下列说法正确的是()
A.a、b两物体运动方向相反
B.a物体的加速度小于b物体的加速度
C.t=1 s时两物体的间距等于t=3 s时两物体的间距
D.t=3 s时,a、b两物体相遇。
高中物理相遇问题解析教案

高中物理相遇问题解析教案
一、教学目标:
1. 理解相遇问题的基本概念和解题方法;
2. 能够独立解决相遇问题,包括两点相遇和三点相遇;
3. 提高学生动手能力和解题能力。
二、教学内容:
1. 相遇问题的概念和基本原理;
2. 两点相遇问题的解题方法;
3. 三点相遇问题的解题方法。
三、教学过程:
1. 引入相遇问题,让学生了解相遇的概念和意义;
2. 讲解两点相遇问题的解题方法,包括相对速度的概念和计算方法;
3. 通过例题练习,巩固学生对两点相遇问题的理解和掌握;
4. 引入三点相遇问题,讲解解题方法和计算步骤;
5. 给学生进行练习,提高解题能力;
6. 结束本节课,总结相遇问题的解题方法和注意事项。
四、教学评价:
1. 根据学生在课堂上的表现和练习成绩,评价其对相遇问题的理解和掌握程度;
2. 针对学生存在的问题,进行及时的辅导和指导;
3. 综合评价学生在本节课的学习情况,为下节课的教学做准备。
五、教学反思:
1. 教学过程中是否存在不足之处,如何改进;
2. 学生对相遇问题的理解和掌握程度是否达到预期目标;
3. 如何提高学生的解题能力和学习兴趣,激发其学习动力。
2024高考物理一轮复习--天体运动专题--卫星的变轨问题、天体追及相遇问题

卫星的变轨问题、天体追及相遇问题一、卫星的变轨、对接问题1.卫星发射及变轨过程概述人造卫星的发射过程要经过多次变轨方可到达预定轨道,如右图所示。
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道 Ⅰ上。
(2)在A 点点火加速,由于速度变大,万有引力不足以提供向心力,卫星做离心运动进入椭圆轨道Ⅰ。
(3)在B 点(远地点)再次点火加速进入圆形轨道Ⅰ。
2.卫星的对接问题(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道(做离心运动)追上高轨道空间站与其完成对接.(2)同一轨道飞船与空间站对接如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度.二、变轨前、后各物理量的比较1.航天器变轨问题的三点注意事项(1)航天器变轨时半径的变化,根据万有引力和所需向心力的大小关系判断;稳定在新圆轨道上的运行速度由v =GM r判断。
(2)航天器在不同轨道上运行时机械能不同,轨道半径越大,机械能越大。
(3)航天器经过不同轨道的相交点时,加速度相等,外轨道的速度大于内轨道的速度。
2.卫星变轨的实质 两类变轨离心运动 近心运动 变轨起因卫星速度突然增大 卫星速度突然减小 受力分析 G Mm r 2<m v 2rG Mm r 2>m v 2r 变轨结果变为椭圆轨道运动或在较大半径圆轨道上运动变为椭圆轨道运动或在较小半径圆轨道上运动 3.变轨过程各物理量分析(1)速度:设卫星在圆轨道Ⅰ和Ⅰ上运行时的速率分别为v 1、v 3,在轨道Ⅰ上过A 点和B 点时速率分别为v A、v B.在A点加速,则v A>v1,在B点加速,则v3>v B,又因v1>v3,故有v A>v1>v3>v B.(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅰ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同.(3)周期:设卫星在Ⅰ、Ⅰ、Ⅰ轨道上的运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律r3T2=k可知T1<T2<T3.(4)机械能:在一个确定的圆(椭圆)轨道上机械能守恒.若卫星在Ⅰ、Ⅰ、Ⅰ轨道的机械能分别为E1、E2、E3,则E1<E2<E3.三、卫星的追及与相遇问题1.相距最近两卫星的运转方向相同,且位于和中心连线的半径上同侧时,两卫星相距最近,从运动关系上,两卫星运动关系应满足(ωA-ωB)t=2nπ(n=1,2,3,…)。
高中物理相遇的问题教案

高中物理相遇的问题教案
教学内容:相遇
教学目标:了解相遇的概念;掌握相遇问题的解题方法;能够应用相遇问题解决实际问题。
教学重点:相遇的基本概念;相遇问题的解题方法。
教学难点:相遇问题的应用。
教学准备:课件、实验器材。
教学过程:
一、导入(5分钟)
通过一个问题引入相遇的概念:两辆小车同时从相距100千米的两地出发,一辆以
60km/h的速度向前行驶,另一辆以40km/h的速度向前行驶,问它们何时相遇?
二、讲解(15分钟)
1. 解释相遇的概念:当两个物体在某一时刻在同一地点相遇时,称它们相遇。
2. 分析相遇问题的解题方法:设第一个物体速度为v1,第二个物体速度为v2,相遇时它
们移动的时间相同,则有v1t = v2t,解方程可得相遇时间。
三、实验展示(10分钟)
利用实验器材展示相遇问题的解决过程,让学生直观地理解相遇的概念和解题方法。
四、练习训练(15分钟)
组织学生进行相遇问题的练习,包括不同速度、不同距离和不同方向的情况,加深对相遇
问题的理解和掌握。
五、巩固拓展(10分钟)
引导学生思考如何应用相遇问题解决实际生活中的问题,如两个人相向而行相遇的问题。
六、作业布置(5分钟)
布置相遇问题的作业,要求学生独立解答并写出解题过程。
七、课堂总结(5分钟)
回顾本节课学习的重点内容,强调相遇问题的重要性和解题方法,激发学生对物理学习的
兴趣。
2021届高考物理沪科版一轮复习教学案:第一章 专题突破 运动图象 追及相遇问题 Word版含解析

姓名,年级:时间:专题突破运动图象追及相遇问题运动图象的理解及应用1.运动学图象主要有x-t图象和v-t图象,运用运动学图象解题可总结为“六看”。
x-t图象v-t图象“一看"轴横轴为时间t,纵轴为位移x横轴为时间t,纵轴为速度v“二看”线倾斜直线表示匀速直线运动倾斜直线表示匀变速直线运动“三看”斜率表示速度表示加速度“四看”面积无实际意义图线和时间轴围成的面积表示位移“五看"纵截距表示初位置表示初速度“六看”特殊点拐点表示从一种运动变为另一种运动,交点表示相遇拐点表示从一种运动变为另一种运动,交点表示速度相等(1)x-t图象、v-t图象都不是物体运动的轨迹,图象中各点的坐标值x、v与t一一对应。
(2)x-t图象、v-t图象的形状由x与t、v与t的函数关系决定。
(3)无论是x-t图象还是v-t图象,所描述的运动情况都是直线运动。
考向1 x-t图象教材引领1。
[人教版必修1·P41·T5]一辆汽车在教练场上沿着平直道路行驶,以x 表示它对于出发点的位移。
图1为汽车在t=0到t=40 s这段时间的x -t图象.通过分析回答以下问题。
汽车行驶的x-t图象图1(1)汽车最远距离出发点多少米?(2)汽车在哪段时间没有行驶?(3)汽车在哪段时间驶离出发点,在哪段时间驶向出发点?答案(1)汽车最远距离出发点30米。
(2)汽车在10~20 s没有行驶。
(3)汽车在0~10 s驶离出发点,在20~40 s驶向出发点。
拓展提升2.(2020·南京开学模拟)如图2所示为一个质点运动的位移x随时间t 变化的图象,由此可知质点在0~4 s内( )图2A.先沿x轴正方向运动,后沿x轴负方向运动B.一直做匀变速运动C.t=2 s时速度一定最小D.速率为5 m/s的时刻有两个解析从图中可知正向位移减小,故质点一直朝着负方向运动,A项错误;图象的斜率表示速度大小,故斜率先增大后减小,说明质点速率先增大后减小,做变速运动,但不能判断是不是做匀变速直线运动,t=2 s 时,斜率最大,速度最大,B、C两项错误;因为斜率先增大后减小,并且平均速度为5 m/s,故速率增大过程中有一时刻速度大小为5 m/s,速率减小过程中有一时刻速度大小为 5 m/s,共有两个时刻速度大小为 5 m/s,D项正确。
2021年高考【物理】一轮复习考点1.7 追及相遇问题(原卷版)

『高考一轮·考点扫描』
『真题剖析·逐一击破』
一轮复习·备战高考
2021 年高考·考点扫描 一轮复习·备战高考
2021 年高考·考点扫描
2021 年一轮考点扫描微专题 专题 1.7 追及相遇问题
目录 目录...................................................................................................................................................................... 1
2.速度大者追速度小者 追及类型 匀减速 追匀速 匀速追 匀加速
匀减速追 匀加速
2021 年高考·考点扫描
设 x0 为开始时两物体间的距离,则应 有下面结论:
①t=t0 以前,后面物体与前面物体间 的距离增大
②t=t0 时,两物体相距最远,为 x0+Δx ③t=t0 以后,后面物体与前面物体间 的距离减小
④一定能追上且只能相遇一次
图象描述
相关结论
设 x0 为开始时两物体间的距离, 开始追及时,后面物体与前面物 体间的距离在减小,当两物体速 度相等时,即 t=t0 时刻:
①若 Δx=x0,则恰能追上,两物 体只能相遇一次,这也是避免相 撞的临界条件
②若 Δx<x0,则不能追上,此时 两物体间距离最小,为 x0-Δx
方法一、地面为参考系, x机
v 舰t
1 2
at 2
,v 飞
v舰
at ,
x舰 v 舰t , x机 x舰 L
方法二、航母为参考系,(v 飞 - v 舰)2 2aL
2021届高考物理一轮复习方略关键能力·题型突破: 1.3 运动图象追及相遇问题

关键能力·题型突破考点一 运动图象的理解及应用x-t图象【典例1】(多选)(2018·全国卷Ⅲ)甲、乙两车在同一平直公路上同向运动,甲做匀加速直线运动,乙做匀速直线运动。
甲、乙两车的位置x随时间t的变化如图所示。
下列说法正确的是( )A.在t1时刻两车速度相等B.从0到t1时间内,两车走过的路程相等C.从t1到t2时间内,两车走过的路程相等D.在t1到t2时间内的某时刻,两车速度相等【通型通法】1.题型特征:x-t图象。
2.思维导引:(1)某点的切线斜率表示该点的速度。
(2)纵坐标之差表示该段时间内的位移。
【解析】选C、D。
由位移—时间图象的意义可知t1时刻两车在x1位置,图线的斜率不同,速度不等,A错;由于甲车起始位置不在原点,从0到t1时间内,两车走过的路程不等,B错;从t1到t2时间内,两车都从x 1位置运动到x 2位置,因此走过的路程相等,C 对;从t 1到t 2时间内甲车图线的斜率先小于后大于乙车,因此在t 1到t 2时间内的某时刻,两车速度相等,D 对。
【多维训练】(2020·泉州模拟)在平直公路上行驶的a 车和b 车,其位移—时间图象分别为图中直线a 和曲线b 。
t=3 s 时,直线a 和曲线b 刚好相切,下列说法正确的是( )A.t=3 s 时,两车具有共同的加速度B.a 车做匀速运动,b 车做加速运动C.在运动过程中,b 车始终没有超过a 车D.在0~3 s 的时间内,a 车的平均速度比b 车的大【解析】选C 。
t=3 s 时,两图线斜率相等,所以两车的速度相等,故A 错误;x-t 图象的斜率表示速度,由图可知,a 车做匀速直线运动,b 车做减速直线运动,故B 错误;由图象可知,b 车的位置始终在a 车的后面,故C 正确;在0~3 s 的时间内,a 车的位移为6m ,b 车的位移为8 m ,由公式=可知,a 车的平均速度小于b 车,v x t 故D 错误。
2021版一轮复习名师导学物理文档:专题突破(四) 天体的相遇问题 Word版含解析

姓名,年级:时间:专题突破(四) 天体的相遇问题对应学生用书p85两卫星在不同轨道绕中心天体在同一平面内做匀速圆周运动,当两星某时相距最近时我们称之为两卫星相遇问题.绕同一中心天体运动的运行天体,由于ω=错误!∝错误!,故在同一轨道上不可能发生相遇,只有在不同轨道上运行的天体才能发生追赶现象,相遇时是指运行天体相距最近的现象.两颗卫星在同一轨道平面内同向绕地球做匀速圆周运动,a卫星的角速度为ωa,b卫星的角速度为ωb,若某时刻两卫星正好同时通过地面同一点正上方,相距最近(如图甲所示).当它们转过的角度之差Δθ=π,即满足ωa Δt-ωbΔt=π时,两卫星第一次相距最远(如图乙所示).当它们转过的角度之差Δθ=2π,即满足ωaΔt-ωbΔt=2π时,两卫星再次相距最近.经过一定的时间,两星又会相距最远和最近.1.两星相距最远的条件:ωaΔt-ωbΔt=(2n+1)π(n=0,1,2,…) 2.两星相距最近的条件:ωaΔt-ωbΔt=2nπ(n=1,2,3…)3.常用结论(1)同方向绕行的两天体转过的角度|θ1-θ2|=2nπ或错误!=n(n=0、1、2、……)时表明两物体相距最近.(2)反方向转动的天体转过的角度|θ1+θ2|=2nπ或错误!=n(n=0、1、2、……)时表明两物体相遇或相距最近.(3)轨道平面不重合时,两天体只有在同一时刻位于中心天体同一侧的同一直线上时发生相遇.1 某行星和地球绕太阳公转的轨道均可视为圆,且绕行方向相同.每过N年,该行星会运行到日地连线的延长线上,如题图所示.该行星与地球的公转半径比为( )A。
错误!错误!B.错误!错误!C.错误!错误!D.错误!错误![解析] 由题意每过N年地球比行星多运动一周,即错误!-错误!=1,T地=1年,再结合开普勒第三定律错误!=C有错误!=错误!=错误!,B正确.[答案]B2 太阳系中某行星运行的轨道半径为R0,周期为T0。
但科学家在长期观测中发现,其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星,则这颗未知行星运动轨道半径为( )A.R=R错误!B.R=R0错误!C.R=R错误!D.R=R0错误![解析] 由题意可知轨道之所以会偏离那是因为受到某颗星体万有引力的作用,相距最近时万有引力最大偏离程度最大.设未知行星的周期为T,则错误!-错误!=1,则T=错误!。
4 追及相遇问题一 2021届高考物理一轮复习教案

第四节追及相遇问题一.复习目标:1.能熟练应用“一个条件,两个关系”来处理追及相遇问题中的常见问题。
2.能描述追及相遇问题中的运动变化过程及速度相等时的关键状态。
3.了解初始条件对所研究问题的影响,体会量变引起质变的哲学思想。
二.复习重难点:1.重点:应用“一个条件,两个关系”来处理追及相遇问题。
2.难点:能抓住速度相等时的关键状态来突破问题。
三.复习方法:讲授法、自主复习法、讨论法、练习法,提问法等。
四.课时安排:1课时五.复习过程:1.追及相遇问题1)两物体同时到达空间的同一位置,物理学中称为相遇。
包括同向运动(追及)中的相遇和相向运动中的相遇。
2)研究追及相遇问题,相比之前研究单个物体的运动而言只不过是在同一时空里同时关注两个物体的运动而已。
从两物体的运动性质来看,在直线运动中最常见的两运动性质的组合是一个物体匀速,而另一个物体匀变速直线运动。
3)处理这类问题的基本方法步骤:a)明确两物体的运动性质及其初始条件b)明确两物体的运动过程,抓住“一个条件,两个关系”来处理问题c)注意实际问题中物体做匀减速运动时,在所研究的时间内物体是否已经停运,即此过程中的运动性质是否发生了变化。
2.例题解析:例1:小汽车从静止开始以a =3m/s2的加速度启动,此时恰有一自行车以v =6m/s的速度从车边匀速驶过。
试求:⑴小汽车从启动到追上自行车之前经过多长时间两者相距最远?最远距离是多少?⑵小汽车经过多长时间追上自行车,此时小汽车的速度是多少?例2:物块A 和物块B 在同一条直线上同向运动,物块B 在物块A 前0x 处时,物块A 正以初速1v ,加速度大小为a 做匀减速直线运动。
而物块B 正以速度0v 做匀速直线运动,且10v v >。
试求:(1)0x 、1v 、0v 、a 满足什么条件物块A 才能追上物块B ?(2)若物块A 不能追上物块B ,则AB 两物块间的最近距离是多少?例3:在平直的公路上甲车经过乙车旁边时,乙车正以v 2=4 m/s 的速度与甲车同向做匀速直线运动,而甲车此时以v 1=10 m/s 的速度开始匀减速刹车,刹车的加速度大小为a =0.5 m/s 2,从甲车刹车开始计时,求:(1)乙车在追上甲车前,两车相距的最大距离。
2021届高三物理一轮复习(匀变速直线运动图像、追及与相遇问题)知识点及教案

匀变速直线运动图像、追及与相遇问题一、本次课知识讲授知识点1:匀变速直线运动的图像问题1.应用运动图像的三点注意(1)无论是x-t图像还是v-t图像都只能描述直线运动。
(2)x-t图像和v-t图像都不表示物体运动的轨迹。
(3)x-t图像和v-t图像的形状由x与t、v与t的函数关系决定。
2.应用运动图像解题“六看”项目x-t图像v-t图像轴横轴为时间t,纵轴为位移x横轴为时间t,纵轴为速度v线倾斜直线表示匀速直线运动倾斜直线表示匀变速直线运动斜率表示速度表示加速度面积无实际意义图线和时间轴围成的面积表示位移纵截距表示初位置表示初速度特殊点拐点表示速度方向变化,交点表示相遇拐点表示加速度方向变化,交点表示速度相同1、匀变速直线运动的图像(一)直线运动的x-t图像(1)意义:反映了直线运动的物体①位移随②时间变化的规律。
(2)图线上某点切线的斜率的意义①斜率的绝对值:表示物体速度的③大小。
②斜率的正负:表示物体速度的④方向。
(3)两种特殊的x-t图像①若x-t图像是一条平行于时间轴的直线,说明物体处于⑤静止状态。
(如图中甲所示)②若x-t图像是一条倾斜的直线,说明物体在做⑥匀速直线运动。
(如图中乙所示)(二)直线运动的v-t图像(1)意义:反映了直线运动的物体⑦速度随⑧时间变化的规律。
(2)图线上某点切线的斜率的意义①斜率的绝对值:表示物体⑨ 加速度 的大小。
②斜率的正负:表示物体⑩ 加速度 的方向。
(3)两种特殊的v -t 图像①匀速直线运动的v -t 图像是与横轴 平行 的直线。
(如图中甲所示) ②匀变速直线运动的v -t 图像是一条倾斜 的直线。
(如图中乙所示)(4)图线与时间轴围成的“面积”的意义①图线与时间轴围成的“面积”表示相应时间内的位移 。
②若此面积在时间轴的上方,表示这段时间内的位移方向为 正方向 ;若此面积在时间轴的下方,表示这段时间内的位移方向为负方向 。
注意 x -t 图像与v -t 图像不是物体的运动轨迹,反映了物体位移或速度随时间变化的规律。
2024高考物理一轮复习第04讲运动图像问题追及相遇问题(讲义)(学生版+解析)

第04讲运动图像问题追及相遇问题目录复习目标网络构建考点一运动图像问题【夯基·必备基础知识梳理】知识点1 v-t图像知识点2 与位移和时间有关的图像知识点3 与v2-v02=2ax有关的图像知识点4 a-t图像【提升·必考题型归纳】考向1 v-t图像考向2 与位移和时间有关的图像考向3 与v2-v02=2ax有关的图像考向4 a-t图像考点二追及相遇问题【夯基·必备基础知识梳理】知识点追击相遇问题的解题思路和技巧【提升·必考题型归纳】考向1 利用图像解决追及相遇问题考向2 一维追及相遇问题考向3 二维相遇问题真题感悟1、明确各种图像的中斜率、面积、截距、拐点等内容的物理含义,并会利用图像处理物理问题。
2、掌握处理追及相遇的方法和技巧,能够利用相应的方法处理实际问题。
考点一运动图像问题知识点1v-t图像知识点2与位移和时间有关的图像知识点3 与ax v v 2202=-有关的图像知识点4 a -t 图像考向1 v -t 图像1.国之重器歼-20完成某次任务后,关闭发动机降落至跑道并打开减速伞,直至速度减为零。
若该机落地时(设为0 t 时刻)具有水平速度0v ,此后始终沿直线运动,经时间0t 停止,其v -t 图像如图所示。
则( )A .P t 时刻,该机的加速度大小一定等于p pv tB .0~0t 时间内,该机发生的位移小于0012v tC .0~0t 时间内,该机受到的阻力逐渐增大D .0~0t 时间内,该机克服阻力做功的功率逐渐减小2.有一种速度叫中国速度,有一种骄傲叫中国高铁。
2022年9月20日,中国中车股份有限公司面向全球发布时速600公里高速磁浮交通系统。
据了解,该磁悬浮列车可以在3.5min 内达到最大速度600km/h 。
假设在某次试运行时起始站到终点站间距离为60km ,加速过程、减速过程都以3.5min 变化600km/h 的加速度变速,请你根据已有数据分析以下试运行方案的v -t 图像,不可能实现的有( )A .B .C .D .考向2 与位移和时间有关的图像3.某质点沿x 轴方向做匀变速直线运动,其位置坐标x 随时间t 变化的关系如图所示,则在0~4s 内,下列说法正确的是( )A .质点的加速度大小为24m/sB .在1s t =时,质点的速度最大C .在0=t 时,质点的速度大小为2m/sD .在0~4s 内,质点的平均速度大小为2.5m/s4.利用函数图像是一种解决物理问题的常用方法。
高中物理天体相遇技巧教案

高中物理天体相遇技巧教案
一、教学内容:
1. 相对速度的概念和计算方法;
2. 天体相遇的条件和计算方法;
3. 天体相遇实例分析。
二、教学目标:
1. 了解相对速度的概念和计算方法;
2. 掌握天体相遇的条件和计算方法;
3. 能够通过实例分析解决天体相遇问题。
三、教学过程:
1. 相对速度的概念和计算方法的讲解:
相对速度是指两个物体相对于彼此的速度。
计算方法为两个速度相减。
如果速度方向相同,则相对速度为两者速度之差;如果速度方向相反,则相对速度为两者速度之和。
2. 天体相遇的条件和计算方法的讲解:
天体相遇的条件为两个天体距离足够近,使得它们在某一时刻处于同一位置。
计算方法为
根据两天体的速度和距离,计算它们相遇的时间。
公式为:时间 = 距离 / 相对速度。
3. 天体相遇实例分析:
通过实例讲解天体相遇的具体计算方法和步骤。
以两个行星相遇为例,分析它们的轨道、
速度和距离,计算它们相遇的时间和位置。
四、教学方法:
1. 理论讲解结合实例分析;
2. 小组讨论和合作学习;
3. 利用多媒体教学工具辅助教学。
五、教学评估:
1. 课堂练习和作业检查;
2. 实例分析和解决问题的能力评估;
3. 学生表现和参与度评价。
六、教学反思:
1. 教学内容是否能够引起学生兴趣和理解;
2. 教学方法和组织是否能够有效提高学生学习效果;
3. 如何进一步提升和完善本次教学。
2021版高考物理一轮复习专题一运动的描述直线运动第4讲运动图象追及和相遇问题学案
2021版高考物理一轮复习专题一运动的描述直线运动第4讲运动图象追及和相遇问题学案一、单项选择题1.(2021年第一次全国大联考)A、B两个物体在同一条直线上做直线运动,它们的at 图象如图K141所示,规定水平向右为正方向.已知在t=0时,两物体的速度均为零,且A在B的左边1.75 m处,则A追上B的时刻是( )图K141A.t=0.5 s B.t=1.5 sC.t=2.5 s D.t=3.5 s2.图K142为物体做直线运动的vt图象.若将该物体的运动过程用st图象表示出来(其中s为物体相对动身点的位移),则图中的四幅图描述正确的是( )图K142A BC D3.(2021年安徽合肥第一中学检测)a、b、c三个物体在同一条直线上运动,三个物体的xt图象如图K143所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法正确的是( )图K143A.a、b两物体都做匀速直线运动,两个物体的速度相同B.a、b两物体都做匀变速直线运动,两个物体的加速度大小相等,方向相反C.在0~5 s内,当t=5 s时,a、b两个物体相距最近D.物体c一定做变速直线运动4.(2021年吉林长春质检)甲、乙两辆汽车从同一地点动身,向同一方向行驶,它们的v t 图象如图K144所示,下列判定正确的是( )图K144A .在t 1时刻前,甲车始终在乙车的前面B .在t 1时刻前,乙车始终在甲车的前面C .在t 1时刻前,乙车的速度始终比甲车增加得快D .在t 1时刻两车第一次相遇5.(2021年湖南岳阳一中检测)光滑的水平面上有一物体在外力作用下做直线运动,物体的加速度随时刻变化的关系如图K145所示.已知t =0时物体的速度为1 m/s ,以现在的速度方向为正方向.下列说法正确的是( )图K145A .0~1 s 内物体做匀加速直线运动B .t =1 s 时物体的速度为3 m/sC .t =1 s 时物体开始反向运动D .t =3 s 时物体离动身点最远二、多项选择题6.甲、乙两车某时刻由同一地点,沿同一方向开始做直线运动,若以该时刻作为计时起点,得到两车的位移时刻图象,即x t 图象如图K146所示,甲图象过O 点的切线与AB 平行,过C 点的切线与OA 平行,则下列说法正确的是( )图K146A .在两车相遇前,t 1时刻两车相距最远B .t 3时刻甲车在乙车的前方C .0~t 2时刻内甲车的瞬时速度始终大于乙车的瞬时速度D .甲车的初速度等于乙车在t 3时刻的速度7.(2021年吉林长春期中)一个物体沿直线运动,从t =0时刻开始,物体的x tt 的图象如图K147所示,图线与纵、横坐标轴的交点分别为0.5和-1,由此可知( )A .物体做匀速直线运动B .物体做匀加速直线运动C .物体的初速度大小为0.5 m/sD .物体的初速度大小为1 m/s图K147 图K1488.(2021年河南南阳第一中学检测)从地面上以初速度v 0竖直上抛一质量为m 的小球,若运动过程中受到的阻力与其速率成正比,小球运动的速率随时刻变化的规律如图K148所示,小球在t 1时刻到达最高点后再落回地面,落地速率为v 1,且落地前小球差不多做匀速运动,已知重力加速度为g ,下列关于小球运动的说法正确的是( )A .t 1时刻小球的加速度为gB .在速度达到v 1之前小球的加速度一直在减小C .小球抛出瞬时的加速度大小为⎝ ⎛⎭⎪⎫1+v 0v 1gD .小球加速下降过程中的平均速度小于v 12三、非选择题9.(2021年辽宁葫芦岛六校大联考)甲、乙两汽车沿同一平直公路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为16 m/s.已知甲车紧急刹车时加速度大小a 1=3 m/s 2,乙车紧急刹车时加速度大小a 2=4 m/s 2,乙车司机的反应时刻为0.5 s(即乙车司机看到甲车开始刹车后0.5 s 才开始刹车).为保证在紧急刹车中两车不相撞,甲、乙两车行驶过程中至少应保持多大距离?10.(2021年湖北重点中学摸底)甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.以动身点为坐标原点,它们在运动过程中的x v 图象(即位置速度图象)如图K149所示(虚线与对应的坐标轴垂直),已知质点甲做初速度为零的匀加速直线运动,加速度大小为a 1;质点乙以某一初速度做匀减速直线运动,加速度大小为a 2,且其速度减为零后保持静止.求:(1)a 1、a 2的大小.(2)开始运动后,两质点通过多长时刻相遇.图K149。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题突破(四)天体的相遇问题
两卫星在不同轨道绕中心天体在同一平面内做匀速圆周运动,当两星某时相距最近时我们称之为两卫星相遇问题.绕同一中心天体运动的运行天体,由于ω=
GM
r 3
∝1
r 3
,故
在同一轨道上不可能发生相遇,只有在不同轨道上运行的天体才能发生追赶现象,相遇时是指运行天体相距最近的现象.
两颗卫星在同一轨道平面内同向绕地球做匀速圆周运动,a 卫星的角速度为ωa ,b 卫星的角速度为ωb ,若某时刻两卫星正好同时通过地面同一点正上方,相距最近(如图甲所示).当它们转过的角度之差Δθ=π,即满足ωa Δt -ωb Δt =π时,两卫星第一次相距最远(如图乙所示).
当它们转过的角度之差Δθ=2π,即满足ωa Δt -ωb Δt =2π时,两卫星再次相距最近.
经过一定的时间,两星又会相距最远和最近.
1.两星相距最远的条件:ωa Δt -ωb Δt =(2n +1)π(n =0,1,2,…) 2.两星相距最近的条件:ωa Δt -ωb Δt =2n π(n =1,2,3…) 3.常用结论
(1)同方向绕行的两天体转过的角度|θ1-θ2|=2n π或⎪⎪⎪⎪
⎪⎪t T 1-t T 2=n (n =0、1、2、……)
时表明两物体相距最近.
(2)反方向转动的天体转过的角度|θ1+θ2|=2n π或⎪
⎪⎪⎪
⎪⎪t
T 1
+t
T
2
=n (n =0、1、2、……)时表明两物体相遇或相距最近.
(3)轨道平面不重合时,两天体只有在同一时刻位于中心天体同一侧的同一直线上时发生相遇.
1 某行星和地球绕太阳公转的轨道均可视为圆,且绕行方向相同.每过N 年,
该行星会运行到日地连线的延长线上,如题图所示.该行星与地球的公转半径比为( )
A .⎝ ⎛⎭
⎪⎫N +1N 2
3
B .⎝ ⎛⎭⎪⎫N N -12
3 C .⎝ ⎛⎭⎪⎫N +1N 3
2 D .⎝ ⎛⎭
⎪⎫N N -13
2 [解析] 由题意每过N 年地球比行星多运动一周,即
N T 地-N
T 行
=1,T 地=1年,再结合开普勒第三定律T 2
R 3=C 有R 行
R 地
=
3
⎝ ⎛⎭
⎪⎫T 行T 地2
=
3
⎝ ⎛⎭
⎪⎫N N -12
,B 正确. [答案] B
2 太阳系中某行星运行的轨道半径为R
0,周期为T 0.但科学家在长期观测中发
现,其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t 0时间发生一次最大的
偏离.天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星,则这颗未知行星运动轨道半径为( )
A .R =R 0
3
⎝ ⎛⎭⎪⎫t 0t 0-T 02
B .R =R 0
t 0t 0-T 0 C .R =R 0
3
⎝ ⎛⎭
⎪⎫t 0-T 0t 02
D .R =R 0
3t 0t 0-T 0
[解析] 由题意可知轨道之所以会偏离那是因为受到某颗星体万有引力的作用,相距最近时万有引力最大偏离程度最大.设未知行星的周期为T ,则t 0T 0-t 0T =1,则T =t 0T 0
t 0-T 0.根据
开普勒第三定律R 3
0T 20=R
3
T
2得R =R 0
3
⎝ ⎛⎭
⎪⎫t 0t 0-T 02
.
[答案] A
3 天文学家发现有一颗类似于地球的宜居行星,经观测得知该行星的自转周
期为T ,半径为R ,该行星的同步卫星A 的圆轨道半径为2R.卫星B 沿半径为2R 的圆轨道在该行星的赤道的正上方运行,其运行方向和该行星的自转方向相同,求:
(1)卫星B 做匀速圆周运动的周期;
(2)卫星A 和卫星B 连续地不能直接通讯的最长时间间隔(信号传输时间可忽略). [审题指导] 不能直接通讯时,是指卫星A 和卫星B 之间有地球阻隔。
假设卫星A 不动, 可以求出不能直接通讯时的卫星B 对应的圆心角,再根据周期和圆心角的关系求解即可.
[解析] (1)对卫星A 和B ,由开普勒第三定律,得(2R )3
T 2=()2R 3
T ′
2
,
得卫星B 的周期为:T′=
24
T. (2)不考虑A 的公转,以A 作为参考系,B 相对于A 的角速度为:ω=ωB -ωA , B 不能连续与A 通讯,有:ωt=2θ,
即()ωB -ωA t =2θ,
而ωB =2πT ′,ωA =2π
T ,
故有 ⎝
⎛⎭
⎪
⎫2πT ′-2πT t =2θ,
又有sin α=R 02R 0=1
2
,
sin β=
R 02R 0
=
22
, 则α=π
6,β=π
4
,
由几何关系知:θ=α+β,故2θ=5π
6
综上,可得t =
54
212⎝⎛
⎭⎫2-42T =512·21
4
⎝ ⎛⎭
⎪
⎫
2-214·T.
,
对于天体追及问题的处理思路:
(1)根据GMm r
2=mrω2
,先判断出谁的角速度大;
(2)两星追上或相距最近时满足两星运行的角度差等于2π的整数倍,相距最远时,两星运行的角度差等于π的奇数倍.
(3)在与地球上物体追及时,要根据地球上物体与同步卫星角速度相同的特点进行判断.)
1.将火星和地球绕太阳的运动近似看成是同一平面内的同方向绕行的匀速圆周运动,
已知火星的轨道半径r 2=2.3×1011 m ,地球的轨道半径为r 1=1.5×1011
m ,根据你所掌握的物理和天文知识,估算出火星与地球相邻两次距离最小的时间间隔约为( )
A .1年
B .2年
C .3年
D .4年
[解析] 已知地球绕太阳的公转周期为T 1=1年,设火星的公转周期为T 2,根据开普勒第三定律r 3
1T 21=r 3
2
T 22
得T 2=T 1
⎝ ⎛⎭
⎪⎫r 2r 13
≈2年,又根据t T 1-t T 2=1,化简得t =T 1T 2T 2-T 1≈2年. [答案] B
2.如图所示,甲、乙两颗卫星绕地球做同向圆周运动,已知甲卫星的周期为N 小时,每过9N 小时,乙卫星都要运动到与甲卫星同居于地球一侧且三者共线的位置上,则甲、乙两颗卫星的线速度之比为( )
A .3
92 B .332 C .
233
D .
239
[解析] 由⎝ ⎛⎭
⎪⎫2πT 1-2πT 29N =2π,T 1=N ,解得:T 2T 1=98.根据开普勒定律,r 2r 1=⎝
⎛
⎭⎪⎫982
3,线速
度v =2πr T ,则v 1v 2=r 1r 2·T 2T 1=⎝ ⎛⎭⎪⎫892
3×98=392
,A 项正确.
[答案] A
3.中国已启动捕捉小行星计划,2034年将摘下第一颗小行星带回地球研究.若小行星被捕捉后将绕地球做匀速圆周运动,运行的轨道与地球的赤道共面,绕行方向与同步卫星相同,且其转动半径是地球同步卫星轨道半径的n 倍(n>1).则地球同步卫星与该小行星连续两次相距最近的时间差为( )
A .n 3
-1n 3天 B .n 3
n 3
-1
天 C .n 天 D .(n -1)天
[解析] 令同步卫星的周期为T =1天,轨道半径为R ,则小行星的轨道半径为nR ,周期为T 行,则据开普勒第三定律有:R 3
T 2=(nR )3
T 2
行,可得小行星的周期T 行=n 3T =n 3
天;令卫星和小行星两次相距最近的时间为t ,则有:⎝ ⎛⎭⎪⎫2πT -2πT 行t =2π,
解得:t =n 3
n 3-1T =n 3
n 3-1天.
[答案] B
4.如图所示,一颗绕地球做匀速圆周运动的卫星,其轨道平面与地球赤道平面重合,离地面的高度等于地球的半径R 0,该卫星不断地向地球发射微波信号.已知地球表面重力加速度为g.
(1)求卫星绕地球做圆周运动的周期T ;
(2)设地球自转周期为T 0,该卫星绕地球转动方向与地球自转方向相同,则在赤道上的任意一点能连续接收到该卫星发射的微波信号的时间是多少?(图中A 1、B 1为开始接收到信号时卫星与接收点的位置关系)
[解析] (1)卫星以半径2R 0绕地球做匀速圆周运动,万有引力提供向心力:GMm
(2R 0)2=
m(2R 0)4π2
T
2,
处于地球表面的物体所受的重力约等于地球对它的万有引力:GMm
R 20=mg ,
所以:T =2π
8R 3
GM
=2π8R 0
g
. (2)设人在B 1位置刚好看见卫星出现在A 1位置,最后在B 2位置刚好看见卫星消失在A 2
位置.OA 1=2OB 1,
有∠A 1OB 1=∠A 2OB 2=π
3
=θ,
设从B 1到B 2时间为t ,显然有:2πT t -2πT 0t =2
3π,
所以:t =TT 0
3(T 0-T )=
2πT 0
8R 0g 3⎝
⎛
⎭
⎪⎫T 0-2π
8R 0g .。
