第四章应力与应变关系PPT课件
合集下载
弹性力学第四章应力应变PPT

2.具有一个弹性对称面的各向异性弹性体
如果物体内每一点都存在这样一个平面,和该面对称的方向 具有相同的弹性性质,则称该平面为物体的弹性对称面。垂 直于弹性对称面的方向称为物体的弹性主方向。 假设yz坐标面为弹性对称面,则x轴为弹性主方向。将x轴绕 动 z 轴转动π 角度,成为新的 Ox'y'z'坐标系。 新旧坐标系之间的转换关系为
等温过程:利用热力学第二定律
x v F x , y v F y , z v F z , x y v x F ,y y z v F y,z x z v F xz
9
统一的形式:
x v x , y v y , z v z , x y v x ,y y z v y,z x z v x z
第四章 应力和应变的关系
在应力分析中,仅从静力学的观点出发,引入了 9个应力分量 ij ,它们满足三个平衡微分(运动方程) 剪应力互等定理,由此得到应力张量对称的结论, 因此独立的应力分量只有六个。在应变分析中,从 物体的几何连续性观点出发,研究物体变形,得到 三个位移分量 u i 和6个独立的应变分量 i j 。这样我们
y z C 4x 1 C 4y 2 C 4z 3 C 4y 4 z C 4x 5 z C 4x 6 y (4-2) x z C 5x 1 C 5y 2 C 5z 3 C 5y 4 z C 5x 5 z C 5x 6 y x y C 6x 1 C 6y 2 C 6z 3 C 6y 4 z C 6x 5 z C 6x 6y
v x z x zC 5x 1 C 5y 2 C 5z 3 C 5y 4 z C 5x 5 z C 5x 6y
2v
xz y
C52
根据偏导数次序可交换原则,可证C25=C52。对于其它的
《材料力学》课件7-4应力与应变间的关系

胡克定律是描述弹性材料的固有性质,它表明应力与应变之间呈线性关系。 弹性模量是表征材料反抗形变的能力,是应力与应变之间的比值。 切变模量是材料抵抗剪切形变的能力,是切应力与切应变之间的比值。
胡克定律
胡克定律是一个简单而重要的材料力学公式,它描述了应力与应变之间的线性关系。
弹性模量与切变模量
弹性模量是一个常用的材料力学参数,它用于衡量材料在受力时的弹性性质。 切变模量是另一个衡量材料性能的参数,它描述了材料抵抗剪切形变的能力。
《材料力学》课件7-4应 力与应变间的关系
本节课将讨论应力与应变之间的关系,以及胡克定律、弹性模量、切变模量、 杨氏模量和泊松比等概念。
应力与应变的定义
应力是单位面积上的力,用于描述物体内部的分子之间的相互作用力。 应变是物体单位长度的发生变化,用于描述物体在受力时的形变程度。
应力与应变之间的关系
杨氏模量
杨氏模量是一个衡量材料刚度的参数,它描于描述材料性质的参数,它衡量了材料在拉伸时的侧向收缩 程度。
剪切模量
剪切模量是一个衡量材料剪切属性的参数,它描述了材料抵抗剪切形变的能力。
胡克定律
胡克定律是一个简单而重要的材料力学公式,它描述了应力与应变之间的线性关系。
弹性模量与切变模量
弹性模量是一个常用的材料力学参数,它用于衡量材料在受力时的弹性性质。 切变模量是另一个衡量材料性能的参数,它描述了材料抵抗剪切形变的能力。
《材料力学》课件7-4应 力与应变间的关系
本节课将讨论应力与应变之间的关系,以及胡克定律、弹性模量、切变模量、 杨氏模量和泊松比等概念。
应力与应变的定义
应力是单位面积上的力,用于描述物体内部的分子之间的相互作用力。 应变是物体单位长度的发生变化,用于描述物体在受力时的形变程度。
应力与应变之间的关系
杨氏模量
杨氏模量是一个衡量材料刚度的参数,它描于描述材料性质的参数,它衡量了材料在拉伸时的侧向收缩 程度。
剪切模量
剪切模量是一个衡量材料剪切属性的参数,它描述了材料抵抗剪切形变的能力。
《应力与应变》课件

《应力与应变》PPT课件
目录
CONTENTS
• 应力概述 • 应变概述 • 应力与应变的关系 • 应力与应变的应用 • 实验与演示 • 总结与展望
01 应力概述
CHAPTER
定义与概念
定义
应力定义为物体内部单位面积上 所承受的力,用于描述物体受力 状态。
概念
应力是物体受力时内部各部分之 间的相互作用,是物体抵抗变形 和破坏的内在能力。
压缩实验
总结词
通过观察物体在压缩过程中的形变,了解应 力和应变的基本性质。
详细描述
压缩实验是应力与应变研究中另一种重要的 实验方法。在实验中,我们将物体的一端固 定,另一端施加逐渐增大的压力,使物体发 生压缩形变。通过测量压缩量,我们可以计 算出物体的应力和应变。通过观察和记录实 验数据,学生可以了解应力和应变的基本性
应力分类
按作用方式
可分为正应力和剪应力。正应力表示 垂直于受力面的力,剪应力表示与受 力面平行且垂直于切线方向的力。
按作用效果
可分为拉应力和压应力。拉应力表示 使物体拉伸的力,压应力表示使物体 压缩的力。
应力单位与表示方法
单位
应力的单位是帕斯卡(Pa),国际单位制中的基本单位。
表示方法
应力的表示方法通常采用符号“σ”或“σxx”(xx表示方向),例如正应力的 表示符号为σ或σxx,剪应力的表示符号为τ或τxy(xy表示剪切方向)。
进步。
谢谢
THANKS
压缩试验
测定材料的抗压强度、弹性模量等指 标,了解材料在受压状态下的性能表 现。
有限元分析
模型建立
根据实际结构或系统建立有限元 模型,将复杂结构离散化为有限
个单元。
加载与约束
目录
CONTENTS
• 应力概述 • 应变概述 • 应力与应变的关系 • 应力与应变的应用 • 实验与演示 • 总结与展望
01 应力概述
CHAPTER
定义与概念
定义
应力定义为物体内部单位面积上 所承受的力,用于描述物体受力 状态。
概念
应力是物体受力时内部各部分之 间的相互作用,是物体抵抗变形 和破坏的内在能力。
压缩实验
总结词
通过观察物体在压缩过程中的形变,了解应 力和应变的基本性质。
详细描述
压缩实验是应力与应变研究中另一种重要的 实验方法。在实验中,我们将物体的一端固 定,另一端施加逐渐增大的压力,使物体发 生压缩形变。通过测量压缩量,我们可以计 算出物体的应力和应变。通过观察和记录实 验数据,学生可以了解应力和应变的基本性
应力分类
按作用方式
可分为正应力和剪应力。正应力表示 垂直于受力面的力,剪应力表示与受 力面平行且垂直于切线方向的力。
按作用效果
可分为拉应力和压应力。拉应力表示 使物体拉伸的力,压应力表示使物体 压缩的力。
应力单位与表示方法
单位
应力的单位是帕斯卡(Pa),国际单位制中的基本单位。
表示方法
应力的表示方法通常采用符号“σ”或“σxx”(xx表示方向),例如正应力的 表示符号为σ或σxx,剪应力的表示符号为τ或τxy(xy表示剪切方向)。
进步。
谢谢
THANKS
压缩试验
测定材料的抗压强度、弹性模量等指 标,了解材料在受压状态下的性能表 现。
有限元分析
模型建立
根据实际结构或系统建立有限元 模型,将复杂结构离散化为有限
个单元。
加载与约束
应力应变概念PPT课件
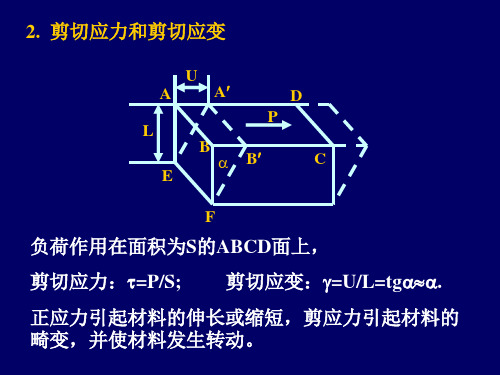
当长方体伸长时,横向收缩:
y=-c/c
z= - b/b
横向变形系数(泊松比):=| y / x| =| z / x |
则
y =- x= - x/E z= - x/E
如果长方体在x y z的正应力作用下,虎克定律表 示为:
x=x/E- y/E - z/E= [x- (y+ z )] /E y=y/E- x/E - y/E= [y- (x+ z )] /E z=z/E- x/E - y/E= [z- (x+ y )] /E
层状硅酸盐
黑云母K(Mg,Fe)3(AlSi3O10)(OH)2 C11=C22=1.9 C33=0.5 白云母KAl2(AlSi3O10 )(OH)2 C11=C22=1.8 C33=0.6 金云母KMg3(AlSi3O10)(OH)2 C11=C22=1.8 C33=0.5 ×1012达因/厘米2
对在电子仪器中的所谓延迟线和标准频率器件十分重要, 因为它们寻求零温度系数材料。
温度补偿材料:一种异常的弹性性质材料(Tc是正 的),补偿一般材料的负Tc值.且压电偶合因子大。
MgO
Tc11=-2.3
SrTiO3 Tc11=-2.6
-SiO2 Tc11=-0.5
Tc44=-1.6
其中:Tc×10-4/oC
2. 应变
(u/y)dy y
(v/y)dy
B
B
dy
yx
C
C
xy
A
(v/x)dx
0
A
x
dx
(u/x)dx
XY面上的剪应变
已知:O点沿x,y,z方向的位移分量分别为u,v,w
(1)正应变
应变为:u/x , 用偏微分表示 : u/ x 在O点 处沿x方向的正应变 是: xx = u/x 同理: yy= v/y
应力与应变之间的关系_图文_图文

例7-5 已知一受力构件自由表面上某点处的
两主应变值为1=240×10-6,3=–160×10-6。 材料的弹性模量E =210GPa,泊松比 =0.3。 求该点处的主应力值数,并求另一应变2的
数值和方向。
解:因主应力和主应变相对应,则由题意可得:
即为平面应力状态,有
联立两式可解得:
主应变2为: 其方向必与1和3垂直,沿构件表面的法线方向。
负面上切应力矢与坐标轴负向一致时,切应力为 正,反之为负。
对应的六个应变分量,
正负号规定:正应变分量同前,拉为正、压为 负;切应变分量以使直角减小为正,反之为负。
对各向同性材料,在线弹性、小变形条件下, 正应力只引起线应变,切应力只引起切应变,应力 分量和应变分量的关系可由叠加原理求得:
三个正应力分量单独作用时,x方向的线应变为:
应力与应变之间的关系_图文_图文.ppt
3)空间应力状态:
sy
dy
sx txy
tdxzxsttzyxtxyttsyzzzxtxyyttzzyyxstzxtdzxyzsx
对图示空间应力状态: 六个应力分量,
正负号规定:正应力分量同前,拉为正、压
为负;切应力分量重新规定,正面(外法线与坐
标轴指向一致)上切应力矢与坐标轴正向一致或
则可得: 同理可得: 对切应力分量与切应变的关系,有:
上述六个关系式即为空间应力状态下,线弹性 和小变形条件下各向同性材料的广义胡克定律。
对平面应力状态:设sz=0,txz=0,tyz=0,有:
若用主应力和主应变来表示广义胡克定律,有:
二向应力状态:
设
有
可见,即使s3 =0,但3 0
而且各向同性材料有
§10-5 广义胡克定律
《材料力学》课件7-4应力与应变间的关系

各向同性材料的体应变
体应变:单位体积的体积变化。
y 2
V a1 1 1 a2 1 2 a3 1 3
z 3
a1
a2
a3
x 1
1 2 3
a2 a2 2
1 2 1 2 3 E
平面纯剪状态 V V 小变形条件下,切应力不引 a1 1 1 a2 1 2 a3 1 3 a1a2 a3 a1a2 a3 1 1 2 3 a1a2 a3 0 起各向同性材料的体积改变 0 V 1 3 22a a1a aa a 3
20MPa
max 20MPa
min 20MPa
20MPa
1 40MPa
max
2 20MPa
1 3
2
3 20MPa
40 20 30MPa 2
2001年长安大学
一受扭圆轴,直径d=20mm,圆轴的材料为 钢,E=200GPa,ν=0.3.现测得圆轴表面上与轴线成450方 向的应变为ε=5.2×10-4,试求圆轴所承受的扭矩.
A. 不变 B. 增大 C. 减小 D. 无法判定
1 x x y z E
z
y
εx仅与正应力有关,而与切应力无关。 所以当切应力增大时,线应变不变。
x
2000年西安建筑科技大学
图示为某点的应力状态,其最大切应力 30 τmax=_____MPa.
40MPa
E
+
1
2
E
+
1
3
E
1 1 1 2 3 E
弹性力学 第四章应力和应变的关系

vI t
x
x
t
y
y
t
z
z
t
yz
yz
t
xz
xz
t
xy
xy
t
若固定x,y,z的值,则得在dt时间内vI 的增量为,即在上式两边乘以dt
dvI xd x yd y zd z yzd yz xz d xz xyd xy
由于内能密度 vI 是状态的单值函数,dvI 必须是全微分,因此
所以
v
1 2
(
x
x
y y
zz
xy xy
xz xz
zy zy )
张量表示
v
1 2
ij
ij
弹性体应变能 V v dV V
§4-3 各向异性弹性体
(一)极端各向异性弹性体
理论具有36个弹性常数
x c11 x c12 y c13 z c14 xy c15 yz c16 zx y c21 x c22 y c23 z c24 xy c25 yz c26 zx
的值,根据无初始应力假设,( f1)0为0。均匀材料,函数 f1
对应变的一阶偏导数为常数。这是因为对物体内各点来说,
承受相同的应力,必产生相同的应变;反之,物体内各点
有相同的应变,必承受同样的应力。
经过上面的处理后,小变形情况就可简化为
广义胡克定律
x C11 x C12 y C13 z C14 xy C15 yz C16 xz y C21 x C22 y C23 z C24 xy C25 yz C26 xz z C31 x C32 y C33 z C34 xy C35 yz C36 xz xy C41 x C42 y C43 z C44 xy C45 yz C46 xz yz C51 x C52 y C53 z C54 xy C55 yz C56 xz xz C61 x C62 y C63 z C64 xy C65 yz C66 xz
工程弹塑性力学课件:第四章应力与应变的关系(肖)

1
弹性力学的基本方程
一、平衡方程 应力分量满足平衡方程:
x yx zx X 0
x y z
xy y zy Y 0
(1.67)
x y z
xz yz z Z 0
x y z
ij, j Fi 0
二、几何方程
x
u x
y
v y
z
w z
xy
u y
v x
yz
v z
xy
120
1 4
x
+
3 4
y
3 4
xy
x y
190 10-6 130 10-6
xy 577 10-6
1,2
x
y
2
( x - y
2
)2 +( xy
2
)2 =30 10-6
330 10-6
1=360 10-6,2 =-300 10-6
2
0
=
arctan(
xy x -
y
)
61。
0
0
30.5。 120.5。
(1.82)
应变与位移的关系→本构关系
材料力学中: x
E x
x
1 E
x
y
z
1 E
x
广义虎克定律: ①正应力→正应变,与剪应变无关
②剪应力→剪应变,与正应变无关
例:贴三角形应变花。
0 =190 10-6,60 =200 10-6,120 =300 10-6, 材料常数:E=206.8109 N / m2, 0.3。
2 y
z 2
2 z
y2
2 yz
yz
0
2 z
x2
弹性力学的基本方程
一、平衡方程 应力分量满足平衡方程:
x yx zx X 0
x y z
xy y zy Y 0
(1.67)
x y z
xz yz z Z 0
x y z
ij, j Fi 0
二、几何方程
x
u x
y
v y
z
w z
xy
u y
v x
yz
v z
xy
120
1 4
x
+
3 4
y
3 4
xy
x y
190 10-6 130 10-6
xy 577 10-6
1,2
x
y
2
( x - y
2
)2 +( xy
2
)2 =30 10-6
330 10-6
1=360 10-6,2 =-300 10-6
2
0
=
arctan(
xy x -
y
)
61。
0
0
30.5。 120.5。
(1.82)
应变与位移的关系→本构关系
材料力学中: x
E x
x
1 E
x
y
z
1 E
x
广义虎克定律: ①正应力→正应变,与剪应变无关
②剪应力→剪应变,与正应变无关
例:贴三角形应变花。
0 =190 10-6,60 =200 10-6,120 =300 10-6, 材料常数:E=206.8109 N / m2, 0.3。
2 y
z 2
2 z
y2
2 yz
yz
0
2 z
x2
《应力与应变》PPT课件

2
e
l1
l0
l0
8 5 0.6 5
2021/3/26
2
l1 l0
(1 e)2
构造地质学—郝建民主讲
11
线 应 变 实 例
2021/3/26
构造地质学—郝建民主讲
12
线应变计算的地质实例
箭石原来长度(l0)82mm 拉长箭石长度( l1)185mm e=1.25 伸长率125%
λ=(1+e)2=5.06
2021/3/26
构造地质学—郝建民主讲
22
伸展盆地的两种动 力学模型
a. 纯剪切模型 (Mckenzie模型);
b. 简单剪切模型 (Wernicke模型)
纯剪盆地从形态上看是对称的,下地壳和上地幔中没有剪切 滑脱面。而简单剪切伸展模式则以一条穿透上地幔或下地壳 的滑脱面为特征,盆地的构造形态不对称,软流圈物质的上 涌不像纯剪模式那样位于盆地的正下方,而是偏移到了盆地 的一侧。
非旋转变形又称无旋转变形, 1和3质点线方向在变形前后
保持不变。如果体积不变而且2=0,则称为纯剪应变。
旋转应变的1和 3质点线方向将 A 会改变。
C 56 20'
O
简单剪
切a
c 33 40'
(单剪)
40
O'
B
最典型的情况是
D
b
d
c
单剪应变,是由 物质中质点沿着 彼此平行的方向
刚体旋转= =22 40'
A
O' 纯剪
b
相对滑动而成。
单剪与纯剪应变
2021/3/26
构造地质学—郝建民主讲
21
2
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)0z
( f1
yz
)0yz
(f1zx)0zx
(f1xy)0xy
-
12
广义虎克定律 展开系数表示函数在其对应变分量一阶导数在应变分 量等于零时的值,而 实( f 1 际) 0 上代表初应力,由于无初应 力假设 等于( f 1零) 0 。 其它分量类推,那么在小变形情况下应力与应变关系 式简化为:
x C11x C12 y C13z C14 yz C15 zx C16 xy
-
15
各向同性体的广义虎克定律
如果物体是各向同性的,则在任何方向上弹性性质相 同,因此在各个方向上应力与应变关系相同。
C15 C25
C16 C26
x y
z
yz
CC3411
C32 C42
C33 C43
C34 C44
C35 C45
C36 C46
z yz
zx
C51
C52
C53
C54
C55
C56
zx
xy C61 C62 C63 C64 C65 C66 xy
(4-4)
可以证明对各向异性体,由于应变能存在,也只有 21个弹性常数独立,对各向同性体,只有两个弹性常 数独立。
地球物理场论 I
海洋地球科学学院 地球探测信息与技术系
宋鹏
-
1
第四章 应力与应变关系
4.1 广义虎克定律 4.2 工程弹性常数及相互间关系式 4.3 简单和复杂应力状态下弹性应变能和应变能密度 4.4 能量密度与能通量密度
-
2
应力与应变关系
在前几章中,从静力学、动力学和几何学的观点分 别研究了应力和应变。前面知道联结应力分量(6个)与 位移分量(3个)有3个方程,联结应变分量(6个)与位移 分量(3个)有6个方程,15个未知数9个方程,还需要6 个方程才能求解弹性动力学问题。
图4-1 某材料应力与应变关系曲线
-
6
广义虎克定律--应力应变曲线
(一)弹性阶段——OB段
在此段内,撤去外力时 (
,为即直变线形,完 说全 明消 当失。通时常,为
A,,称将成 为) 沿B线弹O性(性B关,线极系恢限) 即复。回而原OA点段O
E(4-1)
-
7
广义虎克定律--应力应变曲线
其中E是与材料有关的弹性常数,通常称为弹性模
(二)屈服阶段——BC段
当 后,B出现应变增加很快,而应力在很小范围
内波动的阶段。这种应力变化不大,而应变显著增加的
现象称屈服或流动,屈服阶段的最低应力 称屈 服S 极限
。 (三)强化阶段——CD段
过了屈服阶段以后,材料又恢复了抵抗变形的能力,
要化使 ,它强增化加 阶变 段形 中必 的须最增高加点拉D所力对,应这的种现称象D为称强为度材极料限的。强
-
9
广义虎克定律--应力应变曲线 (四)局部变形阶段——DG段
过了D点以后,在局部范围内,横截面急剧缩小,继 续伸长需要拉力相应减小,到G点处,试件被拉断。
在纯剪应力作用时,与xy 也x y成正比, xy,比G例xy系
数G称剪切弹性模量
-
10
广义虎克定律 在空间应力状态下,描述一点应力状态需6个应力分量 ,与之相应的应变状态也要用6个应变分量来表示。它 们之间存在一定关系。假设应力是应变的函数,分量形 式表示为:
-
3
X x
yx y
zx z
X
2u
t2
xy x
y y
zy z
Y
2v t2
xz x
yz y
z z
Z
2w t2
平衡运动微分方程
-
应力与应变关系
x
u x
y
v y
z
w z
xy
v x
u y
yz
w y
v
z
zx
u z
w x
几何方程 4
应力与应变关系
上式作为虎克定律在复杂受力情况下的一个推广, 因此称为广义虎克定律。式中系数Cm n(m ,n1,是2, ,6) 物质弹性性质的表征,由均匀性假设可知这些弹性性 质与点的位置无关,称为弹性常数。上式也可以写成 矩阵形式
-
14
广义虎克定律
x
y
C11 C21
C12 C22
C13 C23
C14 C24
要解决弹性动力学问题,还要研究应力与应变的关
系,这种关系通常被称为物理方程或本构方程。即还
需要补充应力与应变关系(6个方程)。应力与应变的关
系反映物质固有的物理特性,应力分量与应变分量的
一一对应关系,在线性弹性范围内,便是广义虎克定
律。
-
5
广义虎克定律--应力应变曲线
在常温、静载情况下,由材料拉伸试件可得到 应力与应变关系曲线。不同材料得到的应力应变曲 线不同。图4-1给出低碳钢应力应变曲线。从图中可 看出,该曲线大致可分为四个阶段:
)
x y f 6 ( x , y , z , y z , zx , x y )
-
(4-3a)
11
广义虎克定律
在小变形条件下,应变分量都是微量,(a)式在应变 为零附近做Taylor展开后,忽略2阶以上的微量,例如
对 , 可x 得:
x
(f1)0
(f1x)0x
(f1y)0y
(f1
z
量,E的量纲与 相 同,一般用GN/m2。 则A 称为比
例极限,上式即为虎克定律的数学表达式。
A点与B点非常接近,工程上弹性极限 B和比例极限 并A 不严格区分。这种情况下,横向应变 与' 轴向应
变 绝 对值之比一般是常数,即
'
(4-2)
称为横向变形系数或泊松比。
-
8
广义虎克定律--应力应变曲线
x f1 ( x , y , z , yz , zx , xy )
y
f2
(
x
,
y
,
z
,
yz
,
zx
,
xy
)
z f 3 ( x , y , z , y z , zx , x y )
yz
f4
(
x
,
y
,
z
,
yy
)
zx
f5
(
x
,
y
,
z
,
yz
,
zx
,
xy
C54 yz
C55 zx
C56 xy
xy C61x C62 y C63z C64 yz C65 zx C66 xy
-
13
广义虎克定律
上式表明在弹性体内,任一点的每一应力分量都是 6个应变分量的线性函数,反之亦然。简单拉伸实验已 指出在弹性极限以内,应力与应变呈线性关系,与上 式一致。
y
C21x
C22 y
C23z
C24 yz
C25 zx
C26 xy
z yz
C31x C41x
C32 y C42 y
C33z C43z
C34 yz C44 yz
C35 zx C36 xy C45 zx C46 xy
(4-3b)
zx
C51x
C52 y
C53z
