第12讲_休克尔分子轨道归纳.ppt
合集下载
(整理)休克尔轨道法的分子图.
休克尔轨道法的分子图一、化学家休克尔E.Erich Armand Arthur Josephckel (1896～)联邦德国物理化学家。
1896年8月9日生于柏林夏洛腾堡。
1914年入格丁根大学攻读物理。
曾中断学习，在格丁根大学应用力学研究所研究空气动力学。
1918年重新攻读数学和物理，1921年在P.德拜的指导下获博士学位。
他在格丁根大学工作两年，曾任物理学家M.玻恩的助手。
1922年在苏黎世工业大学再度与德拜合作，任讲师。
1930年在斯图加特工业大学任教。
1937年任马尔堡大学理论物理学教授。
休克尔主要从事结构化学和电化学方面的研究。
他1923年和德拜一起提出强电解质溶液理论，推导出强电解质当量电导的数学表达式。
1931年提出了一种分子轨道的近似计算法即休克尔分子轨道法(HMO 法)，主要用于π电子体系。
他在30年代还对芳香烃的电子特性在理论上作出了解释，并总结出：环状共轭多烯化合物中π电子数符合4n+2（n为1，2或3）者，具有芳香性。
二、休克尔分子轨道法(HMO法)的来源分子轨道理论在处理分子时，并不引进明显的价键结构的概念。
它强调分子的整体性，认为分子中的原子是按一定的空间配置排列起来的，然后电子逐个加到由原子实和其余电子组成的“有效”势场中，构成了分子。
并将分子中单个电子的状态函数称为分子轨道，用波函数ψ(x，y，z)来描述。
每个分子轨道ψi都有一个确定的能值Ei 与之相对应，Ei近似地等于处在这轨道上的电子的电离能的负值，当有一个电子进占ψi 分子轨道时，分子就获得Ei的能量。
分子轨道是按能量高低依次排列的。
参与组合的原子轨道上的电子则将按能量最低原理、鲍里不相容原理和洪特规则进占分子轨道。
根据电子在分子轨道上的分布情况，可以计算分子的总能量。
π键实际上是持有电子的围绕参与组合的原子实的π分子轨道。
1931年，休克尔提出了一种计算π分子轨道及其能值的简单方法，称为休克尔分子轨道法(即HMO 法)。
《休克尔分子轨道法》课件
休克尔分子轨道法的基本原理
分子轨道的构建方式
通过线性组合原子轨道的方式来构建分子轨道。
轨道能级的计算方法
使用哈密顿矩阵的对角化求解方法来计算轨道能级。
分子轨道系数的含义和求解方法
分子轨道系数表示原子轨道在分子轨道中的贡献程度，可以通过求解线性方程组得到。
应用实例
氢分子的构建和计算
通过休克尔分子轨道法可以计 算出氢分子的轨道能级和化学 键的性质。
ห้องสมุดไป่ตู้
苯分子的构建和计算
休克尔分子轨道法可以帮助我 们了解苯分子的共轭体系和芳 香性。
其他分子的构建和计算
休克尔分子轨道法适用于多种 有机分子和配合物的计算和预 测。
休克尔分子轨道法的局限性
1 大分子的计算难度
休克尔分子轨道法在计算大分子时面临计算复杂度增加的挑战。
2 电子相关性的考虑
在处理强关联体系时，休克尔分子轨道法需要考虑电子相关性的影响。
《休克尔分子轨道法》 PPT课件
欢迎来到《休克尔分子轨道法》PPT课件！本课件将详细介绍休克尔分子轨 道法的原理、应用实例、局限性以及未来的发展方向。让我们一起深入了解 这一重要的化学理论。
引言
休克尔分子轨道法是分子轨道理论的重要突破，本节将介绍分子轨道理论的 发展历程以及休克尔分子轨道法的背景和意义。
3 其他局限性
休克尔分子轨道法在处理某些特殊情况时存在一定的限制和不足。
休克尔分子轨道法的发展方向
1
各种扩展方法的简介
介绍了一些休克尔分子轨道法的扩展方法，如密度泛函理论和多配置自洽场方法。
2
对未来应用的展望
展望了休克尔分子轨道法在材料科学、药物设计等领域的未来应用和发展前景。
休克尔轨道法的分子图
休克尔轨道法的分子图一、化学家休克尔E.Erich Armand Arthur Josephckel (1896～)联邦德国物理化学家。
1896年8月9日生于柏林夏洛腾堡。
1914年入格丁根大学攻读物理。
曾中断学习，在格丁根大学应用力学研究所研究空气动力学。
1918年重新攻读数学和物理，1921年在P.德拜的指导下获博士学位。
他在格丁根大学工作两年，曾任物理学家M.玻恩的助手。
1922年在苏黎世工业大学再度与德拜合作，任讲师。
1930年在斯图加特工业大学任教。
1937年任马尔堡大学理论物理学教授。
休克尔主要从事结构化学和电化学方面的研究。
他1923年和德拜一起提出强电解质溶液理论，推导出强电解质当量电导的数学表达式。
1931年提出了一种分子轨道的近似计算法即休克尔分子轨道法(HMO 法)，主要用于π电子体系。
他在30年代还对芳香烃的电子特性在理论上作出了解释，并总结出：环状共轭多烯化合物中π电子数符合4n+2（n为1，2或3）者，具有芳香性。
二、休克尔分子轨道法(HMO法)的来源分子轨道理论在处理分子时，并不引进明显的价键结构的概念。
它强调分子的整体性，认为分子中的原子是按一定的空间配置排列起来的，然后电子逐个加到由原子实和其余电子组成的“有效”势场中，构成了分子。
并将分子中单个电子的状态函数称为分子轨道，用波函数ψ(x，y，z)来描述。
每个分子轨道ψi都有一个确定的能值Ei 与之相对应，Ei近似地等于处在这轨道上的电子的电离能的负值，当有一个电子进占ψi 分子轨道时，分子就获得Ei的能量。
分子轨道是按能量高低依次排列的。
参与组合的原子轨道上的电子则将按能量最低原理、鲍里不相容原理和洪特规则进占分子轨道。
根据电子在分子轨道上的分布情况，可以计算分子的总能量。
π键实际上是持有电子的围绕参与组合的原子实的π分子轨道。
1931年，休克尔提出了一种计算π分子轨道及其能值的简单方法，称为休克尔分子轨道法(即HMO 法)。
第4章 休克尔(Hückel) 分子轨道理论PPT课件
2. 线性变分法
变分法中变分函数的选取广泛采用线性
变分法，变分函数 采用k个线性无关的函
数 1,2,,k 的线性组合, 即:
k
c11c22ckkcii i1
应用于分子体系，1,2,,k常取原子轨道 .
01.08.2020
1122
量子化学 第四章
显然，上述做法体现了原子轨道线性组合构成分 子轨道的思想，即：LCAO-MO。这个思想最早是 由Roothaan提出的。
1,2,,k， 常称为基组，显然，基组越
大，需要确定的系数越多，计算工作量越大，但 同时计算精度越高。
01.08.2020
1133
根据变分原理，
量子化学 第四章
01.08.2020
15
1144
量子化学 第四章
求一套系数（c1 , c2 ,…, ck）使得波函数Ψ下
的能量越接近于E0 越好, 即其值越低越好。 则：
1177
目录
量子化学 第四章
4.2 休克尔分子轨道法
Hückel 将 分 子 轨 道 理 论 应 用 于 共 轭 分 子 ， 形 成 了 Hückel 分 子 轨 道 理 论 ， 简 称 为 HMO (Hückel Molecular Obital)。
HMO理论主要思想是- 分离和 电子近似。
1. - 分离 、 电子分开处理, 针对性地研究 电子。
01.08.2020
33
量子化学 第四章
4.1 变分法
设体系哈密顿算符 的本征值按大小次序排列为： E0≤E1≤E2≤…Ei≤…
等号表示有简并态情形。
设属于每个本征值的本征函数分别为： 0 , 1 , 2 , …,i ,…
则存在 的系列本征方程：
休克尔分子轨道法ppt课件
评估污染物行为
在环境化学领域，休克尔分子轨道法可用于评估污染物的电子结构和性质，从而预测其在环境中的行为和归趋。
04
休克尔分子轨道法的局限性
和挑战
计算复杂度问题
计算资源需求高
由于休克尔分子轨道法涉及大量的矩 阵运算和迭代求解，因此需要高性能 的计算资源，如高性能计算机和大内 存。
计算时间长
并行化难度大
通过基组校正和基组完备性的研究， 可以进一步提高基组的描述能力，从 而得到更准确的结果。
06
结论
休克尔分子轨道法的价值和意义
理论价值
休克尔分子轨道法是量子化学中的重要理论工具，它为理解分子结构和性质提供了基础框 架。通过该方法，我们可以深入探究分子的电子结构和化学键的本质。
实际应用
休克尔分子轨道法在化学、材料科学、生物学等领域有着广泛的应用。它为新材料的合成 、药物设计、环境化学等领域提供了理论支持，有助于我们更好地理解物质性质和行为。
适用于具有共轭结构的分子，如烯烃、炔烃、芳香烃等， 可以用于预测分子的稳定性、反应活性以及电子光谱等性 质。
02
休克尔分子轨道法的基本原
理
分子轨道和电子云
分子轨道
描述分子中电子运动的波函数。
电子云
描述电子在分子中的概率分布。
分子中的电子排布
根据泡利不相容原理，每个分子 轨道最多只能填充两个自旋方向
促进科学发展
休克尔分子轨道法的发展推动了相关学科的进步，促进了化学与其他学科的交叉融合，为 科学技术的整体发展做出了贡献。
对未来研究和应用的建议
深入研究
技术革新
进一步深化对休克尔分子轨道法理论的研 究，探索其在更广泛领域的应用，如生物 大分子的结构和性质研究。
在环境化学领域，休克尔分子轨道法可用于评估污染物的电子结构和性质，从而预测其在环境中的行为和归趋。
04
休克尔分子轨道法的局限性
和挑战
计算复杂度问题
计算资源需求高
由于休克尔分子轨道法涉及大量的矩 阵运算和迭代求解，因此需要高性能 的计算资源，如高性能计算机和大内 存。
计算时间长
并行化难度大
通过基组校正和基组完备性的研究， 可以进一步提高基组的描述能力，从 而得到更准确的结果。
06
结论
休克尔分子轨道法的价值和意义
理论价值
休克尔分子轨道法是量子化学中的重要理论工具，它为理解分子结构和性质提供了基础框 架。通过该方法，我们可以深入探究分子的电子结构和化学键的本质。
实际应用
休克尔分子轨道法在化学、材料科学、生物学等领域有着广泛的应用。它为新材料的合成 、药物设计、环境化学等领域提供了理论支持，有助于我们更好地理解物质性质和行为。
适用于具有共轭结构的分子，如烯烃、炔烃、芳香烃等， 可以用于预测分子的稳定性、反应活性以及电子光谱等性 质。
02
休克尔分子轨道法的基本原
理
分子轨道和电子云
分子轨道
描述分子中电子运动的波函数。
电子云
描述电子在分子中的概率分布。
分子中的电子排布
根据泡利不相容原理，每个分子 轨道最多只能填充两个自旋方向
促进科学发展
休克尔分子轨道法的发展推动了相关学科的进步，促进了化学与其他学科的交叉融合，为 科学技术的整体发展做出了贡献。
对未来研究和应用的建议
深入研究
技术革新
进一步深化对休克尔分子轨道法理论的研 究，探索其在更广泛领域的应用，如生物 大分子的结构和性质研究。
分子轨道(课堂PPT)
43
44
45
46
47Leabharlann 33CF和CF+的键能分别为 548kJ/mol和753kJ/mol。试用 MOT解释。
CF的键级为2.5、CF+的键级为3 键级越大，键能越大。
34
分子极性 偶极矩
在任何一个分子中都可以找到一个正电荷中心和一个负电荷中心。 正、负电荷中心不重合的分子为极性分子。 正、负电荷中心重合的分子为非极性分子
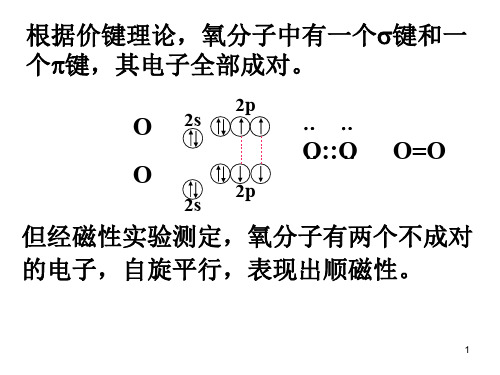
iii) O2 分子有两个成单电子，所以氧分子有顺磁性。
21
F2 分子，含18个电子
[(1s)2 (1s*)2 (2s)2 (2s*)2 (2px)2 (2py)2 =(2pz)2 (2py*)2 =(2pz*)2]
KK 能量抵消
能量抵消 能量抵消
i) F2 分子中有一个 键。
ii)
F2 分子键级=
13
(b) 适用于 1~7 号元素形成的分子或离子
对于 N，B，C原子，2s 和 2p 轨道间能量差小， 相互间排斥作用大，形成分子轨道后，σ2s和σ2Px之间 的排斥也大，结果，出现 B图中σ2Px 的能级反比 π2Py， π2Pz 的能级高的现象。
（Be2）(2py)(2pz) (2px) (2py*)(2pz*) (2px*) KK(2s)(2s*) (2py)(2pz) (2px) (2py*)(2pz*) (2px*) (1s)(1s*) (2s)(2s*) (2py)(2pz) (2px) (2py*)(2pz*) (2px*)14
偶极矩还可帮助判断分子可能的空间构型。例如NH3和BCl3 都是由四个原子组成的分子，可能的空间构型有两种，一种是平 面三角形，一种是三角锥形，根据
(NH3)=5.001030 Cm (BCl3)= 0.00 Cm
休克尔分子轨道理论
0.838 0.391 0.391
0.447
0.838
0.894
H2C 0.894 CH
CH
CH2
1.00
1.00
1.00 分子图
1.00
三、电荷密度、键级、自由价 、分子图
1、电荷密度 ：第r个原子上出现的电子数， r 等于离域电子 在第r个碳原子附近出现的几率：
r n j C jr 2
j
2、键级Prs ：原子 i和 j 间 键的强度：
Prs n j c j对大小： 原子的总成键度： N r 自由价 F r:
同除以并令x
E , 得久期行列式
3 2 4
x 1 0 0
1 x 1 0
2
0 1 x 1
0 0 0 1 x
展开得，x( x 2x) ( x 1) x 3x 1 0 解得，x 0.618 , 1.618 由E x 得
x1 1.618, x 2 0.618, x3 0.618, x 4 1.618,
－
－
2 . 丁二烯的HMO
法处理
（1） HMO 法确定轨道及能量 丁二烯（ H2C CH CH CH2 电子的分子轨道为 c11 c22 c33 c44
c1、c2、c3、c4 满足久期方程：
E 0 0 E 0 0 0 E 0 0 E
可得相应的 4套组合系数
4个碳原子的p轨道线性组合成4个分子轨道：
1 0.372 1 0.602 2 0.602 3 0.372 4
2 0.602 1 0.372 2 0.372 3 0.602 4
3 0.602 1 0.372 2 0.372 3 0.602 4 4 0.372 1 0.602 2 0.602 3 0.372 4
0.447
0.838
0.894
H2C 0.894 CH
CH
CH2
1.00
1.00
1.00 分子图
1.00
三、电荷密度、键级、自由价 、分子图
1、电荷密度 ：第r个原子上出现的电子数， r 等于离域电子 在第r个碳原子附近出现的几率：
r n j C jr 2
j
2、键级Prs ：原子 i和 j 间 键的强度：
Prs n j c j对大小： 原子的总成键度： N r 自由价 F r:
同除以并令x
E , 得久期行列式
3 2 4
x 1 0 0
1 x 1 0
2
0 1 x 1
0 0 0 1 x
展开得，x( x 2x) ( x 1) x 3x 1 0 解得，x 0.618 , 1.618 由E x 得
x1 1.618, x 2 0.618, x3 0.618, x 4 1.618,
－
－
2 . 丁二烯的HMO
法处理
（1） HMO 法确定轨道及能量 丁二烯（ H2C CH CH CH2 电子的分子轨道为 c11 c22 c33 c44
c1、c2、c3、c4 满足久期方程：
E 0 0 E 0 0 0 E 0 0 E
可得相应的 4套组合系数
4个碳原子的p轨道线性组合成4个分子轨道：
1 0.372 1 0.602 2 0.602 3 0.372 4
2 0.602 1 0.372 2 0.372 3 0.602 4
3 0.602 1 0.372 2 0.372 3 0.602 4 4 0.372 1 0.602 2 0.602 3 0.372 4
休克尔分子轨道法PPT课件
• 电子的离域可降低体系的能量，丁二烯离域比定域低0.48β。
•丁二烯有顺、反异构体
C(1) C(2)
C(2) C(3)
C(3) C(4)
C(1)
C(4)
说明C(2)和C(3)之间有一定的双键成分，不能自由旋转。
•丁二烯的键长均匀化：
C1 134.4 C2 146.8 C3 134.4 C4
•丁二烯具有 1，4 加成的化学反应性能。
第4页/共21页
3. 实例丁二烯的HMO 法处理
3.1 分子轨道波函数及能级
丁二烯（H2C CH CH CH2）电子的分子轨道为 c11 c22 c33 c44
c1、c2、c3、c4 满足久期方程：
E
0
0
E
0
0
E
0 c1
0
c2
0
E
cc43
久期方程有非零解，则其系数行列式应为零
第18页/共21页
平面构型的多环芳烃的 HMO 法处理：
(1) 萘(C10H8)
0.555 0.725
1.000
0.518
0.603
1.000
1.000 0.104 0.452
0.404
萘的分子图
142.1
136.1
141.0 142.1
实验测得萘分子键长数据
▲从自由价看， 位自由价为0.452， 位自由价为0.404，桥C原子自由价 为0.104，说明在桥C原子部位不易加成， 位最容易反应。
第3页/共21页
(5) 计算下列数据，作分子图。
•电荷密度i ：第 i个原子上出现的电子数， i 等于离域电子在第 i个碳原
子附近出现的几率： i nk ck2i
分子轨道理论教学课件
密度泛函理论
01
密度泛函理论是一种更高效的计算方法，它将多电子系统的薛 定谔方程简化为单电子系统的方程。
02
它通过电子密度而不是波函数来描述多电子系统，从而大大减
少了计算量。
密度泛函理论在计算化学中得到了广泛应用，可以用于预测分
03
子的电子结构和性质。
分子力学方法
1
分子力学方法是一种基于经典力学原理的计算方 法，它通过势能面来描述分子的运动。
分子轨道理论认为分子中的电子是在一系列的分子轨道上运 动，每个分子轨道都由一个波函数表示，描述了电子在分子 中的运动状态。
分子轨道理论的发展历程
分子轨道理论的起源可以追溯到20世纪初，当时科学家开始尝试用量子力学来描述 分子中的电子行为。
在20世纪30年代，德国物理学家马克思·玻恩和英国化学家罗伯特·玻恩等人发展了 分子轨道理论的基本框架，为后续的研究奠定了基础。
或能级表。
分子轨道能级与化学反应的关系
03
分子轨道能级与化学反应的活化能、反应速率和反应机理等密
切相关，是理解和预测化学反应的重要依据。
03
分子轨道的计算方法
哈特里-福克方法
01
哈特里-福克方法是分子轨道理论 中最早的数值计算方法，它基于 变分原理，通过求解薛定谔方程 来计算分子轨道。
02
该方法适用于较小的分子，但对 于较大的分子和复杂的化学环境 ，计算量会变得非常大。
原子轨道有特定的形状和取向，如球 形、哑铃形、纺锤形等，这些形状和 取向决定了原子中电子云的分布。
分子轨道的形成
1 2 3
分子轨道的概念
分子轨道是指由两个或多个原子轨道相互作用形 成的能量状态，是分子整体的运动状态。
芳香性离域键和休克尔规则最全PPT
Fe
(4) 环庚三烯正离子
七元环的环庚三烯正离子含有6个π电子，按照Hückel规 则应具有芳香性。
环庚三烯与溴加成得到二溴化物，后者在700C时加热失 去一分子溴化氢得一黄色物质，在乙醇中重结晶得黄色棱状 晶体,NMR谱显示δ=9.18ppm单峰，表明为芳香对称结构.
(5) 环壬四烯负离子
，来容纳P原子的孤对电子对，形成P︰ O的σ配键。
二茂铁[Fe(C5H5)2]是芳香性的环戊二烯负离子的另一特例。
子，符合Hückel规则，是芳香化合物。 二茂铁[Fe(C5H5)2]是芳香性的环戊二烯负离子的另一特例。
(2) d－p π键的应用
每个碳原子在32面体的顶点上，均以SP2或近似SP2杂化轨道与相邻碳原子形成3个σ键，每个碳原子剩下的一个P轨道或近似P轨道彼
பைடு நூலகம்HH
+ H+
二茂铁[Fe(C5H5)2]
二茂铁[Fe(C5H5)2]是芳香性的环戊二烯负离子的 另一特例。二茂铁是π络合物类的金属有机化合物， 由两个环戊二烯负离子与亚铁离子构成一种夹心结 构，桔红色，熔点173℃。可以用环戊二烯钠与氯 化亚铁在四氢呋喃中反应或用环戊二烯在二乙胺存 在下直接与亚铁盐反应制备。
其要点是:化合物是轮烯,共平面, 它的π电子数为4n+2 (n为0,1,2,3…,n整数), 共面的原子均为sp2或sp杂化。
一、非苯芳烃举例
1．芳香离子
（1） 环丙烯正离子 环丙烯体系有一个成 键轨道和一对反键轨道，环丙烯正离子的2个 电子占据成键轨道，其碳-碳键长都是 0.140nm，π电子及正电荷离域于三元环共轭 体系中，是芳香性的。
H
H
H
H
+
第12讲_休克尔分子轨道
E1 a 2 E2 E3 a E4 E5 a - E6 a - 2
从而可求出六个 MO的具体形式
I 1/ 6 1 2 3 4 5 6 II 1/12 21 2 -3 - 24 - 5 6 III 1/ 4 2 3 - 5 - 6 IV 1/ 4 2 -3 5 - 6 V 1/12 21 -2 -3 24 -5 -6 VI 1/ 6 1 -2 3 -4 5 -6
i个碳原子附近出现的几率密度
i nk ck2i k
nk —k中的电子数；cki —分子轨道k中第i个原子轨道的组合系数
（2） 键级Pij —原子i和j间 键的强度
Pij nk ckickj k
nk —k中的电子数；cki、ckj —分子轨道k中第i、j原子轨道的组合系数
复习
（3）原子的成键度 分子中某原子与周围其它原子的总键级之和
Dn(x) = 0 1 x 1 0 0 0
00 1 x 1 0
6
5 4
1 2
3
0 00 1x 1 1 0 0 01 x
展开得：x6 – 6x4 + 9x2 – 4 = 0
或 (x – 1) 2(x + 1) 2(x – 2)(x + 2) = 0
第三章 分子的量子力学处理
解出：
x1 -2 x2 x3 -1 x4 x5 1 x6 2
Dn(x)=
1x 1 0 0 …0 0 1 x 1 0 … 0 =0
… … … … … … …
0…… … … 1 x
其解的通式为：
xk
-2
cos
2k
n
k 0,1, 2,3,..., n -1
Ek
a
2
cos
分子轨道理论ppt课件
1、s－s重叠。两个轨道相加成为成键轨道σ，
两者相减则成为反键轨道σ*。若是1s轨道，
则分子轨道分别为σ1s、σ1s*，若是2s轨道，
则写为 σ2s、σ2s*。
节面
σ *ns 能
量
σ ns 11
2、 s-p重叠：形成一个成键轨道 s-p 一个反键轨道 s-p*
2s
2p
σ* s-p
σs-p
12
3、p－p重叠。两个原子的p轨道可以有两 种组合方式，其一是“头碰头”，两个原 子的px轨道重叠后，形成一个成键轨道σp 和一个反键轨道σp*。其二是两个原子的py 或pz轨道垂直于键轴，以“肩并肩”的形 式发生重叠，形成的分子轨道称为π分子轨 道，成键轨道πp，反键轨道πp*。两个原子 各有3个p轨道，可形成6个分子轨道，即 σpx 、σpx* 、πpy 、πpy* 、πpz 、πpz* 。
22
Be2 2s
1s
σ *2s 2s
σ 2s σ *1s
1s σ 1s
(
1s
)
2
(
1s
)
2
(
2s
)
2
(
2s
)
2
KK
(
2
s
)2
(
2s
)2
键级为0，所以Be2不存在。 23
B2
(
1s
)
2
(
1s
)
2
(
2
s
)
2
(
2s
)
2
2 2
1 py
1 pz
键级为0，故不能稳定存在。
18
(3)第二周期，同核双原子分子的分子轨道
《分子轨道理论》PPT课件
O2～F2：σ1s＜σ*1s＜σ2s＜σ*2s ＜σ2pz＜π2py＝π2px＜π*2py＝π*2px＜σ*2pz
异核双原子分子： 1σ＜2σ＜3σ＜4σ＜5σ＜1π＜2π＜6σ
分子轨道理论(MOT)
三十年代，MOT不仅解决了VBT不能解决的许多 问题，并且提出了“单电子键”、“三电子键”等新 化学键，有效地处理多原子的π键体系，解释了诱导 效应、离域效应等。 从三十年代到五十年代，MOT只能作近似的计算， 主要是借助于半经验的方法来总结和探索各种分子中 化学键的本质。 由于计算机的引入，MOT在五十年代得到较快的 发展。 六十年代，定量的分子轨道研究方法（包括从头计 算的自洽场法和半经验法）得到发展。
Hˆ n
E E1 E2 En
分子的波函数
11 n
2 原子轨道线性组合
Linear Combination of Atomic Orbitals（LCAO）
j C j1 1 C j22
分子轨道
n
C jn n C ji i i 1
原子轨道
py、pz、dxy、dxz、dyz py、pz、dxy、dxz、dyz s、px、pz、dyz、dx2-y2、dz2 s、px、py、dxy、dyz、dx2-y2 s、px、pz、dyz、dxz 、dx2-y2 、dz2 s、px 、py 、pz、dxy、dxz 、dx2-y2 、dz2 s、px、py、pz、dxz、dyz、dzy
第三章
结构化学 ——第三章 双原子子的结构
三 分子轨道理论
分子轨道近似 原子轨道线性组合 分子轨道的成键三原则 分子轨道的表示方法
1 分子轨道近似
分子轨道理论假定分子中每个电子是在原子核 形成的库仑场和其它电子形成的平均势场中运 动，其运动状态可用单电子波函数－分子轨道 ψ来描述。
异核双原子分子： 1σ＜2σ＜3σ＜4σ＜5σ＜1π＜2π＜6σ
分子轨道理论(MOT)
三十年代，MOT不仅解决了VBT不能解决的许多 问题，并且提出了“单电子键”、“三电子键”等新 化学键，有效地处理多原子的π键体系，解释了诱导 效应、离域效应等。 从三十年代到五十年代，MOT只能作近似的计算， 主要是借助于半经验的方法来总结和探索各种分子中 化学键的本质。 由于计算机的引入，MOT在五十年代得到较快的 发展。 六十年代，定量的分子轨道研究方法（包括从头计 算的自洽场法和半经验法）得到发展。
Hˆ n
E E1 E2 En
分子的波函数
11 n
2 原子轨道线性组合
Linear Combination of Atomic Orbitals（LCAO）
j C j1 1 C j22
分子轨道
n
C jn n C ji i i 1
原子轨道
py、pz、dxy、dxz、dyz py、pz、dxy、dxz、dyz s、px、pz、dyz、dx2-y2、dz2 s、px、py、dxy、dyz、dx2-y2 s、px、pz、dyz、dxz 、dx2-y2 、dz2 s、px 、py 、pz、dxy、dxz 、dx2-y2 、dz2 s、px、py、pz、dxz、dyz、dzy
第三章
结构化学 ——第三章 双原子子的结构
三 分子轨道理论
分子轨道近似 原子轨道线性组合 分子轨道的成键三原则 分子轨道的表示方法
1 分子轨道近似
分子轨道理论假定分子中每个电子是在原子核 形成的库仑场和其它电子形成的平均势场中运 动，其运动状态可用单电子波函数－分子轨道 ψ来描述。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i个碳原子附近出现的几率密度
i nkck2i
k
nk —k中的电子数；cki —分子轨道k中第i个原子轨道的组合系数
（2） 键级Pij —原子i和j间键的强度
Pij nkckickj k
nk —k中的电子数；cki、ckj —分子轨道k中第i、j原子轨道的组合系数
最新.
7
复习
（3）原子的成键度 分子中某原子与周围其它原子的总键级之和
… … … … … … …
0…… … … 1 x
其解的通式为：
xk
-2
cos
2k
n
k 0,1, 2,3,..., n -1
x1 0 0 0 1 1x 1 0 0 0
Dn(x) = 0 1 x 1 0 0 0
00 1 x 1 0
6
5 4
1 2
3
0 00 1x 1 1 0 0 01 x
展开得：x6 – 6x4 + 9x2 – 4 = 0
或 (x – 1) 2(x + 1) 2(x – 2)(x + 2) = 0
最新.
11
休克尔分子轨道法(HMO法) 的应用
最新.
1
复习
休克尔分子轨道理论
(1)1931年，德国化学家休克尔用分子轨道理 论处理共轭分子体系
(2) HMO法处理共轭分子结构时的假定：
(a) 由于电子在核和 键所形成的整个分子骨 架中运动，可将 键和 键分开处理
Erich Armand Arthur Joseph Hückel (1896-1980)联邦德国物理化学家。
0 0 0 0
…
…
…
0 … … … a-E
… …
… …
… …
…
…
x 1 0 0 0 …0 1x 1 0 0 …0
Dn(x) = 0 1 x 1 0 … 0 0
0…… … … 1 x 最新.
…
x a -E
5
复习
例：苯分子的休克尔行列式
61 2
5 43
休克尔行列式书写方法： 1. 同一碳原子的相应值为x 2. 相邻碳原子的相应值为1 3. 不相邻碳原子的相应值为0
（b）共轭分子具有相对不变的 骨架，而电子
的状态决定分子的性质
（c）对每个电子i的运动状态用i描述，其Schrodinger方程为：
Hˆ i Eii
最新.
2
复习
（3） 休克尔行列式的构成与休克尔近似
非定域的轨道是由具有相同对称性的所有相邻碳原子的2pz 轨道的线性组合而成，按照线性变分法，变分函数可写为：
复习
近似处理
i）对库仑积分α的估计
Hij=α
ii）对交换积分β的估计
｛
Hij=
0
i,j相邻（键连） i,j不相邻（非键连）
iii）重叠积分S
｛1 （ i = j） 归一化所得
Sij=
0 （i≠j）
最新.
4
复习
由以上近似可将久期行列式化为：
a-E 0 0 … a-E 0 … 0 a-E …
Ni Pij
Ni — 分子中第i个原子的成键度
Pij —原子i与其邻接的原子间 键键级之和
（4） 自由价Fi —第i个原子剩余成键能力的相对大小
Fi Fmax－ Pij i
Fmax — 碳原子 键键级中最大者，为 3
Pij —原子i与其邻接的原子间 键键级之和 i
（c）画出分子图
把共轭分子由HMO法求得的电荷密度、键级、自由价都标在一张分
III 1/ 4 2 3 - 5 - 6
IV 1/ 4 2 -3 5 -6
V 1/12 21 -2 -3 24 -5 -6
VI 1/ 6 1 - 2 3 - 4 最新.5 - 6
12
第三章 分子的量子力学处理
苯的 轨 道能 级图
电子的 总能量
E总 2E14E2 6 a 8
注：键级有总键级（键＋π键）和π键级之分
最新.
9
第三章 分子的量子力学处理
对于含n个碳原子的链多烯烃，其休克尔行列式为：
x 1 0 0 0 …0
Dn(x)=
1x 1 0 0 …0 0 1 x 1 0 … 0 =0
… … … … … … …
0…… … … 1 x
其解的通式为：
xj
-2
cos
j
n 1
x1 0 0 0 1
1x 1 0 0 0
Dn(x) = 0 1 x 1 0 0 = 0
00 1 x 1 0
0 00 1x 1
1 0 0 0最新. 1 x
6
复习
(4) HMO法对分子结构和性质的讨论
（a）画出分子轨道k相应的能级Ek图，排布电子，画出k的图形
（b）计算下列数据
（1） 电荷密度i — 第i个原子上出现的电子数，即离域 键中电子在第
子结构图上
最新.
8
复习
分子图及其应用 在共轭分子的碳骨架上标出电核密度、自由价、键级
0.836
键级
0.388
0.0.448
0.896
H2C
CH
CH
CH2
1.0
1.0
1.0
1.0
自由价
分子图是一种较理想的分子结构式图，它本质的表达了 分子的性质。通过分子图的分析和简单计算，可以了解 到有关分子的稳定性、极性及静态化学性质。
第三章 分子的量子力学处理
解出：
x1 -2 x2 x3 -1 x4 x5 1 x6 2
E1 a 2 E2 E3 a E4 E5 a - E6 a - 2
从而可求出六个 MO的具体形式
I 1/ 6 1 2 3 4 5 6
II 1/12 21 2 -3 - 24 -5 6
可见苯的E离的绝对值 比丁二烯的E离要大， 所以可以推知苯比丁二 烯稳定。
相 减
E最新离. = 2
定域键电子 总能量
E定 6 a 6
13
第三章 分子的量子力学处理
对于含n个碳原子的单环共轭烯烃，其休克尔行列式为：
x 1 0 0 0 …0
Dn(x)=
1x 1 0 0 …0 0 1 x 1 0 … 0 =0
久期行列式：
n
c i i(2 pz ) i
n为相共轭的 碳原子数
H11 - ES11 H12 - ES12 … H21 - ES21 H22 - ES22 …
H1n - ES1n H2n - ES2n 0
Hn1 - ESn1 Hn2 - ESn2 … Hnn - ESnn
E的近似处理
最新.
3
j 1, 2,3,..., n
Ej
a
2
cos
j
n 1
j 1, 2,3,..., n
HMO 系数
1
ckJ
2 2 n 1
sin
kj
n 1
最新.
n指共轭原子数，
k指第k条分子轨
道 ，j指第j个原
子轨道.
10
第三章 分子的量子力学处理
单环共轭烯烃（以苯为例）的HMO法处理 苯分子的HMO行列式
i nkck2i
k
nk —k中的电子数；cki —分子轨道k中第i个原子轨道的组合系数
（2） 键级Pij —原子i和j间键的强度
Pij nkckickj k
nk —k中的电子数；cki、ckj —分子轨道k中第i、j原子轨道的组合系数
最新.
7
复习
（3）原子的成键度 分子中某原子与周围其它原子的总键级之和
… … … … … … …
0…… … … 1 x
其解的通式为：
xk
-2
cos
2k
n
k 0,1, 2,3,..., n -1
x1 0 0 0 1 1x 1 0 0 0
Dn(x) = 0 1 x 1 0 0 0
00 1 x 1 0
6
5 4
1 2
3
0 00 1x 1 1 0 0 01 x
展开得：x6 – 6x4 + 9x2 – 4 = 0
或 (x – 1) 2(x + 1) 2(x – 2)(x + 2) = 0
最新.
11
休克尔分子轨道法(HMO法) 的应用
最新.
1
复习
休克尔分子轨道理论
(1)1931年，德国化学家休克尔用分子轨道理 论处理共轭分子体系
(2) HMO法处理共轭分子结构时的假定：
(a) 由于电子在核和 键所形成的整个分子骨 架中运动，可将 键和 键分开处理
Erich Armand Arthur Joseph Hückel (1896-1980)联邦德国物理化学家。
0 0 0 0
…
…
…
0 … … … a-E
… …
… …
… …
…
…
x 1 0 0 0 …0 1x 1 0 0 …0
Dn(x) = 0 1 x 1 0 … 0 0
0…… … … 1 x 最新.
…
x a -E
5
复习
例：苯分子的休克尔行列式
61 2
5 43
休克尔行列式书写方法： 1. 同一碳原子的相应值为x 2. 相邻碳原子的相应值为1 3. 不相邻碳原子的相应值为0
（b）共轭分子具有相对不变的 骨架，而电子
的状态决定分子的性质
（c）对每个电子i的运动状态用i描述，其Schrodinger方程为：
Hˆ i Eii
最新.
2
复习
（3） 休克尔行列式的构成与休克尔近似
非定域的轨道是由具有相同对称性的所有相邻碳原子的2pz 轨道的线性组合而成，按照线性变分法，变分函数可写为：
复习
近似处理
i）对库仑积分α的估计
Hij=α
ii）对交换积分β的估计
｛
Hij=
0
i,j相邻（键连） i,j不相邻（非键连）
iii）重叠积分S
｛1 （ i = j） 归一化所得
Sij=
0 （i≠j）
最新.
4
复习
由以上近似可将久期行列式化为：
a-E 0 0 … a-E 0 … 0 a-E …
Ni Pij
Ni — 分子中第i个原子的成键度
Pij —原子i与其邻接的原子间 键键级之和
（4） 自由价Fi —第i个原子剩余成键能力的相对大小
Fi Fmax－ Pij i
Fmax — 碳原子 键键级中最大者，为 3
Pij —原子i与其邻接的原子间 键键级之和 i
（c）画出分子图
把共轭分子由HMO法求得的电荷密度、键级、自由价都标在一张分
III 1/ 4 2 3 - 5 - 6
IV 1/ 4 2 -3 5 -6
V 1/12 21 -2 -3 24 -5 -6
VI 1/ 6 1 - 2 3 - 4 最新.5 - 6
12
第三章 分子的量子力学处理
苯的 轨 道能 级图
电子的 总能量
E总 2E14E2 6 a 8
注：键级有总键级（键＋π键）和π键级之分
最新.
9
第三章 分子的量子力学处理
对于含n个碳原子的链多烯烃，其休克尔行列式为：
x 1 0 0 0 …0
Dn(x)=
1x 1 0 0 …0 0 1 x 1 0 … 0 =0
… … … … … … …
0…… … … 1 x
其解的通式为：
xj
-2
cos
j
n 1
x1 0 0 0 1
1x 1 0 0 0
Dn(x) = 0 1 x 1 0 0 = 0
00 1 x 1 0
0 00 1x 1
1 0 0 0最新. 1 x
6
复习
(4) HMO法对分子结构和性质的讨论
（a）画出分子轨道k相应的能级Ek图，排布电子，画出k的图形
（b）计算下列数据
（1） 电荷密度i — 第i个原子上出现的电子数，即离域 键中电子在第
子结构图上
最新.
8
复习
分子图及其应用 在共轭分子的碳骨架上标出电核密度、自由价、键级
0.836
键级
0.388
0.0.448
0.896
H2C
CH
CH
CH2
1.0
1.0
1.0
1.0
自由价
分子图是一种较理想的分子结构式图，它本质的表达了 分子的性质。通过分子图的分析和简单计算，可以了解 到有关分子的稳定性、极性及静态化学性质。
第三章 分子的量子力学处理
解出：
x1 -2 x2 x3 -1 x4 x5 1 x6 2
E1 a 2 E2 E3 a E4 E5 a - E6 a - 2
从而可求出六个 MO的具体形式
I 1/ 6 1 2 3 4 5 6
II 1/12 21 2 -3 - 24 -5 6
可见苯的E离的绝对值 比丁二烯的E离要大， 所以可以推知苯比丁二 烯稳定。
相 减
E最新离. = 2
定域键电子 总能量
E定 6 a 6
13
第三章 分子的量子力学处理
对于含n个碳原子的单环共轭烯烃，其休克尔行列式为：
x 1 0 0 0 …0
Dn(x)=
1x 1 0 0 …0 0 1 x 1 0 … 0 =0
久期行列式：
n
c i i(2 pz ) i
n为相共轭的 碳原子数
H11 - ES11 H12 - ES12 … H21 - ES21 H22 - ES22 …
H1n - ES1n H2n - ES2n 0
Hn1 - ESn1 Hn2 - ESn2 … Hnn - ESnn
E的近似处理
最新.
3
j 1, 2,3,..., n
Ej
a
2
cos
j
n 1
j 1, 2,3,..., n
HMO 系数
1
ckJ
2 2 n 1
sin
kj
n 1
最新.
n指共轭原子数，
k指第k条分子轨
道 ，j指第j个原
子轨道.
10
第三章 分子的量子力学处理
单环共轭烯烃（以苯为例）的HMO法处理 苯分子的HMO行列式