按给定的行程速比系数K
机械学基础电子教案-第01章

33
四. 按照传动特性设计 2. 曲柄滑块机构的传动特性 B b C φ0 S C` φ
-α B`
0
+α
α a α0 A D
S=f(α)
d
位移s与转角α的关系公式:
2 2 a cos α 0 − d a cos α − d s = a (sin α − sin α 0 ) + b 1 − 1 − − b b
34Leabharlann 传动比i公式:i=
dα 1 = . ds a
cos α −
1 (a cos α − d )sin α a cos α − d b 1− b
2
位移x与转角α的关系公式:
x = (sin α − sin α 0 ) + λ2 − (cos α 0 − ε ) − λ2 − (cos α − ε )
2
2
相对传动比ia公式:
ia = dα = dx cos α − 1 (cos α − ε )sin α
λ2 − (cos α − ε )2
相对传动比ia公式与i关系:
ia= a ⋅ i
35
(1) 曲柄滑块机构相对传动比曲线 ia
αg
ε=1 λ=2 B
C A
α0
-90º 0º
+90º
α
α
α
α
C
s
A
40
(习题1-4):四杆机构如图所示,已知l1=150mm, l2=120mm, l3=180mm, l4=200mm。试问属哪种机构?
41
(习题1-5):设计一脚踏轧棉机的曲柄摇杆机构。要求踏板CD在 水平位置上下各摆10°,且lCD=500mm, lAD=1000mm,试用图 解法求曲柄AB和连杆BC的长度,如图所示。
机械设计基础ch03 唐林

= 90º –
( 摇杆 CD与连杆 BC之间的夹角 )
Fn C B A D F Ft
α
机械设计基础 东华大学 唐林
34
3.1 平面连杆机构基本型式及特性
压力角 传动角 机构效率愈高 机构传力性能愈好
Fn C B A D F α Ft
机械设计基础 东华大学 唐林
机械设计基础 东华大学 唐林
14
3.1 平面连杆机构基本型式及特性
2.1 曲柄摇杆机构
两个连架杆中,一个为曲柄,一为摇杆。
2.1.1 应用实例 实例 1 雷达天线俯仰角调整机构
机械设计基础 东华大学 唐林
15
3.1 平面连杆机构基本型式及特性
实例 2 搅拌机-1
机械设计基础 东华大学 唐林
16
3.1 平面连杆机构基本型式及特性
20
3.1 平面连杆机构基本型式及特性
实例 7 颚式破碎机
机械设计基础 东华大学 唐林
21
3.1 平面连杆机构基本型式及特性
实例 8 旋转泵
机械设计基础 东华大学 唐林
22
3.1 平面连杆机构基本型式及特性
实例 9 打谷机
机械设计基础 东华大学 唐林
23
3.1 平面连杆机构基本型式及特性
2.1.2 急回运动特性 图示曲柄摇杆机构中 杆AB 曲柄 杆BC 连杆
G’ G C
A
E F
D
B
机械设计基础 东华大学 唐林
56
3.1 平面连杆机构基本型式及特性
2.2.2 反平行四边形机构
对边杆长相等,但连杆与机架不平行 主、从动曲柄沿相反方向转动
摇杆摆角() 摇杆极限位置C1D 与C2D间夹角 极位夹角() 摇杆在C1D、C2D 时,曲柄在对应位置间 所夹锐角。
平面四杆机构设计

1.曲柄摇杆机构 2.曲柄滑块机构 3.导杆机构
1.曲柄摇杆机构
已知条件: 已知条件:行程速比系数K、摇杆的长度 l CD和摇杆的摆角Ψ
K −1 (1)计算极位夹角 K +1 (m/mm), (2)取适当的比例尺μl = l CD/CD(m/mm),并由 l CD 和Ψ 作出两极限位置C1D、C2D; 点作∠ 90° (3)过C2点作∠C1C2N=90°-θ的射线C2N,然后再过C1点作C2C1的垂线C1N 交C2N于P; 为直径作圆, 点必在此圆上; (4)以C2P为直径作圆,圆心为O,则A点必在此圆上; (5)由其他已知条件在圆周上取点A,连AC1、AC2;
例
例
2.给定连杆三个位置设计四杆机构
为连杆所要到达的三个位置,要求设计该四杆机构。 已知B1C1、B2C2、B3C3为连杆所要到达的三个位置,要求设计该四杆机构。 根据已知条件, 根据已知条件,活动铰链B、C 两点的相对位置已定,所以, 两点的相对位置已定,所以,设计 此四杆机构的实质仍然是要求出两 的位置。 固定铰链点A、D的位置。由于连杆 上的铰链中心B和C的轨迹分别为一 圆弧而同时通过三点要求B1、B2、B3 的圆分别只有一个。 和C1、C2、C3的圆分别只有一个。所 以,连架杆的固定铰链中心A和D只 有一个确定的解。 有一个确定的解 。 即 B1B2 和 B2B3 的垂直平分线 b12 和 b23 的交点为 A 以及 C1C2 和
1 EC2 lAB = µ l ( AC2 − AC1 ) = µ l 2 2 l = 1 µ ( AC + AC ) = µ ( AC − EC2 ) 2 1 l 2 BC 2 l 2 (7) 讨论:由于A点可在△C1PC2的外接圆周的弧C1PC2上任意选取,所以,若仅按行 讨论: 点可在△ 上任意选取, 所以, 来设计,可以得到无穷多组解。因此,在未给出其它附加条件的情况下, 程速比系数K来设计,可以得到无穷多组解。因此,在未给出其它附加条件的情况下, 点的位置。 如欲获得良好的传动质量, 如欲获得良好的传动质量,可按照传动角最优或其它辅助条件来确定A点的位置。
按行程速比系数K设计平面四杆机构的几个问题

一
图2 I 取值范 围
首先 根据行程速度变化系数K 求出极 位夹 角 0口 = 1 8 0 o }
圆 8 的 交 于 E、 F两 点 , 如图 1 所示。 1 . 5在 C 。 C 所对优弧 C 。 M C : 上 任 取 一 点 作 为 固定 铰 链 点 A。
解) 。
:
-
2 ・ 1 . 2 出 现 的 问 题
.
可 … 二 B C c 一 : . V 1 l : = B 一
位 于 I : 南 点 乏 接 1 2 x Q t : c i 芝 高 爵 杆
兰
享 、 耒 “ (
・
1 6 6 ・
科技 论坛
按行程速 比系数 K设 计平 面四杆机构 的几个 问题
董 志 刚 ’ 韩 忠义 z 苏 俊 玲
( 1 、 唐 山城 市排水有限公 司, 河北 唐 山 0 6 3 0 0 0 2 、 唐 山学院 , 河北 唐 山 0 6 3 0 0 0 ) 摘 要: 通过对 四杆机构各构件几何 关系的分析、 论证 , 介绍了在 已知行程速比 系数 , 并给定其它辅助 几何条件 时' 用图解法设计四杆
・
1 6 8 ・
科 技 论 坛
的发生提供 了措施依据 。 该事故树的最小径集用布尔代数法求解如下 :
T= = ( xe +X9 ) = x1 ( x5 + X6 + X- ) ( x。 + x, )
I ①f 1 、 =1 / 2 1 ‘ 4 =1 : l f 2 F1 / 2 3 - ’ 1 = 0 . 2 5 ;
2 . 2 已知行程速 比系数 K, 摇杆摆角 , 摇杆长度 l 及连杆长度 l : , 设计铰链 四杆 机构 , 求l 。 , l 4 。 1 . 6求 l 。,l 2,l 4 。 2 . 2 . 1解 题 方 法 图中量取 A C ,、 A C ;则 A B= 1 / 2( A C 一 A C ) ; B C= I / 2 ( A C a . 按图 1 做法 , 先做 出圆 8。 + AC】 ) 。 b . 以 M为 圆心 , 以c M为半径画 圆 B; , 以c 为 圆心 , 以 2 l 2 为 图中量取 A D尺寸 ,则 : 1 1 =A B * l 1 2 = B C * l 1 4 =A D * l 。 半径 画弧与圆 P交于 Y 、 Y : 点。 作直线 c :Y 。 ( 或 c 2 Y ) 与圆 8交点 2 几 种 需 注 意情 况 即为 A点 。两个懈 , 如图 2所示。 2 . 1已知行程速 比系数 K, 摇杆摆 角 , 摇杆长度 l 及机架 长 c. 可得 : A B= 1 / 2 ( A C ,一 A C ) 度l 4 , 设计铰链 四杆 机构 , 确定 l 。 ,l 。 l l : AB l ; 1 4 - AD 1 2 . 1 . 1解 题 方 法 2 . 2 . 2出 现 的 问题 a . 按图 1 做法 , 先 做 出圆 8。 a . 1 : < l c 。 c 时,以 2 l 2 为半径所 画弧与 圆 8 交于 C l c 2 所 对 b . 以 D为 圆心 , 以l 4 为半 径 画弧 与 圆 8 交 于 A、 A’ 点( 两 个 劣弧上 , 不满足设计要求[ 1 1 。
机械原理重点归纳

机械原理不考试内容 六、§8-4 平面四杆机构的设计中
2. 用解析法设计四杆机构
机械原理复习
4.四杆机构的优化设计
§8-5 多杆机构 七、§9-3 凸轮轮廓曲线的设计中
3.用解析法设计凸轮的轮廓曲线
八、§10-11 其他齿轮传动简介 §10-12 齿轮机构动力学简介 九、§11-6 行星轮系的效率 §11-7 行星轮系的类型选择及设计的基本知识中
第8章
1.基本类型:
平面连杆机构及其设计
一、 平面四杆机构的类型和应用 铰链四杆机构:①曲柄摇杆机构 ,②双曲柄机构,③双摇杆机构 2.演化方法: ①改变构件的形状和运动尺寸:曲柄滑块机构、正弦机构
②改变运动副的尺寸:偏心轮机构
③取不同构件为机架:导杆机构、摇块机构 、直动滑杆机构 ④运动副元素的逆换;: 3.应用:举例: ①如何把定轴转动变换为往复直线移动; ②如何把定轴转动变换为往复摆动; ③
作业集7-1——7-3
第7章 机械的运转及其速度波动的调节
三、机械速度波动的调节方法 1.周期性速度波动— 可以利用飞轮储能和放能的特性来调节
2.非周期性速度波动—不能用飞轮进行调节 ,当系统不具有自调性 时,则需要利用调速器来对非周期性速度波动进行调节。 3.飞轮设计的基本问题,是根据 Me、Je、ωm、δ来计算飞轮的转动 惯量 JF ①在一个周期内:Wd=Wr,求未知外力(矩),得出盈功和亏功; ②画出能量指示图,求出最大盈亏功∆Wmax(熟练掌握) ③计算 J Wmax J F C 2
1.应遵循的原则是: 使机械系统在等效前后的动力学效应不变,即
① 动能等效:等效构件所具有的动能,等于整个机械系统的总动能。 ② 外力所做之功等效:作用在等效构件上的外力所做之功,等于作 用在整个机械系统中的所有外力所做之功的总和。 2.要求掌握等效力矩和等效转动惯量的求解
机械原理课后答案第8章
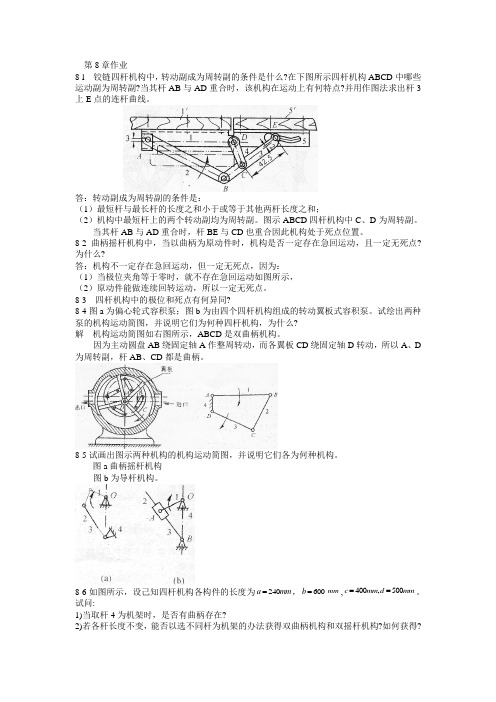
第8章作业8-l 铰链四杆机构中,转动副成为周转副的条件是什么?在下图所示四杆机构ABCD 中哪些运动副为周转副?当其杆AB 与AD 重合时,该机构在运动上有何特点?并用作图法求出杆3上E 点的连杆曲线。
答:转动副成为周转副的条件是:(1)最短杆与最长杆的长度之和小于或等于其他两杆长度之和;(2)机构中最短杆上的两个转动副均为周转副。
图示ABCD 四杆机构中C 、D 为周转副。
当其杆AB 与AD 重合时,杆BE 与CD 也重合因此机构处于死点位置。
8-2曲柄摇杆机构中,当以曲柄为原动件时,机构是否一定存在急回运动,且一定无死点?为什么?答:机构不一定存在急回运动,但一定无死点,因为:(1)当极位夹角等于零时,就不存在急回运动如图所示,(2)原动件能做连续回转运动,所以一定无死点。
8-3 四杆机构中的极位和死点有何异同?8-4图a 为偏心轮式容积泵;图b 为由四个四杆机构组成的转动翼板式容积泵。
试绘出两种泵的机构运动简图,并说明它们为何种四杆机构,为什么?解 机构运动简图如右图所示,ABCD 是双曲柄机构。
因为主动圆盘AB 绕固定轴A 作整周转动,而各翼板CD 绕固定轴D 转动,所以A 、D 为周转副,杆AB 、CD 都是曲柄。
8-5试画出图示两种机构的机构运动简图,并说明它们各为何种机构。
图a 曲柄摇杆机构图b 为导杆机构。
8-6如图所示,设己知四杆机构各构件的长度为240a mm =,600b =mm ,400,500c mm d mm ==。
试问:1)当取杆4为机架时,是否有曲柄存在?2)若各杆长度不变,能否以选不同杆为机架的办法获得双曲柄机构和双摇杆机构?如何获得?3)若a 、b ﹑c 三杆的长度不变,取杆4为机架,要获得曲柄摇杆机构,d 的取值范围为何值? : 解 (1)因a+b=240+600=840≤900=400+500=c+d 且最短杆 1为连架轩.故当取杆4为机架时,有曲柄存在。
(整理)四连杆

2.2.5 平面四杆机构的设计连杆机构的设计方法有作图法、解析法及实验法三种;其中作图法是重点。
用作图法设计四杆机构是根据设计要求及各铰链之间相对运动的几何关系,通过作图来确定四个铰链的位置。
根据不同的设计要求,作图法设计四杆机构可分为三种类型:1)按预定的连杆位置设计四杆机构。
①已知连杆 BC 的三个预定位置B 1 C 1、B 2 C 2、B 3 C 3,设计此四杆机构的实质是求固定铰链中心的位置。
此类问题可用求圆心法来解决,即作铰链 B 的各位置点连线B 1B 2、B 2B 3的中垂线,两中垂线的交点即固定铰链A 的中心。
同样,作铰链C 的各位置点连线C 1C 2、C 2 C 3的中垂线,两中垂线的交点即固定铰链 D 的中心。
若仅给定连杆 BC 的两个预定位置则设计的四杆机构有无穷多解。
②若给定固定铰链中心A 、D 的位置及连杆上标线EF 的三个预定位置,设计此四杆机构的实质是求活动铰链中心B 、C 的位置。
此类问题要用反转法求解,即把机构转化为以原连杆第一位置 E 1 F 1为机架,原机架 AD 为相对连杆,再仿上求得活动铰链 A 的三个相应位置A 、A 2’、A 3’,它们所在圆的圆心就是其相对固定铰链(实际活动铰链)B 的位置B 1,可用前述求圆心法求得。
2)按预定的两连架杆对应位置设计四杆机构。
如已知两连架杆的三组对应位置及机架长度l AD 、原动件长度l AB ,设计此四杆机构的实质是求活动铰链C 的位置。
此问题可用反转法求解,即把从动杆CD 的第一位置C 1D 看做机架,原动件AB 看做连干,求得活动铰链B 的三个相应位置B 、B 2´、B 3´,他们所在圆的圆心就是其相对固定铰链C 的位置C 1,若仅给定两连架杆的两组对应为止,则设计的四杆机构有无穷多解。
3)按给定的行程速比系数K 设计四杆机构已知行程速比系数K 及某些其他条件(如曲柄摇杆机构CD 的长度l CD 、摇杆摆角φ),设计此四杆机构的实质问题是确定曲柄的固定铰链中心A 的位置,进而定出其余三杆长度。
机械原理复习重点

所以: F = f × N = K × f ×Q = fv ×Q
fv——当量摩擦系数 于是:M = F × r = fv × r ×Q 摩擦阻力矩
Q
显然: R21 = -Q,Mf = R21×r ∴ Md=Mf Q×r = R21× =r fv × r × Q ∴ r = fv ×r ——摩擦圆半径 结论: A. 总反力始终切于摩擦圆; B. 总支反力方向与作用点速度方向相反。
F2Ⅱ
Ⅱ
F2 Ⅰ F2
Ⅰ
m r1 1 F1 Ⅰ
m2 r2
m3 r3 F3
F1Ⅱ
F3 Ⅱ
F1 L2
F3 Ⅰ
L1
L3
L
第七章 机械的运转及速度波动的调节 等效转动惯量的一般计算式为: n Je = ∑[JSi ( i=1 等效力矩的一般计算式为: n Me = ∑[Fi cosa( i=1 等效质量的一般计算式为: n me = ∑[JSi ( i=1 等效力的一般计算式为:
P13
P34
1
w1
3 P23
已知w1 求v5,则问题的关键在
P14
于寻找相对瞬心P15
(3) 滑动兼滚动的高副机构(齿轮、凸轮机构) 例 3 :如图所示的凸轮机构。已知各 构件的尺寸、凸轮的角速度 w1,求推 杆速度v2 。
v2= v2P12 = v1P12 = P12 P13 ×ml×w1
2 3 P23 ∞
• 当h=0时,机械处于临界自锁状态; 若h<0,则其绝对值越大,表明自锁越可 靠。
例:图示为一斜面压榨机。求在去掉水 平力P后的机构自锁条件。 解: 1. 确定运动副上的总反力 2. 以受力体2和3为对象,分别 列出平衡方程式为: Q + R42 +R32 = 0 P + R43 + R23 = 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理网络课堂平面四杆机构的设计:按给定的行程速比系数K设计四杆机构
已知:摇杆长度CD,摆角φ,行程速比系数K。
要求:设计曲柄摇杆机构。
解:
1、计算极位夹角θθ=180(K-1)/(K+1)
2、任取一点D为摇杆固定铰链中
心,作等腰三角形C1C2D,两腰长
度等于CD,∠C1DC2=φ。
3、以C1C2为一条边,分别作∠O
C1C2=∠OC2C1=90°_θ。
以O为圆心,
OC1为半径作圆β。
4、连接并延长C 1D ,交圆β于G
点,连接并延长C 2D ,交圆β于F
点。
圆弧C 1F 和GC 2上任意一点A
到C 1和C 2的连线的夹角∠C 1AC 2都等
于极位夹角θ。
曲柄轴心A 点可在
这两段圆弧上选取。
注意:曲柄轴心A 不能
在FG 圆弧上选取,否则机构不满运动连续性要求。
在C 1F 和GC 2两段
圆弧上选取A 点时,当A 点越靠近
F(或G)点时,机构最小传动角将随
之减小。
)
5、A 点选定后,四杆机构尺寸即确定。
设曲柄长度为a ,连杆长度为b,则
AC 1=b _a,
AC 2=b+a,
所以,a=(AC 2_AC 1)/2,
b=(AC 1+AC 2)/2
说明:1)如设计时还给出其它附加条件(如给定机架尺寸或曲柄长度或连杆长度等),则A 点按相应条件确定。
2)对于给定行程速比系数K和滑块行程H时,可以用同样方法求出曲柄滑块机构.
2) 对于摆动导杆机构,由于其导杆
的摆角φ刚好等于其极位夹角
θ,因此,只要给定曲柄长度L
(或给定机架长度L AC)和行程速AB
比系数K就可以由右图求得机构.。
