【课件】第13章磁场中的磁介质
155磁场中的磁介质解读

B0
I0
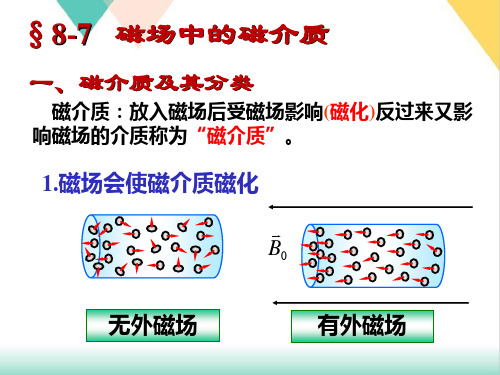
顺 磁 质
IS
I0
2. 磁介质中的安培环路定理
B dl 0 (Ii I s )
L
a
d
b
IS
顺 磁 质
Ii ——为环路所包围的传导电流。 Is ——为环路所包围的是磁化电 流,难以测量。 3. 引入磁场强度 H 令 式中
c
I0
H
B
r
0
B
在外场作用下,每个分子中的所有电子都产生感应磁矩 Pm 则磁介质产生附加磁场 B ' B ' 与外场方向相反
顺磁质磁化 抗磁质磁化
结论:在外场作用下,电子产生附加的转动,从而形成附加
将顺磁质放入外场 B0
分子环流在外场作用下, 产生取向转动, 磁矩将转 向外场方向 —— 宏观上 产生附加磁场
磁畴的磁 化方向
2. 宏观磁化现象 —— 磁滞回线 铁磁质中
B H 不是线性关系
B~H
Br 剩磁
矫顽力
B
B
b
f
a
H
r ~ H
HC
c
H
o
e
o
讨论
d
(1) 实验证明:各种铁磁质的磁化曲线都是“不可逆”的, 具有磁滞现象 (2) 不同材料,矫顽力不同
(3) 铁磁质温度高于某一温度TC 时, 铁磁质转化为顺磁质, 此 临界温度称为居里点。 (4) 铁磁材料的应用
电子自旋磁矩 与轨道磁矩有 相同的数量级
分子磁矩 —— 所有电子磁矩的总和 Pm Pmi i 无外场作用时,对外不显磁性 抗磁质 Pm 0 无外场作用时,由于热运动, 顺磁质 Pm 0
磁场中的磁介质

e ev 电子电流 I 2r / v 2r ev evr 2 m IS r 2r 2
m en
I S
e L 2m e
角动量 L me vr
二、原子的磁矩
2.电子的量子轨道磁矩
h L m, m 0,1,2, 1.05 10 34 J S 2 e 24 一个可能的值 m 9.27 10 J / T 2m e
分子电流为
dI n a 2 dr cos i
n m dr cos
M dr cos M dr
dI M dr
三、磁介质的磁化
若 dr 选在磁介质表面,则 d I 为面束缚电流。
面束缚电流密度
dI M cos M r j dr
电流为i,半径为 a,分子磁 矩为 m ,任取一微小矢量 dr 2 a 元 dr ,它与外磁场 B 的夹角 m i 为,则与 dr 套住的分子电 流的中心都是位于以为 dr 轴、 以 a2 为底面积的斜柱体内。 i
m
B
三、磁介质的磁化
若单位体积内的分子数为n ,则与 dr 套连的总
2.磁化强度
单位体积内分子磁矩的矢量和称作磁介质的 磁化强度。 mi M V
单位 安每米(A/m)
3.实验规律
实验发现,在外磁场不是很强时,对所有磁 介质
r 1 M BB
0 r
三、磁介质的磁化
3.束缚电流与磁化强度之间的关系
以顺磁质为例 , 等效分子
电子的自旋磁矩(内禀磁矩) 电子自旋角动量 内禀磁矩
s 2
玻尔磁子
e e mB s 9.27 10 24 J / T me 2me
高二物理竞赛磁场中的磁介质PPT(课件)
§8-8 有磁介质时的安培环路定理 磁场强度
一、磁化强度
反映磁介质磁化程度(大小与方向)的物理量。
磁化强度:单位体积内所有分子磁矩的矢量
和 m 加上附加磁矩的矢量和 m,称为磁化
强度,用 M表示:
M m m V
磁化强度的单位:A/ m
磁化强度:M m m V
注意:对顺磁质 对抗磁质
(3)磁化电流是分子电流规则排列的宏观反映, (4)由实验,对各向同性均匀磁介质,有
磁化电流是分子电流规则排列的宏观反映,并不伴随电荷的定向运动,不产生热效应;
并不伴随电荷的定向运动,不产生热效应。
三、磁化强度与磁化电流的联系 磁化面电流密度
设无限长直螺线管中充满均匀磁介质。设圆柱体长
为 L,截面积为 S,表面的磁化电流为 I S ,单位长度
质性质有关,是无单位的纯数。
m 0,顺磁质 m 0,抗磁质
(5)由
H
B
0
M 得
B0H0M
将 M代m入H上式得:
B0H0M0H0mH
01mH
令 1m r
则有
——适用于各
B0 rHH向同性磁介质
➢对真空、 导体,磁场 : 由 M 0 , 所 于 B 0 H ,以 m 0 ,r 1
0 电流 I 由中心导体流入,由外面圆筒流出。
顺磁质分子(类有极分子),每个分子的分子磁矩不为零,即分子磁矩
外磁场为零,磁化强度为零。
定义磁场强B度矢量 : H M
0
有介质存在时的安培环路定理为
LHdl I
磁场强度 H沿任一闭合回路的环流,等于闭
合回路所包围并穿过的传导电流的代数和,而在 形式上与磁介质中磁化电流无关。
2R1 抗磁质:分子磁矩为0。
磁场中的磁介质ppt

第五版
一、 H矢量的安培环路定理
几点说明
15
磁场中的介质
H dl I0
L
(1)只与传导电流有关,与束缚电流无关
(2) H 与 D 一样是辅助量,描述电磁场
ED
B H
B 0 H
9
(3)在真空中: M 0 r 1
第五版
15
磁场中的介质
当外磁场由 H m 逐渐减小时,这种 B 的变化落后于H的变 化的现象,叫做磁滞 现象 ,简称磁滞. 由于磁滞, H 0 时,磁感强度 B 0 Br 叫做剩余磁感强 , 度(剩磁).
Bm
H m Br
B
Q
P
Hm
H
O
P
'
Hc
Bm
磁滞回线 矫顽力
Hc
17
第七章 恒定磁场
r
第七章 恒定磁场
13
物理学
第五版
15
磁场中的介质
解 rd R
B H
dR
0 r I
H dl I
l
2π dH I
2π d H dl I I 0
l
r
I
2π dH 0 , H 0
d
I
B H 0
同理可求 d r , B 0
物理学
第五版
15
磁场中的介质
3 铁磁性材料 不同铁磁性物质的磁滞回线形状相差很大.
B B B
O
H
O
H
O
H
软磁材料
硬磁材料
第七章 恒定磁场
矩磁铁氧体材料
大学物理电磁学ppt课件

i
L Er d
B dS S t
--对导线所围面积积分
28
电磁学复习
自感系数 L I
互感系数 M 12 21
i2
i1
自感磁能
WL
1 2
LI 2
互感磁能 WM = M I1I2
L
L
dI dt
12
M
d i2 dt
普适式(L一定)
长直螺线管: B = nI L = n2V
U
q
40 ( x2
R2 )1 2
8
电磁学复习
第11章 导体和电介质的静电场
11-1 导体的静电平衡 11-2 电容器及其电容 11-3 静电场中的电介质 11-4 有电介质时的高斯定理 11-5 静电场中的能量
9
电磁学复习
知识点:
静电平衡状态下导体上电荷分布、电场强度和电势 电容器的电容及其储能 电介质的极化:求D、E、P 电场能量 典型例题: 例11.1; 例11.3; 例11.5 典型习题: P50 11-1, 6, 8, 10, 14, 17, 19, 20, 21, 22
平行板电容器 C 0S
d
充电介质:
圆柱形电容器 C 20L
ln(R2 R1 )
C rC0
球形电容器电容
C 40
RA RB RB - RA
电容器储能: We
1 CU 2 2
Q2 2C
1 QU 2
12
电磁学复习
3. 电介质极化: 在外场E0中
无极分子 --- 位移极化 有极分子 --- 取向极化
电电负内源源载阻充功功功放率率率电II时I22Rr的功率转充放换电电::充外电电电源路U输I输出入功电率I 源U功II 2率r UI 16
磁场中磁介质.ppt

铁磁质的特性
1. 磁导率μ不是一个常量,它的值不仅决定于原线 圈中的电流,还决定于铁磁质样品磁化的历史。 B 和H 不是线性关系。
2. 有很大的磁导率。 放入线圈中时可以使磁场增强102 ~ 104倍。
3. 有剩磁、磁饱和及磁滞现象。
4.温度超过居里点时,铁磁质转变为顺磁质。
三 铁磁质的应用 (1)软磁材料
单位长度上的导线匝数为n。
求:环内的磁场强度和磁感应强度
解:
H
L
dl
H 2r
NI
H NI nI
r
2r
O
B H 0r H
例2 一无限长载流圆柱体,通有电流I ,设电流 I
均匀分布在整个横截面上。柱体的磁导率为μ,柱
外为真空。
求:柱内外各区域的磁场强度和磁感应强度。
静磁场(稳恒磁场)
BH
S B dS 0
L H dl I0 B H
12-3 铁磁质 一 铁磁质的磁化规律
电流表
A
测量H
换 向 开 关
测量磁滞回线的实验装置
测量B 的探头 螺绕环 (霍尔元件)
铁环 狭缝
0 5 10 15 20
磁强计
电阻
A
1、磁化曲线
I
解: r R
LH dl H 2r I
r2 R2 I
Ir
Ir
H 2R2 B 2R2
R
I
0
H
r
r R H2r I
H I B 0I
2r
2r
I R
0
r
H
B
第11章磁场中的磁介质PPT课件

分子磁矩的矢量和:
Pm 0
从介质横截面看,介质内分子电流两两反向,相互抵消。
导体边缘分子电流同向,未被 抵消的分子电流沿柱面流动
⊙ B0
B0
等效
分子电流可等效成磁
介质表面的磁化电流 Is,
Is
B
Is产生附加磁场。
B B0 B B0
磁化电流 Is 可产生附加磁场,但无热效应,因无宏观电 荷移动,磁第化13页电/共流2束6页缚在介质表面,也称为束缚电流。
Hc
矫顽力——加反向磁场Hc, 使介质内部的磁场为 0,
o
Hc
H
结论
继续增加反向磁场,介质
达到反向磁饱和状态; 铁磁质的r不是一个常数,
改变外磁场为正向磁场, 它是 H 的函数。
不断增加外场,介质又达 到正向磁饱和状态。
B的变化落后于H,从而具有 剩磁,即磁滞效应。
第17页/共26页
二、铁磁质的磁化机制
解 (1)当两个无限长的同轴圆柱体和圆柱面中有电流通过
时,它们所激发的磁场是轴对称分布的,而磁介质亦呈轴对
称分布,因而不会改变场的这种对称分布。设圆柱体外圆柱
面内一点到轴的垂直距离是r1,以r1为半径作一圆,取此圆为 积分回路,根据安培环路定理有
r3
I
R1 R2 rr12
II
第9页/共26页
H dl H
抗磁质:分子中各电子的磁矩完全抵消,整个分子无固有磁矩
第12页/共26页
(1)顺磁质的磁化机制
磁介质是由大量分子或原子组成,无外场时,顺磁质分子的磁矩排列杂 乱无章,介质内分子磁矩的矢量和
Pm 0
有外磁场时,这些分子固有磁矩就要受到磁场的力矩
作用,力矩的方向力图使分子磁矩的方向沿外场转向。
有磁介质时的磁场课件

磁场强度的计算公式
磁场强度的单位和物理意义
不同类型磁介质的磁场计算实例
铁氧体的磁导率与磁场强度的关系 硅钢片的磁导率与磁场强度的关系 空气的磁导率与磁场强度的关系
磁场计算中的注意事项
磁介质的磁导率是变化的,需要 考虑不同磁介质对磁场的影响。
磁场强度与距离有关,需要考虑 不同距离对磁场的影响。
磁场强度与电流有关,需要考虑 不同电流对磁场的影响。
变压器
利用磁介质可以制造变压器,实 现电能和磁能的转换。
电机
利用磁介质可以制造电机,实现 电能和机械能的转换。
磁介质在磁场中的局限性
温度稳定性差
磁介质的磁性能容易受到温度的影响,稳定性较 差。
机械强度低
磁介质在机械强度方面较低,容易受到外力的影 响。
成本较高
一些高性能的磁介质成本较高,价格较贵。
05
磁介质的物理性质
磁化
在磁场作用下,磁介质会 发生磁化现象,即产生磁 畴和磁矩。
磁滞
磁介质在交变磁场作用下 会产生滞后现象,即磁滞 。
退磁
当磁场减弱或消失时,磁 介质会失去磁性,即发生 退磁现象。
03
有磁介质时的磁场计算方 法
磁介质的磁场计算公式
01
磁介质的磁化强度矢量
02
磁介质的磁导率
03
04
07
参考文献及致谢
参考文献
教科书
《电磁学》
期刊论文
《磁介质在磁场中的行为研究》
网络资源
各类在线教育平台关于磁场和磁介质的教学视频
致谢
对指导教师表示衷心感谢,感谢他们在 课程设计、内容讲解和答疑解惑方面给
予的大力帮助。
对参与课件制作和资料整理的同学表示 感谢,感谢他们的辛勤付出和团队协作
磁场中的磁介质

实验表明,铁磁质的磁化曲线都是不可逆的。即达到饱和
后,如果逐渐减小电流I,B并不沿起始磁化曲线逆向地随H的 减小而减小,而是沿下图所示中另一条曲线PQ比较缓慢地减 小。这种B的变化落后于H的变化规律称为磁滞现象(简称磁 滞)。由于磁滞的缘故,当磁场强度H减小到零时,磁感应强 度B并不等于零,而是仍有一定的数值Br,Br称为剩余磁感应 强度(简称剩磁)。这时撤去线圈,铁磁质就是一块永磁体。
物理学
磁场中的磁介质
1.1 磁介质
磁介质是指在磁场作用下,其内部状态发生变化,并反过 来影响磁场存在和分布的物质。磁介质在磁场作用下内部状态 的变化称为磁化。
磁化了的磁介质会产生附加磁场,对原磁场产生影响。磁 介质在磁感应强度为B0的外磁场中,受外磁场的作用而被磁化 产生附加磁场B'。此时,在磁介质中的磁场B是这两个磁感应 强度的矢量和,即
2.磁化曲线与磁滞回线
铁磁质的特点是:① r 1 ,可达102~105数量级;② 相 对磁导率μr和磁导率μ会随着磁场强度H的变化而变化,即磁感 应强度B与磁场强度H不成线形关系。以上这些特点可以用B-H 曲线(也称磁化曲线)来描述。
B和H的关系可用实验测定。在实验中,可得出某一铁磁质 开始的B-H曲线,称为初始磁化曲线,如下图所示。从曲线可以 看出,当外加的磁场强度H从零逐渐增大时,可以看出介质的磁 感应强度B也逐渐增加;到达点M后,H继
顺磁质在没有外磁场时,磁介质中各分子磁矩的方向是杂 乱无章的。大量分子的磁矩相互抵消,所以宏观上磁介质不显 磁性。当有外电场B0时,所有分子磁矩都受到磁场力矩的作用 ,使各分子都不同程度地沿磁场方向排列,分子电流产生了一 个沿外磁场B0方向的附加磁场B',从而使总的磁感应强度增加 ,即磁感应强度的值为B=B0+B'>B0。
大学物理-磁场中的磁介质_图文_图文

试 求(1)磁介质中任意点
I
P 的磁感应强度的大小;
(2)圆柱体外面一点Q
I
的磁感强度.
解
I I
同理可求
三 铁磁质
1 磁畴
有 外 磁 场
无外磁场
2 磁化曲线 磁滞回线
B/10-4T
15
ห้องสมุดไป่ตู้10
B=f (H)
5
θ
0
400
600 800 1 000 H/(Am-1)
顺磁质的B-H曲线
当外磁场由 逐渐减小时,这种 B 的变化落后于H的变 化的现象,叫做磁滞 现象 ,简称磁滞.
由于磁滞, 时,磁感强度 , 叫做剩余磁感强 度(剩磁).
O
磁滞回线 矫顽力
3 铁磁性材料 不同铁磁性物质的磁滞回线形状相差很大.
O
O
O
软磁材料
硬磁材料 矩磁铁氧体材料
4 磁屏蔽
把磁导率不 同的两种磁介质 放到磁场中,在 它们的交界面上 磁场要发生突变 ,引起了磁感应 线的折射.
磁屏蔽示意图
大学物理-磁场中的磁介质_图文_图文.ppt
2 顺磁质和抗磁质的磁化 分子圆电流和磁矩
顺磁质的磁化
无外磁场
顺磁质内磁场
有外磁场
无外磁场时抗磁质分子磁矩为零
抗磁质的磁化
同向时
抗磁质内磁场
反向时
3 磁化强度
分子磁矩 的矢量和
体积元
单位:
意义 磁介质中单位体积内分子 的合磁矩.
二 磁介质中的安培环路定理
分子磁矩
C
(单位体积分子磁矩数
)
传导电流 分布电流
B
C
A
D
磁场强度
磁介质响应外磁场而产生磁化电流的过程课件

磁化强度
磁化程度可以用磁化强度 来表示,它反应了磁介质 在磁场中的磁化程度。
磁化过程
起始磁化
当磁场逐渐增加时,磁介 质的磁化强度也随之增加 ,直到到达饱和磁化状态 。
饱和磁化
当磁场继续增加时,磁介 质的磁化强度不再增加, 到达饱和状态。
剩余磁化
当磁场逐渐减小时,磁介 质的磁化强度不会立即消 失,而是保留一部分剩余 磁化。
磁介质响应外磁场而产生磁 化电流的过程课件
目录
• 磁介质简介 • 磁介质响应外磁场的过程 • 磁化电流的产生 • 磁介质在外磁场中的行为
目录
• 外磁场对磁介质的影响 • 磁介质响应外磁场而产生磁化电流的
实验研究
01
磁介质简介
磁介质的定义
01
磁介质
是指能够响应外磁场并产生磁化电流的物质。
02
磁化
磁化电流的应用
电磁感应
磁化电流是电磁感应现象中的重要概念。当线圈中的磁通量产生变化时,会在 线圈中产生感应电动势,进而产生感应电流。这个感应电流就是由磁化电流引 起的。
磁记录
磁化电流在磁记录技术中也有重要应用。通过改变磁介质表面的磁化方向,可 以记录和存储信息。在读取信息时,通过检测磁化电流的大小和方向,可以还 原出存储的信息。
由于磁滞现象的存在,当外磁场变化时,磁介质内部会产生能量 损耗,称为磁滞损耗。
磁滞损耗的产生
磁滞损耗的产生是由于磁畴结构产生变化时,需要克服磁畴之间的 相互作用和摩擦力,从而产生热量和能量损耗。
磁滞损耗的影响
磁滞损耗会导致设备的效率降低、温升增加等问题,因此在实际应 用中需要采取措施减小磁滞损耗。
05
磁化强度的变化
磁化强度的变化
磁场中的磁介质

玩力小。易于磁化和去 磁。
磁滞回线宽。剩磁大。
3. 矩磁材料:磁滞回线接 近矩阵。剩磁接近于饱 和磁感应强度。
例2 如图所示的细螺绕环, 它由表面绝缘的导线在 铁环上密绕而 成,,每厘米绕 10匝。它导线中的电流 I 2.0 A时,测得铁环内 B 的大小为 1.0T,则铁环的相对磁导率 为 __________ ___ 。 解: H dl I
§13.2 顺磁质和抗磁质的磁化
一、原子中电子的磁矩 轨道运动、自旋
1. 轨道运动的磁矩
ev e e I T 2 r 2 r v ev 1 2 IS r evr 2 2 r L rmv e L 2m e L 2m
根据量子理论,任何磁 矩都 是一个最小单元的整数 倍,这个 最小磁矩叫做波尔磁子 B。
2rH 2r 1000 2
H 2000 B H
1 .0 B r 398 7 4 10 2000 0 0 H
作业:13.1,13.2,13.4,
( M为磁介质内(包括表面 )任
内
上式普遍成立。
方向成右手螺旋关系)
§13.3 存在磁介质时磁场的基本规律
一、磁场强度、安培环 路定理 取回路 abcd , B dl 0 ( I 0 I m )
内 内
0 ( I 0 M dl ) B ( 0 M ) dl I 0 B 磁场强度 H M 0
三、顺磁质和抗磁质的 磁化 构成顺磁质的分子本身 磁矩(固有磁矩,一般 比附加磁矩大
5个数量级以上)不为零 ,但各个磁矩随机取向 ,从而 p m 0,
即宏观上不显示磁性。
大学物理磁介质(老师课件)

2)硬磁材料
HC — 104~106 A/m
特点:剩余磁感应强度大 矫顽力大 不容易磁化 也不容易退磁 剩磁性强 磁滞回线宽 磁滞损耗大 应用: 适合制作永久磁铁 永磁喇叭 用于拾音器、扩音 器、麦克风、收录 音机等 B
H
3)矩磁材料: 特点:磁滞回线呈矩形状
应用:作计算机中的记忆元件 磁化时极 性的反转构成了“0”与“1”
二、铁磁质的磁化
三、铁磁性材料的分类
四、磁致伸缩
一、 铁磁质的宏观性质
1. r 1 可使原场大幅度增加 B r B 0 0 r H
2. r与磁化历史(H)有关,不是常数。 B—H和r—H曲线是非线性关系 3. 磁滞现象----B的变化落后 B (B T) 于H 的变化 4. 居里温度----铁磁性 消失的临界温度
B H
四、磁致伸缩 B变 M 磁畴方向改变 晶格间距改变
铁磁体长度和体积改变— 磁致伸缩
长度相对改变约10-5量级 温下可达10 -1
某些材料在低
磁致伸缩有一定固有频率 当外磁场变 化频率和固有频率一致时 发生共振
可用于制作激振器、超声波发生器等
磁介质与电介质的比较
无磁荷 基本场量 B
4
取回路如图,设总匝数为N H dl H 2πr NI
L
O R1 r R2
NI nI H 2πr
细螺绕环
R1 R2 r
H nI B μ H μ nI
长直螺线管亦然
M ( μr 1) H ( μr 1)nI
j M 表
代入数据
M 7.9410 A/m
· 当T > Tc时,铁磁性消失, 铁磁质顺磁质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2第13章物质中的磁性§13-1 磁介质的磁化介质在磁场中被磁化,介质内的磁感应强度B 为真空中的磁感应强度B 0和附加磁感应强度B '之和.电场中电介质极化时束缚电荷产生的附加电场的方向与原电场方向始终相反而使电介质中的电场强度始终小于原场强的特点不同.B B B '+=01. 电介质在电场中极化的特点2. 磁介质在磁场中的磁化3依据附加磁感应强度B '的不同将磁介质分为三类:但磁介质在磁场中的极化与电介质在电场中极化不同铁磁质B >>B 0B '与B 0方向相同,且B '>>B 0B '与B 0方向相同顺磁质B > B 0B '与B 0方向相反抗磁质B < B 0-r II分子磁矩563.分子的附加磁矩∆p m外磁场中,电子旋进运动所产生的附加磁矩之和∆p m ,称分子的附加磁矩,其方向总是与B 0的方向相反.2.外磁场中电子旋进的附加磁矩∆P m有外磁场B 0时, 运动电子受洛伦兹力作用, 作旋进运动, 产生附加磁矩, 方向总是与B 0的方向相反.∆P mL B 0ed Lμμ与B 0夹角小于90︒∆I m I m M∆P m LB 0ed L μμ与B 0夹角大于90︒∆I mI m M L 进动的转向总是和B 0成右手螺旋关系d L = M d tM = μ⨯B 07三、顺磁质和抗磁质的磁化(1)顺磁质中, 每个分子都有一定的固有磁矩p m ≠0, 由于热运动, 任意宏观体积中分子磁矩之和∑p m = 0. 对外不显示磁性.(2)抗磁质中, 每个分子中所有电子磁矩的矢量和等于零, 分子固有磁矩p m =0.对外不显示磁性.无外磁场时的顺磁质(3)在磁场中,都会产生附加磁矩∆p m ,∆p m <<p m .1. 顺磁质和抗磁质的特点8(2)抗磁质磁化时,在外磁场B 0中只有电子旋进运动产生附加磁矩∆p m ,方向与外磁场相反,附加磁场B '与B 0方向相反,表现为抗磁性.(1)顺磁质磁化时,分子磁矩p m 转向外磁场B 0方向,使合磁矩∑p m ≠0,出现宏观磁性,产生附加磁场B ',方向与外磁场相同.(顺磁质磁化时,在外磁场B 0中还有电子旋进运动产生附加磁矩∆p m ,方向与外磁场相反,但∆p m <<p m .)外磁场I∑p m顺磁质的磁化2. 顺磁质和抗磁质的磁化B 'B 0顺磁质:∑∆p m 相对较小,可忽略抗磁质:∑p m =0,只有∑∆p 真空中:M =0表征磁介质磁化的程度介质内各点的M 可不同, 如相同称为均匀磁化(2) 磁化强度的意义V p p VP M mi mi imi ∆∆+=∆=∑∑∑102. 磁化强度与磁化电流的关系介质的磁化程度也可用磁化电流I m 来描述介质被磁场B 0均匀磁化,对顺磁质,磁化强度M 与B 0方向一致I mMI磁化电流也称分子面电流、束缚(面)电流介质内的分子电流相互抵消,外表面形成了环形等效电流I m ,与M 成右手螺旋关系.IIB 0M I∙长直螺线管∙通电后产生均匀磁场B 0∙充满均匀磁介质∙介质被均匀磁化(1) 磁化电流与磁化强度M 之间必有联系!∑⎰=∙内L L I l H 0d 称为有介质时的安培环路定理磁场强度H 沿任意闭合路径过该路径所包围的传导电流的、磁导率H B 0 μ+=⇒由定义式:B H =0μ各向同性的磁介质中B17(a)H 与M 成正比:H M mχ=χm > 0 →顺磁质,χm < 0→抗磁质,χm 很大, 且不是恒量→铁磁质.χm 为磁化率为无量纲量因此顺磁质, H 、M 的方向相同抗磁质, H 、M 的方向相反由于:HM H B m)1(000χμμμ+=+=令:—相对磁导率H H B rμμμ==0μ—磁导率μr =1+χm20(2) 求由磁化电流产生的磁感应强度B 'B B B'+=0由于顺磁质B '与B 0同方向解法一:L∆l B,H μr利用磁介质中的磁场B 为真空中的磁感应强度B0和磁化电流产生的磁感应强度B '的叠加B,H μrB 0=μ0nI B '=B -B 0=μ0μr nI -μ0nI=μ0(μr -1)nIB =B 0 +B '21nI '为单位长度的磁化电流解法二:因为是各向同性均匀顺磁介质, 磁化电流的流动方向→与导体中的传导电流一致, 故磁化电流也相当于一个无限长直螺线管B,HμrB '=μ0nI '=μ0(nI ') = μ0 j m = μ0M=μ0χm H =μ0(μr -1)H =μ0(μr -1)nI例:半径为R的长直载流圆柱导体沿轴向均匀通电流强度为I 的传导电流, 周围充满相对磁导率为μr的各向同性均匀顺磁介质.求(1)磁介质中的磁感应强度(2)和圆柱体导体接触的介质面上的磁化线电流密度和磁化电流大小μrRrIlOP解:磁化电流只分布在介质与导体的接触面上, 它的方向与传导电流的方向相同(顺磁),沿接触面(圆柱面)均匀分布.分析:由于传导电流和磁化电流都具有相同的均匀轴对称分布,故磁场也具有轴对称分布, 即离开轴相等的距离处有大小相等的磁场强度H, 其方向为矢径方向2228铁磁质的主要特性:④存在临界温度T C ,称居里点,高于T C 时铁磁质转化为顺磁质(如铁T C =1040K,镍T C =631K,钴T C =1388K).①B '>>B 0,磁化率χm 高,可达101~105;②μr 、χm 不是常量, 磁化过程为非线性, 过程不可逆;③外场停止作用后,仍能保留部分磁性;§13.4 铁磁质291. 实验装置H =nI 铁芯中磁场强度为:(2) 用磁通计中可测磁感应强度B 由此可得磁场强度与磁感应强度的关系曲线——磁化曲线H = —-MBμ0磁化曲线:B 随H 的变化关系称为磁化曲线.一、铁磁质的磁化规律B = μ0H +μ0M = μH(1) 调节线圈中电流I 可以改变H 次级线圈接磁通计I30oA 段,起始μ较小,B 随H 的增加上升缓慢,AD 段μ较大,B 急剧增加,然后μ又减小,H 达到H S 时,B 趋于极限值B S ,B S 称为饱和磁感应强度.B HoA D SB SH S 3. 磁滞回线BbS H H sc B r o -Hs -H c H cc'S'b'铁磁质的磁滞回线HB μ=2. 起始磁化曲线次级线圈I31(4)磁滞回线:继续增加反向磁场,达到反向磁饱和状态S ',再减小磁场,磁化曲线与正向相曲线相似,形成闭合曲线.(1)剩磁:减小H ,B 随之减小,但并不沿原磁化曲线下降,当H 降至零时,B 并不降至零,有剩余磁感应强度B r ,此时铁磁体成为永磁体.(2)磁滞现象:B 值“落后”于H 值的现象.(3)矫顽力:要使剩磁B r 消失需加反向磁场H c ,使B =0,它反映了铁磁质保留剩磁的能力.B B r S'S b c c'-H s-H c H c H s H b'o 铁磁质的磁滞回线32(5)B 与H 的关系:(a)不仅是非线性的,而且是非单值的;(b)B 与H 当前的数值有关外,还与磁介质的磁化历史有关.4. 磁滞损耗在反复磁化过程中的能量损耗成为磁滞损耗,它与磁滞回线所围成的面积有关硬磁材料-H CH C B r -B r B H 矩形材料-H C H C B r -B rB H 软磁材料-HC H C B r -B r B s -B s BH33例:图示为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是B =μ0H 的关系.说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线:a 代表_______的B ~H 关系曲线;b 代表_______的B ~H 关系曲线;c 代表_______的B ~H 关系曲线.铁磁质顺磁质抗磁质由公式B =μH = μ0μr HHB a b c o 解:铁磁质:μr 为非线性;顺磁质:μr 为线性,B 大于真空中的B 0,虚线表示真空中的关系;抗磁质:μr 为线性,B 小于真空中的B 0.二、铁磁质的微观结构铁磁材料中相邻原子中的电子自旋磁矩通过交换耦合作用而平行磁畴排列, 形成一个自发磁化达饱和状态的微小区域—磁畴.在无外场时, 每个磁畴内的磁矩取同向, 但各磁畴排列杂乱, 宏观不显磁性.在外场作用下, 磁畴转向, 表现为磁化过程.3435(1)由于摩擦阻力, 出现剩磁;(2)温度升高, 磁畴被破坏,表现为居里点, 磁畴的体积为: 10-8~10-12m 3,约1017~1021个原子.磁畴结构的铁粉图形H=0H H H H 磁化过程中磁畴结构变化示意图本章结束!36。
