中值定理及其应用课件
合集下载
数学分析第六章微分中值定理及其应用课件1

即 f '() 0
例如, f ( x) x2 2x 3 ( x 3)(x 1).
在[1,3]上连续, 在(1,3)上可导, 且 f (1) f (3) 0,
f ( x) 2( x 1), 取 1, (1 (1,3)) f () 0.
几何解释:
y
C
在曲线弧AB上至少有一
点C , 在该点处的切线是
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 (1)如果函数 f(x)在 闭区间[a, b]上连续(,2在) 开区间(a, b) 内可导,那末在 (a, b)内至少有一点(a b),使等式
f (b) f (a) f ' ()(b a) 成立.
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
使 f ( x) 0.
又例如,
y
1 0,
x, x
x 0
(0,1] ;
y x, x [0,1].
例1 证明方程 x5 5x 1 0 有且仅有一个小于
1 的正实根.
证 设 f ( x) x5 5x 1, 则 f ( x)在[0,1]连续,
且 f (0) 1, f (1) 3.
由介值定理
所得曲线a, b两端点的函数值相等.
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F ( x) 满足罗尔定理的条件,
则在(a, b)内至少存在一点, 使得 F () 0.
即 f () f (b) f (a) 0 ba
或 f (b) f (a) f ()(b a).
拉格朗日中值公式
例如, f ( x) x2 2x 3 ( x 3)(x 1).
在[1,3]上连续, 在(1,3)上可导, 且 f (1) f (3) 0,
f ( x) 2( x 1), 取 1, (1 (1,3)) f () 0.
几何解释:
y
C
在曲线弧AB上至少有一
点C , 在该点处的切线是
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 (1)如果函数 f(x)在 闭区间[a, b]上连续(,2在) 开区间(a, b) 内可导,那末在 (a, b)内至少有一点(a b),使等式
f (b) f (a) f ' ()(b a) 成立.
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
使 f ( x) 0.
又例如,
y
1 0,
x, x
x 0
(0,1] ;
y x, x [0,1].
例1 证明方程 x5 5x 1 0 有且仅有一个小于
1 的正实根.
证 设 f ( x) x5 5x 1, 则 f ( x)在[0,1]连续,
且 f (0) 1, f (1) 3.
由介值定理
所得曲线a, b两端点的函数值相等.
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F ( x) 满足罗尔定理的条件,
则在(a, b)内至少存在一点, 使得 F () 0.
即 f () f (b) f (a) 0 ba
或 f (b) f (a) f ()(b a).
拉格朗日中值公式
《中值定理》课件

魏尔斯特拉斯逼近定理
魏尔斯特拉斯逼近定理是中值定理中的一种,它指出任何连续函数都可以中值定理是中值定理中的一种,它描述了函数在一个区间内存在某个点,该点处的瞬时变化率等于该区间 平均变化率的值。
柯西中值定理
柯西中值定理是中值定理中的一种,它更具有一般性,适用于实数区间和复 数区间上的函数。它指出了当两个函数经过某个点处函数值相等时,这两个 函数在某个点处的导数也相等。
《中值定理》PPT课件
欢迎来到本次关于《中值定理》的PPT课件。在这个课件中,我们将深入探讨 中值定理的定义、数学表述、证明以及应用,并比较三种不同中值定理之间 的异同。接下来,让我们开始吧!
什么是中值定理
中值定理是微积分中的重要定理之一,它研究函数在一个区间上的平均变化率与瞬时变化率之间的关系。它包括三 种不同的定理,分别是魏尔斯特拉斯逼近定理、拉格朗日中值定理和柯西中值定理。
总结
通过比较三种不同中值定理的异同,我们能更好地了解它们在解决不同问题 时的特点和适用范围。中值定理在微积分、数学物理以及其他领域都有广泛 的应用。继续深入学习中值定理,将为你的数学知识打下坚实的基础。
第三章中值定理与导数的应用课件
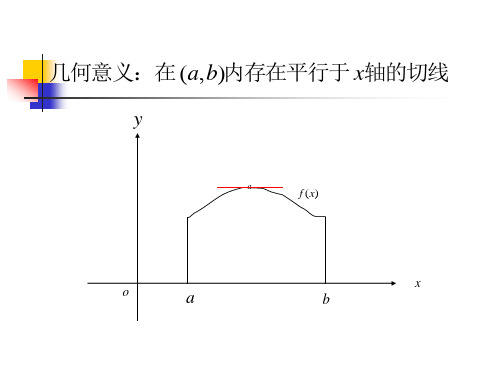
那么在(a,b)内至少有一点 使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
《积分中值定理》课件

积分中值定理在实数理论中有重要应用, 如证明实数的连续性、稠密性等性质。
在其他数学领域的应用实例
复变函数
积分中值定理在复变函数中有广泛的应用, 如在解决柯西积分公式、留数定理等问题时 起到关键作用。
概率论与数理统计
积分中值定理在概率论与数理统计中有重要 应用,如在计算期望、方差等统计量时起到 关键作用。
03
综上所述,积分中值定理是一个具有 重要性和意义的数学定理。在未来的 研究中,我们需要进一步深入探索其 应用范围和条件,并尝试将其应用于 更广泛的领域,以推动数学和其他学 科的发展。
THANKS
感谢观看
利用微积分基本定理证明积分中值定理
总结词
通过利用微积分基本定理和函数的单调性,证明积分中值定理。
详细描述
首先,我们选取一个连续函数$f(x)$,并设其在区间$[a, b]$上非负且不恒为零。然后 ,我们证明函数$F(x) = int_{a}^{x}f(t)dt$在$[a, b]$上单调增加。由于$F(x)$单调增加 ,存在一个点$c in (a, b)$使得$frac{F(b) - F(a)}{b - a} = f(c)$。最后,我们得出结论
对积分中值定理未来的研究方向和展望
01
积分中值定理的研究已经取得了丰硕 的成果,但仍有许多值得探索的问题 。例如,对于更一般的函数空间和更 复杂的积分问题,如何应用积分中值 定理进行有效的处理?这需要我们进 一步深入研究积分中值定理的适用范 围和条件。
02
随着数学和其他学科的不断发展,积 分中值定理的应用领域也在不断扩大 。未来,我们可以尝试将积分中值定 理应用于更广泛的领域,如金融、经 济、生物等,以解决实际问题。同时 ,我们也可以探索积分中值定理与其 他数学理论的交叉应用,以推动数学 的发展。
在其他数学领域的应用实例
复变函数
积分中值定理在复变函数中有广泛的应用, 如在解决柯西积分公式、留数定理等问题时 起到关键作用。
概率论与数理统计
积分中值定理在概率论与数理统计中有重要 应用,如在计算期望、方差等统计量时起到 关键作用。
03
综上所述,积分中值定理是一个具有 重要性和意义的数学定理。在未来的 研究中,我们需要进一步深入探索其 应用范围和条件,并尝试将其应用于 更广泛的领域,以推动数学和其他学 科的发展。
THANKS
感谢观看
利用微积分基本定理证明积分中值定理
总结词
通过利用微积分基本定理和函数的单调性,证明积分中值定理。
详细描述
首先,我们选取一个连续函数$f(x)$,并设其在区间$[a, b]$上非负且不恒为零。然后 ,我们证明函数$F(x) = int_{a}^{x}f(t)dt$在$[a, b]$上单调增加。由于$F(x)$单调增加 ,存在一个点$c in (a, b)$使得$frac{F(b) - F(a)}{b - a} = f(c)$。最后,我们得出结论
对积分中值定理未来的研究方向和展望
01
积分中值定理的研究已经取得了丰硕 的成果,但仍有许多值得探索的问题 。例如,对于更一般的函数空间和更 复杂的积分问题,如何应用积分中值 定理进行有效的处理?这需要我们进 一步深入研究积分中值定理的适用范 围和条件。
02
随着数学和其他学科的不断发展,积 分中值定理的应用领域也在不断扩大 。未来,我们可以尝试将积分中值定 理应用于更广泛的领域,如金融、经 济、生物等,以解决实际问题。同时 ,我们也可以探索积分中值定理与其 他数学理论的交叉应用,以推动数学 的发展。
《中值定理应用》PPT课件

x x0 x x0
(2) f , g在( x0 , x0 )可导 , 且g( x) 0,
f ( x ) ( 3) lim a , ( a 为 有 限 实 数 或 无 穷 大 ) x x0 g( x )
0 ( ) 0
f ( x ) f ( x) lim a . 则 : lim x x x x0 g ( x ) 0 g( x )
在[0, x0 ]上连续, 在(0, x0 )上可导, 且
F (0) F ( x0 ) 0, 则根据 Rolle 定理
(0, x0 ), 使
n n1 F ( ) (a0 x a1 x an1 x )
[na0 x
n1
a1 (n 1) x
f (a ) k f (a ) f (b) f (b) k G (a ) G (b) a b ab
8
因此 (a, b), 使
f ( x) k G( ) 0 x x f ( ) ( f ( ) k ) 即 0 2
16
证 由条件(1), 若f ( x)在x0点不连续 , 只要
补充定义 : f ( x0 ) g( x0 ) 0, 则 f , g 均在
又 g( x ) 0, 因而 f , g满足Cauchy中值定理
且在( x0 , x0 )内可导, [ x0 , x0 ]上连续,
即有
洛
1 x (k ) 1 (k 3,4,, n) ak (e ) 归纳地可得: k! k! x 0
24
于是所求的 n 次多项式为:
Pn ( x) a0 a1 x a2 x an x 1 2 1 n 1 x x x 2! n! 1 2 1 n n x 1 x x x o ( x ) 而 f ( x) e 2! n! f (0) 2 f ( n ) ( 0) n n f ( 0) f ( 0) x x x o( x ) 2! n!
(2) f , g在( x0 , x0 )可导 , 且g( x) 0,
f ( x ) ( 3) lim a , ( a 为 有 限 实 数 或 无 穷 大 ) x x0 g( x )
0 ( ) 0
f ( x ) f ( x) lim a . 则 : lim x x x x0 g ( x ) 0 g( x )
在[0, x0 ]上连续, 在(0, x0 )上可导, 且
F (0) F ( x0 ) 0, 则根据 Rolle 定理
(0, x0 ), 使
n n1 F ( ) (a0 x a1 x an1 x )
[na0 x
n1
a1 (n 1) x
f (a ) k f (a ) f (b) f (b) k G (a ) G (b) a b ab
8
因此 (a, b), 使
f ( x) k G( ) 0 x x f ( ) ( f ( ) k ) 即 0 2
16
证 由条件(1), 若f ( x)在x0点不连续 , 只要
补充定义 : f ( x0 ) g( x0 ) 0, 则 f , g 均在
又 g( x ) 0, 因而 f , g满足Cauchy中值定理
且在( x0 , x0 )内可导, [ x0 , x0 ]上连续,
即有
洛
1 x (k ) 1 (k 3,4,, n) ak (e ) 归纳地可得: k! k! x 0
24
于是所求的 n 次多项式为:
Pn ( x) a0 a1 x a2 x an x 1 2 1 n 1 x x x 2! n! 1 2 1 n n x 1 x x x o ( x ) 而 f ( x) e 2! n! f (0) 2 f ( n ) ( 0) n n f ( 0) f ( 0) x x x o( x ) 2! n!
《中值定理应用》课件

物理学
在物理学中,中值定理被用于解释和预测流体动力学、 电磁学等领域的现象,为物理学家提供了重要的工具。
中值定理的未来研究方向
深化理解
未来研究中,需要进一步深化对中值定理的理解,探索其在数学和其他领域中的更多应用。
交叉学科应用
鼓励跨学科的研究,将中值定理与其他数学分支或其他领域的知识相结合,开拓新的应用领域。
拉格朗日中值定理
如果一个函数在闭区间上连续,开区 间上可导,则存在至少一个点,使得 在该点的导数等于函数在该区间内平 均变化率的乘积。
在微分学中的应用
泰勒中值定理
任何在闭区间上连续的函数都可以用多项式 函数来近似,多项式的阶数取决于所要求的 精度。
柯西中值定理
如果两个函数在闭区间上连续,开区间上可 导,且在区间两端取值相等,则至少存在一 个点,使得两个函数在该点的导数之比等于 它们在该区间内平均变化率的比值。
中值定理应用
目录
CONTENTS
• 中值定理简介 • 中值定理的应用场景 • 中值定理在数学分析中的应用 • 中值定理在其他领域的应用 • 中值定理的最新研究进展
01 中值定理简介
中值定理的定义
罗尔定理
拉格朗日中值定理
柯西中值定理
如果函数$f(x)$在闭区间$[a,b]$上连 续,在开区间(a,b)上可导,且 $f(a)=f(b)$,那么在开区间(a,b)内至 少存在一点$xi$,使得$f'(xi)=0$。
中值定理在数学研究中的新进展
新的证明方法
近年来,数学家们不断探索中值定理的新证明方法, 使得定理的证明更加简洁明了,有助于加深对中值定 理的理解。
扩展到高维空间
随着数学的发展,中值定理的应用范围逐渐扩展到高 维空间,为解决高维数学问题提供了新的思路和方法 。
《微分学中值定理》课件

a. 证明f(x)在区间[a,b]上连续 b. 证明f(x)在(a,b)内可导 c. 利用极限的定义证明柯西定理
结论:柯西定理是微分学中值定理的一个重要结果,对于理解微 分学的基本概念和定理具有重要意义。
单击此处输入你的项正文,文字是您思想的提炼,言简意赅的阐述观点。 Nhomakorabea04
微分学中值定理的推论
推论一:若函数在某区间内可导,则函数在该区间内单调
推论二:若函数在某区间内可导,则函数在该区间内至多 存在一个极值点
极值点的定义:函数在某点处的导数为0,且该点两侧的导数符号相 反
极值点的存在性:若函数在某区间内可导,则函数在该区间内至多 存在一个极值点
极值点的唯一性:若函数在某区间内可导,且该区间内只有一个极 值点,则该极值点为函数的最大值或最小值
极值点的应用:在微分学中,极值点是研究函数性质的重要工具, 可以用于求解函数的最大值和最小值,以及判断函数的单调性等。
推论三:若函数在某区间内可导,则函数在该区间内取得 极值的必要条件
必要条件:函数在某区间内可导
极值:函数在某点处的值大于或小于其附近点的值
证明:通过微分学中值定理的推论,可以证明函数在某区间内取得极值的必要条件
利用微分学中值定理解决实际问题
实例1:求解函数在某点处的导 数
实例2:求解函数在某区间上的 最大值和最小值
实例3:求解函数在某点处的斜 率
实例4:求解函数在某点处的切 线方程
06
微分学中值定理的扩展
泰勒定理与微分学中值定理的关系
泰勒定理是微分 学中值定理的推 广和延伸
泰勒定理将微分 学中值定理中的 函数值扩展到函 数值和导数值
应用:在解决实际问题时,可以利用这个推论来判断函数是否取得极值,从而找到最优解
结论:柯西定理是微分学中值定理的一个重要结果,对于理解微 分学的基本概念和定理具有重要意义。
单击此处输入你的项正文,文字是您思想的提炼,言简意赅的阐述观点。 Nhomakorabea04
微分学中值定理的推论
推论一:若函数在某区间内可导,则函数在该区间内单调
推论二:若函数在某区间内可导,则函数在该区间内至多 存在一个极值点
极值点的定义:函数在某点处的导数为0,且该点两侧的导数符号相 反
极值点的存在性:若函数在某区间内可导,则函数在该区间内至多 存在一个极值点
极值点的唯一性:若函数在某区间内可导,且该区间内只有一个极 值点,则该极值点为函数的最大值或最小值
极值点的应用:在微分学中,极值点是研究函数性质的重要工具, 可以用于求解函数的最大值和最小值,以及判断函数的单调性等。
推论三:若函数在某区间内可导,则函数在该区间内取得 极值的必要条件
必要条件:函数在某区间内可导
极值:函数在某点处的值大于或小于其附近点的值
证明:通过微分学中值定理的推论,可以证明函数在某区间内取得极值的必要条件
利用微分学中值定理解决实际问题
实例1:求解函数在某点处的导 数
实例2:求解函数在某区间上的 最大值和最小值
实例3:求解函数在某点处的斜 率
实例4:求解函数在某点处的切 线方程
06
微分学中值定理的扩展
泰勒定理与微分学中值定理的关系
泰勒定理是微分 学中值定理的推 广和延伸
泰勒定理将微分 学中值定理中的 函数值扩展到函 数值和导数值
应用:在解决实际问题时,可以利用这个推论来判断函数是否取得极值,从而找到最优解
高中数学(人教版)第6章微分中值定理及其应用拉格朗日定理和函数的单调性课件

b a , a b.
注 例3中的不等号可以成为严格的. 事实上, 当
0 a b 和 a b 0时, 显然不为零, 严格不等
式成立.
罗尔定理与拉格朗日定理
当 a 0 b 时,
存在 1 (0, b), 2 (a , 0), 使得
arctan b arctan a arctan b arctan 0 arctan 0 arctan a
x x0
x x0
罗尔定理与拉格朗日定理
证 分别按左右极限来证明.
(1) 任取 x U ( x0 ), f ( x ) 在 [ x0 , x] 上满足拉格朗日
定理条件, 则存在 ( x0 , x ), 使得
f ( x ) f ( x0 ) f ( ). x x0
多项式, 所以 p( x )在[x1 , x2 ]上满足罗尔定理的条件,
从而存在 (a, b), 使得 p( ) 0, 这与条件矛盾. 又若 p( x ) 有一个 k 次重根 x0 , 则
p( x ) ( x x0 )k p1 ( x ), k 2.
( x ), 因为 p( x ) k ( x x0 )k 1 p1 ( x ) ( x x0 )k p1
3.若 f (x) 在(a, b) 上可微, [a, b] 上连续, 则对于任意
x (a , b], 存在 (a , x ), 使
f ( x ) f (a ) f ( )( x a ),
当 x a 时, 必有 a . 从等式
由于x0 x , 因此当x x0 时,随之有 x0 ,
对上式两边求极限,便得
f ( x ) f ( x0 ) lim lim f ( ) f ( x0 0). x x0 x x0 x x0
注 例3中的不等号可以成为严格的. 事实上, 当
0 a b 和 a b 0时, 显然不为零, 严格不等
式成立.
罗尔定理与拉格朗日定理
当 a 0 b 时,
存在 1 (0, b), 2 (a , 0), 使得
arctan b arctan a arctan b arctan 0 arctan 0 arctan a
x x0
x x0
罗尔定理与拉格朗日定理
证 分别按左右极限来证明.
(1) 任取 x U ( x0 ), f ( x ) 在 [ x0 , x] 上满足拉格朗日
定理条件, 则存在 ( x0 , x ), 使得
f ( x ) f ( x0 ) f ( ). x x0
多项式, 所以 p( x )在[x1 , x2 ]上满足罗尔定理的条件,
从而存在 (a, b), 使得 p( ) 0, 这与条件矛盾. 又若 p( x ) 有一个 k 次重根 x0 , 则
p( x ) ( x x0 )k p1 ( x ), k 2.
( x ), 因为 p( x ) k ( x x0 )k 1 p1 ( x ) ( x x0 )k p1
3.若 f (x) 在(a, b) 上可微, [a, b] 上连续, 则对于任意
x (a , b], 存在 (a , x ), 使
f ( x ) f (a ) f ( )( x a ),
当 x a 时, 必有 a . 从等式
由于x0 x , 因此当x x0 时,随之有 x0 ,
对上式两边求极限,便得
f ( x ) f ( x0 ) lim lim f ( ) f ( x0 0). x x0 x x0 x x0
