m法计算弯矩剪力图
合集下载
弯曲应力及强计算
中性轴
正应力沿截面高度呈线性分布，
中性轴上为零，其最大值发生
在截面的上下边缘处。
横力弯曲正应力
横力弯曲时的正应力，用纯弯曲正应力公式计算 不会引起很大的误差，能够满足工程问题所需的 精度。
等直梁 max
Mmax所在横截面 离中性轴最远处
max
Mmax IZ
ymax
等直梁的最大弯曲正应力公式
8 hb 2
12MPa
6
【例2】一矩形截面的简支梁，梁上作用有均布荷载，已
知：l=4m，b=140mm，h=210mm，q=2kN/m，弯曲时木
材的容许正应力 10MPa ，试校核该梁的强度。
解：作梁的弯矩图
q
h
M max
ql 2 8
2 42 8
4kN.m
l
b
WZ
bh 2 6
z
横截面
（1）中性层是对整个截面而言的，中性轴是对某 个截面而言的。
（2）中性轴通过横截面的形心，是截面的 形心主惯性轴。
三、 弯曲正应力公式
My z
I z
M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
MZ: 横截面上的弯矩
y: 所求应力点到中性轴的距离 M
M
IZ: 截面对中性轴的惯性矩
上式表面:弯曲横截面上的
M max W
M max h3
9
取 h=300mm 则：b=200mm
小结：
一、 弯曲正应力公式
梁的剪力和弯矩剪力图和弯矩图
2、计算1-1 截面旳内力 FA
3、计算2-2 截面旳内力
M2
F=8kN
FS1
M1 FS1 FA F 7kN M1 FA 2 F (2 1.5) 26kN m
q=12kN/m
FS2
FB
FS2 q 1.5 FB 11kN
M2
FB
1.5 q 1.5 1.5 2
30kN m
2
1
例题
求下图所示简支梁1-1与2-2截面旳剪力和弯矩。
F=8kN
q=12kN/m
A 2m
FA 1.5m
1 1 1.5m
2
B
2
1.5m
3m
FB
解： 1、求支反力
3 M B 0 FA 6 F 4.5 q 3 2 0 FA 15kN
Fy 0 FA FB F q 3 0 FB 29kN
梁任意横截面上旳剪力，等于作用在该截面左边 （或右边）梁上全部横向外力旳代数和。截面左 边向上旳外力(右边向下旳外力)使截面产生正旳 剪力，反之相反。【左上右下为正，反之为负】 梁任意横截面上旳弯矩，等于作用在该截面左 边（或右边）全部外力（涉及外力偶）对该截面 形心之矩旳代数和。截面左边（或右边）向上旳 外力使截面产生正弯矩，反之相反。【左顺右逆 为正，反之为负】
一、梁平面弯曲旳概念
1、平面弯曲旳概念
弯曲变形：作用于杆件上旳外力垂直于杆件旳轴线，使 杆旳轴线由直线变为曲线。
平面弯曲：梁旳外载荷都作用在纵向对称面内时，则梁旳轴 线在纵向对称面内弯曲成一条平面曲线。
q F
Me 纵 向
对称面
B
A
x
y FAy
FBy
以弯曲变形为主旳直杆称为直梁，简称梁。 平面弯曲是弯曲变形旳一种特殊形式。
剪力与弯矩的计算方法
§7-2剪力与弯矩一、剪力和弯矩根据作用在梁上的已知载荷，求出静定梁的支座反力以后，梁横截面上的内力可利用前面讲过的“截面法”来求解，如图7-8a 所示简支梁在外力作用下处于平衡状态，现在讨论距A 支座距离为x 的m m -截面上的内力。
图7-8简支梁指定截面的剪力、弯矩计算根据截面法计算内力的基本步骤“切、代、平”，计算梁的内力的步骤为：①、首先根据静力平衡方程求支座反力Ay F 和By F ，为推导计算的一般过程，暂且用Ay F 和By F 代替。
②、用截面假想沿m m -处把梁切开为左、右两段，如图7-8b、7-8c 所示，取左段梁为脱离体，因梁原来处于平衡状态，所以被截取的左段梁也同样保持平衡状态。
从图7-8b 中可看到，左段梁上有一向上的支座反力Ay F 、向下的已知力1P 作用，要使左段梁不发生竖向移动，则在m m -截面上必定存在一个竖直方向的内力S F 与之平衡；同时，Ay F 、1P 对m m -截面形心O 点有一个力矩，会引起左段梁转动，为了使其不发生转动，在m m -截面上必须有一个力偶矩M 与之平衡，才能保持左段梁的平衡。
S F 和M 即为梁横截面上的内力，其中内力S F 使横截面有被剪开的趋势，称为剪力；力偶矩M 将使梁发生弯曲变形，称为弯矩。
由于外载荷的作用线垂直于梁的轴线，所以轴力为零，通常不予考虑。
剪力S F 和弯矩M 的大小可由左段梁的静力平衡方程来求解。
由0=∑Y 得：10Ay S F P F --=，得1S Ay F F P =-由0o M =∑得：()01=+-+-M a x P x F Ay 得()a x P x F M Ay --=1如图7-8c 所示，如果取右段梁为脱离体，同样可求得m m -截面的剪力S F 和弯矩M 。
根据作用力与反作用力原理，右段梁在m m -截面上的剪力S F 和弯矩M 与左段梁在m m -截面上的剪力S F 和弯矩M 应大小相等，方向相反。
工程力学内力图-剪力图和弯矩图
例题9-6 图a所示简支梁在C点受矩为Me的集中力偶作用。试作梁的剪力图 和弯矩图。
解：1. 求约束力
FA
Me l
,
FB
Me l
2. 列剪力方程和弯矩方程
FS(x)
M x
x
此简支梁的两支座之间无集中 荷载作用，故作用于AC段梁和BC段 梁任意横截面同一侧的集中力相同， 从而可知两段梁的剪力方程相同，即
说明梁跨中横截面上的弯矩值最大，为
M max
ql 2 8
则x l 2
例题9−5 图a所示的简支梁，在C点处受集中力F的作用， 试作梁的剪力图和弯矩图。
F x
(a) A
aC
b
B
FA
l
FB
解： 1. 求支座反力。利用平衡方程求得
FA
b l
F
a FB l F
2.列剪力方程和弯矩方程
对于AC段梁：
； 集中荷载作用处( x=a)横截面上的
弯矩值最大，
FS,m a x
Fb l
。
M max
Fab l
4. 讨论
由剪力图可见，在梁上 的集中力(包括集中荷载和 约 束力)作用处剪力图有突变， 这是由于集中力实际上是将 作用在梁上很短长度x范围 内的分布力加以简化所致。若将分布力看作在x范围内是 均匀的(图a),则剪力图在x范围内是连续变化的斜直线( 图b)。从而也就可知，要问集中力作用处梁的横截面上的 剪力值是没有意义的。
l
3. 作剪力图和弯矩图
FS x
Me l
0 x l
M x Me x
l
0 x a
剪力图与弯矩图的画法_图文_图文
剪力图与弯矩图的画法_图文_图文.ppt
dM(x) = Q(x)
dx
dQ(x) = q(x)
dx
2
d M(x)
2
= q(x)
dx
公式的几何意义
剪力图上某点处的切线斜率等于该点 处荷载集度的大小 弯矩图上某点处的切线斜率等于该点 处剪力的大小。
梁上最大弯矩可能发生在 Q(x) = 0 的截面上 或梁段 边界的截面上。最大剪力 发生在全梁或梁段的界面。
解： 在AC段中 q=0 ，且 QA=RA
q
A
B
CE
D
0.2
1.6
1
2
q
在AC段中 Qc = 80KN，剪力图
A
B
CE
D
为矩形，MA =0
0.2
1.6
1
2
80KN
(b)
+
80KN
q
在CE段中，剪力图为三角形
A
B
CE
D
QC=80KN，MC=16KN.m
0.2
1.6
1
2
80KN
(b)
+
80KN
81KN
CD段： 向右下方的斜直线
DB段：水平直线
最大剪力发生在 CD 和 DB 段的任一横截面上。
1
A C
0.2
1
q
E
1.6 2
2
B D
80KN
+
80KN
MB = 0
全梁的最大2
1
q
E
1.6 2
2
B D
16 16
+
单位：KN.m
例 作梁的内力图
A
dM(x) = Q(x)
dx
dQ(x) = q(x)
dx
2
d M(x)
2
= q(x)
dx
公式的几何意义
剪力图上某点处的切线斜率等于该点 处荷载集度的大小 弯矩图上某点处的切线斜率等于该点 处剪力的大小。
梁上最大弯矩可能发生在 Q(x) = 0 的截面上 或梁段 边界的截面上。最大剪力 发生在全梁或梁段的界面。
解： 在AC段中 q=0 ，且 QA=RA
q
A
B
CE
D
0.2
1.6
1
2
q
在AC段中 Qc = 80KN，剪力图
A
B
CE
D
为矩形，MA =0
0.2
1.6
1
2
80KN
(b)
+
80KN
q
在CE段中，剪力图为三角形
A
B
CE
D
QC=80KN，MC=16KN.m
0.2
1.6
1
2
80KN
(b)
+
80KN
81KN
CD段： 向右下方的斜直线
DB段：水平直线
最大剪力发生在 CD 和 DB 段的任一横截面上。
1
A C
0.2
1
q
E
1.6 2
2
B D
80KN
+
80KN
MB = 0
全梁的最大2
1
q
E
1.6 2
2
B D
16 16
+
单位：KN.m
例 作梁的内力图
A
剪力以及弯矩剪力图以及弯矩图
剪力图和弯矩图在工程管理中的应用
结构设计：用于计 算结构受力确定结 构尺寸和材料
施工管理：用于 指导施工确保施 工质量和安全
维护管理：用于 评估结构状态制 定维护计划
优化设计：用于 优化结构设计降 低成本和能耗
剪力图和弯矩图的注意 事项
绘制剪力图和弯矩图时应注意的事项
确保数据准确无误 注意单位换算确保单位一致 绘制过程中注意比例尺和坐标轴的设置 绘制完成后检查图例、标题、标注等是否清晰明确
添加副标题
剪力和弯矩剪力图以及弯矩 图
汇报人：
目录
CONTENTS
01 添加目录标题
02 剪力和弯矩的基本 概念
03 剪力图和弯矩图的 绘制
04 剪力图和弯矩图的 解读
05 剪力图和弯矩图的 应用
06 剪力图和弯矩图的 注意事项
添加章节标题
剪力和弯矩的基本概念
剪力和弯矩的定义
剪力：作用在物体表面上的力使物体发生剪切变形 弯矩：作用在物体表面上的力使物体发生弯曲变形 剪力图：表示剪力在物体表面上的分布情况 弯矩图：表示弯矩在物体表面上的分布情况
剪力和弯矩的计算方法
剪力：作用在物体上的力使物体发生剪切变形 弯矩：作用在物体上的力使物体发生弯曲变形 剪力计算方法：根据力的平衡原理利用剪力公式进行计算 弯矩计算方法：根据力的平衡原理利用弯矩公式进行计算
剪力和弯矩的单位和符号
剪力：单位为牛顿（N） 符号为F
弯矩：单位为牛顿·米 （N·m）符号为M
证结构安全
剪力图和弯矩图在施工中的应用
确定结构受力情况： 通过剪力图和弯矩图 可以了解结构的受力 情况为施工提供依据。
优化施工方案：根据 剪力图和弯矩图可以 优化施工方案提高施 工效率和质量。
梁的剪力和弯矩.剪力图和弯矩图
2、集中力偶作用处，M图发生
突变，顺下逆上，大小与M 同，FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN 4.5kN m
2kN m
D
A
C
B
FA 10kN
1m 2m
2m
7
3
x 1.56 2
3
2
2.44 2
E FB 2kN 1m
kN
kNm
例题
4.10
4kN m
6kN
1m
1m
4.5
kN
FL
0 xL 0x L
kNm
例题 4.6
图示外伸梁,,试作剪力图和弯矩图.
20kN 40kN m
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FS x1 20kN
X2
B
0 x1 1
25kN
M x1 20x1
0 x1 1
FS x2 25 10x2
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F FCs F
MC Fl MC Fl
MC 2Fl Fl 0
F
B
D
FDs
MD
F
DB
FDs F MD 0
截开后取左边为示力对象：
❖向上的外力引起正剪力，向下的外力引起负剪力； ❖向上的外力引起正弯矩，向下的外力引起负弯矩； ❖顺时针引起正弯矩，逆时针引起负弯矩。
剪力图是斜直线. 弯矩图是二次抛物线.
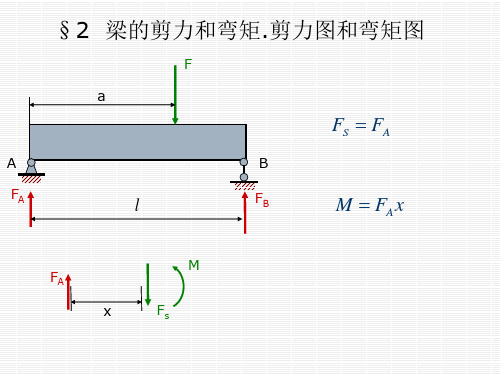
突变，顺下逆上，大小与M 同，FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN 4.5kN m
2kN m
D
A
C
B
FA 10kN
1m 2m
2m
7
3
x 1.56 2
3
2
2.44 2
E FB 2kN 1m
kN
kNm
例题
4.10
4kN m
6kN
1m
1m
4.5
kN
FL
0 xL 0x L
kNm
例题 4.6
图示外伸梁,,试作剪力图和弯矩图.
20kN 40kN m
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FS x1 20kN
X2
B
0 x1 1
25kN
M x1 20x1
0 x1 1
FS x2 25 10x2
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F FCs F
MC Fl MC Fl
MC 2Fl Fl 0
F
B
D
FDs
MD
F
DB
FDs F MD 0
截开后取左边为示力对象：
❖向上的外力引起正剪力，向下的外力引起负剪力； ❖向上的外力引起正弯矩，向下的外力引起负弯矩； ❖顺时针引起正弯矩，逆时针引起负弯矩。
剪力图是斜直线. 弯矩图是二次抛物线.
剪力图和弯矩图
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS(0) 0 FS(l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
绘剪力图和弯矩图的基本方法：首先分别写出梁 的剪力方程和弯矩方程，然后根据它们作图。
Fs(x)
o
x
o
x
Fs 图的坐标系
M(x) M 图的坐标系
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩，而向下 的外力则引起 负值 的弯矩。
例题：图示简支梁 ，在全梁上受集度为 q 的均布荷载作用。 试作此梁的剪力图和弯矩图。
FS 称为 剪力
y
FA
m
C
A
xm
FS x
由平衡方程
a
P
m
m C0
MFAx0
A
B
m
可得 M = FAx
x
内力偶 M 称为 弯矩
y
FA
m FS
C
x
A
xm
M
结论
a
P
m
梁在弯曲变形时，
横截面上的内力有
A
B
两个，即，
m x
剪力 FS 弯矩 M
y
FA
m FS
C
x
A
xm
M
取右段梁为研究对象。
y
FA
m FS
-
FS FS
dx
（2）弯矩符号 横截面上的弯矩使考虑的脱离体下边受拉，上边受压时为 正 。
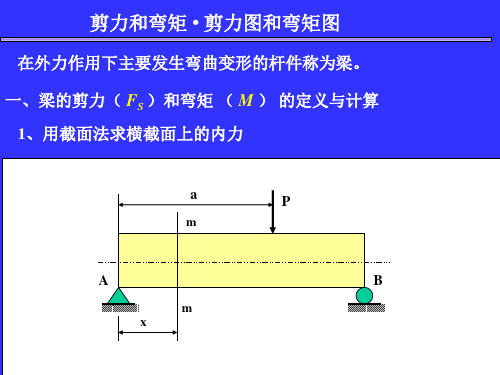
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS(0) 0 FS(l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
绘剪力图和弯矩图的基本方法：首先分别写出梁 的剪力方程和弯矩方程，然后根据它们作图。
Fs(x)
o
x
o
x
Fs 图的坐标系
M(x) M 图的坐标系
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩，而向下 的外力则引起 负值 的弯矩。
例题：图示简支梁 ，在全梁上受集度为 q 的均布荷载作用。 试作此梁的剪力图和弯矩图。
FS 称为 剪力
y
FA
m
C
A
xm
FS x
由平衡方程
a
P
m
m C0
MFAx0
A
B
m
可得 M = FAx
x
内力偶 M 称为 弯矩
y
FA
m FS
C
x
A
xm
M
结论
a
P
m
梁在弯曲变形时，
横截面上的内力有
A
B
两个，即，
m x
剪力 FS 弯矩 M
y
FA
m FS
C
x
A
xm
M
取右段梁为研究对象。
y
FA
m FS
-
FS FS
dx
（2）弯矩符号 横截面上的弯矩使考虑的脱离体下边受拉，上边受压时为 正 。
剪力弯矩计算
由于截面上有弯矩作用，截面各点在垂直于中轴线方向发生 相对位移，在截面内任意一点沿任意方向作用有弯矩。
剪力和弯矩的符号和单位
剪力的符号
用字母F表示，单位为牛顿（N）或千牛顿（kN）。
弯矩的符号
用字母M表示，单位为牛顿·米（N弯矩的关系
1
剪力和弯矩之间的关系可以通过弯曲正应力和 弯曲剪应力来表示。
剪力弯矩对基础的影响
01
02
03
基础沉降
剪力弯矩引起的结构变形 可能导致基础不均匀沉降 。
基础承载力
剪力弯矩会增大基础的承 载力，但也可能导致基础 剪切破坏。
基础稳定性
剪力弯矩可能影响基础的 稳定性，导致基础倾覆、 滑动等问题。
04
剪力弯矩的抗震计算
地震作用下的剪力弯矩计算
竖向地震作用
考虑结构自重以及地震加速度沿高度变化的影响，计算剪力 和弯矩。
矩的变化规律。
02
剪力弯矩的力学计算
静定梁的剪力弯矩计算
计算公式
剪力弯矩的计算公式为M=F*x。其中，F为梁所受的剪力，x为梁的跨度。
符号规定
梁的剪力弯矩符号规定为正，即向下为正，向上为负。
静定刚架的剪力弯矩计算
计算公式
静定刚架的剪力弯矩计算公式与静定梁相同，也为M=F*x。
符号规定
刚架的剪力弯矩符号规定为正，即向下为正，向上为负。
目标性能选择
根据建筑使用功能和结构重要性，选择合适的性能目标，如延性、承载力等 。
多方案比较
针对不同的性能目标，设计多种方案，比较其剪力弯矩等指标，选取最优方 案。
基于地震作用的剪力弯矩优化
地震烈度影响
考虑地震烈度对结构的影响，调整地震作用下的剪力弯矩计算方法。
剪力和弯矩的符号和单位
剪力的符号
用字母F表示，单位为牛顿（N）或千牛顿（kN）。
弯矩的符号
用字母M表示，单位为牛顿·米（N弯矩的关系
1
剪力和弯矩之间的关系可以通过弯曲正应力和 弯曲剪应力来表示。
剪力弯矩对基础的影响
01
02
03
基础沉降
剪力弯矩引起的结构变形 可能导致基础不均匀沉降 。
基础承载力
剪力弯矩会增大基础的承 载力，但也可能导致基础 剪切破坏。
基础稳定性
剪力弯矩可能影响基础的 稳定性，导致基础倾覆、 滑动等问题。
04
剪力弯矩的抗震计算
地震作用下的剪力弯矩计算
竖向地震作用
考虑结构自重以及地震加速度沿高度变化的影响，计算剪力 和弯矩。
矩的变化规律。
02
剪力弯矩的力学计算
静定梁的剪力弯矩计算
计算公式
剪力弯矩的计算公式为M=F*x。其中，F为梁所受的剪力，x为梁的跨度。
符号规定
梁的剪力弯矩符号规定为正，即向下为正，向上为负。
静定刚架的剪力弯矩计算
计算公式
静定刚架的剪力弯矩计算公式与静定梁相同，也为M=F*x。
符号规定
刚架的剪力弯矩符号规定为正，即向下为正，向上为负。
目标性能选择
根据建筑使用功能和结构重要性，选择合适的性能目标，如延性、承载力等 。
多方案比较
针对不同的性能目标，设计多种方案，比较其剪力弯矩等指标，选取最优方 案。
基于地震作用的剪力弯矩优化
地震烈度影响
考虑地震烈度对结构的影响，调整地震作用下的剪力弯矩计算方法。
梁的内力 剪力弯矩方程 剪力弯矩图
q=0 FS M q >0 q<0 当q<0,
(3)若某截面处FS=0
dF S dx
q(x)
dM dx
FS
d M dx
2
2
q(x)
则该截面上M取极值：当q>0, M取到极小值 当q<0, M取到极大值 （4）集中力F作用处，FS突变，跳跃值为F，M有尖点； q>0 q<0
集中力偶M作用处，M突变，跳跃值为M， FS不受影响。 F M
例题
例 题 2
2qa
A
§9 变形体静力学概述 及一般杆件内力分析
qa2 q
B C
解： 1.求约束力
FB q 2 a a 2 qa 3 a qa 2a 7 2 qa ( )
2
D
a
3 2 qa
FB a
a
a 2
FD
F D 4 qa
7 2
qa
1 2
qa ( )
D
FD
FD
F Ax 1 2 2 ( kN )( )
A
FAx
FAy
2m
F Ay 5 3 2 kN ( )
例题
例 题 4
5kN B
§9 变形体静力学概述 及一般杆件内力分析
4kN· m C
2.作内力图 D 3kN 轴力图： AB段 F N 2 kN
1m
1m
(F S )
1 qa
2
2.作内力图
1 2 qa
M
7 2
1 4 qa
2
B
2 qa
2
2qa (M)
qa
8
(3)若某截面处FS=0
dF S dx
q(x)
dM dx
FS
d M dx
2
2
q(x)
则该截面上M取极值：当q>0, M取到极小值 当q<0, M取到极大值 （4）集中力F作用处，FS突变，跳跃值为F，M有尖点； q>0 q<0
集中力偶M作用处，M突变，跳跃值为M， FS不受影响。 F M
例题
例 题 2
2qa
A
§9 变形体静力学概述 及一般杆件内力分析
qa2 q
B C
解： 1.求约束力
FB q 2 a a 2 qa 3 a qa 2a 7 2 qa ( )
2
D
a
3 2 qa
FB a
a
a 2
FD
F D 4 qa
7 2
qa
1 2
qa ( )
D
FD
FD
F Ax 1 2 2 ( kN )( )
A
FAx
FAy
2m
F Ay 5 3 2 kN ( )
例题
例 题 4
5kN B
§9 变形体静力学概述 及一般杆件内力分析
4kN· m C
2.作内力图 D 3kN 轴力图： AB段 F N 2 kN
1m
1m
(F S )
1 qa
2
2.作内力图
1 2 qa
M
7 2
1 4 qa
2
B
2 qa
2
2qa (M)
qa
8
材料力学-5-弯矩图与剪力图
从所得到的剪力图和 弯矩图中不难看出:
在集中力作用点两 侧截面上的剪力是不相 等的，而在集中力偶作 用处两侧截面上的弯矩 是不相等的，其差值分 别为集中力与集中力偶 的数值。
例题5
q
A
4a FAy
梁由一个固定铰链支座和一个辊轴支座所
支承，但是梁的一端向外伸出，这种梁称为外 伸梁(overhanging beam)。梁的受力以及各部 分尺寸均示于图中。
工程中的弯曲构件
工程中可以看作梁的杆件是很多的:
桥式吊车的大梁 可以简化为两端饺支 的简支梁。在起吊重 量(集中力FP)及大梁自 身重量(均布载荷q)的 作用下,大梁将发生弯 曲。
工程中可以看作梁的杆件是很多的:
石油、化工设备中各种直立式反应塔，底部与地面固定 成一体，因此，可以简化为一端固定的悬臂梁。在风力载荷 作用下，反应塔将发生弯曲变形。
Nanjing University of Technology
材料力学 课堂教学(5)
2020年8月12日
第5章 梁的弯曲问题(1)－剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面内的 力偶作用时，其轴线将弯曲成曲线，这种受力与变形形式称为 弯曲（bending）。
主要承受弯曲的杆件称为梁（beam）。
得到梁的剪力方程和弯 矩方程分别为：
M(x)
FQ x＝FRA qx＝ql－qx 0 x 2l
FRA x
M x＝qlx－qx2
0 x 2l
2
这一结果表明，梁上的剪力方程是x的线性函数；弯矩方程是x的 二次函数。
载荷集度、剪力、弯矩之间的 微分关系
绘制剪力图和弯矩图有两种方法：
第一种方法是：根据剪力方程和弯矩方程，在FQx和M-x坐标系中绘制出相应的图线，便得到所需要的 剪力图与弯矩图。
剪力图和弯矩图的画法
Q = - 3KN
F点剪力为零,令 其距A点为x
X=5m
A
c
D
BE
4m
4m
7KN
3KN
+
1KN
F X =5m
4m
3m
2KN
+
-
3KN
弯矩图 AC：( ) CD：( )
DB：( )
BE：()
A
c
D
BE
4m
4m
7KN
3KN
+
1KN
F X =5m
4m
3m
2KN
+
-
3KN
A
cF
D
BE
4m
4m
4m
3m
6
0.2
1.6
1
2
80KN
(b)
+
80KN
例题 用简易法作 所示组合梁旳
剪力图和弯矩图。
解：
已求得支座反力为 RA=81KN RB=29KN
P=50KN
mA
A EC D
M=5KN.m
K
B
mA
1 0.5 1
3
RA
将梁分为AE，EC，
CD，DK，KB五段。
1
RB
剪力图 AE段：水平直线
QA右= QE左 = RA = 81KN
最大剪力发生在DB段中旳 任一横截面上
1P2
A C
P3
B D
200
115
1265
23.6
+
1.7 27
弯矩图
1P2
P3
每段梁旳弯矩图均为斜直线。且 A
C
梁上无集中力偶。故只需计算A、
静定结构的内力—绘制剪力图和弯矩图(建筑力学)
CB段：
Fs
x2
FBy
a l
F
a＜x2＜l
M
x2
FBy
l
x2
a l
F
l
x2
a x2 l
实作训练
（3）画剪力图和弯矩图
剪力图：FS 为常数，剪力图为平行于横坐标
轴的两段水平直线
弯矩图：
x1 0时，M A 0
x1
a时，MC
ab l
F
x2
a时，MC
ab l
F
x2 l时，MB 0
实作训练
弯矩图如图(c)所示。
例题:2：用列方程法作出图示梁的剪
力与弯矩图。
ql 解：由对称性可知，支座反力 FAy FBy 2
取距左端为x的任一横截面n-n，此横截面
的剪力方程和弯矩方程分别为
l Fs ( x) FAy qx q( 2 x)
(0 x l)
xq M ( x) FAy x qx 2 2 x(l x)
➢ 实作训练：
例题1：试列出图示梁的剪力方程与弯矩方程， 并作出剪力图与弯矩图。
解：（1）建立剪力方程和弯矩方程 以梁的左端为坐标原点，沿横截面n-n 将梁截开，取左段梁为分离体，应用求内力的直 接计算法得
FS x F 0＜x＜l a M x Fx 0 x l b
式（a）与（b）分别为剪力方程与弯矩方程。
x
F
x
l 3
3ql
2
4qlx
l/3 l
l/3 FBy
DB 段 FS x FAy F 4ql
M
x
FAy
x
F
x
l 3
Me
4ql 2
剪力图和弯矩图(史上最全面)
极轴，q表示截面m–m的位置。
R
P
A
q
B
O
x
M(q) Px P(R Rcosq) PR(1 cosq) (0 q )
Q(q ) P1 Psinq (0 q )
N(q ) P2 Pcosq (0 q )
35
R
P
A
q
B
A
O
x
2PR
O
+ Q图
M图
B N图
–
+
O
P
O
P
M(q) Px P(R Rcosq) PR(1 cosq) (0 q )
起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M(P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
四、对称性与反对称性的应用： 对称结构在对称载荷作用下，Q图反对称，M图对称；对称结构在反对称载荷作
用下，Q图对称，M图反对称。
39
五、剪力、弯矩与外力间的关系
解：
q — 均布力
10
一、弯曲内力：
§4–2
[举例]已知：如图，P，a，l。 求：距A端x处截面上内力。
解：①求外力
梁的剪力和弯矩
a A
l
X 0, XA 0
mA 0 ,
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
步骤： ①分别作出各项荷载单独作用下梁的弯矩图； ②将其相应的纵坐标叠加即可（注意：不是图形的简单拼凑）。
相关主题