第五章受弯构件斜截面承载力计算
5-受弯构件斜截面承载力

5.1 概述 在受弯构件的剪弯区段,在M、V作用下,有 可能发生斜截面破坏。 斜截面破坏: 斜截面受剪破坏——通过抗剪计算来满足受剪 承载力要求; 斜截面受弯破坏——通过满足构造要求来保证 受弯承载力要求。
5.1.1 斜截面开裂前的应力分析
My0 I0
tp
, 当λ<l.5时,取λ = 1.5,当λ>3
时,取λ=3 。α 为集中荷载作用点到支座或节点边 缘的距离。 独立梁是指不与楼板整体浇筑的梁。
• (3)厚板类受弯构件斜截面受剪承载力应 按下列公式计算:
Vc 0.7 h f t bh0
800 1 / 4 h ( ) h0
一般板类受弯构件主要指受均布荷载作用下的 单向板和双向板需要按单向板计算的构件。
5.2 无腹筋梁的斜截面受剪性能
• 5.2.1 斜裂缝的类型 • (1)弯剪斜裂缝 特点:裂缝下宽上窄 • (2)腹剪斜裂缝
特点:裂缝中间 宽两头窄
5.2.2 剪跨比λ的定义
• 广义剪跨比:
M Vh0
• 集中荷载下的简支梁, 计算剪跨比为:
a h0
M1 V A a1 a1 1 V A h0 V A h0 h0
◆ 临界斜裂缝上部及受压区混凝土相当于受压弦杆(compression
chord)
◆ 纵筋相当于下弦拉杆(tension chord)
第五章 受弯构件斜截面受剪承载力
5.3 有腹筋梁的受剪性能
◆ 箍筋将齿Leabharlann 体混凝土传来的荷载悬吊到受压弦杆,增加了混
凝土传递受压的作用
◆ 斜裂缝间的骨料咬合作用,还将一部分荷载传递到支座(拱
第五章 受弯构件斜截面受剪承载力
《混凝土结构设计原理》第5章 钢筋混凝土受弯构件斜截面承载力

斜拉破坏则是由于梁内配置的腹筋数量过少而引起的,因 此用配置一定数量的箍筋和保证必要的箍筋间距来防止这种破 坏的发生;
对于常见的剪压破坏,通过受剪承载力计算给予保证。
《混凝土结构设计规范》的受剪承载力计算公式就是依据剪 压破坏特征建立的。
5.3.1 计算原则
采用半理论半经验方法建立受剪承载力计算公式
F
5.2.2 有腹筋简支梁的受剪性能
梁沿斜截面破坏的主要形态
剪压破坏的特点
弯剪段下边缘先出现初始垂直 裂缝;
F
随着荷载的增加,这些初始垂直 裂缝将大体上沿着主压应力轨迹 向集中荷载作用点延伸;
临界斜裂缝
在几条斜裂缝中会形成一条主要的斜裂缝,这一斜裂缝被称为临界 斜裂缝; 最后,与临界斜裂缝相交的箍筋应力达到屈服强度,斜裂缝宽度增 大,导致剩余截面减小,剪压区混凝土在剪压复合应力作用下达到混 凝土复合受力强度而破坏,梁丧失受剪承载力。
斜裂缝的形成
矩形截面梁
P
P
弯剪斜裂缝
垂直裂缝
P
I字形截面梁
P
主拉应力超过混 凝土的抗拉强度时, 将出现斜裂缝。 弯剪区段截面下 边缘的主拉应力仍为 水平,在这些区段一 般先出现垂直裂缝, 随着荷载的增大,垂 直裂缝将斜向发展, 形成弯剪斜裂缝。
腹剪斜裂缝
由于腹板很薄,且该处剪应力较大,故斜裂缝首 先在梁腹部中和轴附近出现,随后向梁底和梁顶斜 向发展,这种斜裂缝称为腹剪斜裂缝。
VC
斜截面的受剪承载力的组成
s Va
Vd
DC
Vu = Vc + Vsv + Vsb + Vd + Va
斜截面承载力计算
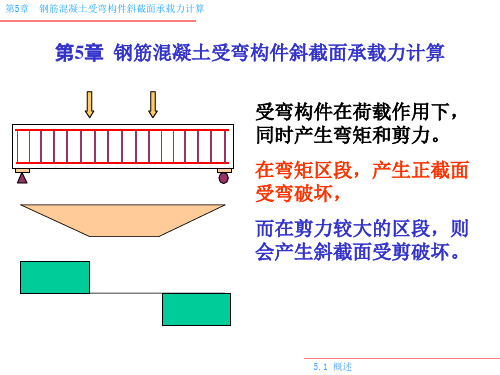
随P 裂缝数 ,W Va , 沿纵筋的混凝土保护层 也可能被撕裂,Vd ,其中一条斜裂缝发展为主要斜裂 缝----临界斜裂缝.无腹筋梁此时如同拱结构,纵筋成 拱的拉杆.
常见的破坏:临界斜裂缝的发展导致混凝土剪压区高 度的不断减小,最后在切应力和压应力的共同作用下, 剪压区混凝土被压碎(拱顶破坏),梁发生破坏.
的受剪承载力来防止由于配箍率而过高产生斜压破坏 ◆ 受剪截面应符合下列截面限制条件
h 当
w
4 时,
V 0.25 f bh
c c
b hw 6 时, V 0.20 c f c bh0 当 b hw < < 6 时,按直线内插法取用。 当4 b
0
上式表明梁的斜截面受剪 承载力的上限,相当于限制 了梁所必须具有的最小截 面尺寸,在只配有箍筋下也 限制了最大配筋率.如不满 足 ?
h 当
w
4 时,
V 0.25 f bh
c c
b hw 6 时, V 0.20 c f c bh0 当 b hw < < 6 时,按直线内插法取用。 当4 b
0
c为高强混凝土的强度折减系 数,当fcu,k ≤50N/mm2时,c =1.0,当fcu,k =80N/mm2时c
表 5-3 梁中箍筋最小直径(mm) 梁高 h(mm) h≤800 h >800 箍筋直径 6 8
5.2 受弯构件斜截面设计方法
第5章 钢筋混凝土受弯构件斜截面承载力计算
2、截面限制条件 上限值---最小截面尺寸和最大配筋率 ◆ 当配箍率超过一定值后,则在箍筋屈服前,斜压杆混凝土已 压坏,故可取斜压破坏作为受剪承载力的上限。 ◆ 斜压破坏取决于混凝土的抗压强度和截面尺寸。
第五章受弯构件斜截面承载力的计算

第五章受弯构件斜截面承载力的计算内容的分析和总结钢筋混凝土受弯构件有可能在弯矩W和剪力V共同作用的区段内,发生沿着与梁轴线成斜交的斜裂缝截面的受剪破坏或受弯破坏。
因此,受弯构件除了要保证正截面受弯承载力以外,还应保证斜截面的受剪和受弯承载力。
在工程设计中,斜截面受剪承载一般是由计算和构造来满足,斜截面受弯承载力则主要通过对纵向钢筋的弯起、锚固、截断以及箍筋的间距等构造要求来满足的。
学习的目的和要求1.了解斜裂缝的出现及其类别。
2.明确剪跨比的概念。
3.观解斜截面受剪破坏的三种主要形态。
4.了解钢筋混凝土简支梁受剪破坏的机理。
5.了解影响斜截面受剪承载力的主要因素。
6.熟练掌握斜截面受剪承载力的计算方法及适用条件的验算。
7.掌握正截面受弯承载力图的绘削方法,熟悉纵向钢筋的弯起、锚固、截断及箍筋间距的主要构造要求,并能在设计中加以应用。
§5-1 受弯构件斜截面承载力的一般概念一、受弯构件斜截面破坏及腹筋布置1.梁受力特点CD段:纯弯段正截面受弯破坏,配纵向钢筋受剪破坏:配腹筋(箍筋和弯筋)AC段:弯剪段斜截面受弯破坏:构造处理图5-1 无腹筋梁斜裂缝出现前的应力状态2.腹筋的布置·将梁中箍筋斜放与斜裂缝正交时受力状态最佳。
但施工难实现;难以适应由于异号弯矩、剪力导致斜裂缝的改变方向。
·在支座附近弯矩较小之处可采用弯起部分纵筋以抵抗部分剪力。
3.关于腹筋布置的规定⑴梁高h<150mm 的梁可以不设置箍筋。
⑵h=150~300mm 时,可仅在梁端各1/4跨度范围内配置箍筋。
当构件中部1/2跨度范围内有集中荷载时,应沿全长布置箍筋。
⑶h>300mm 时,全跨布置箍筋。
二、钢筋混凝土梁开裂前的应力状态1.应力计算方法:接近弹性工作状态,可根据材力公式计算梁中应力。
钢筋按应变相等、合力大小及作用点不变的原则换算成等效混凝土面积αE A s ,把钢筋混凝土的截面变成混凝土单一材料的换算截面,其几何特征值A 0、I 0、S 0、y 0。
05受弯构件斜截面受剪承载力计算

Asi M ui M u As
图5-13
2、纵向钢筋的弯起(如图5-23) (1)钢筋理论充分利用点 图中1、2、3点:是③、②、①号钢筋充分利用 点(图5-23); (2)钢筋理论不需要点 图中的2、3、a点是③、②、①号钢筋不需要点 (图5-23); ; (3) 以③号纵向钢筋弯起为例(图5-23) : 将③号钢筋在E、F点弯起,在G、H点穿过中 和轴进入受压区,对正截面抗弯消失。 分别以E、F点作垂线与③号钢筋交于e、f点。以 G、H点作垂线与②号钢筋交于g、h点,Mu图变成 aigefhb,Mu图>M图,此称之包络图或称材料图
若不满足,则按计算配箍筋 ②最小配箍率(按计算配箍筋)
nAsv1 ft sv sv ,min 0.24 bs f yv
(3)按计算配置腹筋(限制剪压破坏)
当不满足上述(1)、(2) 按计算配制箍筋Asv和弯起筋Asb
三、计算截面位置与剪力设计值的取值
1、计算截面位置:斜截面受剪承载力薄弱部位 截面的抗剪能力沿梁长也是变化的。在剪力或抗剪
hw— 截面的腹板高度,矩形截面取有效高度h0, T形截面取有 效高度减去翼缘高度,工形截面取腹板净高;
βc— 混凝土强度影响系数, (见表5-1)
hf h0 h0 h0 hf
hw
(b) hw = h0 – hf
h
hw hf
(a) hw = h0
(c) hw = h0 – hf – hf
图5-13 hw 取值示意图
临界斜裂缝。梁破坏时与斜裂缝相交的腹筋达
到屈服强度,剪压区的混凝土的面积越来越小,
达到混凝土压应力和剪应力的共同作用下的复
第五章 受弯构件斜截面承载力计算
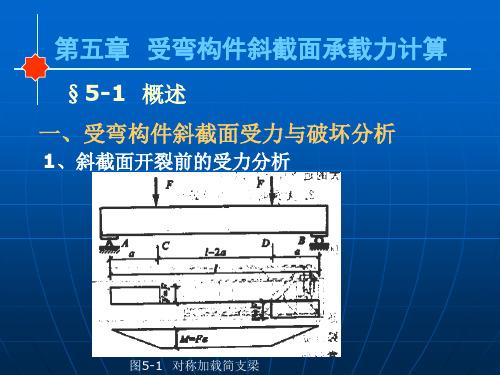
实验表明,当荷载较小, 裂缝未出现时,可将钢筋混 凝土梁视为均质弹性材料的 梁,其受力特点可用材料力 学的方法分析。随着荷载的 增加,梁在支座附近出现斜 裂缝。取CB为隔离体。
图5-3 隔离体受力
与剪力V平衡的力有:AB面上的混凝土切应力合力Vc;由于开裂面BC 两侧凹凸不平产生的骨料咬合力Va的竖向分力;穿过斜裂缝的纵向钢筋 在斜裂缝相交处的销栓力Vd。
图5-12 斜截面受剪承载力计算位置
①支座边缘处截面。
该截面承受的剪力最大。在计算简图中跨度取至支座中心。但支座和 构件连在一起,可以共同承受剪力,所以受剪控制截面是支座边缘截 面。计算该截面剪力设计值时,跨度取净跨。用支座边缘的剪力设计 值确定第一排弯起钢筋和1-1截面的箍筋。
②受拉区弯起钢筋弯起点处截面。(2-2截面和3-3截面)
(2)截面尺寸要求:
为防止斜压破坏,截面尺寸应满足:
当
hw
b£
4 时, V ?
1 (10 60
l0 h)bc fcbh0
当 hw b ³ 6 时, V ? 1 (7 60
l0 h)bc fcbh0
当 4< hw b < 6 时,按线性内插法取用。
2、构造要求:
(1) 截面宽度: ≥140mm; 当l0/h≥1时,h/b≤25; 当l0/h<1时,l0/b≤25。
(2) 混凝土强度: ≥C20 (3)纵向受力钢筋:
图5-25 单跨深梁的钢筋配置
图5-26 连续深梁的钢筋配置
下部纵筋宜均匀布置在梁的下部0.2h范围内,连续深梁中间 支座上纵筋按下图分配:
图 5-27 不同跨高比时连续深梁中间支座上部纵向受拉钢筋在不同高度范围内的分配比例
(4)深梁宜配双排钢筋网,水平和竖向分布钢筋的直径均不应 小于8mm,间距不应大于200mm,且应满足最小配筋百 分率的要求; 当集中荷载作用于连续深梁上部1/4高度范围内,且 l0/h> 1.5时,竖向分布筋最小配筋百分率应增加0.05。
5第五章受弯构件斜截面承载力计算

0.24 1.27 210
0.145%
故:SV SV,min
⑥求VCS(混凝土与箍筋承担的抗剪承载能力设计值 ) VCS=0.7ft bh0+1.25fyvASVh0 /S
=0.7×1.27×250×515+1.25×210×100.6 ×515/200
=182.8(KN )
⑦求ASb(取弯起角度为450)
nAsv1 V 0.7 ftbh0 0.8 f y Asb sin
s
1.25 f yvh0
nAsv1
V
1.75
1.0
ft bh0
0.8 f y Asb
s in
s
1.0 f yvh0
然后验算弯起点的位置是否满足斜截面承载力的 要求。
例1 如图所示一矩形截面简支梁,b×h=250×550mm2,混凝 土等级C25,纵向受力钢筋HRB400级,承受均布荷载设计值 q=80KN/m,按正截面受弯承载力计算配置的纵向受力钢筋为 4 25。试求箍筋用量。
(2) 剪压破坏
破坏前提:剪跨比适中(λ=1~3), 箍筋配置适量,配箍率ρsv适量;
(3) 斜拉破坏
破坏前提:剪跨比较大(λ>3), 箍筋配置过少,配箍率ρsv较小。
受剪破坏三种形态
(1)斜压破坏
破坏前提:
λ<1,ρsv较大
破坏特征: 首先在梁腹出现若干
条较陡的平行斜裂缝,随 着荷载的增加,斜裂缝将 梁腹分割成若干斜向的混 凝土短柱,最后由于混凝 土短柱达到极限抗压强度 而破坏。
钢筋情况: 箍筋应力达到屈服强度
甚至拉断 破坏性质:属于脆性破坏
防止斜拉破坏: 通过控制最小配箍率。
5.2 受弯构件斜截面受剪承载力计算
5.2.1 斜截面受剪承载力计算公式及适用条件
混凝土结构及砌体结构-第五章受弯构件斜截面承载力计算

Asv 1.75 V Vcs f t bh0 f yv h0 1.0 s
注意:
1.5 3
17
2.公式的适用范围 (1)、上限值--最小截面尺寸和最大配箍率:
hw 当 4 时,V 0.25 c f cbh0 b hw 当 6 时,V 0.2 c f c bh0 b hw 当4 6 时,按线性内插法取用 b
250 300 350 500
150 200
24
3.弯起钢筋的要求
1.画出弯矩图和正截面受弯承载力图; 2.根据各根钢筋面积大小按比例分配受弯承载力图,
弯起的钢筋画在外面; 3.找出要弯起钢筋的充分利用点和不需要点; 4.从充分利用点向外延伸0.5h0,作为弯起点,并 找出弯起钢筋与中和轴的交点。如该点在不需要点 的外面,可以,否则再向外延伸; 5.验算是否满足斜截面受剪承载力要求和其它构造 要求。
las≥15d(光面)
37
(2)中间支座直线锚固:
0.7la ≥l a
l ≥0.a7la
38
(3)中间支座的弯折锚固:
≥0.4la ≥0.4la
15d
39
(4)节点或支座范围外的搭接:
ll
40
5.4.5
箍筋的构造要求
单肢箍n=1
双肢箍n=2
四肢箍n=4
41
梁受扭或承受动荷载时,不得使用开口箍筋
45
46
19
-斜截面上弯起钢筋与构件纵向轴线的夹角。
2. 斜截面承载力计算步骤
⑴ 确定计算截面及其剪力设计值; ⑵ 验算截面尺寸是否足够; ⑶ 验算是否可以按构造配筋;
⑷ 当不能按构造配箍筋时,计算腹筋用量;
⑸ 验算箍筋间距、直径和最小配箍率是否 满足要求。
混凝土结构设计原理第五章 受弯构件斜截面

s
s
Asv . . h0 .... b
架立筋
箍筋 纵筋
· · · ·
弯起点 as 弯起筋
箍筋及弯起钢筋 有腹筋梁:箍筋、弯起钢筋(斜筋)、纵筋 无腹筋梁:纵筋
第5章 钢筋混凝土受弯构件斜截面承载力计算
2 无腹筋梁的受力及破坏分析 梁斜裂缝中受力状态图: 现将梁沿斜裂缝AAB切开,取出斜裂缝顶点左边部分脱离体。
第5章 钢筋混凝土受弯构件斜截面承载力计算
拱形桁架模型 此模型把开裂后的有腹筋梁看成为拱形桁架,其拱体是上弦
杆,裂缝间的齿块是受压的斜腹杆,箍筋则是受拉腹杆。如 图所示;与梳形拱模型的主要区别:1)考虑了箍筋的受拉作 用; 2)考虑了斜裂缝间混凝土的受压作用。
拱形桁架模型
第5章 钢筋混凝土受弯构件斜截面承载力计算
当弯剪区的主拉应力tp>ft时,即产生与主拉应力迹线大致垂直 的斜裂缝,故其破坏面与梁轴斜交-称斜截面破坏。
弯剪斜裂缝:裂缝下宽上窄 斜裂缝的类型 腹剪斜裂缝:中间宽两头窄
(a) 腹剪斜裂缝
(b) 弯剪斜裂缝
第5章 钢筋混凝土受弯构件斜截面承载力计算
为了抵抗主拉应力的钢筋: 弯起钢筋,箍筋
梁中设置纵向钢筋承担开裂后的拉力,箍筋、弯筋、纵筋、架 立筋 ––– 形成钢筋骨架,如图所示。
B A Vc D c A
P
D C B A A
P
D C VA
Va Vd Ts B C a MB
(a)
MA
梁中斜裂缝的受力变化
第5章 钢筋混凝土受弯构件斜截面承载力计算
D
C
B
A Vc D c
应力状态变化分析:
VA
Va T B Vd s C a MB
混凝土结构设计受弯构件的斜截面受剪承载力计算

◆(1.5≤ ≤3)
■ ■
剪跨比较小,有一定拱作用
斜裂缝出现后,部分荷载通过 拱作用传递到支座,承载力没 有很快丧失,荷载可继续增加, 并出现其它斜裂缝。 ■最后形成一条临界裂缝,裂缝逐渐向 集中荷载作用点处延伸,致使剪压区 高度不断减小,在剪压区由于混凝土 受剪力和压力的共同作用,达到混凝 土的复合受力下的强度,混凝土被压 碎发生破坏。
箍筋
弯起钢筋
腹筋
5.1概述
抗剪钢筋
第五章 钢筋混凝土受弯构件斜截面承载力计算
弯起钢筋则可利用正截面受弯的纵向钢筋直接弯起而成。弯起 钢筋的方向可与主拉应力方向一致,能较好地起到提高斜截面 承载力的作用,但因其传力较为集中,有可能引起弯起处混凝 土的劈裂裂缝。而且试验研究表明,箍筋对抑制斜裂缝开展的 效果比弯起钢筋好。所以首先选用竖直箍筋,然后再考虑采用 弯起钢筋。选用的弯筋位置不宜在梁侧边缘,且直径不宜过粗。
5.1 概述
受弯构件在荷载作用下,同时 产生弯矩和剪力。
A B C D
BC段仅有弯矩作用,称为纯弯 区段;
支座附近的AB、CD区段内有弯 矩与剪力的共同作用,称为剪 跨。 在弯矩区段,抗弯承载力不足 时,产生正截面受弯破坏,
而在剪力较大的区段(剪跨), 则会产生斜截面破坏。
5.1.1 受弯构件斜截面受力与破坏分析
5.1.2 斜截面的主要破坏形态
对集中荷载作用下的简支梁
h0
a
M a Vh0 h0
计算剪跨比
(狭义剪跨比)
我们把在集中力到支座之间的距离a称之为剪跨, 剪跨a与梁的有效高度h0的比值则称为计算剪跨比。
5.1.2 斜截面的主要破坏形态
1、无腹筋梁
◆(<1.5)或腹板较窄的T形梁或I形梁
斜截面承载力计算

在混凝土梁的受拉区中,弯起钢筋的弯起 点可设在按正截面受弯承载力计算不需要 该钢筋的截面之前,但弯起钢筋与梁中心 线的交点应位于不需要该根钢筋的截面之 外,如图5—15所示;同时弯起点与按充分 利用该钢筋的截面之间的距离不应小于。
钢筋实际截断点 (1)当 V≤0.7ftbh0 时,应延伸至按正截面受弯承载
fcbh0
hw 6 b
V 0.2c fcbh0
当4 hw 6时,按直线内插法取用 b
2.为了防止梁发生斜拉的少筋破坏,规 范用限制梁的配箍率不要低于最小配箍 率的方式来保证。
sv
Asv bs
sv,m in
0.24
ft f yv
四、梁斜截面受剪承载能力计算公式的应用 1.设计计算截面的确定
(2)判断是否需要计算配置腹筋
V 0.7 ftbh0
VHale Waihona Puke 1.751.0ftbh0
(3)按计算配置腹筋
仅配箍筋梁的设计计算
V
0.7
ftbh0
1.25 f yv
Asv s
h0
V
1.75
1.0
ftbh0
1.0 f yv
Asv s
h0
既配箍筋,又配弯起钢筋梁的设计计算
V Asb≥
0.7ftbh0 0.8 f y
V ≤Vcs
Vsb
0.7ftbh0
f yv
nAsv1 s
h0
0.8 f y Asb
sin sb
2.对集中荷载作用时 (1)仅配置箍筋时
V
≤Vcs
=
1.75
1
ftbh0
f yv
Asv s
h0
(2)既配有箍筋也同时配有弯起筋时
第五章--受弯构件斜截面承载力计算分解

河南理工大学土木工程学院
2020/5/18
二、无腹筋梁斜截面受剪性能
(2)斜裂缝出现后,截面B 的钢筋应
力s取决于临界斜裂缝顶点截面A处的
MA,而MA>MB (3)纵筋拉力突增,斜裂缝进一步开 展,受压区面积进一步缩小。
(4)Vd的作用,混凝土沿纵向钢筋 受到撕裂力。
M A Tsd
Vd,TB≈TA
1. 斜裂缝产生前受力性能
tp
2
2 2
4
②
弯腹剪剪斜斜裂裂缝缝
①
A
③
A
2 2
2 cp
4
箍筋 ③
弯起钢筋
河南理工大学土木工程学院
①腹筋
②
2020/5/18
二、无腹筋梁斜截面受剪性能
2. 斜裂缝产生后受力性能
B
Va
Vd Ts
V
c
A Cc
Vc d
MB
河南理工大学土木工程学院
MA
2020/5/18
二、无腹筋梁斜截面受剪性能
B
Va
C
Vd Ts
V
c
A Cc
Vc d
竖向剪力
为简化 力矩平衡
MB
MA
Vd很小
斜裂缝出现前后的应力状态变化:
VA Vc Vay Vd
V V
A
c
M A Tsd Vdc M A Tsd
(1)斜裂缝出现后,受剪面积的减小使受压区混凝土剪应力和压应
力均显著增大(剪压区)
河南理工大学土木工程学院
斜拉破坏 箍筋数量过少或剪跨比较
大时。特点是斜裂缝一出现, 箍筋即屈服。
2020/5/18
三、有腹筋梁斜截面受剪性能
混凝土受弯构件斜截面承载力计算ppt课件

1、抵抗弯矩图应包含设计弯矩图,以保证正截面抗弯的要求; 破坏具有明显的脆性性质,类似于正截面中的超筋破坏,设计和工程中应予以避免。
致与中和轴成45°角的裂缝。随着荷载的增加, ③为使计算公式适用于高强度砼,将原《规范》中砼轴心抗压强度fc表达的砼抗剪承载力改用以砼轴心抗拉强度ft表达。
VVc 1.71.50ftbh0
29
Hale Waihona Puke 布荷载30三、有腹筋梁受剪承载力计算公式
A、计算截面的剪力设计值按如下方法采用; B、计算支座边缘处的截面时,取该处的剪力设计值; C、计算箍筋数量改变处的截面时,取箍筋数量开始改 变处的剪力设计值; D、计算第一排(从支座算起)弯起钢筋时,取支座边 缘处的剪力设计值; E、计算以后每一排弯起钢筋时,取前一排弯起钢筋弯 起点处的剪力设计值。
破坏性质:破坏与裂缝的形成几乎同时发生,承载 力最低,破坏性质类似于正截面破坏中的少筋破坏,脆 性性质最为严重,设计中应当避免发生。
15
19 §5-3 有腹筋梁斜截面受力特点和破坏形态 一、受力特点
16
二、有腹筋梁沿斜截面破坏主要形态
17
§5-4 影响斜截面承载力的主要因素 1、剪跨比或跨高比 剪跨比反映了正应力(弯矩引起)和剪应力(剪力引 起)之间的关系,因而决定截面上各点主应力的大小和方 向,影响承载力。在集中荷载作用下,如果荷载形式简单 ,或者只有一个集中荷载时,采用计算剪跨比;如果是均 布荷载或者荷载形式复杂,采用广义剪跨比。 另外,由于箍筋的抗剪效果较为显著,所以随配箍率 的增大,剪跨比对承载力的影响减小。
21
3、配箍率和箍筋强度
钢筋混凝土受弯构件斜截面承载力计算

关于第五章钢筋混凝土受弯构件斜截面承载力计算的学习报告前言:斜截面受力与破坏机理:主要是支座附近的剪跨区段发生沿斜截面破坏。
斜截面产生原因:当主拉应力值超过混凝土抗拉强度时,将首先在达到该强度的部位产生裂缝其裂缝走向与主拉应力的方向垂直,故是斜裂缝。
腹筋是箍筋和弯起钢筋的总称。
无腹筋梁是指不配箍筋和弯起钢筋的梁。
本章学习思路分析:要研究抵抗钢筋混凝土的斜截面破坏,首先要从无腹筋梁受力及破坏分析入手,然后再从有腹筋梁的受力及破坏分析研究如何抵抗钢筋混凝土的斜截面破坏,从而总结出一般受弯构件斜截面设计方法。
当然,斜截面的抗剪弯设计是建立在正截面抗弯能力的基础之上的,这由前面第4章内容可以计算得到,另外,斜截面的抗剪弯能力必须同时得到保证,计算顺序是先计算斜截面的抗剪能力,再计算斜截面的受弯承载力。
破坏情况大致如下:关于无腹筋梁斜裂缝出现后剪弯段内的应力变化:①开裂前的剪力是全截面承担的,开裂后则主要是由剪压区承担,混凝土剪应力大大增加(随着荷载的增大,斜裂缝宽度增加,骨料咬合力也迅速减小),应力的分布规律不同于斜裂缝出现前的情形。
②混凝土剪压区面积因斜裂缝的出现和发展而减小,剪压区内的混凝土压应力将大大增加。
③与斜裂缝相交处的纵向钢筋应力,由于斜裂缝的出现而突然增大。
因为该处的纵向钢筋拉力T在斜裂缝出现前是由截面C处弯矩Mc决定的(图见书P107),而在斜裂缝出现后,根据力矩平衡的概念,纵向钢筋的拉力T则是由斜裂缝端点处截面AB的弯矩Mb所决定,Mb比Mc要大很多。
④纵向钢筋拉应力的增大导致钢筋与混凝土间粘结应力的增大,有可能出现沿纵向钢筋的粘结裂缝。
关于有腹筋梁的受力及破坏分析得出的相关结论:配置箍筋可以有效提高梁的斜截面受剪承载力。
箍筋最有效的布置方式是与梁腹中的主拉应力方向保持一致,但为了施工方便,一般和梁轴线成90度布置。
斜裂缝出现前,箍筋的应力很小,主要由混凝土传递剪力;斜裂缝出现后,与斜裂缝后相交的箍筋应力增大。
斜截面受弯

T形截面由于存在较大的受压翼缘,增加了剪
截面形状
压区的面积,对斜拉和剪压破坏的承载力有提
高,但对斜压破坏没有提高。
第五章 受弯构件斜截面承载能力计算
5.4 无腹筋梁抗剪承载力的计算
均布荷载
Vc 0.7 f t bh0
第五章 受弯构件斜截面承载能力计算
集中荷载
1.75 Vc f t bh0 1.0
第五章 受弯构件斜截面承载能力计算
第五章 受弯构件斜截面承载能力计算
1. 箍筋的作用
1. 2. 3. 4.
斜裂缝出现后,拉应力由箍筋承担,增强了梁的剪力传递能力; 箍筋控制了斜裂缝的开展,增加了剪压区的面积 ; 吊住纵筋,延缓了撕裂裂缝的开展,增强了纵筋销栓作用; 箍筋有利于提高纵向钢筋与混凝土之间的粘结性能,延缓了沿 着纵筋方向粘结裂缝的出现;
2. 配筋构造是计算模型和构件受力的必要条件,没有可靠的配筋构造
,计算模型和构件受力就不可能成立。 3. 配筋构造与计算设计同等重要,由于疏忽配筋构造而造成工程事故
的情况是很多的。
故切不可重计算,轻构造。
第五章 受弯构件斜截面承载能力计算
例题1 (Example 1)
矩形截面钢筋混凝土简支梁,两端支撑在砖墙上,净跨度为3660mm, 截面尺寸b × h=200×500mm, 保护层厚度30mm。其上作用均布恒荷 载标准值gk= 20 kN/m(未包括自重),活荷载标准值qk= 38 kN/m,混 凝土强度等级选C20,箍筋采用HRB235级。 ( fc =9.6 N/mm2 , ft =1.1 N/mm2 , fy =210 N/mm2 ) 试计算此梁所用的箍筋。
z h0 zw a sin tg 2 sin
第五章-受弯构件斜截面承载力计算

第5章 受弯构件斜截面承载力计算知识点1.斜截面破坏的主要形态,影响斜截面受剪承载力的主要因素;2.无腹筋梁斜裂缝出现后的应力状态及其破坏形态,无腹筋梁斜截面受剪承载力计算公式;3.剪力传递机理,腹筋的作用及其对破坏形态的影响,截面限制条件及最小配箍率的意义;4.有腹筋简支梁和连续梁的抗剪性能,受剪承载力计算方法、计算公式及其适用范围;5.斜截面受弯承载力、抵抗弯矩图、纵筋锚固、弯起及截断、箍筋的构造要求。
要点1.在钢筋混凝土梁斜截面承载力计算中,若o c c bh f V β25.0>,则应采取的措施是加大截面尺寸。
2.对矩形、T 形和工字形截面的一般受弯构件,截面高度大于300mm ,当满足07.0bh f V t ≤时,仅按构造配箍。
3.剪跨比为计算截面至支座截面的距离与截面有效高度的比值。
4.钢筋混凝土简支梁当仅配置箍筋时,承受均布荷载斜截面承载力的计算公式V cs =0.7f t bh 0+1.25f yv (A sv /s)h 0。
5.钢筋混凝土简支梁当仅配置箍筋时,承受集中荷载斜截面承载力的计算公式V cs =)1(75.1λ+f t bh 0+f yv (A sv /s)h 0。
6.影响无腹筋简支梁斜截面受剪承载力的主要因素有:剪跨比、混凝土强度、纵筋配筋率、截面尺寸和形状等。
7.在受弯构件斜截面受剪承载力计算中,通常采用配置腹筋即配置箍筋和弯起钢筋的方法来提高梁的斜截面受剪承载能力。
8.《规范》规定,在梁的受拉区段弯起钢筋时,弯起点与按计算充分利用该钢筋截面面积点之间的距离不应小于o h 5.0。
9.箍筋一般采用HPB235,HRB335级钢筋,其形式有封闭式和开口式两种。
10.梁沿斜裂缝破坏的主要形态及其破坏特征:斜压梁破坏:破坏时,混凝土被腹剪斜裂缝分割成若干个斜向短柱而压坏,破坏是突然发生的。
剪压破坏:临界裂缝出现后迅速延伸,使斜截面剪压区高度缩小,最后导致剪压区混凝土破坏,使斜截面丧失承载力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
先确定弯起筋,再配箍筋,但应满足最小配箍率、箍筋最大间
距和箍筋最小直径的要求。
★截面复核 已知材料强度设计值,截面尺寸,配箍量,要求复核斜截面所 能承受的剪力设计值V。
已知:剪力设计值V,截面尺寸b×h,混凝土强度等级ft,箍筋 级别fyv,纵向受力钢筋的级别和数量As 。求:腹筋数量Asv/S
计算步骤如下:
(1)复核截面尺寸 一般梁的截面尺寸应满足
V 0.25c fcbh0
的要求,否则,应加大截面尺寸或提高混凝土强度等级。
(2)确定是否需按计算配置箍筋 当满足下式条件时,可按构造配置箍筋,否则,需按计算配置箍筋:
(3) 斜拉破坏
破坏前提:剪跨比较大(λ>3), 箍筋配置过少,配箍率ρsv较小。
受剪破坏三种形态
(1)斜压破坏
破坏前提:
λ<1,ρsv较大
破坏特征: 首先在梁腹出现若干
条较陡的平行斜裂缝,随 着荷载的增加,斜裂缝将 梁腹分割成若干斜向的混 凝土短柱,最后由于混凝 土短柱达到极限抗压强度 而破坏。
Vu= Vc +Vsv+Vsb
Vc
Vs
Vsb Vu
受剪承载力的组成
如令Vcs为箍筋和混凝土 共同承受的剪力,即 Vcs=Vc+Vsv
则 Vu=Vcs+Vsb
斜截面承载力计算基本公式
斜截面受剪承载力的组成
Vu=Vc+Vsv+Vsb
Vu──受弯构件斜截面受剪承载力; Vc──剪压区混凝土受剪承载力设计值; Vsv──与斜裂缝相交的箍筋受剪承载力设计值; Vsb──与斜裂缝相交的弯起钢筋受剪承载力设计值。
钢筋情况: 箍筋应力达到屈服强度
甚至拉断 破坏性质:属于脆性破坏
防止斜拉破坏: 通过控制最小配箍率。
5.2 受弯构件斜截面受剪承载力计算
5.2.1 斜截面受剪承载力计算公式及适用条件
假定梁的斜截面受剪承载力Vu由斜裂缝上剪压区混凝 土的抗剪能力Vc,与斜裂缝相交的箍筋的抗剪能力Vsv和与 斜裂缝相交的弯起钢筋的抗剪能力Vsb三部分所组成。由 平衡条件∑Y=0可得:
计算公式的适用条件
上限值—最小截面尺寸
下限值—箍筋最小配筋率
当 hw≤4.0时,属于一般的梁,应满足 b
V 0.25 c fcbh0
当 hbw≥6.0时,属于薄腹梁,应满足
为了避免发生斜拉破 坏,《规范》规定,配箍 率应大于最小配箍率,箍 筋最小配筋率为
V 0.2c fcbh0
当4.0<
5.2.2 斜截面受剪承载力计算方法及步骤
★截面设计 钢筋混凝土梁一般先进行正截面承载力设计,初步确定截面尺
寸和纵向钢筋后,再进行斜截面受剪承载力设计计算。 ◆ 具体计算步骤如下:
⑴验算截面限制条件;如不符合要求,改变截面尺寸,重新确 定;
⑵验算是否需要按计算配置箍筋; ⑶如果需要按计算配置箍筋和弯起筋,此时可根据具体情况选 择其一:
hw b
<6.0时,属于薄腹梁,应满足
s v,m in
nAsv1 bs
0.24
ft fyv
V
0.025(14
hw b
)c
fcbh0
sv
Asv bs
nAsv1 bs
sv,min 0.24
ft
f yv
4 斜截面受剪承载力计算截面位置的确定
(1) 支座边缘截面(1-1); (2)腹板宽度改变处截面(2-2); (3)箍筋直径或间距改变处截面(3-3); (4)受拉区弯起钢筋弯起点处的截面(4-4)。
主要内容:
受弯构件受剪性能的试验研究 斜截面受剪承载力计算 构造要求
重点:
受弯构件受剪性能的试验研究 斜截面受剪承载力计算
斜截面破坏:
由于混凝土抗拉强度远低于抗压强度,当主拉应 力超过混凝土抗拉强度时,梁将出现大致与主拉 应力方向垂直的斜裂缝,称为斜截面破坏。
剪弯段:
梁截面上除作用有弯矩外,往往同时作用有剪力, 弯矩和剪力共同作用的区段称为剪弯段。
集中荷载作用下的简支梁
1
M1 V1h0
VAa1 VAh0
a1 h0
2
M2 V2 h0
VBa2 VB h0
a2 h0
受剪破坏的三种形态
箍筋配置过多,配箍率ρsv较大;
(2) 剪压破坏
破坏前提:剪跨比适中(λ=1~3), 箍筋配置适量,配箍率ρsv适量;
• 只配箍筋而不用弯起钢筋
一般受弯构件
集中荷载作用下的独立梁
Asv V 0.7 ftbh0
s
1.25 f yvh0
Asv
V
1.75
1.0
ftbh0
s
f yvh0
根据Asv/s计算值确定箍筋肢数、直径和间距,并应满足最小配 箍率、箍筋最大间距和箍筋最小直径的要求。
• 既配箍筋又用弯起筋,一般先确定箍筋数量,可参考过去设计
sv
Asv bs
nAsv1 bs
箍筋和弯起钢筋统称为腹筋。
腹筋的作用 箍筋:
①提高斜截面受剪承载力; ②与纵筋绑扎,形成钢筋骨架 → 便于施工; ③防止纵筋过早压曲,约束核心混凝土。 弯起钢筋: 由纵筋弯起形成 承受较大的剪力。
梁的箍筋和弯起钢筋
斜裂缝出现前的应力状态
5.1 受弯构件斜截面承载力的试验研究
钢筋情况: 箍筋应力未不到屈服强度
破坏性质:属于脆性破坏
防止斜压破坏: 通过控制梁的最小截面尺寸
受剪破坏三种形态
(2)剪压破坏
破坏前提:λ=1~3,ρsv适量
破坏特征: 截面出现多条斜裂缝,其中一条延伸最长,开展最宽的斜
裂缝,称为“临界斜裂缝”,与此裂缝相交的箍筋达到屈服强 度,最后,剪压区混凝土达到极限强度而破坏。
梁在弯矩M和剪力V共同作用下的主应力 迹线,其中实线为主拉应力迹线,虚线为 主压应力迹线。
斜截面受剪承载力—通过计算配置腹筋来保证;
斜截面受弯承载力—通过构造措施来保证。
斜截面受剪破坏形态主要取决于配箍率ρsv和剪跨比λ
广义剪跨比 M
Vh0
集中荷载简支梁:
M Pa a
Vh0 Ph0 h0 配箍率:
钢筋情况: 箍筋达到屈服强度
破坏性质:脆性不如斜拉 和斜压明显
防止剪压破坏: 通过斜截面承载力计
算,配置适量腹筋。
受剪破坏三种形态
(3)斜拉破坏
破坏前提:λ>3,ρsv较小
破坏特征: 一旦梁腹出现一条斜裂缝,就很快形成为“临界斜裂缝”,
与其相交的箍筋随即屈服,梁将沿斜裂缝裂成两部分。即使不 裂成两部分,也将因临界斜裂缝的宽度过大而不能继续使用。
