二次函数的应用(2)PPT课件
合集下载
二次函数的应用(经典) PPT

(1)若商场平均每天要盈利1200元,每件 衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天 盈利最多?
最值应用题——销售问题
某商场以每件42元的价钱购进一种服装,根据 试销得知这种服装每天的销售量t(件)与每 件的销售价x(元/件)可看成是一次函数关系: t=-3x+204。 写出商场卖这种服装每天销售利润y(元) 与每件的销售价x(元)间的函数关系式; 通过对所得函数关系式进行配方,指出商场 要想每天获得最大的销售利润,每件的销售 价定为多少最为合适?最大利润为多少?
显而易见:顶点式
已知函数y=ax2+bx+c的图象是以点(2,3) 为顶点的抛物线,并且这个图象通过点(3, 1),求这个函数的解析式。(要求分别用一 般式和顶点式去完成,对比两种方法)
已知某二次函数当x=1时,有最大值-6, 且图象经过点(2,-8),求此二次函数的 解析式。
思维小憩:
用待定系数法求二次函数的解析式,什么 时候使用顶点式y=a(x-m)2+n比较方便?
求函数最值点和最值的若干方法: 直接代入顶点坐标公式 配方成顶点式 借助图象的顶点在对称轴上这一特性,结合 和x轴两个交点坐标求。
二次函数的三种式
一般式:y=ax2+bx+c 顶点式:y=a(x-m)2+n 交点式:y=a(x-x1) (x-x2)
已知二次函数y=ax2+bx+c的图象与x 轴的一个交点坐标是(8,0),顶点是 (6,-12),求这个二次函数的解析式。 (分别用三种办法来求)
窗的形状是矩形上面加一个半圆。窗的 周长等于6cm,要使窗能透过最多的光 线,它的尺寸应该如何设计?
A
O
D
B
(2)每件衬衫降价多少元时,商场平均每天 盈利最多?
最值应用题——销售问题
某商场以每件42元的价钱购进一种服装,根据 试销得知这种服装每天的销售量t(件)与每 件的销售价x(元/件)可看成是一次函数关系: t=-3x+204。 写出商场卖这种服装每天销售利润y(元) 与每件的销售价x(元)间的函数关系式; 通过对所得函数关系式进行配方,指出商场 要想每天获得最大的销售利润,每件的销售 价定为多少最为合适?最大利润为多少?
显而易见:顶点式
已知函数y=ax2+bx+c的图象是以点(2,3) 为顶点的抛物线,并且这个图象通过点(3, 1),求这个函数的解析式。(要求分别用一 般式和顶点式去完成,对比两种方法)
已知某二次函数当x=1时,有最大值-6, 且图象经过点(2,-8),求此二次函数的 解析式。
思维小憩:
用待定系数法求二次函数的解析式,什么 时候使用顶点式y=a(x-m)2+n比较方便?
求函数最值点和最值的若干方法: 直接代入顶点坐标公式 配方成顶点式 借助图象的顶点在对称轴上这一特性,结合 和x轴两个交点坐标求。
二次函数的三种式
一般式:y=ax2+bx+c 顶点式:y=a(x-m)2+n 交点式:y=a(x-x1) (x-x2)
已知二次函数y=ax2+bx+c的图象与x 轴的一个交点坐标是(8,0),顶点是 (6,-12),求这个二次函数的解析式。 (分别用三种办法来求)
窗的形状是矩形上面加一个半圆。窗的 周长等于6cm,要使窗能透过最多的光 线,它的尺寸应该如何设计?
A
O
D
B
二次函数的应用课件ppt课件ppt课件ppt

要点一
导数在二次函数中的应用
利用导数研究二次函数的单调性、极值和拐点,解决实际 问题。
要点二
定积分在二次函数中的应用
利用定积分计算二次函数的面积,解决与面积相关的实际 问题。
THANKS
感谢观看
详细描述
二次函数是数学中一类重要的函数,其形式由参数$a$、$b$ 和$c$决定。当$a > 0$时,函数图像开口向上;当$a < 0$ 时,函数图像开口向下。
二次函数的图像
总结词
二次函数的图像是一个抛物线, 其形状由参数$a$、$b$和$c$决 定。
详细描述
二次函数的图像是一个抛物线, 其顶点的位置由参数$b$和$c$决 定,而开口的大小和方向则由参 数$a$决定。
在生产和生活中,经常需要解决诸如利润最大化、成本最小化等最优化问题。利 用二次函数开口方向和顶点坐标的性质,可以快速找到最优解,为决策提供依据 。
利用二次函数解决周期性问题
总结词
利用二次函数的对称性和周期性,解 决具有周期性规律的问题。
详细描述
在物理学、工程学和生物学等领域, 许多现象具有周期性规律。通过将实 际问题转化为二次函数模型,可以更 好地理解和预测这些周期性现象。
利用二次函数解决面积问题
总结词
利用二次函数与坐标轴的交点,解决 与面积相关的实际问题。
详细描述
在几何学和实际生活中,经常需要计 算图形的面积。通过将问题转化为求 二次函数与坐标轴围成的面积,可以 简化计算过程,提高解决问题的效率 。
04
如何提高二次函数的应用能力
掌握基本概念和性质
理解二次函数的一般 形式: $y=ax^2+bx+c$, 其中$a neq 0$。
导数在二次函数中的应用
利用导数研究二次函数的单调性、极值和拐点,解决实际 问题。
要点二
定积分在二次函数中的应用
利用定积分计算二次函数的面积,解决与面积相关的实际 问题。
THANKS
感谢观看
详细描述
二次函数是数学中一类重要的函数,其形式由参数$a$、$b$ 和$c$决定。当$a > 0$时,函数图像开口向上;当$a < 0$ 时,函数图像开口向下。
二次函数的图像
总结词
二次函数的图像是一个抛物线, 其形状由参数$a$、$b$和$c$决 定。
详细描述
二次函数的图像是一个抛物线, 其顶点的位置由参数$b$和$c$决 定,而开口的大小和方向则由参 数$a$决定。
在生产和生活中,经常需要解决诸如利润最大化、成本最小化等最优化问题。利 用二次函数开口方向和顶点坐标的性质,可以快速找到最优解,为决策提供依据 。
利用二次函数解决周期性问题
总结词
利用二次函数的对称性和周期性,解 决具有周期性规律的问题。
详细描述
在物理学、工程学和生物学等领域, 许多现象具有周期性规律。通过将实 际问题转化为二次函数模型,可以更 好地理解和预测这些周期性现象。
利用二次函数解决面积问题
总结词
利用二次函数与坐标轴的交点,解决 与面积相关的实际问题。
详细描述
在几何学和实际生活中,经常需要计 算图形的面积。通过将问题转化为求 二次函数与坐标轴围成的面积,可以 简化计算过程,提高解决问题的效率 。
04
如何提高二次函数的应用能力
掌握基本概念和性质
理解二次函数的一般 形式: $y=ax^2+bx+c$, 其中$a neq 0$。
二次函数的应用(2)——抛物线型问题

∴水面宽度将增加 2 6 4米.
8.如图,隧道横截面为抛物线,其最大高度为 6 米,OM 为 12 米.
(1)求这条抛物线的解析式; (2)若在隧道 C,D 处装两个路灯,且路灯的高度为 4 米,求 C, D 之间的距离.
解:(1)由题意,得 M 12,0,P6,6
设抛物线的解析式为 y a x 62 6
设抛物线的解析式为 y a x 2 x 2
∵过点C(0,2)
∴2=a0 20 2
,a 1
2Байду номын сангаас
∴抛物线的解析式为y 1 x 2 x 2 ,即 y 1 x2 2
2
2
(2)由题意,得 1= 1 x2 2
2
解得 x1 6,x2 6
(1)求这条抛物线的函数关系式; (2)水池的半径至少要多少米,才能使喷出的水流不落在池 外?
(1)顶点 A1, 4
设抛物线的函数关系式为 y a x 12 4
∵过(0,3) ∴ 3=a 0 12 4 ∴ a 1
∴抛物线的函数关系式为 y x 12 4
PPT课程
主讲老师:
全一册下
第二章 二次函数
第13课 二次函数的应用(2)——抛物线型问题
一、知识储备
1.求抛物线 y=x2-8x 与 x 轴的交点坐标. 解:令 y 0 ,得 0=x2 8x 解得 x1 0,x2 8
∴该抛物线与x轴的交点坐标为0,0,8,0
2.抛物线的顶点为(6,3)且过点(0,0),求它的解析式.
(2)当 x=9 y=-112(9-6)2+3=2.25<2.5 ∴射中球门
5.(例 2)如图,铅球在 A 点被推出,出手时球离地面 1 米, 铅球飞行轨迹是抛物线,当铅球飞行的水平距离为 4 米时达到最高 点 B,最高点离地面 3 米.
新版北师大九年级下2.4二次函数的应用课件ppt
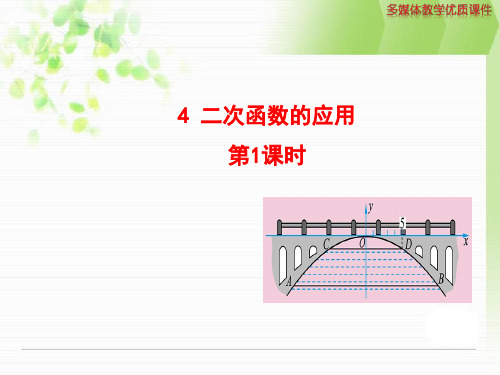
【解析】 (1)设矩形广场四角的小正方形的边长为x米,根据题意 得:4x2+(100-2x)(80-2x)=5 200, 整理得x2-45x+350=0, 解得x1=35,x2=10,经检验x1=35,x2=10均适合题意 , 所以,要使铺设白色地面砖的面积为5 200平方米, 则矩形广场四角的小正方形的边长为35米或者10米.
谢谢观赏
You made my day!
我们,还在路上……
即当x≈1.07m时,窗户通过的光线最多.此时窗户的面积为
4.02m2.
1.(包头·中考)将一条长为20cm的铁丝剪成两段,
并以每一段铁丝的长度为周长各做成一个正方形,则这
两个正方形面积之和的最小值是
cm2.
【答案】 12.5 或 25
2
2.(芜湖·中考)用长度为20m的金属材料制成如图所 示的金属框,下部为矩形,上部为等腰直角三角形,其
4.(南通·中考)如图,在矩形ABCD中,AB=m(m是大于0的常 数),BC=8,E为线段BC上的动点(不与B,C重合).连接DE, 作EF⊥DE,EF与线段BA交于点F,设CE=x,BF=y. (1)求y关于x的函数关系式. (2)若m=8,求x为何值时,y的值最大,最大值是多少? (3)若 y 12 ,要使△DEF为等腰三角形,m的值应为多少?
即△DEF为等腰三角形,m的值应为6或2.
5.(河源·中考)如图,东梅中学要在教学楼后面的空地上用 40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教 学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y. (1)求y与x的函数关系式,并求出自变量x的取值范围. (2)生物园的面积能否达到210平方米?说明理由.
解析:
由4 y 7 x x 15.
人教版初中数学中考复习 一轮复习 二次函数及其应用2(课件)

解方程,得 m1=-2,m2=3(不符合题意,舍去) ∴m=-2
典型例题——二次函数与方程、不等式的关系
9. (2021•泸州)直线 l 过点(0,4)且与 y 轴垂直,若二次函数 y=(x﹣a)2+(x﹣2a)2+
(x﹣3a)2﹣2a2+a(其中 x 是自变量)的图象与直线 l 有两个不同的交点,且其对称轴
解方程,得 m1= 41-1 ,m2= - 41+1 (不符合题意,舍去)
4
4
∴m= 41-1 , 4
1 - m>3,即 m<-3,当 x=3 时,y=6.∴9来自6m+2m2-m=6,
解方程,得 m1=-1,m2= - 3 (均不符合题意,舍去). 2
综上所述,m=-2 或 m=
41-1
.
4
2 1<- m≤3,即-3≤m<-1,当 x=-m 时,y=6. ∴m2-m=6
bx+c=0有 两个不相等的 实数根;
②如果抛物线y=ax2+bx+c(a≠0)与x轴 只有一个 交点,则一元二次方
程ax2+bx+c=0有两个 相等 的实数根;
③如果抛物线y=ax2+bx+c(a≠0)与x轴没有交点,则一元二次方程ax2+bx
+c=0 没有 实数根.
知识点梳理——知识点4:二次函数与一元二次方程及不等式的关系
A(1,0),B(m,0)(-2<m<-1),下列结论①2b+c>0;②2a+c<0;
③a(m+1)-b+c>0;④若方程a(x-m)(x-1)-1=0有两个不等实数根,
A 则4ac-b2<4a;其中正确结论的个数是(
)
A.4
B.3
C.2
D.1
典型例题——二次函数与方程、不等式的关系
山东省九年级鲁教版(五四制)数学上册课件:36二次函数的应用(2)(共16张PPT)

.最大面积的求法
(1)确定自变量x及其取值范围 (2)将面积表示以x为自变量的二 次函数
(3)利用 或 求最大面积. (4)一般地,因为抛物线 的顶点是 最高(低)点,所以当x= 时, 函数有最大(小)值为
议一议
还记得本章一开始的“种多少棵橙子树”的问题吗?
增种橙子树的数量x(棵)与橙子总产量y(个)之
例2:
某旅社有客房120间,每间房的日租金为160元, 每天都客满.经市场调查发现,如果每间客房的日租 金每增加10元时,那么客房每天出租数会减少6间. 不考虑其他因素,旅社将每间客房的日租金提高到 多少元时,客房日租金的总收入最高?
大家自己动手做一做 吧,相信你是最棒的!
分析:有客房120间,每间房的日租金为160元,每天 都. 客满.如果每间客房的日租金每增加10元时,那么客房 每天出租数会减少6间.
件.
厂家批发单价是多少时,可以获利最多?
分析:服装厂生产某品牌的T恤衫,每件的成本是10元. 根. 据市场调查,以单价13元批发给经销商,经销商愿意经 销5000件,并且表示每件降价0.1元,愿意多经销500件.
解:设批发单价为x元(0<x≤13元),那么 销售量可表示为 : 5000+5000(13-;x)
每件小商品的利润为: X-10 元;
所获总利润可表示为: (X-10) [5000还+5有00其0(1他3-x解)]法元吗;?
即y=-5000x2+120000x-700000=-5000(x-12)2+20000
∵-5000<0 ∴当销售单价为
12 元时,可以获得最大利润,
最大利润是 20000
元.
则 y=〔 800-10(30-x) 〕·x
二次函数的应用ppt课件

②根据题意,得绿化区的宽为
= (x-20)(m),
∴y=100×60-4x(x-20).又 ∵28≤100-2x≤52,∴24≤x≤36. 即 y 与 x 的函数关系式及 x 的取值范围为 y=-4x2+80x+6 000 (24≤x≤36);
-7-
2.4 二次函数的应用
(2)y=-4x2+80x+6 000=-4(x-10)2+6 400. ∵a=-4<0,抛物线的开口向下,对称轴为直线 x= 10. 当 24≤x≤36 时,y 随 x 的增大而减小, ∴ 当 x=24 时,y 最大=5 616,即停车场的面积 y 的最大值为 5 616 m2; (3)设费用为 w. 由题意,得 w=100(-4x2+80x+6 000)+50×4x(x- 20)=-200(x-10)2 +620 000, ∴ 当 w=540 000 时,解得 x1=-10,x2=30. ∵24≤x≤36,∴30≤x≤36,且 x 为整数, ∴ 共有 7 种建造方案. 题型解法:本题是确定函数表达式及利用函数的性质设计工程方案的问题. 解题过程中应理解:(1)工程总造价是绿化区造价和停车场造价两部分的和; (2)根据投资额得出方程,结合图象的性质求出完成工程任务的所有方案.
(1)解决此类问题的关键是建立恰当的平面直角坐标系; 注意事项
(2)根据题目特点,设出最容易求解的函数表达式形式
-9-
2.4 二次函数的应用
典题精析 例 1 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系, 其函数的关系式为 y=- x2,当水面离桥拱顶的高度 DO 是 4 m 时,水面宽 度 AB 为 ( ) A. -20 m B. 10 m C. 20 m D. -10 m
北师大版九年级数学下册2.4《二次函数的应用》课件(共18张PPT)

6050 0
60495
60480
6045 5
6042 0
60600 y/个
60500
60400
60300
60200
60100 60000
0 1 2 3 4 5 6 7 8 9 1011 1213 14 x/棵
议一议
何时橙子总产量最大
1.利用函数表达式描述橙子的总产量与增种橙子 树的棵数之间的关系.
(100+x)棵
这时平均每棵树结多少个橙子?
(600-5x)个
(2)如果果园橙子的总产量为y个, 那么请你写出y与x之间的关系式.
想一想
何时橙子总产量最大
果园共有(100+x)棵树,平均每棵树结(600-5x) 个橙子,因此果园橙子的总产量
y=(100+x)(600-5x)=-5x²+100x+60000. 在上述问题中,种多少棵橙子树,可以使果园橙子的总产量 最多?X/棵 1 2 3 4 5 6 7 8 9 10 11 12 13 14
点重合时,等腰△PQR以1cm/s的速度沿直线l向
左方向开始匀速运动,ts后正方形与等腰三角形
重合部分面积为Scm2,解答下列问题:
(1)当t=3s时,求S的值; (2)当t=3s时,求S的值; A
B
(3)当5s≤t≤8s时,求S 与t的函数关系式,并求
MP
S的最大值。
lD Q
C
R
做一做
何时橙子总产量最大
N
2y
xb
x
3
x
30
3
x2
30x
3 x 202
300.
4
4
4
或用公式 :当x
2022九年级数学上册第三章二次函数6二次函数的应用2利用二次函数求实际中应用问题课件鲁教版五四制4
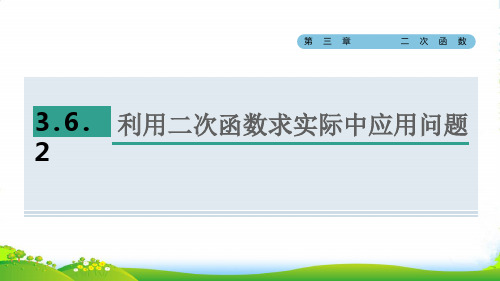
∴(28+12a-6-a)[-100×(28+12a)+5000]-2 000=42 100, ∴a1=2,a2=86. ∵a<4,∴a=2.
8 【2020·十堰】某企业接到生产一批设备的订单,要求不超过 12天完成.这种设备的出厂价为1 200元/台,该企业第一天生 产22台设备,第二天开始,每天比前一天多生产2台.若干天 后,每台设备的生产成本将会增加,设第x天(x为整数)的生 产成本为m(元/台),m与x的关系如图所示. (1)若第x天可以生产这种设备y台,则y与x的函 数关系式为__y_=__2_x_+__2_0,x的取值范围为 __1_≤_x_≤_1_2_.
5 【2020·丹东】某服装批发市场销售一种衬衫,衬衫 每件进货价为50元.规定每件售价不低于进货价,经 市场调查,每月的销售量y(件)与每件的售价x(元)满 足一次函数关系,部分数据如下表:
(1)求出y与x之间的函数表达式(不需要求自变量x的取 值范围).
解:设 y 与 x 之间的函数表达式为 y=kx+b, 则有6605kk+ +bb= =11 430000, ,解得kb= =- 2 62000,, 即 y 与 x 之间的函数表达式是 y=-20x+2 600;
(3)求当天销售利润低于10 800元的天数. 解:由(2)可得,1≤x≤6时,800x+8 000<10 800, 解得x<3.5. 则第1~3天当天销售利润低于10 800元, 当6<x≤12时,-100(x-2)2+14 400<10 800, 解得x<-4(舍去)或x>8, ∴第9~12天当天销售利润低于10 800元, 故当天销售利润低于10 800元的天数有7天.
(2)该批发市场每月想从这种衬衫销售中获 利24 000元,又想尽量给客户实惠,该如何 给这种衬衫定价?
8 【2020·十堰】某企业接到生产一批设备的订单,要求不超过 12天完成.这种设备的出厂价为1 200元/台,该企业第一天生 产22台设备,第二天开始,每天比前一天多生产2台.若干天 后,每台设备的生产成本将会增加,设第x天(x为整数)的生 产成本为m(元/台),m与x的关系如图所示. (1)若第x天可以生产这种设备y台,则y与x的函 数关系式为__y_=__2_x_+__2_0,x的取值范围为 __1_≤_x_≤_1_2_.
5 【2020·丹东】某服装批发市场销售一种衬衫,衬衫 每件进货价为50元.规定每件售价不低于进货价,经 市场调查,每月的销售量y(件)与每件的售价x(元)满 足一次函数关系,部分数据如下表:
(1)求出y与x之间的函数表达式(不需要求自变量x的取 值范围).
解:设 y 与 x 之间的函数表达式为 y=kx+b, 则有6605kk+ +bb= =11 430000, ,解得kb= =- 2 62000,, 即 y 与 x 之间的函数表达式是 y=-20x+2 600;
(3)求当天销售利润低于10 800元的天数. 解:由(2)可得,1≤x≤6时,800x+8 000<10 800, 解得x<3.5. 则第1~3天当天销售利润低于10 800元, 当6<x≤12时,-100(x-2)2+14 400<10 800, 解得x<-4(舍去)或x>8, ∴第9~12天当天销售利润低于10 800元, 故当天销售利润低于10 800元的天数有7天.
(2)该批发市场每月想从这种衬衫销售中获 利24 000元,又想尽量给客户实惠,该如何 给这种衬衫定价?
二次函数的应用ppt课件

∴Q的坐标为(4,0);∠GCF=90°不存在,
综上所述,点Q的坐标为(4,0)或(9,0).
2.4
二次函数的应用(2)
北师大版 九年级数学下册
目
录
00 名师导学
01 基础巩固
02 能力提升
C O N TA N T S
数学
返回目录
◆ 名师导学 ◆
知识点 最大利润问题
(一)这类问题反映的是销售额与单价、销售量以及利润与每
(3)存在.∵y= x +2x+1= (x+3) -2,∴P(-3,-2),
3
3
∴PF=yF-yP=3,CF=xF-xC=3,
∴PF=CF,∴∠PCF=45°.
同理,可得∠EAF=45°,∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的点Q.
设Q(t,1)且AB=9 2,AC=6,CP=3 2.
∵以C,P,Q为顶点的三角形与△ABC相似,
数学
返回目录
①当△CPQ∽△ABC时,
+6 3 2
∴ = ,∴ = ,∴t=-4,∴Q(-4,1);
6
9 2
②当△CQP∽△ABC时,
+6 3 2
∴ = ,∴ = ,∴t=3,∴Q(3,1).
9 2
6
综上所述,在直线AC上存在点Q,使得以C,P,Q为顶点的三角形
数学
返回目录
◆ 基础巩固◆
一、选择题
1.在一个边长为1的正方形中挖去一个边长为 x(0<x<1)的小
正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式
B
为
(
)
2
2
二次函数初三ppt课件ppt课件ppt课件

二次函数初三ppt课件ppt 课件ppt课件
contents
目录
• 二次函数的基本概念 • 二次函数的性质 • 二次函数的应用 • 二次函数的解析式 • 二次函数与一元一次方程的关系 • 综合练习与提高
01 二次函数的基本 概念
二次函数的定义
总结词
二次函数是形如$y=ax^2+bx+c$的 函数,其中$a$、$b$、$c$为常数 ,且$a neq 0$。
详细描述
二次函数的一般形式是 $y=ax^2+bx+c$,其中$a$、$b$、 $c$是常数,且$a neq 0$。这个定义 表明二次函数具有一个自变量$x$,一 个因变量$y$,并且$x$的最高次数为 2。
二次函数的表达式
总结词
二次函数的表达式可以因形式多样而变化,但一般包括三个部分:常数项、一 次项和二次项。
02 二次函数的性质
二次函数的开口方向
总结词
二次函数的开口方向取决于二次 项系数a的正负。
详细描述
如果二次项系数a大于0,则抛物 线开口向上;如果二次项系数a小 于0,则抛物线开口向下。
二次函数的顶点
总结词
二次函数的顶点坐标为(-b/2a, c-b^2/4a)。
详细描述
二次函数的顶点是抛物线的最低点或最高点,其坐标为(-b/2a, c-b^2/4a),其中 a、b、c分别为二次项、一次项和常数项的系数。
解一元二次方程的方法包括公式法和 因式分解法等。
利用二次函数解决一元一次方程问题
当一元一次方程有重根时,可以通过构建二次函数来求解。
构建二次函数的方法是将一元一次方程转化为二次函数的形 式,然后利用二次函数的性质找到根。
06 综合练习与提高
contents
目录
• 二次函数的基本概念 • 二次函数的性质 • 二次函数的应用 • 二次函数的解析式 • 二次函数与一元一次方程的关系 • 综合练习与提高
01 二次函数的基本 概念
二次函数的定义
总结词
二次函数是形如$y=ax^2+bx+c$的 函数,其中$a$、$b$、$c$为常数 ,且$a neq 0$。
详细描述
二次函数的一般形式是 $y=ax^2+bx+c$,其中$a$、$b$、 $c$是常数,且$a neq 0$。这个定义 表明二次函数具有一个自变量$x$,一 个因变量$y$,并且$x$的最高次数为 2。
二次函数的表达式
总结词
二次函数的表达式可以因形式多样而变化,但一般包括三个部分:常数项、一 次项和二次项。
02 二次函数的性质
二次函数的开口方向
总结词
二次函数的开口方向取决于二次 项系数a的正负。
详细描述
如果二次项系数a大于0,则抛物 线开口向上;如果二次项系数a小 于0,则抛物线开口向下。
二次函数的顶点
总结词
二次函数的顶点坐标为(-b/2a, c-b^2/4a)。
详细描述
二次函数的顶点是抛物线的最低点或最高点,其坐标为(-b/2a, c-b^2/4a),其中 a、b、c分别为二次项、一次项和常数项的系数。
解一元二次方程的方法包括公式法和 因式分解法等。
利用二次函数解决一元一次方程问题
当一元一次方程有重根时,可以通过构建二次函数来求解。
构建二次函数的方法是将一元一次方程转化为二次函数的形 式,然后利用二次函数的性质找到根。
06 综合练习与提高
二次函数的应用第二课时最大利润学年北师大版九年级数学下册课件

(2)如果李明想要每月获得2000元的利润,那么销售单价应定 为多少元?
解:(2)由题意,得:- 10x²+700x-10000=2000 解得x1=30,x2=40
∴李明想要每月获得2000元的利润, 销售单价应定为30元或40元.
2.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投 放市场进行试销.据市场调查,销售单价是100元时,每天的销售量 是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单 价不得低于成本. (1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系
y=a(x-h)2+k顶点坐标是(h,k),对称轴是直线x=h 当x=h时,y有最大值或最小值k
y=ax2+bx+c中顶点式,对称轴和顶点坐标公式:
y a x
b
2
4ac
b2
.
2a
4a
顶点坐标是
b 2a
,
4ac 4a
b2
对称轴是直线x b 2a
当x b 时, y有最大或最小值 4ac b2 .
(2)当1≤x<50时,二次函数开口下,二次函数对称轴为x=45, 当x=45时,y最大=﹣2×452+180×45+2000=6050, 当50≤x≤90时,y随x的增大而减小, 当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大利润是6050元;
(3)当20≤x≤60时,每天销售利润不低于4800元.
设旅行团人数为x人,营业额为y元,则 y= x [800-10(x-30)]
= - 10x2+1100x
= - 10(x-55)2+30250
高中数学人教B版必修一课件2.2二次函数应用-不等式

{x|x≠} b 2a
ax2+bx+c<0
(a>0)的解集 {x|x1<x<x2}
Φ
△<0 y
x O 没有实根
R Φ
解一元二次 化为ax2+bx+c>0(或<0),(a>0) 不等式
ax2+bx+c>0 不是
是
(a>0)的过程:
△<0
不是
是
x1=x2
解为两根 之外(或之间)
解为x≠x1(或Ф ) 解为R(或Ф )
高中数学课件
(金戈铁骑 整理制作)
2.2二次函数性质与应用(2)
---不等式问题
一元二次不等式的定义:
我们把只含有一个未知数,并且未知数 的最高次数为2次的不等式称为一元二 次不等式。
其一般形式为:ax2 bx c 0 ax2 bx c 0 ax2 bx c 0 ax2 bx c 0
解:A∩B=A, 则A B
而A:若a≥1则1≤x≤a1≤a≤3 若a<1则a≤x≤1那么 ∴a取值范围是1≤a≤3
A B
练习:已知A {x || x 1 | 2},
B {x | x2 4ax 3a2 0, a 0},
A B , 求a的取值范围
二.一元二次不等式应用
解:
依题意,得- b 5 1, 1
a - 1 ,b a4 .
a
5 1.
5
5
不等式x2 bx a 0为5x2 4x 1 0,
即(5x 1)(x 1) 0,
所求不等式的解集为{x | 1 x 1}. 5
初三二次函数ppt课件ppt课件ppt课件

03
二次函数的图像变换
平移变换
总结词
平移变换是指二次函数的图像在平面坐标系 中沿x轴或y轴方向进行移动。
详细描述
平移变换包括沿x轴方向的左移和右移,以 及沿y轴方向的上移和下移。对于一般形式 的二次函数y=ax^2+bx+c,当b≠0时,图 像为抛物线。当b>0时,图像向右平移b/2a个单位;当b<0时,图像向左平移 |b|/2a个单位。
总结词
顶点式二次函数解析式是y=a(xh)^2+k,其中(h,k)为函数的顶点。
详细描述
顶点式二次函数解析式表示的是一个 开口向上或向下的抛物线,其顶点为 (h,k)。该形式简化了函数的对称轴和 顶点,便于分析函数的性质。
交点式二次函数解析式
总结词
交点式二次函数解析式是y=a(x-x1)(x-x2),其中x1、x2为函数与x轴的交点。
02
二次函数的解析式
一般二次函数解析式
总结词
一般二次函数解析式是y=ax^2+bx+c,其中a、b、c为常数 ,且a≠0。
详细描述
一般二次函数解析式是二次函数的基本形式,它可以表示任 意二次函数。其中a控制函数的开口方向和开口大小,b控制 函数的对称轴,c为函数与y轴的交点。
顶点式二次函数解析式
值的变化。
04
二次函数的实际应用
最大利润问题
总结词
通过建立二次函数模型,解决最大利润问题。
详细描述
在生产和经营过程中,常常需要寻求最大利润。通过将实际问题转化为数学模型,利用二次函数求导 数的方法,可以找到获得最大利润的条件和对应的最大利润值。
抛物线形拱桥问题
总结词
利用二次函数解析式表示抛物线形拱桥的形 状,进而解决相关问题。
二次函数在导数中的应用ppt课件

“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
小结
• 三次求导之后是二次,从而把研究三次函 数的问题转化为研究二次函数的问题,注 意三个二次之间的关系。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
小结
• 分式型导数问题其实可以保持分母为正, 然后只研究分子。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
课后总结 在利用导数研究函数问题时,其实就是 将我们不熟悉的函数问题转化或化归为 二次函数,一次函数及其他我们熟悉的 数学问题.
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
2.4.2北师大版九年级数学下册课件第二章第四节二次函数的应用第二课时最大利润

10
x y 160 x 120 6 当x 20时,y最大 19440 10 这时每间客房的日出租金为160+20=180元 3 x 2 24 x 19200 5
3 x 20 2 19440 5
x 0, 且120 0 x 200
解:设单价是 x 元时可以获利为 y 元. 13-x 则 y=(x - 10)(5000 + 500× )=-5000(x-12)2 +20000 0.1 因此厂家批发单价是 12 元时可以获得最大利润
探究活动一 例2:某旅社有客房120间,每间房的日租金为160元时,每天都 客满,经市场调查发现,如果每间客房的日租金每增加10元时, 那么客房每天出租数会减少6间.不考虑其他因素,旅社将每间客 房的日租金提高到多少元时,客房日租金的总收入最高?
y=(x-8)[100-10(x-10)] =-10x2+280x-1600
=-10(x-14)2+360
解:设每间客房的日租金提高 x 个 10 元, 则每天客房出租数会减少 6x 间。 设客房日租金总收入为 y 元 则 y=(160+10x)(120-6x)= - 60(x-2)2+19440 ∵x≥0,且 120-6x>0 ∴0≤x<20 ∵- 60<0 ∴当 x=2 时,y 有最大值 19440。 这时每间客房的日租金为 160+10×2=180 元。 客房总收入最高为 19440 元。 答:每Байду номын сангаас客房的日租金提高到 180 元时,客房日租金总收入 最高为 19440 元。
b b 4ac b 2 对称轴是直线 x 顶点坐标是 , 2a 2a 4 a b 4ac b 2 当x 时, y有最大或最小值 . 2a 4a
x y 160 x 120 6 当x 20时,y最大 19440 10 这时每间客房的日出租金为160+20=180元 3 x 2 24 x 19200 5
3 x 20 2 19440 5
x 0, 且120 0 x 200
解:设单价是 x 元时可以获利为 y 元. 13-x 则 y=(x - 10)(5000 + 500× )=-5000(x-12)2 +20000 0.1 因此厂家批发单价是 12 元时可以获得最大利润
探究活动一 例2:某旅社有客房120间,每间房的日租金为160元时,每天都 客满,经市场调查发现,如果每间客房的日租金每增加10元时, 那么客房每天出租数会减少6间.不考虑其他因素,旅社将每间客 房的日租金提高到多少元时,客房日租金的总收入最高?
y=(x-8)[100-10(x-10)] =-10x2+280x-1600
=-10(x-14)2+360
解:设每间客房的日租金提高 x 个 10 元, 则每天客房出租数会减少 6x 间。 设客房日租金总收入为 y 元 则 y=(160+10x)(120-6x)= - 60(x-2)2+19440 ∵x≥0,且 120-6x>0 ∴0≤x<20 ∵- 60<0 ∴当 x=2 时,y 有最大值 19440。 这时每间客房的日租金为 160+10×2=180 元。 客房总收入最高为 19440 元。 答:每Байду номын сангаас客房的日租金提高到 180 元时,客房日租金总收入 最高为 19440 元。
b b 4ac b 2 对称轴是直线 x 顶点坐标是 , 2a 2a 4 a b 4ac b 2 当x 时, y有最大或最小值 . 2a 4a
2.4二次函数的应用(2)营销最值问题

每间客房日租金提高到180元时,
三、课堂小结
求一个未知量的值
设一个未知数
方程
求一个未知量的最值
设两个未知数
关键:寻找等量关系
解决实际问题的有效模型
函数
四、课堂检测
1. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么
半月内可售出400件、根据销售经验,提高销售单价会导致销售量的减少,
某种服装,平均每天可销售20件,每件盈利44元. 据市场调查发现:
若每件降价1元,则每天可多售5件. 如果每天要盈利1600元,每件应
降价多少元?
解:设每件应降价 x 元,根据题意,得
( − )( + ) =
解得: = , =
所以,每件应降价4元或36元.
二、新知探究
解:设每间客房日租金提高
∵ ≥ , −
≥
x 元 时,总收入 y 元.
∴ ≤ ≤
= ( + )( −
)
∴.当x=20时,y取得最大值为19440.
= − + +
∴ + = (元)
∴
= − ( − ) +
围内有可能求出最值.故可尝试用函数知识来解决.
例1 某种服装,平均每天可销售20件,每件盈利44元. 据市场调查发
现:若每件降价1元,则每天可多售5件. 每件降价多少时,才能盈利
最多,最多是多少?
分析:函数表达式也是一个等式,是关于两个未知数的等式.可见解
函数应用题的关键也是: 寻找等量关系。本题的主要等量关系:
子.增种多少棵橙子树时果园的产量最高?
三、课堂小结
求一个未知量的值
设一个未知数
方程
求一个未知量的最值
设两个未知数
关键:寻找等量关系
解决实际问题的有效模型
函数
四、课堂检测
1. 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么
半月内可售出400件、根据销售经验,提高销售单价会导致销售量的减少,
某种服装,平均每天可销售20件,每件盈利44元. 据市场调查发现:
若每件降价1元,则每天可多售5件. 如果每天要盈利1600元,每件应
降价多少元?
解:设每件应降价 x 元,根据题意,得
( − )( + ) =
解得: = , =
所以,每件应降价4元或36元.
二、新知探究
解:设每间客房日租金提高
∵ ≥ , −
≥
x 元 时,总收入 y 元.
∴ ≤ ≤
= ( + )( −
)
∴.当x=20时,y取得最大值为19440.
= − + +
∴ + = (元)
∴
= − ( − ) +
围内有可能求出最值.故可尝试用函数知识来解决.
例1 某种服装,平均每天可销售20件,每件盈利44元. 据市场调查发
现:若每件降价1元,则每天可多售5件. 每件降价多少时,才能盈利
最多,最多是多少?
分析:函数表达式也是一个等式,是关于两个未知数的等式.可见解
函数应用题的关键也是: 寻找等量关系。本题的主要等量关系:
子.增种多少棵橙子树时果园的产量最高?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢检查求得的最大值或最小值对应的字变量的值必 须在自变量的取值范围内 。
2020年10月2日
5
例3:
某饮料经营部每天的固定成本为200元,其销 售的饮料每瓶进价为5元。销售单价与日均销售量 的关系如下:
销售单价(元) 678 Nhomakorabea9
10
11
12
日均销售量(瓶) 480 440 400 360 320 280 240
①若记销售单价比每瓶进价多X元,日均毛利润 (毛利润=售价-进价-固定成本)为y元,求Y 关于 X的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多
少元(精确到0.1元)?最大日均毛利润为多少
元?
2020年10月2日
6
练一练
P:47 课内练习
2020年10月2日
7
1、通过这节课的学习活动你 有哪些收获?
➢ ①设经过t时后,A、B两 船分别到达A/、B/(如图), A’ 则两船的距离S应为多少 ?
➢ ②如何求出S的最小值??
A
B’ B
2020年10月2日
4
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值 的一般步骤 : ➢求出函数解析式和自变量的取值范围
➢配方变形,或利用公式求它的最大值或最小值。
浙教版九年级《数学》上册
2020年10月2日
九年级数学备课组 2006.8.
1
复习思考
如何运用二次函数求实际问题中的最大值或最小值?
➢ 首先应当求出函数解析式和自变量的取值范 围,然后通过配方变形,或利用公式求它的最大值 或最小值。
➢注意:有此求得的最大值或最小值对应的
。 字变量的值必须在自变量的取值范围内
汇报人:XXX 汇报日期:20XX年10月10日
9
2020年10月2日
2
例2:
如图,B船位于A船正东26KM处,现在A,B 两船同时出发,A船以12KM/H的速度朝正北方向行 驶,B船以5KM/H的速度朝正西方向行驶,何时两船 相距最近?最近距离是多少?
A’
2020年10月2日
A
B’ B
3
例2:
如图,B船位于A船正东26KM处,现在A,B 两船同时出发,A船以12KM/H的速度朝正北方向行 驶,B船以5KM/H的速度朝正西方向行驶,何时两船 相距最近?最近距离是多少?
2、对这节课的学习,你还有 什么想法吗?
2020年10月2日
8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
2020年10月2日
5
例3:
某饮料经营部每天的固定成本为200元,其销 售的饮料每瓶进价为5元。销售单价与日均销售量 的关系如下:
销售单价(元) 678 Nhomakorabea9
10
11
12
日均销售量(瓶) 480 440 400 360 320 280 240
①若记销售单价比每瓶进价多X元,日均毛利润 (毛利润=售价-进价-固定成本)为y元,求Y 关于 X的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多
少元(精确到0.1元)?最大日均毛利润为多少
元?
2020年10月2日
6
练一练
P:47 课内练习
2020年10月2日
7
1、通过这节课的学习活动你 有哪些收获?
➢ ①设经过t时后,A、B两 船分别到达A/、B/(如图), A’ 则两船的距离S应为多少 ?
➢ ②如何求出S的最小值??
A
B’ B
2020年10月2日
4
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值 的一般步骤 : ➢求出函数解析式和自变量的取值范围
➢配方变形,或利用公式求它的最大值或最小值。
浙教版九年级《数学》上册
2020年10月2日
九年级数学备课组 2006.8.
1
复习思考
如何运用二次函数求实际问题中的最大值或最小值?
➢ 首先应当求出函数解析式和自变量的取值范 围,然后通过配方变形,或利用公式求它的最大值 或最小值。
➢注意:有此求得的最大值或最小值对应的
。 字变量的值必须在自变量的取值范围内
汇报人:XXX 汇报日期:20XX年10月10日
9
2020年10月2日
2
例2:
如图,B船位于A船正东26KM处,现在A,B 两船同时出发,A船以12KM/H的速度朝正北方向行 驶,B船以5KM/H的速度朝正西方向行驶,何时两船 相距最近?最近距离是多少?
A’
2020年10月2日
A
B’ B
3
例2:
如图,B船位于A船正东26KM处,现在A,B 两船同时出发,A船以12KM/H的速度朝正北方向行 驶,B船以5KM/H的速度朝正西方向行驶,何时两船 相距最近?最近距离是多少?
2、对这节课的学习,你还有 什么想法吗?
2020年10月2日
8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
