(地图学课件)第2讲(第三章常用的地图投影)
常用的地图投影

第一节圆锥投影一、圆锥投影的基本概念1.圆锥投影的定义圆锥投影的概念可用图5-1来说明:设想将一个圆锥套在地球椭球上而把地球椭球上的经纬线网投影到圆锥面上,然后沿着某一条母线(经线)将圆锥面切开面展成平面,就得到圆锥投影。
2.圆锥投影的分类①按圆锥面与地球相对位置的不同,可分正轴、横轴、斜轴圆锥投影,见图5-2,但横轴、斜轴圆锥投影实际上很少应用。
所以凡在地图上注明是圆锥投影的,一般都是正轴圆锥投影。
②按标准纬线分为切圆锥投影和割圆锥投影切圆锥投影,视点在球心,纬线投影到圆锥面上仍是圆,不同的纬线投影为不同的圆,这些圆是互相平行的,经线投影为相交于圆锥顶点的一束直线,如果将圆锥沿一条母线剪开展为平面,则呈扇形,其顶角小于360度。
在平面上纬线不再是圆,而是以圆锥顶点为圆心的同心圆弧,经线成为由圆锥顶点向外放射的直线束,经线间的夹角与相应的经差成正比,但比经差小。
在割圆锥投影上,两条纬线投影后没有变形,是双标准纬线,两条割线符合主比例尺,离开这两条标准纬线向外投影变形逐渐增大,离开这两条标准纬线向里投影变形逐渐减小,凡是距标准纬线相等距离的地方,变形数量相等,因此圆锥投影上等变形线与纬线平行。
③圆锥投影按变形性质分为等角、等积和等距圆锥投影三种。
构成圆锥投影需确定纬线的半径ρ和经线间的夹角δ,ρ是纬度的函数用公式表示为。
δ是经差λ的函数。
用公式表示为,对于不同的圆锥投影它是不同的。
但对于某一具体的圆锥投影(),它的值是相同的。
当=1时(圆锥顶角为180 度),为方位投影;=0 时(圆锥体的顶角小到0度),为圆柱投影。
方位投影和圆柱投影都可看成是圆锥投影的特例。
3.基本公式在制图实践中,广泛采用正轴圆锥投影。
对于斜轴、横轴圆锥投影,由于计算时需经过坐标换算,且投影后的经纬形状均为复杂曲线,所以较少应用。
因此本文只研究正轴圆锥投影。
下面研究正轴圆锥投影的一般公式。
圆锥投影中纬线投影后为同心圆圆弧,经线投影后相交于一点的直线束,且夹角与经差成正比见图5-3。
(地图学课件)第2讲(第三章常用的地图投影)

§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影(墨卡托投影) 3、等角航线
在该投影图上,不仅保持了方向和相对位置的正确,而且能使等角航线表 示为直线,因此对航海、航空具有重要的实际应用价值。只要在图上将航 行的两点间连一直线,并量好该直线与经线的夹角,一直保持这个角度即 可到达终点。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.1 等差分纬线多圆锥投影
2、变形特点
• 该投影是属于面积变形不大的任意投影,从 整体构图上有较好的球形感; • 陆地部分变形分布比较均匀,其轮廓形状比 较接近真实,并配置在较为适中的位置,完整 地表现了太平洋及沿岸国家,突出了我国与太 平洋各国之间的联系; • 中央经线和±44纬线的交点处没有角度变形 ,我国境内绝大部分地区的角度变形在10以 内,只有少数地区可达13左右 ; • 面积比等于1的等变形线自西向东贯穿我国中 部,我国境内绝大部分地区的面积变形在10% 以内 。
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
3. 地图的内容 主题和内容不同,对投影的要求也不同。
• 要求方向正确,应选择等角投影 • 要求面积对比正确,应选择等积投影 • 教学或一般参考图,要求各方面变形都不大,则 应选择任意投影
现代地图学教程 第3章 地图投影及其判别与变换
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
2.制图比例尺 不同比例尺地图对精度要求不同,投影亦不同。 大比例尺地形图,对精度要求高,宜采用变形小的投影
3.2地图投影及其分类,3.3常用的地图投影解析PPT参考幻灯片
轴投影
5
§3 常用的地图投影
❖ 1.墨卡托投影(等角正圆柱投影) 投影原理:设想地球为一透明球体,球心置一点光
源,将圆柱投影面沿赤道与地球相切,地球上的经纬网格投 影到圆柱面上
6
墨卡托投影绘制的世界地图
§3 常用的地图投影
❖ (一)地图投影
利用一定的数学法则把地球表面上的经纬线网表 示到平面上
F(, ) f (x, y)
1
❖ 1. 地图投影的失真
由于地球椭球体表面是曲面,而地图通常是要绘制在平 面图纸上,因此制图时首先要把曲面展为平面,然而球 面是个不可展的曲面,即把它直接展为平面时,不可能 不发生破裂或褶皱。
为了保证地图的精度,采用分带投影方法,即将投 影范围的东西界加以限制,使其失真不超过一定的 限度,这样把许多带结合起来,可成为整个区域的 投影。
我国规定1:1 万、1:2.5 万、1:5 万、1:10万、 1:25 万、1:50 万比例尺地形图,均采用高斯克 -吕格投影。1:2.5 至1:50 万比例尺地形图采用 经差6 °分带,1:1 万比例尺地形图采用经差3° 分带。
绘制机场专用航图和涉及仪表飞行程序的基础用图; 国家大地测量和五十万分之一及更大比例尺的国家基本地形
图
13
❖ 高斯投影坐标网
经纬网(地理坐标网)
114°00 14
16
30° 202
40´
α
3396
94 -δ TH/TC
92
18 20 A( 20218 , 3394 )
90
TH/TC= α+(± δ)
第03章 地图投影
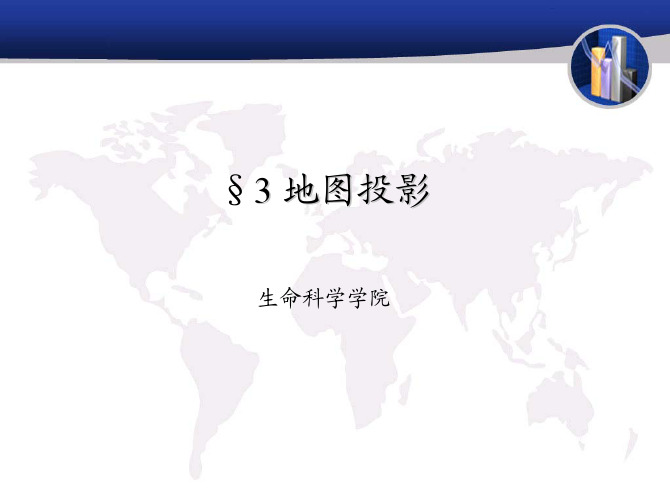
⑵ 不同变形性质投影的变形分布
⑶应用范围 • 根据圆柱投影的变形规律和经纬网的特点,在赤道附近沿 东西方向延伸地区的地图,最适宜采用各种变形性质的圆 柱投影; • 全球区域的地图可采用等角或等距圆柱投影,航海和航空 图上常常采用墨卡托投影; • 由于圆柱投影的经线为平行直线,便于显示时区的划分, 因此它也是世界时区图的主要投影。
⑵条件投影 • 根据某些条件,用数学解析法确定球面与平面之间点与点的 函数关系。 • 伪方位投影:在方位投影的基础上,根据某些条件改变经线 形状而成,除中央经线为直线外,其余均投影为对称中央经 线的曲线。 • 伪圆柱投影:在圆柱投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 伪圆锥投影:在圆锥投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 多圆锥投影:设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在中央经线 的延长线上。中央经线为直线,其余经线投影为对称于中央 经线的曲线。
§3 地图投影
生命科学学院
§1. 常用的地图坐标系
• 1.1 平面直角坐标系
x,y
• 1.2 平面极坐标系
ρ,δ
• 1.3 平面直角坐标与极坐标的关系
x q cos y sin
§2. 地图投影的基本概念
• 2.1 地图投影的定义
为什么要进行地图投影?
2
ab ab
当投影后经纬线正交,即θ=90°时:
,b n ; P ab mn ;
a m
sin
2
(地图学课件)第2讲链接(第三章我国地形图采用的地图投影)
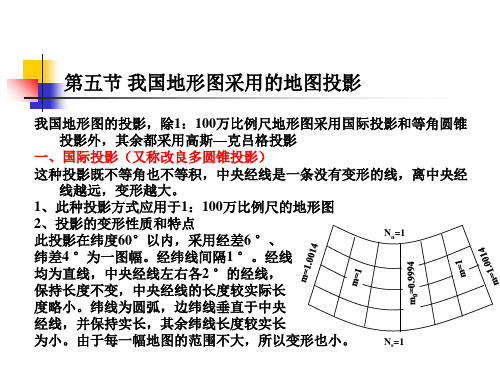
此投影在纬度60°以内,采用经差6 °、
Nn=1
纬差4 °为一图幅。经纬线间隔1 °。经线
均为直线,中央经线左右各2 °的经线,
保持长度不变,中央经线的长度较实际长
度略小。纬线为圆弧,边纬线垂直于中央
经线,并保持实长,其余纬线长度较实长
为小。由于每一幅地图的范围不大,所以变形也小。 Ns=1
第五节 我国地形图采用的地图投影
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 5、对多圆锥投影原理的解释 多圆锥投影,中央经线投影为直线且保持长度不变,其余经线投影为对
称于中央经线的曲线;赤道投影为直线,其余纬线投影为同轴圆弧, 圆心位于中央经线上,各纬线投影后保持长度不变且与中央经线正 交。
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 3、拼接时产生的后果 由于各幅地图均系单独投影,虽然同一列与同一行图幅可以密切拼接,
但上下左右四幅拼接在一起,则发生裂隙。如果九幅或更多幅地图 拼接在一起,则变形更大,但仍可有效的进行研究地区的阅读。 4、七十年代以前,我国1/100万地图一直采用国际投影,现在改用等角 圆锥投影。
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥
投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影)
这种投影既不等角也不等积,中央经线是一条没有变形的线,离中央经
线越远,变形越大。
1、此种投影方式应用于1:100万比例尺的地形图
三种常用地图投影介绍地理ppt

λ
椭球面上经线的夹角
m d Md
α
小于1的常数
n
r
sin a b
2 ab
或者:
tan 45 a
4 b
6
思考: 正轴圆锥投影的变形主要受什么因素影响?
7
2、双标准纬线等角圆锥投影
8
投影公式:
K U
,
x s cos
y sin
m
n
3
正轴:圆锥轴与地轴重合 横轴:圆锥轴与地轴垂直 斜轴:圆锥轴与地轴斜交
横轴、斜轴圆锥投影实际上很少应用。 凡在地图上注明是圆锥投影的,一般都是正轴圆锥投影。
4
对正轴圆锥投影,设区域中央经线投影作为X轴, 区域最低纬线与中央经线交点为原点。
5
1、圆锥投影(正轴)的一般公式:
f
x s cos y sin
由于每幅图的纬差仅为4°,因此投影的变形极小,长度变形 在边纬与中纬上为±0.030%,面积变形约为长度变形的两倍。
14
拼接裂隙: 投影的特点决定了:
图幅的东西方向拼接不会产 生裂隙;但南北方向拼接时, 因投影带不同,会产生裂隙。
裂隙距 裂隙角 图幅经差 L 边长 当纬度较低时,裂隙角增大, L也增大,裂隙距自然也增大。
r
K
rU
P
m2
n2
K
rU
2
0
α, K 均为投影常数:
lg r1 lg r2
lg U2 lg U1
K
r1U1
r2U
2
tan 45
U
2 ,sin e sin
tane 45
2
9
面积比等 变形线
中国常用的地图投影

中国常用的地图投影举例第三节中国常用的地图投影举例科学事业的发展同社会制度和经济基础是密切相联系的,旧中国是一个半封建半殖民地的国家,测绘事业也濒于停顿,编制出版的少量地图质量也很差,更少考虑到采用自己设计及计算的地图投影。
在解放前出版的几种地图中曾采用过的几种地图投影,也多半是因循国外陈旧的地图投影,很少自行设计新投影。
解放后,在党和政府的领导下,非常重视测绘科学事业的发展,我国测绘工作者不仅在地图投影的理论上有了研究,同时结合我国具体情况,设计了一些适合于我国情况的新的地图投影。
下面介绍我国出版的地图中常用的一些地图投影。
世界地图的投影等差分纬线多圆锥投影正切差分纬线多圆锥投影(1976年方案)任意伪圆柱投影:a=0.87740,6=0.85当φ=65°时P=1.20正轴等角割圆柱投影半球地图的投影东半球图横轴等面积方位投影φ0=0°,λ0=+70°横轴等角方位投影φ0=0°,λ0=+70°西半球图横轴等面积方位投影φ0=0°,λ0=-110°横轴等角方位投影φ0=0°,λ0=-110°南、北半球地图正轴等距离方位投影正轴等角方位投影正轴等面积方位投影亚洲地图的投影斜轴等面积方位投影φ0=+40°,λ0=+90°φ0=+40°,λ0=+90°彭纳投影标准纬线φ0=+40°,中央经线λ0=+80°标准纬线φ0=+40°,中央经线λ0=+80°欧洲地图的投影斜轴等面积方位投影φ0=52°30′,λ0=20°正轴等角圆锥投影φ1=40°30′,λ0=65°30′北美洲地图的投影斜轴等面积方位投影φ0=+45°,λ0=-100°彭纳投影南美洲地图的投影斜轴等面积方位投影φ0=0°,λ0=+20°桑逊投影λ0=+20°澳洲地图的投影斜轴等面积方位投影φ0=-25°,λ0=+135°正轴等角圆锥投影φ1=34°30′,φ2=-15°20′拉丁美洲地图的投影斜轴等面积方位投影φ0=-10°,λ0=-60°中国地图的投影中国全图斜轴等面积方位投影φ0=-27°30′λ0=+105°或φ0=30°00′λ0=+105°或φ0=35°00′λ0=+105°斜轴等角方位投影(中心点位置同上)彭纳投影伪方位投影中国全图(南海诸岛作插图)正轴等面积割圆锥投影两条标准纬线曾采用φ1=24°00′,φ2=48°00′或φ1=25°00′,φ2=45°00′或φ1=23°30′,φ2=48°30′目前常采用φ1=25°00′,φ2=47°00′正轴等角割圆锥投影中国分省(区)地图的投影正轴等角割圆锥投影正轴等面积割圆锥投影正轴等角圆柱投影高斯-克吕格投影(宽带)中国大比例尺地图的投影多面体投影(北洋军阀时期)等角割圆锥投影(兰勃特投影) (解放前)高斯-克吕格投影(中华人民共和国成立以后)。
地图学(2.投影)

地球椭球体元素及定义
• 首子午面:亦称起始经线面(本初 子午面),通过格林尼治天文台中 心的子午面。 • 首子午圈:亦称起始经线(本初子 午线),通过格林尼治天文台中心 的子午圈。 • 平行面:亦称纬线面,垂直与地轴 的平面。 • 平行圈:亦称纬线、纬圈,平行面 与椭球面的交线。 • 赤道面:垂直于地轴并过地心的平 面。
1
5 4 3
2
§5 常用小比例尺地图投影
5.1 方位投影
1) 等积方位投影 由德国数学家兰勃特(mbert)创制于1772年,又 名兰勃特投影。 其投影条件是:P=a×b=1
(1) 变形特点
① 极点无变形; ② 经线从切点往外作负向增大,即经线长随远离切点越短; ③ 纬线作正向增大; ④ 角度变形随远离切点逐渐增大。
设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在 中央经线的延长线上。中央经线为直线,其余经线 投影为对称于中央经线的曲线。
2) 条件投影(非几何投影或解析投影) (1) 多圆锥投影
经纬线形状: 经线: 中央经线为直线,其余为对称 于中央经线的曲线。 纬线: 赤道为直线,其余为对称于赤 道的同轴圆弧。
第二章
地图投影中的地球体
静止海平面
大地水准面
1.地球自然表面:地球是一个近似球体,其自然表面是一个极其复杂而 又不规则的曲面。 2. 地球物理表面:是假定海水处于 “完全” 静止状态,把海水面延伸到 (大地水准面)大陆之下形成包围整个地球的连续表面。 3. 大地体:由大地水准面包围而成的球状体。
地球椭球体元素及定义
• 赤道圈:赤道面与椭球面的交线, 简称赤道,它是最大的平行圈。 • 法线:垂直于椭球面某点的切面的 直线,一般不交于地心。 • 法截面:包含法线的一切平面。 • 卯酉面:与子午面垂直的法截面。 • 卯酉圈:卯酉面与椭球面的交线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影(墨卡托投影)
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影(墨卡托投影) 1、投影特点
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影(墨卡托投影) 3、等角航线
在该投影图上,不仅保持了方向和相对位置的正确,而且能使等角航线表 示为直线,因此对航海、航空具有重要的实际应用价值。只要在图上将航 行的两点间连一直线,并量好该直线与经线的夹角,一直保持这个角度即 可到达终点。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.2 正切差分纬线多圆锥投影
1、投影特点
该投影和等差分纬线多圆锥投影比较相似,它是一种任意性质、不等分纬 线的多圆锥投影,称之为正切差分纬线多圆锥投影。
2、变形特点
该投影属于角度变形不大的任意投影,角度无变形点位于中央经线与纬度 ±44交点处,愈向高纬度其角度变形递增愈快。面积等变形线与纬线方向 大致一致,在纬度±30以内面积变形为10%~20%,愈向高纬其面积变形愈 大,在纬度±60处增至200%,到纬度±80以上区域可增至400%~500%。 总体看来,世界的大陆轮廓形状无明显变形。我国的图形形状比较正确, 大陆部分最大角度变形均在6以内;大部分地区的面积变形在10%~20%以 内,少部分地区最多可达±60%左右。中国地图出版社1981年出版的1:1400 万世界地图,使用的就是该投影。
第3章 地图投影及其判别与变换
§1 地图投影的基本概念 §2 地图投影的分类 §3 常用的地图投影 §4 地图投影的选择、判别与变换 §5 我国地形图投影及其分幅与编号
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
地图投影的种类有很多,具体到常用的地图投影就是有限 的几个,这些地图投影主要用来编制世界地图、半球图、 大洋图、分洲图、分国图以及小区域的大中比例尺地图时 采用,其结果作为这些种类地图的数学基础。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.5 摩尔威特投影
1、投影特点
中央经线为直线,距离中央经线东西经差±90的经线构成一个大圆,其面 积等于地球面积的1/2,其余经线为椭圆;赤道长度是中央经线的2倍,纬线
间隔是由赤道向两极逐渐缩小的平行直线;同一条纬线上经线的间隔相等
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.1 等差分纬线多圆锥投影
1、投影特点
• 赤道和中央经线投影后是互相垂直的直 线,赤道长度比大于1,中央经线长度比 等于1; • 其它纬线为对称于赤道的同轴圆弧,其 圆心均在中央经线的延长线上; • 其它经线为对称于中央经线的曲线,其 经线间隔随离中央经线距离的增加而按等 差级数递减; • 极点投影成圆弧,其长度为赤道的1/2。
该投影的经纬线是互相垂直的平行直线,经线间隔相等,纬线间隔由赤道 向两极逐渐扩大。
2、变形特点
图上任取一点,由该点向各方向长度比皆相等,即角度变形ω=0。在正轴等 角切圆柱投影中,赤道为没有变形的线,随纬度增高面积变形增大。在正 轴等角割圆柱投影中,两条割线为没有变形的线,在两条标准纬线之间变 形为负值,离标准纬线愈远变形愈大,赤道上负向变形最大,两条标准纬 线以外呈正变形,同样离标准纬线愈远变形愈大,到极点为无限大。
2、变形特点
为等积性质的伪圆柱投影, 中央经线和±404411.8的 交点为没有变形的点,离这 两点距离愈远变形愈大,而 且向高纬比向低纬增大的速 度快。该投影用于用于编制 世界地图或东西半球图。
40°44 ′11.8 ″
S90 = Searth / 2
现代地图学教程 第3章 地图投影及其判别与变换
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.7 摩尔威特+桑逊-古ห้องสมุดไป่ตู้投影
投影和变形特点
古德除了将某一种伪圆柱投影 进行分瓣外,古德还采用了桑 逊投影和摩尔威特投影结合在 一起的分瓣方法;在南北纬 404411.8以内采用桑逊投影, 在此纬线以外采用摩尔威特投 影,两者在南北纬404411.8 部位结合起来,这样就可以使 投影变形减小。在国外(美、 日)出版的世界地图集中的世 界地图经常采用这种投影。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.1 等差分纬线多圆锥投影
2、变形特点
• 该投影是属于面积变形不大的任意投影,从 整体构图上有较好的球形感; • 陆地部分变形分布比较均匀,其轮廓形状比 较接近真实,并配置在较为适中的位置,完整 地表现了太平洋及沿岸国家,突出了我国与太 平洋各国之间的联系; • 中央经线和±44纬线的交点处没有角度变形 ,我国境内绝大部分地区的角度变形在10以 内,只有少数地区可达13左右 ; • 面积比等于1的等变形线自西向东贯穿我国中 部,我国境内绝大部分地区的面积变形在10% 以内 。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.4 桑逊投影 1、投影特点
经线为正弦曲线的等积伪圆柱投影,纬线为间隔相等的平行直线,每条纬 线上经线间隔相等。
2、变形特点
所有纬线长度比均等于1 ,即n=1;中央经线长度 比大于1,距中央经线愈 远其长度比愈大;面积 比等于1,即面积变形等 于0。适合编制位于赤道 附近南北延伸的地图。
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.6 古德投影 1、投影特点
即分瓣伪圆柱投影,用来绘制世界地图。其设计思想是将全制图区域根据 需要,确定若干个中央经线位置,然后进行分瓣投影,但要求分裂的各部 分必须在赤道处连接在一起。
2、变形特点
每瓣中央经线两侧投影区域 不至于过大,因此每瓣经线 的弯曲度减小,即经线交角 与实地差别减少,变形也就 减小。
