第五章时间序列的模型识别汇总
5时间序列模型

方差函数: 自协方差函数:
? ? 2 t
?
D(Y) t
?
?
[ yE?
??
(Y) td]2 FYt ( y)
?? Cov(Yt ,Ys ) ??E ???Yt EYt ??Ys ??EYs ??? t,s ? (t, s)
自相关函数(ACF):
? ?ts, ? ?? ts, ?
?(ts,) ??tt, ????s,
模型
? 完善阶段 :
? 异方差场合
? Robert F.Engle,1982年,ARCH模型 ? Bollerslov,1986年GARCH模型
? 多变量场合
? C.A.Sims等,1980年,向量自回归模型 ? C.Granger ,1987年,提出了协整(co-integration)理论
模拟时间序列数据:
8
? 随机过程与时间序列的关系如下所示:
随机过程: {y1, y2, …, yT-1, yT,} 第1次观测:{y11, y21, …, yT-11, yT1} 第2次观测:{y12, y22, …, yT-12, yT2}
???? ? 第n次观测:{y1n, y2n, …, yT-1n, yTn}
一般的,对于任意 m ? N,,t,1 t2 L , tm ? T,Yt1 ,L ,Ytm 的联合分布函数为:
FYt1 ,Yt2 ,L ,Ytm ( y1 ,,y,)2 L ymP ?? (Yt1 y1Y,,L tm ? ym )
均值方程:
? ?t ? E(Yt ) ?
?
?? ydFYt ( y)
9
2、随机过程的分布及其数字特征
设{Yt}为一个随机过程,对任意一个 t ? T ,Yt的分布函数为:
第五章 时间序列模型

5.时间序列模型
5.1 时间序列 5.2 自回归(AR)模型 5.3 滑动平均(MA)模型 5.4 自回归滑动平均(ARMA)模型
2/40
5.1 时间序列
数字化技术的应用和发展使得随机序列的分析变得日
益广泛和重要,并由平稳随机过程在时间轴上的 取样引
出平稳离散随机信号或时间序列的概念。对于这类随机序 列,主要采用相关函数和功率谱进行分析。对于平稳离散 时间信号,还常用时间序列描述方法进行研究,由此提出 时间序列模型法。它是采用各种随机差分方程表示时间序
当 z1, 2 1 时,上式右边齐次解随 n 的增大而趋于零,而特 解部分具有有限方差,在均方意义下收敛,随 n 的增大而 渐近收敛于特解公式的平稳结果。 实际上,二阶模型的平稳条件与其系数 a1和 a 2是有关
的,这可通过 a1和 a 2 平面表示。设 z1, 2 1 ,并设z1 z2 a1
1 H ( z) (1 z1 z 1 )(1 z 2 z 1 )(1 z p z 1 )
所以,AR模型的传递函数只有极点,除原点外没有任何 零点,属于全极点模型,对应于全极点滤波器,具有无限 冲激响应(IIR)。因此,模型传递函数的性质完全取决于 p
个极点在 z 平面上的分布情况。可以证明,如果所有 p 个
1 k 1 k 1 k z1 z 2 D (n) z1 z 2 k 0 k z1k 1 z 2 1 (n k ) z1 z 2 k 0
15/40
5.2 自回归(AR)模型
根据模型差分方程,零输入下得齐次方程
x(n) a1 x(n 1) a2 x(n 2) 0
11/40
《时间序列模型识别》课件

外汇汇率预测
外汇汇率预测是时间序列模型的又一重要应用。通过分析历史外汇汇率数据,时 间序列模型可以预测未来的汇率走势,帮助投资者制定外汇交易策略。
常用的时间序列模型同样适用于外汇汇率预测,如ARIMA、SARIMA、VAR、 VARMA等。这些模型能够捕捉外汇汇率的动态变化规律,为投资者提供有价值 的参考信息。
总结词
气候变化趋势分析是全球气候治理的重要基 础,利用时间序列模型可以对气候变化趋势 进行定量评估,为政策制定提供科学依据。
详细述
通过长时间尺度的历史气候数据,建立时间 序列模型,并利用该模型分析气候变化的趋 势。分析结果可以为应对气候变化、制定减 排政策等提供决策支持。
06
时间序列模型在生产领域 的应用
解释性
选择易于解释的模型,有助于 理解时间序列数据的内在规律 。
计算效率
考虑模型的计算效率和可扩展 性,以便在实际应用中快速处
理大量数据。
03
时间序列模型性能评估
预测精度评估
01
均方误差(MSE)
衡量预测值与实际值之间的平均 差异,值越小表示预测精度越高 。
02
平均绝对误差( MAE)
计算预测值与实际值之间的绝对 差值的平均值,值越小表示预测 精度越高。
03
均方根误差( RMSE)
将预测误差的平方和开方,反映 预测值的离散程度,值越小表示 预测精度越高。
模型稳定性评估
模型参数稳定性
评估模型参数在多次运行或不同数据集上的稳定性, 以确保模型的可靠性。
模型结构稳定性
时间序列分析

n 1
an + 2
时间间隔不等时:加权平均法。 时间间隔不等时:加权平均法。
+ an a + a3 a a1 + a 2 f1 + 2 f 2 + + n 1 f n 1 2 2 2 a = ∑f
式中f1,f2,…,fn-1:相邻时点指标间隔的月(季)数。
序时平均数计算示例
(三)平均发展水平的计算
1.绝对数时间序列的序时平均数 绝对数时间序列 时期数列的序时平均数(简单算术平均 ( 1 ) 时期数列 简单算术平均 法)。
a =
a1 + a
2
+ + a n
n
=
∑
n
a
(2) 时点数列的序时平均数
①连续时点数列:逐日登记。 连续时点数列:逐日登记。
未分组资料: 逐日登记,每日都有数据(简单算术平 未分组资料 : 逐日登记 , 每日都有数据 简单算术平 均法)。
某企业2005年上半年统计资料
二月 126 600 三月 124 610 四月 122 640 五月 126 640 六月 128 700 七月 124 700
例5-3答案
时间间隔相等的间断时点数列, [分析] 属于时间间隔相等的间断时点数列,采用首末折 分析] 时间间隔相等的间断时点数列 首末折 半法计算。 半法 上半年平均职工人数为:
a =
a1 + a
2
+ + a n
n
=
∑
n
a
分组资料: 逐日登记, 非每日都有数据(加权算术平 分组资料 : 逐日登记 , 非每日都有数据 加权算术平 均法)。
a1 f1 + a 2 f 2 + + a n f n a = = f1 + f 2 + + f n
统计学原理第5章:时间序列分析

a a
n 118729 129034 132616 132410 124000 5
127357.8
②时点序列
若是连续时点序列: 计算方法与时期序列一样; 若是间断时点序列: 则必须先假设两个条件,分别是 假设上期期末水平等于本期期初水平; 假设现象在间隔期内数量变化是均匀的。 间隔期相等的时点序列 采用一般首尾折半法计算。 例如:数列 a i , i 0,1,2, n 有 n 1 个数据,计算 期内的平均水平 a n a n 1 a 0 a1 a1 a 2
(3)联系
环比发展速度的乘积等于相应的定基发展速度,
n n i 0 i 1 i 1
相邻两期的定基发展速度之商等于后期的环比发展速度
i i 1 i 0 0 i 1
(二)增减速度
1、定义:增长量与基期水平之比 2、反映内容:现象的增长程度 3、公式:增长速度
0.55
二、时间序列的速度分析指标
(一)发展速度 (二)增长速度 (三)平均发展水平
(四)平均增长速度
(一)发展速度
1、定义:现象两个不同发展水平的比值 2、反映内容:反映社会经济现象发展变化快慢相对程度 3、公式:v 报告期水平 100%
基期水平
(1)定基发展速度
是时间数列中报告期期发展水平与固定基期发展水平对比所 得到的相对数,说明某种社会经济现象在较长时期内总的发 展方向和速度,故亦称为总速度。 (2)环比发展速度 是时间数列中报告期发展水平与前期发展水平之比,说明某 种社会经济现象的逐期发展方向和速度。
c
a
b
均为时期或时点数列,一个时期数列一个时点数列,注意平均的时间长度 ,比如计算季度的月平均数,时点数据需要四个月的数据,而时期数据则 只需要三个月的数据。
第五章 平稳时间序列模型的建立

2. 样本偏自相关函数截尾性的判断方法
可以证明:若序列xt为AR(p)序列,则
k>p后,序列的样本偏自相关函数ˆkk 服
从渐近正态分布,即近似的有:
ˆkk
~
N (0, 1 ) n
此处n表示样本容量。于是可得:
P( ˆkk
1 ) 31.7% n
P( ˆkk
2 ) 4.5% n
在实际进行检验时,可对每个k>0,分
将上式展开得:
xt 1xt1 p xtp 0 at 1at1 2at2 qatq
此时,所要估计的未知参数有p+q+1个。
式中:
0 (1 1 2 p )
即有:
0
11 2 p
在实际估计模型时,可将θ0看作一个常数估计, 若θ0显著不为0,则μ≠0,此时θ0 、 μ 有如上关系。 若θ0显著为0,则可认为μ=0,在最终模型中将此常数 项去掉即可。
– 原假设:序列非平稳
H0:1 1
– 备择假设:序列平稳
检验统计量
H0:1 1
– –
时 1 1 时 1 1
t (1 )
ˆ1 1 S (ˆ1 )
渐近 N (0,1)
ˆ1 1 S(ˆ1)
DF统计量
1 1 时
t (1 )
ˆ1 1 S (ˆ1 )
渐近 N (0,1)
1 1 时
ˆ1 S (ˆ1
对ACF和PACF的截尾性作一判断。
1. 样本自相关函数截尾性的判断方法
理 则论k>上q后证,明序:列若的序样列本xt自为相MA关(q函)序数列ˆ k,渐
近服从正态分布,即:
ˆ k
~
N (0, 1 (1 2 q
n
时间序列的模型识别课件
时间序列的模型基础
1 自回归模型(AR)
利用过去时刻的观测值来预测未来时刻的值。
2 移动平均模型(MA)
根据过去时刻的预测误差来预测未来时刻的值。
3 自回归移动平均模型(ARMA)
结合自回归和移动平均模型的特点,适用于一般的时间序列。
时间序列的平稳性检验
1 平稳性的概念
时间序列的均值和方差在时间上保持恒定。
ARMA模型
自回归移动平均模型是自回归模型和移动平均模型的综合应用。它能够捕捉 时间序列的长期和短期动态特征。
ARIMA模型
自回归积分移动平均模型是自回归模型、差分和移动平均模型的组合应用。 它适用于具有趋势和季节性的时间序列。
季节性调整
对具有季节性的时间序列进行季节性调整可以消除季节性的影响,使时间序 列更具可预测性。
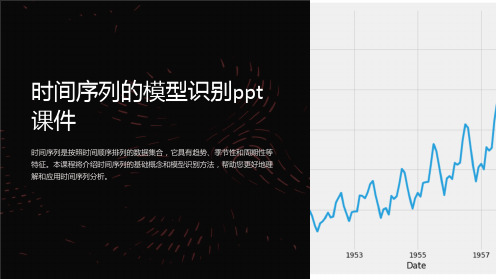
时间序列的模型识别ppt 课件
时间序列是按照时间顺序排列的数据集合,它具有趋势、季节性和周期性等 特征。本课程将介绍时间序列的基础概念和模型识别方法,帮助您更好地理 解和应用时间序列分析。
介绍时间序列
时间序列是按照时间顺序排列的数据集合,常见于经济、金融、气象等领域。了解时间序列的基 本概念和特征对于进行模型识别和预测至关重要。
2 单位根检验
用于判断时间序列是否具有单位根,进而确定是否为平稳序列。
3 差分
通过对时间序列进行差分,将非平稳序列转化为平稳序列。
AR模型
自回归模型是基于过去时刻的观测值进行预测的模型。它的特点是具有记忆性,各个时刻的值受 前面时刻的影响。
MA模型
移动平均模型是根据过去时刻的预测误差进行预测的模型。它的特点来自对预 测误差有很好的适应能力。
时间序列的模型识

• 时间序列的基本概念 • 时间序列的模型 • 时间序列的模型识别方法 • 时间序列的预测 • 时间序列的应用
01
时间序列的基本概念
时间序列的定义
总结词
时间序列是指按照时间顺序排列的一系列观测值。
详细描述
时间序列是按照时间顺序排列的一系列数据点,可以是数字、文本或其他类型 的数据。这些数据点通常表示在某个特定时间点上的测量值或观察结果。
详细描述
参数法通常需要预先设定一些数学模型,如AR模型、MA模型、ARMA模型等,然后通过最小二乘法 、最大似然估计等方法估计模型的参数。如果实际数据与某个模型的拟合度较高,则认为该模型适用 于该时间序列。
图形法
总结词
图形法是一种直观的方法,通过绘制时间序 列的图形和各种统计量来识别模型。
详细描述
图形法包括绘制时间序列的时序图、自相关 图、偏自相关图等,以及计算各种统计量如 峰度、偏度等。通过观察图形的特征和统计 量的值,可以初步判断时间序列的模型类型。
信息准则法
总结词
信息准则法是一种基于信息论的方法,通过比较不同模型的复杂度和拟合度来选择最优 模型。
详细描述
信息准则法包括AIC准则、BIC准则等,它们通过计算模型的复杂度和拟合度来选择最 优模型。复杂度越小、拟合度越高的模型被认为是更好的模型。信息准则法可以自动选
详细描述
差分自回归移动平均模型
ARIMA模型
总结词
详细描述
总结词
详细描述
自回归积分滑动平均模 型
ARIMA模型是一种结合 了自回归、积分和移动 平均三种模型的混合模 型。它通过同时考虑时 间序列中的过去值、过 去误差值和时间序列的 非平稳性来预测未来值 。
时间序列分析模型汇总

平滑法
平滑法是进行趋势分析和预测时常用的一 种方法。它是利用修匀技术,削弱短期随 机波动对序列的影响,使序列平滑化,从 而显示出长期趋势变化的规律
• 简单平均数法 :也称算术平均法。即把若干历史 时期的统计数值作为观察值,求出算术平均数作 为下期预测值。这种方法基于下列假设:“过去 这样,今后也将这样”,把近期和远期数据等同 化和平均化,因此只能适用于事物变化不大的趋 势预测。如果事物呈现某种上升或下降的趋势, 就不宜采用此法。 • 加权平均数法: 就是把各个时期的历史数据按近 期和远期影响程度进行加权,求出平均值,作为 下期预测值。
例如,取线性方程、一期滞后以及白噪声随 机扰动项( n =n),模型将是一个1阶自回 归过程AR(1): Yn=aYn-1+ n 这里, n特指一白噪声。
一般的p阶自回归过程AR(p)是 Yn=a1Yn-1+ a2Yn-2 + … + apYn-p + n
(*)
一般的p阶自回归过程AR(p)是 Yn=a1Yn-1+ a2Yn-2 + … + apYn-p + n
三、确定性时间序列分析与随机性时间序列分 析: 时间序列依据其特征,有以下几种表现形式, 并产生与之相适应的分析方法: (1)长期趋势变化 受某种基本因素的影响,数据依时间变化时 表现为一种确定倾向,它按某种规则稳步地 增长或下降。 使用的分析方法有:移动平均法、指数平滑法、 模型拟和法等;
(2)季节性周期变化 受季节更替等因素影响,序列依一固 定周期规则性的变化,又称商业循环。 采用的方法:季节指数; (3)循环变化 周期不固定的波动变化。
例:拟合澳大利亚政府1981——1990年 每季度的消费支出序列
第5章 时间序列的模型识别PPT参考课件

原理(模型阶数简约原则 parsimony principle):
设Xt(1≤t≤N)是零均值平稳序列,用模型AR模型拟合
AR p : Xt 1Xt1 2 Xt2 L p Xt p t 残差平方和Q0
AR p 1 : Xt 1Xt1 2 Xt2 L p1Xt p1 t 残差平方和Q1
2020/2/15
25
结论:对于给定的显著性水平α
若F>Fα(s,N-r),则拒绝原假设,认为后面s个回归因子对 因变量的影响是显著的,表明M1合适;
若F<Fα(s,N-r),则接受原假设,认为这s个回归因子对因 变量的影响是不显著的,表明M2合适。
2020/2/15
14
AR(p)模型定阶的F准则
1967年,瑞典控制论专家K.J.Aström教授将F检验准则用于 对时间序列模型的定阶。
2020/2/15
23
BIC准则
AIC准则是样本容量N的线性函数,在N→∞时不收敛 于真实模型,它通常比真实模型所含的未知参数要多, 是过相容的。
为了弥补AIC准则的不足,Akaike于1976年提出BIC准 则,而Schwartz在1978年根据Bayes理论也得出同样的 判别标准,称为SBC准则。理论上已证明,SBC准则 是最优模型的真实阶数的相合估计。
Xt 1Xt1 L p Xt p t 1t1 L qtq , t : WN 0, 2 AIC T ln ˆ 2 2 p q 1
说明:
第一项:体现了模型拟合的好坏,它随着阶数的增大而减小; 第二项:体现了模型参数的多少,它随着阶数的增大而变大。
2020/2/15
21
AIC准则用于ARMA模型的定阶
时间序列分析简介与模型

第二篇 预测方法与模型预测是研究客观事物未来发展方向与趋势的一门科学。
统计预测是以统计调查资料为依据,以经济、社会、科学技术理论为基础,以数学模型为主要手段,对客观事物未来发展所作的定量推断和估计。
根据社会、经济、科技的预测结论,人们可以调整发展战略,制定管理措施,平衡市场供求,进行各种各样的决策。
预测也是制定政策,编制规划、计划,具体组织生产经营活动的科学基础。
20世纪三四十年代以来,随着人类社会生产力水平的不断提高和科学技术的迅猛发展,特别是近年来以计算机为主的信息技术的飞速发展,更进一步推动了预测技术在国民经济、社会发展和科学技术各个领域的应用。
预测包含定性预测法、因果关系预测法和时间序列预测法三类。
本篇对定性预测法不加以介绍,对后两类方法选择以下几种介绍方法的原理、模型的建立和实际应用,分别为:时间序列分析、微分方程模型、灰色预测模型、人工神经网络。
第五章 时间序列分析在预测实践中,预测者们发现和总结了许多行之有效的预测理论和方法,但以概率统计理论为基础的预测方法目前仍然是最基本和最常用的方法。
本章介绍其中的时间序列分析预测法。
此方法是根据预测对象过去的统计数据找到其随时间变化的规律,建立时间序列模型,以推断未来数值的预测方法。
时间序列分析在微观经济计量模型、宏观经济计量模型以及经济控制论中有广泛的应用。
第一节 时间序列简介所谓时间序列是指将同一现象在不同时间的观测值,按时间先后顺序排列所形成的数列。
时间序列一般用 ,,,,21n y y y 来表示,可以简记为}{t y 。
它的时间单位可以是分钟、时、日、周、旬、月、季、年等。
一、时间序列预测法时间序列预测法就是通过编制和分析时间序列,根据时间序列所反应出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年可能达到的水平。
其容包括:收集与整理某种社会现象的历史资料;将这些资料进行检查鉴别,排成数列;分析时间序列,从中寻找该社会现象随时间变化而变化的规律,得出一定的模型,以此模型去预测该社会现象将来的情况。
05 时间序列信号模型

令 z = e jω , 得到
2 Pxx (e jω ) = σ w V (cos ω )
这就说明有理谱信号的功率谱是 e jω 或者 cos ω 的有理函数.
2. 谱分解定理 (1) 定理
如果功率谱 Pxx (e jω ) 是平稳随机序列 x(n) 的有理谱, 则一定存在 一个零极点均在单位园内的有理函数 H ( z )
2. 自回归模型(Auto-Regressive, 简称 AR 模型) (3)
差分方程与系统函数
若 a0 = 1 , b0 = 1 , 其它 bk = 0,(k = 1, 2," , q ) , 则模型差分方程为
“ 自回归 ” 的含义是 : 该 模型当前的输出, 是当前 的输入和过去 p 个输出 的加权和.
p
q
(1.3.9)
1+ H ( z) = 1+
(2)
∑b z
k
q
−k
∑a z
k k =1
k =1 p
(1.3.10)
−k
特点
典型 IIR 滤波器.
极点-零点模型(ARMA 模型); 分子部分称为 MA 部分; 分子部分称为 AR 部分, 应分别满足稳 定性和可逆性条件.
关于滤波器长度和阶数的说明: MA 模型或 RIR 滤波器——滤波器长度就是单位冲激响应 bk 的长 度(有限长), 即系数的个数.其阶数是差分方程或系统函数式中 q 的 大小(等于长度减 1).
154自相关函数功率谱与时间序列信号模型的关系上面已经说明已知信号模型参数可求得输出功率谱用z变换形式表本节讨论已知信号的功率谱或自相关函数如何按上式唯一分解出一个因果稳定的模型系统函数
时间序列的分析——模型的识别与预测

模型的识别与预测一、实验内容依照某AR 模型生成一段数据(1000),同时用另一MA 模型生成一段数据(200),合成一段1200长度的数据1)依赖于这1200个数据的前800个数据,识别这段数据背后的AR 模型。
2)在1)的基础上对新数据进行预测,并通过后续的400个数据进行判别(数据模型是否匹配)或者模型的修正(修正只需要提供思路和方法)。
二、理论基础 1.时间序列模型介绍时间序列是随时间改变而随机地变化的序列。
时间序列分析的目的是找出它的变化规律,即线性模型,主要有三种:AR 模型(自回归模型)、MA 模型(滑动平均模型)和ARMA 模型(自回归滑动平均模型或混合模型)。
设{X t }为零均值的实平稳时间序列,阶数为p 的AR 模型定义为t p t p t t t a X X X X ++++=---ϕϕϕ (2211)其 ,0][ =t a E ⎩⎨⎧≠==,,0,,][2s t s t a a E a t s δt s X a E t s >=,0][其中{p k k ,...,2,1,=ϕ}成为自回归系数,白噪声序列{t a }成为新信息序列;阶数为q 的MA 模型定义为211...-----=t q t t t a a a X θθ其中{q k k ,...,2,1,=θ}称为滑动平均系数;P 阶自回归q 阶ARMA 模型定义为q t q t t p t p t t a a a X X X -------=---θθϕϕ (1111)记为ARMA (p ,q )。
2. 模型的识别根据教材对平稳时间序列的特性分析,对初步识别平稳时间序列的类型提供了依据,如表1所示:表1 各时间序列模型的特性3. 模型阶数的确定1)样本自相关函数和样本偏相关函数设有零均值平稳时间序列{t X }的一段样本观测值N x x x ,...,,21,样本协方差函数估计式为1,...,1,011^-==+-=∑N k xx Nki k N i i k γ同理样本自相关函数定义为1,...,1,0^^^-==N k k k γγρ2)MA 模型阶数的确定设{t X }是正态的零均值平稳MA (q )序列,而对于充分大的N ,可以认为^kρ的分布近似于正态分布))/1(,0(2N N ,从而,^k ρ的截尾性判断如下:首先计算^^2^1,...,,M ρρρ(取10/N M ≈),因为q 值未知,故令q 值从小到大,分别检验M q q q +++^2^1^,...,,ρρρ满足N k 1^≤ρ 或N k 2^≤ρ 的比例是否占总个数M 的68.3%或95.5%。
时间序列分析模型汇总

时间序列分析模型汇总时间序列分析是一种广泛应用于各个领域的统计分析方法,它用来研究一组随时间而变化的数据。
时间序列数据通常具有趋势、季节性和随机性等特征,时间序列分析的目的是通过建立适当的模型来描述和预测这些特征。
本文将汇总一些常用的时间序列分析模型,包括AR、MA、ARIMA、GARCH和VAR等。
1.AR模型(自回归模型):AR模型是根据过去的观测值来预测未来的观测值。
它假设未来的观测值与过去的一系列观测值有关,且与其他因素无关。
AR模型的一般形式为:Y_t=c+Σ(φ_i*Y_t-i)+ε_t,其中Y_t表示时间t的观测值,c 为常数,φ_i为系数,ε_t为误差项。
2.MA模型(移动平均模型):MA模型是根据过去的误差项来预测未来的观测值。
它假设未来的观测值与过去的一系列误差项有关,且与其他因素无关。
MA模型的一般形式为:Y_t=μ+ε_t+Σ(θ_i*ε_t-i),其中Y_t表示时间t的观测值,μ为平均值,θ_i为系数,ε_t为误差项。
3.ARIMA模型(自回归积分移动平均模型):ARIMA模型是AR和MA模型的组合,它结合了时间序列数据的趋势和随机性特征。
ARIMA模型的一般形式为:Y_t=c+Σ(φ_i*Y_t-i)+Σ(θ_i*ε_t-i)+ε_t,其中Y_t表示时间t的观测值,c为常数,φ_i和θ_i为系数,ε_t为误差项。
4.GARCH模型(广义自回归条件异方差模型):GARCH模型用于建模并预测时间序列数据的波动性。
它假设波动性是由过去观测值的平方误差和波动性的自相关引起的。
GARCH模型的一般形式为:σ_t^2=ω+Σ(α_i*ε^2_t-i)+Σ(β_i*σ^2_t-i),其中σ_t^2为时间t的波动性,ω为常数,α_i和β_i为系数,ε_t为误差项。
5.VAR模型(向量自回归模型):VAR模型用于建模并预测多个时间序列变量之间的相互关系。
它假设多个变量之间存在相互依赖的关系,即一个变量的变动会对其他变量产生影响。
时间序列模型归纳总结复习

时间序列模型归纳总结复习时间序列模型可以分为线性模型和非线性模型两类。
线性模型假设时间序列数据之间的关系是线性的,并且基于这种线性关系进行预测。
常见的线性时间序列模型有AR模型(自回归模型)、MA模型(滑动平均模型)和ARMA模型(自回归滑动平均模型)。
AR模型是通过对时间序列数据的当前值和过去的值进行线性组合来预测未来值。
MA模型是通过对时间序列数据的误差项进行线性组合来预测未来值。
ARMA模型是AR模型和MA模型的结合。
这些模型通常需要对时间序列数据进行平稳性和白噪声检验。
非线性时间序列模型则放松了线性假设,认为时间序列数据之间的关系是非线性的。
常见的非线性时间序列模型有ARCH模型(自回归条件异方差模型)和GARCH模型(广义条件异方差模型)。
ARCH模型和GARCH模型可以描述时间序列数据中的异方差性,即波动性不稳定。
这些模型通常采用极大似然估计方法进行参数估计。
除了上述模型之外,还有一些高级的时间序列模型,如VAR模型(向量自回归模型),VAR模型可以同时预测多个时间序列变量之间的关系;VARMA模型(向量自回归滑动平均模型),VARMA模型是VAR模型和MA模型的结合;VARIMA模型(向量自回归移动平均模型),VARIMA模型是VAR模型和ARIMA模型的结合。
建立时间序列模型的一般步骤如下:首先,对时间序列数据进行可视化和描述性统计分析,了解数据的基本特征。
然后,判断时间序列数据是否满足平稳性和白噪声检验的要求,如果不满足需要进行差分或转换。
接下来,根据数据的特征选择合适的时间序列模型,并进行参数估计。
最后,使用模型进行预测和评估,并进行模型选择和调整。
时间序列模型的评估一般采用残差分析和预测误差分析。
残差分析用于检验模型的拟合效果,常见的检验方法有自相关函数(ACF)和偏自相关函数(PACF)。
预测误差分析用于评估模型的预测能力,常见的评估指标有均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)。
第五章-时间序列的模型识别汇总
第五章-时间序列的模型识别汇总第五章时间序列的模型识别前面四章我们讨论了时间序列的平稳性问题、可逆性问题,关于线性平稳时间序列模型,引入了自相关系数和偏自相关系数,由此得到ARMA(p, q)统计特性。
从本章开始,我们将运用数据开始进行时间序列的建模工作,其工作流程如下:图5.1 建立时间序列模型流程图在ARMA(p,q)的建模过程中,对于阶数(p,q)的确定,是建模中比较重要的步骤,也是比较困难的。
需要说明的是,模型的识别和估计过程必然会交叉,所以,我们可以先估计一个比我们希望找到的阶数更高的模型,然后决定哪些方面可能被简化。
在这里我们使用估计过程去完成一部分模型识别,但是这样得到的模型识别必然是不精确的,而且在模型识别阶段对于有关问题没有精确的公式可以利用,初步识别可以我们提供有关模型类型的试探性的考虑。
对于线性平稳时间序列模型来说,模型的识别问题就是确定ARMA(p,q)过程的阶数,从而判定模型的具体类别,为我们下一步进行模型的参数估计做准备。
所采用的基本方法主要是依据样本的自相关系数(ACF)和偏自相关系数(PACF)初步判定其阶数,如果利用这种方法无法明确判定模型的类别,就需要借助诸如AIC、BIC 等信息准则。
我们分别给出几种定阶方法,它们分别是(1)利用时间序列的相关特性,这是识别模型的基本理论依据。
如果样本的自相关系数(ACF)在滞后q+1阶时突然截断,即在q处截尾,那么我们可以判定该序列为MA(q)序列。
同样的道理,如果样本的偏自相关系数(PACF)在p处截尾,那么我们可以判定该序列为AR(p)序列。
如果ACF和PACF都不截尾,只是按指数衰减为零,则应判定该序列为ARMA(p,q)序列,此时阶次尚需作进一步的判断;(2)利用数理统计方法检验高阶模型新增加的参数是否近似为零,根据模型参数的置信区间是否含零来确定模型阶次,检验模型残差的相关特性等;(3)利用信息准则,确定一个与模型阶数有关的准则函数,既考虑模型对原始观测值的接近程度,又考虑模型中所含待定参数的个数,最终选取使该函数达到最小值的阶数,常用的该类准则有AI C、BIC 、FP E等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ˆkk ~ N 0, 1 T
这样根据正态分布的性质,我们有
(5.5)
P
ˆkk
1
68.3%
T
(5.6)
P
ˆkk
2
95.5%
T
(5.7)
这样,关于偏自相关系数 kk 的截尾性的判断,转化为利用上述性质(5.6)或者(5.7),
可以判断 ˆkk 的截尾性。具体方法为对于每一个 p>0,考查p1, p1 , p2, p2 ,…, pM , pM
内容,一个比较直观的方法,就是通过观察自相关系数(ACF)和偏自相关系数(PACF)
可以对拟合模型有一个初步的识别,这是因为从理论上说,平稳 AR、MA 和 ARMA 模型的
ACF 和 PACF 有如下特性:
模型(序列)
AR(p)
MA(q)
ARMA(p,q)
自相关系数(ACF) 拖尾
q 阶截尾
拖尾
偏自相关系数(PACF) p 阶截尾
第五章 时间序列的模型识别
前面四章我们讨论了时间序列的平稳性问题、可逆性问题,关于线性平稳时间序列模型, 引入了自相关系数和偏自相关系数,由此得到 ARMA(p, q)统计特性。从本章开始,我们将 运用数据开始进行时间序列的建模工作,其工作流程如下:
1. 模型识别 用相关图和偏相关图识别模型 形式(确定参数 p, q)
T
1 k
T k j 1
xj x
xjk x , 1 k T 1
(5.3)
ˆk ˆk , 1 k T 1
在上述两种估计中,当样本容量T 很大,而 k 的绝对值较小时,上述两种估计值相差不 大,其中由(5.1)定义的第一种估计值的绝对值较小。根据前面章节的讨论,因为 AR( p ),
MA( q )或者 ARMA( p, q )模型的自协方差系数 k 都是以负指数阶收敛到零,所以在对平
其中 x
1 T
T
x j 为样本均值,则样本自协方差系数ˆk 是Xt 的自协方差系数 k 的估
j 1
计。样本自相关系数定义为
ˆk ˆk ˆ0 , k T 1
(5.2)
是Xt 的自相关系数k 的估计。
作为Xt 的自协方差系数 k 的估计,根据数理统计知识,样本自协方差系数还可以
写为
2 / 17
ˆk
截尾性,进而由此可以给出模型的初步识别。首先,我们需要给出样本的自相关系数 ˆk 和
偏自相关系数 ˆkk 的定义。
设平稳时间序列Xt 的一个样本 x1, , xT 。则样本自协方差系数定义为ˆkFra bibliotek1 T
T k j 1
xj x
xjk x , 1 k T 1
(5.1)
ˆk ˆk , 1 k T 1
对于线性平稳时间序列模型来说,模型的识别问题就是确定 ARMA(p,q)过程的阶数, 从而判定模型的具体类别,为我们下一步进行模型的参数估计做准备。所采用的基本方法主 要是依据样本的自相关系数(ACF)和偏自相关系数(PACF)初步判定其阶数,如果利用 这种方法无法明确判定模型的类别,就需要借助诸如 AIC、BIC 等信息准则。我们分别给 出几种定阶方法,它们分别是(1)利用时间序列的相关特性,这是识别模型的基本理论依 据。如果样本的自相关系数(ACF)在滞后 q+1 阶时突然截断,即在 q 处截尾,那么我们 可以判定该序列为 MA(q)序列。同样的道理,如果样本的偏自相关系数(PACF)在 p 处截 尾,那么我们可以判定该序列为 AR(p)序列。如果 ACF 和 PACF 都不截尾,只是按指数衰 减为零,则应判定该序列为 ARMA(p,q)序列,此时阶次尚需作进一步的判断;(2)利用数 理统计方法检验高阶模型新增加的参数是否近似为零,根据模型参数的置信区间是否含零来 确定模型阶次,检验模型残差的相关特性等;(3)利用信息准则,确定一个与模型阶数有关
1 / 17
的准则函数,既考虑模型对原始观测值的接近程度,又考虑模型中所含待定参数的个数,最 终选取使该函数达到最小值的阶数,常用的该类准则有 AIC、BIC、FPE 等。实际应用中, 往往是几种方法交叉使用,然后选择最为合适的阶数(p,q)作为待建模型的阶数。
§5.1 自相关和偏自相关系数法
在平稳时间序列分析中,最关键的过程就是利用数据去识别和建模,根据第三章讨论的
稳时间序列的数据拟合 AR( p ),MA( q )或者 ARMA( p, q )模型时,希望实际计算的样本自
协方差系数ˆk 能以很快的速度收敛。因此,我们一般选择由(5.1)定义的第一种估计值作
为 k 的点估计。
根据第三章偏自相关系数的计算,利用样本自相关系数 ˆk 的值,定义样本偏自相关
系数 ˆkk 如下:
2. 参数估计 对初步选取的模型进行参数估计
3. 诊断与检验 包括参数的显著性检验和 残差的随机性检验
模型是否可取
吗 可取
停止
不可取
图 5.1 建立时间序列模型流程图
在 ARMA(p,q)的建模过程中,对于阶数(p,q)的确定,是建模中比较重要的步骤,也是比较 困难的。需要说明的是,模型的识别和估计过程必然会交叉,所以,我们可以先估计一个比 我们希望找到的阶数更高的模型,然后决定哪些方面可能被简化。在这里我们使用估计过程 去完成一部分模型识别,但是这样得到的模型识别必然是不精确的,而且在模型识别阶段对 于有关问题没有精确的公式可以利用,初步识别可以我们提供有关模型类型的试探性的考 虑。
拖尾
拖尾
但是,在实际中 ACF 和 PACF 是未知的,对于给定的时间序列观测值 x1, x2 , , xT ,我们
需要使用样本的自相关系数 ˆk 和偏自相关系数 ˆkk 对其进行估计。然而由于ˆk 和
ˆkk 均是随机变量,对于相应的模型不可能具有严格的“截尾性”,只能呈现出在某步之后
围绕零值上、下波动,因此,我们需要借助 ˆk 和 ˆkk 的“截尾性”来判断k 和kk 的
ˆkk
Dˆ k Dˆ
,
k 1, 2,
,T
(5.4)
其中
1 ˆ1
ˆ k 1
1 ˆ1
ˆ1
Dˆ ˆ1 1
ˆk2 , Dˆk ˆ1
1
ˆ2
ˆk1 ˆk2
1
ˆk1 ˆk2
ˆk
关于样本的自相关系数ˆk 的统计性质,我们将在下一章给予讨论。
Quenouille 证明, ˆkk 也满足 Bartlett 公式,即当样本容量 T 充分大时,
