§3 波面双光束干涉
合集下载
双光束干涉PPT课件

从一个条纹过渡到另一个条纹,平板的厚度均改变
/ (2n)。
L h sin
h 2n
46
(2)劈尖的等厚干涉条纹
L2nsin (33)
劈角 小,条纹间距大;反之,劈角 大,条纹
间距小。因此,当劈尖上表面绕棱线旋转时, 随着
的增大, 条纹间距变小, 条纹将向棱线方向移动。
47
(2)劈尖的等厚干涉条纹
49
(2)劈尖的等厚干涉条纹 应用:
Δh
b
b'
50
(3)牛顿环 在一块平面玻璃上放置一曲率半径 R 很大的平凸透 镜,在透镜凸表面和玻璃板的平面之间便形成一厚 度由零逐渐增大的空气薄层。
S
R
r
o
h
51
(3)牛顿环 当以单色光垂直照射时,在空气层上会形成一组以 接触点 O 为中心的中央硫、边缘密的圆环条纹,称 为牛顿环。
II12 00..906016 V0.0814
所以,在平行板表面反射率较低的情况下,通常应
用的是反射光的等倾干涉。
35
2)楔形平板产生的干涉——等厚干涉 扩展光源中的某点 S0 发出一束光,经楔形板两表面 反射的两支光相交于 P 点,产生干涉,其光程差为
n ( A B B C ) n 0 ( A P A C )
23
②等倾亮圆环的半径
一般情况下,1N 和 2N 都很小,近似有 nn01N/ 2N
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2 ,因而由上式可得
1Nn10
n N1
h
(23)
2 n h ( 1 c o s2 N ) ( N 1 ) ]
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2
/ (2n)。
L h sin
h 2n
46
(2)劈尖的等厚干涉条纹
L2nsin (33)
劈角 小,条纹间距大;反之,劈角 大,条纹
间距小。因此,当劈尖上表面绕棱线旋转时, 随着
的增大, 条纹间距变小, 条纹将向棱线方向移动。
47
(2)劈尖的等厚干涉条纹
49
(2)劈尖的等厚干涉条纹 应用:
Δh
b
b'
50
(3)牛顿环 在一块平面玻璃上放置一曲率半径 R 很大的平凸透 镜,在透镜凸表面和玻璃板的平面之间便形成一厚 度由零逐渐增大的空气薄层。
S
R
r
o
h
51
(3)牛顿环 当以单色光垂直照射时,在空气层上会形成一组以 接触点 O 为中心的中央硫、边缘密的圆环条纹,称 为牛顿环。
II12 00..906016 V0.0814
所以,在平行板表面反射率较低的情况下,通常应
用的是反射光的等倾干涉。
35
2)楔形平板产生的干涉——等厚干涉 扩展光源中的某点 S0 发出一束光,经楔形板两表面 反射的两支光相交于 P 点,产生干涉,其光程差为
n ( A B B C ) n 0 ( A P A C )
23
②等倾亮圆环的半径
一般情况下,1N 和 2N 都很小,近似有 nn01N/ 2N
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2 ,因而由上式可得
1Nn10
n N1
h
(23)
2 n h ( 1 c o s2 N ) ( N 1 ) ]
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2
《双光束干涉》课件

扩展光源
对于某些实验需求,可以使用扩 展光源代替激光器,以模拟自然 光或实现更大的干涉条纹可见度 。
分束器
半透半反镜
将一束光分成两束相同的光,一束反 射,一束透射,是常用的分束器。
分束棱镜
利用棱镜的折射特性将一束光分成两 束不同角度的光,常用于产生不同路 径长度的干涉。
反射镜和干涉仪
反射镜
用于改变光路,使两束光在空间上交叠,形成干涉。
干涉条纹的移动与变化
当一束光波的波长或相位发生变化时,干涉条纹的位置 和形状也会随之改变。
当两束光波的振幅(强度)发生变化时,干涉条纹的可 见度和强度也会受到影响。
当一束光波在空间中传播时,遇到不均匀介质或受到外 界扰动时,干涉条纹的位置和形状也会发生变化。
干涉条纹的可见度与强度
01
干涉条纹的可见度与两束光波的 相位差和振幅有关。相位差越小 ,可见度越高;振幅越大,可见 度越高。
双光束干涉的原理
光程差
01
两束光在相遇点产生的光程差会导致相位发生变化,进而影响
干涉结果。
干涉加强
02
当两束光的光程差为半波长的偶数倍时,光强增强,形成明条
纹。
干涉减弱
03
当两束光的光程差为半波长的奇数倍时,光强减弱,形成暗条
纹。
02
双光束干涉实验装置
Chapter
光源
激光器
作为相干性好的光源,激光器能 够产生单色性好的光束,是双光 束干涉实验中的理想选择。
激光器稳定性误差
激光器的输出功率和波长可能会随时间变化,导 致干涉条纹的移动和变化。
探测器响应误差
探测器的响应速度和精度会影响对干涉条纹的记 录和分析。
THANKS
对于某些实验需求,可以使用扩 展光源代替激光器,以模拟自然 光或实现更大的干涉条纹可见度 。
分束器
半透半反镜
将一束光分成两束相同的光,一束反 射,一束透射,是常用的分束器。
分束棱镜
利用棱镜的折射特性将一束光分成两 束不同角度的光,常用于产生不同路 径长度的干涉。
反射镜和干涉仪
反射镜
用于改变光路,使两束光在空间上交叠,形成干涉。
干涉条纹的移动与变化
当一束光波的波长或相位发生变化时,干涉条纹的位置 和形状也会随之改变。
当两束光波的振幅(强度)发生变化时,干涉条纹的可 见度和强度也会受到影响。
当一束光波在空间中传播时,遇到不均匀介质或受到外 界扰动时,干涉条纹的位置和形状也会发生变化。
干涉条纹的可见度与强度
01
干涉条纹的可见度与两束光波的 相位差和振幅有关。相位差越小 ,可见度越高;振幅越大,可见 度越高。
双光束干涉的原理
光程差
01
两束光在相遇点产生的光程差会导致相位发生变化,进而影响
干涉结果。
干涉加强
02
当两束光的光程差为半波长的偶数倍时,光强增强,形成明条
纹。
干涉减弱
03
当两束光的光程差为半波长的奇数倍时,光强减弱,形成暗条
纹。
02
双光束干涉实验装置
Chapter
光源
激光器
作为相干性好的光源,激光器能 够产生单色性好的光束,是双光 束干涉实验中的理想选择。
激光器稳定性误差
激光器的输出功率和波长可能会随时间变化,导 致干涉条纹的移动和变化。
探测器响应误差
探测器的响应速度和精度会影响对干涉条纹的记 录和分析。
THANKS
物理光学13第十三次课球面波干涉和分波面双光束干涉

其中I1(P)和I2(P)分是S1和S2单独在P点产生的强度。
(20 10 ) 是初始位相差,它是常量。
(L2 L1)
(29)
是P点对S1和S2的光程差。
余弦函数的宗量是P点相对于光源点S1和S2的位相差。
7
2、干涉场的分析
y P(x, y, z)
(1)、等强度面与等光程差面
d2
S2
-l/2
一、两束球面波的干涉
内容
1、概述 2、光程和光程差 3、干涉场的分析
(1)、等强度面与等光程差面 (2)、干涉级、极值强度面和局部空间频率 4、二维观察屏面上干涉条纹的性质 (1)、观察屏沿着y轴并垂直于y轴放置 (2)、观察屏沿着x轴并垂直于x轴放置
1
1、概述
同平面波一样,球面波也是最基本的简单光波,而且在 实际中,球面波比平面波更加普遍,因此了解球面波的 干涉也是极其必要的。 两束球面波在空间相遇叠加,如果要产生稳定的干涉现 象,它们也要满足前面讲述的三个基本条件,即在相遇 点波振动方向不垂直,两束球面光波的频率相同,初始 位相差恒定,满足这种条件的球面波称为相干球面波。 我们知道点光源发射球面波,如果两个点光源发射的球 面波叠加时能够产生干涉现象,可以称这两个点光源为 相干点光源。
O
I (P) I1(P) I2(P) 2 I1(P)I2(P) cos2m z
最大强度面与整数 m 相对应, 最小强度面与半整数 m 相对应。
d1
S1
l/2 x
(28)式仍表明干涉场的强度分布近似是光程差Δ或干涉级 m 的周期函数; 但是因为Δ和 m 不再与考察点位置坐标成正比,所以干涉场强度分布不具 有空间周期性。
杨氏条纹的强度分布
x
22
物理光学-第三章 光的干涉3.19

行等距直条纹。
5、干涉条纹的反衬度: 当两束光波满足获得稳定干涉的条件时有:
2 E 1 E 2 E 1 0 E 2 0 c o s k 2 k 1 r 2 0 1 0
干涉场强度为:
I r I 1 r I 2 r 2 I 1 I 2 c o s k 2 k 1 r 2 0 1 0
在三维干涉场中放置一个二维
y
的观察屏Π,Π上将出现强度
变化的干涉图形,这实际上是
极值强度面与观察平面的交线,
r
因此所谓的干涉图形又称为干
涉条纹。
O
z
P(r) Δk P0 Π
x
等强度面是按余弦规律变化的平行等距平面,Π平面上的干涉
条纹是一组平行等距的直线性条纹,条纹的方向及空间频率与
观察屏Π的方向有关
令Δ=L2-L1 ,称为P点对S1和S2的光程差
P点相对于光源点S1和S2的位相差: k 0 L 1 L 2 2 01 0
注意:
I1(P)和I2(P)分别是S1和S2单独在P点产生的强度 由于初始位相差是常量, 两光波在P点的位相位差取决于Δ
3、干涉场的分析 (1)、等强度面与等光程差面
y f
Π1垂直于f,该平面上|f1|=0,
Π4
Π2
Π1
干涉条纹为无限宽条纹
Π2平行于f,有|f2|=2 sin(θ/2)/λ,
α x
干涉条纹为平行等距直条纹;
Π3 二维观察屏的干涉条纹
Π3平行于x轴,该平面|f3|=2sin(θ/2)cosα/λ,干涉条纹为平行等 距直条纹;
Π4平行于y轴,该平面|f4|=2 sin(θ/2)sinα/ λ,干涉条纹也是平
将干涉强度的极大值和干涉强度的极小值代入,得到两束平 面波干涉的条纹反衬度公式:
5、干涉条纹的反衬度: 当两束光波满足获得稳定干涉的条件时有:
2 E 1 E 2 E 1 0 E 2 0 c o s k 2 k 1 r 2 0 1 0
干涉场强度为:
I r I 1 r I 2 r 2 I 1 I 2 c o s k 2 k 1 r 2 0 1 0
在三维干涉场中放置一个二维
y
的观察屏Π,Π上将出现强度
变化的干涉图形,这实际上是
极值强度面与观察平面的交线,
r
因此所谓的干涉图形又称为干
涉条纹。
O
z
P(r) Δk P0 Π
x
等强度面是按余弦规律变化的平行等距平面,Π平面上的干涉
条纹是一组平行等距的直线性条纹,条纹的方向及空间频率与
观察屏Π的方向有关
令Δ=L2-L1 ,称为P点对S1和S2的光程差
P点相对于光源点S1和S2的位相差: k 0 L 1 L 2 2 01 0
注意:
I1(P)和I2(P)分别是S1和S2单独在P点产生的强度 由于初始位相差是常量, 两光波在P点的位相位差取决于Δ
3、干涉场的分析 (1)、等强度面与等光程差面
y f
Π1垂直于f,该平面上|f1|=0,
Π4
Π2
Π1
干涉条纹为无限宽条纹
Π2平行于f,有|f2|=2 sin(θ/2)/λ,
α x
干涉条纹为平行等距直条纹;
Π3 二维观察屏的干涉条纹
Π3平行于x轴,该平面|f3|=2sin(θ/2)cosα/λ,干涉条纹为平行等 距直条纹;
Π4平行于y轴,该平面|f4|=2 sin(θ/2)sinα/ λ,干涉条纹也是平
将干涉强度的极大值和干涉强度的极小值代入,得到两束平 面波干涉的条纹反衬度公式:
《双光束干涉》PPT课件

18
返回
菲涅耳双面镜装置示意图
P
s
P1
M1
L
s1
d
s2
C
M2
P2
11/24/2020
r0
19
返回
劳埃德镜示意图
P'
P
s1
d
ML
P0
s2
d'
狭缝S1被强单色光照射,作为单色线状光源;
S1经M所成的虚像S2与S1构成相干光源;
入射角i1接近90o-掠射,可使很小。
注意
•1当1/2屏4/2与020M接触时,P0点出现暗纹,原因是光在M
• 也就是说,凡入射角相同的光,形成同一干涉 条纹。通常把这种干涉条纹称为等倾干涉。
11/24/2020
25
从点光源发出的单条光线的光路
11/24/2020
26
等倾干涉 从点光源发出的锥面上光线的光路
11/24/2020
27
(2) 等倾干涉条纹的特性
• 一等倾干涉条纹的 形状与观察透镜放 置的方位有关。
时,肉眼或探测仪器就将观察不到稳定的条纹分布。 • 因此11/,24为/20了20 产生干涉现象,要求两叠加光束的频率尽量相等6。
(2) 对叠加光束振动方向的要求
• 当两光束光强相等,则条纹可见度为V=cosθ
• 若θ=0,两光束的振动方向相同时,V=1,干涉条纹最
清晰; • 若θ=π/2,两光束正交振动时,V=0,不发生干涉; • 当0<θ<π/2时,0<V<1,干涉条纹清晰度介于上
• 对应于光源S发出的同一入射角的光束,经平板产生的两束透射
光和两束反射光的光程差恰好相差λ/2,相位差相差π; • 透射光与反射光的等倾干涉条纹是互补的,即对应反射光干涉条
《分波面双光束干涉》课件

在物理实验中,分波面双光 束干涉被用于验证光的波动 性和相干性原理,以及研究 量子力学中的干涉现象。
在工程领域,分波面双光束 干涉被用于光学仪器和传感 器的校准和检测,以及光学 信号处理和通信技术中。
02 分波面双光束干涉的实验装置
光源
总结词
光源是干涉实验中的重要组成部分, 它负责产生用于干涉的光束。
《分波面双光束干涉 》PPT课件
目录
• 分波面双光束干涉的基本概念 • 分波面双光束干涉的实验装置 • 分波面双光束干涉的实验结果与分
析 • 分波面双光束干涉的结论与展望
01 分波面双光束干涉的基本概念
分波面双光束干涉的定义
01
分波面双光束干涉是指将一束光分成两个波面,然后让 这两个波面在空间中相遇,形成干涉现象。
创新成果。
未来研究方向
研究不同类型的光源和光波在 分波面双光束干涉中的表现, 探索提高干涉测量精度和稳定
性的方法。
探讨分波面双光束干涉在生 物医学、环境监测等领域的 应用前景,拓展其应用范围
。
研究分波面双光束干涉与其他 光学干涉技术相结合的可能性 ,开发新型的光学测量和信息
处理技术。
谢谢聆听
使用普通直尺测的方法
• 环境因素:温度和湿度的变化可能影响光学元件的 位置和光学特性,从而影响干涉效果。
误差来源与减小误差的方法
01
减小误差的方法
02
03
使用稳频激光作为光源,确保光强的稳定性 。
使用高精度的测量工具,如显微镜下的测微 器。
04
在恒温、恒湿的环境中进行实验,并定期检 查和调整光学元件的位置。
条纹间距与光程差的关系
通过理论推导,验证了条纹间距与光程差之间的 线性关系,为实验结果提供了理论支持。
光学 1.3分波面双光束干涉.ppt

(4)复色光(白光)
红
大
K+1
紫
红
K
小
紫
2、菲涅耳双面镜
图3.3菲涅耳双面镜实验
d 2r sin ;
r0 rcos l
间隔:
x r cos l r l
2r sin
2r
x
r cos 2r sin
l
即平r 行 光入射
2 A1A2
A1 A2
2
( j 0,1,2, )
(3)条纹间距:
x
xj1
xj
r0 d
(7)
(4)干涉图样:
这些点的轨迹是以s1s2 为轴线的双叶旋转双曲面
5、特征:
(1)各级亮条纹的光强相等,条纹间距相等
x r0 / d
(2) 一定:x r0 / d
(3) r0,d一定,x
2sin
4、 洛埃镜
图3.5洛埃镜实验
揭示了光在介质表面上反射,且入射角接近90° (掠射)时,产生了半波损失。
r2
r1
2
xd r0
2
原为明纹处:xd 2 j 时 (2 j 1) 暗
r0
2
2
原为暗纹处: xd (2 j 1) 时 2 j
1、杨氏干涉实验: (1)装置
x px
r1
·
s
R1
S1 d
R2
S2
r2
r0
x
0
x0
x
I
图3.2 杨氏实验装置
红
大
K+1
紫
红
K
小
紫
2、菲涅耳双面镜
图3.3菲涅耳双面镜实验
d 2r sin ;
r0 rcos l
间隔:
x r cos l r l
2r sin
2r
x
r cos 2r sin
l
即平r 行 光入射
2 A1A2
A1 A2
2
( j 0,1,2, )
(3)条纹间距:
x
xj1
xj
r0 d
(7)
(4)干涉图样:
这些点的轨迹是以s1s2 为轴线的双叶旋转双曲面
5、特征:
(1)各级亮条纹的光强相等,条纹间距相等
x r0 / d
(2) 一定:x r0 / d
(3) r0,d一定,x
2sin
4、 洛埃镜
图3.5洛埃镜实验
揭示了光在介质表面上反射,且入射角接近90° (掠射)时,产生了半波损失。
r2
r1
2
xd r0
2
原为明纹处:xd 2 j 时 (2 j 1) 暗
r0
2
2
原为暗纹处: xd (2 j 1) 时 2 j
1、杨氏干涉实验: (1)装置
x px
r1
·
s
R1
S1 d
R2
S2
r2
r0
x
0
x0
x
I
图3.2 杨氏实验装置
《双光束干涉》课件

在双光束干涉实验中,测量仪器通常 包括显微镜、测微器和光电探测器等。
03
双光束干涉的实验操作
实验准备
01
02
03
实验器材
包括分束器、反射镜、光 屏、激光器、测量尺等。
实验环境
确保实验室环境安静、无 风,避免外界因素干扰实 验结果。
安全措施
确保实验人员佩戴护目镜, 避免激光直接照射眼睛。
实验步骤
安装调试
按照实验要求,正确安 装和调试实验器材,确
保光路正确。
开启激光器
调整激光器输出功率, 使光束稳定。
观察干涉现象
观察双光束在光屏上的 干涉现象,记录干涉条
纹。
改变实验条件
可改变光束角度、光束 间距等条件,观察干涉
现象的变化。
数据处理与分析
数据记录
详细记录不同实验条件下 干涉条纹的数量、宽度和 分布。
改进方法一
使用更稳定的光源,如激光, 以减小光波相位差的不稳定性
。
改进方法二
使用高精度测量设备,确保双 缝宽度和间距的准确性。
THANKS
感谢观看
干涉现象
干涉现象是指两束或多束相干波在空 间某些区域相遇时,相互叠加而形成 的稳定强度分布现象。
干涉现象是波动性的重要特征之一, 是双光束干涉的基础。
双光束干涉的形成原理
双光束干涉是指两束相干光在空间相遇并相互叠加,形成稳 定的干涉现象。
双光束干涉的形成原理基于光的波动性和相干性,当两束相 干光波的相位差恒定时,它们在空间某些区域形成稳定的干 涉图案。
数据处理
对记录的数据进行计算和 处理,求出干涉条纹的间 距和角度。
结果分析
根据数据处理结果,分析 双光束干涉的规律和特点, 得出结论。
1.4分波面双光束干涉(Wavefront splitting)

r2 r 1 之值)
( k =1,2…)(整数级)
λ
暗纹 ±(2k+1)/2 ( k =1,2…)(半整数级)
●
来定0级位置),其余级明纹构成彩带,第2级开始 出现重叠(为什么?)
白光入射时,0级明纹中心为白色(可用 y ∝ λ ,
红光入射的杨氏双缝干涉照片
白光入射的杨氏双缝干涉照片
▲
光强分布 设狭缝 迭加后 若
1.4 分波面双光束干涉 分波面双光束干涉(Wavefront splitting)
实现干涉的方法
将一个光源的一束光波分割成两束或多束, 将一个光源的一束光波分割成两束或多束, 分割成两束或多束 再使其相互交会,在交会区域可能产生干涉条纹. 再使其相互交会,在交会区域可能产生干涉条纹.
波前分割法 光波的分割方法: 光波的分割方法: 振幅分割法
杨氏双缝干涉实验
扬氏双缝干涉光强分布的计算机模拟实验
▲
明暗条纹满足的条件
光程差: δ = r = r2 r1 ≈ d sin θ 相位差:
程差条件
δ = 2π λ 明纹 δ = d sin θ = ± jλ ( j = ±0,1,2,)
暗纹
代入
明纹 位置条件 暗纹
y 2 d sin θ ≈ d tgθ = d r0 r y = ± j 0 λ ( j = 0,1,2 …) d r y = ± (2 j + 1) 0 λ (j = ±0,1,2 ) 2d
s1
d
r0
r1 r2
例 [1-1]:
p s2 未贴薄片: 0 为零光程差处 p0
p
s2
p s2 贴薄片: 为零光程差处
t
零光程差处移动 y = p0 p = 1cm
《物理光学》3-3 分波前干涉的其它实验装置Ⅰ

如果它们之中有一个是“ 如果它们之中有一个是“虚”点光源,也即 形成干涉场的不是两个发散球面波,而是一 个发散球面波和一个会聚球面波, 则等光程差面的形状将由旋转双曲面变成旋 转椭球面。 实际上,例如当s 实际上,例如当s1是“虚”点光源时,向s1会 点光源时,向s 聚的球面波将先经过观察点P,然后到达s 聚的球面波将先经过观察点P,然后到达s1, 则考虑点p 则考虑点p和s1之间的光程可以看作是“负” 之间的光程可以看作是“ 值,使得“光程差”在空间上表现为“ 值,使得“光程差”在空间上表现为“距离 和”,而与两个定点(s1和s2)之间距离和等 ,而与两个定点(s 于常数的动点的轨迹是旋转椭球面。
ρ = x0
若m0是整数,即干涉条纹中心恰好是极大 强度,则,由里往外计数的第N 强度,则,由里往外计数的第N个“亮纹” 亮纹” 的半径ρ 的半径ρN为 2λ
ρN = x0
0
nl
N = ρ1 N
即各亮纹的半径按N 即各亮纹的半径按N1/2的规律增大,再次说 明条纹内疏外密的特点。 以上讨论了s 都是“ 点光源的情形。 以上讨论了s1和s2都是“实”点光源的情形。
0 20 10
λ0 ∆ = mλ0 − (ϕ20 −ϕ10 ) 2π
用极限形式定义强度分布的局部空间频率φ 用极限形式定义强度分布的局部空间频率φ
f • dr = dm ⇒ f = 1
此为φ的一般计算公式。 此为φ的一般计算公式。 观察屏上干涉条纹的性质: 观察屏上干涉条纹的性质: 1.假定观察屏П放置y=y0=常数的平面上,并 1.假定观察屏 放置y=y 常数的平面上, 假定观察屏П 假定考察范围集中在y轴附近,使x 假定考察范围集中在y轴附近,使x、z值均远 y 小于y 小于y0,如图所示: P (x , y , z) y Π 则等光程差面与观察屏的交线方程:
3.1.2 双光束干涉

P
O
x
d
S2
θ
Q2
λ
r2
D
∆ = d sinθ
问:(1) 当待测气体的折射率大于空气的折射率时, 当待测气体的折射率大于空气的折射率时, 干涉条纹应如何移动? 干涉条纹应如何移动? (2) 设 l = 2.0cm,条纹移动 20 条,光波的波长为 , 5893Å,空气的折射率为 n =1.000276,求待测气体 , , 的折射率。 的折射率。 解:(1) 设薄壁容器中充入空气时,零级条纹出现 设薄壁容器中充入空气时, 而充入待测气体时, 在 O 点,而充入待测气体时,零级条纹出现于 P 点。此时的光程差
2π yd ϕ = ∆ = (∆r + ∆R) ≈ ( + ∆R) ( ) 10 λ λ λ D
1.分波面法双光束干涉 . ①如果 S1、S2 到 S 的距离相等 如果 的距离相等,∆R=0, 则对应 ϕ = 2mπ (m=0, ± 1, ± 2L ) 的空间点
Dλ y=m d (11)
光强极大,呈现干涉亮条纹; 为光强极大,呈现干涉亮条纹;
在d<<D,且在 y 很小的范围内考察时,相应二光的 且在 很小的范围内考察时, 相位差为
2π yd ϕ = ∆ ≈ ( + ∆R) ( ) 10 λ λ D 2π
S
R1 R2
S1
θ
θ
r1
y
P
0
y
d
S2
λ
r2
D
∆ = d sinθ
∆r = d sin θ sin θ ≈ y / D
2π 2π
∆r ≈ dy / D
1.分波面法双光束干涉 . ②如果 S1、S2 到 S 的距离不相等 如果 的距离不相等,∆R≠0, 则对应
《光学教程》第五版 姚启钧 第三章 光的干涉.解析

2
r2 r1
2
3.3.2 干涉图样
2 I A12 A2 2 A1 A2 cos 2 A1 A2 2 A1 A2 2
2 j
干涉相长
2 j 1 干涉相消
j 干涉相长(明纹) 1 j 2 干涉相消( 暗纹)
1 A1 A2 2 A1 A2 2 A1 A2 V 2 2 2 A1 A2 1 A1 A2 0 A1 A2
——验证了干涉条件之一 振幅相差不能太大 令
I 0 I1 I 2 A A
2 1
2 1 2 2
2 2
2 A1 A2 I A A 1 2 cos 2 A1 A2 I 0 1 V cos
由光强公式
1 I1 4 I10Cos , 2 2 2 I 2 4 I 20Cos 2
2
1
2
1 2 2 2
I I1 I 2
,
yd l
dy 2dy 4 I10Cos 4 I 20Cos l1 l2
2
3.5菲涅耳公式
As1 n1 n2 Ap1 A’s1 A’p1
400 430 450 500 570 600 630 760 nm
紫
蓝
青
cyan
绿
green
黄
橙
红
purple blue
yellow orange red
可见光 4~7.6 × 1014Hz
ν——频率,表征发光机制的物理量 真空中, 介质中,
c 0
0
n
折射率的定义:
r2 r1
2
3.3.2 干涉图样
2 I A12 A2 2 A1 A2 cos 2 A1 A2 2 A1 A2 2
2 j
干涉相长
2 j 1 干涉相消
j 干涉相长(明纹) 1 j 2 干涉相消( 暗纹)
1 A1 A2 2 A1 A2 2 A1 A2 V 2 2 2 A1 A2 1 A1 A2 0 A1 A2
——验证了干涉条件之一 振幅相差不能太大 令
I 0 I1 I 2 A A
2 1
2 1 2 2
2 2
2 A1 A2 I A A 1 2 cos 2 A1 A2 I 0 1 V cos
由光强公式
1 I1 4 I10Cos , 2 2 2 I 2 4 I 20Cos 2
2
1
2
1 2 2 2
I I1 I 2
,
yd l
dy 2dy 4 I10Cos 4 I 20Cos l1 l2
2
3.5菲涅耳公式
As1 n1 n2 Ap1 A’s1 A’p1
400 430 450 500 570 600 630 760 nm
紫
蓝
青
cyan
绿
green
黄
橙
红
purple blue
yellow orange red
可见光 4~7.6 × 1014Hz
ν——频率,表征发光机制的物理量 真空中, 介质中,
c 0
0
n
折射率的定义:
1.3分波面双光束干涉
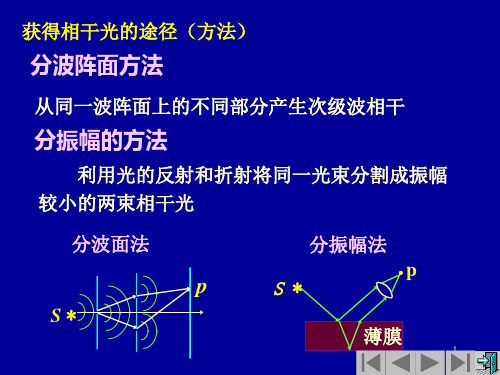
一系列平行的明暗相间的条纹; ● 一系列平行的明暗相间的条纹;
● ∆y ∝ λ ,白光入射时 , 0 级明纹中心为白色 白光入射时, 可用来定0级位置) 其余级明纹构成彩带, ( 可用来定 0 级位置 ) , 其余级明纹构成彩带 , 级开始出现重叠(为什么? 第2级开始出现重叠(为什么?)
17
红光入射的杨氏双缝干涉照片
22
例题1 1 例题1-1
s1
d
p25页 页
r0
r1
p s2 未贴薄片: 0 为零光程差处 未贴薄片: p0
p
s2
p s2 贴薄片: 为零光程差处 贴薄片:
t
r2
零光程差处移动 y = p0 p = 1cm
两列光通过狭缝前已有光程差 两列光通过狭缝后到 p 点的光程差
p为零光程差处 零光程差处
( n − 1) t = r1 − r2 = d y r0
24
2、菲涅耳双面镜
▲
实验装置
y
P
L
S1
d
M1 θ
S
C
S2
o
M2
d′
l
s1 和 s2 发出的光为相干光,在相遇 虚光源 发出的光为相干光, 区域(阴影部分)发生干涉 干涉。 区域(阴影部分)发生干涉。
25
▲
明暗条纹满足的条件
M1 θ
S
L
y
P
S1
d
C
S2
o
M2
d′
l
s s s 为圆心, 由几何关系知, 、1 、 2 在以 c 为圆心,半径为 r 的圆上
ν = (E2-E1)/h
E1 波列长L = τ c 波列长
τ < 10−8 秒
3.1.2 双光束干涉解析

S1 S
双棱 镜
d
S2
D
菲涅耳双棱镜的干涉
S
M1 S1 S2
M2
菲涅耳双面镜的干涉
S
d
S’
M
D 洛 埃 镜 的 干 涉
1.分波面法双光束干涉 这些实验的共同点是: ①在两束光的叠加区内,到处都可以观察到干涉 条纹,只是不同地方条纹的间距、形状不同而已。 这种在整个光波叠加区内随处可见干涉条纹的干涉, 称为非定域干涉。与非定域干涉相对应的是定域干 涉,有关于涉的定域问题,将在以后中讨论。
y ml R
(14)
的空间点是亮条纹;
对应
(m 1/2)l R y
(15)
的空间点是暗条纹。即干涉图样相对于 R=0 的情况, 沿着 y 方向发生了平移。
1.分波面法双光束干涉 除了上述杨氏干涉实验外,菲涅耳双棱镜、菲 涅耳双面镜和洛埃镜都属于分波面法双光束干涉的 实验装置。
2nh cosq 2
l
2
(17)
(1)等倾干涉的强度分布 由此可以得到焦平面上的光强分布:
I I1 I 2 2 I1I 2 cos(k ) (18)
显然,形成亮暗干涉条纹的位置,由下述条件决定 : 相应于光程差 = ml(m = 0,1,2)的位置为亮条 纹; 相应于光程差 = (m+1/2)l 的位置为暗条纹。
为了研究分波而法双光束干涉现象的特性,下 而进一步讨论杨氏双缝干涉实验。在图实验原理图 中,Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出 很小的两部分作为相干光源,它们发出的两列光波 在观察屏上叠加,形成干涉条纹。
S1 S
点 光 源单 缝
r1 r2
双 缝
物理光学教程 第三章 光的干涉

2 2
(3(3-26)
= I1 + I 2 + 2 I1 I 2 cos( )
2. 干涉强度分布特点
(1) 等强度面 (2) 峰值强度面 (3) 干涉强度的空间频率和空间周期 (4) 二 维观察平面上的强度分布— 维观察平面上的强度分布—干涉图形 (5) 干涉条纹的反衬度
3. 平面波在薄膜波导中的传输
3.1.3 双光束干涉的基本条件
1. 干涉场强度
根据光的干涉的定义, 根据光的干涉的定义,干涉场中光能量密度的空间分布是干涉现象 是否存在的判据. 是否存在的判据.
2. 干涉项
干涉项不为零的条件是: 干涉项不为零的条件是:
ω2 = ω1
E10 E20 ≠ 0
(3(3-22) (3(3-23) (3(3-24)
第三章
§3.1 干涉的基本 理论
3.1.1 3.1.2 3.1.3 3.1.4 3.1.5 波的叠加原理 光波叠加综述 双光束干涉的基本条件 两个平面波的干涉 两个球面波的干涉
光的干涉
§3.3 分振幅干涉
3.3.1 3.3.2 3.3.3 3.3.4 干涉条纹的定域性质 平行平板的等倾干涉 楔形板和薄膜的等厚干涉 双臂式分振幅干涉仪及其应用
薄膜波导又称为平面波导,是一种重要的集成光学器件,它根据集成电路原理, 薄膜波导又称为平面波导,是一种重要的集成光学器件,它根据集成电路原理, 将各种独立的光源器件,光放大器件,光调制器件, 将各种独立的光源器件,光放大器件,光调制器件,光耦合器件以及光接收器 件等,以薄膜的形式集成在同一基底上,形成具有某种功能的微光学系统. 件等,以薄膜的形式集成在同一基底上,形成具有某种功能的微光学系统. 上一页 下一页 返回
2. 时间相干性
(3(3-26)
= I1 + I 2 + 2 I1 I 2 cos( )
2. 干涉强度分布特点
(1) 等强度面 (2) 峰值强度面 (3) 干涉强度的空间频率和空间周期 (4) 二 维观察平面上的强度分布— 维观察平面上的强度分布—干涉图形 (5) 干涉条纹的反衬度
3. 平面波在薄膜波导中的传输
3.1.3 双光束干涉的基本条件
1. 干涉场强度
根据光的干涉的定义, 根据光的干涉的定义,干涉场中光能量密度的空间分布是干涉现象 是否存在的判据. 是否存在的判据.
2. 干涉项
干涉项不为零的条件是: 干涉项不为零的条件是:
ω2 = ω1
E10 E20 ≠ 0
(3(3-22) (3(3-23) (3(3-24)
第三章
§3.1 干涉的基本 理论
3.1.1 3.1.2 3.1.3 3.1.4 3.1.5 波的叠加原理 光波叠加综述 双光束干涉的基本条件 两个平面波的干涉 两个球面波的干涉
光的干涉
§3.3 分振幅干涉
3.3.1 3.3.2 3.3.3 3.3.4 干涉条纹的定域性质 平行平板的等倾干涉 楔形板和薄膜的等厚干涉 双臂式分振幅干涉仪及其应用
薄膜波导又称为平面波导,是一种重要的集成光学器件,它根据集成电路原理, 薄膜波导又称为平面波导,是一种重要的集成光学器件,它根据集成电路原理, 将各种独立的光源器件,光放大器件,光调制器件, 将各种独立的光源器件,光放大器件,光调制器件,光耦合器件以及光接收器 件等,以薄膜的形式集成在同一基底上,形成具有某种功能的微光学系统. 件等,以薄膜的形式集成在同一基底上,形成具有某种功能的微光学系统. 上一页 下一页 返回
2. 时间相干性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3 波面双光束干涉
一、产生干涉的四件可分为三种 1、分波面干涉 2、分振幅 3、分振动面
二、几种典型的分波面干涉实验
a 、杨氏实验(双缝干涉)
211 , ,s s s 足够小
21 ,s s 为相干光源
b 、菲涅耳双面镜
\
特例:两独立激光光源(或两平行光相干)
∞→r
θ
λ
s i n 2r y =∆
C 、洛埃镜(21p p 为干涉区) 实验结果分析:
当屏与镜接触,接触点0p 出现暗纹。
θ
θλ
θθsin 2cos cos sin 20r l r y l rd r r d +=∆+==
说明反射光的光程在介质表面反射时损失了半个波长,这现象称为半波损失。
D 、维纳驻波实验
G G '片涂一落层感光乳胶
入射波和反射波相遇在一起,也会发生相干迭加而形成驻波。
在Ga (与M M '接触的地方)无感光,即波切,即光产生了丰波损失。
例:杨氏实验
已知0,r y 放n -λ的透明片遮住一孔,使条纹移动距离y 。
求:薄片厚度l 。
解:θsin 12d r r =- l nl r r -+=12 0
)1(r n d
y l -⋅=
s i n r y tg =
=θθ 例:复合光入射,含(21λλ>) 求:第二级明纹的宽度l ∆
解:d
r
j y 0λ=
d
r
y y l 02121)(2λλ-=-=∆。
