2012-2013-1线性代数1-A期末试题
(完整版)线性代数期末测试题及其答案.doc

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题 5 分,共 25 分)1 3 1 1.若0 5 x 0,则__________。
1 2 2x1 x2 x3 02.若齐次线性方程组x1 x2 x3 0 只有零解,则应满足。
x1x2x303.已知矩阵A,B,C (c ij )s n,满足 AC CB ,则 A 与 B 分别是阶矩阵。
4.已知矩阵A为 3 3的矩阵,且| A| 3,则| 2A|。
5.n阶方阵A满足A23A E 0 ,则A1。
二、选择题(每小题 5 分,共 25 分)6.已知二次型 f x12 x22 5x32 2tx1x2 2x1 x3 4x2 x3,当t取何值时,该二次型为正定?()A. 40 B.4 4C. 0 t4 4 1t5t D. t2 5 5 5 51 42 1 2 37.已知矩阵A 0 3 4 , B 0 x 6 ,且 A ~ B ,求x的值()0 4 3 0 0 5A.3B.-2C.5D.-58 .设 A 为 n 阶可逆矩阵,则下述说法不正确的是()A. A0B. A 1 0C.r (A) nD.A 的行向量组线性相关9 .过点( 0, 2, 4)且与两平面x 2z 1和 y 3z 2 的交线平行的直线方程为()1xy 2 z 4A.312xy 2 z 4C.31 2x y2 z 4B.32 2x y2 z 4D.322103 1 .已知矩阵 A, 其特征值为()51A. 12, 2 4 B. C.12,24D.三、解答题(每小题 10 分,共 50 分)1 12,2, 22441 1 00 2 1 3 40 2 1 30 1 1 011.设B, C 0 2 1 且 矩 阵满足关系式0 0 1 1 00 10 0 0 2T X(C B)E,求。
a1 12212. 问 a 取何值时,下列向量组线性相关?111, 2a ,3。
2 1 21 a22x 1 x 2x 3 313.为何值时,线性方程组x 1 x 2x 3 2有唯一解,无解和有无穷多解?当方x 1 x 2x 32程组有无穷多解时求其通解。
12-13-1《线性代数试卷A》第一学期期末考试试卷

河南理工大学 2012-2013 学年第 1 学期《线性代数》试卷(A 卷)1.设()()(),,,,,,,,t 3,1321111321===βββ若321βββ,,线性相关,则t =.2.矩阵()nn ija ⨯=A 的全体特征值的和等于 , 全体特征值的积等于.3.设A 为4阶方阵,2-=A ,则A 3-= .4.()234321,,B ,A =⎪⎪⎪⎭⎫ ⎝⎛=,则=AB.5.设三阶方阵⎪⎪⎪⎭⎫ ⎝⎛--=120350002A ,则A 的逆矩阵1-A =.6.设3阶方阵A 按列分块为()321ααα,,A =,且Ad e t =5,又设()231215432ααααα,,B ++=,则B =.7.设⎪⎪⎪⎭⎫ ⎝⎛--=11334221xA ,x 为某常数,B 为3阶非零矩阵,且0AB =,则x = . 8.设三元非齐次线性方程组的系数矩阵的秩为2,已知21ηη,是它的两个解向量.且⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=42232121ηη,该方程组的通解为.1.设A 与B 均为n 阶方阵,则下列结论中成立的为().(A) det(AB ) = 0,则0A =或0B =; (B) det(AB ) = 0,则det A = 0或det B = 0; (C) AB = 0,则0A =或0B =; (D) AB ≠ 0,则det A ≠ 0或det B ≠ 0.2. 设n 阶矩阵A 的行列式0≠A ,*A 是A 的伴随矩阵,则( ).(A) 2-=n *A A ; (B) 1+=n *A A ; (C) 1-=n *AA ;(D) 2+=n *AA .3. 已知A 、B 均为3阶方阵,且A 与B 相似,若A 的特征值为1,2,3,则()12-B 的特征值为( )(A) 2312,,; (B) 614121,,; (C) 321,,;(D) 3212,,.4. 向量组321,,βββ线性无关,324,,βββ线性相关,则有 .(A)1β可由324,,βββ线性表示; (B)3β可由42ββ,线性表示 ;(C)2β可由43ββ,线性表示;(D)4β可由32ββ,线性表示 .三、计算题1.(7分)计算行列式211112111121=n D .一、填空题,每小题4分二、选择题,每小题5分2.(7分)设⎪⎪⎪⎭⎫⎝⎛---=121011332A ,求1-A .3.(7分)求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛---=1401131********12211A 的列向量组的一个最大线性无关组.4.(12分)λ取何值时,非齐次线性方程组⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x ,,(1)有唯一解;(2)无解;(3)有无穷多个解?5.(15分)已知二次型()322221321434x x x x x ,x ,x f ++=,求一个正交变换Py x =,把二次型()321x ,x ,x f 化为标准型.。
线性代数期末考试试题(含答案)

江西理工大学《线性代数》考题一、填空题(每空3分,共15分)1。
设矩阵,且,则______2.二次型是正定的,则t的取值范围__________3.为3阶方阵,且,则___________4.设n阶矩阵A的元素全为1,则A的n个特征值是___________5.设A为n阶方阵,为A的n个列向量,若方程组只有零解,则向量组()的秩为_____二、选择题(每题3分,共15分)6.设线性方程组,则下列结论正确的是()(A)当取任意实数时,方程组均有解(B)当a=0时,方程组无解(C)当b=0时,方程组无解(D)当c=0时,方程组无解7. A.B同为n阶方阵,则()成立(A)(B)(C)(D)8.设,,,则( )成立(A) (B)(C)(D)9.,均为n阶可逆方阵,则的伴随矩阵()(A)(B) (C)(D)10.设A为矩阵,<,那么A的n个列向量中()(A)任意r个列向量线性无关(B) 必有某r个列向量线性无关(C) 任意r个列向量均构成极大线性无关组(D)任意1个列向量均可由其余n-1个列向量线性表示三、计算题(每题7分,共21分)11.设.求12.计算行列式13.已知矩阵与相似,求a和b的值四、计算题(每题7分,共14分)14.设方阵的逆矩阵的特征向量为,求k的值15.设,,,(1)问为何值时,线性无关(2)当线性无关时,将表示成它们的线性组合五、证明题(每题7分,共14分)16.设3阶方阵,的每一列都是方程组的解(1)求的值(2)证明:17.已知为n维线性无关向量,设,证明:向量线性无关六、解答题(10分)18.方程组,满足什么条件时,方程组(1)有惟一解(2)无解(3)有无穷多解,并在此时求出其通解七、解答题(11分)19。
已知二次型,试写出二次型的矩阵,并用正交变换法化二次型为标准型. (一)1、202、 3 4 5、n(二)ACCDB(三)11、12、()13、()(四)14、(或) 15、()(五)16 ( 略) 17略(六)18、( (1)且;(2);(3),解略)(七)19、(,其余略)。
线性代数期末考试试题

《线性代数》重点题一. 单项选择题1.设A 为3阶方阵,数λ = -3,|A | =2,则 |λA | =( ).A .54;B .-54;C .6;D .-6.解. .54227)3(33-=⨯-=-==A A A λλ 所以填: B.2、设A 为n 阶方阵,λ为实数,则|λA |=( )A 、λ|A |;B 、|λ||A |;C 、λn |A |;D 、|λ|n |A |. 解. |λA |=λn |A |.所以填: C.3.设矩阵()1,2,12A B ⎛⎫==- ⎪⎝⎭ 则AB =( ).解. ().24121,221⎪⎪⎭⎫⎝⎛--=-⎪⎪⎭⎫ ⎝⎛=AB 所以填: D.A. 0;B. ()2,2-;C. 22⎛⎫ ⎪-⎝⎭;D. 2142-⎛⎫⎪-⎝⎭.4、123,,a a a 是3维列向量,矩阵123(,,)A a a a =.若|A |=4,则|-2A |=( ). A 、-32; B 、-4; C 、4; D 、32.解. |-2A |=(-2)3A =-8⨯4=-32. 所以填: D. 5.以下结论正确的是( ).A .一个零向量一定线性无关;B .一个非零向量一定线性相关;C .含有零向量的向量组一定线性相关;D .不含零向量的向量组一定线性无关.解. A .一个零向量一定线性无关;不对,应该是线性相关.B .一个非零向量一定线性相关;不对,应该是线性无关.C .含有零向量的向量组一定线性相关;对.D .不含零向量的向量组一定线性无关. 不对, 应该是:不能判断. 所以填: C.6、 1234(1,1,0,0),(0,0,1,1),(1,0,1,0),(1,1,1,1),αααα====设则它的极大无关组为( )A 、 12,; ααB 、 123,, ;αααC 、 124,, ;αααD 、1234,, ,αααα解. (B)93页7.设A,B,C 是n 阶矩阵,下列选项中不正确的是( ).A .若A 可逆,则*1A A A-=,其中*A 为A 的伴随矩阵;B .若AB E =,则1B A -=;C .若矩阵A 可逆,数k ≠ 0,则()11kA kA --=;D .对标准矩阵方程AXB C =,若A ,B 可逆,则11X A CB --=.解. A .若A 可逆,则*1A A A-=,其中*A 为A 的伴随矩阵;对.B .若AB E =,则1B A -=;对.C .若矩阵A 可逆,数k ≠ 0,则()11kA kA --=;不对,应该是().111--=A kkA D .对标准矩阵方程AXB C =,若A ,B 可逆,则11X A CB --=.对.所以填: C.8、 矩阵A =1111-⎛⎫ ⎪-⎝⎭的伴随矩阵A *=( ). A 、1111⎛⎫⎪⎝⎭;B 、⎪⎪⎭⎫ ⎝⎛--1111;C 、⎪⎪⎭⎫⎝⎛--1111; D 、⎪⎪⎭⎫ ⎝⎛--1111.解.因为112112221,(1)11,(1)11,1A A A A ==--⋅==--⋅==.所以1121*12221111AA A A A ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦ 故填A.41页9.若n 元齐次线性方程组0Ax =有非零解, 则( ). A . ()R A n <; B . ()R A n =;C . ()0R A =;D .A 、B 、C 都不对.解. A . ()R A n <;对.B . ()R A n =;不对, 此时应该0Ax =有且仅有零解.C . ()0R A =;不对. 此时, 仅是0Ax =有非零解的一种情况.D .A 、B 、C 都不对. 不对.所以填:A.10、 ,A B n 与均为阶方阵则下列结论中成立的是( ).A 、det()0,,;AB A O B O ===则或 B 、det()0,det 0,det 0;AB A B ===则或C 、,,;AB O A O B O ===则或;D 、,det 0,det 0.AB O A B ≠≠≠则或 解. A 、不对. B 、40页(iii),AB A B =.即有det()0,det 0,det 0AB A B ===则或.所以填: B .11.设向量组123,,ααα线性相关,234,,ααα线性无关,则下列成立是( ).A . 2α可由34,αα线性表示;B .4α可由23,αα线性表示;C . 4α不可由123,,,ααα线性表示;D .3α可由2,α4α线性表示.解.(p90例7.) 由题设“设向量组123,,ααα线性相关,234,,ααα线性无关”.①因234,,ααα线性无关,则23,αα线性无关.再由123,,ααα线性相关.则1α可由23,αα线性表示.②用反证法.假设4α可由123,,,ααα线性表示,而由①知1α可由23,αα线性表示.因此4α可由23,αα线性表示.这与题设234,,ααα线性无关相矛盾.所以4α不可由123,,,ααα线性表示. 所以填: C.12、设123,,a a a 是二维实向量,则( ).A 、123,,a a a 一定线性无关;B 、1a 一定可由23,a a 线性表出;C 、123,,a a a 一定线性相关;D.12,a a 一定线性无关.解. A 不对. B 不对. C.因为105页:n 维实向量12,,,n e e e 叫做n R 中的自然基.因此二维实向量123,,a a a 的自然基为二维实向量12,e e .当然123,,a a a 是线性相关的.即C 对. D 不对. 所以填: C.13.向量空间3R 的一组基为( )A . 1231200,3,1000ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;B . 1231000,1,0001ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;C . 1231010,3,1000ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;D . 1230210,0,0130ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.解. A .1231200,3,1000ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;不是.因31232ααα+=, 所以123,,ααα不是向量空间3R 的一组基.B . 1231000,1,0001ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;是向量空间3R 的一组基.C . 1231010,3,1000ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;不是.因13233ααα-=, 所以123,,ααα不是向量空间3R 的一组基.D . 1230210,0,0130ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.不是.因31223ααα+=, 所以123,,ααα不是向量空间3R 的一组基.所以填: B.14、设A 是4×6矩阵,R (A )=3,则齐次线性方程组Ax =0的基础解系中所含向量的个数是( ).A 、 4;B 、 3 ;C 、 2;D 、1.解.由97页,定理7.设m n ⨯矩阵A 的秩()R A r =,则n 元齐次线性方程组0Ax =的解集S 的秩.S R n r =-现在6, 3.n r ==因此63 3.-= 即填: B.15.设矩阵111213212223212223111213313233311132123313,,a a a a a a A a a a B a a a a a a a a a a a a ⎛⎫⎛⎫⎪⎪== ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭12010100100,010,001101P P ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭则必有( ). A .12APP B =; B .21AP P B =; C .12PP A B =; D .21P P A B =.解. A . 12APP B =?.10101000110101000110000101033313332232123221311131233313223212213111233323123222113121121B a a aa a a a a a a a a a a a a a a a a a a a a a a a a a a P AP ≠⎪⎪⎪⎭⎫⎝⎛+++=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=因此A 不对.B .21AP P B = ?11121311121321212223212223313233313233121113132221232332313333100010010010100100101001011.a a a a a a AP P a a a a a a a a a a a a a a a a a a a a B a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪⎪⎪⎪== ⎪⎪⎪ ⎪⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭+⎛⎫ ⎪=+≠ ⎪ ⎪+⎝⎭因此B 不对.C .12PP A B = ?11121311121312212223212223313233313233212223111213113112321333010100010100010100001101101.a a a a a a PP A a a a a a a a a a a a a a a a a a a B a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪⎪ ⎪⎪== ⎪⎪⎪ ⎪⎪ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫ ⎪== ⎪ ⎪+++⎝⎭因此C 对.D .21P P A B = ?11121311121321212223212223313233313233212223111213213122322333100010010010100100101001011.a a a a a a P P A a a a a a a a a a a a a a a a a a a B a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪⎪ ⎪⎪== ⎪⎪⎪ ⎪⎪ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫ ⎪=≠ ⎪ ⎪+++⎝⎭所以填: C.16、设A ,B ,C 为同阶可逆方阵,则1()ABC -=( ).A 、111ABC ---; B 、111C A B ---; C 、111C B A ---;D 、111B A C ---解。
大一线性代数期末考试试卷+答案

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=TA A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 s n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④ s ααα,,, 21中不含零向量3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
线性代数期末试题及参考答案

线性代数期末试题及参考答案一、单项选择题<每小题3分,共15分)1.下列矩阵中,< )不是初等矩阵。
<A )001010100⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ (B>100000010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ (C> 100020001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(D> 100012001⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦ 2.设向量组123,,ααα线性无关,则下列向量组中线性无关的是< )。
<A )122331,,αααααα--- <B )1231,,αααα+ <C )1212,,23αααα- <D )2323,,2αααα+3.设A 为n 阶方阵,且250A A E +-=。
则1(2)A E -+=< )(A> A E - (B> E A + (C> 1()3A E - (D> 1()3A E +4.设A 为n m ⨯矩阵,则有< )。
<A )若n m <,则b Ax =有无穷多解;<B )若n m <,则0=Ax 有非零解,且基础解系含有m n -个线性无关解向量;<C )若A 有n 阶子式不为零,则b Ax =有唯一解; <D )若A 有n 阶子式不为零,则0=Ax 仅有零解。
5.若n 阶矩阵A ,B 有共同的特征值,且各有n 个线性无关的特征向量,则< )<A )A 与B 相似 <B )A B ≠,但|A-B|=0<C )A=B <D )A 与B 不一定相似,但|A|=|B|二、判断题(正确填T ,错误填F 。
每小题2分,共10分>1. A 是n 阶方阵,R ∈λ,则有A A λλ=。
< )2. A ,B 是同阶方阵,且0≠AB ,则111)(---=A B AB 。
< )3.如果A 与B 等价,则A 的行向量组与B 的行向量组等价。
线性代数期末考试题及答案

《线性代数》期末考试题及答案一、单项选择题(每小题3分,共24分).1.设行列式1112132122233132331a a a a a a a a a =,则111112132121222331313233234234234a a a a a a a a a a a a --=-( ). A. 6; B. -6; C. 8; D. -8.2.设B A ,都是n 阶矩阵,且0=AB , 则下列一定成立的是( ).A. 0A =或0B =;B. 0A =且0B =;C. 0=A 或0=B ;D. 0=A 且0=B .3.设A ,B 均为n 阶可逆矩阵,则下列各式中不正确...的是( ). A. ()T T T A B A B +=+; B . 111()A B A B ---+=+; C. 111()AB B A ---= ; D. ()T T T AB B A =.4.设12,αα是非齐次线性方程组Ax b =的解,是β对应的齐次方程组0Ax =的解,则Ax b =必有一个解是( ).A .21α+α;B .21α-α;C . 21α+α+β ;D .121122βαα++.5.齐次线性方程组123234 020x x x x x x ++=⎧⎨--=⎩的基础解系所含解向量的个数为( ).A. 1;B. 2;C. 3;D. 4. 6.向量组12,,αα…,s α(2)s ≥线性无关的充分必要条件是( ).A. 12,,αα…,s α都不是零向量;B. 12,,αα…,s α任意两个向量的分量不成比例;C. 12,,αα…,s α每一个向量均不可由其余向量线性表示;D. 12,,αα…,s α至少有一个向量不可由其余向量线性表示. 7.若( ),则A 相似于B .A. A B = ; B . 秩(A )=秩(B );C. A 与B 有相同的特征多项式;D. n 阶矩阵A 与B 有相同的特征值,且n 个特征值各不相同. 8.正定二次型1234(,,,)f x x x x 的矩阵为A ,则( )必成立.A. A 的所有顺序主子式为非负数;B. A 的所有顺序主子式大于零;C. A 的所有特征值为非负数;D. A 的所有特征值互不相同.二、填空题(每小题3分,共18分)1.设3阶矩阵100220333A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,*A 为A 的伴随矩阵,则*A A =_____________.2.1111n⎛⎫⎪⎝⎭=__________________(n 为正整数). 3.设a b A c d ⎛⎫= ⎪⎝⎭,且det()0A ad bc =-≠,则1A -=________________.4.已知4阶方阵A 的秩为2,则秩(*A )=_________________.5.已知向量组123(1,3,1),(0,1,1),(1,4,)a a a k ===线性相关,则k =____________.6.3阶方阵A 的特征值分别为1,-2,3,则1A -的特征值为_________.三、计算题(10分,共44分)1.(7分)计算行列式01231000100001x x a a a a ---2.(7分)设矩阵121348412363A a -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,问a 为何值时,(1) 秩(A )=1; (2) 秩(A )=2.3.(15分)给定向量组12103a -⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭=,21324a ⎛⎫⎪- ⎪ ⎪ ⎪ ⎪⎝⎭=,33021a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭=,40149a ⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭=,试判断4a 是否为123,,a a a 的线性组合;若是,则求出组合系数4.(15分)λ取何实值时,线性方程组12233414x x x x x x x x λλλλλλλλ-=⎧⎪-=⎪⎨-=⎪⎪-+=⎩有唯一解、无穷多解、无解?在有无穷多解的情况求通解。
线代期末试题及答案

线代期末试题及答案一、选择题(每题3分,共30分)1. 在三维向量空间中,以下向量中线性无关的是:A) (1, 0, 0)B) (0, 1, 0)C) (0, 0, 1)D) (1, 1, 1)答案:D2. 设矩阵A = [a b; c d],若行列式det(A) = 0,则以下哪个等式成立?A) ad - bc = 0B) ab - bc = 0C) ac - bd = 0D) ad - bd = 0答案:A3. 给定矩阵A = [1 2 3; 4 5 6; 7 8 9],则A的逆矩阵为:A) [-1/6 -1/3 1/6; -1/6 2/3 -1/6; 1/6 -1/3 1/6]B) [-1 -2 -3; -4 -5 -6; -7 -8 -9]C) [1/6 1/3 -1/6; 1/6 -2/3 1/6; -1/6 1/3 -1/6]D) [1 2 3; 4 5 6; 7 8 9]答案:A4. 给定矩阵A = [2 0; 0 3],B = [1 2; 3 4],则A与B的乘积为:A) [2 4; 6 8]B) [2 0; 0 3]C) [1 2; 9 12]D) [4 6; 6 12]答案:B5. 给定向量a = (1, 2, 3)和b = (4, 5, 6),则a与b的内积为:A) 32B) 22C) 14D) 6答案:C6. 若向量a = (1, 2, 3),b = (4, -2, 5),c = (3, 1, -2),则以下哪个等式成立?A) a × b = cB) b × c = aC) c × a = bD) a × c = b答案:B7. 给定矩阵A = [1 2; 3 4],则A的特征值为:A) 1, 2B) 2, 3C) 3, 4D) 4, 5答案:A8. 设向量a = (1, 2, 3),b = (4, 5, 6),c = (2, 1, 3),则向量集合{a, b, c}的维数为:A) 1B) 2C) 3D) 4答案:C9. 给定矩阵A = [1 2; 3 4],A的转置矩阵为:A) [1 3; 2 4]B) [4 3; 2 1]C) [1 2; 3 4]D) [3 4; 1 2]答案:A10. 设矩阵A = [2 1; 3 4],则A的伴随矩阵为:A) [4 -1; -3 2]B) [2 -1; 3 4]C) [-4 1; 3 -2]D) [-2 1; -3 -4]答案:A二、计算题(共70分)1. 设矩阵A = [1 2; 3 4],求A的逆矩阵。
大一线性代数期末考试试题

大一线性代数期末考试试题大一线性代数期末考试试题线性代数作为大一学生的一门重要课程,对于培养学生的数学思维能力和解决实际问题的能力具有重要意义。
而期末考试则是对学生所学知识的一次全面检验。
下面我们就来看一下大一线性代数期末考试试题。
第一题:矩阵的运算已知矩阵A=(1 2 3,4 5 6,7 8 9),求矩阵A的转置矩阵、逆矩阵和行列式的值。
解析:首先,矩阵A的转置矩阵可以通过将矩阵A的行变为列得到,即A^T=(1 4 7,2 5 8,3 6 9)。
其次,逆矩阵的计算可以通过求解方程AX=I,其中I为单位矩阵。
假设矩阵A的逆矩阵为B,那么AB=BA=I。
通过高斯-约当消元法可以求解出逆矩阵B。
最后,行列式的计算可以通过拉普拉斯展开式或者初等行变换来进行。
对于本题中的矩阵A,可以通过对第一行进行展开得到行列式的值。
第二题:向量的内积和外积已知向量a=(1,2,3),b=(4,5,6),求向量a和b的内积和外积。
解析:向量的内积可以通过将对应分量相乘再相加来计算,即a·b=1*4+2*5+3*6=32。
向量的外积可以通过行列式的形式来计算,即a×b=|i j k| |1 2 3| |4 5 6|。
其中i、j、k分别为单位向量。
通过计算可以得到向量a和b的外积为(-3,6,-3)。
第三题:矩阵的特征值和特征向量已知矩阵A=(2 1,1 2),求矩阵A的特征值和特征向量。
解析:特征值和特征向量的求解可以通过求解方程Ax=λx来进行。
其中,A为矩阵,λ为特征值,x为特征向量。
首先,我们需要求解矩阵A的特征值。
可以通过求解矩阵A的特征多项式的根来得到特征值。
特征多项式为|A-λI|=0,其中I为单位矩阵。
对于本题中的矩阵A,可以得到特征多项式为(2-λ)(2-λ)-1*1=λ^2-4λ+3=0。
解这个二次方程可以得到特征值λ1=1和λ2=3。
然后,我们需要求解矩阵A的特征向量。
可以通过代入特征值到方程(A-λI)x=0来求解特征向量。
北京理工大学2012级线性代数(A)A卷及答案

课程编号:A073122 北京理工大学2012-2013学年第一学期线性代数A 试题 A 卷班级 ________ 学号 _________ 姓名 __________ 成绩 ___________一、(10分)已知3阶方阵123035002A ⎛⎫⎪= ⎪ ⎪⎝⎭,计算行列式*123A I+。
二、(10分) 设423110, 2123A AX A X ⎛⎫ ⎪⎪==+ ⎪ ⎪-⎝⎭, 求X 。
三、(10分)已知线性空间4][x F 的自然基为231,,,x x x 。
(1) 证明:2231,12,123,1234x x x x x x ++++++为4][x F 的一个基;(2) 求自然基231,,,x x x 到基2231,12,123,1234x x x x x x ++++++的过渡矩阵,以及23()1h x x x x =--+在后一个基下的坐标。
四、(10分)已知123(1,0,1), (2,2,0), (0,1,1)TTTααα=-==。
(1) 求向量组123,,ααα的一个极大无关组;(2) 求生成子空间123(,,)L ααα的一个标准正交基。
五、(10分)设A 是5阶方阵,且已知存在5阶可逆矩阵P ,使得111112P AP --⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭试写出A 的初等因子,同时判断P 的哪几列是A 的特征向量。
六、(10分)在多项式空间4[]R x 中定义变换σ:233012330201()()a a x a x a x a a a x a a x σ+++=-+++(1)证明:σ是4[]R x 上的线性变换;(2)求σ在4[]R x 的自然基231,,,x x x 下的矩阵,并判断σ是否可逆。
七、(10分)假设A 是m n ⨯的实矩阵,证明:()()TA A A =秩秩八 (10分)已知(1,1,1)T ξ=-是矩阵2125312A a b -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦的一个特征向量, (1)确定参数a , b 及特征向量ξ所对应的特征值; (2)判断A 是否可以相似对角化,说明理由。
2012-2013-1线性代数A试卷与答案

,,s、向量组的秩为r,则向量组中三、计算题(每题12分,共60分)1、计算行列式:32142143143243212、已知=⎪⎪⎪⎭⎫ ⎝⎛--101111121X ⎪⎪⎪⎭⎫ ⎝⎛523231141,求矩阵X3、求线性方程组⎪⎪⎩⎪⎪⎨⎧-=----=+-+-=+-+=+-+261782314620324321432143214321x x x x x x x x x x x x x x x x 的通解。
4、求向量组1234(1,1,1),(1,1,0),(1,0,0),(1,2,3)αααα====-的一个极大线性无关组,并把其余向量用极大无关组线性表示.5、求⎪⎪⎪⎭⎫ ⎝⎛--=100010221A 的特征值与特征向量.分)若123,,ξξξ是方程组0AX =的基础解系,证明1323122,2,2ξ+ξξ+ξξ+ξ也是该方程组的基础解系.2012-2013-1线性代数A 参考答案与评分标准一、 判断题(每题2分,共20分)二、填空题(每空2分,共10分)1、-2;2、43、41; 4、1; 5、111,,632三、计算题(每题12分,共60分)1、解:原式=32110214101431043210……………………………………………(2分) =111022203110432110321121411431432110------= …………………………(6分) =11314021113112011111131120----=----=---- …………(10分)=160113140=- ……………………………………………………(12分)2、解:1141121132111325101X -⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦----------------------4分 121100121100111010012110101001022101⎡⎤⎡⎤⎢⎥⎢⎥-→---⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦1310011031202201211001001100212111001122⎡⎤--⎢⎥--⎡⎤⎢⎥⎢⎥---→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦--⎢⎥⎣⎦--------------10分131221141223113201102232511465122⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥----⎢⎥⎣⎦⎣⎦--------------------------12分 3、解:先对增广矩阵进行初等行变换⎪⎪⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎪⎪⎭⎫⎝⎛-------------→⎪⎪⎪⎪⎪⎭⎫⎝⎛---------000000000012210032112442012210122100321121611178231461203211--------------------6分同解方程组⎪⎩⎪⎨⎧=++=+-+1220324324321x x x x x x x ,一个特解⎪⎪⎪⎪⎪⎭⎫⎝⎛-0011-----------------------8分选4x 为自由未知量,得到齐次线性方程组的一个基础解系:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-210121,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1105----------------------10分原方程组的通解为+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2101211k ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-11052k +⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-0011-------------------------12分 4、解:秩为 3,--------------------------6分一个极大线性无关组为123,,ααα. --------------------------10分412335αααα=-+-;--------------------------12分5、解:特征方程为|λE -A|=1010221---+λλλ=(λ+1) (λ-1)2 =0,------4分 ∴A 的全部特征值为λ1=-1,λ2=λ3=1。
(完整word版)线性代数期末考试试题答案解析合集

XXX 大学线性代数期末考试题、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1 -3 11.若 05 x =0,则-12 -2| /..X| x 2x 3 = 02 .若齐次线性方程组 +h x 2 +x3 =0只有零解,则 乙应满足X ! +x 2 +x 3 =05. n 阶方阵A 满足A 2-3A-E=0,则A 」= ___________________ 。
二、 判断正误(正确的在括号内填“V” ,错误的在括号内填“X” 。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则 D 0 o ()2. 零向量一定可以表示成任意一组向量的线性组合。
()3. 向量组a 1? a 2, , a m 中,如果a 1与a m 对应的分量成比例,则向量组a 1? a 2, , a s 线性相关。
()0 1 1 04. A =0 0 卫05. 若■为可逆矩阵A 的特征值,则 A ,的特征值为■ o ()三、单项选择题(每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且A =2,则|AA^= ( )o①2n② 2n4③2n 1④42. n 维向量组〉2,…,s (3 - s _n )线性无关的充要条件是()。
①:-1,' 2 , , 〉s 中任意两个向量都线性无关②-■1,' 2,, 〉s 中存在一个向量不能用其余向量线性表示 0 0_0 01 “),贝y A =Ao (0 11 03.已知矩阵A , B ,C = (C j )s n ,满足AC 二CB ,则A 与B 分别是 ________________ 阶矩阵。
a ii4 .矩阵 A = a 21 l a31ai2a 22的行向量组线性a32」③-■1,' 2, , 〉s中任一个向量都不能用其余向量线性表示④:-1,- 2, , 〉s 中不含零向量3. 下列命题中正确的是()。
(完整版)线性代数试题套卷及答案

(线性代数) ( A 卷)专业年级: 学号: 姓名:一、单项选择题(本大题共5小题,每小题5分,共25分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设n m A ⨯为实矩阵,则线性方程组0=Ax 只有零解是矩阵)(A A T为正定矩阵的(A) 充分条件; (B) 必要条件; (C) 充要条件; (D) 无关条件。
2.已知32121,,,,αααββ为四维列向量组,且行列式 4,,,1321-==βαααA ,1,,,2321-==βαααB ,则行列式 =+B A(A) 40; (B) 16-; (C) 3-; (D) 40-。
3.设向量组s ααα,,,21)2(≥s 线性无关,且可由向量组s βββ,,, 21线 性表示,则以下结论中不能成立的是(A) 向量组s βββ,,,21线性无关; (B) 对任一个j α,向量组s j ββα,,,2线性相关; (C) 存在一个j α,向量组s j ββα,,,2线性无关; (D) 向量组s ααα,,,21与向量组s βββ,,, 21等价。
4.对于n 元齐次线性方程组0=Ax ,以下命题中,正确的是(A) 若A 的列向量组线性无关,则0=Ax 有非零解; (B) 若A 的行向量组线性无关,则0=Ax 有非零解; (C) 若A 的列向量组线性相关,则0=Ax 有非零解; (D) 若A 的行向量组线性相关,则0=Ax 有非零解。
5.设A 为n 阶非奇异矩阵)2(>n ,*A 为A 的伴随矩阵,则√√(A) A A A 11||)(-*-=; (B) A A A ||)(1=*-;(C) 111||)(--*-=A A A ; (D) 11||)(-*-=A A A 。
二、填空题(本大题共5小题,每小题5分,共25分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6. 列向量⎪⎪⎪⎭⎫ ⎝⎛-=111α 是矩阵⎪⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的对应特征值λ的一个特征向量. 则λ= ,a = ,b = 。
2012-2013-1-线性代数A 期末试卷及答案

②若秩 (A) ≥ 秩 (B) ,则 Ax = 0 的解均是 Bx = 0 的解;
③若 Ax = 0 与 Bx = 0 同解,则秩 (A) = 秩 (B) ;
④若秩 (A) = 秩 (B) ,则 AX = 0 与 BX = 0 同解。
以上命题中正确的是
。
(A)①②
(B)①③
(C)②④
(D)③④
5. 方阵 A 与 B 相似的充分必要条件是
北京科技大学 2012--2013 学年第一学期
线性代数 试卷(A 卷)
院(系)
班级
学号
姓名
试卷卷面成绩
题 号
一
二
三
四
五
六
七
八
得
分
评
阅
审
核
小计
占课程 考核成 绩 70%
平时 成绩 占 30%
课程考 核成绩
注意事项: (1)本试卷共八道大题,共八页,请认真核对。 (2)正确填写学院、班级、姓名、学号等个人信息,空填或错填的试卷为无效试卷。 (3)请使用钢笔、签字笔或者圆珠笔答卷,使用铅笔答卷无效。
(A)2000
(B)-2000
。 (C)2300
(D)-2300
3.设向量组α1,α2 ,α3 线性无关,向量 β1 可由α1,α2 ,α3 线性表示,而向量 β2 不能由α1,α2 ,α3 线性表示,
则对于任意常数 k ,必有
。
(A)α1,α2 ,α3, kβ1 + β2 线性无关;
(B)α1,α2 ,α3, kβ1 + β2 线性相关;
⎟ ⎟ ⎟
,
α
3
⎜
=
⎜ ⎜
0 7
⎟
线性代数 期末测试题及其答案
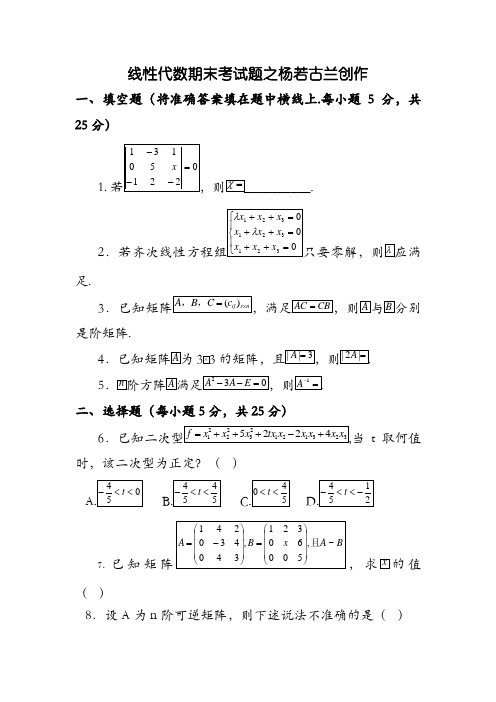
线性代数期末考试题之杨若古兰创作一、填空题(将准确答案填在题中横线上.每小题5分,共25分)1.2足.3是阶矩阵.45二、选择题(每小题5分,共25分)6当t 取何值时,该二次型为正定?( )7.已知矩阵,求的值( )8.设A 为n 阶可逆矩阵,则下述说法不准确的是( )A的行向量组线性相干9.过点(0,2,4行的直线方程为()10其特征值为()三、解答题(每小题10分,共50分)11.矩足关系式12.问取何值时,以下向量组线性相干?解和有没有量多解?当方程组有没有量多解时求其通解.14.求此向量组的秩和一个极大有关组,并将其余向量用该极大有关组线性暗示. 15.证实其中线性代数期末考试题答案一、填空题1. 5.解析:采取对角线法则,考查常识点:行列式的计算.难度系数:解析:要使该现行方程组只要零解,考查常识点:线性方程组的求解难度系数:解析;,,,阶矩阵.考查常识点:n 阶矩阵的性质难度系数: 4. 24解析:由题可知3考查常识点:矩阵的运算 难度系数: 解析:考查常识点:求解矩阵的逆矩阵 难度系数:二、选择题 6. A解析:由题可知,该二次型矩阵为,而此时,该二次型正定.考查常识点:二次型正定的判断难度系数7. C解析:由矩阵特征值性质有1-3+3=1+x+5,可解得x=-5. 考查常识点:n 阶矩阵特征值的性质 难度系数:8. D解析:由题可知,A 为n 阶可逆矩阵,则A 的行向量组线性有关.考查常识点:n 阶可逆矩阵的性质 难度系数:9. A.解析:由题可知,两平面法向量分别为,则所求直线的方向向量为考查常识点:求空间平面交线平行的直线方程 难度系数:10. C.考查常识点:求解矩阵的特征值三、解答题11.解:考查常识点:矩阵方程的运算求解难度系数:12.解:.考查常识点:向量组的线性相干性难度系数:13.解:③当时,有没有量多组解,通解为考查常识点:线性方程组的求解14.解:由题可知,且线性关系为考查常识点:向量组的秩与最大有关组难度系数:15.证实:由题可知,考查常识点:n 阶方阵的性质难度系数:。
2012-2013线性代数(32学时)期末试卷A卷答案 本科

所以
2 0 1 1 2 1 B ( A E ) ( A E ) ( A E ) ( A E )( A E ) A E 0 3 0 (6 分) 1 0 2
14、 (10 分)计算行列式 D
0 0 d2 c2
解:在等式两边同时左乘 A1 ,得: X A1 B (2 分) , 因为: A 34 0 ,所以 A 可逆, (4 分)
21 19 4 , 又因为 A 的伴随矩阵是: A 19 35 2 4 2 4
=( a 2 b2 - d 2 c 2) ( a1b1 - d1c1) (10 分)
21 19 4 1 故 A 19 35 2 (7 分) 34 2 4 4
1
21 19 4 1 -3 -29 -21 1 1 所以 X A B 19 35 2 2 -2 57 -15 (10 分) 34 34 12 2 4 4 4 3 -1
0 0 0
1
2 0 0 1 1 3 0 2 2 1 4 1 0 0 0 1 0 0 0 1 0 0 0 1
0 0 1 r3 1 0 0 r4 3 r3 0 2 r2 0 1 0 r4 1 r3 4 0 0 1
0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 1 1 0 2 2 1 1 1 2 6 3 5 1 1 8 24 12
1
五、
阅卷教师 得分
计算题(共 3 题,共 24 分)
2012-2013第一学期线性代数A(A卷)

北京信息科技大学2012 ~2013 学年第一学期《线性代数A 》课程期末考试试卷A课程所在学院:理学院 适用专业班级:工科48学时考试形式:(闭卷)一、完成下列各题(本题满分48分,共含8道小题,每题6分)1、求排列3154726的逆序数,并判断奇偶性。
2、设101310124D -=-,D 的(i,j )元的代数余子式A ,ij 求313233A A A ++。
3、计算行列式1234111100,0,1,2,3,4100100i a a D a i a a =≠=其中。
4、设111123111,124111051A B ⎛⎫⎛⎫ ⎪ ⎪=-=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,求2T A B A -。
5、120213,121A ⎛⎫ ⎪= ⎪ ⎪⎝⎭求:12+3A E -。
6、设1121212==+r r βαβααβααα=+++,,且向量组12,,,r ααα线性无关,证明:向量组12,,,r βββ组线性无关。
7、若12,t β⎛⎫ ⎪= ⎪ ⎪⎝⎭可由1232211,2,1174ααα-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭线性表出,求t 的值 8、判断二次型12222312133924f x x x x x x x =++-+的正定性。
二、计算题(本题满分40分,共含5道小题,每题8分)1、设110011,2,101A AX X A X -⎛⎫ ⎪=-=+ ⎪ ⎪-⎝⎭求。
2、求非齐次线性方程组 的通解。
3、设11021α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,21201α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,32514α⎛⎫ ⎪ ⎪= ⎪- ⎪⎝⎭,41131α⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭,(1)求向量组4321,,,αααα的秩;(2)求该向量组的一个最大线性无关组;(3)将其余向量用最大无关组表示。
4、已知向量1111a ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求一组非零向量23,,a a 使得123,,a a a 两两正交。
线代期末试题及答案共享

线代期末试题及答案共享线性代数是一门重要的数学学科,在各个领域都有广泛的应用。
为了帮助同学们更好地复习线性代数课程,我将在本文中提供线性代数期末试题及答案供大家共享。
一、选择题1. 下列哪个向量不是向量组{(1, -2, 3), (2, -4, 6), (3, -6, 9)}的一个线性组合?A. (4, -8, 12)B. (5, -10, 15)C. (-1, 2, -3)D. (0, 0, 0)答案:A. (4, -8, 12)2. 给定矩阵A = (1, 2, 3; 4, 5, 6; 7, 8, 9),则A的转置矩阵是:A. (1, 4, 7; 2, 5, 8; 3, 6, 9)B. (1, 2, 3; 4, 5, 6; 7, 8, 9)C. (1, 2, 3; 7, 8, 9)D. (1, 4, 7; 2, 5, 8; 3, 6, 9)答案:A. (1, 4, 7; 2, 5, 8; 3, 6, 9)3. 设矩阵A = (1, 2; 3, 4),则A的逆矩阵是:A. (-2, 1; 3/2, -1/2)B. (1, -1; -3/2, 1/2)C. (-1, 2; 3/2, -1/2)D. (1/2, -1/2; -3/2, 1/2)答案:A. (-2, 1; 3/2, -1/2)二、填空题1. 设A是一个n阶矩阵,若A的行列式为5,则A的伴随矩阵的元素之和为_______。
答案:02. 设向量组{(1, 2, 3), (4, 5, 6), (7, 8, k)}是线性相关的,则k的取值范围为_________。
答案:[-3, 3]三、计算题1. 设向量a = (2, 1, 3),向量b = (4, 2, 1),求向量a与向量b的点积。
答案:a·b = 2*4 + 1*2 + 3*1 = 112. 设向量a = (-1, 2, 3),向量b = (2, -1, 1),求向量a与向量b的叉积。
线性代数期末考试试卷合集(共十一套)

线性代数期末考试试卷合集(共十一套)目录线性代数期末试卷及参考答案(第一套) .............................................................................. 1 线性代数期末试卷及参考答案(第二套) .............................................................................. 9 南京工程学院期末试卷(第一套) ........................................................................................ 17 南京工程学院期末试卷(第二套) ........................................................................................ 24 南京工程学院期末试卷(第三套) ........................................................................................ 30 线性代数 期末试卷(A 卷) .................................................................................................. 36 线性代数 期末试卷(B 卷) .................................................................................................. 41 线性代数 期末试卷(C 卷) .................................................................................................. 46 线性代数 期末试卷(D 卷) .................................................................................................. 51 线性代数 期末试卷(E 卷) .................................................................................................. 57 线性代数 期末试卷(F 卷) (62)线性代数期末试卷及参考答案(第一套)一、单项选择题(本大题共5小题,每小题3分,共15分)1、设矩阵⎪⎪⎭⎫ ⎝⎛=3223A 满足B AB =,则矩阵=B ( )(A ) ⎪⎪⎭⎫⎝⎛21k k ; (B )⎪⎪⎭⎫ ⎝⎛11; (C ) ⎪⎪⎭⎫ ⎝⎛--2121k k k k ; (D ) ⎪⎪⎭⎫ ⎝⎛-2111k k .(21k k ,为任意常数) 2、设n 阶方阵A ,B 满足E AB =,则下列一定成立的是 ( ) (A )E B A == ; (B )E B A =+ ; (C )1=A 或1=B ; (D )1=⋅B A .3、设矩阵,⎪⎪⎪⎭⎫ ⎝⎛=001010100A 则 =-++)()(E A R E A R ( )(A ) 2; (B ) 3; (C ) 4; (D ) 5 .4、设向量组A :r a a a,,,21可由向量组B :s b b b ,,,21线性表示,则正确的是 ( )(A )当s r >时,向量组A 必线性相关; (B ) 当s r <时,向量组A 必线性相关; (C )当s r >时,向量组B 必线性相关; (D ) 当s r <时,向量组B 必线性相关.5、设A 为n m ⨯的矩阵,0=x A 是非齐次线性方程组b x A =所对应的齐次线性方程组,则下列结论正确的是( )(A ) 若0=x A 仅有零解,则b x A =有唯一解;(B ) 若b x A =有无穷多解,则0=x A 有非零解;(C ) 若n m =,则b x A=有唯一解;(D ) 若A 的秩m A R <)(,则b x A=有无穷多解.二、填空题(本大题共5小题,每小题3分,共15分)1、设方阵⎪⎪⎪⎭⎫⎝⎛=010002cb a A ,当c b a ,,满足 时,A 为可逆方阵.2、若可逆方阵A 的有一个特征值3,则13-)(A 必有一个特征值为 .3、设A 为54⨯的矩阵,且秩2=)(A R ,则齐次方程组0=x A 的基础解系所含向量个数是 .4、若三阶行列式222023z y x =1,则行列式1117110111------z y x = . 5、设向量组⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛13232121,,x 线性相关,则常数x= .三、计算题(本题共6小题,共50分)1、(6分)设矩阵⎪⎪⎪⎭⎫ ⎝⎛-=b a a A 140132121的秩2=)(A R , 求常数b a ,及一个最高阶非零子式.2、(8分)求矩阵⎪⎪⎪⎭⎫ ⎝⎛--=314020112A 的特征值和特征向量. 3、(8分)设3阶方阵A 与B 满足BA A BA A 22+=*, 其中,⎪⎪⎪⎭⎫⎝⎛=400030001A 求B .4、(10分)设向量组A :.,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=77103 1301 3192 01414321αααα 求: (1) 向量组A 的秩; (2) 向量组A 的一个最大线性无关组; (3) 将此最大无关组之外的其它向量用最大无关组线性表示.5、(8分)计算行列式aa a a D ++++=4321432143214321,其中0≠a .6、(10分)设线性方程组⎪⎩⎪⎨⎧=+-=--=--532403321321321x x x b ax x x x x x , 问:当参数b a ,取何值时,(1)此方程组有唯一解? (2)此方程组无解? (3)此方程组有无穷多解? 并求出通解.四、判断题(本大题共5小题,每小题2分,共10分) 1、设矩阵B A ,为3阶方阵,且42==B A ,,则121=-AB.( )2、由3维向量构成的向量组4321a a a a,,,中必有一个可由其余向量线性表示. ( ) 3、对任意n 阶方阵C B A ,,,若AC AB =,且O A ≠,则一定有C B =.( )4、设向量21ηη ,是线性方程组b x A =的解,则212ηη -也是此方程组的一个解.( ) 5、正交向量组321a a a ,,线性无关.( )五、证明题(本题共2小题,每小题5分,共10分) 1、设n 阶对称矩阵A 满足关系式O E A A =++862,证明:(1)E A 3+是可逆矩阵,并写出逆矩阵; (2) E A 3+是正交矩阵.2、若3210a a a a,,,是n 元非齐次线性方程组b x A =的线性无关解,且,)(3-=n A R证明:030201a a a a a a---,,是其对应的齐次线性方程组0 =x A 的基础解系.参考答案一、选择题(本题5小题, 每小题3分, 共15分)1. C ;2. D ;3. B ;4. A ;5. B .二、填空题(本题5小题, 每小题3分, 共15分)1. c ab 2≠;2.91; 3. 3; 4. 23- ; 5. 5. 三、计算题(本题6小题, 共50分)1. 解: A →⎪⎪⎪⎭⎫ ⎝⎛------210022170121b a a a (2分), 由R (A ) = 2知,⎩⎨⎧=-=--0201b a , ⎩⎨⎧=-=∴21b a ,一个最高阶非零子式3221-. 2.解: 由λλλλ-----=-314020112E A (),)(0212=-+-=λλ 得A 的特征值为.,21321==-=λλλ当11-=λ时, 解 ().0=+x E A,⎪⎪⎪⎭⎫ ⎝⎛-−→−⎪⎪⎪⎭⎫ ⎝⎛--=+000010101414030111r E A得基础解系:,⎪⎪⎪⎭⎫⎝⎛=1011p 对应11-=λ的全部特征向量为)(0111≠k p k当232==λλ时, 解().02=-x E A,⎪⎪⎪⎪⎪⎭⎫⎝⎛--−→−⎪⎪⎪⎭⎫⎝⎛--=-000000414111140001142r E A 得基础解系:,⎪⎪⎪⎭⎫ ⎝⎛=401 2p ,⎪⎪⎪⎭⎫ ⎝⎛=041 3p对应232==λλ的特征向量为)0,(323322不全为k k p k p k+ 3. 解: B= 2(|A |E -2A ) -1 A |A |=12(|A |E -2A ) -1 =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛4100061000101, B=2⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛410061000101⎪⎪⎪⎭⎫⎝⎛400030001 =⎪⎪⎪⎪⎪⎭⎫⎝⎛20001000514. 解: ),,,(4321αααα=A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------71307311100943121→⎪⎪⎪⎪⎪⎭⎫⎝⎛--0000110024103121 → ⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000110020102001 所以,秩3=A R , (1分)一个最大线性无关组为,,,321ααα(2分)且321422αααα++-=5. 解:aa a a D ++++=43214321432143214321c c c c +++aa a a a a a +++++++432104321043210432101r r i -aa a a 00000000043210+=)(103+a a 6. 解: 增广矩阵⎪⎪⎪⎭⎫⎝⎛-----==5312410131b ab A B ),( →⎪⎪⎪⎭⎫⎝⎛+---120011100131b a(1) 当12-≠=b a ,时, 32=<=)()(B R A R ,此时方程组无解. (2) 当b a ,2≠取任意数时, 3==)()(B R A R ,此时方程组有唯一解. (3) 当12-==b a ,时, 32<==)()(B R A R ,此时方程组有无穷多解.B →⎪⎪⎪⎭⎫ ⎝⎛--000011100131 →⎪⎪⎪⎭⎫ ⎝⎛000011103201即⎩⎨⎧+-=+-=1323231x x x x 原方程组的通解为)(R c c ∈⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛--013112.四、判断题(本题5小题, 每小题2分, 共10分)1. ×;2. √;3. ×;4. √;5. √.五、证明题(本题2小题, 每小题5分, 共10分)1.证明: (1)由O E A A =++862得E E A A =++962,即E E A E A =++))((33 所以E A 3+可逆,且E A E A 331+=+-)(.(2)由A 为n 阶对称矩阵知,E A E A E A TT T 333+=+=+)()(,故()()()E E A E A E A E A T=++=++333)3(,所以E A 3+是正交矩阵.2. 证明: 3210a a a a,,,是n 元非齐次线性方程组b x A =的解,030201a a a a a a---∴,,是对应齐次方程组0 =x A 的解;又,)(3-=n A R 所以0 =x A 的基础解系中含向量个数为3)(=-A R n 个; 下证 030201a a a a a a---,,线性无关即可.设0033022011 =-+-+-)()()(a a k a a k a a k 即00321332211=++-++a k k k a k a k a k )(又 3210a a a a ,,,线性无关, 故⎪⎪⎩⎪⎪⎨⎧=++-===0000321321)(k k k k k k 有唯一解0321===k k k所以030201a a a a a a---,, 线性无关,从而030201a a a a a a---,,是其对应的齐次方程组0 =x A 的基础解系线性代数期末试卷及参考答案(第二套)一、填空题(本大题共7小题,每小题3分,共21分)1、设向量⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=123,321βα ,则当k = 时,.正交与βαα +k2、设方阵A 满足关系式O A A =+322,则1)(-+E A = .3、若三阶行列式930021-=x xxx ,则 =x . 4、设矩阵⎪⎪⎭⎫⎝⎛-=0211A ,多项式x x x f 2)(2+=,则=)(A f . 5、设向量组⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-13,032,101λ线性相关,则常数λ= .6、n 元非齐次线性方程组b x A=有无穷多解的充要条件是 .7、设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的对应特征值λ的一个特征向量为⎪⎪⎪⎭⎫ ⎝⎛-111,则 ._______________,______,===b a λ二、单项选择题(本大题共5小题,每小题3分,共15分)1、设A ,B 是任意n 阶方阵(2≥n ),则下列各式正确的是 ( )(A ) B A B A +=+; (B ) 22B A B A B A -=-⋅+; (C ) B A B A ⋅=; (D ) A B AB T⋅= .2、下列4个条件中,①A 可逆 ; ②A 为列满秩(即A 的秩等于A 的列数); ③A 的列向量组线性无关; ④ O A ≠ ;可使推理“ 若O AB =, 则O B = ”成立的条件个数是 ( )(A ) 1个 ; (B ) 2个; (C ) 3个; (D ) 4个.3、向量组s ααα,,,21)2(≥s 线性无关,且可由向量组s βββ ,,,21线性表示, 则下列结论中不成立的是( )(A ) 向量组s βββ,,,21线性无关;(B ) 对任一个j α )1(s j ≤≤,向量组s j βββα,,,,21线性相关;(C ) 存在一个j α )1(s j ≤≤,向量组s j βββα,,,,21线性无关;(D ) 向量组s ααα,,,21与向量组s βββ ,,,21等价. 4、设A ,B 均为3阶方阵, 3)(=A R ,2)(=B R , 则=)(AB R( )(A ) 1; (B ) 2; (C ) 3; (D ) 6 .5、设A 为n m ⨯的矩阵,r A R =)(,则非齐次线性方程组b x A=( )(A ) 当n r = 时有唯一解; (B ) 当n m r == 时有唯一解;(C ) 当n m = 时有唯一解; (D ) 当n r < 时有无穷多解. 三、计算题(本题共6小题,共54分)1、(7分)设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=61011152121λλA 的秩2)(=A R , 求常数λ及一个最高阶非零子式.2、(9分)求矩阵⎪⎪⎪⎭⎫ ⎝⎛=320230001A 的全部特征值和特征向量.3、(8分)设3阶方阵C B A ,,满足方程 A B A C =-)2(,试求矩阵A ,其中 ⎪⎪⎪⎭⎫ ⎝⎛=100010301B , ⎪⎪⎪⎭⎫ ⎝⎛=300020001C .4、(10分)设向量组A :.6721 ,11313 ,5652 ,21214321⎪⎪⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=αααα 求: (1) 向量组A 的秩; (2) 向量组A 的一个最大线性无关组; (3) 将此最大无关组之外的其它向量用最大无关组线性表示.5、(8分)计算行列式cc b b a a x x x x D ---=000000, 其中x c b a ,,,全不为0.6、(12分)设线性方程组⎪⎩⎪⎨⎧=++=++=++bx x x x a x x x x x 3213213214231202, 问:当参数b a ,取何值时,(1)此方程组有唯一解? (2)此方程组无解? (3)此方程组有无穷多解? 并求出通解.四、证明题(本题共2小题,每小题5分,共10分)1、若向量321,,ααα线性无关, 求证 2132αα +,324αα +,135αα + 也线性无关.2、设矩阵T E A ηη -=, 其中E 是3阶单位矩阵,⎪⎪⎪⎭⎫⎝⎛=321x x x η 是单位向量,证明:(1) A A =2; (2) A 不可逆.参考答案一、填空题(本题7小题, 每小题3分, 共21分)1. 75-; 2. E A +2; 3. 3±; 4. ⎪⎪⎭⎫ ⎝⎛--2631 ; 5. 6 ; 6. n b A R A R <=),()(; 7. -1 ,-3 ,0 .二、选择题(本题5小题, 每小题3分, 共15分)1. D ;2. C ;3. C ;4. B ;5. B .三、计算题(本题6小题, 共54分)1. 解: A →⎪⎪⎪⎭⎫⎝⎛--+---3390022110121λλλλλ(3分), 由R (A ) = 2知,⎩⎨⎧=-=-03039λλ,3=∴λ (2分), 一个最高阶非零子式5221 .2.解: 由λλλλ---=-32230001E A (),01)5(2=--=λλ得A 的特征值为.1,5321===λλλ当51=λ时, 解 ().05=-x E A,0001100012202200045⎪⎪⎪⎭⎫⎝⎛-−→−⎪⎪⎪⎭⎫ ⎝⎛---=-r E A得基础解系:,1101⎪⎪⎪⎭⎫⎝⎛=p 对应51=λ的全部特征向量为)(0111≠k p k当132==λλ时, 解().0=-x E A,000000110220220000⎪⎪⎪⎭⎫ ⎝⎛−→−⎪⎪⎪⎭⎫ ⎝⎛=-r E A 得基础解系:,001 2⎪⎪⎪⎭⎫ ⎝⎛=p ,110 3⎪⎪⎪⎭⎫ ⎝⎛-=p对应132==λλ的特征向量为)0,(323322不全为k k p k p k+.3. 解: CB A E C =-)2( ;⎪⎪⎪⎭⎫ ⎝⎛=-5000300012E C ; ⎪⎪⎪⎪⎭⎫ ⎝⎛=--51000310001)2(1E C ; ⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛=⋅-=-5300032030110001030130002000151000310001)2(1CB E C A . 4. 解: ),,,(4321αααα =A →⎪⎪⎪⎪⎪⎭⎫⎝⎛---00210045101321 → ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000021********001 (初等变换步骤不一,请酌情给分)所以,秩3=A R , (1分) 一个最大线性无关组为,,,321ααα(2分)且32142617αααα--=5. 解:)1,2,3(1=++i c c i i Dcb a xx x x---0000000234=xabc 4- .6. 解: 增广矩阵⎪⎪⎪⎭⎫⎝⎛==b a b A B 4231120211),( →⎪⎪⎪⎭⎫⎝⎛----120014100211b a a , (1) 当b a ,2≠取任意数时, 3)()(==B R A R , 此时方程组有唯一解; (2). 当1,2≠=b a 时, 3)(2)(=<=B R A R ,此时方程组无解;(3) 当1,2==b a 时, 32)()(<==B R A R ,此时方程组有无穷多解.B →⎪⎪⎪⎭⎫ ⎝⎛-000012100211 →⎪⎪⎪⎭⎫⎝⎛-000012101001 即⎩⎨⎧--==121321x x x原方程组的通解为)(011120R c c ∈⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-.四、证明题(本题2小题, 每小题5分, 共10分)1.证明: 由题意 ⎪⎪⎪⎭⎫⎝⎛=+++540013102),,()5,4,32(321133221ααααααααα , 记 AK B = .K K ∴≠=,022 可逆, 又321,,ααα线性无关,所以)5,4,32(133221αααααα +++R 3),,(321==αααR , 即 2132αα +,324αα +,135αα+ 也线性无关.2. 证明: (1) η为单位向量,1=∴ηηT ,A E E E E A T T T T T T T =-=+--=--=∴ηηηηηηηηηηηηηη)())((2.(2) 由(1)知,A A =2, 即 O E A A =-)(,3)()(≤-+∴E A R A R ,η为单位向量,O E A T ≠-=-∴ηη , 1)(≥-E A R ,从而32)(<≤A R , 所以0=A , 故A 不可逆.另一证法: 0)(=-=-=-=ηηηηηηηηηηT T E A ,的非零解,为线性方程组0=∴ηηA所以0=A , 故A 不可逆.南京工程学院期末试卷(第一套)共6 页第1页课程所属部门:基础部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科南京工程学院试卷共 6 页第 4 页南京工程学院期末试卷(第二套)共6 页第1页课程所属部门:基础部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科南京工程学院期末试卷(第三套)共6 页第1页课程所属部门:数理部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科线性代数 期末试卷(A 卷)一、(本大题共8小题,每题3分,共24分)1. 设B A ,均为n 阶方阵,则下面各式正确的是----------------------------------( C ) (A)TTTB A AB =)( (B) 222)(B A AB = (C) || ||AB BA = (D)AB BA = 2. 下列命题正确的是--------------------------------------------------------------------( C ) (A) 若02=A ,则0=A (B) 若A A =2,则0=A 或E A = (C) 若E A =,则E A n = (D) 若E A =2,则E A ±=3. 若行列式的所有元素都变号,则--------------------------------------------------( D ) (A) 行列式一定变号 (B) 行列式一定不变号 (C) 偶阶行列式变号 (D) 奇阶行列式变号4. 设k c c c b b b a a a =321321321,则112311231123232323a a a a b b b b c c c c ++=+-------------------------------( B ) (A) k 6 (B) k 3 (C) k 2 (D) k5. 若某线性方程组的系数行列式为零,则该方程组------------------------------( D ) (A) 有唯一解 (B) 有非零解 (C) 无解 (D) 有非零解或无解6.已知TT T t ),3,1(,)3,2,1(,)1,1,1(321===ααα线性相关的,则t =-----( B )(A) 4 (B) 5 (C) 6 (D) 77. 设方阵A 相似于(1,1,1)diag -,则10A =---------------------------------------- ( A )(A) E (B) 10E (C) E - (D) 10E - 8. 设A 为n 阶方阵,则下列说法中正确的是--------------------------------------( B ) (A) 若A 可对角化,则A 为实对称阵 (B) 若A 为实对称阵,则A 可对角化 (C) 若A 可对角化,则A 必可逆 (D) 若A 可逆,则A 可对角化二、填空题(本大题共4小题,每题4分,共16分)1.设2110A ⎛⎫=⎪-⎝⎭,则*A =0112-⎛⎫ ⎪⎝⎭,1A-=0112-⎛⎫ ⎪⎝⎭。
2013级线性代数期末考试题(A卷)答案

2013—2014学年第一学期线性代数课程期末考试试卷参考答案(A 卷)一、(每小题2分,共8小题)1 错;2 对;3 对;4 C ;5 B ;6 B ;7 A ;8 B二、行列式计算 (本题共14分,第1小题6分,第2小题8分)1、计算四阶行列式1110110110110111D =.解:根据行列式的性质,原行列式等于:1(234)21311/3414*3/211103333110111012101110110111011111111111110100103*3*21011010001111003*(1)*1*(1)*(1)*(1)32r r r r r r r r r r r D +++---==-==--=----=-分分分2、计算n 阶行列式11111222(2)1233123n n>.解:根据行列式的性质,原行列式等于:12111110111001100011n n r r r r ---==原式6分2分三、矩阵X ,A ,B 满足3AX X B =+,其中 (本题共8分)301050303A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,111222369B -⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,求矩阵X 。
解:由 3AX X B =+ 可得:(3)A E X B -= 2分又因为 0010203003A E ⎛⎫⎪⎪ ⎪⎝⎭-= 且它是可逆矩阵 1分所以 1(3)X A E B -=- 1分通过计算可得:1001/301/20100(3)A E -⎛⎫⎪= ⎪ ⎪⎝⎭- 2分所以 123111111X ⎛⎫⎪-- ⎪ ⎪-⎝⎭= 2分四、当a 取何值时,线性方程组:1232312343133(1)0x x x ax x x x a x ---+==+++=⎧⎪⎨⎪⎩无解,有惟一解,有无穷多解?并在方程组有无穷多解时求其通解。
(本题14分) 解:方程组的增广矩阵为:⎪⎪⎪⎭⎫ ⎝⎛+---01313301141a a 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012~2013 学年度第一学期 《线性代数》期末考试 试题
课程代码: 1590046 试卷编号: 1-A 命题日期: 2012 年 12 月 6 日 答题时限: 120 分钟 考试形式:闭卷 笔试
一、单项选择题(从4个备选答案中选择最适合的一项,每小题2分,共20分)
1.下列关于行列式性质的的叙述错误的是
A .行列式与其转置行列式相等;
B. 某两行或两列元素对应相等的行列式等于零; C .换行或换列偶数次,行列式的值不变; D .换行或换列奇数次,行列式的值不变 。
2.设ij A 表示3 阶行列式行列式D =2
231323
21中元素ij a 的代数余子式,下列结果错误的是
A . D A A A =++31211132 ;
B . D A A A =++13121132;
C .
D A A A =++13121132; D . 032131211=++A A A ;
3. 以下结论正确的是
A .非零方阵的乘积一定不为零矩阵;
B .若AY AX =,且0≠A ,则Y X =
C .222()2A B A AB B +=++;
D . 若O A =2,则O A =
4. 设B A ,是n 阶可逆矩阵,以下结论不一定成立的是 A .()+A B X C =解为()11+A B C --; B .B XA =的解为1BA -; C. B AX =的解为1A B -; D. C AXB =的解为11--CB A .
5. 设*A 是n 阶方阵A 的伴随矩阵,以下结论错误的是 A .n
A A =*;
B .若A 的秩等于n ,则*A 的秩等于n ; C. 若A 的秩小于-1n ,则*A 的秩等于0 D .若A 的秩等于-1n ,则*A 的秩等于1 。
6. 已知向量组51αα,, 的秩为5, 则以下结论正确的是
A .组41αα,, 线性相关;
B . 组51αα,, 线性无关
C .组5,1,αα 线性相关;
D . 1α可由组2345αααα,,, 线性表示.
7.设321ααα,,是O AX =的基础解系,则还可以当做方程组的基础解系的是
A .与321,,ααα等价的一个向量组;
B .与321ααα,,等秩的一个向量组;
C .321211,,αααααα+++ ;
D .,,3221αααα++31αα-.
8.设12λλ≠为n 阶方阵A 的特征值,21,ξξ为对应的特征向量,下列结论正确的是
A .21ξξ+也是特征向量;
B .21,ξξ线性相关;
C .21,ξξ线性无关;
D .21ξξ=
9.设B A ,均是n 阶矩阵,且E BC E AC ==2,2,则()=---1
1B A C
A .E 23;
B .E 3
2
; C .C 3; D .C 2.
10.与矩阵⎥
⎦
⎤
⎢⎣⎡-1111对应的二次型是 A .2221212x x x x -+; B .2221212x x x x --; C .2221212y y y y --; D .2
221y y -.
二、填空题(每空3分,共30分)
1.若排列1234p p p p 的逆序数是3,则排列4321p p p p 的逆序数是 .
2. 2
2
21
11
z y x z y x
= 。
3.已知某个3元非齐次线性方程组AX=b 的增广矩阵A 经初等行变换化为:
12
31021200(1)1a a a --⎛⎫ ⎪→- ⎪ ⎪--⎝⎭
A ,若方程组无解,则a =____________.
4.设A ,B 均为三阶方阵,2,1A B ==,则=-)(21B A .
5.设E (i,j)是将单位矩阵的第i,j 两行(列)互换所得3阶初等方阵,
则()=⎪⎪⎪
⎭
⎫ ⎝⎛)1,2(3213.2E z y x c b a E
6.设向量组(1,2,3)=T α,(3,1,2)=-T β,(2,3,)=T m γ线性相关,则=m _______________.
7.设A 为43⨯的矩阵,方程组O AX =的基础解系包含2个解向量,则矩阵A 的秩等于 .
8.已知3阶方阵A 的特征值分别为1,-2,1
2
;则=+-1A A .
9. 非齐次方程组⎩⎨⎧=+++=+++n x x x m
x x x n n 3332121 有解的充分必要条件是 .
10.二次型212)(x x x f =的标准型为 .
三、计算题(每小题10分,共40分)
1. 计算n 阶行列式1
111141111311112+n
2. 设有向量组设向量组
()()()(),2,1,1,2,2,1,6,1,1,4,1,24321T
T
T
T
-=--=--==αααα
(1)求向量组4321,,αααα,的一个极大无关组; (2)用所求极大无关组表示其余向量.
3.求λ为何值时方程组⎪⎩⎪
⎨⎧=+--=++=++λ
λλλ32
132132131
x x x x x x x x x (1)有唯一解;(2)无解;(3)有无穷多解。
4.用正交变换,将二次型323121222x x x x x x f -+=化为标准形,写出所用正交变换阵。
四、证明题(每小题5分,共10分)
1. 已知4321,,αααα,线性无关,设411ααβ-=,422ααβ-=,433ααβ-=, 求证:321,,βββ线性无关.
2. 设A 是n 阶正交矩阵,向量α与β满足αβA =,试证明:αβ=。
