用MATLAB解决_条件平差和间接平差(可编辑)
平差实验报告及完整matlab程序
fprintf(fn,'%6.3f\n',v);
fprintf(fn,'%s\n','未知参数估值x');
fprintf(fn,'%6.3f\n',x1);
fprintf(fn,'%s\n','各点高程平差值');
fprintf(fn,'%6.3f\n',x2);
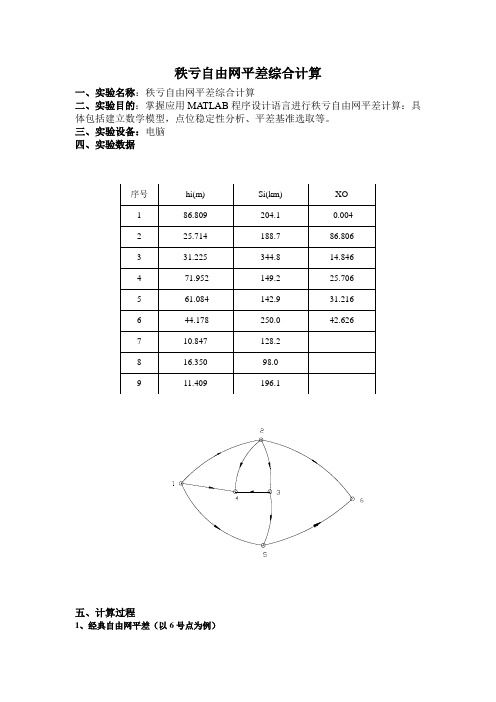
86.806
3
31.225
344.8
14.846
4
-71.952
149.2
25.706
5
-61.084
142.9
31.216
6
-44.178
250.0
42.626
7
10.847
128.2
8
16.350
98.0
9
11.409
196.1
五、计算过程
1、经典自由网平差(以6号点为例)
由已知可列出误差方程
(1)
fnal=strcat(p1,f);fpath=p1;
fm=fopen(fnal,'r');
while (~feof(fm))
s=fscanf(fm,'%f',inf)
end
%---------------从文件获取数据----------------------------------------------
switch dh_index
case 1
b=b(:,2:6);
x0=x0(2:6,:);
间接平差 精度评定

Thank you for listening to my class and have a good life
定权,得法方程;
QXˆXˆ
N 1 BB
测量LO平GO差
例2 如下图水准网,(1)求未知点高程平差值及其协 因数;(2)求观测高差平差值的协因数。
解:(1)设C、D点高程为参数,即
Xˆ Xˆ 1 Xˆ 2 T Hˆ C Hˆ D T
参数近似值为:X 0
X
0 1
X
0 2
T
H A h1
二、水准网平差示例
例5-8:如图,A、B是已知的高程点(无误差),C、D、E是 待定点。已知数据与观测数据列于下表。按条件平差求(1)各 待定点的平差高程(2)C至D点间高差平差值的中误差(3)待 定点C、D高程平差值的中误差。
路线号 1
观测高差 (m)
+1.359
路线长度 (km)
1.1
已知高程 (m)
H B h3 T
平差值方程为:
测量LO平GO差
hˆ1 Xˆ 1
HA
hˆ2 Xˆ 1 Xˆ 2
hˆ3
Xˆ 2 H B
误差方程常数项计算:
l1
h1
X
0 1
HA 0
l2
h2
X
0 1
X
0 2
l3 h3
X
0 2
HB
0
误差方程为:v1 xˆ1
v2 xˆ1 xˆ2 l2
v3
xˆ2
令C=4,P1=4/4=1; P2=4/2=2; P3=4/4=1
0
V
BN
1 BB
MATLAB在测量平差中的应用

MATLAB在测量平差中的应用作者:夏浩军来源:《价值工程》2015年第10期摘要:本文采用MATLAB对测量平差中的平差处理进行了应用,并给出了相应的函数程序。
结果证明,MATLAB算法语言及编程简单并具有运算速度快的特点,极大地提升了测量平差数据处理的效率和质量。
Abstract: This paper uses MATLAB for the adjustment processing in measuring adjustment and gives the corresponding function program. The results prove that the MATLAB ALGOL and programming is simple and has the characteristics of fast operation and it has greatly improved the efficiency and quality of the data processing in measuring adjustment.关键词: MATLAB;数据处理;测量误差;测量平差;运算效率Key words: MATLAB;data processing;measurement error;measuring adjustment;operational efficiency0; 引言随着我国信息技术的飞速发展,计算机软件被广泛地应用于测绘领域,并在测绘处理中发挥了十分重要的作用。
为提高测量数据质量,减少测量过程中的误差,观测值的个数要多于确定未知量所必须观测的个数,也就是要进行多余观测。
有了多余观测,必定会在观测结果之间产生矛盾,测量平差的主要目的就在于消除矛盾,从而求得观测量的最可靠结果并评测测量成果的精度。
在所有的测量中,只要有多余观测,就存在平差问题。
而平差计算涉及大量的矩阵运算,不仅计算量大,且运算程序复杂。
条件平差与间接平差的相互关系

条件平差与间接平差的相互关系
一、条件平差与间接平差
1、条件平差与间接平差是指:条件平差是指基础数据是现有被观
测坐标信息,假定各点位置坐标值满足一定近似关系时(即解算中假
定有约束关系或条件,以达到所求结果的平差方法);而间接平差是指,基础数据是待测点的被观测量,包括方位量、距离量等,无任何
关系的前提条件,是一种完全无条件的平差方法。
二、条件平差
2、条件平差一般会把条件设置为两个系统中坐标值的差值最小,
这样就能够更容易地实现平差。
条件平差的典型应用是重叠法平差,
它会利用各观测值之间的内在联系,并通过设定一定的几何条件,使
其之间被观测量满足某一关系,以解决无条件方程组的平差问题。
三、间接平差
3、间接平差是指以被观测量构成的方程组,可以以各种迭代方法
求解,但是必须有一定的条件限制才能使解出的坐标值符合实际要求。
加拿大匹兹堡大学的Bloch教授认为,从下面几个原因考虑起,最好
用间接平差来解决坐标转换的问题:
(1)传统的解算序号很容易引起原点偏移和比例错误;
(2)间接平差可以很好地表示待解系统中的不确定性;
(3)使用间接平差可以很好地降低待解系统中分量精度和消隐关
系统时发生的偏差。
四、条件平差与间接平差的关系
4、条件平差与间接平差是有联系的,相互之间的联系是:可以把
条件平差看做是一种特殊的间接平差,即在无条件间接平差的基础上,再加入解算中的限制条件,以达到所求结果。
可以说,条件平差是间
接平差的分支,而间接平差是条件平差的总集合。
水准网间接平差及可视化程序设计

水准网间接平差及可视化程序设计
段艳慧;葛于祥;张晓莹;郭伟
【期刊名称】《北京测绘》
【年(卷),期】2022(36)4
【摘要】针对测量平差烦琐的矩阵运算问题,本文利用矩阵实验室(matrix laboratory,MATLAB)平台进行水准网平差、精度评价与可视化展示。
由于间接平差误差方程式建立的规律性很强,而条件平差的条件方程式的规律不够明显,本文根据间接平差的原理进行程序设计并进行实例验证,实现了水准网间接平差的程序化及可视化表达,该程序的设计与可视化界面的设计降低了误差出现的概率,极大提高了水准网平差及精度评价的速度和精度,可应用于水准网间接平差的计算中。
【总页数】5页(P488-492)
【作者】段艳慧;葛于祥;张晓莹;郭伟
【作者单位】中国矿业大学(北京)地球科学与测绘工程学院;中国矿业大学环境与测绘学院
【正文语种】中文
【中图分类】P207
【相关文献】
1.粗差探测在水准网平差程序设计中的实现
2.基于Matlab的水准网间接平差程序设计
3.浅议同一水准网条件平差与间接平差处理之异同
4.水准网条件平差粗差检测程序设计方法
5.水准网条件平差粗差检测程序设计方法
因版权原因,仅展示原文概要,查看原文内容请购买。
第五章条件平差

二、法方程及改正数方程
将V T PV min的原则作用于条件方程 。
组成新函数:
V T PV-2k T AV W
式中
r 1
k k a , kb , k r 条件方程联系数
T
对新函数求导: T T 2V P 2A k ---改正数方程
dSCD ˆ f T dL SCD ˆ SCD T 2 T ˆ f D f f QL ˆL ˆ ˆL ˆ f 0 L S CD
得测边相对中误差为: 3、大地四边形测角网
2
ˆS
CD
SCD
=
ˆ 0 f T QL ˆL ˆ f
设
F ( f1 , f 2 , f m )
T T
G ( g1 , g 2 , g m ) 有
均为m维向量函数,且 f i、g i 均为x的函数, d F G dG F T dG T dF F G dx dx dx dx
注意:当N为满秩方阵时,才有 N 1唯一存在,法方程才有唯
测方向网
测角网
测角网
三角网
测边网
测边长
测边+测方向
边角网
(导线网) 测边+测角
三、三角网的布设--从高级到低级逐级布设 四、三角网平差的方法 1。严密平差 ----遵守VTPV=min原则 ; 2。近似平差
5.3 测角网条件平差
独立网(经典自由网)---只有必要起算数据d。
非独立网(附合网)---已知条件超过必要起算数据。
3 图形条件: n=12 t=2×2+4=8 r =4 1 极条件:
v2 v1 v6 v5 v11 v10 W1 0
测量程序设计_条件平差和间接平差

程序代码如下:
disp(‘-------水准网间接平差示例-------------’) disp(‘已知高程’) Ha = 5.015 % 已知点高程,单位m Hb = 6.016 % 已知点高程,单位m
A h2 D h1
C h6 E h7 B h4
h5
h3
disp(‘观测高差,单位m’)
L = [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp(‘系数矩阵B’)
则: PV AT K
V P A K QA K
T
1 T
4、法方程: 将条件方程 AV+W=0代入到改正数方程V=QATK 中,则得到:
AQAT K W 0
r1 r1 r1
记作: 由于
N aa K W 0
rr
R( Naa ) R( AQAT ) R( A) r
Naa为满秩方阵, K Naa1W ( AQAT )1 ( AL A0 )
if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确') else disp(‘检核错误') end disp(‘平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
其中l=L-d.
ˆ 设误差Δ和参数X的估计值分别为V 和 X
则有
ˆ V AX l
X0 为了便于计算,通常给参数估计一个充分接近的近似值
ˆ ˆ X X0 x
则误差方程表示为
matlab常见经典平差程序

matlab常见经典平差程序希望本人编写的经典平差可以对matlab初学者以及测绘专业的学生有用By cowboyfunction void()sprintf('请选择平差类型')sprintf('1: 参数平差\n2: 条件平差\n3:具有条件的参数平差\n4: 具有参数的条件平差\n') a=input('请输入对应号码\n');switch (a)case 1% 参数平差V=AX-Lsprintf('1:参数平差V=AX-L')n=input('请输入n=');t=input('请输入t=');A=input('请输入系数矩阵A=');L=input('请输入常数项矩阵L=');P=diag(input('请输入权阵P='))%P=input('请输入权阵P=');N=A'*P*A;U=A'*P*L;sprintf('开始计算')X=inv(N)*(U);V=A*X-L;Qx=inv(N);u=sqrt((V'*P*V)/(n-t));fid=fopen('data.txt','wt'); %写入文件路径,文件输出fprintf(fid,'=====================参数平差: V=AX-L =====================\n');fprintf(fid,'输出n,t\n') ;fprintf(fid,'%12.5f %12.5f\n',n ,t) ;%n,t fprintf(fid,'输出矩阵A\n')[m,n]=size(A); %Afor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',A(i,j));elsefprintf(fid,'%12.5f\t',A(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵L\n') ;[m,n]=size(L); %Lfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',L(i,j));elsefprintf(fid,'%12.5f\t',L(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵P\n') ;[m,n]=size(P); %P for i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',P(i,j));elsefprintf(fid,'%12.5f\t',P(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵X\n'); [m,n]=size(X); %X for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',X(i,j));elsefprintf(fid,'%12.5f\t',X(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵V\n'); [m,n]=size(V); %V for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',V(i,j));elsefprintf(fid,'%12.5f\t',V(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵Qx\n'); [m,n]=size(Qx); %Qx for i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',Qx(i,j)); elsefprintf(fid,'%12.5f\t',Qx(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出单位权中误差u\n'); [m,n]=size(u); %u for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',u(i,j));elsefprintf(fid,'%12.5f\t',u(i,j));endendendfprintf(fid,'\n');fclose(fid);case 2% 条件平差BV+W=0sprintf('2:条件平差BV+W=0')n=input('请输入n=');t=input('请输入t=');B=input('请输入系数矩阵B=');W=input('请输入自由项向量W='); P=input('请输入权阵P='); sprintf('开始计算')K=-inv((B*inv(P)*B'))*W;V=inv(P)*B'*K;u=sqrt((V'*P*V)/(n-t));Ql=inv(P)-inv(P)*B'*inv(B*inv(P)*B')*B*inv(P);fid=fopen('data.txt','wt'); %写入文件路径,文件输出fprintf(fid,'=====================条件平差: BV+W=0 =====================\n'); fprintf(fid,'输出n,t\n') ;fprintf(fid,'%12.5f %12.5f\n',n ,t) ;%n,tfprintf(fid,'输出矩阵B\n');[m,n]=size(B); %Bfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',B(i,j));elsefprintf(fid,'%12.5f\t',B(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵W\n');[m,n]=size(W); %Wfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',W(i,j));elsefprintf(fid,'%12.5f\t',W(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵P\n'); [m,n]=size(P); %Pfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',P(i,j)); elsefprintf(fid,'%12.5f\t',P(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵V\n'); [m,n]=size(V); %Vfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',V(i,j)); elsefprintf(fid,'%12.5f\t',V(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵Qx\n'); [m,n]=size(Ql); %Ql for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',Ql(i,j));elsefprintf(fid,'%12.5f\t',Ql(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出单位权中误差u\n');[m,n]=size(u); %u for i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',u(i,j));elsefprintf(fid,'%12.5f\t',u(i,j));endendendfprintf(fid,'\n');fclose(fid);case 3% 具有条件的参数平差% 参数平差V=AX-L% 条件平差BX+W=0sprintf('3:具有条件的参数平差V=AX-L;BX+W=0') n=input('请输入n=');t=input('请输入t=');r=input('请输入r=');A=input('请输入误差方程系数矩阵A=');L=input('请输入常数项矩阵L=');B=input('请输入条件方程系数矩阵B=');W=input('请输入自由项向量W=');P=input('请输入权阵P=');sprintf('开始计算')K=-(inv(B*inv(A'*P*A)*B'))*(W+B*inv(A'*P*A)*A'*P*L)X=(inv(A'*P*A))*(B'*K+A'*P*L)N=(A'*P*A)M=B*inv(N)*B'Qx=inv(N)-inv(N)*B'*inv(M)*B*inv(N)u=sqrt((V'*P*V)/(n-t+r))fid=fopen('data.txt','wt'); %写入文件路径,文件输出fprintf(fid,'=====================具有条件的参数平差: V=AX-L;BX+W=0 ===========================\n');fprintf(fid,'输出n,t,r\n') ;fprintf(fid,'%12.5f %12.5f %12.5f\n',n ,t,r); %n,t,rfprintf(fid,'输出矩阵A\n');[m,n]=size(A); %Afor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',A(i,j));elsefprintf(fid,'%12.5f\t',A(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵L\n');[m,n]=size(L); %Lfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',L(i,j)); elsefprintf(fid,'%12.5f\t',L(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵B\n'); [m,n]=size(B); %Bfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',B(i,j)); fprintf(fid,'%12.5f\t',B(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵W\n'); [m,n]=size(W); %W for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',W(i,j)); elsefprintf(fid,'%12.5f\t',W(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵P\n'); [m,n]=size(P); %P for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',P(i,j)); elsefprintf(fid,'%12.5f\t',P(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵X\n'); [m,n]=size(X); %X for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',X(i,j)); elsefprintf(fid,'%12.5f\t',X(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵V\n'); [m,n]=size(V); %Vfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',V(i,j)); elsefprintf(fid,'%12.5f\t',V(i,j));endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵Qx\n'); [m,n]=size(Qx); %Qx for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',Qx(i,j)); elsefprintf(fid,'%12.5f\t',Qx(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出单位权中误差\n'); [m,n]=size(u); %u for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',u(i,j));elsefprintf(fid,'%12.5f\t',u(i,j));endendendfprintf(fid,'\n');fclose(fid);case 4% 具有参数的条件平差% 具有参数的条件方程式BV+AX+W=0sprintf('4:具有参数的条件平差BV+AX+W=0 ')n=input('请输入n=');t=input('请输入t=');r=input('请输入r=');B=input('请输入条件方程中V的系数矩阵B=');A=input('请输入条件方程中X的系数矩阵A=');W=input('请输入条件方程自由向量W=');P=input('请输入权阵P=');sprintf('开始计算')N=(B*inv(P)*B')M=(A'*inv(N)*A)X=-inv(M)*A'*inv(N)*WK=-inv(N)*(A*X+W)V=inv(P)*B'*KQx=inv(M)u=sqrt((V'*P*V)/(r-t))fid=fopen('data.txt','wt'); %写入文件路径,文件输出fprintf(fid,'=====================具有参数的条件平差: BV+AX+W=0 ================================\n');fprintf(fid,'输出n,t,r\n') ;fprintf(fid,'%12.5f %12.5f %12.5f\n',n ,t,r) ; %n,t,rfprintf(fid,'输出矩阵B\n');[m,n]=size(B); %Bfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',B(i,j));elsefprintf(fid,'%12.5f\t',B(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵A\n'); [m,n]=size(A); %Afor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',A(i,j)); elsefprintf(fid,'%12.5f\t',A(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵W\n'); [m,n]=size(W); %Wfor i=1:1:mfor j=1:1:nif j==nfprintf(fid,'%12.5f\n',W(i,j)); elsefprintf(fid,'%12.5f\t',W(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵P\n');[m,n]=size(P); %P for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',P(i,j)); elsefprintf(fid,'%12.5f\t',P(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵X\n'); [m,n]=size(X); %X for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',X(i,j)); elsefprintf(fid,'%12.5f\t',X(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵V\n'); [m,n]=size(V); %V for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',V(i,j)); elsefprintf(fid,'%12.5f\t',V(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出矩阵Qx\n'); [m,n]=size(Qx); %Qx for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',Qx(i,j)); elsefprintf(fid,'%12.5f\t',Qx(i,j)); endendendfprintf(fid,'\n');fprintf(fid,'输出单位权中误差\n'); [m,n]=size(u); %u for i=1:1:m for j=1:1:nif j==nfprintf(fid,'%12.5f\n',u(i,j));elsefprintf(fid,'%12.5f\t',u(i,j));endendendfprintf(fid,'\n');fclose(fid);otherwisedisp('代号输入有误')end。
实验三-利用matlab程序设计语言完成某工程导线网平差计算

实验三利用mat lab程序设计语言完成某工程导线网平差计算实验数据;某工程项目按城市测量规范(CJJ8-99)不设一个二级导线网作为首级平面控制网,主要技术要求为:平均边长200cm,测角中误差±8,导线全长相对闭合差<1/10000,最弱点的点位中误差不得大于5cm,经过测量得到观测数据,设角度为等精度观测值、测角中误差为山=±8秒,鞭长光电测距、测距中误差为m二± Vsmm,根据所学的‘误差理论与测量平差基础'提出一个最佳的平差方案,利用matlab完成该网的严密平差级精度评定计算;平差程序设计思路:1采用间接平差方法,12个点的坐标的平差值作为参数.利用matlab进行坐标反算,求出已知坐标方位角;根据已知图形各观测方向方位角;2计算各待定点的近似坐标,然后反算出近似方位角,近似边. 计算各边坐标方位角改正数系数;3确定角和边的权,角度权Pj=1 ;边长权Ps=100/S;4计算角度和边长的误差方程系数和常数项,列出误差方程系数矩阵 B,算出Nbb=B’ PB,W=B’ Pl,参数改正数 x=inv(Nbb)*W;角度和边长改正数V=Bx-l; 6建立法方程和解算x,计算坐标平差值,精度计算;程序代码以及说明:s10=;s20=;s30=;s40=;s50=;s60=;s70=;s80=;s90=;s100=;s110=;s120=;s130=;s140=; %已知点间距离Xa=;Ya二;Xb=;Yb=;Xc=;Yc=;Xd=;Yd=;Xe=;Ye=;Xf=;Yf=; %已知点坐标值a0=atand((Yb-Ya)/(Xb-Xa))+180;d0=atand((Yd-Yc)/(Xd-Xc));f0=atand((Yf-Ye)/(Xf-Xe))+360; %坐标反算方位角a1=a0+(163+45/60+4/3600)-180a2=a1+(64+58/60+37/3600)-180;a3=a2+(250+18/60+11/3600)-180;a4=a3+(103+57/60+34/3600)-180;a5=d0+(83+8/60+5/3600)+180;a6=a5+(258+54/60+18/3600)-180-360;a7=a6+(249+13/60+17/3600)-180;a8=a7+(207+32/60+34/3600)-180;a9=a8+(169+10/60+30/3600)-180;a10=a9+(98+22/60+4/3600)-180;a12=f0+(111+14/60+23/3600)-180;a13=a12+(79+20/60+18/3600)-180;a14=a13+(268+6/60+4/3600)-180;a15=a14+(180+41/60+18/3600)-180; %推算个点方位角 aa=[a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a12 a13 a14 a15]'X20=Xb+s10*cosd(a1);X30=X20+s20*cosd(a2);X40=X30+s30*cosd(a3);X50a=X40+s40*cosd(a4);X60=Xd+s50*cosd(a5);X70=X60+s60*cosd(a6);X80=X70+s70*cosd(a7);X90=X80+s80*cosd(a8);X100=X90+s90*cosd(a9);X50c=X100+s100*cosd(a10);X130二Xf+s110*cosd(a12);X140=X130+s120*cosd(a13);X150=X140+s130*cosd(a14);X50e=X150+s140*cosd(a15); %各点横坐标近似值X0=[X20 X30 X40 X60 X70 X80 X90 X100 X130 X140 X150 X50a X50c X50e]'Y20=Yb+s10*sind(a1);Y30=Y20+s20*sind(a2);Y40=Y30+s30*sind(a3);Y50a=Y40+s40*sind(a4);Y60=Yd+s50*sind(a5);Y70=Y60+s60*sind(a6);Y80=Y70+s70*sind(a7);Y90=Y80+s80*sind(a8);Y100=Y90+s90*sind(a9);Y50c=Y100+s100*sind(a10);Y130=Yf+s110*sind(a12);Y140=Y130+s120*sind(a13);Y150=Y140+s130*sind(a14);Y50e=Y150+s140*sind(a15); %个点从坐标近似值Y0=[Y20 Y30 Y40 Y60 Y70 Y80 Y90 Y100 Y130 Y140 Y150 Y50a Y50c Y50e]'P=[X0 Y0];X50=(X50a+X50c+X50e)/3Y50=(Y50a+Y50c+Y50e)/3s4二sqrt((Y40-Y50)"2+(X40-X50厂2);si二sqrt((Y100-Y50厂2+(X100-X50厂2);s14二sqrt((Y150-Y50)"2+(X150-X50厂2);A1=[cosd(a1) cosd(a2) cosd(a3) cosd(a4) cos(a5) cosd(a6) cosd(a7) cosd(a8) cosd(a9) cosd(a10) cosd(a12) cosd(a13) cosd(a14) cosd(a15)]';B11=[sind(a1) sind(a2) sind(a3) sind(a4) sin(a5) sind(a6) sind(a7) sind(a8) sind(a9) sind(a10) sind(a12) sind(a13) sind(a14) sind(a15)]';s=blkdiag(s10,s20,s30,s4,s50,s60,s70,s80,s90,s10',s110,s120,s130,s14);a=*inv(s)*B11b=*inv(s)*A1ab4=atand((Y50-Y40)/(X50-X40))+180;ab10=atand((Y50-Y100)/(X50-X100));ab14=atand((Y50-Y150)/(X50-X150))+360;m4=ab4-a3+180;m10=ab10-a9+180;m11=ab4-ab10;m15=ab14-a14+180;m16=ab10-ab14+360;m04=103+57/60+34/3600;m010=98+22/60+4/3600;m011=94+53/60+50/3600;m015=180+41/60+18/3600;m016=ab10-ab14+360;l=[0 0 0 m4-103-57/60-34/3600 0 0 0 0 0 m10-98-22/60-4/3600 m11-94-53/60-50/3600 0 0 0 m15T80-41/60T8/3600m16-103-23/60-8/3600 0 0 0 s40-s4 0 0 0 0 0 s100-s1 0 0 0 s140-s14]';e1=(abs(X20-Xb))/s10;e2=(abs(X30-X20))/s20;e3=(abs(X40-X30))/s30;e4=(abs(X50-X40))/s4;e5=(abs(X60-Xd))/s50;e6= (abs(X70-X60))/s60;e7=(abs(X80-X70))/s70;e8=(abs(X90-X80))/s80;e9=(abs(X100-X90))/s90;e10=(abs(X50-X100))/s1;e11=(abs(X130-Xf))/s110;e12=(abs(X140-X130 ))/s120;e13=(abs(X150-X140))/s130;e14=(abs(X50-X150))/s 14;e=[e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14]' m1=(abs(Y20-Yb))/s10;m2=(abs(Y30-Y20))/s20;m3=(abs(Y40-Y30))/s30;m4=(abs(Y50-Y40))/s4;m5=(abs(Y60-Yd))/s50;m6= (abs(Y70-Y60))/s60;m7=(abs(Y80-Y70))/s70;m8=(abs(Y90-Y80))/s80;m9=(abs(Y100-Y90))/s90;m10=(abs(Y50-Y100))/s1;m11=(abs(Y130-Yf))/s110;m12=(abs(Y140-Y130 ))/s120;m13=(abs(Y150-Y140))/s130;m14=(abs(Y50-Y150))/s 14;m=[m1 m2 m3 m4 m5 m6 m7 m8 m9 m10 m11 m12 m13 m14]' % 以上为求得误差方程系数B=[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0%系数矩阵B0 0 ]P=blkdiag(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,100/s10,100/s 20,100/s30,100/s40,100/s50,100/s60,100/s70,100/s80,100/ s90,100/s100,100/s110,100/s120,100/s130,100/s140); %定义权矩阵Nbb二B'*P*BW=B'*P*l;x=inv(Nbb)*WV=B*x-l;inv(Nbb);Y=V'*P*V;O二sqrt(Y/6)*3600 %精度评定计算结果:平差值坐标X:+003 *Qx1= Qy1= Qx2= Qy2= ……Qx15= Qy15=。
基于Matlab的水准网间接平差程序设计

基于Matlab的水准网间接平差程序设计赵亚红;周文国【摘要】设计水准网数据结构,存储在文本中,按照水准网的起点、终点、观测数据相对应关系建立矩阵,利用Matlab强大的矩阵运算功能,通过间接平差方法,按照最小二乘原理,求得任意水准网的未知点的最或然高程值,对平差结果输出存储,程序直观、简便。
并用实例验证了其正确性及通用性。
%On the basis of data structure designed, the relation of point s and lines of level net, the surveying data and the known data are st ored in the text, the matrixs were set up through the relation of the jupping -off points, end -points and the surveying data. And a program is designed in MATLAB to get the value of most probable by its strong abilty of calculating matrix, the result was output and stored. At last,the example proved the programme was right.【期刊名称】《华北科技学院学报》【年(卷),期】2011(008)003【总页数】3页(P58-60)【关键词】水准网;间接平差;Matlab【作者】赵亚红;周文国【作者单位】华北科技学院土木工程系,北京东燕郊101601;华北科技学院土木工程系,北京东燕郊101601【正文语种】中文【中图分类】P207.2水准网间接平差的的具体过程是:(1)根据水准网形进行分析,列误差方程;(2)根据误差方程系数列法方程;(3)解算法方程,求参数X及V;(4)求最或然值、精度评定。
基于MATLAB的测量平差计算

序。M A T L A B与 其 他 算 法 语 言相 比 , 具有编程简单 、 运 算速 度 快 的 特 点 , 特 别 是 在 矩 阵运 算 方 面 , 在 最 小 二 乘
平 差 中可 以发 挥 很 好 的作 用 , 能 大 大 提 高 工 程 测 量 中 的数 据处 理 效 率 。 关键 词 : 平 差; M A T L A B优 化 箱 ; 附 线 性 不 等 式 约 束
2 0 1 3年第 7 期
中州 煤炭
总第 2 1 1 期
基 于 MAT L A B 的 测 量 平 差 计 算
高 思培 , 陈冠 宇 , 范新 华 , 王 耀鑫 , 王强昆
( 1 , 河 南理 工 大 学 测绘 与 国 土 信 息 工 程 学 院 , 河 南 焦作 2 . 桂林理 工大学 测绘地理信 息学院, 广西 桂林 4 5 4 0 0 0 ; 7 1 0 0 4 3 ) 5 4 1 0 0 6 ; 3 . 机械工业勘察设计研 究院, 陕西 西安
=
( 胎 ) B P 1 , P为 观测 值 的权 阵。
平差值 向量 的协 因数阵 :
Q L L= B( 曰 P Z ) 曰
计 算 软件 , 它 以矩 阵 运算 为基 础 , 把计算 、 绘 图及 动 态 系统 仿真 等功 能有 机 融合在 一起 。MA T L A B将 高 性 能 的数值 和符 号计 算功 能 、 强 大 的绘 图功 能 、 程 序 语 言设 计功 能 以及为 数众 多 的应用 工具 箱集 成在 一
H a= 2 3 7 . 4 8 3 m, 为求 B、 C、 D三点 的高 程 , 进 行 了水
准测 量 , 其结果 见表 1 , 试 按 间 接 平 差 求 定 B、 C 、 D
MATLAB软件在测量平差解算中的应用

3 . 2 用间接平差的方法求解 间接平差误差方程为 : V = Bx - l 法方程为: N bbx- W = 0 观测值改正数 V 为 :
V = - 0. 2427 2. 8552 - 4. 2427 - 0. 1448 - 3. 9021 - 0. 6151 - 1. 1423
观测量或选用独立的参数列方程式, 然后根据最小 二乘法原理平差 , 由最小二乘法原理平差一般会得 到法方程, 法方程的求解即求解线性方程组。如线 性方程组 AX = b, A 为系数矩阵, b 为常数项矩阵 , X 为未知量, 当方程存在唯一解时 , 直接使用矩阵求逆 X = inv(A ) * b, 或采用左除运算 X = A \ b, 其实这两 种方法都是高斯消去法求解 , 只是采用左除运算不 是求逆 , 而是直接进行高斯消去法计算。当然也可 以采用 LU 分解、 QR 分解、 Cho lesky 分解 , 以及 Schur 分解、 H essenberg 分解、 奇异分解等来求解线性方程 组。另外当方程数与未知量数目不等时, 通常不存 在唯一解, 在约束条件下可以得到唯一解。此时在 MATLAB 中 X = P in v (A ) * b, 或采用左除运算 X = A \b会得到最小二乘解。当方程存在无穷多个解的 时 , 如果采用求逆或除法只能得到其中的一个解。
此时在matlab中xmatlab在测量平差解算中的应用如图1所示的水准网中b是已知高程水准点并设这些已知高程点无误差图中b点的高程观测高差和相应的水准路线长度见表水准网观测数据观测号观测高差水准路线长度km已知高程结合测量平差的原理并对观测数据做适当的加工分别用条件平差和间接平差的原理在matlab中实现观测量的平差其代码如下
用MATLAB解决 条件平差和间接平差

C h6 E h3 h5 h7 B h4
disp(‘C是单位权观测高差的线路公里数,S是线路长度’) 是单位权观测高差的线路公里数, 是线路长度 是线路长度’ 是单位权观测高差的线路公里数 C = l*ones(1,6)
S = [1.1, 1.7, 2.3, 2.7, 2.4, 4.0] P = C./S % 定义观测值的权, 定义观测值的权, P = diag(P) % 定义权阵 disp(‘参数的解’) 参数的解’ 参数的解 x = inv(B’*P*B)*B’*P*l disp(‘误差 误差V(mm), 各待定点的高程平差值 (m)’) 各待定点的高程平差值L1( ) 误差 V = B*x - l % 误差方程 误差方程(mm) L1 = L + V/1000 % 观测值的平差值, 观测值的平差值, disp(‘精度评定’) 精度评定’ 精度评定 n = 6; % 观测值的个数 t = 2; % 必要观测数 delta = sqrt(V’*P*V/(n – t))
H(1,1)+H(2,1)-H(3,1)+HAH(2,1)if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确 检核正确') disp( 检核正确') else disp(‘检核错误 检核错误') disp( 检核错误') end disp(‘平差后的高程值 平差后的高程值') disp( 平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
在一个控制网中,设有t个独立参数, 在一个控制网中,设有t个独立参数,将每一个观测值都表达 成所选参数的函数,以此为基础进行平差, 成所选参数的函数,以此为基础进行平差,最终求得参数的估 计值。 计值。 选择参数应做到足数(参数的个数等于必要观测数)和独 选择参数应做到足数(参数的个数等于必要观测数) 参数间不存在函数关系)。 )。利用参数将观测值表示为 立(参数间不存在函数关系)。利用参数将观测值表示为
浅议同一水准网条件平差与间接平差处理之异同

浅议同一水准网条件平差与间接平差处理之异同马自军【摘要】测量平差是据最小二秉法原理,正确地消除各观测值之间的矛盾,合理分配误差,以求出观测值的最或是值并评定测量成果的精度.据不同条件下的测量问题,测量平差的方法也不尽相同.本论述试图以某水准网为例,分别采用条件平差、间接平差对各观测值最或是值进行计算,揭示两种平差方法对同一问题处理过程及结果之异同,以便引导学生在以后的测量工作中针对具体观测条件对平差方法有准确、灵活的选定.【期刊名称】《甘肃科技纵横》【年(卷),期】2011(040)003【总页数】3页(P161-162,181)【关键词】条件平差;间接平差;最或是值【作者】马自军【作者单位】兰州铁路技师学院,甘肃兰州730050【正文语种】中文如图1所示某闭合环水准网,A点是已知高程点:HA=153.768m(假设无误差),各点间的高差观测值分别为:h1=11.105m,h2=-5.728m,h3=-2.090m,h4=-13.215m,h5=16.857m,h6=-3.622m各水准路线长度分别为s1=3.4km,s2=4.0km,s3=3.8km,s4=5.0km,s5=5.3km,s6=5.5km现分别采用条件平差和间接平差计算B、C、D点高程最或是值。
图1 闭合环水准网1 条件平差条件平差是据各观测值改正数应满足的几何条件方程,采用最小二乘法原理消除因多余观测而产生的不符值从而求得各观测值的最或是值的平差方法。
(1)已知:n=6,t=3则r=n-t=3,选定1km观测高差为单位权观测值。
(2)设有:n个观测值为:L1、L 2……L n平差值为:L 1/、L2/ ……L n/相应的权为:P1、P2……Pn条件方程的常数项为:a0、b0……r0观测值的改正数为:v1、v2......vn条件方程的闭合差为:wa、wb……wr则:各条件方程系数=各观测值:条件方程改正数:条件方程闭合差:条件方程常数项:据得条件方程为:(3)依上述各条件方程据:得法方程:据:令则法方程为:NK+W=0由:K=N-1W解得:ka=0.433 kb=-2.336 kc=-1.783(4)通过改正数方程计算各测段高差改正数:由或:vi=1′pi(aika+bikb+cikc)得:v1=10mm v2=-2mm v3=-8mmv4=2mm v5=-12mm v6=-10mm(5)计算各测段高差最或是值:由:hi′=hi+vih1′=h1+v1=+11.115m h2′=h2+v2=-5.730mh3′=h3+v3=-2.098m h4′=h4+v4=-13.213mh5′=h5+v5=+16.845m h6′=h6+v6=-3.632m (6)把各测段高差最或是值hi/分别代人闭合环检核: H1′-h3′+h4′=0H1′-h2′-h5′=0H2′-h3′-h6′=0结论:各测段高差最或是值计算无误。
MATLAB平差程序

function BJPC2ZB=[];ZJ=[];BC=[];%%format long[filename,filepath]=uigetfile('*.txt','选择平差文件:'); name=[filepath filename];fid1=fopen(name,'rt');if(fid1==-1)disp('文件未打开,请重试!');return;endn=fscanf(fid1,'%f',1);%输入边的个数b=fscanf(fid1,'%f',1);%输入多余观测个数E=fscanf(fid1,'%f',1);%输入测角中误差t=fscanf(fid1,'%f',1);%输入坐标个数ZB=fscanf(fid1,'%f',[2 t]);dms1=fscanf(fid1,'%f',[3 n+1]);BC=fscanf(fid1,'%f',[1 n]);T0=fscanf(fid1,'%f',1);T1=fscanf(fid1,'%f',1);fclose(fid1);dms=dms1';ZJ=dms2degrees(dms);%%if t==2T0=T0;%若告诉起始方位角就直接输入endif t==4 %若没有告诉起始方位角由坐标反算Xa=ZB(1,1);Xb=ZB(1,2);Ya=ZB(2,1);Yb=ZB(2,2);Tx=Xb-Xa; Ty=Yb-Ya;T0=atan(Ty/Tx)*180/pi;%对方位角的讨论if ((Tx>0)&&(Ty>0))T0;endif (((Tx<0)&&(Ty>0))||((Tx<0)&&(Ty<0)))T0=T0+180;endif ((Tx>0)&&(Ty<0))T0=T0+360;endif ((Tx==0)&&(Ty>0))T0=90;endif ((Tx==0)&&(Ty<0))T0=270;endif((Ty==0)&&(Tx>0))T0=0;endif ((Ty==0)&&(Tx<0))T0=180;endenda0=T0;x0=ZB(1,t/2);y0=ZB(2,t/2);A=[0,0];FWJ=[];%开始计算近似方位角J=1;while(J<=n+1)belta=ZJ(J);%讨论方位角if J==1a=a0+belta;elsea=a+belta;endif a>=180a=a-180;elsea=a+180;endif a>=360a=a-360;endFWJ(J)=a;J=J+1;endFWJ;%%J=1;%开始计算近似坐标Awhile(J<=n)if J==1A(1,1)=x0+BC(1)*cos(FWJ(1)*pi/180);A(2,1)=y0+BC(1)*sin(FWJ(1)*pi/180);elseA(1,J)=A(1,J-1)+BC(J)*cos(FWJ(J)*pi/180); A(2,J)=A(2,J-1)+BC(J)*sin(FWJ(J)*pi/180);endJ=J+1;endA;%%W=[];%开始计算闭合差if t==2T1=T1;endif t==4Xa=ZB(1,3);Xb=ZB(1,4);Ya=ZB(2,3);Yb=ZB(2,4);Tx=Xb-Xa; Ty=Yb-Ya;T1=atan(Ty/Tx)*180/pi;if ((Tx>0)&&(Ty>0))T1;endif (((Tx<0)&&(Ty>0))||((Tx<0)&&(Ty<0)))T1=T1+180;endif ((Tx>0)&&(Ty<0))T1=T1+360;endif ((Tx==0)&&(Ty>0))T1=90;endif ((Tx==0)&&(Ty<0))T1=270;endif((Ty==0)&&(Tx>0))T1=0;endif ((Ty==0)&&(Tx<0))T1=180;endendW(1,1)=-(FWJ(n+1)-T1)*3600;%以秒为单位W(2,1)=-(A(1,n)-ZB(1,t/2+1))*100;%以厘米为单位W(3,1)=-(A(2,n)-ZB(2,t/2+1))*100;W;%%XS=zeros(3,2*n+1);%开始计算系数阵,XS是系数阵e=n+1;while(e<=2*n+1)XS(1,e)=1;e=e+1;endf=1;while(f<=n)XS(2,f)=cos(FWJ(f)*pi/180);%纵坐标边长改正数的系数 XS(3,f)=sin(FWJ(f)*pi/180);%横坐标边长改正数的系数 f=f+1;endu=1;y0=A(2,n);x0=A(1,n);Y=[];X=[];y1=[];x1=[];while(u<=n+1)if u==1Y(1)=ZB(2,t/2);X(1)=ZB(1,t/2);elseY(u)=A(2,u-1);X(u)=A(1,u-1);endu=u+1;endy1=-1/2062.65*(y0-Y);%纵坐标转角改正数的系数x1=1/2062.65*(x0-X);%横坐标转角改正数的系数y1;x1;d=n+1;z=1;while(d<=2*n+1)XS(2,d)=y1(1,z);XS(3,d)=x1(1,z);d=d+1;z=z+1;endXS;%%r=[];h=1;while (h<=n)s=(5+5*BC(h)/1000)/10;%求中误差厘米为单位r(h)=E^2/s^2;%计算距离的权h=h+1;endaa=[];y=1;while(y<=n)aa(y)=r(y);%将距离的权赋给矩阵aay=y+1;endc=n+1;while(c<=2*n+1)aa(c)=1;%转角的权都是1c=c+1;endP=diag(aa);%形成权阵P;%%Q=inv(P);N=XS*Q*XS';N1=inv(N);K=inv(N)*W;V=Q*XS'*K;V;BC1=BC'+V(1:n)/100;%将改正数加到观测值以求平差边长(除一百统一单位)ZJ1=ZJ+V(n+1:2*n+1)/3600;%同上BC1;i=1;while (i<=n+1)ZJ2(i,1)=fix(ZJ(i));ZJ2(i,2)=fix((ZJ(i)-fix(ZJ(i)))*60);ZJ2(i,3)=((ZJ(i)-fix(ZJ(i)))*60-fix((ZJ(i)-fix(ZJ(i)))*60))*60;i=i+1;endZJ2;%%A1=[0,0];FWJ1=[];J=1;while(J<=n+1)belta=ZJ1(J);if J==1a=a0+belta;elsea=a+belta;endif a>=180a=a-180;elsea=a+180;endif a>=360a=a-360;endFWJ1(J)=a;J=J+1;endi=1;while (i<=n+1)FWJ3(i,1)=fix(FWJ(i));FWJ3(i,2)=fix((FWJ(i)-fix(FWJ(i)))*60);FWJ3(i,3)=((FWJ(i)-fix(FWJ(i)))*60-fix((FWJ(i)-fix(FWJ(i)))*60))*60;FWJ2(i,1)=fix(FWJ1(i));FWJ2(i,2)=fix((FWJ1(i)-fix(FWJ1(i)))*60);FWJ2(i,3)=((FWJ1(i)-fix(FWJ1(i)))*60-fix((FWJ1(i)-fix(FWJ1(i)))*60))*60; i=i+1;endFWJ3;FWJ2;%%J=1;%开始计算平差坐标A1while(J<=n)if J==1A1(1,1)=ZB(1,t/2)+BC1(1)*cos(FWJ1(1)*pi/180);A1(2,1)=ZB(2,t/2)+BC1(1)*sin(FWJ1(1)*pi/180);elseA1(1,J)=A1(1,J-1)+BC1(J)*cos(FWJ1(J)*pi/180);A1(2,J)=A1(2,J-1)+BC1(J)*sin(FWJ1(J)*pi/180);endJ=J+1;endA1;m=sqrt(V'*P*V/b);%测量精度单位权中误差。
用MATLAB解决_条件平差和间接平差(可编辑)

用MATLAB解决_条件平差和间接平差测量程序设计条件平差和间接平差一、条件平差基本原理A LA0函数模型 A VW0r n n 1 r 1r 12 21随机模型D? Q? P0 0TV P Vm i n平差准则条件平差就是在满足r个条件方程式条件下,求使函数V‘PV最小的V值,满足此条件极值问题用拉格朗日乘法可以求出满足条件的V值。
?A LA01、平差值条件方程: 0r n n 1r 1r 1a La L a La01 12 2 n n 0b Lb L b Lb01 12 2 n n 0?r Lr L r Lr01 12 2 n n 0a ,b ,, r i1 , 2 ,, n 条件方程系数i i ia ,b ,, r0 0 0常数项?A LA02、条件方程: 0r n n 1r 1r 1将LLV代入平差值条件方程中,得到A VW0r 1 n 1 r 1 r 1w , w ,, wa b r为条件方程闭合差WA LA闭合差等于观测值减去其应有值。
3、改正数方程:按求函数条件极值的方法引入常数TK k , k ,, ka b rr 1称为联系系数向量,组成新的函数:T T? V P V2 K A VW将Ω对V求一阶导数并令其为零?T T2 V P2 K A0VT1 T TP VA K则: VP A KQ A K4、法方程: 将条件方程 AV+W0代入到改正数方程VQATK 中,则得到:TA Q A KW0N KW0记作: a ar 1 r 1 r 1r rTR N R A Q A R A r由于 a a1 T1K? N W? A Q A A LANaa为满秩方阵,a a 0TLLVVQ A K按条件平差求平差值计算步骤A VW01、列出rn-t个条件方程r 1 n 1 r 1 r 1T1 TN KW0NA Q AA P A2、组成法方程a aa ar 1 r 1 r 1r r1K? N Wa a3、求解联系系数向量4、将 K值代入改正数方程VP-1ATKQATk中,求出V值,并求出平差值LL+V。
基于MATLAB的测量平差数据处理

基于MATLAB的测量平差数据处理摘要MATLAB是目前在研究机构广泛应用的一种数值计算及图形工具软件,它的特点是语法结构简明、数值计算高效、图形功能完备,特别适合非专业编程员完成数值计算、科学试验处理等任务。
以往的测量数据处理方法需要编制特定的处理矩阵运算程序,而且程度复杂,难度大。
本文介绍一种基于MATLAB的水准网和测边网的程序设计方法,与其它算法语言相比,具有编程简单,运算速度快的特点。
文中分别阐述了水准网和测边网程序的理论基础、实现步骤和运行结果。
通过实例的分析,总结出利用MATLAB对测量数据处理有很大的应用价值,它缩短了编程的时间,提高工作效率。
关键词:MATLAB;平差;程序设计ABSTRAC TMATLAB is one species of numerical-values calculation and graphic tools software which is widely used to apply at research institutions at present. The particularities are: concise grammar-structure、highly efficient in numerical values calculating、complete function of graphs、especially it is adapted to evildoing professional programmer to accomplish the tasks that are numerical-values calculating and scientific experiments treating. The ancient methods of measured data-processing need establishing special proceedings of treating matrices operation, moreover, it is complex and greatly difficult.This article introduces one programming method dealing with leveling and measuring edge network based on MATLAB. Compared with other algorithm language, it has particularities which are simply programming and quickly operating. The article separately expatiate the theories basics、realizing steps and running results at leveling and measuring edge network. With the analysis of examples, it has prodigious application value in measured data-processing by use of MATLAB. Moreover, it shortens programming time and improves working effectiveness.Key words:MATLAB;programming绪论作为一名测量技术人员,如果不掌握一门PC机编程语言与便携计算工具,要想提高测量工作的效率几乎寸步难行。
MATLAB 在水准测量平差中的应用1

MATLAB 在水准测量平差中的应用1摘要:文中阐述了水准网从程序设计到实现的整个过程。
通过实例可看出,利用MATLAB对测量数据处理不仅可以缩短了编程的时间,还可以提高工作效率。
关键词:测量平差;水准网;程序设计Matlab Application In Leveling AdjustmentWang QinMinnan University of Science and Technology,Depart. of Civil Engineering,Quanzhou 362700,ChinaAbstract:The article separately expatiate the theories basics、realizing steps and running results at leveling. With the analysis of examples,it has prodigious application value in measured data-processing by use of MATLAB. Moreover,it shortens programming time and improves working effectiveness.Key words:MATLAB;leveling network;programming0 引言测量平差数据处理主要是基于矩阵的运算。
在MATLAB环境中,不需要对创建的变量对象给出类型说明和维数,它是一种程序化和解释性相结合的编程语言,不仅使程序容易调试、计算更为简捷,而且使平差原理理解和掌握变得更容易,这些优点都依托于它是逐行解释运行程序。
再有,MATLAB语言容易掌握和理解,这一点与数学语言相类似。
1 测量平差原理的概述根据所选参数的个数,对于一个实际平差问题,附有条件的间接平差模型本身实际上就是各种经典平差模型的概括模型,这一点经过仔细推敲可以发现,其余的经典平差模型都是它的特例。
Matlab软件在测绘平差计算中的应用

Matlab软件在测绘平差计算中的应用摘要:测绘平差计算主要是矩阵运算,矩阵运算主要包括矩阵的转置、求逆等。
而在Matlab软件中创建变量对象不需要给出具体类型说明和维数,程序计算简捷,容易调试,能更容易地理解和掌握测量原理。
关键词:Matlab;平差计算1、Matlab软件简介Matla是一款集数值计算、数据分析与可视化、动态仿真、文字图像处理等功能于一体的软件。
它执行数据操作的基本单位是矩阵,在Matlab中矩阵的生成、运算、转置、求逆等计算非常容易,此外它的统计工具箱功能非常强大,可以方便快速地进行数据统计和处理。
2、Matlab在测绘中的应用在测量数据平差处理中,最常见的问题是解线性方程组AX+L=0,式中A为系数矩阵,L为常数项矩阵,X为待求未知数。
当存在解时,有高斯消去法、LU分解法或直接使用矩阵求逆,其解可写为X=A-1L。
当A不是方阵,通常不存在唯一解,在Matlab中此时会给出最小二乘解。
“\”表示左算子,“Aorkest.txt’,’r’);可以用Matlab绘制出均方差为σ=1的正态分布概率密度函数的误差分布曲线,具体操作为:x=-2:0.1:2y=normpdf(x,0,1)holdonplot(x,y,’b’)holdoff显示的误差分布曲线如下图所示:从文中的算例可以看出,测量的计算问题用Matlab软件处理可以从繁琐的数值计算中解脱出来,简单明了便于检查。
Matlab软件的使用有利于专业知识与软件应用相结合。
因其强大的矩阵计算、简洁的程序编写方法等特点,使Matlab软件非常适合测量平差的计算,可以达到事半功倍的效果。
参考文献:[1]武汉大学测量平差教研室.测量平差基础:3版[M].北京:测绘出版社,2006.[2]孙祥,徐流美,吴清.Matlab基础教程[M].北京:清华大学出版社,2005.[3]陈杰,Matlab宝典[M].电子工业出版社,2011.[4]聂桂根,Matlab在测量数据处理中的应用[J].测绘通报,2001.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用MATLAB解决_条件平差和间接平差
测量程序设计
条件平差和间接平差一、条件平差基本原理A LA0
函数模型 A VW0
r n n 1 r 1
r 1
2 21
随机模型
D? Q? P
0 0
T
V P Vm i n
平差准则条件平差就是在满足r个条件方程式条件下,求
使函数V‘PV最小的V值,满足此条件极值问题用
拉格朗日乘法可以求出满足条件的V值。
?
A LA0
1、平差值条件方程: 0
r n n 1
r 1
r 1
a La L a La0
1 1
2 2 n n 0
b Lb L b Lb0
1 1
2 2 n n 0?
r Lr L r Lr0
1 1
2 2 n n 0
a ,
b ,, r i1 , 2 ,, n 条件方程系数
i i i
a ,
b ,, r
0 0 0
常数项?
A LA0
2、条件方程: 0
r n n 1
r 1
r 1将
LLV
代入平差值条件方程中,得到A VW0
r 1 n 1 r 1 r 1
w , w ,, w
a b r
为条件方程闭合差
WA LA
闭合差等于观测值减去其应有值。
3、改正数方程:
按求函数条件极值的方法引入常数
T
K k , k ,, k
a b r
r 1
称为联系系数向量,组成新的函数:
T T? V P V2 K A VW
将Ω对V求一阶导数并令其为零?
T T2 V P2 K A0V
T1 T T
P VA K
则: VP A KQ A K4、法方程: 将条件方程 AV+W0代入到改正数方程VQATK 中,则得到:
T
A Q A KW0
N KW0
记作: a a
r 1 r 1 r 1
r r
T
R N R A Q A R A r
由于 a a1 T1
K? N W? A Q A A LA
Naa为满秩方阵,
a a 0
TLLV
VQ A K按条件平差求平差值计算步骤
A VW0
1、列出rn-t个条件方程
r 1 n 1 r 1 r 1
T1 T
N KW0
NA Q AA P A
2、组成法方程
a a
a a
r 1 r 1 r 1
r r1
K? N W
a a
3、求解联系系数向量
4、将 K值代入改正数方程VP-1ATKQATk中,求
出V值,并求出平差值LL+V。
5、检核。
例《误差理论与测量平差基础》P74
设对下图中的三个内角作同精度观测,得观测值:
o o o
L 42 12’20’’,L 78 09’09’’,L 59 38’40’’,试按条1 2 3
件平差求三个内角得平差值。
clc
Disp‘条件平差示例2’
Disp‘三角形内角观测值’
L1 [42 12 20]
L2 [78 9 9]
L3 [59 38 40]
L [L1; L2; L3]
Disp‘将角度单位由度分秒转换为弧度’
LL dms2radmat2dmsLL1 L + V
A [1 1 1]
LL
w sumLL: - pi
dms2radmat2dmsL1
w dms2matrad2dmsw
sumLL sumLL
P eye3;
ifsumLL pi disp‘检核正确’
Naa A*invP*A'
else
Ka -invNaa*w disp‘检核错误’
end
V A'*Ka例《误差理论与测量平差基础》P75
在下图中,A、B为已知水准点,其高程为
HA12.013m, HB 10.013m, 可视为无误差。
为了确定点C及D点的高程,共观测了四个高差,高差观测值及相应的水准路线的距离为:
h1 -1.004m, S1 2km;
h2 1.516m, S2 1km;
h3 2.512m, S3 2km;
h4 1.520m, S4 1.5km
试求C和D点高程的平差值。
clc
clear
A [1 1 -1 0; 0 1 0
h1 -1.004;
-1]
h2 1.516;
w1 h1 + h2 - h3 +
h3 2.512;
HA - HB;
h4 1.520;
w2 h2 - h4;
HA 12.013
w [w1; w2]
HB 10.013
P diag1./s
h [h1 h2 h3 h4]'
Naa A*invP*A'
s1 2;
Ka -invNaa*w
s2 1;
V invP*A'*Ka
s3 2;
s4 1.5;
H h + V;
s [s1 s2 s3 s4]'
if H1,1+H2,1-H3,1+HA-HB0 && H2,1-
H4,10 disp‘检核正确'
else disp‘检核错误'
end
disp‘平差后的高程值'
HC HA + H1,1
HD HA + H1,1 + H4,1二、间接平差的基本原理
在一个控制网中,设有t个独立参数,将每一个观测值都表达成所选参数的函数,以此为基础进行平差,最终求得参数的估计值。
选择参数应做到足数(参数的个数等于必要观测数)和独
立(参数间不存在函数关系)。
利用参数将观测值表示为
~
L A Xd
其中L为观测值,Δ为误差,或者表示为
~? A Xl
其中l=L-dX
设误差Δ和参数X的估计值分别为V 和
则有VA Xl
X
为了便于计算,通常给参数估计一个充分接近的近似值
0?
则误差方程表示为VA xl
其中常数项为
lL A Xd 由最小二乘准则,所求参数的改正数应该满足T
V P Vm i n
目标函数对x求一阶导数,并令其为零
T
d V P V dV
T T2 V P2 V P A0?
d x d x
T
A P V0
转置后得到
把误差方程代入上式后得到
T TA P A xA P l0T T
设 NA P A UA P l
A
则法方程为N xU0
A
由此求得参数改正数的唯一解为1xN U
将其代入误差方程,可求得改正数V,最后得到观测值得平差值及参数的平差值分别为LLV
0?
XXx精度评定
计算单位权中误差的公式为
T
V P V0
nt
按误差传播定律得参数的权逆阵为1
Nx x A
X X
参数的中误差为 Q?
X 0
j X X
j j设参数的函数为Ff X , X ,, X
1 2 t
0以代入,并按泰勒级数展开,取一次项XXx
Fff x f x
0 1 1 t t
记为
T? f x f xf x1 1 t t
F
由此得到参数函数的权逆阵为
T T1
Qf Q ff N fA
F F X X中误差为 Q
F F F
改正数为1 TVA xl A N A PI l
A1 T
A N A
V V A
平差值及其协因数阵分别为LLV1 T
QA N A?
L L L V V L V V A
L L二、水准网间接平差程序设计
例教材P124,
A和B是已知高程的水准点,
并设这些点已知高程无误差,
C、D、E是待定点,A、B高程、
观测高差和相应的水准路线
长度见下表,试按间接平差
求各待定点的高程平差值;线路编号观测高差线路长度已知高程
( m ) ( km ) (m )
1 + 13 5 9 11 H A 50 1 6
2 + 20 0 9 17 H B 60 1 6
3 + 03 6 3 23
4 + 10 1 2 27
5 + 0
6 5
7 24
6 + 02 3 8 14
7 - 05 9 5 26程序代码如下:
disp‘-------水准网间接平差示例-------------’disp‘已知高程’
Ha 5.015 % 已知点高程,单位m
Hb 6.016 % 已知点高程,单位m
disp‘观测高差,单位m’
L [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp‘系数矩阵B’
B [1 0; 0 1; 1 0; 0 1; -1 1; -1 0]
l [0; 0; 4; 3; 7; 2]
disp‘C是单位权观测高差的线路公里数,S是线路长度’C l*ones1,6。
