材料科学基础 chp8三元相图PPT课件
合集下载
三元相图ppt

三元相图的分析技巧
相态的分析
确定三元相图的三个相态
根据三元相图中的三个区域,可以确定三元相图的三个相态,即液相、固相和气 相。
确定相态之间的转化
三元相图中不同相态之间的转化与成分和温度有关,可以根据相图中的成分和温 度范围确定不同相态之间的转化条件。
结晶过程的分析
分析结晶过程
三元相图中的结晶过程分析需要了解不同成分的溶液中结晶 过程的特点,以及结晶过程中成分的变化规律。
材料科学的基础研究
三元相图的研究也是材料科学基础研 究的重要组成部分。通过对三元相图 的深入研究,可以更好地理解物质的 本质和规律,为材料科学的其他领域 提供基础支撑。
THANKS
谢谢您的观看
新型材料的探索
研究者们通过实验探索新型材料的三元相图,以寻找具有更优性能的相变材料, 应用于能源、环保等领域。
理论研究进展
计算方法的改进
研究者们不断改进计算方法,以更准确地预测三元相图中的 相行为。
分子动力学模拟
利用分子动力学模拟技术,研究者们可以模拟真实材料的三 元相图,为理论预测提供更为准确的依据。
多晶型和同素异构体的存在
在某些三元体系中,可能存在多种晶型和同素异构体,这些不同结构的物质在物理和化学 性能上可能存在显著的差异,因此如何考虑这些差异对三元相图的影响也是一个重要的问 题。
三元相图未来研究方向的建议
加强实验研究
由于三元相图的复杂性,实验研究仍然是确定三元相图最准确的方法。因此,需要发展新的实验技术,提高实验的精度和效 率,同时需要建立更加完善的数据库和理论模型来描述和预测三元相图。
应用研究进展
能源储存与运输
研究者们正在研究如何利用三元相图优化能源储存与运输过程中的性能。例 如,优化相变材料在储存和运输过程中的热力学性质。
相态的分析
确定三元相图的三个相态
根据三元相图中的三个区域,可以确定三元相图的三个相态,即液相、固相和气 相。
确定相态之间的转化
三元相图中不同相态之间的转化与成分和温度有关,可以根据相图中的成分和温 度范围确定不同相态之间的转化条件。
结晶过程的分析
分析结晶过程
三元相图中的结晶过程分析需要了解不同成分的溶液中结晶 过程的特点,以及结晶过程中成分的变化规律。
材料科学的基础研究
三元相图的研究也是材料科学基础研 究的重要组成部分。通过对三元相图 的深入研究,可以更好地理解物质的 本质和规律,为材料科学的其他领域 提供基础支撑。
THANKS
谢谢您的观看
新型材料的探索
研究者们通过实验探索新型材料的三元相图,以寻找具有更优性能的相变材料, 应用于能源、环保等领域。
理论研究进展
计算方法的改进
研究者们不断改进计算方法,以更准确地预测三元相图中的 相行为。
分子动力学模拟
利用分子动力学模拟技术,研究者们可以模拟真实材料的三 元相图,为理论预测提供更为准确的依据。
多晶型和同素异构体的存在
在某些三元体系中,可能存在多种晶型和同素异构体,这些不同结构的物质在物理和化学 性能上可能存在显著的差异,因此如何考虑这些差异对三元相图的影响也是一个重要的问 题。
三元相图未来研究方向的建议
加强实验研究
由于三元相图的复杂性,实验研究仍然是确定三元相图最准确的方法。因此,需要发展新的实验技术,提高实验的精度和效 率,同时需要建立更加完善的数据库和理论模型来描述和预测三元相图。
应用研究进展
能源储存与运输
研究者们正在研究如何利用三元相图优化能源储存与运输过程中的性能。例 如,优化相变材料在储存和运输过程中的热力学性质。
材料科学基础三元相图PPT课件

代表的两组元的比值恒定。
17
与某一边平行的直线
B
含对角组元浓度相等
B%
C%
P
Q
A
← A%
C
18
过某一顶点作直线
A% C a1 Ba '1 Ba '2 C a2 常 数 C % Bc1 Bc1 Bc2 Bc2
B
a1′ a2′
c1
c2 E
F
C%
B%
A
← A% D a2 a1 C
19
课堂练习
↑
N
B%
A
C%→
13
14
3 成分三角形中特殊的点和线 (1)三个顶点:代表三个纯组元; (2)三个边上的点:二元系合金的成分点;
15
II 点:40%A- 0%B- 60%C 90
III 点:20%A- 20%B- 60%C IV点:20%A- 50%B- 30%C 80
70
60 B% 50
B
10
还有偏共晶、共析、包析、包共析转变等。
22
5 共线法则与杠杆定律 (1)共线法则:在一定温度下,三元合金两相平衡时,合
金的成分点和两个平衡相的成分点必然位 于成分三角形内的同一条直线上。 (由相率可知,此时系统有一个自由度,表示一个相的成 分可以独立改变,另一相的成分随之改变。) (2)杠杆定律:用法与二元相同。
26
二元匀晶相图
液相线 固相线
T (℃)
单相区 双相区
L
L +
A
B
27
三元匀晶相图
70 60 B% 50 40
30
20
10
10
20
30
40
II
17
与某一边平行的直线
B
含对角组元浓度相等
B%
C%
P
Q
A
← A%
C
18
过某一顶点作直线
A% C a1 Ba '1 Ba '2 C a2 常 数 C % Bc1 Bc1 Bc2 Bc2
B
a1′ a2′
c1
c2 E
F
C%
B%
A
← A% D a2 a1 C
19
课堂练习
↑
N
B%
A
C%→
13
14
3 成分三角形中特殊的点和线 (1)三个顶点:代表三个纯组元; (2)三个边上的点:二元系合金的成分点;
15
II 点:40%A- 0%B- 60%C 90
III 点:20%A- 20%B- 60%C IV点:20%A- 50%B- 30%C 80
70
60 B% 50
B
10
还有偏共晶、共析、包析、包共析转变等。
22
5 共线法则与杠杆定律 (1)共线法则:在一定温度下,三元合金两相平衡时,合
金的成分点和两个平衡相的成分点必然位 于成分三角形内的同一条直线上。 (由相率可知,此时系统有一个自由度,表示一个相的成 分可以独立改变,另一相的成分随之改变。) (2)杠杆定律:用法与二元相同。
26
二元匀晶相图
液相线 固相线
T (℃)
单相区 双相区
L
L +
A
B
27
三元匀晶相图
70 60 B% 50 40
30
20
10
10
20
30
40
II
三元相图分析 ppt课件

单相区与之点接 (水平截面与棱边的交点,表 示三个平衡相成分。)
相率相区的相数差1; 相区接触法则: 单相区/两相区曲线相接;
两相区/三相区直线相接。
三元相图分析 22
三元相图分析 23
合金结晶过程分析; (4)投影图 相组成物相对量计算(杠杆定律、重心定律)
组织组成物相对量计算(杠杆定律、重心定律)
三元相图分析 8
6.2.2 重心定律 在一定温度下,三元合金三相平衡时,合金的成分点为三
个平衡相的成分点组成的三角形的质量重心。(由相率可知, 此时系统有一个自由度,温度一定时,三个平衡相的成分是 确定的。)
平衡相含量的计算:所计算相的成分点、合金成分点和二 者连线的延长线与对边的交点组成一个杠杆。合金成分点为 支点。计算方法同杠杆定律。
三元相图分析 13
6.4 三元共晶相图
6.4.1 组元在固态互不溶,具有共晶转变的相图 1. 相图分析 点:熔点;二元共晶点;三元共晶点。
三元相图分析 14
面: 区:
液相面 固相面 两相共晶面 三相共晶面 两相区:3个 单相区:4个 三相区:4个 四相区:1个
三元相图分析 15
三元相图分析
❖ 投影图
三元相图分析
三元相图的主要特点 (1)是立体图形,主要由曲面构成; (2)可发生四相平衡转变; (3)一、二、三相区为一空间。
三元相图分析 3
6.1三元相图的成分表示法 6.1.1 浓度三角形(等边、等腰、直角三角形) (1)已知点确定成分; (2)已知成分确定点。
等边浓度三角形
三元相图分析 4
三元相图分析 28
6.6 具有化合物的三元相图及三元相图的简化分割
三元相图分析 29
❖ 6.7 三元合金相图应用举例 6.7.1
相率相区的相数差1; 相区接触法则: 单相区/两相区曲线相接;
两相区/三相区直线相接。
三元相图分析 22
三元相图分析 23
合金结晶过程分析; (4)投影图 相组成物相对量计算(杠杆定律、重心定律)
组织组成物相对量计算(杠杆定律、重心定律)
三元相图分析 8
6.2.2 重心定律 在一定温度下,三元合金三相平衡时,合金的成分点为三
个平衡相的成分点组成的三角形的质量重心。(由相率可知, 此时系统有一个自由度,温度一定时,三个平衡相的成分是 确定的。)
平衡相含量的计算:所计算相的成分点、合金成分点和二 者连线的延长线与对边的交点组成一个杠杆。合金成分点为 支点。计算方法同杠杆定律。
三元相图分析 13
6.4 三元共晶相图
6.4.1 组元在固态互不溶,具有共晶转变的相图 1. 相图分析 点:熔点;二元共晶点;三元共晶点。
三元相图分析 14
面: 区:
液相面 固相面 两相共晶面 三相共晶面 两相区:3个 单相区:4个 三相区:4个 四相区:1个
三元相图分析 15
三元相图分析
❖ 投影图
三元相图分析
三元相图的主要特点 (1)是立体图形,主要由曲面构成; (2)可发生四相平衡转变; (3)一、二、三相区为一空间。
三元相图分析 3
6.1三元相图的成分表示法 6.1.1 浓度三角形(等边、等腰、直角三角形) (1)已知点确定成分; (2)已知成分确定点。
等边浓度三角形
三元相图分析 4
三元相图分析 28
6.6 具有化合物的三元相图及三元相图的简化分割
三元相图分析 29
❖ 6.7 三元合金相图应用举例 6.7.1
材料科学基础第八章 三元相图

材料科学基础 第八章 三元相图
1
本章章节结构 8.1 三元相图基础 8.2 固态互不溶解的三元共晶相图 8.3 固态有限互溶的三元共晶相图
2
内容预报
• 三元相图基础 • 三元相图有很多面
水平、垂直截面图 • 由平面回溯立体
3
8.1 三元相图基础
8.1.1 成分表示方法 1.成分三角形 2.成分三角形中的特殊线 3.杠杆定律及重心定律
49
典型合金的平衡结晶过程-3
3. 位于三相平衡共晶转变终了面及双析溶解度曲面 投影内的合金(图8.19中Ⅴ区)。 结晶过程:L→L+α初→α初+(α+β)共→α初+ (α+β)共+γⅡ
50
典型合金的平衡结晶过程-4
4. 位于三相平衡共晶转变终了面但不在双析溶解度 曲面投影内的合金Ⅳ(图8.19中)。 结晶过程:L→L+α初→α初+(α+β)共 可用同 样的方法分析其它合金的结晶过程,图8.19中所 标注的六个区域。
• 在垂直截面图中发生两相共晶转变的三相区为尖 点向上的曲边三角形。
43
投影图
44
45
相区接触法则
• 空间相图、水平截面、垂直截面相图。 • 相邻相区的相数差1; • 立体相图中在面两侧判断,截面图中在线两侧判
断; • 除截到的零变量点外,所有的点均有四条相界线
相交。
46
8.1 三元相图基础 8.2 固态互不溶解的三元共晶相图
B% 50
10
20
30
40 C%
50
40 30 20
AxC4x-B
60
70 80
10
90
A
90 80 70
1
本章章节结构 8.1 三元相图基础 8.2 固态互不溶解的三元共晶相图 8.3 固态有限互溶的三元共晶相图
2
内容预报
• 三元相图基础 • 三元相图有很多面
水平、垂直截面图 • 由平面回溯立体
3
8.1 三元相图基础
8.1.1 成分表示方法 1.成分三角形 2.成分三角形中的特殊线 3.杠杆定律及重心定律
49
典型合金的平衡结晶过程-3
3. 位于三相平衡共晶转变终了面及双析溶解度曲面 投影内的合金(图8.19中Ⅴ区)。 结晶过程:L→L+α初→α初+(α+β)共→α初+ (α+β)共+γⅡ
50
典型合金的平衡结晶过程-4
4. 位于三相平衡共晶转变终了面但不在双析溶解度 曲面投影内的合金Ⅳ(图8.19中)。 结晶过程:L→L+α初→α初+(α+β)共 可用同 样的方法分析其它合金的结晶过程,图8.19中所 标注的六个区域。
• 在垂直截面图中发生两相共晶转变的三相区为尖 点向上的曲边三角形。
43
投影图
44
45
相区接触法则
• 空间相图、水平截面、垂直截面相图。 • 相邻相区的相数差1; • 立体相图中在面两侧判断,截面图中在线两侧判
断; • 除截到的零变量点外,所有的点均有四条相界线
相交。
46
8.1 三元相图基础 8.2 固态互不溶解的三元共晶相图
B% 50
10
20
30
40 C%
50
40 30 20
AxC4x-B
60
70 80
10
90
A
90 80 70
材料科学基础三元相图ppt

• 3)判断无变点性质: 15个无变 量点。
• 4)副三角形:有多少无变点就 对应多少副三角形。
• 5)观察相图中是否存在晶型转 变、液相分层或固溶体等。
• 水泥的矿物组成(wt%):
• C3S:40~60%;C2S:15~30%;C3A:6~12%; C4AF:10~16%
• 根据△规则,配料点落在何副△内,最后析晶产物便为这 个副△顶点所表示的晶相。可知,配料点在△C3S-C2S -C3A浓度△内
M
W D
3.MgO-Al2O3-SiO2 系统
4. Na2O-CaO-SiO2 系统
实际生产过程:
• 配料
• 水泥的配料组成(化学组成wt%):
• 原料: 石灰石
粘土
Fe粉
成份 CaO Al2O3 SiO2 Fe2O3
wt% 60~67 5~7 20~24 4~6
在 CaO-Al2O3-SiO2系统中,各种重 要的硅酸盐制品的组成区
• 2. K2O-Al2O3-SiO2 系统
Q
线规则 • 三、判断界线性质——切线规则 • 四、划分副三角形 • 五、标出并确定三元无变量点的性质(刚达到该点
时各相是多少)——重心原理 • 六、冷却(或加热)过程分析(M点析晶性质,过
程)——三角形规则、初晶区规则 • 七、过程量计算(确定析晶结束时各晶体相对数
量)——杠杆规则
• 1. CaO-Al2O3-SiO2 系统
• 1)判断化合物的性质:
共有十个二元化合物、二个三 元化合物。
一致熔融二元化合物: CS、 C2S、 C12A7、A3S2。
• 不一致熔融二元化合物: C3S2 、C3S、C3A、CA、 CA2、CA6
• 一致熔融三元化合物:CAS2、 C2AS。
• 4)副三角形:有多少无变点就 对应多少副三角形。
• 5)观察相图中是否存在晶型转 变、液相分层或固溶体等。
• 水泥的矿物组成(wt%):
• C3S:40~60%;C2S:15~30%;C3A:6~12%; C4AF:10~16%
• 根据△规则,配料点落在何副△内,最后析晶产物便为这 个副△顶点所表示的晶相。可知,配料点在△C3S-C2S -C3A浓度△内
M
W D
3.MgO-Al2O3-SiO2 系统
4. Na2O-CaO-SiO2 系统
实际生产过程:
• 配料
• 水泥的配料组成(化学组成wt%):
• 原料: 石灰石
粘土
Fe粉
成份 CaO Al2O3 SiO2 Fe2O3
wt% 60~67 5~7 20~24 4~6
在 CaO-Al2O3-SiO2系统中,各种重 要的硅酸盐制品的组成区
• 2. K2O-Al2O3-SiO2 系统
Q
线规则 • 三、判断界线性质——切线规则 • 四、划分副三角形 • 五、标出并确定三元无变量点的性质(刚达到该点
时各相是多少)——重心原理 • 六、冷却(或加热)过程分析(M点析晶性质,过
程)——三角形规则、初晶区规则 • 七、过程量计算(确定析晶结束时各晶体相对数
量)——杠杆规则
• 1. CaO-Al2O3-SiO2 系统
• 1)判断化合物的性质:
共有十个二元化合物、二个三 元化合物。
一致熔融二元化合物: CS、 C2S、 C12A7、A3S2。
• 不一致熔融二元化合物: C3S2 、C3S、C3A、CA、 CA2、CA6
• 一致熔融三元化合物:CAS2、 C2AS。
第8章三元相图课件

可以利用垂直截面图分析合金的结晶过程和相变临界温度,及结晶所 得组成物。但在利用垂直截面图时,不能分析相变过程中相的成分变化, 也不能利用直线法则(或杠杆定律)计算相和组织的相对量。在垂直截面图 上,不能套用二元相图中的相接触法则。 在垂直截面图中发生两相共晶转变的三相区为尖点向上的曲边三角 形,且向上的顶点与反应相L相区相接,在下方的另两个顶点与生成相的 相区相接。这时两相共晶转变三相区的基本特征之一。
7.绘出A / C =1/4的 ↗ 60 B% 50 合金
40 30 20 10 A
3. 直线法则与重心法则
1)直线法则
—— 适用于两相平衡的情况 投影到任何一边上,按二 元杠杆定律计算
↗ B%
B
C% ↘
fg f ' g ' Rβ Wα = = = ef e' f ' αR Wβ
e’ A
g’ f’ α e R f
A
E
B
C3 C2
C1
L⇔A+C
C L⇔B +C
两相共晶面和液固三相区
TA TB A3 E1 A2 A1 E3 TC E2 B3 B2 B1
A
E
B
A+B+C
C3 C2
L⇔A+B +C
C1
C
TA E1
TB
L⇔B
E2
L⇔A
E1
E E3 E TA E TB A3 E1 A2 A1 E3 TC E2 B3 B2 B1 E3 TC E2
L⇔C
A
E
B
C3 C2
C1
C
曲面的立体图
E1
液 相 面
E2 E3
材料科学基础-第7章-三元相图ppt课件

材料科学基础-第7章-三元相 图
1
7.8 三元合金相图
7.8.1三元合金相图的成分表示方法 7.8.2三元系平衡相的定量法则 . 7.8.3三元匀晶相图 7.8.4三元共晶相图 7.8.5两相平衡、三相平衡和四相平衡的 类型和一般规律 7.8.6三元相图应用举例
2
2
7.8.1三元合金相图的成分表示方法
A% Ca1 Ba '1 Ba '2 Ca2 常数 C % Bc1 Bc1 Bc 2 Bc 2
a2 ′
a1 ′
c1 c2 E F C%
B% A
8
← A%
D a2 a1
8
C
7.8.2 三元系平衡相的定量法则
1.直线法则和杠杆定律(适用于两相平衡)
在一定温度下三组元材料两相平衡时,材料的 成分点和其两个平衡相的成分点必然位于成分 三角形内的一条直线上,该规律称为直线法则 或三点共线原则。
1.成分三角形(浓度三角形)
等边成分三角形
等腰成分三角形
直角成分三角形
3
3
7.8.1三元合金相图的成分表示方法
(1)已知点确定成分
过O作平行于BC边的直线 求平行线与A坐标的截距 得组元A的含量XA。 同理求组元B、C的含量 XB、 XC。
B% C% B
O
XA+XB+X24
7.8.4 三元共晶相图 应用:
可确定合金在该温度下的相组成; 可运用杠杆定律和重心法则确定合金中各相 的成分及其含量。
25
25
7.8.4三元共晶相图
2.垂直截面与投影图 b1 O点合金室温相组成物: A+B+C
c1
(1)投影图
1
7.8 三元合金相图
7.8.1三元合金相图的成分表示方法 7.8.2三元系平衡相的定量法则 . 7.8.3三元匀晶相图 7.8.4三元共晶相图 7.8.5两相平衡、三相平衡和四相平衡的 类型和一般规律 7.8.6三元相图应用举例
2
2
7.8.1三元合金相图的成分表示方法
A% Ca1 Ba '1 Ba '2 Ca2 常数 C % Bc1 Bc1 Bc 2 Bc 2
a2 ′
a1 ′
c1 c2 E F C%
B% A
8
← A%
D a2 a1
8
C
7.8.2 三元系平衡相的定量法则
1.直线法则和杠杆定律(适用于两相平衡)
在一定温度下三组元材料两相平衡时,材料的 成分点和其两个平衡相的成分点必然位于成分 三角形内的一条直线上,该规律称为直线法则 或三点共线原则。
1.成分三角形(浓度三角形)
等边成分三角形
等腰成分三角形
直角成分三角形
3
3
7.8.1三元合金相图的成分表示方法
(1)已知点确定成分
过O作平行于BC边的直线 求平行线与A坐标的截距 得组元A的含量XA。 同理求组元B、C的含量 XB、 XC。
B% C% B
O
XA+XB+X24
7.8.4 三元共晶相图 应用:
可确定合金在该温度下的相组成; 可运用杠杆定律和重心法则确定合金中各相 的成分及其含量。
25
25
7.8.4三元共晶相图
2.垂直截面与投影图 b1 O点合金室温相组成物: A+B+C
c1
(1)投影图
材料科学基础――三元合金相图PPT课件
26
2 重心定律
适用于三相平衡的情况
w%W WR
Rf10% 0 cf
B%
a
A
B
fb d
R e
c
C%
← A% C
27
但是,作图求三相平衡不够准确而产生误差, 用代数法求解,可避免误差。已知条件: ✓R合金中A,B,C组元含量为xR,yR,zR ✓α相中A,B,C组元含量为xα,yα,zα ✓β相中A,B,C组元含量为xβ,yβ,zβ ✓γ相中A,B,C组元含量为xγ,yγ,zγ
24
杠杆定律
W L+W =W 0 W L X X rb W 0 X X L ab W X X L ar W 0 X X L ab
L
a
rb
α
A
XL
X
Xα B
25
★杠杆定律 由直线法则导出
即三元合金系中两相平衡的杠杆定律 应用条件 a,某一温度下,成分给定三元合金处于液固平衡, 其中成分可知,可求另一成分 b,已知成分的固相在某一温度下析出一新相时,新 相成分已知,可确定母相成分
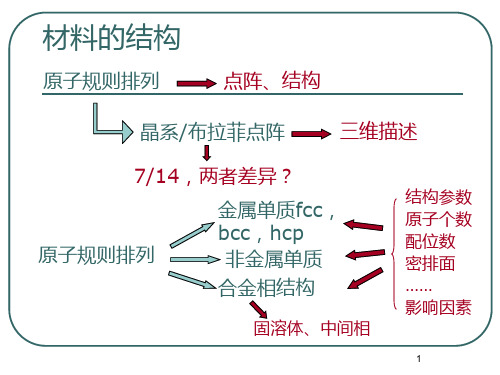
材料的结构
原子规则排列
点阵、结构
晶系/布拉菲点阵
三维描述
7/14,两者差异?
原子规则排列
金属单质fcc, bcc,hcp
非金属单质
合金相结构
固溶体、中间相
结构参数 原子个数 配位数 密排面 …… 影响因素
1
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
15
2) 直角浓度三角形
当合金成分以某一组 元为主,其它两组元 含量很少时,合金成 分将靠近等边三角形 某一顶角,采用直角 坐标,则可使该部分 相图清楚地表示出来。
2 重心定律
适用于三相平衡的情况
w%W WR
Rf10% 0 cf
B%
a
A
B
fb d
R e
c
C%
← A% C
27
但是,作图求三相平衡不够准确而产生误差, 用代数法求解,可避免误差。已知条件: ✓R合金中A,B,C组元含量为xR,yR,zR ✓α相中A,B,C组元含量为xα,yα,zα ✓β相中A,B,C组元含量为xβ,yβ,zβ ✓γ相中A,B,C组元含量为xγ,yγ,zγ
24
杠杆定律
W L+W =W 0 W L X X rb W 0 X X L ab W X X L ar W 0 X X L ab
L
a
rb
α
A
XL
X
Xα B
25
★杠杆定律 由直线法则导出
即三元合金系中两相平衡的杠杆定律 应用条件 a,某一温度下,成分给定三元合金处于液固平衡, 其中成分可知,可求另一成分 b,已知成分的固相在某一温度下析出一新相时,新 相成分已知,可确定母相成分
材料的结构
原子规则排列
点阵、结构
晶系/布拉菲点阵
三维描述
7/14,两者差异?
原子规则排列
金属单质fcc, bcc,hcp
非金属单质
合金相结构
固溶体、中间相
结构参数 原子个数 配位数 密排面 …… 影响因素
1
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
15
2) 直角浓度三角形
当合金成分以某一组 元为主,其它两组元 含量很少时,合金成 分将靠近等边三角形 某一顶角,采用直角 坐标,则可使该部分 相图清楚地表示出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/11/7
T℃等温面
A
B
L+α
α
N
K
M
O
K
bL
C
ML T
L+α
α K
O
返回
N K
2020/11/7
截面两相区不能代表两相浓 度,且不能用杠杆定律确定 两相相对量。
返回
变温截面的功能:
• 定性地揭示不同成分的系统的结晶过程 • 确定相变的临界温度 • 不能揭示多个平衡相的成分,故也不能揭示各平 衡相的质量分数
=xxCA
N
=EAE C=常数
N
PQ E
%A
xAN xAM C
2020/11/7
返回
8.2 平衡相的定量法则
B
一、直线定律
• 已知成分的两合金P、Q,熔 配成新合金R,R必在PQ连
α Oβ
线上,且在重量重心上。
PR Q
wPRP=wQRQ
A
C
• 成分为O的合金,分解为αβ两相,则αβ连线必过O点。
w % = o 10 % 0w % = o 10 % 0
2020/11/7
返回
二、重心定律
• 已知成分的三个合金P、Q、N,
B
熔配成一个新的合金R,R成分
点必在△PQN内,且在△重量
Q
重心上。
wP·RP = wQ ·RQ = wN ·RN
nR p
Pq
N
A
C
• 证:将PQ合金按直线定律熔配
成n,再由n和N按直线定律熔
在TE等温四相面以上有三个三相区,以下有一个,称 为3/1转变。
三相区由三相平衡三角形滑动而成。三相区棱边为三
个相的浓度变温线。
E
e
αβ
2020/11/7
L→α+β α
β L
γ
β
α
γ
返回
• 四相面:L+α+β+γ; 反应式:LE→(α+β+γ)共 f=0 水平面
★ 相区接触法则:
α
• 以面相邻相数差一
A T3
T4 T5
T2
T1 α
B
O
L
C
TB > TA > TC
2020/11/7
返回
• 等温截面图中,两相区平衡 相成分及相对量的确定,只 能由实测才知道。
• 连接线的方向,可根据纯组 元熔点高低大致判定。 ∵ TA>TC,低温相α偏向于A。
• 垂直截面两相区不能代表两 相浓度,且不能用杠杆定律 确定两相相对量。
xA + xB + xC = 100%
B
↑
• 独立变量为二,需用平面表示。
常用直边三角形和等边三角形表 xB
O
示,统称为浓度三角形。
2020/11/7
A
xC
返回
→C
等边三角形表示法:
• 浓度三角形顶点代表纯组元
• 三角形的边代表二元合金
%B
AB = BC = CA = 100%
B
xc
%C
• 三角形内任意一点都代表一 xb
α
2020/11/7
返回
特殊成分的合金:
• O合金(线接触) 单(L)→三(L+α+β)→
Aα
e1
O
M
E
e2
→双(α+β)→三(α+β+γ)
γ
• M合金(线接触)
C
单(L)→双(L+α)→双(α+γ)→三(α+β+γ)
配成R。
2020/11/7
返回
• 由合金O,分解成αβγ三个相,
则O位于△αβγ的重量重心处。
B
• 各相相对量:
w %
= o ' 100 '
%
o '
w %
=
100 '
%
w %
=
o ' 100 '
%
β
γ’ O α’
α β’
A
γ
C
2020/11/7
返回
8.3 三元匀晶相图
一、立体图
• 熔点:TA、TB、TC • 二元匀晶相图:
• 以线相邻相数差二或零
• 以点相邻相数差三
β
L E
γ
2020/11/7
返回
二、投影图
12
e1
Aα
97
11
5
E
e2
3
4 β
B
8 10
6
12
e3
2020/11/7
γ C
返回
三、平衡结晶过程
• Ⅰ合金:
L L+ L++
L
室温组织:α固溶体
• Ⅱ合金:
e1
A Ⅰ Ⅱα LⅢ+α+β α+β+γ
L+α+γE
2020/11/7
返回
8.4 三元共晶相图(3/1转变)
一、立体图
TB
由相 三图 个发 二展 元而 共来 晶。
TA
α
e1
β
e3
e2
TC
E
B
γ
2020/11/7
A C
TA> TB > TC > e1 > e2 > e3 > TE
返回
相 区:
• 单相区:L、α、β、γ f=3 任意形状空间区域。 与三个两相区衔接。
L+α
α
A
2020/11/7
返回
• 双相区: L+α、L+β、L+γ、α+β、α+γ、β+γ; 一对成分共轭面包围的空间区域,两平衡相的浓度在
共轭面上按蝴蝶规律变化。 f=2
e1
e1
e2
E
A
2020/11/7
L+α
α+β
返回
三相区: • L+α+β、 L+α+γ、 L+β+γ、 α+β+γ
f=1L→α+β、L→α+γ、 L→β+γ
L+α O xL
L
C
2020/11/7
TB>T2>TA
BA
L+α α B
L
C
TC>T4
BA
B
α
C
返回
三、垂直截面图
TA
f=0
L TA
L+α f=1
L
TB
L+α
α
α
A
TC
B
A
a
• 两相区由一对共轭线包围 • 平衡相浓度不在共轭线上
a
C
TB>TA> TC
2020/11/7
返回
四、凝固过程
• 结晶过程中,两 平衡相浓度按蝴蝶 形规律变化。
第八章 三元相图ቤተ መጻሕፍቲ ባይዱ
• 三维空间立体图 • 多元可作伪三元处理
2020/11/7
返回
章 目 录:
8.1 三元合金相图的表示方法 8.2 平衡相的定量法则 8.3 三元匀晶相图 8.4 三元共晶相图 8.5 其它三元相图 8.6 举例
2020/11/7
返回
8.1 三元合金相图的表示方法
一、浓度三角形
三元合金组元 A、B、C,应满足约束条件:
e2
γ
βB
e3
LL+ + ++
L
2020/11/7
Ⅱ
Ⅱ Ⅱ
返回
C
室温组织: α+βⅡ+γⅡ
• Ⅲ合金:
AⅠ
Ⅱ
单(L)→双(L+α) →三(L+α+β)
→双(α+β) →三(α+β+γ)
e2
e1
LⅢ+α+β α+β+γ
E
βB
e3
L L(+)
Ⅱ
Ⅱ Ⅱ
γ
(α+β)
C
βⅡ+γⅡ
室温组织:α+(α+β)+βⅡ+γⅡ
A-B、A-C、B-C • 固液相面:(共轭) • 单相区:L、α • 双相区:L+α
DL
TB
TA
E
D L+Dα
E
E
α
A
TC
B
C
TB > TA > TC
2020/11/7
返回
二、等温截面图
A
• 两相区由
T1>TB
L
一对共轭线
包围,两平
C
衡相浓度在
共轭线上,
A
TA>T3>TC α xα
用连接线连 接(实测)
O
个三元合金。如图O点
A
xa D xb
C
%A
xa + xb + xc = 100 % = 边长
2020/11/7
返回
二、△中具有特殊意义的线
• 平边线等浓度关系: P、Q合金,B组元相等
• 顶角线等比浓度关系:
B xCM
%B
M
xCN
F %C
任意两点M、N合金, A、C组元浓度之比相等。
xB
A
xxCAM
T℃等温面
A
B
L+α
α
N
K
M
O
K
bL
C
ML T
L+α
α K
O
返回
N K
2020/11/7
截面两相区不能代表两相浓 度,且不能用杠杆定律确定 两相相对量。
返回
变温截面的功能:
• 定性地揭示不同成分的系统的结晶过程 • 确定相变的临界温度 • 不能揭示多个平衡相的成分,故也不能揭示各平 衡相的质量分数
=xxCA
N
=EAE C=常数
N
PQ E
%A
xAN xAM C
2020/11/7
返回
8.2 平衡相的定量法则
B
一、直线定律
• 已知成分的两合金P、Q,熔 配成新合金R,R必在PQ连
α Oβ
线上,且在重量重心上。
PR Q
wPRP=wQRQ
A
C
• 成分为O的合金,分解为αβ两相,则αβ连线必过O点。
w % = o 10 % 0w % = o 10 % 0
2020/11/7
返回
二、重心定律
• 已知成分的三个合金P、Q、N,
B
熔配成一个新的合金R,R成分
点必在△PQN内,且在△重量
Q
重心上。
wP·RP = wQ ·RQ = wN ·RN
nR p
Pq
N
A
C
• 证:将PQ合金按直线定律熔配
成n,再由n和N按直线定律熔
在TE等温四相面以上有三个三相区,以下有一个,称 为3/1转变。
三相区由三相平衡三角形滑动而成。三相区棱边为三
个相的浓度变温线。
E
e
αβ
2020/11/7
L→α+β α
β L
γ
β
α
γ
返回
• 四相面:L+α+β+γ; 反应式:LE→(α+β+γ)共 f=0 水平面
★ 相区接触法则:
α
• 以面相邻相数差一
A T3
T4 T5
T2
T1 α
B
O
L
C
TB > TA > TC
2020/11/7
返回
• 等温截面图中,两相区平衡 相成分及相对量的确定,只 能由实测才知道。
• 连接线的方向,可根据纯组 元熔点高低大致判定。 ∵ TA>TC,低温相α偏向于A。
• 垂直截面两相区不能代表两 相浓度,且不能用杠杆定律 确定两相相对量。
xA + xB + xC = 100%
B
↑
• 独立变量为二,需用平面表示。
常用直边三角形和等边三角形表 xB
O
示,统称为浓度三角形。
2020/11/7
A
xC
返回
→C
等边三角形表示法:
• 浓度三角形顶点代表纯组元
• 三角形的边代表二元合金
%B
AB = BC = CA = 100%
B
xc
%C
• 三角形内任意一点都代表一 xb
α
2020/11/7
返回
特殊成分的合金:
• O合金(线接触) 单(L)→三(L+α+β)→
Aα
e1
O
M
E
e2
→双(α+β)→三(α+β+γ)
γ
• M合金(线接触)
C
单(L)→双(L+α)→双(α+γ)→三(α+β+γ)
配成R。
2020/11/7
返回
• 由合金O,分解成αβγ三个相,
则O位于△αβγ的重量重心处。
B
• 各相相对量:
w %
= o ' 100 '
%
o '
w %
=
100 '
%
w %
=
o ' 100 '
%
β
γ’ O α’
α β’
A
γ
C
2020/11/7
返回
8.3 三元匀晶相图
一、立体图
• 熔点:TA、TB、TC • 二元匀晶相图:
• 以线相邻相数差二或零
• 以点相邻相数差三
β
L E
γ
2020/11/7
返回
二、投影图
12
e1
Aα
97
11
5
E
e2
3
4 β
B
8 10
6
12
e3
2020/11/7
γ C
返回
三、平衡结晶过程
• Ⅰ合金:
L L+ L++
L
室温组织:α固溶体
• Ⅱ合金:
e1
A Ⅰ Ⅱα LⅢ+α+β α+β+γ
L+α+γE
2020/11/7
返回
8.4 三元共晶相图(3/1转变)
一、立体图
TB
由相 三图 个发 二展 元而 共来 晶。
TA
α
e1
β
e3
e2
TC
E
B
γ
2020/11/7
A C
TA> TB > TC > e1 > e2 > e3 > TE
返回
相 区:
• 单相区:L、α、β、γ f=3 任意形状空间区域。 与三个两相区衔接。
L+α
α
A
2020/11/7
返回
• 双相区: L+α、L+β、L+γ、α+β、α+γ、β+γ; 一对成分共轭面包围的空间区域,两平衡相的浓度在
共轭面上按蝴蝶规律变化。 f=2
e1
e1
e2
E
A
2020/11/7
L+α
α+β
返回
三相区: • L+α+β、 L+α+γ、 L+β+γ、 α+β+γ
f=1L→α+β、L→α+γ、 L→β+γ
L+α O xL
L
C
2020/11/7
TB>T2>TA
BA
L+α α B
L
C
TC>T4
BA
B
α
C
返回
三、垂直截面图
TA
f=0
L TA
L+α f=1
L
TB
L+α
α
α
A
TC
B
A
a
• 两相区由一对共轭线包围 • 平衡相浓度不在共轭线上
a
C
TB>TA> TC
2020/11/7
返回
四、凝固过程
• 结晶过程中,两 平衡相浓度按蝴蝶 形规律变化。
第八章 三元相图ቤተ መጻሕፍቲ ባይዱ
• 三维空间立体图 • 多元可作伪三元处理
2020/11/7
返回
章 目 录:
8.1 三元合金相图的表示方法 8.2 平衡相的定量法则 8.3 三元匀晶相图 8.4 三元共晶相图 8.5 其它三元相图 8.6 举例
2020/11/7
返回
8.1 三元合金相图的表示方法
一、浓度三角形
三元合金组元 A、B、C,应满足约束条件:
e2
γ
βB
e3
LL+ + ++
L
2020/11/7
Ⅱ
Ⅱ Ⅱ
返回
C
室温组织: α+βⅡ+γⅡ
• Ⅲ合金:
AⅠ
Ⅱ
单(L)→双(L+α) →三(L+α+β)
→双(α+β) →三(α+β+γ)
e2
e1
LⅢ+α+β α+β+γ
E
βB
e3
L L(+)
Ⅱ
Ⅱ Ⅱ
γ
(α+β)
C
βⅡ+γⅡ
室温组织:α+(α+β)+βⅡ+γⅡ
A-B、A-C、B-C • 固液相面:(共轭) • 单相区:L、α • 双相区:L+α
DL
TB
TA
E
D L+Dα
E
E
α
A
TC
B
C
TB > TA > TC
2020/11/7
返回
二、等温截面图
A
• 两相区由
T1>TB
L
一对共轭线
包围,两平
C
衡相浓度在
共轭线上,
A
TA>T3>TC α xα
用连接线连 接(实测)
O
个三元合金。如图O点
A
xa D xb
C
%A
xa + xb + xc = 100 % = 边长
2020/11/7
返回
二、△中具有特殊意义的线
• 平边线等浓度关系: P、Q合金,B组元相等
• 顶角线等比浓度关系:
B xCM
%B
M
xCN
F %C
任意两点M、N合金, A、C组元浓度之比相等。
xB
A
xxCAM
