《材料力学》课件2-4拉(压)杆的变形.胡克定律
合集下载
轴向拉(压)杆的变形-胡克定律

1.2 胡克定律
英国科学家胡克在1678 年首先通过实验发现:当杆件的应力不超过某一限度 时,杆件的轴向变形 Δl 与杆件所受的外力 F 和杆长 l 成正比,而与杆件横截面面 积 A 成反比,即
l ∝ Fl A
引入比例常数 E ,同时由于横截面上轴力FN = F ,于是有
l = FNl EA
(6-10)
l l
(6-7)
应变 ε 是无量纲的量。
2. 横向变形和应变
设杆原横向尺寸为 d ,受力后变为 d1 ,如图6-10b 所示,则杆的横向变形为 Δd = d1 ‒ d 。相应的横向线应变为
' d d
(6-8)
横向线应变 '也是无量纲的量。
正负号规定:Δl 、 Δd 以伸长为正,缩短为负; ε 和 ' 的正负号分别与 Δl 和 Δd 一致,即拉应变为正,压应变为负。显然, 轴向线应变 ε 与横向线应变 ' 恒为 异号。
E
(6-11)
从式( 6-11) 可以得知, 当杆的应力在线弹性范围内时,应力与应变成正比。 E 与 μ 都是材料弹性性质的常数,表6-2 列出了几种常用工程材料的 E、μ 值。
表6-2 几种常用工程材料的E、μ 值
【例6-7】一截面为正方形的阶梯形柱,由上、下两段组成。其各段长度、截面尺寸 和受力情况如图6-11所示。已知材料的弹性模量 E = 0.03×105 MPa,外力F = 50 kN, 试求该柱A 、B 截面的位移。
lA
50 103 3 0.03105 106 0.252
150 103 4 0.03105 106 0.372
2.26 mm
(向下)
lB
150 103 4 0.03105 106 0.372
西南交大 材料力学 龚晖 拉压变形
分段累加
100kN
75kN 50kN
A
BC
D
1.75m 1.25m 1.50m
75kN
100kN (1)
50kN
(2)
(3)
lAC lAC1 lAC2 lAC3 lAB1 lAC2 lAC3
=
(-100)×103 ×1.75×103 70×103×800
75×103 ×3.0×103 + 70×103×800
l 1 FN l EA
E
称为单轴应力状态下的胡克定律
例 求各段的线应变。
100kN
A
B
75kN 50kN
C
D
1.75m 1.25m 1.50m
解:lAB 0.78mm
lBC 2.79mm
lCD 2.14mm
AB
l AB lAB
0.78 1.75103
5.2104
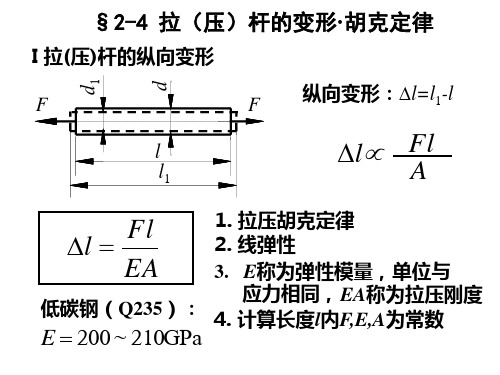
§2-4 拉(压)杆的变形·胡克定律
I 拉(压)杆的纵向变形
d1 d
F
F
纵向变形:l=l1-l
l l1
l
Fl A
l Fl
1. 拉压胡克定律 2. 线弹性
EA
3. E称为弹性模量,单位与
低碳钢(Q235):
4.
应力相同, EA称为拉压刚度 计算长度l内F,E,A为常数
E 200 ~ 210GPa
-ν
520106
520με
II 拉(压)杆的横向变形
d1 d
F
F
l l1
绝对变形 d d1 - d
相对变形
ν
' d
(压)杆的变形· 胡克定律 - 材料力学

内力。
第二章 轴向拉伸和压缩
Ⅱ. 截面法· 轴力及轴力图
步骤: (1)断开 (2)代替 (3)平衡
解得:轴力FN=F ,方向:拉为正,压为负。
第二章 轴向拉伸和压缩
思考题 静力学中力的可传递性原理,在用截面法求内力的 过程中是否可用?
轴力图:平行于杆轴线的坐标表示横截面的位置。 垂直于杆轴线的坐标表示横截面轴力的数值。
3
第二章 轴向拉伸和压缩
例题2-5 如图所示杆系,荷载 P = 100 kN,试求结点A 的位移ΔA。已知: = 30° ,l = 2 m,d = 25 mm,杆的材
料(钢)的弹性模量为E = 210 GPa。
第二章 轴向拉伸和压缩
解:结点A的位移ΔA系由两杆的伸长变形引起,故需先
求两杆的伸长。 1. 求杆的轴力及伸长 由结点 A 的平衡(如图)有
说,拉杆在其任意两个横截面之间的纵向线段的伸长是均
匀的。
第二章 轴向拉伸和压缩
FN s A
推论:横截面上各点处的正应力s 都相等
第二章 轴向拉伸和压缩
注意: 由于杆端连接方式的不同,等直杆在外力作用点附近, 横截面上的应力情况复杂。圣维南原理:“力作用于杆端方
式的不同,只会使与杆端距离不大于杆的横向尺寸的范围内
受到影响”。
第二章 轴向拉伸和压缩
例题2-2 试求此正
方形砖柱由于荷载引起
的横截面上的最大工作 应力。已知F = 50 kN。
第二章 轴向拉伸和压缩
解:Ⅰ段柱横截面上的正应力
FN1 50 103 N s1 A1 (0.24 m) (0.24 m) 0.87 106 P a 0.87 MP a (压应力)
化阶段中,Δl=Δle+Δlp。
第四节 胡克定律

b b1 b 应变: b b
b
b
b1
b
b1
3)横向变形量(应变)---或伸长或缩短
横向变形量: d d1 d
d d1 d 横向应变: d d
/
b
d
b
b1
d1 d1
b
b1
4)符号: 受拉为正,受压为负
二、胡克定律:
1、胡克定律
在弹性限度内,应变与应力成正比,即:
解:
例2阶梯状直杆受力如图所示。已知AD段横截面面积AAD=1000mm2, DB段横截面面积ADB=500mm2,材料的弹性模量E=200GPa。求该 杆的总变形量ΔlAB。
解:由截面法可以计算出AC,CB段轴力FNAC=-50kN(压),FNCB=30kN
(拉)。
例3:圆截面阶梯状杆件如图所示,受到F=150kN的轴向拉力作用。 已知中间部分的直径d1=30mm,两端部分直径为d2=50mm,整个杆
E
E 弹性模量
2、胡克定律变形:
E
l l
N A
Nl l EA
3、泊松比: 在弹性限度内,轴向应变与横向应变之比是定值,成 为泊松比
/
三、习题:
例1 圆截面钢杆长l=3m,直径d=25mm,两端受到F=100kN的轴向 拉力作用时伸长Δl=2.5mm。试计算钢杆横截面上的正应力σ和纵向 线应变ε。
习题
P127:
8-5 8-6
1胡克定律eanl在弹性限度内轴向应变与横向应变之比是定值成为泊松比圆截面钢杆长l3m直径d25mm两端受到f100kn的轴向拉力作用时伸长l25mm
第一节 材料力学的基本概念
一、拉杆变形:
b
b
b1
b
b1
3)横向变形量(应变)---或伸长或缩短
横向变形量: d d1 d
d d1 d 横向应变: d d
/
b
d
b
b1
d1 d1
b
b1
4)符号: 受拉为正,受压为负
二、胡克定律:
1、胡克定律
在弹性限度内,应变与应力成正比,即:
解:
例2阶梯状直杆受力如图所示。已知AD段横截面面积AAD=1000mm2, DB段横截面面积ADB=500mm2,材料的弹性模量E=200GPa。求该 杆的总变形量ΔlAB。
解:由截面法可以计算出AC,CB段轴力FNAC=-50kN(压),FNCB=30kN
(拉)。
例3:圆截面阶梯状杆件如图所示,受到F=150kN的轴向拉力作用。 已知中间部分的直径d1=30mm,两端部分直径为d2=50mm,整个杆
E
E 弹性模量
2、胡克定律变形:
E
l l
N A
Nl l EA
3、泊松比: 在弹性限度内,轴向应变与横向应变之比是定值,成 为泊松比
/
三、习题:
例1 圆截面钢杆长l=3m,直径d=25mm,两端受到F=100kN的轴向 拉力作用时伸长Δl=2.5mm。试计算钢杆横截面上的正应力σ和纵向 线应变ε。
习题
P127:
8-5 8-6
1胡克定律eanl在弹性限度内轴向应变与横向应变之比是定值成为泊松比圆截面钢杆长l3m直径d25mm两端受到f100kn的轴向拉力作用时伸长l25mm
第一节 材料力学的基本概念
一、拉杆变形:
材料力学 拉压2-4

3·设计板宽b 四个铆钉可布置成一排或二排,只要 使外力的作用线通过钉群图形的形心,则 可假定各钉受力相等。 若布置二排,有矩形和菱形二种排列 如图,则拉伸危险截面在虚线处。 对于矩形布置,轴力图如图 则有: =P/2t1(b-2d)[] 即得: b2d+P/2t1[] =40+210×103/2×5×160=172mm
Fb P 110 bs 10 7 171 .9MPa bs Abs 4td 4 11.6
钢板的2--2和3--3面为危险面 3P 3 110 2 107 155 .7MPa 4t (b 2d ) 4 (8.5 2 1.6) P 110 3 107 159 .4MPa 综上,接头安全。 t (b d ) 1 (8.5 1.6) 1 2 3 P P P
P/2
P/2
P/2 P/4
矩形排列轴力图
对于菱形布置,轴力图如图
则有: =P/2t1(b-d)[] 即得: bd+P/2t1[]=152mm。
P/8 P/4
P/2
菱形排列轴力图
问题讨论1: 木榫接头如图。 接头总高度H给定,试设计其 他尺寸。 问题讨论2:铰接正方形铸 铁框架,各杆直径均为d。 []压=3[]拉, 试求Pmax并设 计销钉C的尺寸。 问题讨论3:刚性梁AB支承如 图,试设计A处销钉的尺寸。
t
d
t
P/4
1 2 3
例: 平键连接轮与轴。 转速n=200转/分,传递功率20千瓦。 平键尺寸b=20mm, L=40mm。d=60mm。 []=80MPa。试校核平键的剪切强度。
b
d
h/2
L
m
解: 1) 依据功率、转速与传递的扭矩m之关系,有: m=9.55NP/n=9.55×20/200=0.955kN.m 2) 轴受力如图 由平衡方程: mO(F)=m-Qd/2=0 求得剪力: Q=2m/d=2×0.955/0.06=31.8kN 3) 平键剪切面面积为: A=bL=20×40=800 mm2. 剪应力为: =Q/A=31.8×103/800=39.6MPa<[]=80MPa 故平键剪切强度足够。
胡克定律与拉压杆的变形

n 按结构原有几何形状与尺寸,计算约束力与内力 o 采用切线代圆弧的方法确定节点位移
例 7-3 F1= F2/ 2 = F,求截面 A 的位移∆Ay
刚体 EA
解:1. 计算 FN
∑M B =0, F1⋅2l+F2⋅l−FN⋅lsin30D =0
FN
=
2F1 + F2 sin 30D
=
8F
刚体 EA
−
F
)⋅2l
=0
FN2 =4FN1
FN2=4FN1=88
2F = 4.59 × 104 2 +1
N
5. 截面设计
FN1− 拉力
FN2 − 压力
A1 ≥[FσNt1] =71.7 mm2 A2 ≥[FσNc2] =383 mm2
结论: A1 = A2 = 383 mm2
例 8-3 图示两端固定杆,试分析当温度升高 ∆T 时,横
单辉祖:工程力学(材料力学)
87
应变能与功能原理
应变能与外力功 z 弹性体因变形而储存的能量-应变能 Vε z 外力在变形过程中所作之功-外力功 W
解:1. 破坏形式分析
单辉祖:工程力学(材料力学)
81
2. 许用载荷 [F]
n
τ
=
4F πd 2
≤ [τ
]
F ≤ πd 2[τ ] = 1.257 kN
4
o
σ bs
=
F
δd
≤ [σ bs ]
F ≤ δd[σ bs ] = 2.40 kN
p
σ max
=
F
(b − d )δ
≤ [σ ]
F ≤ (b − d )δ [σ ] = 3.52 kN
例 7-3 F1= F2/ 2 = F,求截面 A 的位移∆Ay
刚体 EA
解:1. 计算 FN
∑M B =0, F1⋅2l+F2⋅l−FN⋅lsin30D =0
FN
=
2F1 + F2 sin 30D
=
8F
刚体 EA
−
F
)⋅2l
=0
FN2 =4FN1
FN2=4FN1=88
2F = 4.59 × 104 2 +1
N
5. 截面设计
FN1− 拉力
FN2 − 压力
A1 ≥[FσNt1] =71.7 mm2 A2 ≥[FσNc2] =383 mm2
结论: A1 = A2 = 383 mm2
例 8-3 图示两端固定杆,试分析当温度升高 ∆T 时,横
单辉祖:工程力学(材料力学)
87
应变能与功能原理
应变能与外力功 z 弹性体因变形而储存的能量-应变能 Vε z 外力在变形过程中所作之功-外力功 W
解:1. 破坏形式分析
单辉祖:工程力学(材料力学)
81
2. 许用载荷 [F]
n
τ
=
4F πd 2
≤ [τ
]
F ≤ πd 2[τ ] = 1.257 kN
4
o
σ bs
=
F
δd
≤ [σ bs ]
F ≤ δd[σ bs ] = 2.40 kN
p
σ max
=
F
(b − d )δ
≤ [σ ]
F ≤ (b − d )δ [σ ] = 3.52 kN
《材料力学》课件2-4拉(压)杆的变形.胡克定律

拉(压)杆的综合变形
综合变形
杆件在受到拉力或压力作用时,不仅会发生轴向变形和横向变形,还可能发生弯曲变形 等其他形式的变形。
胡克定律的应用
胡克定律只适用于描述杆件的轴向变形,对于其他形式的变形,需要使用更复杂的力学 公式来描述。
Part
02
胡克定律
胡克定律的表述
总结词
胡克定律是材料力学中一个重要的基本定律,它表述了材料 在拉伸或压缩过程中所遵循的应力和应变之间的关系。
胡克定律的局限性
总结词
胡克定律的应用有一定的局限性,它仅适用于线弹性材料,且只考虑了单向受力的情况。
详细描述
胡克定律的应用范围仅限于线弹性材料,对于非线性材料或塑性材料,胡克定律不再适用。此外,胡克定律只考 虑了单向拉伸或压缩受力的情况,对于剪切、弯曲等复杂受力情况,需要引入更复杂的力学模型进行分析。
详细描述
胡克定律指出,在弹性范围内,材料所受的应力与产生的应变 之间成正比,即应力与应变之比为常数,这个常数称为材料的 弹性模量或杨氏模量,用符号E表示。数学表达式为:σ=E*ε, 其中σ为应力,ε为应变。
胡克定律的应用
总结词
胡克定律在工程实践中广泛应用于材料的强度分析、结构设计等方面。
详细描述
通过胡克定律,可以计算出材料在受到拉伸或压缩力时的应力和应变,从而评估 材料的承载能力和安全性。在结构设计时,可以利用胡克定律进行受力分析和优 化设计,以确保结构的稳定性和可靠性。
详细描述
均匀性假设意味着材料在各个部分都 具有相同的性质,如密度、弹性模量 等。这一假设使得我们能够将材料的 性质视为空间位置的常数,从而简化 分析过程。
各向同性假设
总结词
各向同性假设认为材料在各个方向上都 具有相同的性质。
§4 拉(压)杆的变形.胡克定律`

h2
z
y
max
h2
y0
A
y
max
3F s F sh 2 F sh 2 3 2A bh 8I Z 8 12
例题 4.13
F
矩形截面简支梁,加载于梁中点C,如图示。 求σmax , τmax 。
h
M max
FL 4
bh 2 WZ 6
l 2
l 2
Fs max
max
F 3 2 3 Fs 3 F 2 bh 2 A 4 bh
5m
I
2m
2m
2m
查表:
I
WZ 237 103 mm3
M 52.7 MPa WZ
4IN0 20
例题 4.10
试对图示结构布置图中的L-2梁进行截面选择。两梁均采用工字钢截 面,[σ]=215MPa,已知L-1梁上简支板的荷载设计值为3.5kN/m2。
q 3.5 2 7kN / m
150kN吊车
B
200kN吊车
1.确定F加在辅助梁的位置
A
C
辅助梁
M M
A
0 0
FA
F
l
x
FB
B
FP l x F F B B l F l x 0 l F Fx FAl 0 FAx l
令: FA Fx 200kN l
FB
F l x l
2F
1400 600
z
200 50
12kNm
16kNm
A
M Ayl 16 103 250 96.4 24.09MPa 8 IZ 1.02 10
拉压变形

∑F = 0 ∑F = 0
x y
FN1 = FN 2
2 FN1 cos α = F
FN1 = FN 2
F = 2 cos α
B 1 2
C
由胡克定律得两杆的伸长: 由胡克定律得两杆的伸长:
FN1l FN 2l = l1 = l2 = EA EA
A F B 1
Fl = 2EA cos α
C 2 A1 A A' A' A 2 A'' 1 2
S l = EA
ql 2 ql × l S = = = EA 2EA 2EA
d1
F l l1 绝对变形 相对变形
d
F
l = l1 - l
长度量纲 线应变,无量纲
l ε= l
l 1 FN FNl = l = l E A EA σ ε= 称为单轴应力状态下的 单轴应力状态下的胡克定律 称为单轴应力状态下的胡克定律 E
杆的变形胡克定律 §2-4 拉(压)杆的变形 胡克定律
I 拉(压)杆的纵向变形 d1 F l l1 F 纵向变形: 纵向变形:l=l1-l d
Fl l∝ A
1. 拉压胡克定律 2. 线弹性 3. E称为弹性模量,单位与 称为弹性模量, 称为弹性模量 应力相同, 称为拉压刚度 应力相同,EA称为拉压刚度 低碳钢( 低碳钢(Q235): ): 计算长度l内 4. 计算长度 内F,E,A为常数 为常数
求各段的线应变. 例 求各段的线应变.
100kN A B C 75kN 50kN D
1.75m 1.25m 1.50m
解:l AB = 0.78mm
l BC = 2.79mm lCD = 2.14mm 0.78 l AB = 5.2 ×10 4 = 520 ×10 6 = ε AB = l AB 1.75 ×103 = 520ε
《材料力学》2-4拉(压)杆的变形.胡克定律

拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
1、纵向变形
LLL 绝对变形
线应变: 受力物体变形时,一点处沿 某一方向微小线段的相对变 形
当杆沿长度均匀变形时
L L
纵向线应变 (无量纲)
y
C
O
x
A
B
z △x
当杆沿长度非均匀变形时
αD
B1 BB2C1 C
FNCD
F
A
C
a
CC1
CL CCD ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LC FD LFN1 2CEL D A cLC o DsFCD
2Fa
EAcos2
B
4Fa
EAco3s
移δB。1、已经测出CD杆的轴向应变ε;2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCDa
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B2LCD 2a
2. 已知EA
LCD
FNCDa EA
mA 0
FNCD2F
B 2L 2 LC FN DCD 4EFFAaL0
例题
2.12
B
图示的杆系是由两根圆截面钢杆铰接而成。已知
L AB L AC F N EA L A C 2 EF c A o Ls
A
A AA
L AC
cos
FL
2EAcos2
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
1、纵向变形
LLL 绝对变形
线应变: 受力物体变形时,一点处沿 某一方向微小线段的相对变 形
当杆沿长度均匀变形时
L L
纵向线应变 (无量纲)
y
C
O
x
A
B
z △x
当杆沿长度非均匀变形时
αD
B1 BB2C1 C
FNCD
F
A
C
a
CC1
CL CCD ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LC FD LFN1 2CEL D A cLC o DsFCD
2Fa
EAcos2
B
4Fa
EAco3s
移δB。1、已经测出CD杆的轴向应变ε;2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCDa
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B2LCD 2a
2. 已知EA
LCD
FNCDa EA
mA 0
FNCD2F
B 2L 2 LC FN DCD 4EFFAaL0
例题
2.12
B
图示的杆系是由两根圆截面钢杆铰接而成。已知
L AB L AC F N EA L A C 2 EF c A o Ls
A
A AA
L AC
cos
FL
2EAcos2
轴向拉伸与压缩—轴向拉(压)杆的变形和胡克定律(建筑力学)

轴向拉(压)杆的变形和胡克定律
4 例题
一木方柱受轴向荷载作用,横截面边长a=200mm,材料的弹性模量 E=10GPa,杆的自重不计。求各段柱的纵向线应变及柱的总变形。
解: (1)由于上下两段柱的轴力不等,故两段柱 的变形要分别计算。经计算各段柱的轴力为
FNBC=-100kN FNAB=-260kN
正负号恒相反
利用上式,可由纵向线应变或正应力求横向线应变。反之亦然。
轴向拉(压)杆的变形和胡克定律
3 胡克定律
实验表明工程上大多数材料都有一个弹性阶段,在此弹性范围内,正
应力与线应变成正比.
由
E
FN
A
Δl
l
上式改写为
Δl FNl EA
式中 E 称为弹性模量 ,EA称为抗拉(压)刚度。
6.5 ×10-4
Ch5 轴向拉伸或压缩变形
03 轴向拉(压)杆的变形和胡克定律
轴向拉(压)杆的变形和胡克定律
1 纵向、横向变形
纵向变形 纵向应变
l l1 l
= l
l
横向变形 横向应变
h h1 h
h1 h Δh
hh
轴向拉(压)杆的变形和胡克定律
2 泊松比
称为泊松比。 E 和 都是表征材料弹性的常量。考虑到 与 的ຫໍສະໝຸດ 轴向拉(压)杆的变形和胡克定律
4 例题
(2)各段柱的纵向变形为
△lBC=
FNBClBC EA
100 103 N 2m 10 109 Pa (0.2m)
2 =-0.5 ×10-3 m=-0.5mm
△lAB=
FNABlAB EA
260 103 10 109 Pa
N
1.5m (0.2m)
材料力学-课件2-4拉杆的变形.胡克定律

EA L L
L
i
FNiLi
EAi
FN EA L E
A AL
在计算ΔL的L长度内,FN,E,A均 为常数。
在材料的线弹性范围内,正应力与线应变呈正比关系。
2、横向变形
△b=b1-b
b1 b
b
b
横向线应变
泊松比
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
α=300,杆长L=2m,杆的直径d=25mm,材
料的弹性模量E=2.1×105MPa,设在结点A处悬
挂一重物F=100kN,试求结点A的位移δA。
1
2
FNAB FNAC
X 0 C Y 0
F N F FN c N A AA C s C o C FiN F s n N AB F N c A 2cA s F B o oB isF n s 0 0
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例题
2.10
例:图示直杆,其抗拉刚度为EA,试 求杆件的轴向变形△L,B点的位移 δB和C点的位移δC
A L
F
F
B
LAB
FL EA
B
C
L
C
B
FL EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆,
B点受荷载P作用,试在下面两种情况下分别计算B点的位
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
材料力学第2章+轴向拉伸与压缩

第二章 轴向拉伸和压缩
§2-3应力·拉(压)杆内的应力
1. 应力的概念
若考察受力杆截面上M点处
应力:指受力杆件某一横 截面上一点处的内力集度 (内力分布的密集程度)
应力,可在M点周围取一很
小面积ΔA,设 ΔA面积上分 布内力的合力为ΔF,则 ΔA
上内力平均集度为:
F M A
26
Pm = F/A
Pm即A上的平均应力
第二章 轴向拉伸和压缩
若将力F由自内端A至杆B点处(图d),则其AB段内任一横 截面上的轴力都将等于零(图e).而BC段内任一横截面n-n上的 轴力仍等于F(图f),保持不变。
FN = 0
14
§2-2内力·截面法·轴力及轴力图 2.截面法、轴力
第二章 轴向拉伸和压缩
原因:这是因为集中力F由自由端A移至B点 后,改变了杆件AB段的变形。而并不改变BC 段的变形
第二步、绘制轴力图
第二章 轴向拉伸和压缩
FN kN
10
FN图kN
25
_
x
10
20
第二章 轴向拉伸和压缩
§2-2内力·截面法·轴力及轴力图
例2.2
30kN
A
30kN
作图示杆件的轴力图,并指出| FN |max
1
2
90kN
60kN
1
B
2
解:1、计算杆件各段的轴力。
C
AB 段
1
2
x FN1
FN2
1
2
60kN
第二章 轴向拉伸和压缩
§2-2内力·截面法·轴力及轴力图 2.截面法、轴力
注意:静力学中的力(或力偶)的可移性原理,在用截面法 求内力的过程中是有限制的。如图a所示拉杆在自由端A承 受集中力F,由截面法可得,杆任一横截面m—m或n—n” 上的轴力FN、均等于F(图b,c)。
材料力学 胡克定律

地加以描述的知识王国”。 3
1
2.4 拉压杆的变形 胡克定律 东汉经学家郑玄(127—200)对《考工记·弓人》中“量其力,
有三均”作了 这样的注释:“假令弓力胜三石,引之中三尺,弛 其弦,以绳缓擐之,每加物一石,则张一尺。” (图) 胡:请问,“弛其弦,以绳缓援之”
是什么意思 ? 郑:这是讲测量弓力时,先将弓的弦
松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
2
2.4 拉压杆的变形 胡克定律 郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说:
郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
必知弓力三石者,当弛其弦以绳缓擐之者,谓不张之,别以
一条 绳系两箭,乃加物一石张一尺、二石张二尺、三石张三 尺。其中 “两萧”就是指弓的两端。 胡:郑老先生讲“每加物一石,则张一尺”。和我讲的完全是同一 个意思。您比我早1500 中就记录下这种正比关系,的确了不起, 真是令人佩服之至』我在1686 年《关于中国文字和语言的研究 和推测》一文中早就推崇过贵国的古代文化:“目前我们还只 是刚刚走到这个知识领域的边缘,然而一旦对它有了充分的认 识,就将会在我们面 前展现出一个迄今为止只被人们神话般
ቤተ መጻሕፍቲ ባይዱ2.4 拉压杆的变形 胡克定律
3、单向应力状态下的弹性定律
(dx) 1 FN (x) 1
dx E A(x) E
4、泊松比(或横向变形系数)
即: 1
E
或 :
三、是谁首先提出弹性定律 弹性定律是材料力学等固体力学一个非常重要的基础。一般
认为它是由英国科学家胡克(1635一1703)首先提出来的,所以通 常叫做胡克定律。其实,在胡克之前1500年,我国早就有了关于 力和变形成正比关系的记载。
1
2.4 拉压杆的变形 胡克定律 东汉经学家郑玄(127—200)对《考工记·弓人》中“量其力,
有三均”作了 这样的注释:“假令弓力胜三石,引之中三尺,弛 其弦,以绳缓擐之,每加物一石,则张一尺。” (图) 胡:请问,“弛其弦,以绳缓援之”
是什么意思 ? 郑:这是讲测量弓力时,先将弓的弦
松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
2
2.4 拉压杆的变形 胡克定律 郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说:
郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
必知弓力三石者,当弛其弦以绳缓擐之者,谓不张之,别以
一条 绳系两箭,乃加物一石张一尺、二石张二尺、三石张三 尺。其中 “两萧”就是指弓的两端。 胡:郑老先生讲“每加物一石,则张一尺”。和我讲的完全是同一 个意思。您比我早1500 中就记录下这种正比关系,的确了不起, 真是令人佩服之至』我在1686 年《关于中国文字和语言的研究 和推测》一文中早就推崇过贵国的古代文化:“目前我们还只 是刚刚走到这个知识领域的边缘,然而一旦对它有了充分的认 识,就将会在我们面 前展现出一个迄今为止只被人们神话般
ቤተ መጻሕፍቲ ባይዱ2.4 拉压杆的变形 胡克定律
3、单向应力状态下的弹性定律
(dx) 1 FN (x) 1
dx E A(x) E
4、泊松比(或横向变形系数)
即: 1
E
或 :
三、是谁首先提出弹性定律 弹性定律是材料力学等固体力学一个非常重要的基础。一般
认为它是由英国科学家胡克(1635一1703)首先提出来的,所以通 常叫做胡克定律。其实,在胡克之前1500年,我国早就有了关于 力和变形成正比关系的记载。
材料力学PPT第二章

Q235钢的主要强度指标:s = 240 MPa,
b = 390 MPa
低碳钢拉伸试件图片
试件拉伸破坏断口图片
结合压缩曲线得到结论:颈缩过程,材 料的力学性质发生变化
塑性指标
1.延伸率
l1 l 100%
l
2.断面收缩率
A A1 A
100%
l1----试件拉断后的长度
A1----试件拉断后断口处的最小 横截面面积
F 用截面法取节点B为研究对象
Fx 0 FN1 cos 45 FN 2 0
x
Fy 0 FN1 sin 45 F 0
FN1 28.3kN
FN 2 20kN
A
FN1 28.3kN FN 2 20kN
1
2、计算各杆件的应力。
45° B
C
2
FN1
F
y
FN 2 45° B x
F
a
c
b
d
F FN dA
bd
A
dA A
A
FN
A
A 1
45°
C
2
FN1
y
FN 2 45° B
F
例题2.2
图示结构,试求杆件AB、CB的
应力。已知 F=20kN;斜杆AB为直
径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆)
≥5%—塑性材料 <5%—脆性材料 σ
Q235钢: 20% ~ 30% ≈60%
冷作硬化
O
应力-应变(σ-ε)图
注意:
(1) 低碳钢的s,b都还是以相应的抗力除以试
材料力学2-4

300
A A2 l 2 P
C
2
ቤተ መጻሕፍቲ ባይዱl 1
A1
A2 A A2 A3 0 tg 30 l 2 l 1 0 tg 30 sin 300
2 2 AA3 ( AA2) ( A2 A3)
A2
A
A’
l 2
l1
300
A1
300
3.78mm
A3
补充题 : 一等直杆受自重及集中力P作用。杆的长度为l,横
截面面积为A,材料的容重为,弹性模量为E,许用应力 为[]。试分析杆的自重对强度的影响,并求杆的伸长。 解: N(x)=P+ Ax Nmax=P+ Al
m m
N(x)
P+ Al
l
m Ax m
+
x
P
P P
P+ Ax
Nmax=P+ Al
N(x)
强度条件为
m
m
l
m Ax m
+
x
P γ l [σ ] A
(1) 1—1,11—11,111—111截面的轴力,作轴力图 (2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
111
11
1
P3 C
111
P2
11
P1 A
1
D
B
l3
111
l2
11
l1
1
R
P3 C
111
P2
11
P1 A
1
D
B
l3
l2
l1
解:求支座反力
R = -50KN
111
11
1
A A2 l 2 P
C
2
ቤተ መጻሕፍቲ ባይዱl 1
A1
A2 A A2 A3 0 tg 30 l 2 l 1 0 tg 30 sin 300
2 2 AA3 ( AA2) ( A2 A3)
A2
A
A’
l 2
l1
300
A1
300
3.78mm
A3
补充题 : 一等直杆受自重及集中力P作用。杆的长度为l,横
截面面积为A,材料的容重为,弹性模量为E,许用应力 为[]。试分析杆的自重对强度的影响,并求杆的伸长。 解: N(x)=P+ Ax Nmax=P+ Al
m m
N(x)
P+ Al
l
m Ax m
+
x
P
P P
P+ Ax
Nmax=P+ Al
N(x)
强度条件为
m
m
l
m Ax m
+
x
P γ l [σ ] A
(1) 1—1,11—11,111—111截面的轴力,作轴力图 (2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
111
11
1
P3 C
111
P2
11
P1 A
1
D
B
l3
111
l2
11
l1
1
R
P3 C
111
P2
11
P1 A
1
D
B
l3
l2
l1
解:求支座反力
R = -50KN
111
11
1
2材料力学轴向拉压.ppt课件

斜FA 布p纵α上切截=。截应c±面面力o4A5上FA上成so的截对p面全A dFA应Ac力mmm oia 可nxp9s i分0AAn 4α45解—A —59 ——为d0 c2 正横 斜Ao20 截截应s面面p力面面9 和积A 积0 4 4切550 应2F2力
pcos co2s22co2s psincossin2sin2
U
W
n i1
12Fii
利用外力功计算应变能并不方便,在更多情况下主 要是通过内力功来计算。
单向应力状态单元体微面上的力在变形过程中做的功为
y
x
dy dx
x
dz x
dW 1 2xdydzxdx1 2xxdV
不考虑能量损耗,则力做的功全部转化为单元体的应变能
dUdW12xxdV
单位体积内储存的应变能,称为应变能密度,单向应力状态有
2.3
F
F
b b1
拉压杆的变形
F 二、拉压杆的横向变形
l l1
bb1b
b
b
横向变形
横向线应变
实验表明,在胡克定律适用的范围时,有:
or
F/ A 即 横向线应变与轴向线应变恒异号,两者之 比的绝对值为一常数,称为泊松比。
00.5
弹性模量 E 和泊松比μ都是材料的弹性常数, 由实验测得。
l
l /l
第二章 轴向拉伸和压缩
A
F
连杆
A
钢拉杆
B
B
F
F
F
F
F
F
F
F
F
F
受力(简)图
受力变形特点: 外力或其合力的作用线沿杆件的轴线(轴载), 主要变形为轴向伸缩。这样的杆件称拉压杆。
pcos co2s22co2s psincossin2sin2
U
W
n i1
12Fii
利用外力功计算应变能并不方便,在更多情况下主 要是通过内力功来计算。
单向应力状态单元体微面上的力在变形过程中做的功为
y
x
dy dx
x
dz x
dW 1 2xdydzxdx1 2xxdV
不考虑能量损耗,则力做的功全部转化为单元体的应变能
dUdW12xxdV
单位体积内储存的应变能,称为应变能密度,单向应力状态有
2.3
F
F
b b1
拉压杆的变形
F 二、拉压杆的横向变形
l l1
bb1b
b
b
横向变形
横向线应变
实验表明,在胡克定律适用的范围时,有:
or
F/ A 即 横向线应变与轴向线应变恒异号,两者之 比的绝对值为一常数,称为泊松比。
00.5
弹性模量 E 和泊松比μ都是材料的弹性常数, 由实验测得。
l
l /l
第二章 轴向拉伸和压缩
A
F
连杆
A
钢拉杆
B
B
F
F
F
F
F
F
F
F
F
F
受力(简)图
受力变形特点: 外力或其合力的作用线沿杆件的轴线(轴载), 主要变形为轴向伸缩。这样的杆件称拉压杆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
移δB。1、已经测出CD杆的轴向应变ε;2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCD a
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B 2LCD 2a
2. 已知EA
0
FNCD 2F
B
2L2LCFDNCD
4FFa L EA
0
例题
2.12
图示的杆系是由两根圆截面钢杆铰接而成。已知
EA L L
L
i
FNi Li
EAi
FN EA L E
A AL
在计算ΔL的L长度内,FN,E,A均 为常数。
在材料的线弹性范围内,正应力与线应变呈正比关系。
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例题
2.10
例:图示直杆,其抗拉刚度为EA,试 求杆件的轴向变形△L,B点的位移 δB和C点的位移δC
A L
F
F
B
LAB
FL EA
B
C
L
C
B
FL EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆,
B点受荷载P作用,试在下面两种情况下分别计算B点的位
α=300,杆长L=2m,杆的直径d=25mm,材
料的弹性模量E=2.1×105MPa,设在结点A处悬
挂一重物F=100kN,试求结点A的位移δA。
X 0
FNAC sin FNAB sFin 0
B1
2
C Y 0
FNAC
FNAC cos
FNFANBAB c2ocsos F
0
FNAB FNAC
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
L
L
实验表明:在材料的线弹性范围内,△L与外力F
和杆长L成正比,与横截面面积A成反比。
L FN L EA
胡克定律 EA :拉抗(压)刚度
当拉(压)杆有两个以上的外力作用时,需要先画出轴力图,然后 分段计算各段的变形,各段变形的代数和即为杆的总伸长量。
αD
BB1 B 2CC1
FNCD
F
A
C
a
CC1
CLCCD
ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LCFDLFNC12DELAcLoCsD FCD
2F a
EA cos2
B
4Fa
EAcos3
αα
LAB
LAC
FNAC L EA
FL
2 EA cos
A
A
A
AA
LAC
cos
FL
2EAcos2
F
LAC
A
LAB
1.3mm 100103 2
2 2.1105 106 252 106
4
cos 300
A
图所示结构,刚性横梁AB由斜杆CD吊在水 例题 平位置上,斜杆CD的抗拉刚度为EA,B点 2.13 处受荷载F作用,试求B点的位移δB。
1. 已知ε
LCD
a
LCD a
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B 2LCD 2a
2. 已知EA
0
FNCD 2F
B
2L2LCFDNCD
4FFa L EA
0
例题
2.12
图示的杆系是由两根圆截面钢杆铰接而成。已知
EA L L
L
i
FNi Li
EAi
FN EA L E
A AL
在计算ΔL的L长度内,FN,E,A均 为常数。
在材料的线弹性范围内,正应力与线应变呈正比关系。
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例题
2.10
例:图示直杆,其抗拉刚度为EA,试 求杆件的轴向变形△L,B点的位移 δB和C点的位移δC
A L
F
F
B
LAB
FL EA
B
C
L
C
B
FL EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆,
B点受荷载P作用,试在下面两种情况下分别计算B点的位
α=300,杆长L=2m,杆的直径d=25mm,材
料的弹性模量E=2.1×105MPa,设在结点A处悬
挂一重物F=100kN,试求结点A的位移δA。
X 0
FNAC sin FNAB sFin 0
B1
2
C Y 0
FNAC
FNAC cos
FNFANBAB c2ocsos F
0
FNAB FNAC
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
L
L
实验表明:在材料的线弹性范围内,△L与外力F
和杆长L成正比,与横截面面积A成反比。
L FN L EA
胡克定律 EA :拉抗(压)刚度
当拉(压)杆有两个以上的外力作用时,需要先画出轴力图,然后 分段计算各段的变形,各段变形的代数和即为杆的总伸长量。
αD
BB1 B 2CC1
FNCD
F
A
C
a
CC1
CLCCD
ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LCFDLFNC12DELAcLoCsD FCD
2F a
EA cos2
B
4Fa
EAcos3
αα
LAB
LAC
FNAC L EA
FL
2 EA cos
A
A
A
AA
LAC
cos
FL
2EAcos2
F
LAC
A
LAB
1.3mm 100103 2
2 2.1105 106 252 106
4
cos 300
A
图所示结构,刚性横梁AB由斜杆CD吊在水 例题 平位置上,斜杆CD的抗拉刚度为EA,B点 2.13 处受荷载F作用,试求B点的位移δB。
