斐波那契数列(普通和递归实现)
r语言斐波那契数列递归实现

r语言斐波那契数列递归实现斐波那契数列是一种非常经典的数列,它的定义如下:第一项和第二项都是1,从第三项开始,每一项都是前两项的和。
因此,斐波那契数列的前几项是1、1、2、3、5、8、13、21、34、55、89、144……。
在r语言中,我们可以使用递归的方式来实现斐波那契数列。
递归是一种函数调用自身的方法,它可以让我们更加简洁地实现一些复杂的算法。
下面是使用r语言实现斐波那契数列的递归函数:```fibonacci <- function(n) {if (n == 1 || n == 2) {return(1)} else {return(fibonacci(n-1) + fibonacci(n-2))}}```这个函数接受一个整数n作为参数,返回斐波那契数列的第n项。
如果n等于1或2,那么直接返回1;否则,递归调用fibonacci函数计算前两项的和。
我们可以使用这个函数来计算斐波那契数列的前几项:```for (i in 1:10) {print(fibonacci(i))}```这段代码会输出斐波那契数列的前10项:1、1、2、3、5、8、13、21、34、55。
需要注意的是,递归函数的效率并不高,因为它会重复计算很多项。
例如,计算fibonacci(5)时,会重复计算fibonacci(3)和fibonacci(4)。
因此,当n比较大时,递归函数的效率会非常低下。
为了提高效率,我们可以使用循环的方式来实现斐波那契数列。
下面是使用循环实现斐波那契数列的代码:```fibonacci <- function(n) {if (n == 1 || n == 2) {return(1)} else {a <- 1b <- 1for (i in 3:n) {c <- a + ba <- bb <- c}return(b)}}```这个函数的实现方式与递归函数类似,但是使用了循环来避免重复计算。
尾递归实现斐波那契数列

尾递归实现斐波那契数列尾递归实现斐波那契数列斐波那契数列是一组无限序列,其中第一个和第二个数字都是1,之后的数字则是前两个数字之和。
例如:1, 1, 2, 3, 5, 8, 13, 21, 34, ...实现斐波那契数列有很多种方法,其中一种高效的方式是使用尾递归。
尾递归是指递归过程中,最后一步是调用自身。
下面是用尾递归实现斐波那契数列的代码:```def fibonacci(n, a=1, b=1):if n == 1:return aelif n == 2:return belse:return fibonacci(n-1, b, a+b)```这个函数接受一个整数n作为输入,以及两个默认值a和b(默认值分别为1),然后返回序列中的第n个数字。
函数的主要逻辑是这样的:如果n等于1,则返回a;如果n等于2,则返回b;否则,调用自身,输入n-1,以及新的a为b,新的b为a+b,然后返回结果。
使用这种方式实现斐波那契数列的好处是,每一次递归都会把之前的计算结果传递给下一次递归,避免了重复计算,节省了计算时间。
下面是一个完整的实现示例:```def fibonacci(n, a=1, b=1):"""使用尾递归实现斐波那契数列"""if n == 1:return aelif n == 2:return belse:return fibonacci(n-1, b, a+b)def main():"""主函数,输出前20个斐波那契数列数字"""result = []for i in range(1, 21):result.append(fibonacci(i))# 划分列表divided_result = [result[i:i+5] for i in range(0, len(result), 5)]# 输出结果for item in divided_result:print(item)if __name__ == '__main__':main()```在这个完整的实现示例中,我们定义了一个main函数,它首先生成前20个斐波那契数列数字并将它们添加到一个结果列表中,然后使用列表划分功能,将结果列表划分为多个子列表,使输出更加整齐。
python经典代码

python经典代码Python是一门功能强大且易于学习的编程语言,广泛应用于各个领域。
它的简洁性和灵活性使得Python成为许多开发者的首选语言。
在这篇文章中,我们将探讨一些经典的Python代码示例,展示Python的魅力和实用性。
一、斐波那契数列斐波那契数列是一个经典的数学问题,定义如下:第一个和第二个数字是1,之后的数字是前两个数字之和。
下面是使用Python实现斐波那契数列的代码:```def fibonacci(n):fib = [1, 1]for i in range(2, n):fib.append(fib[i - 1] + fib[i - 2])return fibn = 10result = fibonacci(n)print(result)```二、冒泡排序冒泡排序是一种简单但有效的排序算法。
它通过多次比较和交换相邻元素的方式,将最大值逐步“冒泡”到最右侧。
下面是使用Python实现冒泡排序的代码:```def bubble_sort(arr):n = len(arr)for i in range(n - 1):for j in range(n - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]arr = [4, 2, 6, 1, 9]bubble_sort(arr)print(arr)```三、递归实现阶乘阶乘是另一个常见的数学问题,定义如下:n的阶乘(表示为n!)等于1乘以2乘以3一直乘到n。
下面是使用递归方式实现计算阶乘的Python代码:```def factorial(n):if n == 0:return 1else:return n * factorial(n - 1)n = 5result = factorial(n)print(result)```四、矩阵转置矩阵转置是将矩阵的行转换为对应的列,列转换为对应的行。
母牛问题(递归实现、非递归)实现两种以及斐波那契数列的实现

母⽜问题(递归实现、⾮递归)实现两种以及斐波那契数列的实现【题⽬】假设农场中成熟的母⽜每年只会⽣1头⼩母⽜,并且永远不会死。
第⼀年农场有1只成熟的母⽜,从第⼆年开始,母⽜开始⽣⼩母⽜。
每只⼩母⽜3年之后成熟⼜可以⽣⼩母⽜。
给定整数N,求出N年后⽜的数量。
【举例】N=6,第1年1头成熟母⽜记为a;第2年a⽣了新的⼩母⽜,记为b,总⽜数为2;第3年a⽣了新的⼩母⽜,记为c,总数为3;第4年a⽣了新⽜d,总数4;第5年b成熟了,ab分别⽣了⼀只,总数为6;第6年c也成熟了,abc分别⽣了⼀只,总数为9,故返回9.斐波那契数列的递归和⾮递归实现斐波那契数列:public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.println("请输⼊第⼏年?"); int n = scanner.nextInt(); int sum = dg(n);//递归⽅式// int sum = fdg(n);//⾮递归⽅式 System.out.println("第" + n + "年总共有" + sum + "头⽜");}//递归实现 public static int dg(int n) {if (n < 1) { return 0; }if (n == 1 || n == 2 || n == 3 || n == 4) { return n; }return dg(n - 1) + dg(n - 3);}//⾮递归实现 public static int fdg(int n) {int a = 1; //初始化第⼀项 int b = 2;//初始化第⼆项 int res = 3;//初始化第三项 int t = 0;//res 的原来值if (n == 1 || n == 2 || n == 3) { return n; }for (int i = 4; i <= n; i++) { t = res; res = b + a; a = b; b = t; } return res; }递归的原理:每⼀级的函数调⽤都有⾃⼰的变量。
C语言中斐波那契数列的三种实现方式(递归、循环、矩阵)
C语⾔中斐波那契数列的三种实现⽅式(递归、循环、矩阵)⽬录⼀、递归⼆、循环三、矩阵《剑指offer》⾥讲到了⼀种斐波那契数列的 O(logN) 时间复杂度的实现,觉得挺有意思的,三种⽅法都记录⼀下。
⼀、递归⼀般来说递归实现的代码都要⽐循环要简洁,但是效率不⾼,⽐如递归计算斐波那契数列第n个元素。
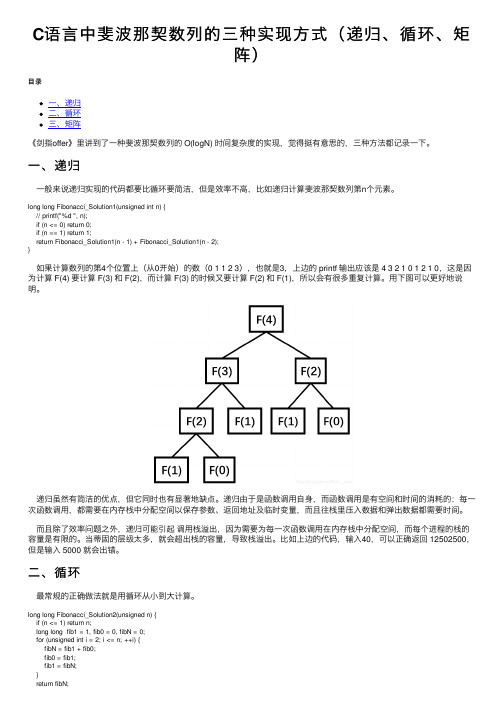
long long Fibonacci_Solution1(unsigned int n) {// printf("%d ", n);if (n <= 0) return 0;if (n == 1) return 1;return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);}如果计算数列的第4个位置上(从0开始)的数(0 1 1 2 3),也就是3,上边的 printf 输出应该是 4 3 2 1 0 1 2 1 0,这是因为计算 F(4) 要计算 F(3) 和 F(2),⽽计算 F(3) 的时候⼜要计算 F(2) 和 F(1),所以会有很多重复计算。
⽤下图可以更好地说明。
递归虽然有简洁的优点,但它同时也有显著地缺点。
递归由于是函数调⽤⾃⾝,⽽函数调⽤是有空间和时间的消耗的:每⼀次函数调⽤,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,⽽且往栈⾥压⼊数据和弹出数据都需要时间。
⽽且除了效率问题之外,递归可能引起调⽤栈溢出,因为需要为每⼀次函数调⽤在内存栈中分配空间,⽽每个进程的栈的容量是有限的。
当蒂固的层级太多,就会超出栈的容量,导致栈溢出。
⽐如上边的代码,输⼊40,可以正确返回 12502500,但是输⼊ 5000 就会出错。
⼆、循环最常规的正确做法就是⽤循环从⼩到⼤计算。
long long Fibonacci_Solution2(unsigned n) {if (n <= 1) return n;long long fib1 = 1, fib0 = 0, fibN = 0;for (unsigned int i = 2; i <= n; ++i) {fibN = fib1 + fib0;fib0 = fib1;fib1 = fibN;}return fibN;}或者下边这种long long Fibonacci_Solution2(unsigned n) {if (n <= 1) return n;long long a = 0, b = 1;for (unsigned int i = 2; i <= n; ++i) {b = a + b;a =b - a;}return b;}三、矩阵数中提到了⼀种 O(logN) 时间复杂度的算法,就是利⽤数学公式计算。
斐波那契数列.实现斐波那契数列的计算,程序使用循环结构和递归算法计算斐波那契数

斐波那契数列是一个非常有名的数列,在这个数列中,前两个数是0和1,后面的每个数都是前两个数的和。
这里有两种实现斐波那契数列的方式,一种是使用循环结构,另一种是使用递归算法。
1. 循环结构实现pythondef fibonacci_iterative(n):if n <= 0:return []elif n == 1:return [0]elif n == 2:return [0, 1]else:fib_seq = [0, 1]for i in range(2, n):fib_seq.append(fib_seq[i-1] + fib_seq[i-2])return fib_seqprint(fibonacci_iterative(10)) # 输出斐波那契数列的前10项2. 递归算法实现pythondef fibonacci_recursive(n):if n <= 0:return []elif n == 1:return [0]elif n == 2:return [0, 1]else:fib_seq = fibonacci_recursive(n-1)fib_seq.append(fib_seq[-1] + fib_seq[-2])return fib_seqprint(fibonacci_recursive(10)) # 输出斐波那契数列的前10项注意:虽然递归算法在理解上可能更为直观,但对于大的n值,递归算法可能会因为重复计算和栈溢出而变得非常慢。
在实际应用中,通常会使用循环结构或者带有记忆功能的递归(也就是动态规划)来优化斐波那契数列的计算。
此外,以上代码中的fibonacci_iterative和fibonacci_recursive函数返回的都是斐波那契数列的前n项,如果你只需要计算第n项,可以对这些代码进行相应的修改。
斐波那契数列(递归、非递归算法)

斐波那契数列(递归、⾮递归算法)题⽬斐波那契数,亦称之为斐波那契数列(意⼤利语: Successione di Fibonacci),⼜称黄⾦分割数列、费波那西数列、费波拿契数、费⽒数列,指的是这样⼀个数列:1、1、2、3、5、8、13、21、……在数学上,斐波那契数列以如下被以递归的⽅法定义:F0=0,F1=1,Fn=Fn-1+Fn-2(n>=2,n∈N*),⽤⽂字来说,就是斐波那契数列由 0 和 1 开始,之后的斐波那契数列系数就由之前的两数相加。
限制时间限制:1秒空间限制:32768Kpackage com.algorithm;import java.util.Scanner;/*** ⼤家都知道斐波那契数列,现在要求输⼊⼀个整数n,请你输出斐波那契数列的第n项。
n<=39* @⽇期:2018年6⽉30⽇下午10:11:43* @作者:Chendb*/public class Fibonacci {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();System.out.println(fibonacciRecursion(n));System.out.println(fibonacci(n));}/*** 递归算法* @param n* @return*/public static int fibonacciRecursion(int n) {if (n < 1) {return 0;}if( n == 1 || n == 2) {return 1;}return fibonacciRecursion(n-1) + fibonacciRecursion(n-2);}/*** ⾮递归算法* @param n* @return*/public static int fibonacci(int n) {if (n < 1) {return 0;}if( n == 1 || n == 2) {return 1;}int result = 1;int preResult = 1; // n - 2项int currentResult = 1; // n - 1项for (int i = 3; i <= n; i++) {result = preResult + currentResult; // n = f(n-1) + f(n-2)preResult = currentResult; // f(n-2) = f(n-1)currentResult = result; // f(n-1) = n}return result;}}View Code。
使用递归算法求斐波那契数列的第n项

使用递归算法求斐波那契数列的第n项使用递归算法求解斐波那契数列的第n项是一个经典的数学问题。
斐波那契数列是指从0和1开始,后一项是前两项之和的数列。
数学表达式可以表示为:Fn = Fn-1 + Fn-2,其中n表示数列的项数。
递归算法是一种通过调用自身函数来解决问题的方法。
在求解斐波那契数列的第n项时,可以利用递归算法的特性,将问题不断拆分为更小的子问题,直到最终达到基本情况。
为了使用递归算法求解斐波那契数列的第n项,首先需要定义一个递归函数。
这个函数接受一个整数n作为参数,表示要求解的斐波那契数列的第n项。
然后,通过判断n的值,确定是否已经达到基本情况。
当n等于0或1时,斐波那契数列的第n项分别为0和1,即F0=0,F1=1。
这是递归算法的基本情况,可以直接返回结果。
当n大于1时,可以通过递归调用自身函数来求解斐波那契数列的第n项。
具体思路是,先递归求解第n-1项和第n-2项,然后将两者相加得到第n项的值。
下面是使用递归算法求解斐波那契数列的第n项的示例代码:```pythondef fibonacci(n):if n == 0:return 0elif n == 1:return 1else:return fibonacci(n-1) + fibonacci(n-2)```通过上述递归函数,我们可以很方便地求解斐波那契数列的任意一项。
例如,要求解斐波那契数列的第10项,可以调用`fibonacci(10)`,得到结果55。
然而,尽管递归算法简洁明了,但也存在一些问题。
递归算法的时间复杂度较高,随着n的增大,计算量呈指数级增加。
这是因为递归算法需要重复计算相同的子问题,造成了重复的工作量。
此外,递归算法还会占用较多的内存空间,因为每次递归调用都需要在栈中保存一些临时变量。
为了解决递归算法的效率问题,可以考虑使用迭代算法来求解斐波那契数列。
迭代算法通过循环的方式,逐步计算每一项的值,避免了重复计算和大量的函数调用。
用python写斐波那契数列

用python写斐波那契数列斐波那契数列就是一系列的数字构成的序列,这个序列以如下方式进行定义:开头的两个数字是 0 1,之后的数字是前两个数字之和。
斐波那契数列具有独特的特性,它有着广泛的应用。
本文就通过Python来写斐波那契数列,供读者参考。
首先,我们来看一下Python如何写斐波那契数列。
Python可以快速的生成斐波那契数列,最常用的方法就是使用递归。
递归即函数调用它自身,在斐波那契数列中,递归实现就是用第一个和第二个数字初始化,之后每次调用函数自身就能得到下一个数字。
下面是Python实现斐波那契数列的简单代码:def Fibonacci(num):if num == 0:return 0elif num == 1:return 1else:return Fibonacci(num - 1) + Fibonacci(num - 2)for i in range(10):print(Fibonacci(i))上面的代码就实现了前10个数字的斐波那契数列,调用Fibonacci()函数可以输出斐波那契数列的任意一个数字,只需要把函数中的参数num改变即可。
另外,Python也可以使用迭代来实现斐波那契数列,迭代是一种算法,它将一个问题分解成多个子问题,逐个解决每一个子问题。
要使用迭代实现斐波那契数列,就要把前一个数字和前两个数字之和作为下一个数字,把这个过程重复做下去,就可以实现斐波那契数列。
下面就是使用迭代实现斐波那契数列的代码:def Fibonacci(num):if num == 0:return 0elif num == 1:return 1else:n_2 = 0n_1 = 1for i in range(num-1):n = n_2 + n_1n_2 = n_1n_1 = nreturn nfor i in range(10):print(Fibonacci(i))上面的代码也能实现前10个斐波那契数列,和递归实现的方法完全一样,只是迭代定义了两个变量,分别是n_2和n_1,表示前两个数字,通过这两个变量的更新,循环进行之后就能得到斐波那契数列的下一个数字。
c++递归求斐波那契数列

c++递归求斐波那契数列斐波那契数列是指每个数字都是前两个数字之和的数列,其前几个数字依次为0、1、1、2、3、5、8、13、21、34等。
下面我将通过递归的方法来实现斐波那契数列的求解。
递归是一种将问题分解成更小规模的子问题,并通过调用自身来解决问题的方法。
在斐波那契数列中,我们可以将问题定义为:给定一个正整数n,求解斐波那契数列的第n个数字。
首先,我们需要定义递归的终止条件。
在斐波那契数列中,当n 等于0或1时,其值是已知的(分别为0和1),不需要再进行递归调用,可以直接返回结果。
接下来,我们可以定义递归的求解过程。
对于任意大于1的n,我们可以通过递归求解n-1和n-2的斐波那契数列,然后将两者的和作为结果返回。
具体实现如下:```c++#include<iostream>using namespace std;int fibonacci(int n) {if (n == 0 || n == 1) { //终止条件return n;} else {return fibonacci(n - 1) + fibonacci(n - 2); //递归调用}}int main() {int n;cout << "请输入一个正整数n:" << endl;cin >> n;int result = fibonacci(n);cout << "斐波那契数列的第" << n << "个数字为:" << result << endl;return 0;}```在上述代码中,`fibonacci`函数用于求解斐波那契数列的第n个数字。
首先判断n是否为0或1,若是,则直接返回n;否则,通过递归调用`fibonacci`函数来求解n-1和n-2的斐波那契数列,并将两者的和作为结果返回。
php实现斐波那契数列,返回第n个斐波那契

斐波那契数列是数学中经典的问题之一,以意大利数学家斐波那契的名字命名。
斐波那契数列的定义是:F(0)=0,F(1)=1,对于n>1,F(n)=F(n-1)+F(n-2)。
显然,斐波那契数列是一个递归定义的数列,它的前几个数字依次是0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ……在实际编程中,经常会遇到要求返回斐波那契数列的第n个数的问题。
PHP作为一种广泛应用于Web开发的编程语言,它也可以很方便地实现斐波那契数列的计算。
本文将介绍如何在PHP中实现斐波那契数列的计算,并返回第n个斐波那契数。
二、使用递归算法实现斐波那契数列1. 递归算法的特点递归算法是指在算法的定义中包含对自身的调用。
在斐波那契数列的计算中,其定义本身就是递归的,因此可以使用递归算法来实现。
2. 递归实现斐波那契数列的PHP代码<?function fibonacci($n){if ($n<=0){return 0;}elseif ($n==1){return 1;return fibonacci($n-1)+fibonacci($n-2);}}>3. 递归算法的优缺点递归算法实现简单,直接套用斐波那契数列的定义即可,代码量少,易于理解。
但是,递归算法的效率较低,计算复杂度较高,特别是对于大的n值,递归算法的效率更是低下。
当n较大时,递归算法不适合用于计算斐波那契数列。
三、使用迭代算法实现斐波那契数列1. 迭代算法的特点迭代算法是指在算法中使用循环结构来重复执行一段代码,从而达到求解问题的目的。
在斐波那契数列的计算中,可以通过迭代算法来实现,并且迭代算法的效率比递归算法高。
2. 迭代实现斐波那契数列的PHP代码<?function fibonacci($n){$prev = 0;$sum = 1;for ($i = 2; $i <= $n; $i++){$temp = $sum;$sum = $prev + $sum;$prev = $temp;}return $sum;}>3. 迭代算法的优缺点迭代算法的效率高,计算复杂度低,适合用于大规模的斐波那契数列的计算。
斐波那契数列的四种实现方式

斐波那契数列的四种实现方式F(0)=0F(1)=1F(n)=F(n-1)+F(n-2)(n>=2)在C语言中,我们可以使用四种不同的方法来实现斐波那契数列。
1.递归实现:递归是一种自身调用的方法。
可以通过递归函数来实现斐波那契数列的计算。
代码如下:```c#include <stdio.h>int fibonacci(int n)if (n <= 1)return n;}return fibonacci(n-1) + fibonacci(n-2);int maiint n = 10;printf("斐波那契数列前%d个数为: ", n);for (int i = 0; i < n; i++)printf("%d, ", fibonacci(i));}return 0;```该代码先定义了一个递归函数`fibonacci`,该函数根据斐波那契数列的定义,通过递归调用自身来计算每个数。
在主函数中,通过调用`fibonacci`函数来打印斐波那契数列的前n个数。
2.迭代实现:迭代是一种重复执行的方法。
我们可以通过循环来实现斐波那契数列的计算。
代码如下:```c#include <stdio.h>void fibonacci(int n)int a = 0, b = 1, c;printf("斐波那契数列前%d个数为: ", n);for (int i = 0; i < n; i++)printf("%d, ", a);c=a+b;a=b;b=c;int maiint n = 10;fibonacci(n);return 0;```该代码使用三个变量a、b和c来存储斐波那契数列的前两个数和计算的当前数。
通过循环,我们可以连续计算出斐波那契数列的n个数,并打印出来。
3.动态规划实现:动态规划是一种自底向上的方法,通过将问题分解为子问题来解决复杂问题。
c语言实现斐波那契数列的常见方法

c语言实现斐波那契数列的常见方法C语言实现斐波那契数列的常见方法介绍斐波那契数列是一个经典的数学问题,在计算机编程中也经常用到。
它的定义是:第一个和第二个数为1,之后的每个数都是前两个数的和。
本文将介绍几种常见的C语言实现斐波那契数列的方法。
方法一:递归递归是最直观的实现方法之一,通过不断调用函数自身来计算斐波那契数列。
int fibonacci(int n) {if (n <= 1)return n;return fibonacci(n-1) + fibonacci(n-2);}方法二:迭代迭代是一种更高效的方法,通过循环来计算斐波那契数列。
int fibonacci(int n) {int a = 0, b = 1, c;if (n == 0)return a;for (int i = 2; i <= n; i++) {c = a + b;a = b;b = c;}return b;}方法三:动态规划动态规划是一种将问题分解为子问题并保存结果的方法,可以用来解决斐波那契数列的计算。
int fibonacci(int n) {int f[n+1];f[0] = 0;f[1] = 1;for (int i = 2; i <= n; i++) {f[i] = f[i-1] + f[i-2];}return f[n];}方法四:矩阵快速幂这是一种更高级的方法,利用矩阵的性质来计算斐波那契数列。
typedef struct {int m[2][2];} Matrix;Matrix matrixMultiply(Matrix a, Matrix b) {Matrix c;[0][0] = [0][0]*[0][0] + [0][1]*[1][0];[0][1] = [0][0]*[0][1] + [0][1]*[1][1];[1][0] = [1][0]*[0][0] + [1][1]*[1][0];[1][1] = [1][0]*[0][1] + [1][1]*[1][1];return c;}Matrix matrixPow(Matrix a, int n) {if (n == 1)return a;Matrix half = matrixPow(a, n/2);Matrix result = matrixMultiply(half, half); if (n % 2 == 1)result = matrixMultiply(result, a);return result;}int fibonacci(int n) {if (n <= 1)return n;Matrix a;[0][0] = 1;[0][1] = 1;[1][0] = 1;[1][1] = 0;Matrix result = matrixPow(a, n-1);return [0][0];}总结通过递归、迭代、动态规划和矩阵快速幂等方法,我们可以在C 语言中实现斐波那契数列的计算。
java中斐波那契数列

java中斐波那契数列斐波那契数列是一个经典的数学问题,在计算机科学中也得到了广泛应用。
它的定义非常简单明了:第一个和第二个数为1,从第三个数开始,每个数都是前两个数之和。
具体的数列如下:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...在Java中,我们可以使用递归或迭代的方式来计算斐波那契数列。
下面我们将分别介绍这两种方法的实现。
一、递归方法:递归是一种通过调用自身来解决问题的方法。
对于斐波那契数列,我们可以定义一个递归函数来计算第n个数的值。
具体代码如下:```public static int fibonacci(int n) {if (n <= 2) {return 1;}return fibonacci(n - 1) + fibonacci(n - 2);}```在这段代码中,我们首先判断n是否小于等于2,如果是,则直接返回1,否则,递归调用函数自身来计算第n-1和n-2个数的值,并将它们相加作为结果返回。
二、迭代方法:迭代是一种通过循环来解决问题的方法。
对于斐波那契数列,我们可以使用循环来计算第n个数的值。
具体代码如下:```public static int fibonacci(int n) {if (n <= 2) {return 1;}int a = 1;int b = 1;for (int i = 3; i <= n; i++) {int temp = a + b;a = b;b = temp;}return b;}```在这段代码中,我们首先判断n是否小于等于2,如果是,则直接返回1。
接下来,我们使用两个变量a和b来分别保存第n-2和n-1个数的值,然后通过循环计算第n个数的值。
在每次循环中,我们将a+b的结果保存在临时变量temp中,然后将b的值赋给a,将temp的值赋给b,最后返回b作为结果。
以上就是使用递归和迭代两种方法来计算斐波那契数列的代码。
斐波那契数列

斐波那契数列“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacc i,生于公元1170年,卒于1240年,籍贯大概是比萨)。
他被人称作“比萨的列昂纳多”。
1202年,他撰写了《珠算原理》(Liber Abaci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、……这个数列从第三项开始,每一项都等于前两项之和。
它的通项公式为:(1/√5)*{[(1 +√5)/2]^n - [(1-√5)/2]^n}(又叫“比内公式”,是用无理数表示有理数的一个范例。
)(√5表示根号5)有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。
[编辑本段]【奇妙的属性】随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割的数值0.61803 39887……从第二项开始,每个奇数项的平方都比前后两项之积多1,每个偶数项的平方都比前后两项之积少1。
(注:奇数项和偶数项是指项数的奇偶,而并不是指数列的数字本身的奇偶,比如第五项的平方比前后两项之积多1,第四项的平方比前后两项之积少1)如果你看到有这样一个题目:某人把一个8*8的方格切成四块,拼成一个5*13的长方形,故作惊讶地问你:为什么64=65?其实就是利用了斐波那契数列的这个性质:5、8、13正是数列中相邻的三项,事实上前后两块的面积确实差1,只不过后面那个图中有一条细长的狭缝,一般人不容易注意到。
斐波那契数列的第n项同时也代表了集合{1,2,...,n}中所有不包含相邻正整数的子集个数。
斐波那契数列(f(n),f(0)=0,f(1)=1,f(2)=1,f(3)=2……)的其他性质:1.f(0)+f(1)+f(2)+…+f(n)=f(n+2)-12.f(1)+f(3)+f(5)+…+f(2n-1)=f(2n)-13.f(0)+f(2)+f(4)+…+f(2n)=f(2n+1)-14.[f(0)]^2+[f(1)]^2+…+[f(n)]^2=f(n)·f(n+1)5.f(0)-f(1)+f(2)-…+(-1)^n·f(n)=(-1)^n·[f(n+1)-f(n)]+16.f(m+n)=f(m-1)·f(n-1)+f(m)·f(n)利用这一点,可以用程序编出时间复杂度仅为O(log n)的程序。
递归法求斐波那契数列第n项

递归法求斐波那契数列第n项斐波那契数列是数学中一个著名的数列,它的定义是:前两项为0和1,从第三项起,每一项都等于前两项之和。
用数学公式表示为:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2)。
斐波那契数列可以用递归的方法来求解。
递归是一种将一个大问题分解成更简单的子问题的方法,通过不断地调用自身来解决问题。
对于斐波那契数列,可以使用递归算法来计算第n项的值。
要求斐波那契数列的第n项,可以先考虑递归的终止条件,即边界条件。
根据斐波那契数列的定义,前两项为0和1,因此当n为0或1时,直接返回0或1即可。
这是一个递归的终止条件,可以作为递归算法的基准情况。
当n大于1时,需要计算第n项的值。
根据斐波那契数列的定义,第n项等于前两项之和,因此可以通过递归调用求解第n-1项和第n-2项的值,然后将两者相加得到第n项的值。
具体递归的表达式为:F(n)=F(n-1)+F(n-2)。
递归算法的思想是将大问题分解成更小的子问题,然后通过不断地调用自身来解决子问题。
在这个过程中,递归算法会不断地调用自身,直到达到终止条件。
然后从最小的子问题开始,逐步解决更大的子问题,最终解决整个问题。
递归算法的实现需要注意两个问题:递归的终止条件和递归表达式的正确性。
递归的终止条件是确定的,就是当n为0或1时,直接返回0或1;递归表达式的正确性是基于斐波那契数列的定义的,通过不断地调用自身求解子问题,并将子问题的解合并得到整个问题的解。
递归算法的效率并不高。
由于递归算法会进行多次重复计算,因此在计算较大的斐波那契数列时,会出现严重的效率问题。
例如,计算F(50)时就需要进行大量的重复计算,造成了很大的时间消耗。
为了提高效率,可以使用动态规划的方法来解决斐波那契数列的问题。
动态规划是一种将大问题分解成更小的子问题,并保存子问题的解以供重复使用的方法。
通过动态规划,可以避免重复计算,提高算法的效率。
动态规划方法的基本思想是,首先确定递推关系式,然后根据递推关系式计算每个子问题的解,最后根据子问题的解计算整个问题的解。
使用递归求斐波那契数列第十项的值

斐波那契数列是数学中常见的一个序列,其特点是前两项之和等于后一项,即F(n) = F(n-1) + F(n-2),其中F(1) = 1,F(2) = 1。
斐波那契数列的前几项为1, 1, 2, 3, 5, 8, 13, 21, 34, 55...要求使用递归的方式求斐波那契数列第十项的值。
1. 理解递归在介绍递归之前,我们需要首先了解递归的概念。
递归是指一个函数在内部调用自身的过程。
在编程中,递归通常用于解决能够被拆分为相似子问题的任务。
2. 编写递归函数我们需要编写一个递归函数来计算斐波那契数列的第n项。
递归函数的基本结构为:```def fibonacci(n):if n <= 0:return 0elif n == 1 or n == 2:return 1else:return fibonacci(n-1) + fibonacci(n-2)```在这个函数中,当n小于等于0时,返回0;当n等于1或2时,返回1;其他情况下,返回fibonacci(n-1)与fibonacci(n-2)的和。
3. 调用递归函数接下来,我们可以在主程序中调用这个递归函数,计算斐波那契数列的第十项。
代码如下:```result = fibonacci(10)print(result)```运行该程序,将会输出斐波那契数列的第十项的值。
4. 注意事项虽然递归是一种优雅的解决方案,但也需要注意一些问题。
递归算法存在重复计算的问题,会导致计算效率低下。
递归的层级过深可能会导致栈溢出的问题,因此在使用递归时需要注意优化算法,避免出现不必要的性能问题。
5. 结论通过使用递归的方式,我们成功求得了斐波那契数列的第十项的值。
递归是一种强大的计算工具,能够简洁地解决许多复杂的问题,但在使用时需要谨慎考虑算法的效率和性能。
希望本文能够帮助读者更好地理解递归的概念及其在斐波那契数列中的应用。
递归是计算机科学中一个非常重要的概念,它不仅在算法设计中有着广泛的应用,也是解决许多数学问题的重要方法。
c语言编写递归函数,实现斐波那契数列前20项的和。

c语言编写递归函数,实现斐波那契数列前20项的和。
篇一:斐波那契数列是一组以2为首项、以5为公差值的等差数列。
在数学中,这个数列通常用符号斐波那契数列来表示,例如,1、1、2、3、5、8、13、21、34、55、89、144等等。
在C语言中,我们可以使用递归函数来计算斐波那契数列的前n项和。
递归函数是一种函数调用自身的函数,这种函数调用可以在程序中循环执行,从而实现复杂的计算。
下面是一个简单的C语言代码示例,用于计算斐波那契数列前20项的和: ```c#include <stdio.h>int fibonacci(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;} else {return fibonacci(n - 1) + fibonacci(n - 2);}}int main() {int n;printf("Enter the number of terms: ");scanf("%d", &n);printf("Fibonacci sum of %d terms: %d", n, fibonacci(n));return 0;}```在这个示例中,`fibonacci`函数是递归函数,用于计算斐波那契数列的前n 项和。
在函数中,如果n等于0,返回0;如果n等于1,返回1;否则,返回fibonacci(n-1)加上fibonacci(n-2)。
在`main`函数中,我们输入要计算的斐波那契数列项数n,然后调用`fibonacci`函数来计算前n项和,并将结果打印出来。
需要注意的是,递归函数的返回值是一个整数,如果需要使用浮点数,需要使用`double`类型来传递参数。
另外,在使用递归函数时,需要注意递归条件的设置,以避免无限递归导致程序崩溃。
采用递归方法求斐波那契数列的前20项

采用递归方法求斐波那契数列的前20项
斐波那契数列是指从0和1开始,后面每一项都是前面两项的和。
即:0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765……
本文将采用递归方法求斐波那契数列的前20项。
递归方法是指在函数内部调用自身的方法。
在求斐波那契数列时,我们可以定义一个函数,输入一个正整数n,返回斐波那契数列的第n项。
具体实现如下:
```python
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
```
在上述代码中,我们首先判断n的值是否为0或1,如果是,则直接返回0或1;否则,递归调用函数本身,返回前两项的和。
接下来,我们可以使用for循环调用上述函数,输出斐波那契数列的前20项:
```python
for i in range(20):
print(fibonacci(i), end=' ')
```
运行上述代码,即可得到斐波那契数列的前20项:0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181。
通过递归方法求斐波那契数列,我们可以看到,递归方法虽然简单,但是在计算大量数据时,会出现效率低下的问题。
因此,在实际应用中,我们需要根据具体情况选择合适的算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
System.out.println("请输入数列的项数(输入-1结束):");
Scanner sin = new Scanner(System.in);
int num = sin.nextInt();
if (num == -1) {
break;
} else {
public static long fibonacci(int iNum)
{
if(iNum == 1) return 1;
if(iNum == 2) return 1;
return fibonacci(iNum - 1) + fibonacci(iNum - 2);
long start=System.currentTimeMillis();
sum = getFibonacciSequenceSum(num);
long stop=System.currentTimeMillis();
long time=stop-start;
}
public static long CallFibocacci(int n)
{
long sum = 0;
for(int i = 1;i <= n; ++i)
{
long ltemp = fibonacci(i);
sum += ltemp;
}
}
}
}
Scanner sin = new Scanner(System.in);
int num = sin.nextInt();
if (num == -1) {
break;
} else {
long start = System.currentTimeMillis();
long num1 = 1;
long num2 = 1;
long temp = 0;
long sum = 0;
if (num == 1) {
sum = 1;
System.out.println(num1);
} else {
sum = num1 + num2;
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、……
这个数列从第三项开始,每一项都等于前两项之和。它的通项公式为:(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}(又叫“比内公式”,是用无理数表示有理数的一个范例。)(√5表示根号5)
有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。
sum = CallFibocacci(num);
long stop = System.currentTimeMillis();
long time = stop - start;
System.out.println("sum=" + sum + "\ntime=" + time);
System.out.println("sum=" + sum+"\ntime="+time);
}
}
}
}
package com.testdata;
import java.util.Scanner;
public class FibonacciRecursion {
package com.testdata;
import java.util.Scanner;
import org.omg.CORBA.Current;
public class FibonacciSequence {
private static long getFibonacciSequenceSum(int num) {
System.out.println(ltemp + ",");
}
return sum;
}
public static void main(String[] args) {
long sum;
while (true) {
System.out.println("请输入数列的项数(输入-1结束):");
System.out.print(num1 + "," + num2);
}
for (int i = 3; i <= num; i++) {
temp = num2;
num2 = num1 + num2;
num1 =ystem.out.print("," + num2);
}
System.out.println();
return sum;
}
public static void main(String[] args) {
long sum;
while (true) {
“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨)。他被人称作“比萨的列昂纳多”。1202年,他撰写了《珠算原理》(Liber Abaci)一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。
