4.3非欧几何学解析
不可思议的几何──非欧几何

不可思议的几何──非欧几何非欧几何的来源非欧几何学是一门大的数学分支,普通来讲,他有狭义、狭义、通常意义这三个方面的不同含义。
所谓狭义式泛指一切和欧几里的几何学不同的几何学,狭义的非欧几何只是指罗式几何来说的,至于通常意义的非欧几何,就是指罗式几何和黎曼几何这两种几何。
欧几里得的«几何原本»提出了五条公设,临时以来,数学家们发现第五公设和前四个公设比拟起来,显得文字表达冗长,而且也不那么显而易见。
有些数学家还留意到欧几里得在«几何原本»一书中直到第二十九个命题中才用到,而且以后再也没有运用。
也就是说,在«几何原本»中可以不依托第五公设而推出前二十八个命题。
因此,一些数学家提出,第五公设能不能不作为公设,而作为定理?能不能依托前四个公设来证明第五公设?这就是几何开展史上最著名的,争论了长达两千多年的关于〝平行线实际〞的讨论。
由于证明第五公设的效果一直得不到处置,人们逐渐疑心证明的路子走的对不对?第五公设究竟能不能证明?到了十九世纪二十年代,俄国喀山大学教授罗巴切夫斯基在证明第五公设的进程中,他走了另一条路子。
他提出了一个和欧式平行公理相矛盾的命题,用它来替代第五公设,然后与欧式几何的前四个公设结分解一个公理系统,展开一系列的推理。
他以为假设这个系统为基础的推理中出现矛盾,就等于证明了第五公设。
我们知道,这其实就是数学中的反证法。
但是,在他极为细致深化的推理进程中,得出了一个又一个在直觉上匪夷所思,但在逻辑上毫无矛盾的命题。
最后,罗巴切夫斯基得出两个重要的结论:第一,第五公设不能被证明。
第二,在新的公理体系中展开的一连串推理,失掉了一系列在逻辑上无矛盾的新的定理,并构成了新的实际。
这个实际像欧式几何一样是完善的、严密的几何学。
这种几何学被称为罗巴切夫斯基几何,简称罗氏几何。
这是第一个被提出的非欧几何学。
从罗巴切夫斯基创立的非欧几何学中,可以得出一个极为重要的、具有普遍意义的结论:逻辑上互不矛盾的一组假定都有能够提供一种几何学。
非欧几何简介Non

非欧几何简介Non
一、欧几里得几何与欧几里得空间
这里的欧氏几何描述二维平面的几何,高维的欧氏几何叫欧几里得空间(三维欧氏几何叫做立体几何)。
一句话概括,欧氏空间是欧氏几何在多维情况下的推广。
所以欧几里得几何又叫平面几何(plane geometry)(两要素:二维、曲率为0),它基于五条公设:
二、欧几里得几何与非欧几何
俄罗斯数学家罗巴切夫斯基和匈牙利数学家波约指出,第五条平行公理不一定在所有的几何情况下都成立,并非几何真理,也就是三角形内角和不一定为180。
基于“三角形内角≠180°”的几何学叫做非欧几何。
以下图为例,在球上的三角形的内角和就大于180°,所以在球上的几何是非欧几何,叫做球面几何(spherical geometry),它描述的是二维球面(2-dim surface)的几何,而不是包括球内部的球体(ball, solid sphere)。
三、第五公理/平行公理
第五公理为:
它也可以等价为:
如果将公设改为“可引最少两条平行线”引申的几何为罗氏几何(双曲几何);
如果将公设改为“一条平行线也不能引”引申的几何为黎曼几何(椭圆几何)。
这第五公理的三个版本不能说都错或者都对,只是需要一定条件。
如果(曲面的)曲率=0,原公理成立;曲率<0,双曲几何的平行公理成立;曲率>0,椭圆几何的平行公理成立。
非欧几里得几何学(non-Euclidean

⾮欧⼏⾥得⼏何学(non-Euclidean geometry)⾮欧⼏⾥得⼏何学(non-Euclidean geometry)不同于欧⼏⾥得⼏何学的⼏何体系。
简称为⾮欧⼏何。
⼀般是指罗巴切夫斯基⼏何(双曲⼏何)和黎曼的椭圆⼏何。
它们与欧⽒⼏何最主要的区别在于公理体系中采⽤了不同的平⾏公理。
⾮欧⼏何起源于对欧⼏⾥得平⾏公设的讨论。
公元前3世纪初,欧⼏⾥得《⼏何原本》问世,开篇列出定义、公理和公设,其中第五公设是:同⼀平⾯内⼀条直线与另外两条直线相交,若在某⼀侧的两个内⾓之和⼩于⼆直⾓,则这⼆直线经过⽆限延长后在这⼀侧相交。
它不像其他公设那样显然,因此很快就引起⼈们的争议,认为欧⼏⾥得把它放在公理(公设)之列,不是因为它不能证明,⽽是找不到证明,这是欧⼏⾥得⼏何体系的唯⼀“污点”。
2000多年来,许多⼏何学家⽤不同的⽅法试图证明第五公设,可是都失败了,因为在他们的每⼀个所谓“证明”中都引进⼀个新的假定,⽽这个假定等价于第五公设。
公元2世纪,古希腊数学家托勒密试图从欧⼏⾥得其他9个公理、公设以及与平⾏公设⽆关的欧⼏⾥得命题1~28来证明平⾏公设,但假设了两直线平⾏后,另⼀与之相交直线⼀侧内⾓成⽴的东西也必在另⼀侧同样成⽴。
公元5世纪的普罗克洛斯基于亚⾥⼠多德⽤于证明宇宙有限的公理来证明平⾏公设,实际上是把⼀个有问题的公理⽤另⼀个来代替09世纪阿拉伯数学家塔⽐·伊本·库拉在《欧⼏⾥得著名的公设证明》中假设:如果两条直线与第三条直线相交,并且它们在(第三条直线的)某⼀侧靠近或相离,则它的(在第三条直线的)另⼀侧就相离或靠近。
13世纪的纳西尔丁在《平⾏线问题释疑》中也应⽤了这样的假设:同⼀平⾯上的若⼲直线,若在⼀个⽅向上是分离的,则它们在这个⽅向上就不会靠近。
他在此基础上证明了垂线与斜线⼀定相交,⾃⾓内任⼀点必可作⼀直线与⾓的两边都相交等命题,这些都与第五公设等价。
纳西尔丁的⼯作于1663年由英国数学家沃利斯重新阐发,引起欧洲⼈的重视。
数学中的非欧几何与应用知识点

数学中的非欧几何与应用知识点数学作为一门学科,其中的几何学一直以来都是研究空间、形状和变换的重要分支。
而欧几里得几何作为传统几何学的基础,主要研究了平面和空间中的几何关系和性质。
然而,19世纪的数学家们通过对平行公设的思考和推翻,引入了非欧几何的概念,开辟了几何学的新篇章。
本文将介绍非欧几何的概念、基本理论和应用知识点。
一、非欧几何的概念和分类非欧几何是与欧几里得几何相对应的一个几何学分支,它不满足欧几里得几何中的平行公设。
根据非欧几何的不同特性,可以将其分为以下两种类型:1. 椭圆几何椭圆几何是一种非欧几何,其中的平行公设被取否定,即不存在平行线。
相反,任意两条直线在某一点处相交。
椭圆几何主要研究了曲率为正的几何空间,如球面。
2. 双曲几何双曲几何也是一种非欧几何,其中的平行公设被替换为双曲公设,即通过一点外一直线的平行线可以有无数条。
相比于椭圆几何,双曲几何研究的是曲率为负的几何空间。
二、非欧几何的基础理论非欧几何的基础理论包括非欧空间、非欧几何公设和非欧运动等。
1. 非欧空间非欧空间,也称为开平面,是非欧几何的基础。
它是一个无穷大的平面空间,没有边界和界限。
在非欧空间中,平行线不再存在,给几何学带来了全新的视角。
2. 非欧几何公设非欧几何的公设与欧几里得几何不同。
非欧几何中的公设包括反证法、证明方法和平行公设的改变等。
其中最为重要的是改变平行公设,也是区分椭圆几何和双曲几何的关键因素。
3. 非欧运动非欧运动是指在非欧几何中的刚体运动。
在椭圆几何和双曲几何中,刚体在空间中的平移、旋转和翻转等运动被重新定义,不再满足欧几里得几何中的性质。
三、非欧几何的应用知识点非欧几何在现实生活中有着广泛的应用,特别是在相对论、地理学和计算机图形学等领域。
1. 相对论相对论是物理学中的一项重要理论,其中的时空观念受到了非欧几何的影响。
爱因斯坦的相对论通过引入非欧几何的概念,重新定义了时空的结构,改变了传统的欧几里得空间观念,从而对现代物理学产生了深远影响。
非欧几何简介
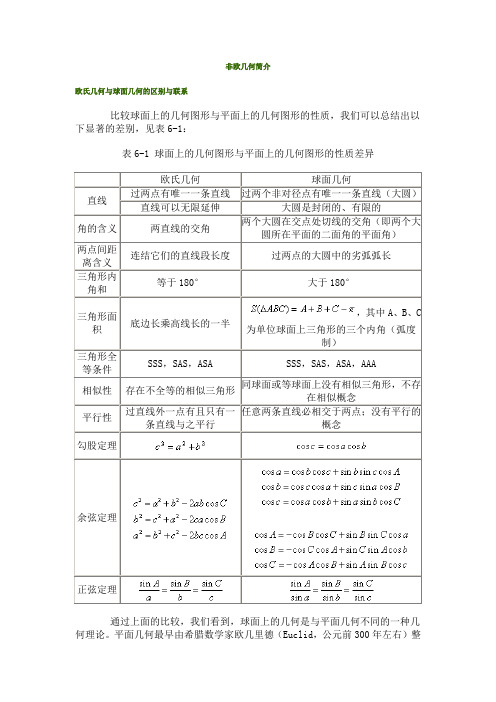
非欧几何简介欧氏几何与球面几何的区别与联系比较球面上的几何图形与平面上的几何图形的性质,我们可以总结出以下显著的差别,见表6-1:表6-1 球面上的几何图形与平面上的几何图形的性质差异,其中A、B、C为单位球面上三角形的三个内角(弧度制)通过上面的比较,我们看到,球面上的几何是与平面几何不同的一种几何理论。
平面几何最早由希腊数学家欧几里德(Euclid,公元前300年左右)整理成系统的理论。
他的不朽之作《几何原本》不仅包含了平面几何,也包含了立体几何。
为了纪念他对人类做出的伟大贡献,后来就把这种几何称为欧氏几何。
球面上的几何是与欧氏几何不同的几何,所以叫做非欧几何。
球面上的几何与欧氏几何有不相同之处,但他们之间也有一些共同特征,见表6-2。
表6-2 球面上的几何与欧氏几何的共同特征两种几何的这些相同之处,说明它们之间应该有某种内在的联系。
首先分析一下球面三角形的面积公式把这个公式改写成这个等式的左端称为球面三角形的角超,它反映出球面上的几何与平面几何的差距。
在平面几何中三角形三内角之和等于,角超等于零。
在球面上的几何中角超大于零。
不难看出当球面半径R无限增大时,球面逐渐趋向于平面,越来越小,即三角形的角超越来越小,球面三角形逐渐趋向于平面三角形,球面几何的性质逐渐接近于平面几何的性质。
所以我们可以说:当球面半径趋向于无穷大时,球面上的几何以平面几何为极限。
因为地球的半径非常大,当我们研究的范围相对于地球半径很小时,三角形的角超就一定很小。
因此,可以用平面几何的知识来代替球面几何知识,所产生的误差很小。
另一种非欧几何通过前一小节的分析,我们发现三角形的三个内角之和的大小,在很大程度上反映了平面欧氏几何与球面几何的差别。
当三角形的三个内角之和等于时,就是欧氏几何,当三角形的三个内角之和大于时,就反映出球面几何的主要特征。
有没有三角形三个内角之和小于的几何呢?我们简单回顾一段几何发展史。
在十七世纪以前,人们认为只有一种几何,就是欧氏几何,它是一切科学的基础。
非欧几何

非欧几何罗巴切夫斯基几何的公理系统和欧几里得几何不同的地方仅仅是把欧式几何平行公理用“在平面内,从直线外一点,至少可以做两条直线和这条直线平行”来代替,其他公理基本相同。
由于平行公理不同,经过演绎推理却引出了一连串和欧式几何内容不同的新的几何命题。
我们知道,罗氏几何除了一个平行公理之外采用了欧式几何的一切公理。
因此,凡是不涉及到平行公理的几何命题,在欧式几何中如果是正确的,在罗氏几何中也同样是正确的。
在欧式几何中,凡涉及到平行公理的命题,在罗氏几何中都不成立,他们都相应地含有新的意义。
下面举几个例子加以说明:欧式几何:同一直线的垂线和斜线相交。
垂直于同一直线的两条直线互相平行。
存在相似的多边形。
过不在同一直线上的三点可以做且仅能做一个圆。
罗氏几何:同一直线的垂线和斜线不一定相交。
垂直于同一直线的两条直线,当两端延长的时候,离散到无穷。
不存在相似的多边形。
过不在同一直线上的三点,不一定能做一个圆。
从上面所列举得罗氏几何的一些命题可以看到,这些命题和我们所习惯的直观形象有矛盾。
所以罗氏几何中的一些几何事实没有像欧式几何那样容易被接受。
但是,数学家们经过研究,提出可以用我们习惯的欧式几何中的事实作一个直观“模型”来解释罗氏几何是正确的。
1868年,意大利数学家贝特拉米发表了一篇著名论文《非欧几何解释的尝试》,证明非欧几何可以在欧几里得空间的曲面(例如拟球曲面)上实现。
这就是说,非欧几何命题可以“翻译”成相应的欧几里得几何命题,如果欧几里得几何没有矛盾,非欧几何也就自然没有矛盾。
直到这时,长期无人问津的非欧几何才开始获得学术界的普遍注意和深入研究,罗巴切夫斯基的独创性研究也就由此得到学术界的高度评价和一致赞美,他本人则被人们赞誉为“几何学中的哥白尼”。
欧氏几何与罗氏几何中关于结合公理、顺序公理、连续公理及合同公理都是相同的,只是平行公理不一样。
欧式几何讲“过直线外一点有且只有一条直线与已知直线平行”。
罗氏几何讲“过直线外一点至少存在两条直线和已知直线平行”。
几何中的非欧几何和几何证明

几何中的非欧几何和几何证明几何学作为数学的一个重要分支,研究着空间和形状的关系。
传统欧几何中,我们通常研究的是平面几何和立体几何,但在20世纪,人们开始发现了非欧几何的存在,它颠覆了我们对传统几何的认识并带来了新的思维方式。
非欧几何的出现不仅丰富了几何学的研究领域,也对几何证明提出了新的挑战。
一、非欧几何的基本概念非欧几何诞生于19世纪,它与欧几何最大的区别在于第五公设的不同。
在欧几何中,第五公设也被称为平行公设,它规定了通过一点外一直线上的平行线只有一条。
而在非欧几何中,第五公设被拓展了,提出了多种关于平行线的不同假设。
这就导致了非欧几何与欧几何有着不同的几何性质。
非欧几何的两个经典例子是椭圆几何和双曲几何。
椭圆几何是典型的非欧几何,它的特点是不存在平行线,任意两条直线都会相交。
而双曲几何则是另一种非欧几何,它的特点是存在无数条平行线,且相交角的和小于180度。
二、非欧几何的影响和应用非欧几何的提出对几何学的发展产生了深远的影响。
首先,非欧几何推动了数学的发展。
它挑战了传统几何的思维方式,促使数学家们重新思考几何的基本原理和公设。
这对后来的研究起到了积极的推动作用,并且促成了更加深入的几何学研究。
其次,非欧几何对物理学的发展也有一定的贡献。
爱因斯坦的广义相对论理论中,空间被看作是弯曲的,而非欧几何正是提供了一种新的模型来描述这种弯曲的空间,从而有助于解释物理现象。
因此,非欧几何为物理学的发展提供了新的视角。
此外,非欧几何还在现代通信、计算机图形学等领域得到了广泛应用。
在通信领域,非欧几何被用来研究信号传输中的误差控制和编码技术。
在计算机图形学中,非欧几何被应用于三维模型的建模和渲染,能够更加真实地反映物体之间的关系。
三、几何证明的挑战几何证明是几何学的重要部分,它通过推理和逻辑推断来证明几何定理的正确性。
在传统欧几何中,几何证明的过程通常基于欧几里德几何的公理和定理,逻辑推理比较简单明确。
然而,在非欧几何中,几何证明面临着更大的挑战。
人教高中数学欧氏几何与非欧几何的意义PPT

人教高中数学欧氏几何与非欧几何的 意义PPT
人教高中数学欧氏几何与非欧几何的 意义PPT
那么,为什么把大圆作为“直线”呢? 在球面上,大圆具有直线在平面上的 一些最基本的性质。例如,过两点有且只有 一条直线;两点之间的连线中直线最短,等 等,这些性质球面上的大圆都具备。所以大 圆可以作为直线所具有的基本性质的一种说 明或解释,这种解释可以视为一种模型。
下面,我们给出法国数学家庞加莱建立 的满足非欧平行公理的一种几何模型。
A
l
x
图8-1
A l
x
人教高中数学欧氏几何与非欧几何的 意义PPT
人教高中数学欧氏几何与非欧几何的 意义PPT
在欧氏平面上做一条直线x,以x为边缘 的上半平面(不包含x 上的点)记为 ( 图81),现在考虑 内部的点,我们规定 内部 的点为“非欧点”,圆心在x上的半圆或垂直 于x的射线称为“非欧直线”。
欧几里得
庞加莱
旧知回顾
通过前面的学习,我们知道球面 几何与平面几何中的许多定理是“相 同”的,但也有一些定理是不相同的。
导入新课
在本讲,我们首先通过平面几何与 球面几何的比较,追溯某些定理不相同 的根源,给出欧氏几何与非欧几何的定 义;然后通过欧氏平行公理的分析,给 出非欧几何的一种模型——庞加莱模型。
人教高中数学欧氏几何与非欧几何的 意义PPT
球面上的大圆可视为“直线”。在球 面上有这样一个结论:任意两条“直线” (大圆)都相交,即过“直线”外一点, 没有一条“直线”与该“直线”不相交。
欧氏几何与非欧几何中的几何思考与证明

● 03
第3章 欧氏几何与非欧几何 的比较Biblioteka 欧氏几何与非欧几何 的异同
01 欧氏几何基于直觉和直线的概念
欧氏几何
02 非欧几何基于曲线和曲面的概念
非欧几何
03 欧氏几何受限于第五公设
欧氏几何
欧氏几何和非欧几何的几何思考
更侧重于直线和角
度的关系
欧氏几何
01
更注重于曲线和曲 面之间的关系
非欧几何
02
Unified fonts make reading more fluent.
Theme color makes PPT more convenient to change.
Adjust the spacing to adapt to Chinese typesetting, use the reference line in PPT.
非欧几何的未来前景
01 现代数学地位
非欧几何将更突出
02 广泛应用
领域发展需求
03 新思路方法
为数学研究提供
欧氏几何与非欧几何的融合
相互影响 创新性提升
领域融合
创新实用
01
融合效果 实践应用
02
发展推动 04
促进数学研究
03
前沿探索
欧氏几何与非欧几 何的发展趋势展望
数学研究领域扩展 多元化前沿性
02
解决特殊问题
为特殊问题提供新的解决思路
03
推动数学的创新发展
几何思考与证明
01 推理与证明方法
通过逻辑推理确立几何定理
02 几何形状分析
探索图形形状的几何特征
03 数学定律应用
运用数学定律解决实际问题
非欧几何(Non-Euclidean.

非欧几何(Non-Euclidean geometry)简介福州大学林鸿仁非欧几何就是非欧几里得几何,是针对欧几里得几何而言的,非欧几何通常指的是罗巴切夫斯基几何和黎曼几何。
众所周知,素有“几何之父”之称的古希腊的数学家欧几里得( Euclid,希腊文:Ευκλειδης,约公元前330年-前275年)有一本传世之作叫《几何原本》,已经传了两千多年了。
其中的基本内容,至今还是我们孩子们学习的课程,包括《平面几何》和《立体几何》。
西方的几何学大概兴于公元前7世纪的古埃及,对古代埃及人来说,几何学就是“测地术”,几何是在测量地块中获得的,是一种经验的几何知识,所以大都十分零散杂乱,缺乏系统。
古希腊的欧几里得首先觉察到,很有必要对这些“上帝的杰作”进行整理,于是特地到古埃及的亚历山大,收集整理并于公元前3世纪写成《几何原本》这一巨著,开创了数学理论的系统化逻辑化的先河,除了使几何成为一门独立学科之外,也成为西方科学研究方法的典范。
欧几里得的《几何原本》全书共分13卷,包含了5条“公理”、5条“公设”、23个定义和467个命题。
在每一卷中,欧几里得都采用了完全不同的叙述方式,先提出公理、公设和定义,再将命题进行逻辑推理和证明。
他先后对直边形、圆、比例论、相似形、数、立体几何等进行系统的论述。
在这里,作为定义的基本概念,如点、线、面、直角等,已不是具体的图形或图像,而是抽象的一般概念;推演定理的方法,也尽量避开直观,而采用“三段论式”的逻辑方法。
欧几里得的成功之处在于,从一些被认为是不证自明的事实出发,通过逻辑演绎,用很少的几个公理公设,令人信服地推出了很多的定理,而且它们与现实世界又是一致的。
欧几里得建立的这一个几何学公理体系一直受到后世数学家的普遍称颂,被公认为数学严格性的典范。
因此,在相当长的历史时期里,人们一直把几何称为“欧几里得几何”简称“欧氏几何”,并把它奉为金科玉律。
但由于时代的局限,他的5条公设中的第5条一直被质疑。
非欧几何

非欧几何19世纪,由于各国数学家对欧几里得《几何原本≮五公设(见第五公设)的怀疑和探索,出现了许多不同于欧几里得几何的几何。
通常把这些称为非欧几何。
第一非欧几何——罗巴切夫基几何,就是在对平行公设的研究中诞生的。
罗巴切夫斯基是俄国数学家,1792年生于高尔基城的一个穷职员家庭。
他从小聪明好学,才思过人,15岁时以高材生的资格进入喀山大学,毕业即获硕士学位,后留校任教,历任教授、数学—物理系系主任、校长等职。
从1816年起,罗巴切夫斯基开始像他的前人一样尝试证明第五公设,但很快发现他的证明无法逃脱循环论证的错误。
于是他改变了研究方法。
罗巴切夫斯基首先提出两个不同的假设:(1)过直线AB外一点P只能作一条直线与AB不相交;(2)过直线AB外一点P不止作一条直线与AB不相交。
如采用(1)作公理,可以导出我们熟悉的欧几里得几何。
罗巴切夫斯基从(2)出发,推导出一系列前后一贯的命题,构成了逻辑上没有矛盾,但与欧几里得几何完全不同的另外一种几何。
罗巴切夫斯称这种新的几何系统为“虚几何学”。
1826年2月23日,俄国喀山大学物理—数学系的学术会议上,罗巴切夫斯基宣读了他的论文《几何原理概述及平行线定理的严格证明》,向被称颂为“几何学经典”的欧氏几何发出了挑战:“直到今天为止,几何学中的平行线理论是不完全的。
从欧几里得时代以来,两千年徒劳无益的努力,使我怀疑在概念(指…第五公设‟)本身之中,并未包含那样的真实情况!”1829—1830年他在《喀山学报》上发表《论几何基础》,这是世界上最早的非欧几何的文献;1837年他用法文发表了《虚几何学》;1840年用德文写他影响最大的专著《平行理论的几何研究》。
但由于罗巴切夫斯基的新学说背离了几千年的传统思想,动摇了欧氏几何“神圣不可侵犯”的权威,也违反了人们的“常识”,因此,他的学说一发表,就遭到社会上的攻击、侮辱和谩骂。
科学院拒绝接受他的论文,大主教宣布他的学说是“邪说”,有人在杂志上谩骂罗巴切夫斯基是“疯子”。
小学生数学认识数学中的非欧几何

小学生数学认识数学中的非欧几何在我们的日常生活中,数学是一个无处不在的学科。
而对于小学生来说,数学是他们初步接触的学科之一,它帮助他们培养逻辑思维和问题解决能力。
然而,除了我们在学校中所学到的欧几里德几何之外,还有一个神秘莫测的数学分支被称为“非欧几何”。
在本文中,我们将一起探索小学生如何认识数学中的非欧几何。
一、什么是非欧几何1.1 定义与由来非欧几何是一种与欧几里德几何不同的几何学分支。
欧几里德几何以其公设和证明方法而闻名,被普遍接受为准确且可靠的几何学。
然而,在19世纪,数学家们开始发现一些违背欧几里德几何公设的几何系统。
这些几何系统被称为非欧几何,其形成了一个全新而有趣的数学领域。
1.2 非欧几何的特点非欧几何与欧几里德几何不同之处在于其公设的差异。
对于欧几里德几何而言,公设中包括了平行公设和直角公设,这些公设一直以来都被认为是几何学的基石。
然而,非欧几何并不满足这些公设,例如,可以存在多条与一直线平行的线,且平行线之间的角度和为180度。
二、小学生认识非欧几何的重要性2.1 拓宽数学思维通过认识非欧几何,小学生可以开拓他们的数学思维。
在欧几里德几何中,许多问题似乎是确定和规范的。
然而,非欧几何给予小学生一种创造性和非常规思考的机会。
他们可以开始质疑曾经被认为是几何学中唯一正确答案的概念。
2.2 培养逻辑推理能力研究非欧几何需要一定的逻辑推理能力。
小学生通过解决非欧几何的问题,可以提高他们的分析和推理能力。
他们将学会关注细节,挖掘问题背后的规律,培养独立思考的能力。
三、小学生如何学习非欧几何3.1 寓教于乐对于小学生来说,学习应该是有趣和有意义的事情。
教师可以通过游戏、故事等方式,将非欧几何的概念引入到课堂中。
小学生可以通过探索、讨论和实践,逐渐理解非欧几何的特点和思维方式。
3.2 创设问题情境教师可以创设一些与非欧几何相关的问题情境,帮助小学生进行实际应用和思考。
例如,设计一个非欧几何的迷宫,让学生通过探索迷宫中的角度和线段关系,来发现非欧几何的独特性质。
非欧几何的基本特点

非欧几何的基本特点非欧几何是对传统欧几何的扩展与挑战,主要研究那些不遵循欧几里得第五公设(平行公设)的几何结构。
这种几何体系的提出,对数学、物理、哲学等领域产生了深远影响。
本文将从非欧几何的定义、基本特点、主要分支及其应用等方面进行详细探讨。
非欧几何的定义非欧几何是指不满足欧几里得几何中“通过平面上某一点,且不在直线上,可以画一条唯一的平行线”的公设的几何。
它建立了一种新颖的空间观念,揭示了在不同公理体系下,几何形状和性质可以发生剧变。
例如,在非欧几何中,平行线不是唯一的,因此形成了全新的数学结构和思维模式。
基本特点1. 平行公设的替代非欧几何最显著的特点就是对平行公设的替代。
在欧几里得几何中,只允许存在一条平行线通过一点,而在非欧几何中,这一限制被打破:超球面几何: 在球面上,任何两条直线(大圆)相交,因此不存在平行线。
双曲几何: 在双曲面上,对于一个给定点,可以画出无限多条不相交于该点的直线。
这种对平行线多样性的探索,使得非欧几何成为数学研究的重要领域。
2. 三角形和内角和单位三角形内角和在不同的非欧空间中表现出截然不同的特性:球面几何: 三角形内角和大于180度。
如在极地附近,三角形可以有较大的内角,例如近乎183度。
双曲几何: 三角形内角和小于180度。
例如,通过适当设定,可以构造出一个仅有90度内角和的小三角形。
以上特性使得研究三角形成为了非欧几何的重要内容,不同形式下三角形性质的变化为其提供了丰富的研究方向。
3. 空间结构与距离概念在非欧几何中,空间结构和距离的定义也与传统意义上有所不同。
例如:在球面几何中,距离通常由弧长来测量,而不是在平面上的直线距离。
在双曲空间中,随着空间维度增加,其距离测量也呈现出复杂化。
这些变化推动了对于“空间”的全新理解,特别是在较高维度情况下,更加复杂的距离计算有助于推动其他学科之间的相互交融,如物理学中的相对论模型等。
4. 曼哈顿几何曼哈顿几何是一种以城市街道网络为基础而发展的理论。
非欧几何

罗巴切夫斯基非欧几何的基本思想与高斯、波约是 一致的,即用与欧几里得第五公设相反的断言: 通过直线外一点,可以引不止一条而至少是两条直 线与已知直线不相交。 作为替代公设,由此出发进行逻辑推导而得出一连串新 几何学的定理。 罗巴切夫斯基明确指出,这些定理并不包含矛盾,因而 它的总体就形成了一个逻辑上可能的、无矛盾的理论, 这个理论就是一种新的几何学-——非欧几里得几何学。
1733年,意大利数学家萨凯里:《欧几里得无懈可击》 锐角?直角?钝角?
萨凯里四边形 锐角?三角形内角之和小于两直角;过给定直线外一 给定点,有无穷多条直线不与该给定直线相交;等等
无逻辑矛盾,但不合乎情理。
• 1763年,德国数学家克吕格尔(G.S.Klugel) 在其博士论文中首先指出萨凯里的工作实际 上并未导出矛盾,只是得到了似乎与经验不 符的结论。克吕格尔是第一位对平行公设是 否可以由其它公设加以证明表示怀疑的数学 家。
在非欧几何的三位发 明人中,罗巴切夫斯 基最早、最系统地发 表了自己的研究成果, 并且也最坚定地宣传 和捍卫自己的新思想。 “几何学中的哥白尼”
Н. И. Лобачевский 1792-1856
罗氏几何满足如下公理 • • • • •
π(α)
过两点可连一直线 直线可无限延长 以一点为中心任意长为半径可做一个圆 所有直角相等 过直线外一点至少有两条直线与已知直线平行
直到18世纪末,几何领域仍然是欧几里得一统 天下。解析几何改变了几何研究的方法,但没 有从实质上改变欧几里得几何本身的内容。解 析方法的运用虽然在相当长的时间内冲淡了人 们对综合几何的兴趣,但欧几里得几何作为数 学严格性的典范始终保持着神圣的地位。
第五公设(平行公设)
• 第五公设:若一直线落在两直线上所 构成的同旁内角和小于两直角,那么 把两直线无限延长,它们将在同旁内 角和小于两直角的一侧相交。
大学 数学专业 空间解析几何第五章 非欧几何简介 PPT

19世纪初,俄罗斯人罗巴切夫斯 基在否定第五公理的同时,假设其 反面之一:“过已知直线外一点, 可作多于一条的直线与已知直线平 行”,得到了一系列定理,并且认 为他得到了一门新的几何学。这是 过去2000年以来的重大突破。
π(α)
罗巴切夫斯基1826年2月11日宣布 自己建立了新的几何学之后,得到 了许多数学大家的嘲笑、讽刺,德 国诗人歌德也出来讽刺他。实际上, 罗巴切夫斯基的理论得到世界的认 可是在他去世几十年后的事了.
欧氏几何
欧氏几何在公元前300年就已产生。 欧几里德在他的名著《几何原本》中,以5 个基本假设为基础,把当时人类已经掌握的纷杂 的几何知识变成一个演绎系统,使用逻辑推理方 法,一共推出了465个定埋。 这个系统所依据的只是几个虽然没有加以证 明,但是看起来相当明显,并且合乎人类经验的 假设。这几个“不证自明”的事实叫做公理 (axioms)。
1854年黎曼(德, 1826-1866)《关于 几何基础的假设》
(黎曼非欧几何)
(罗氏几何)
(欧氏几何)
椭圆几何 双曲几何 抛物几何
A+B+C=π
第五平行公理的研究(公元前3世纪至1800年)
欧几里得
普莱菲尔(苏格兰, 1748-1819) 勒让德(法, 1752-1833)
平行公理
A
这个平行公理在所有公理之中是最不明显的, 所以数学家或是对数学有兴趣的人便想从其他的 公理去推得平行公理。 而这努力延持了两千年, 后来证明这是不可能的,于是有了非欧几何学的 发现,这在人类思想史上是非常特别、有意思的 事实,是西方数学和中国数学不同的地方。
这五个公理是
1. 两点间必可连一条直线; 2. 直线可以任意延长; 3. 已知圆心及半径可作一圆; 4. 凡直角皆相等;
并不神秘的非欧几何,它究竟讲的是什么?今天带你搞懂

并不神秘的非欧几何,它究竟讲的是什么?今天带你搞懂欧氏几何是人类创立的第一个完整的严密的(相对而言)科学体系。
它于公元前三世纪由古希腊数学家欧几里得完成,欧洲数学2000年发展史,几乎有四分之三的时间里欧氏几何一统天下,对科学和哲学的影响极其深远。
直到魏尔斯特拉斯发起的分析算术化运动使代数从欧氏几何中完全脱离以及非欧几何的诞生才结束了欧氏几何的统治地位。
其中,非欧几何的诞生影响着现代自然科学、现代数学和数学哲学的发展,今天我们就来谈一下非欧几何与发展。
欧氏几何第五公设问题掀起的风波欧几里得的《几何原本》标志着非欧几何的诞生,在《几何原本》里,欧几里得给出了 23 条定义、5条公理、5条公设,由此推证出48个命题。
公理是指在任何数学学科里都适用的不需要证明的基本原理,公设则是几何学里的不需要证明的基本原理。
近代数学则对此不再区分,都称“公理”。
这五大公设中,由于第五公设的内容和叙述比前四条公设复杂,所以引起后人的不断研究和探讨。
因为前四条公设都可以用《几何原本》中的其余公设、公理和推论证明,而人们始终相信欧氏几何是物理空间的正确理想化,所以众多数学家就尝试用前4个公设、5个公理以及由它们推证出的命题来证明第五公设,然而都没有成功。
第五公设难题:如果一条线段与两条直线相交,在某一侧的内角和小于两直角和,那么这两条直线在不断延伸后,会在内角和小于两直角和的一侧相交。
论证的不成功引发了数学家的疑义,数学界由此开始了对“第五公设难题”的讨论。
数学家还尝试用更简单、明畅的语言来叙述这条公设,从而更好地理解它并解决它,古希腊数学家普罗克鲁斯在公元5世纪就曾经试图重现陈述它,然而这些替代性陈述效果并不比原来的文字更好。
直到 18 世纪普莱菲尔才算总结出一个比较简单的替代性公设:过已知直线外一点能且只能作一条直线与已知直线平行”。
(我们中学教材就常用这个叙述形式来替代第五公设。
)从公元前三世纪一直到公元十八世纪期间,近2000 年的时光过去,整个数学体系已经初具雏形。
非欧几何的产生

编号(学号):本科学生毕业论文(设计)手册题目:非欧几何与平行第五公社 学院名称:数学与信息学院 专业名称:数学与应用数学 年 级:2008级 学生姓名:何蓉学 号:200808140609指导教师: 杨孝斌 职称/学历:教授●评定等级标准:“优”(90分以上); “良”(80~89); “中”(70~79); “及格”(60~69); “不及格”(60以下)。
教务处 制目录(一)毕业论文(设计)承诺书…………………(二)毕业论文(设计)任务书…………………(三)开题报告…………………………………………………………(四)指导教师指导毕业论文内容记录表…………………………………(五)指导教师评价表(毕业论文)……………………………………(六)指导教师评价表(毕业设计)……………………………………………(七)评阅人评价表(毕业论文)…………………(八)评阅人评价表(毕业设计)………………(九)答辩评分参考标准…………………………………………………(十)答辩记录……………………………………………………(十一)毕业论文(设计)撰写规范与要求…………(十二)毕业论文(设计)格式及排版要求…………西华师范大学本科学生毕业论文(设计)承诺书本人承诺:在即将开始的毕业论文(设计)过程中,严格遵守学术道德规范和学校纪律,在学院和指导教师的安排与指导下,独立完成毕业论文(设计)工作,不弄虚作假,不请人代做毕业论文(设计)或抄袭别人的成果。
按照“西华师范大学本科生毕业论文(设计)规定”的要求,完成毕业论文(设计)的撰写、答辩、装订整理等工作。
学生签名:何蓉2012年 3 月 28 日西华师范大学本科学生毕业论文(设计)任务书注:1、任务书由指导老师填写。
2、任务书必须在第七学期开学一周内下达给学生。
附件三:西华师范大学本科学生毕业论文(设计)开题报告附件四:西华师范大学本科学生毕业论文(设计)指导记录表附件五:西华师范大学本科学生毕业论文评价表(指导教师用)附件六:西华师范大学本科学生毕业设计评价表(指导教师用)西华师范大学本科学生毕业论文评价表(评阅人用)西华师范大学本科学生毕业设计评价表(评阅人用)附件九:西华师范大学本科学生毕业论文(设计)答辩评分参考标准附件十:西华师范大学本科学生毕业论文(设计)答辩记录附件十一:西华师范大学本科生毕业论文(设计)撰写规范与要求撰写毕业论文(设计)是培养学生综合运用本学科的基本知识和基本技能,分析、解决实际问题和某些理论问题,培养学生科学研究、创新意识、创新能力,提高学生素质的重要途径,是高校教学的重要实践环节。
非欧几何

对非欧几何的认识摘要:本文简单的介绍了公理化体系中的基本概念,对非欧几何的产生进行了阐述。
介绍了两种非欧几何——罗氏几何,黎氏几何.即罗氏几何在欧氏几何公理化体系的基础上对平行公理进行修改,改为:过直线外一点至少可以做两条直线与已知直线平行,从而推出一个新的几何体系。
而黎氏几何则在此基础上将平行公理修改为:平面上任何两条直线都相交或者说平面上不存在平行直线。
本文还对非欧几何诞生的意义及应用进行了探讨。
关键字:公理化体系非欧几何罗氏几何黎氏几何引言为了研究非欧几何,必须对公理化体系有较清楚地认识,所以本文从公理化体系着手,简单介绍公理化体系的概念,由公理化体系引出“第五公设问题”再由此引出非欧几何的产生.非欧几何所包含的内容是本文重点要讨论的问题,即第三部分内容:简介非欧几何的主要内容.最后简单介绍非欧几何产生的几何意义及应用以结束本文。
1 简单叙述公理化体系及其产生人们对《几何原本》中在逻辑结果方面存在的一些漏洞、破绽的研究和发现,推动了几何学不断向前发展.德国数学家希尔伯特在总结前人工作的基础上在他1898年发表的《几何基础》一书中提出了一个比较完善的几何学的公理体系,这个公理体系就被叫做希尔伯特公理体系.希尔伯特不仅提出了建立一个公理体系所应遵循的原则就是在一个几何公理体系中采取哪些公理,应该包含多少条公理,应考虑如下三个方面的问题:第一、和谐性(共存性)在一个公理体系中,各条公理应该是不矛盾的,他们和谐而共存在同一系统中,这显然是必要条件.给定一组公理,具体挑选一组事物,使这组公理得到满足,就是说给这组公理做了一个实现或解.实现这些公理的对象的集合,构成这一公理的一个模型,而这一公理体系若能以某种方法用模型来实现,那么这个公理体系就是和谐的.第二、独立性,公理体系中的每一条公理应该是各自独立而互不依附的,没有一条公理是可以从其它公理引申出来的.如果公理体系中有一个公理可以从其余的公理中推导出来,它就不是独立的,可以把它从公理体系中挪走,减少一个公理.但是应当注意,一种几何可以用不同的公理体系作为基础,因此去掉多余的公理后,一般说来,可以得到不同的最少个数的体系,因此最少个数的公理体系不是唯一的.第三、完备性,公理体系中所包含的公理应该是足够能证明本学科的任何新命题.设一个∑,如果在∑和的'∑对象之间能够建立这样的一一对应,使得公理体系具有两个模型∑和'∑中元素之间的相互关系或命题总是'∑中相应元素间的相互关系或命题相对应,则称这两个模型是同构的,如果一个公理体系中的各个模型是同构的,那么这个公理体系就称它为完备的.这种用公理系统来定义几何学的基本对象和它的关系的研究方法,成了数学中所谓的“公理化方法”,而把欧几里德在《几何原本》提出的体系叫做古典公理法.公理化的方法给几何学的研究带来了一个新颖的观点,在公理化理论中,由于涉及的对象不予定义,因此就不必探究对象的直观形象是什么,指专门研究抽象的对象之间的关系、性质.从公理法的角度看,我们可以任意的用点、线、面代表具体的事物,只要这些具体事物间满足公理中的结合关系,顺序关系,合同关系等,使这些关系满足公理系统中所规定的要求,则构成了几何学.这里的几何学研究对象更加广泛,几何学的含义比欧几里德时代更为抽象.2 欧氏几何公理化体系及第五公设问题欧氏几何的公理体系不止一组,当各组彼此是等价的.在欧氏几何的所有公理体系中,希尔伯特系统概念和陈述最简单,如下所述:第一组、结合公理公理1 通过任意给定的两点有一直线.公理2 通过任意给定的两点至多有一直线.公理3 每一直线上至少有两点,至多有三点不共线.公理4 通过任意给定不共线的三点有一平面,每平面上至少有一点.公理5 通过任意给定不共线的三点,至多有一平面.公理6 若一直线上的两点在一平面上,则这一直线上的每一点都不在这平面上.公理7 若平面上有一公共点,则至少还有一公共点.公理8 至少有四点不同在一平面上.第二组、顺序公理公理1 若点B 在两点A 、C 之间,则A 、B 、C 是一直线上的不同点,且B 也在C 、A 之间.公理2 对于任意两点A 、B 直线AB 上至少有一点C 存在,使得B 在A 、C 之间.公理3 在共线的三点中,一点在其它两点之间的情况不多于一次.公理4 设A 、B 、C 是不共线的三点,L 是平面ABC 上部通过A 、B 、C 中任何一点的直线,若直线L 通过线段AB 的一个点,则直线L 要通过线段AC 或BC 的内点.第三组、合同公理公理1若A 、B 是直线L 上的两点,A ′是同一或另一直线L ′上的点,则在L ′上点A ′给定的一侧有一点且仅有一点B ′使线段A ′B ′合同于或等于线段AB ,且对于每一线段AB 要求AB 合同BA.公理2 线段A ′B ′及A 〞B 〞都与同一线段AB 合同,则A ′B ′与A 〞B 〞合同.公理3 设AB 与BC 是直线L 上没有公共内点的两线段,而A ′B ′和B ′C ′是同一或另一直线L ′上的两线段,也没有公共内点.若AB ≡A ′B ′及BC ≡B ′C ′,则AC ≡A ′C ′ .公理 4 在平面π上给定了AOB ∠,在同一或另一平面'π上给定一直线'L ,且在以'L 为边缘的半平面'H 上有射线''AO 在'L 上,则过点'O 在半平面'H 内有唯一的射线 ''B O 使得AOB B O A ∠=∠'''公理5 在ABC ∆与'''C B A ∆之间,若AB ≡A ′B ′,AC ≡A ′C ′,∠B ′A ′C ′=∠BAC ,则AOB B O A ∠=∠'''第四组、连续公理公理1 设AB 与CD 是任意两线段,在直线AB 上存在着有限个点n A A A 21使得1A 在2A 和A 之间,2A 在 1A 和3A 之间,等等.且线段n n A A A A AA 1211, ,与线段CD 合同,最后使得点B 在点A 和n A 之间.公理2 设直线L 上有由线段组成的一个无穷序列11B A ,22B A 其中在后的每一线段都包含在前一个内部,并且任意给定一线段,总有一个自然数n 使得线段n n B A 比它小,那么在直线L 上存在一点X 落在每条线段11B A , 22B A 的内部.第五组、平行公理设有一直线及线外一点,在这直线和这点确定的平面上,经过这点最多有一条直线与该直线平行.以上便是欧氏几何公理体系的全部内容,由此便可推到处欧氏几何的全部内容.了解了欧氏几何的公理化体系,现在回过头来谈谈欧几里德的第五.欧氏几何公理化体系中的五个公设是:○1给定两点,可以连接一线段. ○2线段可以无限延长. ○3给定一点为中心和通过任意一点可以作一圆. ○4所有直角彼此相等. ○5如果一条直线与两条直线相交,并且在同一侧所交出的两角之和小于两个直角,这两条直线无限延长后,必在该侧相交.长期以来,人们对欧氏几何公理系统中前四个公设没有异议,而对第五公设特别注意,这是因为:第一,它没有其他公理那样简单,第二,可能连欧几里德本人也曾试着证明过第五公设,因为欧氏《几何原本》中前二十八个命题都未曾利用过第五公设,似乎是欧几里德本人也推迟使用它.第五公设能不能从欧氏表中挪走,用其余的公设、公理将它作为定理证出来,便是著名的“第五公设问题”.人们在假设平行公理不成立的时候,自然想到做出与“过已知直线外一点,可作一条也只可作一条直线与已知直线平行”相悖的假设.如假设“过已知直线外一点,可作出多于一条的直线平行于已知直线”,然后,人们总是在这一假定下希望通过一长串的推理,从中得出两个相互矛盾的命题,但都以失败而告终.德国的高斯是真正预见到非欧几何的第一人,1792年,当他15岁时,已经有了第五公设不可证和非欧几何的思想萌芽.以后相继得到许多这方面的重要结果.但他动摇徘徊了25年之久,直到1817年才牢固树立起坚定信念.不幸的是,由于康德的唯心主义空间学说和在 数学界占统治地位的所谓现实空间只能是欧氏空间这旧传统观念,给高斯以很大的精神压力,因而毕其一生关于此问题也没有发表什么见解.匈牙利的J-波尔约是预见到非欧几何的第二人,他在青年时代就醉心于第五公设的证明.不顾父亲的劝告,坚持研究,终于建立了非欧几何.1823年11月3日,他高兴地写信告诉父亲:“我已从乌有中创造了另一个新奇的世界.”当他父亲把J-波尔约的研究成果写信告诉高斯的时候,高斯感到十分吃惊,回信说:“这和我40年来沉思的结果不谋而合.”J-波尔约看到高斯的回信,大大刺伤了自己的自尊心,怀疑高斯剽窃他的成果.从此消沉下去,不再研究这一问题.只有俄国的罗巴切夫斯基无愧于享有这门新学说的创建者和捍卫者的光荣称号.他试图证明第五公设,并在独立的在完成一个个推论被严密论证后发现了一个新的几何体系,之后他不顾来自各方面的嘲讽和压力,忠实的捍卫着这一伟大的理论成果,并于1826年2月23日在喀山大学数理系做了《几何学原理的扼要阐述,暨平行线定理的一个严格证明》的报告上宣读了他关于非欧几何的研究工作.我们称这一天文非欧几何的诞生日.3 简介非欧几何的主要内容非欧几何是一门大的数学分支,一般说来,它有广义、狭义和通常意义三个方面不同的含义.所谓广义的非欧几何时泛指一切和欧几里德几何学不同的几何学,而狭义的几何学只是指罗氏几何而言,通常意义上的非欧几何,就是指罗氏几何和黎氏几何这两种几何.下面重点阐述罗氏几何和黎氏几何.罗氏几何罗巴切夫斯基几何学的公理系统和欧氏几何学不同的地方仅仅是把欧氏几何平行公理用“从直线外一点至少可以做两条直线和已知直线平行”来替代,其他公理相同.故罗氏几何公理可表述为:第一组:结合公理;第二组:顺序公理;第三组:合同公理;第四组:连续公理;(前四组公理如前所述欧氏几何公理体系)第五组:平行公理,过直线外一点,至少可以做两条直线和已知直线平行.这五组公理推出一个新的几何体系,又称为双曲形几何,其模型可描述为:在欧氏平面上取一个圆∆,在圆∆内作为非欧平面,圆内任意一点P 称为非欧点,圆的边界点用∆∂表示,∂垂直的圆弧或直线段称为非欧直线.由此∂上的点是非欧平面上的无穷远点,在∆内与∆所有过原点的直线都是非欧直线,两条非欧直线间的夹角,由交点处两圆弧切线间的夹角来度量,此即在圆内建立了一个无限的非欧平面.如图所示:其中,非欧直线L与∆∂的交点是A、B,过L外一点Z作两条非欧直线分别与之相切于A、B两点,此两条直线为过Z点与L平行的非欧直线.由于平行公理不同经过演绎推理引出一连串新的不同于欧氏几何的几何命题,且因为罗氏几何除了第五组平行公理之外,其余四条公理全部采用欧氏几何的公理,故凡不涉及到平行公理的几何命题在欧氏几何中成立,在罗氏几何中同样正确,在欧氏几何中凡涉及到平行公理的命题在罗氏几何中均不成立.例如,欧氏几何中同一直线的垂线和斜线相交;垂直于同一直线的两条直线互相平行;存在相似的多边形;过不同在一条直线上的三点可以做且仅可以做一个圆;而罗氏几何中,同一直线的垂线和斜线不一定相交;垂直于同一直线的两条直线,当两端延长时可以离散到无穷;不存在相似的多边形;过不同在一条直线上的三点,不一定可以做一个圆.同时,在这个新的几何中一些与平行公理有关的命题被新的定理代替,如:三角形的内角和小于180°;两三角形若三组对应角分别相等则两三角形必然全等.黎氏几何欧氏几何与罗氏几何中关于结合公理,顺序公理,连续公理及合同公理都是相同的,其不同之处在于平行公理.欧氏几何讲:“过直线外一点犹且只有一条直线与已知直线平行”,罗氏几何中:“过直线外一点至少存在两条直线和已知直线平行”,而黎氏几何则提出:“过直线外一点,不能做出直线与已知直线平行”.这与前面四条公理结合即形成另一种新的非欧几何体系,称之为黎氏几何.因为黎曼几何公理化体系同欧氏几何的公理化体系也仅在第五组平行公理上有所不同,故黎氏几何的公理化体系可表述为:第一组:结合公理;第二组:顺序公理;第三组:合同公理;第四组:连续公理;(前四组公理如前所述欧氏几何公理体系)第五组:平行公理,即平面上任何两条直线都相交,或者平面上不存在相交直线.黎曼提出的非欧几何又称为椭圆几何,如图所示:首先,对图形的基本对象点、直线、平面作如下约定:第一,点:把欧氏球面上对径的两点同一起来,看成一点,这个约定点称为黎曼几何的点.第二,直线:把欧氏球面上对径点合一后,得到的大圆约定为黎曼几何中的直线.第三,平面:把对径点合一后的欧氏球面约定为黎曼几何中的平面.上图中,A点为一黎曼点.大圆APA是一条封闭的黎曼直线.其模型又可描述为:若将球面上的大圆视为直线,那么球面上的几何中任何两条直线都相交,而且存在两个交点.亦即,黎曼于1851年所作论文《论几何学作为基础的假设》中明确提出的一条基本规定:同一平面内任何两条直线都有公共点(交点).其实际意义可认为是:赤道为一大圆,所有的纬线也都是大圆,它们均为与赤道垂直的,且交于南北极,有两个交点.我们可以推导出在该模型上三角形的内角和必然大于180°;一条直线的所有垂线都相交于一点.同时,黎曼几何学中不承认有平行直线的存在,另一基本规定是:直线可以无限延长,但总长度有限,故我们可以将黎氏几何的模型看作一个经适当修改的球面.4 探讨非欧几何的产生所具有的几何意义及其应用非欧几何产生的几何意义首先,随着几何学的不断发展,非欧几何的产生引起了数学家们对几何基础的研究,从而从根本上改变了人们的几何观念,扩大了几何学的研究对象,对几何学的研究对象由性质进入到抽象空间,即更一般的空间形式,使几何学的发展进入了一个以抽象为特征的新阶段.其次,几何学本身也从其传统的束缚中被解放出来,并在这基础上发现了大批有趣的几何,如:非阿基米德几何,非笛沙格几何,非黎曼几何,有限几何,等等.非欧几何的产生,也引发了一些重要的数学分支的产生,数学家们围绕着几何的基础问题,几何的真实性问题或者几何的应用可靠性问题的讨论,在完善数学基础的过程中,相继出现了一些新的数学分支,如数的概念,分析基础,数学基础,数理逻辑,等.非欧几何的应用我们知道,非欧几何的出现不仅仅影响了人们的价值观,思维方式,世界观及人类的文化,更重要的是非欧几何对一般难以把握的,据一般生活更远的实际中得到了广泛的应用.比如,近代的黎曼几何在相对论中有重要的应用.广义相对论中,爱因斯坦放弃了关于时空均匀性的观念,他认为时空只是在充分小的空间里是一种近似均匀的,而整个时空是不均匀的.物理学里广义相对论中的空间几何即是黎曼几何.在日常生活中,就是说在我们所处的这个不大不小,不远不近的空间里,欧氏几何是适用的;延伸到宇宙空间中或者原子核世界里,罗氏几何更加适用;在地表研究航海,航空等实际问题则更多的需要用到黎曼几何.参考文献[1]郑崇友、王汇淳等编著几何学引论 [M] 北京高等教育出版社 1994[2]朱德祥编高等几何 [M] 北京高等教育出版社 1983年9月[3]傅章秀编几何基础 [M] 北京北京师范大学出版社 1984[4]梅向明、刘增贤编高等几何 [M] 北京高等教育出版社 1983[5]方德植陈亦培编射影几何 [M] 北京高等教育出版社 1983年2月[6]姚俊凡编高等几何讲义 [M] 贵州贵州人民出版社 1981Carries out official duties the physics and chemistry system tolookat the non- European geometryAuthor:HUANG Xiaolin Supervisor:XU TianchangAbstract:In this paper,basic conceptions in the system of Axiomatizing are briefly introduced and some statements of the generation of non-Euclidean geometries are given.Two forms of the non-Euclidean geometries: Lobachevskian geometry and Ricmmanian geometry will be discussed.The Lobachevskian geometry is a new geometry which is given by changing the parallel postulate in the system of Axiomatizing of Euclidean geometries to : through one point beyond a given line ,there are at least two lines parallel to the given line.In the Ricmmanian geometry,the parallel postulate is changed to: two arbitrary lines in a surface always intersect or there exist no parallel lines.Furthermore,the significance of the generation of non-Euclidean geometries is studied in this paper.Key words:system of Axiomatizing; non-Euclidean geometries;Lobachevskian geometry; Ricmmanian geometry.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反 证 法 。
证 明 了 第 五 公 设 。 我 们 知 道 , 这 其 实 就 是 数 学 中 的
为 如 果 这 个 系 统 为 基 础 的 推 理 中 出 现 矛 盾 , 就 等 于
设 结 合 成 一 个 公 理 系 统 , 展 开 一 系 列 的 推 理 。 他 认
用 它 来 代 替 第 五 公 设 , 然 后 与 欧 式 几 何 的 前 四 个 公
4.3 非欧几何学
欧氏几何学与罗氏几何学定理的不同
08理 邹亚君 24号
一、 回 顾 欧 式 几 何 学
二、非 欧 几 何 学
一、回 顾 欧 式 几 何 学
欧 几 里 得
约公元前 300年,古希腊数 学家欧几里得集前人之大成, 总结了人们在生产、生活实践 中获得的大量的几何知识,规 定了少数几个原始假定为公理、 公设,并定义了一些名词概念, 通过逻辑推理,得到一系列的 几何命题,形成了欧几里得几 何学,简称欧氏几何。
互 不 矛 盾 的 一 组 假 设 都 有 可 能 提 供 一 种 几 何 学 。
出 一 个 极 为 重 要 的 、 具 有 普 遍 意 义 的 结 论 : 逻 辑 上
从 罗 巴 切 夫 斯 基 创 立 的 非 欧 几 何 学 中 , 可 以 得
氏 几 何 。 这 是 第 一 个 被 提 出 的 非 欧 几 何 学 。
1.几 何 原 本
2. 几 何 原 本 介 绍
1.几 何 原 本
欧几里得著有《几何原本》(以下简称《原本》)一书,该书
共13卷,除第5、7、 8、9、10卷是用几何方法讲述比例和算术理论 以外,其他各卷都是论述几何问题的。这部书成为传播几何知识的 教科书达2000年之久,现代初等几何学(即平面几何和立体几何) 的内容基本全包括在此书内 。中国最早的译本是明代万历年间 (1607)由大学士徐光启与意大利天主教传教士利玛窦合译的《几 何原本》前 6 卷。《原本》之所以具有价值,不仅因为欧几里得非 常详尽地搜集了当时所知道的一切几何资料,而更重要的是把那些 分散的知识用逻辑推理的方法编排成一个有系统的演绎的几何学体 系。他是历史上第一个创造了一个比较完整的数学理论的人。
结 矛 了 论 盾 一 第 : 的 个 但 命 又 是 一 题 一 , , 。 个 在 第 最 在 他 五 后 直 极 公 , 觉 为 设 罗 上 细 不 巴 匪 致 能 切 夷 深 被 夫 所 入 证 斯 思 的 明 基 , 推 。 得 但 理 出 在 过 两 逻 程 个 辑 中 重 上 , 要 毫 得 的 无 出
路 子 。 他 提 出 了 一 个 和 欧 式 平 行 公 理 相 矛 盾 的 命 题 ,
切 夫 斯 基 在 证 明 第 五 公 设 的 过 程 中 , 他 走 了 另 一 条
到 了 十 九 世 纪 二 十 年 代 , 俄 国 喀 山 大 学 教 授
罗 巴
2. 罗 氏 几 何 学
罗巴切夫斯基几何的公理系统 和欧几里得几何不同的地方仅仅是 把欧式几何平行公理用“在平面内, 从直线外一点,至少可以做两条直 线和这条直线平行”来代替,其他 公理基本相同。由于平行公理不同, 经过演绎推理却引出了一连串和欧何原本》共有23个定义,5条公设,5条公理, 他力图把几何学建立在这些原始的定义、公理和公设的基础上,然 后以这些显然的假设为依据推证出体系里的一切定理。由于欧几里 得所处的时代是人类文明的初期,受时代的局限,《原本》的逻辑 系统不可能完美无缺,在许多地方出现了漏洞。例如:常常使用未 经定义过的概念来解释一个新的概念;用了既不是公理,又不是公 设,也没有证明过的结论作为论证命题的依据;等等。正因为如此, 在《原本》问世后2000年中,一方面《原本》作为用逻辑来叙述科 学的典范,对数学其他分支甚至整个科学发展起着深远的影响;另 一方面,对于《原本》在逻辑上的欠缺进行修改、补充和研究工作 从未停止过,对于《原本》中的定义、公理、公设的研究成了历代 数学家的重要课题。尤其对于《原本》中的第五公设,许多数学家 对它产生了怀疑,最终导致非欧几何的创建。
二、非 欧 几 何 学
非欧几何学(Non-Euclidean geometry )是一门大 的数学分支,一般来讲 ,它有广义、狭义、通常 意义这三个方面的不同含义。所谓广义式泛指一切 和欧几里得几何不同的几何学,所以又叫非欧几里 得几何学;狭义的非欧几何只是指罗氏几何来说的, 至于通常意义的非欧几何,就是指罗氏几何和黎曼 几何这两种几何。
这 种 几 何 学 被 称 为 罗 巴 切 夫 斯 基 几 何 , 简 称 罗
严 密 的 几 何 学 。
了 新 的 理 论 。 这 个 理 论 像 欧 式 几 何 一 样 是 完 善 的 、
得 到 了 一 系 列 在 逻 辑 上 无 矛 盾 的 新 的 定 理 , 并 形 成
第 二 , 在 新 的 公 理 体 系 中 展 开 的 一 连 串 推 理 ,
1.非欧几何学的诞生 2. 罗 氏 几 何 学 3. 黎 曼 几 何 学
4.罗氏几何学中不一定成立的 欧式几何学定理 5.罗氏几何学与欧式几何学截 然不同的定理
1.非欧几何学的诞生
欧几里得的《几何原本》提出了五条公设,头四条公设分别为: 1.由任意一点到任意一点可作直线。 2.一条有限直线可以继续延长。 3.以任意点为心及任意的距离可以画圆。 4.凡直角都相等。 第五条公设说:同一平面内一条直线和另外两条直线相交,若在某一侧的两 个内角的和小于两直角,则这两直线经无限延长后在这一侧相交。 长期以来,数学家们发现第五公设和前四个公设比较起来,显得文字叙述冗 长,而且也不那么显而易见。有些数学家还注意到欧几里得在《几何原本》一书 中直到第二十九个命题中才用到,而且以后再也没有使用。也就是说,在《几何 原本》中可以不依靠第五公设而推出前二十八个命题。因此,一些数学家提出, 第五公设能不能不作为公设,而作为定理?能不能依靠前四个公设来证明第五公 设?这就是几何发展史上最著名的,争论了长达两千多年的关于“平行线理论” 的讨论。 由于证明第五公设的问题始终得不到解决,人们逐渐怀疑证明的路子走的对 不对?第五公设到底能不能证明?
