五年级奥数第5讲--等积变形剖析
小学五年级奥数精讲等积变形求面积(含答案)

小学奥数精讲:等积变形求面积“三角形的面积等于底与高的积的一半”这个结论是大家熟知的,据此我们立刻就可以知道: 等底等高的两个三角形面积相等. 这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等,当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”.另一类是两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边的所对的顶点在一条与底边平行的直线上,如右图中的三角形A 1BC 与A 2BC 、A 3BC 的面积都相等。
图形割补是求图形面积的重要方法,利用割补可以把—些形状不规则的图形转换成与之面积相等但形状规则的图形,或把不易求面积的图形转换成易求面积的图形.利用添平行线或添垂线的办法,常常是进行面积割补的有效方法,利用等底等高的三角形面积相等这个性质则是面积割补的重要依据,抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键.进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案.不要盲目地乱动手.本讲中.的几个例子都是经过仔细计算才切拼成功的。
例1、已知三角形ABC 的面积为1,BE = 2AB ,BC =CD ,求三角形BDE 的面积?例2、如下图,A 为△CDE 的DE 边上中点,BC=31 CD ,若△ABC(阴影部分)面积为5平方厘米,求△ABD 及△ACE 的面积.例3、 2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角基本概念例题分析三角形拼成(直角边长为2和3),问:大正方形面积是多少?例4、下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积.练习提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD 是平行四边形,DC =CE ,如果△BCE 的面积是15平方厘米,那么梯形ABED 的面积是多少平方厘米?4、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,三角形DEF 的面积是多少平方厘米?CF 长多少厘米?5、如图,在平行四边形ABCD 中,AE =ED ,BF =FC ,CG =GD ,平行四边形ABCD 的面积是阴影三角形EFG 的多少倍?(4)6、一个长方形被两条直线分成四个长方形,其中三个面积分别是20平方米,25平方米和30平方米,阴影部分的面积是多少平方米?7、如右图,平行四边形ABCD 的面积是240平方厘米,如果平行四边形内任取一点0,连接AO 、BO 、CO 、DO ,三角形AOD 与三角形BOC 的面积和的21,加上三角形AOB 与三角形DOC 的面积和的31,结果是多少?8、图8-17中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的2倍,求三角形CDE的面积.9、如图,正方形的边长为10厘米,用一根铁丝弯成直角,把这根铁丝放到正方形上,使直角顶点与正方形的中心O重合,问正方形在直角内部的部分有多大面积?答案:【例题分析】例1. 4例2.三角形ABD=10平方厘米三角形ACE=15平方厘米例3. 13例4. 27【练习提高】1. 22.52. 1203. 454. 三角形DEF=24平方厘米 CF=6厘米5. 4倍6. 37.57. 1008. 59. 25。
奥数-等积变形

奥数-教学教案
授课时间:年月日备课时间年月日年级五课程类别课时学生姓名
授课主题三角形等积变形授课教师
教学目标理解和掌握三角形形状变化但是面积不变
教学
重难点
理解三角形形状变化但是面积不变
教学方法讲练结合
教学过程1、课程导入/错题讲解:
点
拨
教学过程2.知识点讲解
学
习
札
记
教学过程
3、例题分析:
1、如图所示三角形ABC,D为AC上一点,CD=2AD。
问:三角形ABC的面积是三角形
ADB的几倍?方法与技巧
2.如图平行四边形ABCD,E为AB中点,F为DB中点。
已知三角形BEF面积为4平方厘米,问:平行四边形ABCD面积是多少平方厘米?
教学过程4、随堂练习
小
提
本课小结
及下节预告。
五年级奥数第5讲等积变形

第五讲长方体、正方体的表面积和体积等积变形例一、一个装有水的长方体水槽,底面积为80平方厘米,水深8厘米。
现将一个底面积为16平方厘米的长方体铁块竖放入水底,仍有部分铁块露在外面,现在水深多少厘米?分析:根据题意可知,水槽中的水的体积在放入铁块后没有变化,依然是80×8=640(立方厘米),这时底面积为80-16=64(平方厘米)。
根据体积=底面积×高,再求出现在的水深。
80×8÷(80-16)=640÷64=10(厘米)答:现在水深是10厘米。
巩固练习1(1)一个底面积为360平方厘米的水槽内,水深12厘米,现将一个底面积为72平方厘米的长方体铁块竖放入水槽底部,仍有部分铁块露在外面,现在水深多少厘米?(2)在一个长5分米、宽4分米、高6分米的水箱中,水深4分米,现将一个底面边长20厘米、高10分米的的长方体铁块,竖放入水底,现在水面距离水箱口多少分米?(3)一个底面积为1200平方厘米、深为30厘米的水槽内,水深10厘米,现将一个底面边长为20厘米的长方体铁块竖放入水底,这时铁块仍高于水面,现在水面高是多少厘米?例二、有一个长方体水槽,它的底面是边长是边长为20厘米的正方形,有一段横截面积是80平方厘米的长方形钢材浸没在其中,当钢材从水槽中取出以后,水槽的水面下降了3厘米,求这段钢材的长。
分析:根据题意可知,钢材的体积相当于水槽内下降部分的体积,即20×20×3=1200(立方厘米),再根据横截面面积×长=体积,求出这段钢材的长。
20×20×3÷8=1200÷80=15(厘米)答:这段钢材的长是15厘米。
巩固练习2(1)在一个棱长是24厘米的正方体容器中注入水。
有一根横截面积是192平方厘米的长方形铁棒浸没在水中,当把铁棒从容器中取出后,容器中的水面下降了5厘米,求这根铁棒的长度。
小学五年级 等积变形
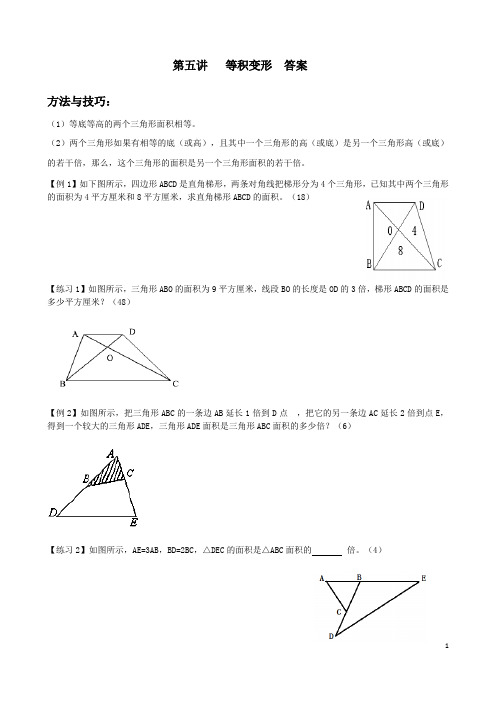
第五讲等积变形答案方法与技巧:(1)等底等高的两个三角形面积相等。
(2)两个三角形如果有相等的底(或高),且其中一个三角形的高(或底)是另一个三角形高(或底)的若干倍,那么,这个三角形的面积是另一个三角形面积的若干倍。
【例1】如下图所示,四边形ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为4平方厘米和8平方厘米,求直角梯形ABCD的面积。
(18)【练习1】如图所示,三角形ABO的面积为9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?(48)【例2】如图所示,把三角形ABC的一条边AB延长1倍到D点,把它的另一条边AC延长2倍到点E,得到一个较大的三角形ADE,三角形ADE面积是三角形ABC面积的多少倍?(6)【练习2】如图所示,AE=3AB,BD=2BC,△DEC的面积是△ABC面积的倍。
(4)【例3】已知三角形ABC面积为56平方厘米,是平行四边形DEFC的2倍,则阴影部分的面积是多少平方厘米?(14)【例4】如图所示,矩形ABCD的面积为24平方厘米,三角形ADM与三角形BCN的面积和为7.8平方厘米,则四边形PMON的面积是多少平方厘米?(1.8)【例5】如图所示,点M、N、P、Q分别在平行四边形ABCD的边AB、BC、CD、DA上,且PE//GM//CB,HN//QF//AB。
若平行四边形ABCD的面积为600平方厘米、阴影部分的面积为80平方厘米。
请问四边形MNPQ的面积为多少平方厘米?(340)【例6】如图所示,在正方形ABCD的BC边上取一动点E,以DE为边作矩形DEFG,且FG边通过点A。
在点E从点B移动到点C过程中,矩形DEFG的面积()(E)(A)一直变大。
(B)一直变小。
(C)先变小后变大。
(D)先变大后变小。
(E)保持不变。
【练习1】如左下图,△ABC中,D、E分别为边BC、AB的中点。
若图中阴影部分面积为1,则△ABC的面积为多少?(4)【练习2】如右上图所示,图中阴影部分的面积为多少平方厘米?(24)【练习3】如图,六角形的6个顶点恰好是一个正六边形的6个顶点。
五年级奥数第5讲--等积变形
5
例1 用四种不同的方法,把任意一个三角形分成四个面
积相等的三角形. A
A
E
F
B DEF C
B
D
C
方法1:如左图,将BC四等分,
(BD=DE=EF=FC=BC/4)、连结AD、AE、AF,则
△ABD、△ADE、 △AEF、 △AFC等积.
方法2:如右图,先将BC二等分,分点D、连结AD,
得到两个等积三角形,即△ABD与△ADC等积.然
2021/10/10
白汀水
14
例8 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,
DC=CG,AD=DH.求四边形EFGH的面积.
H
G
C
D S11 S2 B
E A?
F
解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有 S△FBD=S△DBC=S1 所以S△CGF=S△DFC= S△FBD+S△DBC=2S1.
2
为便于实际问题的研究,我们还会常常用到以下结论:
①等底等高的两个三角形面积相等.
②底在同一条直线上并且相等,该底所对的角的顶点是同一
个点或在与底平行的直线上,这两个三角形面积相等.
③若两个三角形的高(或底)相等,其中一个三角形的底(
或高)是另一个三角形的几倍,那么这个三角形的面积也是
另一个三角形面积的几倍.
2021/10/10
白汀水
10
例4 如右图,把四边形ABCD改成一个等积的三角形.
D
A
A′ B
C
分析 本题有两点要求,一是把四边形改成一个三角形,二是
改成的三角形与原四边形面积相等.我们可以利用三角形等积
变形的方法,如上图, 把顶点A移到CB的延长线上的A′处,
小学五年级数学思维专题训练—等积变形(含答案解析)
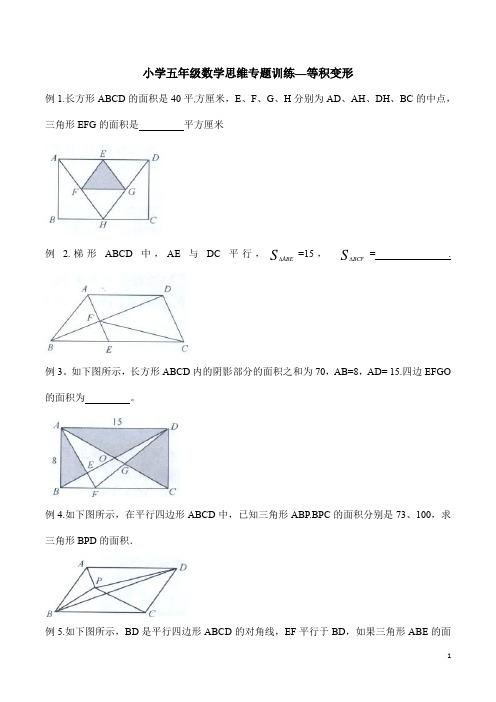
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
五年级奥数专题 等积变换、切割、平移、旋转(学生版)

学科培优数学等积变换、切割、平移、旋转学生姓名授课日期教师姓名授课时长知识定位本讲是几何知识体系中的一个基石同时也是一个升华,等积变换试平面几何的基础,解决三角形问题几乎无处不在,切割、平移、旋转是解决个性问题的个性思想,在几何中举足轻重,能使复杂的问题巧妙化解。
所以本讲是非常重要的一讲,也是竞赛常考的知识板块。
重点难点:1. 等积变换中等地等高三角形的寻找。
2.化未知图形为已知图形。
3. 合理做辅助线4. 平移、旋转、切割等知识的适用范围主要考点:1. 面积和边的比例关系2. 利用平移、旋转解复杂问题知识梳理常见图形面积的解题方法我们已经知道三角形面积的计算公式:三角形面积=底×高÷2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小);如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。
这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: 1、等底等高的两个三角形面积相等.2、若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍. 3、夹在一组平行线之间的等积变形,如下图,和夹在一组平行线之间,且有公共底边那么;反之,如果,则可知直线平行于。
4、把未知图形转化为三角形、长方形、正方形来求解。
小学奥数-直线型面积讲义图文版

1. 熟练运用直线型面积的最基本性质——等积变形;2. 熟练掌握直线型面积的两个模型: (1)等积变形 (2)鸟头模型直线型面积求解是在以三角形、长方形、正方形、梯形等一些规则图形为基础上进行的。
最基本的思想是等积变形。
一、等积变形①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =baS 2S 1 DC BA③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDA知识精讲教学目标第一讲 直线型面积(一)板块一、等积变形【例 1】 如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.FE CBAFE C【解析】 本题是等底等高的两个三角形面积相等的应用.连接BH 、CH . ∵AE EB =,∴AEH BEH S S =△△.同理,BFH CFH S S =△△,S =S CGH DGH ,∴11562822ABCD S S ==⨯=阴影长方形(平方厘米).【巩固】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E GCB654321HBCG E【例 2】 如图,有三个正方形的顶点D 、G 、K 恰好在同一条直线上,其中正方形GFEB 的边长为10厘米,求阴影部分的面积.KO QH G F EB A K O QH GF EBA【解析】 对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接FK 、GE 、BD ,则////BD GE FK ,根据几何五大模型中的面积比例模型,可得DGE BGE S S ∆∆=,KGE FGE S S ∆∆=,所以阴影部分的面积就等于正方形GFEB 的面积,即为210100=平方厘米.【巩固】右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.GAB CDGAB CDF【巩固】(2008年西城实验考题)如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为 .BE FHBCEFH【巩固】正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?D G HE CCEHG D【例 3】 长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?HGE【解析】 解法一:寻找可利用的条件,连接BH 、HC ,如下图:H E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++= 即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=;而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影 解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:GE (H )这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影.【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.P CAA CPCA【例 4】 (2007首届全国资优生思维能力测试)ABCD 是边长为12的正方形,如图所示,P 是内部任意一点,4BL DM ==、5BK DN ==,那么阴影部分的面积是 .PKK P【解析】 (法1)特殊点法.由于P 是内部任意一点,不妨设P 点与A 点重合(如上中图),那么阴影部分就是AMN ∆和ALK ∆.而AMN ∆的面积为(125)4214-⨯÷=,ALK ∆的面积为(124)5220-⨯÷=,所以阴影部分的面积为142034+=.(法2)寻找可以利用的条件,连接AP 、BP 、CP 、DP 可得右上图所示:则有:211127222PDC PAB ABCD S S S ∆∆+==⨯=同理可得:72PAD PBC S S ∆∆+=;而::4:121:3PDM PDC S S DM DC ∆∆===,即13PDM PDC S S ∆∆=;同理:13PBL PAB S S ∆∆=,512PND PDA S S ∆∆=,512PBK PBC S S ∆∆=;所以:15()()()()312PDM PBL PND PBK PDC PAB PDA PBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++而()()()()PDM PBL PND PBK PNM PLK DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++阴影面积;145102DNM BLK S S ∆∆==⨯⨯=;所以阴影部分的面积是:15()()()312PNM PLK PDC PAB PDA PBC DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+=+++-+即为:15727210224302034312⨯+⨯-⨯=+-=.【例 5】 (2008年四中考题)如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC∆的面积是 平方厘米.DADA【解析】 连接CD .根据题意可知,DEF ∆的面积为DAC ∆面积的13,DAC ∆的面积为ABC ∆面积的12,所以DEF ∆的面积为ABC ∆面积的111236⨯=.而DEF ∆的面积为5平方厘米,所以ABC ∆的面积为15306÷=(平方厘米).【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF长的3倍.那么三角形AEF 的面积是多少平方厘米?F ECBA【例 6】 如图,大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成.求阴影部分的面积.48cm 224cm 236cm 212cm 2MNB A12cm 236cm 224cm 248cm 2【解析】 如图,将大长方形的长的长度设为1,则12112364AB ==+,24124483CD ==+,所以1113412MN =-=,阴影部分面积为211(12243648)5(cm )212+++⨯⨯=.【例 7】 (2009年第七届”希望杯”二试六年级)如图,在三角形ABC 中,已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89,28,26.那么三角形DBE 的面积是 .D【解析】 根据题意可知,8928117ADCADE DCE S S S ∆∆∆=+=+=,所以::26:1172:9BDC ADC BD AD S S ∆∆===, 那么::2:9DBE ADE S S BD AD ∆∆==,故222789(901)2019S =⨯=-⨯=-=.【例 8】 O 是长方形ABCD 内一点,已知OBC ∆的面积是25cm ,OAB ∆的面积是22cm ,求OBD ∆的面积是多少?POD C B【解析】 由于ABCD 是长方形,所以12AOD BOC ABCD S S S ∆∆+=,而12ABD ABCD S S ∆=,所以AOD BOC ABD S S S ∆∆∆+=,则BOC OAB OBD S S S ∆∆∆=+,所以2523cm OBD BOC OAB S S S ∆∆∆=-=-=.【例 9】 如右图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若PBD ∆的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?CEFHPCEFH P【解析】 根据差不变原理,要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差,相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差. 如右上图,连接CP 、AP .由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=,所以BCP ABP BDP S S S ∆∆∆-=.而12BCP BCFE S S ∆=,12ABP ABHG S S ∆=,所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米).【例 10】 如右图,正方形ABCD 的面积是20,正三角形BPC ∆的面积是15,求阴影BPD ∆的面积.PBAOAB P【解析】 连接AC 交BD 于O 点,并连接PO .如下图所示,可得//PO DC ,所以DPO ∆与CPO ∆面积相等(同底等高),所以有:BPO CPO BPO PDO BPD S S S S S ∆∆∆∆∆+=+=,因为1120544BOC ABCD S S ∆==⨯=,所以15510BPD S ∆=-=.【巩固】如右图,正方形ABCD 的面积是12,正三角形BPC ∆的面积是5,求阴影BPD ∆的面积.PBAOAB DP【例 11】 (2008年”华杯赛”决赛)右图中,ABCD 和CGEF 是两个正方形,AG 和CF 相交于H ,已知CH等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积.HG F E D C B AHGF ED CB A【解析】 连接AC 、GF ,由于AC 与GF 平行,可知四边形ACGF 构成一个梯形.由于HCG ∆面积为6平方厘米,且CH 等于CF 的三分之一,所以CH 等于FH 的12,根据梯形蝴蝶定理或相似三角形性质,可知FHG ∆的面积为12平方厘米,AHF ∆的面积为6平方厘米,AHC ∆的面积为3平方厘米.那么正方形CGEF 的面积为()612236+⨯=平方厘米,所以其边长为6厘米.又AFC ∆的面积为639+=平方厘米,所以9263AD =⨯÷=(厘米),即正方形ABCD 的边长为3厘米.那么,五边形ABGEF 的面积为:21369349.52++⨯=(平方厘米).【例 12】 如图,已知长方形ADEF 的面积16,三角形ADB 的面积是3,三角形ACF 的面积是4,那么三角形ABC 的面积是多少?F ED CB AF ED CB A F ED CB A【解析】 方法一:连接对角线AE . ∵ADEF 是长方形∴12ADE AEF ADEF S S S ∆∆==∴38ADB ADE S DB DE S ∆∆==, 12ACF AEF S FC EF S ∆∆== 5BE DE DB -1CE FE CF -∴1515162822BEC S ∆=⨯⨯⨯=∴132ABC ADEFADB ACF CBE S SS S S ∆∆∆∆=---=. 方法二:连接BF ,由图知1628ABF S =÷=△,所以16835BEF S =--=△,又由4ACF S =△,恰好是AEF △面积的一半,所以C 是EF 的中点,因此52 2.5BCE BCF S S ==÷=△△,所以1634 2.5 6.5ABC S =---=△【例 13】 (第七届”小机灵杯”数学竞赛五年级复赛)如图所示,三角形ABC 中,D 是AB 边的中点,E 是AC边上的一点,且3AE EC =,O 为DC 与BE 的交点.若CEO ∆的面积为a 平方厘米,BDO ∆的面积为b 平方厘米.且b a -是2.5平方厘米,那么三角形ABC 的面积是 平方厘米.E baOD CBA【解析】 12ABC BCD BCO S S b S ∆∆∆==+,14ABC BCE BCO S S a S ∆∆∆==+,所以112.524ABC ABC S S b a ∆∆-=-=(平方厘米).所以 2.5410ABC S ∆=⨯=(平方厘米).【例 14】 如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?G FD C【解析】 如下图,连接FC ,DBF 、BFG 的面积相等,设为x 平方厘米;FGC 、DFC 的面积相等,设为y 平方厘米,那么DEF 的面积为13y 平方厘米.xyy x GFE DCBA221BCD S x y =+=,BDE 111S =x+y=l 333⨯=.所以有0.531x y x y +=⎧⎨+=⎩①②.比较②、①式,②式左边比①式左边多2x ,②式右边比①式右边大0.5,有20.5x =,即0.25x =,0.25y =.而阴影部分面积为2550.253312y y +=⨯=平方厘米.【例 15】 (2008年第一届”学而思杯”综合素质测评六年级2试)如图,45BC =,21AC =,ABC ∆被分成9个面积相等的小三角形,那么DI FK += .KJIH GFE DC B A【解析】 由题意可知,::2:9BAD ABC BD BC S S ∆∆==,所以2109BD BC ==,35CD BC BD =-=;又::2:5DIF DFC DI DC S S ∆∆==,所以2145DI DC ==,同样分析可得10FK =,所以141024DI FK +=+=.【巩固】(2009年清华附中入学测试题)如图,在角MON 的两边上分别有A 、C 、E 及B 、D 、F 六个点,并且OAB ∆、ABC ∆、BCD ∆、CDE ∆、DEF ∆的面积都等于1,则DCF ∆的面积等于 .OBD FN【例 16】 (2009年四中入学测试题)如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【解析】 连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=;所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=,于是:2115652827ADG CBF S S ∆∆+=;712382827ADG CBF S S ∆∆+=;可得40ADG S ∆=.故三角形ADG 的面积是40.【例 17】 (2008年走美六年级初赛)如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .O GFEDBA【解析】 利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=;又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=. 另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【巩固】(2008年”华杯赛”初赛)如图所示,矩形ABCD 的面积为24平方厘米.三角形ADM 与三角形BCN的面积之和为7.8平方厘米,则四边形PMON 的面积是 平方厘米.NOMPDCBA【例 18】 (清华附中分班考试题)如图,如果长方形ABCD 的面积是56平方厘米,那么四边形MNPQ 的面积是多少平方厘米?3PD C B333D CB【解析】 如图,过M 、N 、P 、Q 分别作长方形ABCD 的各边的平行线.易知交成中间的阴影正方形的边长为3厘米,面积等于9平方厘米.设MQD ∆、NAM ∆、PBN ∆、QCP ∆的面积之和为S ,四边形MNPQ的面积等于x ,则569x S x S +=⎧⎨-=⎩,解得32.5x =(平方厘米).板块二 鸟头模型【例 19】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 20】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 21】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 22】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 23】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =,1ABC S =, ∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯. 又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES=.所以186318DEFABCFCEADFBDESS SS S=+++=+++=.【例 24】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【例 25】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 26】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.练习1. (第三届“华杯赛”初赛试题)一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是221cm .问:长方形的面积是多少平方厘米?红绿黄红练习2. 如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与BEC 等积的三角形一共有哪几个三角形?F DECBA练习3. (97迎春杯决赛)如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且2AN BN =.那么,阴影部分的面积是多少?课后练习练习4. 如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FE DCBA练习5. 如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E D CBA AB CD E练习6. 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF。
五年级奥数——等积变形

年 级授课日期 授课主题 第5讲——等积变形教学内容i.检测定位两个平面图形面积相等,称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积.其中三角形的等积变形的技巧是各种等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则,并由此衍生出因题而宜的种种精巧的等积变形的技巧.【例1】如图5-1,ABCD 是直角梯形,两条对角线把梯形分为4个三角形.已知其中两个三角形的面积为3平方厘米和6平方厘米,求直角梯形ABCD 的面积.分析与解 因为三角形ADC 和三角形ADB 同底等高,所以ADB ADC S S ∆∆=,又三角形AOD 是公共部分,可知).(3平方厘米==∆∆COD AOB S S在三角形BOC 与三角形DOC 中,BO 、OD 边上的高相等,6是3的2倍,可知OD BO 2=,得AOD AOB S S ∆∆=2,这样).(5.123平方厘米=÷=∆AOD S 因此,).(5.13)36(3336平方厘米梯形=÷÷+++=ABCD S随堂练习1如图5-2,三角形ABO 的面积为9平方厘米,线段BO 的长度是线段OD 的3倍,梯形ABCD 的面积是多少平方厘米?【例2】如图5-3,把三角形ABC 的一条边AB 延长1倍到D ,把它的另一边AC 延长2倍到E ,得到一个较大的三角形ADE ,三角形ADE 的面积是三角形ABC 面积的多少倍?分析与解 如图5-4,连结BE ,因为AC CE 2=,所以ABC BCE S S ∆∆=2,即ABC ABE S S ∆∆=3.又因为BD AB =,则BDE ABE S S ∆∆=,ABC ADE S S ∆∆=6.随堂练习2如图5-5,DBE BC BD AB AE ∆==,2,3面积是ABC ∆面积的________倍.【例3】如图5-6,已知三角形ABC 的面积为56平方厘米,是平行四边形DEFC 的2倍,阴影部分的面积是多少平方厘米?分析与解 如图5-7,连结EC .EC 为平行四边形DEFC 的对角线.平行四边形DEFC 的面积是(平方厘米)28256=÷,由平行四边形的性质有.2S DEC ÷=∆DEFC S 平行四边形在ED CED AED 中,与∆∆为公共底,,AC DE 平行于则 ED 边上的高相等,因此.DEC AED S S ∆∆=).(1422562平方厘米=÷÷=÷==∆∆DEFC DEC AED S S S随堂练习3如图5-8,ABC ∆的面积等于24平方厘米,M 为AB 中点,E 为AM 上任意一点,MD 与EC 平行.求EBD ∆的面积.【例4】如图5-9所示,矩形ABCD 的面积为24平方厘米,三角形ADM 与三角形BCN 的面积之和为7.8平方厘米,则四边形PMON 的面积是__________平方厘米.分析与解 三角形AOD 与三角形BOC 的面积之和为矩形ABCD 面积的一半,先求出三角形AOM 和三角形NOB 的面积之和,由三角形ABP 的面积减去三角形AOB 的面积,再减去三角形AOM 和三角形NOB 的面积和,就可求出四边形PMON 的面积了.).(2.48.7224平方厘米=-÷=+∆∆NOB AOM S S).(8.14242.4224平方厘米四边形=÷--÷=PMON S说明 本题说求的阴影部分面积看似无从下手,实质上只要我们理清楚解题的思路分步考虑,脚踏实地地去做,求出本题的答案是不难的.随堂练习4如图5-10,平行四边形ABCD 中DF BF 2=,.的中点是BC E 平方厘米,8=∆BEF S 求平行四边形ABCD 的面积.【例5】如图5-11,梯形ABCD 的面积是45平方厘米,高是6厘米,BC AD //.三角形AED 的面积是5平方厘米,厘米10=BC ,求三角形BCE 的面积.分析与解 由已知量,可先求出上底AD ,进而求出三角形ABD (或ACD )面积及三角形ABE 面积,利用等积变换可知三角形ABE 与三角形CDE 等积.最后得到三角形BCE 的面积.由梯形的面积公式得 6102145⨯+⨯=)(AD , 解得厘米5=AD ,进而 )(155621平方厘米=⨯⨯=∆ABD S . 由等积变形知 ACD ABD S S ∆∆=,从而 )(10515平方厘米=-==∆∆CDE ABE S S .所以 )(20210545平方厘米=⨯--=∆BCE S .【例6】如图5-12,已知长方形宽是长的32,平方厘米14=∆ABC S ,AD AC 31=,EF DE =.求阴影部分的面积.分析与解 连结BD ,因为AD AC 31=,所以,)(421433平方厘米=⨯=⨯=∆∆ABC ABD S S , 从而)(84422平方厘米长方形=⨯=ABFD S .又因为EF DE =,所以 )(21844141平方厘米长方形=⨯==∆ABFD BFE S S , 从而 )(49211484平方厘米长方形阴影面积=--=--=∆∆BFE ABC ABFD S S S S .随堂练习5如图5-13,梯形ABCD 中,BC AD //,对角线交于O ,三角形AOD 面积为20,三角形ABO 面积为30.求梯形ABCD 的面积.(单位:平方厘米)读一读不要轻易放弃题目 平面上有7个点,任意三点不在同一直线上.以上这7个点作为定点作三角形,使任意两个三角形至多只有一个公共顶点.问最多可以作出多少个满足上述条件的三角形?我在纸上画了很多草图,费尽心思,想得到合乎要求的7个三角形,但没有结果.只好向单墫请教,他很快就给出了解答,非常精彩.在他的解答中有一句话使我心头一震:“在构造这7个三角形时,每一个点恰好用了3次”.事后,我又回顾了自己的思路,有两张草图印象很深.第一张是开始时的草图(图1),这是第一个念头,只能作出3个符合要求的三角形.于是想在此图基础上连线增加符合要求的三角形,虽然有所改进,但毫无章法,很快就放弃了.为了改进作图,我先将7个点放在圆上,可保证无3个点共线,两两连线,得到以给定7个点为顶点的所有三角形(图2),我知道要求的7个三角形必在其中.但要把他们找出来,并加以说明又很困难.然而当单老师的信息“每个点恰用3次”出现时,我的第1个年头立刻浮现在眼前,图中的“1”不正好直观地被用了3次吗?如果对1进行轮换,用2、3、4、5、6、7替换1,就可产生2173=⨯个符合要求的三角形,而因为每个点恰好用了3次,因此,合乎题目要求的三角形正好是7个,这7个三角形的3个顶点分别为(1,2,3),(3,4,5),(5,6,1),(1,7,4),(3,7,6),(5,7,2),(2,4,6).上面的想法几乎在一瞬间完成,再去复查2,7个三角形很容易找出来了.单老师在谈解题思路是常说,做不出来不要紧,很多想法虽然没有解决全部问题,但其中或解决了部分问题,或隐含着解决问题的合理成分.关键是要会总结,碰了钉子不要紧,不一定全部放弃你原来的想法.ii.针对培养1.如图,ABC ∆中,D 、E 分别为各边重点.若阴影部分面积为1,则ABC ∆的面积为_________.2.如图,同种阴影部分的面积为__________平方厘米.3.如图,梯形的下底长为10厘米,高为6厘米,阴影部分的面积是________平方厘米.4.如图,平行四边形中,A 、M 、N 分别为对应线段的中点,且阴影部分面积为15平方厘米,则大平行四边形的面积是__________平方厘米.5.如图,将ABC ∆的AB 边延长1倍,将BC 边延长2倍,得ADE ∆,则ADE ∆的面积是ABC ∆面积的________倍.6.如图,,4,3CD AC BE BC ==则ABC ∆的面积是DEA ∆面积的________倍.7.如图,求平行四边形中阴影部分面积.(单位:厘米)8.如图,ABC ∆中,.32==BD AD ,四边形DBEF 的面积等于ABE ∆的面积.若ABC ∆的面积等于10,则四边形DBEF 的面积是多少?9.如图,梯形ABCD 中,BC AD //,ABE ∆的面积为30平方厘米,.2AE EC =求梯形ABCD 的面积.10.如图,ABC ∆的面积是72平方厘米,D 是BC 的中点,.2,3EF FD AE BE ==求三角形AFD 面积.11.如图,ABC ∆的面积为14平方厘米,.,3ED AE DB DC ==求阴影部分面积.12.如图,长方形ABCD 中,,2,,GF EG FC DF ED AE ===且长方形的长和宽分别是10厘米、6厘米.则BFG ∆的面积是多少?。
最新小学奥数 三角形的等积变形学生版

最新小学奥数三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.,它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.例如在右图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如右图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC 高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1 用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.例2 用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.例3 如右图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.例4 如右图,把四边形ABCD改成一个等积的三角形.例5 如右图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.例6 如下页图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=例7 如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF 的面积.例8 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.例9 如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.课后练习:1、如图,BDA长12厘米,DC长4厘米,B、C和D在同一条直线上。
小学五年级奥数精讲等积变形求面积(含答案)

小学五年级奥数精讲等积变形求面积(含答案)小学奥数精讲:等积变形求面积基本概念我们都知道“三角形的面积等于底与高的积的一半”,因此,我们可以得出等底等高的两个三角形面积相等的结论。
这意味着,即使两个三角形的形状不同,只要它们的底和高分别相等,它们的面积就相等。
但是,不能反过来说“面积相等的两个三角形的底和高一定分别相等”。
另一类三角形有一条公共底边,但这条底边上的高相等,即这条底边所对的顶点在一条与底边平行的直线上。
例如,右图中的三角形A1BC、A2BC和A3BC的面积都相等。
图形割补是求图形面积的重要方法。
通过割补,我们可以将一些形状不规则的图形转换成形状规则但面积相等的图形,或者将不易求面积的图形转换成易求面积的图形。
常用的割补方法包括添加平行线或垂线。
利用等底等高的三角形面积相等这个性质是面积割补的重要依据,而抓住具体的图形特点进行分析以确定正确的割补方法则是面积割补的关键。
在进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案。
不要盲目地乱动手。
本讲中的几个例子都是经过仔细计算才切拼成功的。
例题分析例1:已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积。
例2:如下图,A为△XXX的DE边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米,求△ABD及△XXX的面积。
例3:2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角三角形拼成(直角边长为2和3)。
问:大正方形的面积是多少?例4:下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积。
练提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD是平行四边形,DC=CE,如果△BCE的面积是15平方厘米,那么梯形ABED的面积是多少平方厘米?4、正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,三角形DEF的面积是多少平方厘米?CF长多少厘米?在平行四边形ABCD中,如果AE=ED,BF=FC,CG=GD,求平行四边形ABCD的面积是阴影三角形EFG的多少倍。
小学五年级奥数 等积变形

奥数拓展:等积变形(一)故事导入:有一个富翁留了一块三角形的土地给两个儿子,两个儿子要求平分这块地,这可伤透了他们的脑筋,因为他们不知道怎样去测量、平分。
同学们,你们能想出多少种方法将这块土地平分成2个面积相等的三角形吗?根据这个问题,你能得出什么结论?结论一:。
(二)即学即练:1.你有什么方法将任意一个三角形分成3个面积相等的三角形?2.如图,把△ABC的底边BC四等分,那么甲、乙两个三角形的面积谁大,为什么?如图.三角形ABC中.D是AB的中点.点E、F.G、H把BC平均分成五份.阴影部分的面积占三角形ABC面积的几分之几?(三)思维探索:(平行线间的等积变形)如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边,那么△ACD和△BCD的面积关系是怎样的?为什么?(四)即学即练:1.如图,在梯形ABCD中共有8个三角形,其中面积相等的三角形有哪几对?(五)结论总结:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状。
为便于实际问题的研究,我们还会常常用到以下结论:(1)等底等高的两个三角形面积相等;(2)底在同一条直线上并且相等,该底所对的角的的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等;(3)若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(六)例题梳理【例1】等积变形的等分点应用1.如图,在直角三角形ABC中,D、E分别是AB、AC的中点,如果△AED的面积是30平方厘米.求△ABC 的面积?结论2:夹在间的一组同底三角形面积相等2.如图,A为三角形DE边上的中点,BF为CD边上的三等分点,如果三角形ABC的面积为5,求三角形ABD和三角形ACE的面积。
3.在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若三角形ADE的面积是1,求三角形BEF的面积。
等积变形PPT教学课件

加彩壶(清代)
壶盖呈扁圆形,壶身 呈扁圆柱形,口及底渐收, 有圈足,短流,把手上圆 下方。周身以深浅蓝珐琅 彩满绘花纹带。盖上绘花 卉、如意纹,壶口下部一 周是回纹,回纹外一周是 如意纹,腹中部一周绘花 卉卷草纹,近底部绘变形 莲瓣纹。花纹的颜色和紫 砂胎本色既对比又和谐, 在加彩装饰的紫砂器中堪 称佳作。
金银彩绘山水茶壶 (清代)
通体呈方形,直口,口以 下渐广,方圈足。曲形柄,流、 柄均凸起四棱,与壶体相呼应。 口上附盖与壶体相吻合。用紫 色砂泥制作,形体古朴大方。 腹部一面用金银彩绘山水、楼 阁和松柏。另一面为金彩篆书 御制诗:“御制 花港观鱼, 锦梭不籍。天孙掷练,影中堆 万。族云设兴,水仙作春。服 天边风,月傲清华。”共三十 四字。盖面用金彩彩描绘卷枝 纹作边饰,壶口边、足边刻络 绎纤细的回纹。底阳印“乾隆 年制”四字篆款。彩绘技法娴 熟,书意清逸典雅,篆书用笔 流畅,是紫砂器中的珍品。
4×3×2= 1.5 2πx
解得 x 3.4
经检验,符合题意。
答:圆柱的高为 3.4 厘米。
2.分析:
圆柱形瓶内装满水,则水的体积为:
( 5)2 18 112.5 (立方厘米)
2
圆柱形玻璃杯的容积为:
(6)2 10 90 (立方厘米)
2 因此:水的体积大于杯的容积。
可见:圆柱形玻璃杯装不下,圆柱 形瓶内仍剩余部分的水。
注壶 (清代)
壶为梅花形, 并有梅花形盖,盖 上塑二桃形钮。壶 流朝天,为半圆形。 梅花形矮圈足。底 心有一圆形戳记, 字模糊不清。整体 造型俊秀,小巧玲 珑。
彩绘山水注壶 (清代)
壶身似杯,有短平 流,无把。盖身、圈足 均作四瓣瓜棱形。盖顶 堆塑双桃,瓜棱腹两侧 用胭脂红、蓝、青、黄、 黑等多种色料绘山水画。 器形规整,制作讲究。 盖内及壶底均刻草书 “王伦”二字,底又印 有椭圆形款记,惜字迹 模糊,难以辨认。1959 年浙江杭州半山清乾隆 年间墓葬出土。
五年级奥数第5讲等积变形

学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第05 讲,本讲课题:等积变形内容概要熟知各种规则图形的面积求法,结合等积变形来求出不规则图形面积。
两个平面图形面积相等,称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题.其中三角形的等积变形的技巧是各种等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则,并由此衍生出因题而宜的种种精巧的等积变形的技巧。
【例1】计算:如图,5-1,ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为3平方厘米和6平方厘米,求直角梯形ABCD的面积。
随堂练习1如图5-2,三角形ABO的面积为9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?【例2】如图5-3,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的多少倍?随堂练习2如图5-5,AE=3AB,BD=2BC,△DBE面积是△ABC面积的多少倍?【例3】如图5-6,已知三角形ABC的面积为56平方厘米,是平行四边形DEFC的2倍,阴影部分的面积是多少平方厘米?随堂练习3如图5-8,△ABC面积=24平方厘米,M为AB中点,E 为AM上任意一点,MD与EC平行,求EBD的面积。
【例4】如图5-9所示,矩形ABCD的面积为24平方厘米,三角形ADM 与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是多少平方厘米。
随堂练习4如图5-10,平行四边形ABCD中BF=2DF.E是BC中点。
三角形BEF的面积等于8平方厘米,求平行四边形ABCD的面积。
【例5】如图5-11,梯形ABCD的面积是45平方厘米,高6厘米,AD∥BC,三角形AED的面积是5平方厘米,BC=10厘米。
求三角形BCE的面积。
五年级奥数第5讲等积变形

【例1】计学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第05讲,本讲课题:等积变形内容概要熟知各种规则图形的面积求法,结合等积变形来求出不规则图形面积。
两个平面图形面积相等,称为这两个图形等积•解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题•其中三角形的等积变形的技巧是各种等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则, 并由此衍生出因题而宜的种种精巧的等积变形的技巧。
如图,5-1,ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为3平方厘米和6平方厘米求直角梯形ABCD的面积。
◎I 多少平方厘米?A 界C梦想从这里起飞【例2】如图5-3,把三角形ABC 的一条边 少平方厘米?AB 延长1倍到D,把它的 另一边AC 延长2倍到E, 得到一个较大的三角形ADE ,三角形ADE 的面积是三角形ABC 面积的多少【例3】如图5-6,已知三角形ABC 的面积为56平方厘米,是平行四边形DEFC 的2倍,阴影部分的面积是多倍?随堂练习3随堂练习2 如图5-5,AE=3AB BD=2BC,ADBE 面积是△ ABC 面积的多少倍? 如图5-8,^ABC 面积=24平方厘米,M 为AB 中点,E 为AM 上任意一点,MD 与EC 平行,求EBD 的面积。
as-sE和为7.8平方厘米,则1'■只—9四边形PMON的面积是BC=10厘米。
求三角形BCE的面积。
【例4】如图5-9所示, 矩形ABCD的面积为24 平方厘米,三角形ADM 与三角形BCN的面积之【例5】如图5-11,梯形ABCD的面积是45平方厘米,高6厘米,AD〃BC,三角形AED的面积是5平方厘米,多少平方厘米。
随堂练习4如图5-10,平行四边形ABCD中BF=2DF.E是BC中点。
三角形BEF的面积等于8平方厘米,求平行四边形ABCD的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
白汀水
例5 如右图,已知在△ABC中,BE=3AE,CD=2AD.若 △ADE的面积为1平方厘米.求三角形ABC的面积.
解法1:连结BD,在△ABD中 ∵ BE=3AE, ∴ S△ABD=4S△ADE=4(平方厘米). 在△ABC中,∵CD=2AD, B ∴ S△ABC=3S△ABD=3×4=12(平方厘米). 解法2:连结CE,如右图所示,在△ACE中,
A D
B
C
白汀水
例如下图中,△ABC与△DBC的底相同(它们的底都 是BC),△ABC的高是△DBC高的2倍(D是AB中点, AB=2BD,有AH=2DE),则△ABC的面积是△DBC 面积的2倍.
A
D
B E H
C
上述结论,是我们研究三角形等积变形的重要依据.
白汀水
例1 用四种不同的方法,把任意一个三角形分成四个面 A 积相等的三角形. A
D A
A′
B
C
分析 本题有两点要求,一是把四边形改成一个三角形,二是 改成的三角形与原四边形面积相等.我们可以利用三角形等积 变形的方法,如上图, 把顶点A移到CB的延长线上的A′处, △A′BD与△ABD面积相等,从而△A′DC面积与原四边形ABCD面 积也相等.这样就把四边形ABCD等积地改成了三角形 △A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A′点。
E F
B
D
E
F
C
B
D
C
方法1:如左图,将BC四等分, (BD=DE=EF=FC=BC/4)、连结AD、AE、AF,则 △ABD、△ADE、 △AEF、 △AFC等积. 方法2:如右图,先将BC二等分,分点D、连结AD, 得到两个等积三角形,即△ABD与△ADC等积.然 后取AB、AC中点E、F,并连结DE、DF.从而得到 四个等积三角形,即△ADE、△BDE、△DCF、 △ADF等积.
、
DE,从而得到三个三角形:△ADE、△BDE、△ACD.其面积 比为1∶3∶4.
白汀水
方法2:如下图,先取AB中点D,再连结CD,再取CD上的1/4分 点E,连结AE,从而得到三个三角形:△ACE、△ADE、 △BCD.其面积比为1∶3∶4.
A
D 4 B
3 1
E
C
当然本题还有许多种其他分法,同学们可以自己寻找解决.
小学奥数
三角形的等积变形
A 相 相 似 B C 等 D
白汀水
三角形的等积变形
三角形面积的计算公式: 三角形面积=底×高÷2
高 底
这个公式告诉我们:三角形面积的大小,取决于三角形底和高 的乘积.如果三角形的底不变,高越大(小),三角形面积也 就越大(小)。同样若三角形的高不变,底越大(小),三角 形面积也就越大(小)。这说明;当三角形的面积变化时,它 的底和高之中至少有一个要发生变化。但是,当三角形的底和 高同时发生变化时,三角形的面积不一定变化.当三角形的底 和高 的积保持不变,三角形的面积就不变。只有当三角形底 和高的乘积 变化时,三角形的面积才发生变化。
白汀水
A
A
E
F
F
E
B
D
C
B
D
C
方法3:如左图, 取△ABC三条边的中点D、E、F 连结DE、DF、EF,则△BED、△EAF、 △DFC、 △EFD等积.
方法4:如右图, 取点D,使BD=BC/3,连结AD、 取点E、F,使AE=EF=FD,则△ABD、△CAE、 △CEF 、 △CFD等积.
白汀水
解:连结BG,在△ABG中,
∵ BD=2AD, ∴S ⊿ADG=S⊿ABG,在⊿ABC中, ∵ AG=2CG, ∴S ⊿ABG=2/3S⊿ABC,
B D G E F C A
∴S ⊿ADG=(1/3)×(2/3)S⊿ABC=(2/9)S ⊿ABC 。
同理S ⊿BDE=(2/ቤተ መጻሕፍቲ ባይዱ)S ⊿ABC ; S ⊿CFG=(1/9)S ⊿ABC
B
D
E
C
它们所对的顶点同为A点,(也就是它们的高相等)那么 这两个三角形的面积相等. 同时也可以知道△ABC的面积是△ABD或△AEC面积的 3倍.
白汀水
例如在下图中,△ABC与△DBC的底相同(它们的底都是BC), 它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们 的高相等),那么这两个三角形的面积相等.
A D
E 1
C
A E 1 D
∵ CD=2AD, ∴ S△ACE=3S△ADE=3(平方厘米). 在△ABC中,∵BE=3AE ∴ S△ABC=4S△ACE =4×3=12(平方厘米).
B
C
白汀水
例6 如下页图,在△ABC中,BD=2AD,AG=2CG, BE=EF=FC=BC/3,求阴影部分面积占三角形面积的几分之几?
∴ S△ADG+S△BDE+S△CFG =(2/9+2/9+1/9)S ⊿ABC=5/9⊿ABC ∴ 阴影部分面积=(1-5/9)S△ABC=4/9 △ABC
白汀水
例3 如右图,在梯形ABCD中,AC与BD是对角线,其交点O,求 证:△AOB与△COD面积相等.
A O D
B
C
证明:∵△ABC与△DBC等底等高, ∴S△ABC=S△DBC 又∵ S△AOB=S△ABC—S△BOC S△DOC=S△DBC—S△BOC ∴S△AOB=S△COD.
白汀水
例4 如右图,把四边形ABCD改成一个等积的三角形.
例2 用三种不同的方法将任意一个三角形分成三个小三角形, 使它们的面积比为及1∶3∶4.
A A E 1 3 C B D 4 C
B
1 D
3 E
4
方法 1:如上左图,将BC边八等分,取1∶3∶4的分点D、E, 连结AD、AE,从而得到△ABD、△ADE、△AEC的面积比为 1∶3∶4. 方法2:如上右图,先取BC中点,再取AB的1/4分点,连结AD
一个三角形在面积不改变的情况下,可以有无数多个 不同的形状.本讲即研究面积相同的三角形的各种形 状以及它们之间的关系。
白汀水
为便于实际问题的研究,我们还会常常用到以下结论:
①等底等高的两个三角形面积相等.
②底在同一条直线上并且相等,该底所对的角的顶点是同一 个点或在与底平行的直线上,这两个三角形面积相等. ③若两个三角形的高(或底)相等,其中一个三角形的底( 或高)是另一个三角形的几倍,那么这个三角形的面积也是 另一个三角形面积的几倍. A
