代数方程与差分方程模型PPT课件
合集下载
第三章差分方程模型 ppt课件

输入必要信息 轻击鼠标即得
单利和复利 两种计算利息的基本方式
单利 ~1万元存5年定期, 年利率4.75%, 到期后本 息(本金加利息):10000(1+0.04755)=12375元.
复利 ~1万元存1年定期, 年利率为3%, 到期不取则 自动转存, 5年后本息:10000 (1+0.03)5=11593元.
3. 差分方程模型
• 差分方程的基本类型及求解 3.1 贷款购房 3.2 管住嘴迈开腿 3.3 物价的波动 3.4 动物的繁殖与收获 3.5 中国人口增长预测——全国大学生
数学建模竞赛2007年A 题
差分方程的基本类型及求解
xk~未知变量x在时段k的数值(k=0,1,2, …)
1. 一阶线性常系数差分方程 xk 1 axk b, x0已知,k 0,1,2,
• 由x0, x1按照方程递推地计算x2, x3,…
•
求解公式
xk
c11k
c2k2
b 1 a1 a2
,
k 0,1,2,
1, 2~特征根 2 a1 a2 0 ~ 特征方程
c1, c2 ~常数, பைடு நூலகம்始值x0, x1代入求解公式确定.
1, 2<1
k→∞,
xk
x
1
b a1 a2
~稳定平衡点
3. 线性常系数差分方程组
x1(k), x2(k),, xn(k) ~n个未知变量在时段k的数值
x1(k 1) a11x1(k) a12x2 (k) a1n xn (k) b1 x2 (k 1) a21x1(k) a22x2 (k) a2n xn (k) b2 xn (k 1) an1x1(k) an2x2 (k) ann xn (k) bn
M06代数方程与差分方程模型市公开课获奖课件省名师示范课获奖课件

• 1971年第一代供临床应用旳CT设备问世.
• 螺旋式CT机等新型设备被医疗机构普遍采用.
• CT技术在工业无损探测、资源勘探、生态监测 等领域也得到了广泛旳应用.
什么是CT,它与老式旳X射线成像有什么区别?
概念图示 一种半透明物体嵌入5个不同透明度旳球
单方向观察无法拟定 让物体旋转从多角度观察能
aij~直接消耗系数——第j部门单位产出 对第i部门旳直接消耗
aij xij / x j
每个部门旳总产出等于总投入
xj~第j部门旳总投入
A (aij )nn
x (x ,x )T
1
n
d (d ,d )T
1
n
n
xi aij x j di j 1
x Ax d
模型应用 x Ax d (I A)x d, x (I A)1d
农业 工业 建筑业
0.159 0.171 0.002
0.047 0.512 0.001
0.080 0.502 0.001
0.008 0.257 0.013
0.054 0.238 0.010
0.002 0.226 0.023
• 运送 0.021 邮电
0.031
0.045
0.104
0.029
0.027
批农零业餐每饮1亿元产0.0出27直接消耗0.004.1559亿元0农.04业9产品 0直.02接7 消耗00.1.07516亿元工业0.0产50品
• 根据各部门间投入和产出旳平衡关系,拟定各部 门旳产出水平以满足社会旳需求 .
• 20世纪30年代由美国经济学家列昂节夫提出和研究.
• 从静态扩展到动态,与数量经济分析措施日益融合, 应用领域不断扩大 .
第4讲 差分方程方法(new)PPT课件

它的平衡点 x* 0 是稳定的充要条件是 A 的所有特
征根都有 i 1(i 1,2,, n) 。
对于一阶线性常系数非齐次差分方程组
x(k 1) Ax(k) B(k 0,1,2,)
的情况同样给出。
11
2020年11月23日
二 差分方程的平衡点及其稳定性
3.二阶线性常系数差分方程的平衡点
二阶线性常系数齐次差分方程的一般形式为
则 x* 也是一阶线性差分方程 xk1 f (x*)(xk x*) f (x*)
的平衡点. 故平衡点 x* 稳定的充要条件是 f (x* ) 1 。
2020年11月23日
三 连续模型的差分方法
1. 微分的差分方法
问题:已知 f (x) 在点 xk 处的函数值 f (xk )(k 0,1,, n 1) ,且 a x0 x1 xn1 b,试求函数的导数值 f (xk )(k 1,2,, n) 。
二 差分方程的平衡点及其稳定性
4.一阶非线性差分方程的平衡点
一阶非线性差分方程的一般形式为
xk1 f (xk ),k 0,1,2,
其中 f 为已知函数,其平衡点定义为方程 x f (x) 的解 x* 。
事实上:将 f (xk ) 在 x* 处作一阶的台勒展开有
xk1 f (x* )( xk x* ) f (x* )
, n)
14
2020年11月23日
三 连续模型的差分方法
2. 定积分的差分方法
问题:已知 f (x) 在点 xk 处的函数值 f (xk )(k 0,1,, n) ,
b
且在[a,b]上可积,试求 f (x) 在[a,b] 上的积分值 f (x)dx 。 a
对应代数方程:
k a1k1 a2k2 ak 0
征根都有 i 1(i 1,2,, n) 。
对于一阶线性常系数非齐次差分方程组
x(k 1) Ax(k) B(k 0,1,2,)
的情况同样给出。
11
2020年11月23日
二 差分方程的平衡点及其稳定性
3.二阶线性常系数差分方程的平衡点
二阶线性常系数齐次差分方程的一般形式为
则 x* 也是一阶线性差分方程 xk1 f (x*)(xk x*) f (x*)
的平衡点. 故平衡点 x* 稳定的充要条件是 f (x* ) 1 。
2020年11月23日
三 连续模型的差分方法
1. 微分的差分方法
问题:已知 f (x) 在点 xk 处的函数值 f (xk )(k 0,1,, n 1) ,且 a x0 x1 xn1 b,试求函数的导数值 f (xk )(k 1,2,, n) 。
二 差分方程的平衡点及其稳定性
4.一阶非线性差分方程的平衡点
一阶非线性差分方程的一般形式为
xk1 f (xk ),k 0,1,2,
其中 f 为已知函数,其平衡点定义为方程 x f (x) 的解 x* 。
事实上:将 f (xk ) 在 x* 处作一阶的台勒展开有
xk1 f (x* )( xk x* ) f (x* )
, n)
14
2020年11月23日
三 连续模型的差分方法
2. 定积分的差分方法
问题:已知 f (x) 在点 xk 处的函数值 f (xk )(k 0,1,, n) ,
b
且在[a,b]上可积,试求 f (x) 在[a,b] 上的积分值 f (x)dx 。 a
对应代数方程:
k a1k1 a2k2 ak 0
差分方程模型PPT课件

回到全国竞赛题。这里提出了新的问题: (1)潜伏期病人如何描述? (2)死亡病人在模型中的描述。 (3)需要考虑人口的迁移影响,如何描述? (4)如何控制疾病的蔓延?
问题的图示
b O
a
d
d
利用简单的几何关系即得到 yk1 f ( yk ), y1 b
例2:按年龄分组的种群增长模型。
问题考虑两个要点:增长和人口分布 人口分布:对于连续问题,可以利用分布函数和 密度函数描绘。
我们也可以利用离散的方法描述人口分布。把t时
刻人口从小到大分为n组,第k 组人数xk(t),则离 散人口分布可以利用向量
试从中国的实际情况和人口增长的上述特点出发, 参考附录2中的相关数据(也可以搜索相关文献和 补充新的数据),建立中国人口增长的数学模型, 并由此对中国人口增长的中短期和长期趋势做出 预测;特别要指出你们模型中的优点与不足之处。
附录1 《国家人口发展战略研究报告》 附录2 人口数据(《中国人口统计年鉴》中的部 分数据)及其说明
差分方程建模:设第k天病人所占比例为i(k),健 康人数量为s(k),则第k天病人数量变化为
Ni(k 1) Ni(k) s(k)Ni(k) Ni(k)
第k天健康人数量变化为
Ns(k 1) Ns(k) s(k)Ni(k)
把两个式子化简即得到差分方程组。
差分方程和微分方程的建模过程没有差异,差别 在于:变化率和的意义不同。
一阶线性差分方程组的稳定性: 设一阶线性差分方程组的解为{Xk}, 而受扰动解为 {Yk}。记扰动误差为
k X k Yk 则扰动误差满足
k1 A k
对任意初始扰动0,k0的充分必要条件为
( A) 1
这就是差分方程的稳定性条件。
《差分方程》PPT课件

方程变为yt+1+ayt=b, a,b均为非零常数.
试以 yt (为待定常数)形式的特解代入方程得 +a (1+a) b.
当a≠-1时,可求得特解
b yt 1 a
当a1时,改设特解 yt t (为待定系数),将其代 入方程得 (t+1)+a t(1+a) t+ b
返回 上页 下页 求得特解 yt bt
6
返回 上页 下页
三、 差分方程的解 定义4 如果将已知函数yt=j(t)代入方程F(t,yt,yt+1,…, yt+n)=0, 使 其 对 t=…,-2,-1,0,1,2,… 成 为 恒 等 式 , 则 称 yt=j(t) 为方程的解.含有n个任意(独立)常数C1,C2,…,Cn的解
yt=(t,C1,C2,…,Cn)
依此定义类推,有
D2yt+1= Dyt+2- Dyt+1=yt+3-2yt+2+yt+1, D2yt+2= Dyt+3- Dyt+2=yt+4-2yt+3+yt+2,
………………
类推,计算两个相继的二阶差分之差,便得到三阶差分 D3yt= D2yt+1- D2yt=yt+3-3yt+2+3yt+1-yt,
5
返回 上页 下页
定义3′ 含有两个或两个以上函数值yt,yt+1,…的函数方 程,称为(常)差分方程,出现在差分方程中未知函数下 标的最大差,称为差分方程的阶.
n阶差分方程的一般形式为 F(t,yt,yt+1,…,yt+n)=0,
数学模型-第06章(第五版)市公开课一等奖省赛课获奖PPT课件

零存整取 累计存入金额180,000元 计算器 到期本息总额196,012.50元
勤俭节约、科学理财
第5页
单利和复利 按单利计算业务——零存整取
a~每个月存入金额, r ~月利率, n ~ 存期 (x月k ~)存入k个月后本息 x1=a+ar x2= x1+a+a2r
xk= xk-1+a+akr, k=2,3,…, n k=n递推至k=1 xn= na+ar(1+2+…+n) a =3000, r =0.035/12, n =125 (月) xn= 196,012.50
a=7485.2(元), A1=1796447.27(元) 与房贷计算器给出相同
第10页
等额本息贷款和等额本金贷款
例2 “房贷计算器”选择等额本金还款, 输入: 商业 贷款总额100万元, 期限20年, 年利率6.55%. 点击“开 始计算”得到: 还款总额1657729.17元, 每个月还款金 额由第1月9625元逐月递减, 最终1月为4189.41元. 建立等额本金还款方式数学模型, 并作数值计算.
比两阶段计划时间长,吸 收热量突减对身体不利.
75kg
c =1时
c =14000时
w(40)=75kg w(72)=75kg
第27页
7. 到达目标体重所需时间与每七天吸收热量关系
k=1递推至k=n
w(n 1) (1 )n w(1) c[1 (1 ) (1 )n1] (1 )n[w(1) c / ] c /
1)r, n
k 1,2,n
第12页Βιβλιοθήκη 额本金还款模型x0 ~贷款总额 r ~月利率 n ~贷款期限(月)
xk ~第k月还款金额
勤俭节约、科学理财
第5页
单利和复利 按单利计算业务——零存整取
a~每个月存入金额, r ~月利率, n ~ 存期 (x月k ~)存入k个月后本息 x1=a+ar x2= x1+a+a2r
xk= xk-1+a+akr, k=2,3,…, n k=n递推至k=1 xn= na+ar(1+2+…+n) a =3000, r =0.035/12, n =125 (月) xn= 196,012.50
a=7485.2(元), A1=1796447.27(元) 与房贷计算器给出相同
第10页
等额本息贷款和等额本金贷款
例2 “房贷计算器”选择等额本金还款, 输入: 商业 贷款总额100万元, 期限20年, 年利率6.55%. 点击“开 始计算”得到: 还款总额1657729.17元, 每个月还款金 额由第1月9625元逐月递减, 最终1月为4189.41元. 建立等额本金还款方式数学模型, 并作数值计算.
比两阶段计划时间长,吸 收热量突减对身体不利.
75kg
c =1时
c =14000时
w(40)=75kg w(72)=75kg
第27页
7. 到达目标体重所需时间与每七天吸收热量关系
k=1递推至k=n
w(n 1) (1 )n w(1) c[1 (1 ) (1 )n1] (1 )n[w(1) c / ] c /
1)r, n
k 1,2,n
第12页Βιβλιοθήκη 额本金还款模型x0 ~贷款总额 r ~月利率 n ~贷款期限(月)
xk ~第k月还款金额
《高数3差分方程》PPT课件

( yt2 yt1 ) ( yt1 yt ) yt1 yt 2 yt ,
则原方程还可化为 2 yt 3t.
10
又如: 可化为
yt2 2 yt1 yt 3t , yt 2 yt1 yt2 3t2 ,
2 yt 2 yt 3t.
定义5.1.3 如果一个函数代入差分方程后,方程两边 恒等,则称此函数为差分方程的解.
yt (t 2 ) (t 1)2 t 2 2t 1,
2( yt ) 2(t 2 ) (yt ) (2t 1)
2(t 1) 1 (2t 1) 2,
3( yt ) (2 yt ) (2) 2 2 0. 例2 设 yt at (0 a 1), 求 ( yt ). 解 ( yt ) at1 at at (a 1).
kbt1 akbt cbt 即 k(b a) c ,
于是
yt*
b
c
a
bt
.
28
(2) 当 b a 时 , 令yt* ktbt 代 入 方 程(6) , 得 :
k(t 1)bt1 aktbt cbt
即 k(t 1)b akt c ,
解得 k c . a
于是
yt*
c a
tbt
ctbt1 .
当b a 和 b a 时,方程(6) 的通解分别为:
yt
c ba
bt
Aa t
和
yt ctbt1 Aat .
29
例6 求差分方程
yt 1
1 2
yt
5 t
的2 通解。
解 对应齐次差分方程的通解为 Y A 1 t .
2
由于 a 1 , b 5 , a b,
22
故可设其特解为: yt* kbt .
差分方程ppt

其他特 VIP专享精彩活动权 NhomakorabeaVIP专属身份标识
开通VIP后可以享受不定期的VIP随时随地彰显尊贵身份。
专属客服
VIP专属客服,第一时间解决你的问题。专属客服Q全部权益:1.海量精选书免费读2.热门好书抢先看3.独家精品资源4.VIP专属身份标识5.全站去广告6.名
(4)
称为齐次差分方程; 当 f (x) 0时, 称为非齐次差分方程.
先求齐次差分方程 yx+1 ayx = 0的解 设 y0 已知, 代入方程可知
y1 = ay0, y2 = a2y0,
yx = axy0,
令y0 = C, 则得齐次差分方程的通解为
yx = Cax.
(5)
例4 求差分方程 yx+1 + 2yx = 0的通解. 解 这里 a = 2, 由公式(5)得, 通解为
yx B0 B1x Bm xm (1 a b 0),
yx (B0 B1x Bm xm )x (1 a b 0且a 2 0) yx (B0 B1x Bm xm )x2 (1 a b a 2 0).
其中B0 , B1 , , Bm为待定系数.
例10 求差分方程 yx+2 + yx+1 2yx = 12x的通解.
包权
人书友圈7.三端同步
例1 求(x3), 2(x3), 3(x3), 4(x3). 解 (x3) = (x + 1)3 x3 = 3x2 + 3x + 1,
2(x3) = (3x2 + 3x + 1) = 3(x + 1)2 + 3(x + 1) + 1 (3x2 + 3x + 1) = 6x + 6,
代数方程与差分方程模型 PPT

代数方程与差分方程模型
投入产出表
国民经济各部门间生产和消耗、投入和产出的数量关系
中国2002年投入产出表(产值单位:亿元)
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务 初始投入 总投入
农业
464 499
5 62 79 146 1663 2918
工业
788 8605
9 527 749 1285 4851 16814
原子弹爆炸的能量估计
爆炸产生的冲击波以爆炸点为中心呈球面向四周传播, 爆炸的能量越大,在一定时刻冲击波传播得越远、
冲击波由爆炸形成的“蘑菇云”反映出来、
泰勒测量: 时刻t 所对应的“蘑菇云”的半径r
t(ms) r(m) t(ms) r(m) t(ms) r(m) t(ms) r(m) t(ms) r(m) 0、10 11、1 0、80 34、2 1、50 44、4 3、53 61、1 15、0 106、
σ
1 1 0 0 1
10
0
1
1 0 0 1 1 0 0 1 1
1
23
4
5
L5
7
8
L6
L7 L8
6
L1
9 L2 L3 L4
A
0 1
0 0
0 0
0 0
0 0
0 0
1 0
1 0
0
0
0 1 0 1 1 0 1 0 0
0 0 1 0 1 1 0 1 0
0 0 0 0 0 1 0 0 1
根据A和b, 由 Ax b 确定像素的衰减系数向量x
m
q 则 s
ysj j
为m-r 个相互独立的无量纲量, 且
j 1
F( 1, 2,…, m-r ) = 0 与 f (q1, q2, , qm) =0 等价, F未定、
投入产出表
国民经济各部门间生产和消耗、投入和产出的数量关系
中国2002年投入产出表(产值单位:亿元)
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务 初始投入 总投入
农业
464 499
5 62 79 146 1663 2918
工业
788 8605
9 527 749 1285 4851 16814
原子弹爆炸的能量估计
爆炸产生的冲击波以爆炸点为中心呈球面向四周传播, 爆炸的能量越大,在一定时刻冲击波传播得越远、
冲击波由爆炸形成的“蘑菇云”反映出来、
泰勒测量: 时刻t 所对应的“蘑菇云”的半径r
t(ms) r(m) t(ms) r(m) t(ms) r(m) t(ms) r(m) t(ms) r(m) 0、10 11、1 0、80 34、2 1、50 44、4 3、53 61、1 15、0 106、
σ
1 1 0 0 1
10
0
1
1 0 0 1 1 0 0 1 1
1
23
4
5
L5
7
8
L6
L7 L8
6
L1
9 L2 L3 L4
A
0 1
0 0
0 0
0 0
0 0
0 0
1 0
1 0
0
0
0 1 0 1 1 0 1 0 0
0 0 1 0 1 1 0 1 0
0 0 0 0 0 1 0 0 1
根据A和b, 由 Ax b 确定像素的衰减系数向量x
m
q 则 s
ysj j
为m-r 个相互独立的无量纲量, 且
j 1
F( 1, 2,…, m-r ) = 0 与 f (q1, q2, , qm) =0 等价, F未定、
最新数模(差分方程模型)1概要教学讲义PPT

设贷款额为a0,每月还贷额为x,月利率为r,第n个月后的欠 款额为an,则
a0=200000, a1=(1+r)a0-x, a2=(1+r)a1-x, ……
an=(1+r)an-1-x, n=1,2,3,…
重庆邮电大学市级精品课程------数学建模
一阶线性差分方程
在上述模型中,给出了an+1与an之间的递推公式. 将它们写成 统一的形式:
重庆邮电大学市级精品课程------数学建模
7.1 差分方程基本知识
• 1、差分方程: 差分方程反映的是关于离散变量的取值 与变化规律。通过建立一个或几个离散变量取值所满 足的平衡关系,从而建立差分方程。
• 差分方程就是针对要解决的目标,引入系统或过程中 的离散变量,根据实际背景的规律、性质、平衡关系, 建立离散变量所满足的平衡关系等式,从而建立差分 方程。通过求出和分析方程的解,或者分析得到方程 解的 特别性质(平衡性、稳定性、渐近性、振动性、 周期性等),从而把握这个离散变量的变化过程的规 律,进一步再结合其他分析,得到原问题的解。
此规律对于(7.1)也成立。
重庆邮电大学市级精品课程------数学建模
的形式,其对应的齐次方程为
a 0 x n t a 1 x n t 1 . .a .n x t 0 (7.2)
容易证明,若序列
x
( t
1
)
与
x (2) t
均为方程(7.2)的解,则
xt c1xt(1)c2xt(2)
也是方程(7.2)的解,其 中c1、c2为任意常数,这说明, 齐次方程的解构成一个 线性空间(解空间)。
1. 银行存款与利率
假如你在银行开设了一个1000元的存款账户,银行的年利 率为7%. 用an表示n年后你账户上的存款额,那么下面的数列 就是你每年的存款额:
《数学建模》课件:第7章 差分方程模型(投影版)
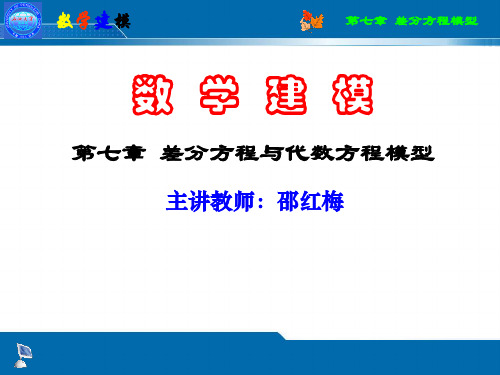
k 1
0
k
0
x x ( )k (x x )
k 1
0
1
0
1 ( 1/ ) xk x0 P0稳定 K f K g
1 ( 1/ ) xk P0不稳定 K f K g
方程模型与蛛网模型的一致
K f 1/ Kg
数学建模
第七章 差分方程模型
结果解释
考察 , 的含义
差分方程稳定性理论简介
数学建模
第七章 差分方程模型
二、n阶线性常系数差分方程的平衡点和稳定性
定理1 考虑n阶线性常系数差分方程
an xkn a1xk1 a0 xk b
(I)
设其对应的特征方程的根为
1, 2, ,n, 则方程(I)的平衡点
x=x =
b
n
稳定的充要条件是: i 1, i 1, 2, n.
4. n阶线性常系数差分方程
形如 an xkn a1xk1 a0 xk b, 其中 ai和 b 都是常数,
的方程称为n阶线性常系数差分方程。
接下来,我们讨论n阶线性常系数差分方程的平衡点及 稳定性问题。
差分方程稳定性理论简介
数学建模
第七章 差分方程模型
5. 平衡点及稳定性
在方程 an xkn a1xk1 a0xk b 中令 xk+i =x i 0,1, , n
x= b 1 a
稳定的充要条件是
a 1.
差分方程稳定性理论简介
数学建模
第七章 差分方程模型
三、一阶非线性差分方程的平衡点和稳定性
考虑方程 xk1 f (xk )
(II)
其平衡点 x 由代数方程 x f (x) 解出。为了分析 x 的稳定性,
将f ( x )在 x 点作Taylor展开,只取一次项,方程(II)近似为
代数和差分方程模型36页PPT

❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
代数和差分方程模型
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
代数和差分方程模型
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
什么是CT,它与传统的X射线成像有什么区别?
概念图示 一个半透明物体嵌入5个不同透明度的球
单方向观察无法确定 让物体旋转从多角度观察能
球的数目和透明度
分辨出5个球及各自的透明度
光源
X 射 线
人眼
胶 片
光源
X 光 管
人眼 探
测 器
人体内脏
传统的X射线成像原理
人体内脏Biblioteka 图像CT技术原理 重建
CT技术: 在不同深度的断面上,从各个角度用探测器接 收旋转的X光管发出、穿过人体而使强度衰减的射线; 经过测量和计算将人体器官和组织的影像重新构建.
技术水平没有明显提高 假设直接消耗系数不变
问题1 如果某年对农业、工业、建筑业、运输邮 电、批零餐饮和其他服务的外部需求分别为1500, 4200, 3000, 500, 950, 3000亿元, 问这6个部门的总 产出分别应为多少?
求解 A由直接消耗系数表给出
d=(1500, 4200, 3000, 500, 950, 3000)T 6个部门的总产出 x=(3277, 17872, 3210, 1672, 2478, 5888)(亿元).
运输 邮电 13 403 20 163 43 225 703 1570
批零 餐饮 127 557 23 67 130 219 1218 2341
其他 服务 13 1223 124 146 273 542 3093 5414
外部 需求 1284 4083 2691 477 927 2725
总产出
2918 16814 2875 1570 2341 5414
模型应用 x Ax d (I A)x d, x (I A)1d
问题2 如果6个部门的外部需求分别增加1个单位, 问它们的总产出应分别增加多少?
求解 总产出对外部需求线性
Δd~d增加1个单位 x的增量 x (I A)1d
若农业的外部需求增加1单位 d (1,0,0,0,0,0)T Δx为(I A)1 的第1列 6个部门的总产出分别增加1.2266,0.5624, 0.0075,0.0549,0.0709,0.1325单位.
• 根据各部门间投入和产出的平衡关系,确定各部 门的产出水平以满足社会的需求 .
• 20世纪30年代由美国经济学家列昂节夫提出和研究.
• 从静态扩展到动态,与数量经济分析方法日益融合, 应用领域不断扩大 .
建立静态投入产出数学模型,讨论具体应用.
投入产出表
国民经济各部门间生产和消耗、投入和产出的数量关系
其余外部需求增加1单位 Δx为 (I A)1 的其余各列
2 CT技术的图像重建 背景
• CT(计算机断层成像 )技术是20世纪50至70年代由 美国科学家科马克和英国科学家豪斯费尔德发明的. • 1971年第一代供临床应用的CT设备问世. • 螺旋式CT机等新型设备被医疗机构普遍采用.
• CT技术在工业无损探测、资源勘探、生态监测 等领域也得到了广泛的应用.
X射线强度衰减与图像重建的数学原理
I~射线强度 l~物质在射线方向的厚度
I0~入射强度 μ~物质对射线的衰减系数
• 射线强度的衰减 率与强度成正比.
dI I
dl
I I 0e l
y I0
• 射线沿直线L穿行, 穿过由
不同衰减系数的物质组成的 非均匀物体(人体器官).
l L (x, y)dl)
I
建筑业 运输邮电 批零餐饮 其他服务
0.080 0.502 0.001 0.045 0.049 0.095
0.008 0.257 0.013 0.104 0.027 0.143
0.054 0.238 0.010 0.029 0.056 0.094
0.002 0.226 0.023 0.027 0.050 0.100
数学 原理
Pf (L)
f (x, y)dl
L
拉东变换
f (Q) 1 dFQ (q)
0 q
拉东逆变换
FQ(q)~与Q相距q的直线L的线积分Pf(L)对所有q的平均值
I0
exp(
(x,
L
y)dl)
μ(x, y) L
0
x
(x, y)dl ln I0
L
I
X射线强度衰减与图像重建的数学原理
(x, y)dl ln I0
L
I
右端数值可从CT 的测量数据得到
图像 多条直线L的线积分 L (x, y)dl 被积函数μ(x, y)
重建 反映人体器官大小、形状、密度的图像
农业每1亿元产出直接消耗0.159亿元农业产品 直接消耗0.171亿元工业产品
反映国民经济各个部门之间的投入产出关系
投入产出的数学模型
设共有n个部门
xi~第i部门的总产
di~对第i部门的外部需求
x出ij~第i部门对第j部门的投入
n
xi xij di
xij~第j部门总产出对第i部门的直接消耗
j 1
中国2002年投入产出表(产值单位:亿元)
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务 初始投入 总投入
农业
464 499
5 62 79 146 1663 2918
工业
788 8605
9 527 749 1285 4851 16814
建筑 业 229 1444 3 128 140 272 659 2875
直接消耗系数表
由投入产出表直接得到
一个部门的单位产出对各个部门的直接消耗
中国2002年直接消耗系数表
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务
农业
0.159 0.171 0.002 0.021 0.027 0.050
工业
0.047 0.512 0.001 0.031 0.045 0.076
aij~直接消耗系数——第j部门单位产出 aij xij / x j
对第i部门的直接消耗
每个部门的总产出等于总投入
xj~第j部门的总投入
A (aij )nn
x (x ,x )T
1
n
d (d ,d )T
1
n
n
xi aij x j di j 1
x Ax d
模型应用 x Ax d (I A)x d, x (I A)1d
代数方程与差分方程模型
1 投入产出模型 2 CT技术的图像重建 3 原子弹爆炸的能量估计 4 市场经济中的蛛网模型 5 减肥计划——节食与运动 6 按年龄分组的种群增长
背景
1 投入产出模型
• 国民经济各个部门之间存在着相互依存和制约关系, 每个部门将其他部门的产品或半成品经过加工(投入) 变为自己的产品(产出).
概念图示 一个半透明物体嵌入5个不同透明度的球
单方向观察无法确定 让物体旋转从多角度观察能
球的数目和透明度
分辨出5个球及各自的透明度
光源
X 射 线
人眼
胶 片
光源
X 光 管
人眼 探
测 器
人体内脏
传统的X射线成像原理
人体内脏Biblioteka 图像CT技术原理 重建
CT技术: 在不同深度的断面上,从各个角度用探测器接 收旋转的X光管发出、穿过人体而使强度衰减的射线; 经过测量和计算将人体器官和组织的影像重新构建.
技术水平没有明显提高 假设直接消耗系数不变
问题1 如果某年对农业、工业、建筑业、运输邮 电、批零餐饮和其他服务的外部需求分别为1500, 4200, 3000, 500, 950, 3000亿元, 问这6个部门的总 产出分别应为多少?
求解 A由直接消耗系数表给出
d=(1500, 4200, 3000, 500, 950, 3000)T 6个部门的总产出 x=(3277, 17872, 3210, 1672, 2478, 5888)(亿元).
运输 邮电 13 403 20 163 43 225 703 1570
批零 餐饮 127 557 23 67 130 219 1218 2341
其他 服务 13 1223 124 146 273 542 3093 5414
外部 需求 1284 4083 2691 477 927 2725
总产出
2918 16814 2875 1570 2341 5414
模型应用 x Ax d (I A)x d, x (I A)1d
问题2 如果6个部门的外部需求分别增加1个单位, 问它们的总产出应分别增加多少?
求解 总产出对外部需求线性
Δd~d增加1个单位 x的增量 x (I A)1d
若农业的外部需求增加1单位 d (1,0,0,0,0,0)T Δx为(I A)1 的第1列 6个部门的总产出分别增加1.2266,0.5624, 0.0075,0.0549,0.0709,0.1325单位.
• 根据各部门间投入和产出的平衡关系,确定各部 门的产出水平以满足社会的需求 .
• 20世纪30年代由美国经济学家列昂节夫提出和研究.
• 从静态扩展到动态,与数量经济分析方法日益融合, 应用领域不断扩大 .
建立静态投入产出数学模型,讨论具体应用.
投入产出表
国民经济各部门间生产和消耗、投入和产出的数量关系
其余外部需求增加1单位 Δx为 (I A)1 的其余各列
2 CT技术的图像重建 背景
• CT(计算机断层成像 )技术是20世纪50至70年代由 美国科学家科马克和英国科学家豪斯费尔德发明的. • 1971年第一代供临床应用的CT设备问世. • 螺旋式CT机等新型设备被医疗机构普遍采用.
• CT技术在工业无损探测、资源勘探、生态监测 等领域也得到了广泛的应用.
X射线强度衰减与图像重建的数学原理
I~射线强度 l~物质在射线方向的厚度
I0~入射强度 μ~物质对射线的衰减系数
• 射线强度的衰减 率与强度成正比.
dI I
dl
I I 0e l
y I0
• 射线沿直线L穿行, 穿过由
不同衰减系数的物质组成的 非均匀物体(人体器官).
l L (x, y)dl)
I
建筑业 运输邮电 批零餐饮 其他服务
0.080 0.502 0.001 0.045 0.049 0.095
0.008 0.257 0.013 0.104 0.027 0.143
0.054 0.238 0.010 0.029 0.056 0.094
0.002 0.226 0.023 0.027 0.050 0.100
数学 原理
Pf (L)
f (x, y)dl
L
拉东变换
f (Q) 1 dFQ (q)
0 q
拉东逆变换
FQ(q)~与Q相距q的直线L的线积分Pf(L)对所有q的平均值
I0
exp(
(x,
L
y)dl)
μ(x, y) L
0
x
(x, y)dl ln I0
L
I
X射线强度衰减与图像重建的数学原理
(x, y)dl ln I0
L
I
右端数值可从CT 的测量数据得到
图像 多条直线L的线积分 L (x, y)dl 被积函数μ(x, y)
重建 反映人体器官大小、形状、密度的图像
农业每1亿元产出直接消耗0.159亿元农业产品 直接消耗0.171亿元工业产品
反映国民经济各个部门之间的投入产出关系
投入产出的数学模型
设共有n个部门
xi~第i部门的总产
di~对第i部门的外部需求
x出ij~第i部门对第j部门的投入
n
xi xij di
xij~第j部门总产出对第i部门的直接消耗
j 1
中国2002年投入产出表(产值单位:亿元)
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务 初始投入 总投入
农业
464 499
5 62 79 146 1663 2918
工业
788 8605
9 527 749 1285 4851 16814
建筑 业 229 1444 3 128 140 272 659 2875
直接消耗系数表
由投入产出表直接得到
一个部门的单位产出对各个部门的直接消耗
中国2002年直接消耗系数表
产出 投入 农业 工业 建筑业 运输邮电 批零餐饮 其他服务
农业
0.159 0.171 0.002 0.021 0.027 0.050
工业
0.047 0.512 0.001 0.031 0.045 0.076
aij~直接消耗系数——第j部门单位产出 aij xij / x j
对第i部门的直接消耗
每个部门的总产出等于总投入
xj~第j部门的总投入
A (aij )nn
x (x ,x )T
1
n
d (d ,d )T
1
n
n
xi aij x j di j 1
x Ax d
模型应用 x Ax d (I A)x d, x (I A)1d
代数方程与差分方程模型
1 投入产出模型 2 CT技术的图像重建 3 原子弹爆炸的能量估计 4 市场经济中的蛛网模型 5 减肥计划——节食与运动 6 按年龄分组的种群增长
背景
1 投入产出模型
• 国民经济各个部门之间存在着相互依存和制约关系, 每个部门将其他部门的产品或半成品经过加工(投入) 变为自己的产品(产出).
