人教版初中数学七年级上册第一章有理数ppt
合集下载
初中数学人教七年级上册第一章有理数数轴 PPT
3、选取适当的长度作为单位长度，直线上从原点向右 ，每隔一个单位长度取一个点，依次表示1，2，…；从 原点向左，用类似方法依次表示-1，-2，-3，……。
※分数和小数也可以用数轴上的点表示，如从原点向 右3.5个单位长度的点表示小数3.5，从原点向左 个单位 长度的点表示分数
共同归纳
（1）数轴的三要素：原点、正方向、单位长度． （2）数轴的规范画法：是条直线，数字在下，字母在上．
-3 -2 -1 0 1 2 3
动手画一个数轴，然后进行交流讨论. 思考： 1.数轴的规范画法. 2.数轴必须满足什规范画法： 3
2
2
3.5 -4 -3 -2 -1 0 1 2 3 4
1、画一条水平直线，在直线上取一点0，叫原点；
2、通常规定直线上从原点向右（或上）的方向为正方 向，从原点向左（或下）的方向为负方向；
正确地画出一条数轴的方法可概括为：
一画
二找
三定
四取
-3 -2 -1 0 1 2 3
课堂练习 判断下图中所画的数轴是否正确？如不正确，指出错在哪里？
(1) 错
(2) 错
2
(3) 错
(4)
错
1 -1
(5)
错
1
(6) 对
01
(7) 错
-2 -1 1
(8) 错
-1-2-3 0 1 2 3
(9) 错
例题演示
课堂练习
1.写出数轴上点A、B、C、D、E所表示的数：
EB
AC D
Ａ：0 Ｃ：1 Ｅ：-3
Ｂ：-2 Ｄ：2.5
巩固练习
2.借助数轴回答下列问题： （1）写出到原点的距离小于3的整数 ±1,±2,0．
-3 -2 -1 0 1 2 3
※分数和小数也可以用数轴上的点表示，如从原点向 右3.5个单位长度的点表示小数3.5，从原点向左 个单位 长度的点表示分数
共同归纳
（1）数轴的三要素：原点、正方向、单位长度． （2）数轴的规范画法：是条直线，数字在下，字母在上．
-3 -2 -1 0 1 2 3
动手画一个数轴，然后进行交流讨论. 思考： 1.数轴的规范画法. 2.数轴必须满足什规范画法： 3
2
2
3.5 -4 -3 -2 -1 0 1 2 3 4
1、画一条水平直线，在直线上取一点0，叫原点；
2、通常规定直线上从原点向右（或上）的方向为正方 向，从原点向左（或下）的方向为负方向；
正确地画出一条数轴的方法可概括为：
一画
二找
三定
四取
-3 -2 -1 0 1 2 3
课堂练习 判断下图中所画的数轴是否正确？如不正确，指出错在哪里？
(1) 错
(2) 错
2
(3) 错
(4)
错
1 -1
(5)
错
1
(6) 对
01
(7) 错
-2 -1 1
(8) 错
-1-2-3 0 1 2 3
(9) 错
例题演示
课堂练习
1.写出数轴上点A、B、C、D、E所表示的数：
EB
AC D
Ａ：0 Ｃ：1 Ｅ：-3
Ｂ：-2 Ｄ：2.5
巩固练习
2.借助数轴回答下列问题： （1）写出到原点的距离小于3的整数 ±1,±2,0．
-3 -2 -1 0 1 2 3
七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1
![七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1](https://img.taocdn.com/s3/m/99109955ef06eff9aef8941ea76e58fafbb04568.png)
请大家玩一玩这个游戏，并思考，如何猜想能更快地猜中？至少猜想几次 就一定能猜中？多做几次游戏，检验一下你的猜数策略是否有效.
50
猜想
回答
0 0与50的中间数→ 25 25与50的中间数→ 38 38与50的中间数→ 44
47 49 50
小了 小了 小了 小了 小了 小了
√
－30
猜想
回答
0 0与－50的中间数→ －25 －25与－50的中间数→ －38 －25与－38的中间数→ －32
3．一个正数的绝对值是__它__本__身__；一个负数的绝对值是 __它__的__相__反__数__；0的绝对值是__0__．即
（1）如果a＞0，那么__|a_|_＝__a_； （2）如果a＝0，那么__|a_|_＝__0_； （3）如果a＜0，那么__|a_|_＝__－__a_．
4．绝对值的非负性：任何一个有理数的绝对值总是__正__数__或__0__． 即对任意有理数a，总有__|a_|_≥__0__．若|a|＋|b|＝0，则必有__a_＝__b_＝___0__．
示的数大，可得a，b，－a，－b的大小关系为b＜－a＜a＜－b．
在对多个数进行大小 比较时，运用数轴比较法 比较合适．
数学活动——猜数游戏
两个人合作，按下面的步骤完成游戏： （1）第一位同学默想一个－50~50的整数记住； （2）第二位同学对第一位同学默想出的数提出一个猜想，第一位同学比较 这个数和自己心中所想数的大小，然后回答“大了”“小了”或者“相等”， 若相等则说明第二位同学猜中； （3）若第二位同学没有猜中，则根据第一位同学的回答，调整猜想； （4）重复步骤（2）（3），直到猜中.
5．求一个数的绝对值的两种方法： 方法1：求某个数的绝对值，首先要确定这个数的__符__号___，然后根 据__绝__对__值___的__性__质___进行求值． 方法2：根据__绝__对__值__的__几__何__意___义__进行求解．
50
猜想
回答
0 0与50的中间数→ 25 25与50的中间数→ 38 38与50的中间数→ 44
47 49 50
小了 小了 小了 小了 小了 小了
√
－30
猜想
回答
0 0与－50的中间数→ －25 －25与－50的中间数→ －38 －25与－38的中间数→ －32
3．一个正数的绝对值是__它__本__身__；一个负数的绝对值是 __它__的__相__反__数__；0的绝对值是__0__．即
（1）如果a＞0，那么__|a_|_＝__a_； （2）如果a＝0，那么__|a_|_＝__0_； （3）如果a＜0，那么__|a_|_＝__－__a_．
4．绝对值的非负性：任何一个有理数的绝对值总是__正__数__或__0__． 即对任意有理数a，总有__|a_|_≥__0__．若|a|＋|b|＝0，则必有__a_＝__b_＝___0__．
示的数大，可得a，b，－a，－b的大小关系为b＜－a＜a＜－b．
在对多个数进行大小 比较时，运用数轴比较法 比较合适．
数学活动——猜数游戏
两个人合作，按下面的步骤完成游戏： （1）第一位同学默想一个－50~50的整数记住； （2）第二位同学对第一位同学默想出的数提出一个猜想，第一位同学比较 这个数和自己心中所想数的大小，然后回答“大了”“小了”或者“相等”， 若相等则说明第二位同学猜中； （3）若第二位同学没有猜中，则根据第一位同学的回答，调整猜想； （4）重复步骤（2）（3），直到猜中.
5．求一个数的绝对值的两种方法： 方法1：求某个数的绝对值，首先要确定这个数的__符__号___，然后根 据__绝__对__值___的__性__质___进行求值． 方法2：根据__绝__对__值__的__几__何__意___义__进行求解．
初中数学人教七年级上册第一章有理数相反数(可直接用)PPT
如图：是一个正方形纸盒的展开图，若在其中的 三个正方形Ａ，Ｂ，Ｃ内分别填入适当的数，使 得它们折成正方体后相对的面上的两个数互为相 反数，则填入正方形Ａ，Ｂ，Ｃ内的三个数依次 为__1___ __-_2___ __0___
A
应用创新
C B0 -1
2
巩固练习
已知数轴上A、B两点互为相反数，它们 分别表示为m ，n(m>n)，并且A、B两 点间的距离是6，则m= 3 ， n= -3 ．
2. 在一个数的前面添上“+”号,即表示这个数本身.
例如： + ( - 4 ) = - 4
+ ( + 5.5 ) = 5.5
练习: 化简下列各数:
(1) – ( + 10 ) (2) + (–20.15 )
(3) + ( + 3 )
(4) – (–20 )
解: (1) 原式 = - 10 (2) 原式 = - 20.15 (3) 原式 = 3 (4) 原式 = 20
例2:化简下列各数：
① –（+10） ；
② +（ – 0.15）；
③ +（ + 3 ） ；
④ – ( –128 )
解：① –（+10）= –10 ；
(5)-[-(-3.6)]
② +（ – 0.15）= – 0.15；
③ +（ + 3 ）= 3 ；
方法： ④ – ( –128 ) = 128 ;
一个数的前面添一个“ + ”号，仍然表示这个数，不变；
课堂练习
1．－1.6是____的相反数，___的相反数是0.3．
2．下列几对数中互为相反数的一对为（ ）．
第一章 有理数(单元解读课件)-人教版初中数学七年级上册
(一)对标课程标准，把握好教学要求；
◆再次，有理数的加、减、乘、除、乘方运算中涉及的数应简单一些， 特别是混合运算，课程标准明确提出“以三步以内为主”，不要在数字 的复杂性、运算技巧、运算速度等方面提出过高要求，应当强调的是运 用运算法则确定结果的符号、用运算律简化运算、运用有理数的运算解 决简单实际问题等方面的运算，尽力体现有理数运算教学的思维训练价 值，使学生感受到数学应用于实际的熏陶。
(二)聚焦核心素养，整体建构知识体系；
◆教学目标的定位要聚焦到人的发展和解决问题的能力，而不仅仅是知识与技能 的习得。本章要聚焦发展抽象能力和运算能力，让学生理解字母表示数的意义， 建立符号意识，感悟数学结论的一般性。要对本阶段教学有一个全面的把控和整 体的设计，准确把握知识的“生长点”和“延伸点”，把每堂课教学的知识置于 整体知识结构和体系中。 ◆首先要把握数与式的整体性，注重研究方法和研究策略的学习。本章学习了有 理数的表示、分类、大小比较、相反数、绝对值、运算等内容，基于生活实例的 研究方法特殊到一般的归纳法;当数系扩充到实数范围后，也要用这些方法研究 这些内容，而且运算原理、运算法则、运算律可以自然地的迁移到“整式的加 减”“实数的运算”等的学习中去。
(三)立足学生实际，站在未知者的角度看问题；
◆教学的出发点不是“我怎么认为”而是“学生怎么认为”.站在已知者 (教师)的角度看待问题，思维的路线是直线的；站在未知者(学生)的角 度看待问题，思维的路线是曲线的.好老师就是要将自己变身为学生，变 身为差学生，从这个角度去寻找思维的真实路线.
(四)抓住核心内容，凸出培养运算能力.
(二)聚焦核心素养，整体建构知识体系；
◆其次要发挥“转化思想”的统领应用。有理数运算的基本方法将正数与负数 之间的运算转化为正数之间的运算；加法与乘法运算法则都是“先定符号，再 算绝对值”，当符号确定后，就转化为已学过的运算；减法与除法运算转化为 加法与乘法运算；乘方转化为乘法运算等.这种由未知转化为已知的思 想是数学学习中解决问题的基本思维方式.
初中数学人教版七年级上册《1.有理数的除法》课件
最后求出结果（乘除混合运算按从左到右的顺序进行计算）.
如果两个有理数的和除以它们的积，所得的商为 0，那么这两个有
理数( D )
A.和为 0
B.互为倒数
C.有一个等于0
D.互为相反数且都不等于 0
若有理数 a，b满足 ab<0，则
||
+
||
的值为. 0
谢谢大家
2.理解除法法则，体验除法与乘法的转化关系.
3.掌握有理数的除法及乘除混合运算.
根据“除法是乘法的逆运算”填空：
-2
8÷(-4)=___
-6
-36÷6=___
4
12
3
5
- ÷(- )=___
25
5
-8
-72÷9=___
-2
8÷(-4)=___
-6
-36÷6=___
1
-2
8×(- )=___
4
1
-36×
2.两个数相除，若商是1，则这两个数相等；若商是 -1，则这两
个数互为相反数.
例 计算：
(1) (-36)÷9；
12
3
(2) (- ) (- )
25
5
解：(1) (-36)÷9=-(36÷9)=-4；
12
3
12
5
4
(2) (- ) (- ) (- ) (- ) .
25
5
25
3
5
6 （- ）=
2
-3
+3
互为倒数
“÷”变“×”
(2)
(+6)÷(-2)=
-3
互为倒数
从中你能得出什么结论？
初中数学人教七年级上册第一章 有理数 函数奇偶性PPT
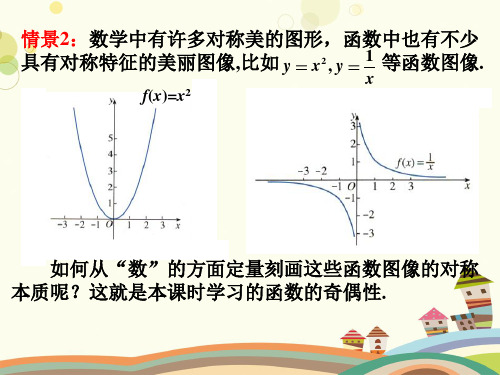
(3) f ( x) x 1 x
解：(1)定义域为(-∞,+∞) ∵ f(-x)=(-x)4=f(x) 即 f(-x)=f(x) ∴ f(x)是偶函数.
1 (4) f ( x) x2
(2)定义域为(-∞,+∞) ∵ f(-x)=(-x)5= - x5 = -f(x) 即 f(-x) = -f(x) ∴ f(x)是奇函数.
(3)定义域为{x|x≠0}
(4)定义域为{x|x≠0}
∵ f(-x)=-x+1/(-x)=-f(x)∵ f(-x)=1/(-x)2=f(x)
即 f(-x) = -f(x)
即 f(-x)=f(x)
∴ f(x)是奇函数.
∴ f(x)是偶函数.
用定义判断函数奇偶性的步骤：
(1)、先求定义域，看是否关于原点对称； (2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.
∴函数f(x)既不是奇函数也不是偶函数.
（4）f ( x)
x(1
x(1
x) x)
(x (x
0) 0) .
解：∵f(x)的定义域是(－∞，0)∪(0，+∞)，
当x＞0时，－x＜0， ∴f(－x)=(－x)[1－(－x)]=－x(1+x) =－f(x) (x＞0). 当x＜0时，－x＞0，
∴f(－x)= (－x)[1＋ (－x)]=－x(1－x) =－f(x) (x＜0)，
实际上，对于R内任意的一个x,都有f(-x)=-x=-f(x),这
时我们称函数y=x为奇函数.
定义:一般地,对于函数f(x)的定义域内的任意一个x， 都有f(－x)= －f(x)，那么f(x)就叫做奇函数．
定义
偶函数:一般地,对于函数f(x)的定义域内的任意一个x， 都有f(－x)=f(x)，那么f(x)就叫做偶函数．
七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1
![七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1](https://img.taocdn.com/s3/m/3857a617a517866fb84ae45c3b3567ec102ddc8c.png)
ICU护士职业倦怠及其与离职意愿的相关性调查谭朝霞;邹颢宇;刘怡素;胡霞红【期刊名称】《海南医学》【年(卷),期】2014(000)011【摘要】目的：探讨ICU护士职业倦怠及其与离职意愿之间的关系。
方法采用Maslach职业倦怠量表、离职意愿量表对长沙市四所省级综合性三甲医院207名ICU护士进行问卷调查。
结果 ICU护士职业倦怠中情绪衰竭维度得分为(23.20±9.71)分、去人格化维度得分为(6.43±5.81)分，均属于中度倦怠；个人成绩感得分为(32.34±9.40)分，属于高度倦怠。
76.3%(158名)的ICU护士存在离职意愿，其中17.4%(36名)的ICU护士离职意愿强烈。
情绪衰竭和去人格化与离职意愿呈正相关(r=0.531，r=0.384，P＜0.05)，而个人成就感与离职意愿呈负相关(r=-0.310，P＜0.05)。
结论 ICU护士职业倦怠较严重，离职意愿率较高。
应注意降低ICU护士的职业倦怠感，从而减弱离职意愿，以便有效预防ICU护士离职行为的发生。
%Objective To investigate the job burnout and its relationship with turnover intention in nurses in Intensive Care Unit. Methods The Chinese Maslach Burnout Inventory and Turnover intention questionnaire were used to conduct a survey in 207 ICU nurses from four provincial third-level comprehensive hospitals in Changsha. Results"Emotional exhaustion"(23.20±9.71) and"Depersonalization"(6.43±5.81) were moderate burnout and“Per-sonal accomplishment”(32.34 ± 9.40) was in a high degree of burnout among ICU nurses. 76.3 percentages of the ICU nurses (158) have turnover intention, of which 17.4 percentages (36) holdserious turnover intention. Turnover intention was significantly positive correlation with emotional exhaustion and depersonalization(r=0.531,r=0.384, P<0.05) and significantly negative correlation with personal accomplishment (r=-0.310,P<0.05) in ICU nurses. Conclusion The problem of job burnout is serious and the turnover intention is common in ICU nurses. Attention should be paid to reduce the job burnout in ICU nurses and weaken the turnover intention in order to effectively pre-vent the occurrence of ICU nurses leaving behavior.【总页数】3页(P1695-1697)【作者】谭朝霞;邹颢宇;刘怡素;胡霞红【作者单位】湖南省人民医院肝胆外科，湖南长沙 410005;湖南省人民医院肝胆外科，湖南长沙 410005;湖南省人民医院肝胆外科，湖南长沙 410005;湖南省人民医院肝胆外科，湖南长沙 410005【正文语种】中文【中图分类】R195【相关文献】1.男护士职业倦怠与离职意愿的相关性研究 [J], 马秀娥2.惠州市民营医院护士离职意愿与工作压力源相关性调查 [J], 余秋容;游彩芬;黎秀珍;杨淑芬;李美娟;冯燕;黄雪兰;魏琴3.男护士职业倦怠与离职意愿的相关性研究 [J], 武施凯4.护士职业倦怠、离职意愿相关因素研究 [J], 陈先梅; 吴庆芳5.护士职业尊重感、职业倦怠及离职意愿的相关性 [J], 史晓普;李莹;张丛丛因版权原因，仅展示原文概要，查看原文内容请购买。
七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1
![七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1](https://img.taocdn.com/s3/m/69966e29ce84b9d528ea81c758f5f61fb73628a0.png)
C
BD
A
－3 －2 －1 0 1 2
解：点
A表示
3，点
2
B表示－
1 2
，点
C表示－
5，点
2
D表示0.
由点读数：先由位置（哪一侧）确定符号， 再由距离读出数.
例4 画出数轴，并在数轴上画出表示下列各数的点.
4，－2，－4.5，4 ，0.
3
解：如图所示.
4
－4.5 －2
03
4
－5 －4 －3 －2 －1 0 1 2 3 4 5
－5 －4 －3 －2 －1 0 1 2 3 4 5
例1 画出数轴，并在数轴上表示下列各数： 3，－4，4，0.5，0， 5 ，－1. 2
－4
5 2
－1 0
0.5
34
－5 －4 －3 －2 －1 0 1 2 3 4 5
例2 下面画出的直线中，哪条是数轴？为什么？
（1） 0
没有单位长度
（2） 012
原点
正方向
－5 －4 －3 －2 －1 0 1 2 3 4 5
我是直线！
单位长度
思考 仔细观察下面的动图，想一想它有什么特点？
思考 仔细观察下面的动图，想一想它有什么特点？
像这样，规定了原点、正方向和单位长度的直线叫作数轴. 0是正数和负数的分界；原点是数轴的“基准点”. 原点将数轴（原点除外）分成两部分，其中正方向一侧的 部分叫作数轴的正半轴；另一侧的部分叫作数轴的负半轴.
7.5
思考
右图中的温度计可以看作表示正数、0和负数
50
120
的直线. 它和前面我们画出的用数简明表示位置 关系的图形有什么共同点，有什么不同点？
40
人教版初中数学七年级上册精品教学课件 第1章 有理数 1.5.1 乘方
1.5.1 乘方
快乐预习感知
1.求n个 相同因数 的积的运算,叫做乘方,乘方的结果叫 做 幂 .在an中,a叫做 底数 ,n叫做 指数 .
2.正数的任何次幂都是 正数 ,0的任何正整数次幂都是 0 ; 负数的 奇次幂 是 负数 ,负数的 偶次幂 是 正数 .
3.下列关于 -3 4的说法中正确的是( D ) A.-3是底数,4是指数,12是幂 B.-3是底数,4是指数,-12是幂 C.3是底数,4是指数,81是幂 D.-3是底数,4是指数,81是幂
是
.
解析:在数组中其相邻的数字之间依次扩大相同的倍数时,可用
乘方来探索其中的规律.探索规律时,常从符号和绝对值两方面考
虑.如从这组数的符号看,正负交替出现;从绝对值上看,这组数可写
成:30,31,32,33,34,35,….因此第2 021个数是32 021-1.32=3×2
C.
-
1 2
3=-12
×
1 2
×
1 2
D.23=32
快乐预习感知
3.-95表示( C )
A.5个-9相乘
B.9个-5相乘
C.5个9相乘的相反数
D.5个9相乘
4.
-
2 3
5
的底数为
-23
,指数为 5 .
快乐预习感知
5.计算:(1)-13-[1-(1-0.5×43)];
(2)(-2)2-(-1)3×
1 2
-
1 3
÷ 16.
解: (1)-13-[1-(1-0.5×43)] =-1-[1-(1-0.5×64)]
=-1-[1-(1-32)]=-1-(1+31)
=-1-32=-33.
(2)(-2)2-(-1)3×
快乐预习感知
1.求n个 相同因数 的积的运算,叫做乘方,乘方的结果叫 做 幂 .在an中,a叫做 底数 ,n叫做 指数 .
2.正数的任何次幂都是 正数 ,0的任何正整数次幂都是 0 ; 负数的 奇次幂 是 负数 ,负数的 偶次幂 是 正数 .
3.下列关于 -3 4的说法中正确的是( D ) A.-3是底数,4是指数,12是幂 B.-3是底数,4是指数,-12是幂 C.3是底数,4是指数,81是幂 D.-3是底数,4是指数,81是幂
是
.
解析:在数组中其相邻的数字之间依次扩大相同的倍数时,可用
乘方来探索其中的规律.探索规律时,常从符号和绝对值两方面考
虑.如从这组数的符号看,正负交替出现;从绝对值上看,这组数可写
成:30,31,32,33,34,35,….因此第2 021个数是32 021-1.32=3×2
C.
-
1 2
3=-12
×
1 2
×
1 2
D.23=32
快乐预习感知
3.-95表示( C )
A.5个-9相乘
B.9个-5相乘
C.5个9相乘的相反数
D.5个9相乘
4.
-
2 3
5
的底数为
-23
,指数为 5 .
快乐预习感知
5.计算:(1)-13-[1-(1-0.5×43)];
(2)(-2)2-(-1)3×
1 2
-
1 3
÷ 16.
解: (1)-13-[1-(1-0.5×43)] =-1-[1-(1-0.5×64)]
=-1-[1-(1-32)]=-1-(1+31)
=-1-32=-33.
(2)(-2)2-(-1)3×
初中数学人教七年级上册第一章 有理数 《乘方》PPT
C. 2017
D. –2017
课堂检测
基础巩固题
1.填空： （1）–(–4)2= –16 ;
（2）–32= –;9
（3）(–5)3= –125;
（4）0.13= 0.00; 1
（5）(–1)9= –1;
（6）(–1)12= ;1
（7）(–1)2n= 1;
（8）(–1)2n+1= –; 1
-1 （当n为奇数时）
探究新知 分裂方式如下所示:
第一次
第二次
第三次
探究新知
【思考】 这个细胞分裂一次可得多少个细胞? 分裂两次呢?
分裂三次呢?四次呢？ 那么，3小时共分裂了多少次?有多少个细胞？
解:
一次： 2个；
两次：
2×2个；
三次： 2×2×2个；
四次： 2×2×2×2个； 六次: 2×2×2×2×2×2个.
探究新知 请比较细胞分裂四次后的个数式子:2×2×2×2和细
课堂检测
拓广探索题
厚度是0.1毫米的纸,将它对折1次后,厚度为0.2毫米.
（1）对折3次后,厚度为多少毫米?
0.1×23=0.8毫米
（2）对折7次后,厚度为多少毫米?
0.1×27=12.8毫米.
（3）用计算器计算对折30次后纸的厚度.
0.1×230=0.1×1073741824=107374182.4（毫米） 107374182.4毫米=107374.1824米 ＞8848米
负数有t个，则m n k t （6）
（3）
2 3
3
.
解：（1）(–4)3=(–4)×(–4)×(–4)= – 64；
（2）(–2)4 =(–2)×(–2)×(–2)×(–2)=16；
人教版初中数学七年级上册精品教学课件 第1章 有理数 1.1 正数和负数
答案:C
互动课堂理解
2.用正、负数表示具有相反意义的量 【例2】 某水泥厂计划每月生产水泥900 t,1月份实际生产了850 t,2月份实际生产了900 t,3月份实际生产了1 000 t,试用正数和负数 表示每月超额完成计划的吨数. 分析:习惯上我们把多生产的水泥吨数用正数表示,少生产的水 泥吨数用负数表示.因此1月份比原计划少生产50 t,记作-50 t;2月份 与原计划相同,记作0 t;3月份比原计划多生产了100 t,记作+100 t. 解:1月份、2月份、3月份超额完成计划的吨数分别为-50,0,+100.
8.指出下列各数哪些是正数,哪些是负数. 7,-9,-190,-301,+247,112,+2 021,0. 分析: 可由大于0的数是正数和正数前面加上符号“-”的数是负数进 行判断. 解: 正数:7,+247,112,+2 021;负数:-9,-190,-301.
互动课堂理解
1.正数和负数 【例1】 下列说法正确的个数是( )
①-a是负数;②-7是负数;③正数前面加上符号“-”的数为负数;④
+2是正数. A.1 B.2 C.3 D.4
解析:②③④符合正数、负数的概念,都正确.单独一个字母既可
以表示正数,又可以表示负数,还可以表示0.只有在正数前面加上符
号“-”的数才是负数,因此①错误.
快乐预习感知
4.在-212,+170,-3.314,0,4.5,-1 中,负数有 ( C )
A.1 个
B.2 个
C.3 个
D.4 个
5.在数学课上,甲、乙、丙、丁四名同学分别对“0”作了如下描述: 甲:“0”可以表示“没有”; 乙:“0”可以表示特定的意义,比如“0 ℃”; 丙:0既不是正数,也不是负数; 丁:0是正数和负数的分界点. 其中描述正确的个数是( D ) A.1 B.2 C.3 D.4
互动课堂理解
2.用正、负数表示具有相反意义的量 【例2】 某水泥厂计划每月生产水泥900 t,1月份实际生产了850 t,2月份实际生产了900 t,3月份实际生产了1 000 t,试用正数和负数 表示每月超额完成计划的吨数. 分析:习惯上我们把多生产的水泥吨数用正数表示,少生产的水 泥吨数用负数表示.因此1月份比原计划少生产50 t,记作-50 t;2月份 与原计划相同,记作0 t;3月份比原计划多生产了100 t,记作+100 t. 解:1月份、2月份、3月份超额完成计划的吨数分别为-50,0,+100.
8.指出下列各数哪些是正数,哪些是负数. 7,-9,-190,-301,+247,112,+2 021,0. 分析: 可由大于0的数是正数和正数前面加上符号“-”的数是负数进 行判断. 解: 正数:7,+247,112,+2 021;负数:-9,-190,-301.
互动课堂理解
1.正数和负数 【例1】 下列说法正确的个数是( )
①-a是负数;②-7是负数;③正数前面加上符号“-”的数为负数;④
+2是正数. A.1 B.2 C.3 D.4
解析:②③④符合正数、负数的概念,都正确.单独一个字母既可
以表示正数,又可以表示负数,还可以表示0.只有在正数前面加上符
号“-”的数才是负数,因此①错误.
快乐预习感知
4.在-212,+170,-3.314,0,4.5,-1 中,负数有 ( C )
A.1 个
B.2 个
C.3 个
D.4 个
5.在数学课上,甲、乙、丙、丁四名同学分别对“0”作了如下描述: 甲:“0”可以表示“没有”; 乙:“0”可以表示特定的意义,比如“0 ℃”; 丙:0既不是正数,也不是负数; 丁:0是正数和负数的分界点. 其中描述正确的个数是( D ) A.1 B.2 C.3 D.4
最新人教版七年级数学上册全套PPT课件-七年级数学上ppt精选全文
*
1.什么是负数?
我们将前面带有“－”的数叫负数,那么为什么要引入负数?通常我们在日常生活中用正数和负数分别表示怎样的量呢?.
*
中国男蓝在雅典奥运会上: 58:83负于西班牙 69:62战胜新西兰 57:82负于阿根廷 52:89负于意大利 积分:5分 67:66战胜塞黑
*
比标准重量多出5克
比标准重量少出5克
*
1.2.1有理数
*
复习与回顾：
上一节课我们讲了些什么内容？
1，正数和负数。 2，0既不是正数，也不是负数。 3，正数与负数通常用来表示具有相反意义的 量。 4，“0”所表示的意思。 5，在生产中，通常用正负数来表示允许误差；
*
1、粮食每袋标准重量是50千克，先测得甲、乙、丙三袋粮 食重量如下：52千克，49千克，49.8千克，如果超重部分 用正数表示，请用正数和负数记录甲、乙、丙三袋粮食的 超重数和不足数；
*
“不是正数的数一定是负数,不是负数的数一定是正数”的说法对吗?
答案肯定是不对的，还有0的存在．
*
在生活中，我们将海平面高度计为0米，根据图的标识，你能说出我国的最高峰珠穆朗玛峰和吐鲁番盆地的海拔高度吗？
8848
-155
类似题中0可以都有怎样的意义？
0只是一个基准，它具有丰富的意义，不是简简单单的只表示没有．
2、国际乒联在正式比赛中采用打球，对大球的直径有严格的标准，现有5个乒乓球，测量它们的直径，超过标准的毫米数记为正数，不足的记为负数，测量结果如下： A.-0.1mm B.-0.2mm C.+0.25mm D.-0.05mm E.+0.15mm 你认为应该选哪一个4，7，142，－12，0，-37， 中，负整数共有（ ） A．3个 B．2个 C．1 个 D．0个
1.什么是负数?
我们将前面带有“－”的数叫负数,那么为什么要引入负数?通常我们在日常生活中用正数和负数分别表示怎样的量呢?.
*
中国男蓝在雅典奥运会上: 58:83负于西班牙 69:62战胜新西兰 57:82负于阿根廷 52:89负于意大利 积分:5分 67:66战胜塞黑
*
比标准重量多出5克
比标准重量少出5克
*
1.2.1有理数
*
复习与回顾：
上一节课我们讲了些什么内容？
1，正数和负数。 2，0既不是正数，也不是负数。 3，正数与负数通常用来表示具有相反意义的 量。 4，“0”所表示的意思。 5，在生产中，通常用正负数来表示允许误差；
*
1、粮食每袋标准重量是50千克，先测得甲、乙、丙三袋粮 食重量如下：52千克，49千克，49.8千克，如果超重部分 用正数表示，请用正数和负数记录甲、乙、丙三袋粮食的 超重数和不足数；
*
“不是正数的数一定是负数,不是负数的数一定是正数”的说法对吗?
答案肯定是不对的，还有0的存在．
*
在生活中，我们将海平面高度计为0米，根据图的标识，你能说出我国的最高峰珠穆朗玛峰和吐鲁番盆地的海拔高度吗？
8848
-155
类似题中0可以都有怎样的意义？
0只是一个基准，它具有丰富的意义，不是简简单单的只表示没有．
2、国际乒联在正式比赛中采用打球，对大球的直径有严格的标准，现有5个乒乓球，测量它们的直径，超过标准的毫米数记为正数，不足的记为负数，测量结果如下： A.-0.1mm B.-0.2mm C.+0.25mm D.-0.05mm E.+0.15mm 你认为应该选哪一个4，7，142，－12，0，-37， 中，负整数共有（ ） A．3个 B．2个 C．1 个 D．0个
七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1
![七年级-人教版(2024新版)-数学-上册-[课件]初中数学-七年级上册-第一章--1](https://img.taocdn.com/s3/m/3dbde40a24c52cc58bd63186bceb19e8b9f6ec75.png)
1 整数可以写成分数的形式.
负整数 ，如－1，－2，－3，…；写成负分数 －3＝－3 1
分
正分数
，如
1 2
，
2 3
，175，0.1，5.32，0.3• ，…；
数
负分数 ，如－ 5 ，－ 2
23
，－ 1
7
，－0.5，－150.5，…．
1
－1 1
10
23
有限小数和无限循环小数都可以化为分数．
归纳
可以写成分数形式的数称为有理数．其中，可以写 成正分数形式的数为正有理数，可以写成负分数形式的 数为负有理数.
为4．
圆周率 π 是正数，但不是有理数，千万要注意，类 似 π ，－ π 等同样也不是有理数．
23
例4 把下列各数填入相应的集合内．
172，－3.141
6，0，2
019，－
8 5
，10%，10.1，0.67，－89．
正数集合： 12，2 019，10%，10.1，； 0.67， 7
；
负数集合： －3.141 6，－ 8 ，－89，
9
负有理数：－3 ，－30，－12%，－7.5，－60 ． 8
例2 下列说法中，正确的是（ D ）． A．在有理数中，0的意义仅仅表示没有 B．一个有理数，它不是正数就是负数 C．正有理数和负有理数组成有理数 D．0是自然数 解析：0的意义不仅仅表示没有，在一些具体情境中有特殊的 表示，故选项A错误；一个有理数，它有可能是正数，也有可能是 负数，还有可能是0，故选项B错误；正有理数、0和负有理数组成 有理数，故选项C错误．0是自然数，故选项D正确．
“0”的意义
_表__示__没__有_____ _某__种__量__的_基__准__ _分__界__点_______
初中数学人教七年级上册第一章有理数有理数的分类PPT
正数集合 分数集合
8:如果用一个字母表示一个数，那a可能是什么样的数？ 一定是正数吗？
答：不一定，a可能是正数，可能是负数，也可 能是0。
9: 观察下列各组数，请找出它们的规律，并在横线上填 上相应的数字；
(1)2,0,2,4,_6____8___,__;
(2)1,1 2,3 2,4 3,5 4__65 ____76__, __;
124.由前__面_的_结_43论,,小_学_里_学_的_85数,可_以_分_为_哪_几, 类? 25.引入__负_数_后_5，,整数__除_了_小_2学,学的__整_数_外._，还包含其它的整数吗？ 3分数除了小学6学的分数外，7还包含其它的分数吗？
正整数: ＋10，18，29，＋75， 110，305，1，2，3，… 零: ０
不能”)算做分数；
21
2，，－两3个.14整等数）的、比无（限如循环3 小, 数2等（）如、有限0.小3,数1等（.4）如7都0.2是
分数；但无限不循环小数（如 等）不是分数；
3，无限不循环小数不是有理数；(无理数)
4，整数中除了正整数和负整数，还有___0__.
练一练
1．把下列各数填入它所属于的集合的圈内：
同桌 探究
110, 122.5, 182.5,
12.91, 12.96, 0, －52 1.1,
＋75, 305,
18, －7.5, ＋10.
1.在以上各数中,哪些是在小学里学过的数?它们可以分为哪几类?
2.在小学里学过的数中,有没有哪类数在上面没有出现?请举例说明.
3.计算下列各分数的值,说明所有分数都可以化作什么数?
复习与回顾：
上一节课我们讲了些什么内容？ 1，正数和负数。 2，0既不是正数，也不是负数。 3，正数与负数通常用来表示具有相反意义的量 。 4，“0”所表示的意思。 5，在生产中，通常用正负数来表示允许误差；
8:如果用一个字母表示一个数，那a可能是什么样的数？ 一定是正数吗？
答：不一定，a可能是正数，可能是负数，也可 能是0。
9: 观察下列各组数，请找出它们的规律，并在横线上填 上相应的数字；
(1)2,0,2,4,_6____8___,__;
(2)1,1 2,3 2,4 3,5 4__65 ____76__, __;
124.由前__面_的_结_43论,,小_学_里_学_的_85数,可_以_分_为_哪_几, 类? 25.引入__负_数_后_5，,整数__除_了_小_2学,学的__整_数_外._，还包含其它的整数吗？ 3分数除了小学6学的分数外，7还包含其它的分数吗？
正整数: ＋10，18，29，＋75， 110，305，1，2，3，… 零: ０
不能”)算做分数；
21
2，，－两3个.14整等数）的、比无（限如循环3 小, 数2等（）如、有限0.小3,数1等（.4）如7都0.2是
分数；但无限不循环小数（如 等）不是分数；
3，无限不循环小数不是有理数；(无理数)
4，整数中除了正整数和负整数，还有___0__.
练一练
1．把下列各数填入它所属于的集合的圈内：
同桌 探究
110, 122.5, 182.5,
12.91, 12.96, 0, －52 1.1,
＋75, 305,
18, －7.5, ＋10.
1.在以上各数中,哪些是在小学里学过的数?它们可以分为哪几类?
2.在小学里学过的数中,有没有哪类数在上面没有出现?请举例说明.
3.计算下列各分数的值,说明所有分数都可以化作什么数?
复习与回顾：
上一节课我们讲了些什么内容？ 1，正数和负数。 2，0既不是正数，也不是负数。 3，正数与负数通常用来表示具有相反意义的量 。 4，“0”所表示的意思。 5，在生产中，通常用正负数来表示允许误差；
初中数学人教七年级上册第一章 有理数算术平方根PPT
实战演练 运用新知
• 例1 分别求下列各数的算术平方根： • 例2 计算： • 练一练
探究二：算术平方根的非负性
• 例3 ： 几个非负数的和为0，则每个数均为0，现阶段学过的非负数有绝
对值、一个数的平方及算术平方根.
巩固新知 深化理解
• 1.填空： • 2.求下列各数的算术平方根 • 3.下列式子表示什么意义？你能求出它们的值吗？
x2=a,那么这个正数x叫做 a的算术平方根.
实战演练 运用新知
1.因为22=4 ，所以4的算术平方根是（
)
2.下列说法正确的是( )
①5是25的算术平方根
Hale Waihona Puke ② 0.01是0.1的算术平方根
合作探究 获取新知:算术平方根的性质
• 1.一个正数的算术平方根有几个？ • 2.0的算术平方有几个？ • 3.-1有算术平方根吗？负数有算术平方根
教学目标：
1.了解算术平方根的概念，会用根号表示一个数的算术平根;
2.掌握算术平方根的非负性，会求非负数的算术平方根．
•
•
教学重点：
• 了解算术平方根的概念，会用根号表示一个数的算术平 方根;
•
•
教学重点：
• 掌握算术平方根的非负性，会求非负数的算术平方根．
一、新课引入：
1、阅读教材引入。 2、填表。 3、二次根式的概念： 一般地，如果一个正数x的平方等于a，即
• 思维方法：求一个正数的算术平方根运算和开 平方求一个正数的二次幂运算互为逆运算.
• 探究策略：由特殊到一般，再由一般到特殊， 是发现问题和解决 问题的基本方法和途径.
回顾与反思
• 通过今天的学习, • 能说说你的收获和体会吗? • 你有什么经验与收获让同学们共享呢？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1)在-13与11之间按从小到大 依次插入三个数，使这五个数 中每相邻两个数之间的差相等， 则这三个数的和是 ___________.Байду номын сангаас(2) 4-(12-18)=_______.
乘方
下列各对数中，值相等的一对是（ ） A. 32与23 B. -23与(-2)3 C. -32与(-3)2 D. (-3×2)3与-3×23
注意：有理数的乘法可以使用： 乘法交换律、结合律、分配律
有 理 数 的 除 法
除以一个不为0的 数，等于乘乘这个数 的倒数。 两数相除，同号 得正，异号得负，并 把绝对值相除。0除 以任何一个不等于0 的数，都得0.
乘 方
求n个相同因数的积 的运算，叫做乘方， 乘方的结果叫做幂。 在an中，a叫做底数， n叫做指数，当an看 作a的n次方的结果时， 也可读作“a的n次 幂”。
（1）在直线上任取一个点表示0这
数 轴
个点叫做原点； （2）通常规定直线上从原点向右 （或上）为正方向，从原点向左 （或下）为负方向； （3）选取适当的长度为单位长度， 直线上从原点向右，每隔一个单 位长度取一个点，依次表示1，2， 3，…；从原点向左，用类似方 法依次表示-1，-2…。
做 一 做
亲们：哦！ O(∩_∩)O
有 理 数 知 识 结 构 图
正 数 和 负 数
正数：大于0的数叫做正数 负数：小于0的数叫做负数 数0既不是正数，也不是 负数，它是正、负数的届限， 表示“基准”的数，零不是 表示“没有”，它表示一个 实际存在的数量。正数负数 的“+”“-”的符号是表示 性质相反的量，符号写在数 字前面，这种符号叫做性质 符号。
绝 对 值
一般地，数轴上表示数a的 点与原点的距离叫做a的绝对 值，记作|a|。 (1)当 a>0时，|a|=a; (2)当a=0时，|a|=0; (3)当a<0时，|a|=-a.
①正数大于0，0大于负数， 正数大于负数 ②两个负数，绝对值大的反 而小
有 理 数 的 加 法
符号相同的两个数相 加，结果的符号不变，绝 对值相加；符号相反的两 个数相加，结果的符号与 绝对值较大的加数的符号 相同，并用较大的绝对值 减去较小的绝对值。 注意： 有理数加法中可以使用 加法交换律、结合律
负数的奇次幂是负数，负数的偶次幂是正数。 正数的任何次幂都是正数，0的任何正整数次 幂都是0.
有理数混合运算顺序： 1、先乘方，再乘除，最后加减; 2、同级运算，从左到右进行； 3、如有括号，先做括号内的运算，按小括号、中括号、 大括号依次进行。
科学计数法
把一个大于10的数表示成a×10n的形式 (其中a大于或等于1且小于10，n是正整数)， 使用的是科学计数法。 有效数字: 从一个数的左边第一个非0数字起，到末尾 数字止，所有的数字都是这个数的有效数字。
在数轴上，若点A 表示-1.5，点B表 示3，则A、B两点 间的距离是 ________。
相 反 数
只有符号不同 的两个数叫做 互为相反数。
做一做
（1）当x=_____时，式子|x-1|+2 的值最小，为_______。 （2）将下列各式分别填入相应的 横线上： -(-3),+|-3|,-|-3|,-|+3|,+(-3),-(+3) 化简结果为-3： ___________________________
有 理 数
正整数、0、负 整数统称为整数; 正分数、负分数 统称为分数。 整数和分数统 称为有理数。
找 规 律
一列数：0，-1，-1，-2, -3，-3…按照这样的规 律，第十个数是_____, 第2013个数是_______, 第n个数是_________。 （n为正整数）
在数学中，可以用一条直线 上的点表示数，这条直线叫做 数轴，它满足以下要求：
有理数的减法
减去一个数， 等于加这个数的相反数.
例：(-20)+(+3)-(-5)-(+7) =-20+3+5-7 =-20-7+3+5 =-27+8 =-19
有理数的乘法
负数乘负数，积为正数，乘积的 绝对值等于各乘数绝对值的积。
有理数乘法法则： 两数相乘，同号得正，异号得负， 并把绝对值相乘。 任何数与0相乘，都得0.