人教版数学七年级下册-练习对顶角_相交线
人教版七年级数学下册《第五章 相交线与平行线》练习题-附带答案

人教版七年级数学下册《第五章相交线与平行线》练习题-附带答案一、选择题:在每小题给出的四个选项中只有一项是符合题目要求的.1.下列图形中∠1与∠2是对顶角的是A.B.C.D.【答案】C2.下列说法正确的是A.大小相等的两个角互为对顶角B.有公共顶点且相等的两个角是对顶角C.两角之和为180°则这两个角互为邻补角D.—个角的邻补角可能是锐角、钝角或直角【答案】D【解析】A.大小相等的两个角互为对顶角错误;B.有公共顶点且相等的两个角是对顶角;错误;C.两角之和为180°则这两个角互为邻补角错误;D.—个角的邻补角可能是锐角、钝角或直角正确.故选D.3.如图直线AB CD相交于点O所形成的∠1、∠2、∠3和∠4中一定相等的角有A.0对B.1对C.2对D.4对【答案】C4.如图直线AB CD相交于点O若∠1+80°=∠BOC则∠BOC等于A.130°B.140°C.150°D.160°【答案】A【解析】因为∠1+∠BOC=180°∠1+80°=∠BOC所以∠1+∠1+80°=180°解得:∠1=50°所以∠BOC=130°.故选A.二、填空题:请将答案填在题中横线上.5.如图所示AB与CD相交所成的四个角中∠1的邻补角是__________∠1的对顶角是__________.【答案】∠2和∠4;∠3【解析】根据对顶角和邻补角的定义解答注意两直线相交一个角的对顶角只有一个但邻补角有两个.由图形可知∠1的对顶角是∠3∠1的邻补角是∠2和∠4.6.如图是一把剪刀其中∠1=40°则∠2=_________其理由是_________.【答案】40°对顶角相等【解析】因为对顶角相等所以∠2=∠1=40°.故答案为:40°对顶角相等.三、解答题:解答应写出文字说明、证明过程或演算步骤.7.如图所示AB CD EF交于点O∠1=20°∠2=60°求∠BOC的度数.【解析】因为∠BOF=∠2=60°所以∠BOC=∠1+∠BOF=20°+60°=80°.8.如图直线AB CD相交于点O∠EOC=70°OA平分∠EOC求∠BOD的度数.9.探究题:(1)三条直线相交最少有_________个交点;最多有_________个交点画出图形并数出图形中的对顶角和邻补角的对数;(2)四条直线相交最少有_________个交点;最多有_________个交点画出图形并数出图形中的对顶角和邻补角的对数;(3)依次类推n条直线相交最少有_________个交点;最多有_________个交点对顶角有_________对邻补角有_________对.【解析】当直线同交于一点时只有一个交点;当直线两两相交且不过同一点时交点个数最多;根据对顶角与邻补角的定义找出即可.(1)三条直线相交最少有1个交点最多有3个交点如图:对顶角:6对邻补角:12对;。
人教版七年级下学期数学-5.1相交线(练习题)

人教版七年级下学期数学-5.1相交线练习题一、单选题1.如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是()A.B.C.D.2.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为()A.30°B.45°C.60°D.75°3.如图,直线AB,CD相交于点O,,OF平分,则的大小为()A.40°B.50°C.65°D.70°4.如图,在中,,,垂足为点D,那么点A到直线的距离是线段()的长.A.B.C.D.5.如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD 的度数为()A.40°B.37°C.36°D.35°6.如图所示,与∠α构成同位角的角的个数为()A.1B.2C.3D.47.在下列语句中,正确的是().A.在平面上,一条直线只有一条垂线;B.过直线上一点的直线只有一条;C.过直线上一点且垂直于这条直线的直线有且只有一条;D.垂线段的长度就是点到直线的距离8.平面上三条直线两两相交最多能构成对顶角的对数是().A.7B.6C.5D.49.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD =∠BOC.A.①②③B.①②④C.①③④D.②③④10.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有()A.1个B.2个C.3个D.4个二、填空题11.已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为.12.如图,直线AB、CD、EF相交于点O,若∠1+∠2=150°,则∠3=°.13.如图,直线AB、CD相交于点O,OE平分,OF平分.若,则的度数为°.14.若与是对顶角,与互余,且,则的度数为°.15.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为.三、计算题16.如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.17.如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.四、综合题18.如图,在所标注的角中.(1)对顶角有对,邻补角有对;(2)若,,求与的度数.19.如图,点在直线外,点在直线上,连接.选择适当的工具作图.(1)在直线上作点,使,连接;(2)在的延长线上任取一点,连接;(3)在,,中,最短的线段是,依据是.20.如图,直线、相交于点,且平分,平分.(1)求证:平分;(2)求的度数.答案解析部分1.【答案】D【解析】【解答】解:依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是:故答案为:D.【分析】利用垂线段最短,以及两点之间线段最短求解即可。
人教版最全七年级数学下册全册同步练习及单元测验卷及答案

第五章相交线与平行线5.1.1 相交线复习检测(5分钟):1、如图所示,/1和/2是对顶角的图形有()A.1个B.2 个C.3 个D.4 个2、如图,若/ 1=60° ,那么/ 2=3、如图是一把剪刀,其中 1 40,则24、如图三条直线AB,CD,EF相交于一点O, /AOD勺对顶角是,/AOC勺邻补角是,若/ A0C=50 ,贝U/ BOD= ./ COB= J AOE+ DOB + COF=5、如图,直线AB,CD相交于0,0评分/ AOC若/ AOD/DOB=50 ,?求/EOB勺度数.6、如图,直线a,b,c两两相交,/1=2/ 3, / 2=68° ,求/4的度数5.1.2 垂线复习检测(5分钟):1、两条直线互相垂直,则所有的邻补角都相等.()2、一条直线不可能与两条相交直线都垂直.()3、两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.()4、两条直线相交有一组对顶角互补,那么这两条直线互相垂直.().5、如图1,OAL OB,OCL OC,O为垂足,若/AOC=3 5,则/BOD=.6、如图2,A0± BO,O为垂足,直线CDi点O,且/ BOD=2AOC则/ BOD=.7、如图3,直线AB CD相交于点0,若/E0D=40 , /B0C=130,那么射线0E与直线AB的位置关系是C8、已知:如图,直线AB,射线0位于点的位置关系.9、如图,AC± BC,C为垂足,CD± AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6 ,那么点C 到AB 的距离是,点A 到BC 的距离是,点B 到CD 的距离是 ,A 、B 两点间的距离是.10、如图,在线段AB AG AD AE AF 中AD 最短.小明说垂线段最短,因此线段AD 的 长是点A 到BF 的距离,对小明的说法,你认为对吗?11、用三角尺画一个是30的/AOB 在边OA±任取一点P,过P 作POL OB,垂足为Q, 量一量OP 的长,你发现点P 到OB 的距离与OP 长的关系吗?5.1.3同位角、内错角、同旁内角3、如图(6),直线DE 截AB, AC,构成八个角: ①、指出图中所有的同位角、内错角、同旁内角复习检测(5分钟):1、如图(4),卜列说法不正确的是( )人./1与/2是同位角 B. / 2与/ 3是同位角C. / 1与/ 3是同位角D. / 1与/ 4不是同位角2、如图(5),直线AB CDM 直线EF 所g, / A 和一 错角,/A 班是同旁内角.^ /\ \ /--- ---------- 4 届 -------------------- R图⑷ 图⑸—是同位角,/ A 和 ________ 是内A40(3) c'②、/人与/5, /A 与/6, /A 与/8,分别是哪一条直线截哪两条直线而成的什么 角?4、如图(7),在直角 ABCt\ / C= 90 , DU AC 于 E,交 A.一 L①、指出当BG DE 被AB 所截时,/ 3的同位角、内错角和礴内他(门②、若/ 3+/ 4=180试说明/ 1 = /2=/3的理由.5.2.1平行线复习检测(5分钟):1、在同一平面内,两条直线的位置关系有2、两条直线L 1与L 2相交点A,如果L 1//L ,那么12与L ()3、在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必.D ./3=/4 D. /BACW ACD4、两条直线相交,交点的个数是 ,两条直线平行,交点的个数是 _____________ 个.判断题5、6、7、85、不相交的两条直线叫做平行线.()6、如果一条直线与两条平行线中的一条直线平行,那么它与另一条直线也互相平行.()7、过一点有且只有一条直线平行于已知直线.()8、读下列语句,并画出图形后判断.(1)直线a 、b 互相垂直,点P 是直线a 、b 外一点,过P 点的直线c 垂直于直线b. (2)判断直线a 、c 的位置关系,并借助于三角尺、直尺验证.9、试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况5.2.2平行线的判定复习检测(10分钟):1、如图1所示,下列条件中,能判断AB// CD 的是()DAFCA./BADh BCDB. /1 = /2;C.AD C B如图5,直线a,b 被直线c 所截,现给出下列四个条件: ?①/ 1 = /5;②/ 1=/7;③/ 2+/ 3=180 ;@Z4=Z 7.其中能说明 a // b 的条件序号为() A.①② B.①③ C.①④ D. ③④如果/ 9=,那么AD// BC;如果/ 9=,那么AB// CD.7、在同一平面内,若直线a,b,c 满足a±b,a ±c,则b 与c 的位置户系是8、如图所示,BE 是AB 的延长线,量得/ CBEh A=/ C. //.... AB E(1) 由/ CBEh A 可以判断//,根据是.⑵ 由/ CBEh C 可以判断//,根据是2、 如图2所示,如果/ D=/ EFC 那么()A.AD // BCB.EF // BC 3、 F 列说法错误的是()A.同位角不一定相等B. 内错角都相等C. 同旁内角可能相等D.同旁内角互补,两直线平行4、 5、如图5,如果/ 3=/7,那么,理由是 如果/ 5=/ 3,那么 ,理由是 如果/ 2+ /5=那么a // b,理由是6、如图4,若/ 2=/6,则,如果/3+/4+/ 5+/ 6=180 ,那么(4)C.AB // DCD.AD9、已知直线a、b被直线c所截,且/1+/ 2= 试判断直线a、b的位置关系,并说明理由.10、如图,已知AEM DG , 1 2 ,试问EF是否平行GH并说明理由.11、如图所示,已知/ 1=/ 2,AC平分/ DAB试说明DCI AB.12、如图所示,已知直线EF和AB,CM别相交于K,H,且EGL AB,/CHF=60 / E=30°试说明AB// CD.13、提高训练:如图所示,已知直线a,b,c,d,e,且/ 1=/ 2, / 3+/4=180° ,则a与c平行吗?劝什么?5.3.1平行线的性质复习检测(10分钟):1、如图1所示,AB//CD则与/ 1相等的角(/1除外)共有()A.5 个B.4 个C.3 个D.2 个 B AA B —(4) (5) (6)5、如图5,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是南偏西(3)2、如图 2 所示,CD// AB,O 评分/ AOD,OFOE,/D=50,则/BOF 为(A.35B.30C.253、如图 3 所示,AB II CD,Z D=80CAD=, /ACD=?.4、如图 4,若 AD// BC,则/=/ D.20/ABC 廿=180 ;若 DC/ZAB,则/=/A,/ CAD:/ BAC=3:2则/56° ,甲、乙两地同时开工,若干天后公路准确接通,则乙地所修公路的走向是,因为.6、河南)如图6所示,已知AB// CD直线EF分别交AB,CD于E,F,EG?平分/ B-EF,若/ 1=72 ,贝U/2=.7、如图,AB/ZCQ / 1 = 102° ,求/ 2、/3、/4、/ 5的度数,并说明根据?8、如图,ERiz\ABC勺一个顶点A,且EF// BC 如果/ B= 40° , / 2= 75° ,那么/1、/3、/G / BAO /B+ 是多少度,并说明依据?9、如图,已知:DE/ZCB,/1 = /2,求证:CD平分/ ECB.10、如图所示,把一张长方形纸片ABCD& EF折叠,若/ EFG=50 ,求/ DEG勺度数.1111、如图所示,已知:AE平分/BAC CE平分/ACD且AB//CD求证:/1+/ 2=90° . 证明:・•. AB//CD (已知)・♦/BAC/ACD180 , ()又.. AE平分/ BAC C评分/ ACD (). 1 1•• 1 - BAC , 2 万ACD,( ___________________ ) __________1 1 0 0. .1 2 -( BAC ACD) —1800 90°.2 2即Z1+Z 2=90 .结论:若两条平行线被第三条直线所截,则一组同旁内角的平分线互相.推广:若两条平行线被第三条直线所截,则一组同位角的平分线互相^5.3.2命题、定理、证明复习检测(5分钟):1、判断下列语句是不是命题(1)延长线段AB( ) (3)画线段AB的中点( (2)两条直线相交,只有一交点((4)若|x|=2 ,则x=2 ( )134、命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有()A.1 个B.2个C.3个D.4个5、分别指出下列各命题的题设和结论(1)如果a// b, b // c,那么all c ⑵ 同旁内角互补,两直线平行 6、分别把下列命题写成“如果……,那么……”的形式 (1)两点确定一条直线; (2)等角的补角相等;(3)内错角相等.7、如图,已知直线a 、b 被直线c 所截,在括号内为下面各小题的推理填上适当的根据(1) '.'all b,「•/ 1=/ 3( ); (2) ・// 1=/ 3, ..・all b( ); (3) '.'all b,「•/ 1=/ 2( );(4) 「a// b,「./ 1+/ 4=180o ( (5) ・// 1=/ 2, ..・all b( ); (6) •// 1+/ 4=180o,「.a// b( ). 8、已知:如图 ABL BG BCLCD 且/ 1=/ 2, 证明:.「AB!BG BCLCD (已知)= =90(5)角平分线是一条射线( 2、下列语句不是命题的是( A.两点之间,线段最短 C.x 与y 的和等于0吗? 3、下列命题中真命题是( )A.两个锐角之和为钝角)B.不平行的两条直线有一个交点 D.对顶角不相等.B.两个锐角之和为锐角D.锐角小于它的余角・ ・•/ 1 = /2 (已知)(等式性质)/ ACB=90 ()・ ••/ BCD^/ ACD 勺余角・ ・•/BCD^/B 的余角(已知) ・•・ / ACDN B ()5.4平移复习检测(5分钟):1、下列哪个图形是由左图平移得到的( )B.沿射线EC 的方向移动C 冰C.沿射线BD 的方向移动BD 长;D.沿射线BD 的方向移动DC 长3、下列四组图形中,?有一组中的两个图形经过平移其中一个能得到 -另一个,这组图形9、已知: 求证: 证明: BE// CF (/ ACDM B・•. ACL BC (已知)2、如图所示,4FDE 经过怎样的平移可得到4A.沿射线EC 的方向移动DB 长; 如图,ACL BCC 垂足为CABC.()4、如图所示,△ DEF经过平移可以得到△ ABC那的对应角和ED的对应边分-别是()A. / F,ACB. / BOD,BA;C. / F,BAD.5、在平移过程中,对应线段()A.互相平行且相等;B.互相垂直且相等C.互相平行(或在同一条直线上)且相等6、在平移过程中,平移后的图形与原来的图形________ 都相同,?因-此对应线段和对应角7、如图所示,平移△ ABC可得到△ DEF,如果// C=60 ,那么/ E=?-度,/ EDF=/F= ______ 度,/DOB= .........8、将正方形ABCDg对角线AC方向平移,且平移后的图形的一个顶点恰好在AC的中点。
春七年级数学下册 第10章 相交线、平行线和平移 10.1 相交线 第1课时 对顶角及其性质课时作业

第10章相交线、平行线与平移10.1相交线第1课时对顶角及其性质知识要点基础练知识点1对顶角的概念1.如图,∠1和∠2是对顶角的是(B)2.如图,在所标识的角中,互为对顶角的两个角是(A)A.∠2和∠3B.∠1和∠3C.∠1和∠4D.∠1和∠2知识点2对顶角的性质3.直线AB,CD相交于点O,OE平分∠BOC.已知∠BOE=65°,则∠AOD的度数是(D)A.32.5°B.65°C.110°D.130°4.如图,已知直线AB,CD,EF相交于点O,∠1=95°,∠2=32°,则∠BOE=53°.5.直线AB,CD,EF相交于点O,如图.(1)写出∠AOD,∠EOC的对顶角;(2)已知∠AOC=50°,求∠BOD的度数;(3)若∠BOD+∠COF=140°,求∠BOE的度数.解:(1)∠AOD的对顶角是∠BOC,∠EOC的对顶角是∠DOF.(2)∠BOD=50°.(3)因为∠BOE=∠EOD+∠BOD,∠EOD=∠COF,所以∠BOE=∠BOD+∠COF=140°.综合能力提升练6.如图,当光线从空气射入水中,光线的传播发生了改变,这就是折射现象.∠1的对顶角是(A)A.∠AOBB.∠BOCC.∠AOCD.都不是7.下列说法:①两条直线相交,有公共顶点的角是对顶角;②对顶角相等;③相等的两个角是对顶角;④两个角互为对顶角,这两个角度数之和不会超过180°.其中正确的有(A) A.1个 B.2个 C.3个 D.4个8.如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠BOE=4∶1,则∠AOF 等于(B) A.130° B.120° C.110° D.100°9.如图,直线AB,CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=28°,则∠EOF的度数为62°.10.如图,有两堵墙,要测量地面上形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外.如何测量?并说明理由.解:延长AO,BO分别至点C,点D,测量∠COD的度数即可.理由:对顶角相等.11.如图,直线AB与CD相交于点O,OD恰为∠BOE的平分线.(1)请直接写出和∠AOD互补的角;(把符合条件的角都写出来)(2)若∠AOD=142°,求∠AOE的度数.解:(1)∠AOC,∠BOD,∠EOD.(2)由(1)知∠DOE=∠BOD=180°-∠AOD=38°,∴∠AOE=∠AOD-∠DOE=104°.12.如图,直线AB,CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE∶∠EOC=2∶3.(1)求∠AOE的度数;(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.解:(1)∠AOE=30°.(2)OB是∠DOF的平分线.理由:∵∠AOE=30°,∴∠BOE=180°-∠AOE=150°,∵OF平分∠BOE,∴∠BOF=75°,又∵∠BOD=75°,∴∠BOD=∠BOF,∴OB是∠DOF的平分线.13.如图,已知直线AB与CD交于点O,OE平分∠BOD,OF平分∠AOB.(1)若∠BOE=40°,求∠AOF与∠COF的度数;(2)若∠BOE=x(x<45°),请用含x的代数式表示∠COF的度数.解:(1)∵OE平分∠BOD,∠BOE=40°,∴∠BOD=80°,∴∠BOC=100°.∵OF平分∠AOB,∴∠AOF=∠BOF=90°,∴∠COF=100°-90°=10°.(2)∠COF=180°-2x-90°=90°-2x.拓展探究突破练14.观察下列图形,寻找对顶角(不含平角).(1)两条直线相交于一点,如图①,共有2对对顶角;(2)三条直线相交于一点,如图②,共有6对对顶角;(3)四条直线相交于一点,如图③,共有12对对顶角;…(4)根据填空结果探究:当n条直线相交于一点时,所构成的对顶角的对数与直线条数之间的关系;(5)根据探究结果,求2019条直线相交于一点时,所构成的对顶角的对数.解:(4)n(n-1).(5)2018×2019=4074342.。
2012-2013人教版数学七年级下册《相交线与平行线》知识复习与练习(基础)

相交线与平行线知识复习及训练【知识复习】1.对顶角:概念(1):两条直线相交形成的四个角中,(填“相邻”或“不相邻”)的两个角叫做对顶角。
如右图中的∠1与∠3。
概念(2):一个角的两边分别是另一角的两边的,这样的两个角叫做对顶角.对顶角的性质是:。
2.邻补角:两条直线相交所构成的四个角中,(填“相邻”或“不相邻”)的两个角叫做邻补角。
如右图中的∠1与∠2。
特点是:这两个角有一条公共边OA,另一条边OC、OD互为。
3.垂线:两条直线相交成直角时,叫做互相,其中一条线叫做另一条线的。
4.垂线的性质:性质1:过一点有且只有(填“一条”或“很多条”)直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,最短。
简称:。
7.平行线:在同一平面内,的两条直线叫做平行线。
8.平行公理:经过一点有且只有(填“一条”或“很多条”)直线与已知直线平行。
9.平行公理的推论:如果两条直线都与平行,那么这两条直线。
10.平行线的判定方法:(如图a)方法1:同位角,两直线平行。
∵∠1=∠3(已知)∴a∥b(同位角,两直线平行)方法2:内错角 ,两直线平行。
∵∠1=∠4(已知)∴a ∥b (内错角 ,两直线平行) 方法3:同旁内角 ,两直线平行。
∵∠1+∠2=180°(已知)∴a ∥b (同旁内角 ,两直线平行)11.平行线的性质:(如图a )方法1:两直线平行,同位角 。
∵a ∥b (已知)∴∠1=∠3(两直线平行,同位角 ) 方法2:两直线平行,内错角 。
∵a ∥b (已知)∴∠1=∠4(两直线平行,内错角 ) 方法3:两直线平行,同旁内角 。
∵a ∥b (已知)∴∠1+∠2=180°(两直线平行,同旁内角 )【基础训练】 一、选择题1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )A .50°B .60°C .140°D .160°2、已知:如图2,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠ 与2∠的关系一定成立的是( ) A .相等B .互余C .互补D .互为对顶角ACDE F2 1 O图2图1a b 1 2O图3图a3、如右图所示,已知BC AC ⊥ ,AB CD ⊥,垂足分别是C 、D ,那么以下线段大小的比较必定成立....的是( ) A. AD CD > B. BC AC < C. BD BC > D. BD CD <4、如图3,小明从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20方向行走至C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )A .右转80°B .左转80°C .右转100°D .左转100° 5、如右图所示,点E 在AC 的延长线上,下列条件中能判断...CD AB //( )A. 43∠=∠B. 21∠=∠C. DCE D ∠=∠D. 180=∠+∠ACD D6、下列语句:①不相交的两条直线叫做平行线。
新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)

新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)第五章相交线与平行线5.1.1相交线教学目标:1.理解对顶角和邻补角的概念,能在图形中辨认.2.掌握对顶角相等的性质和它的推证过程.3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.重点:在较复杂的图形中准确辨认对顶角和邻补角.难点:在较复杂的图形中准确辨认对顶角和邻补角.教学过程一、创设情境,引入课题先请同学观察本章的章前图,然后引导学生观察,并回答问题.学生活动:口答哪些道路是交错的,哪些道路是平行的.教师导入:图中的道路是有宽度的,是有限长的,而且也不是完全直的,当我们把它们看成直线时,这些直线有些是相交线,有些是平行线.相交线、平行线都有许多重要性质,并且在生产和生活中有广泛应用.所以研究这些问题对今后的工作和学习都是有用的,也将为后面的学习做些准备.我们先研究直线相交的问题,引入本节课题.二、探究新知,讲授新课1.对顶角和邻补角的概念学生活动:观察上图,同桌讨论,教师统一学生观点并板书.【板书】∠1与∠3是直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角.学生活动:让学生找一找上图中还有没有对顶角,如果有,是哪两个角?学生口答:∠2和∠4再也是对顶角.紧扣对顶角定义强调以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边.符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行.(2)对顶角是成对存在的,它们互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.2.对顶角的性质提出问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?学生活动:学生以小组为单位展开讨论,选代表发言,井口答为什么.【板书】∵∠1与∠2互补,∠3与∠2互补(邻补角定义),∴∠l=∠3(同角的补角相等).注意:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而填邻补角定义.或写成:∵∠1=180°-∠2,∠3=180°-∠2(邻补角定义),∴∠1=∠3(等量代换).学生活动:例题比较简单,教师不做任何提示,让学生在练习本上独立完成解题过程,请一个学生板演。
【初中数学】相交线(1)邻补角与对顶角讲练课件 2023—2024学年人教版数学七年级下册

4. 如图,直线AB与CD相交于点O,若∠1+∠2=140°, 则∠1=_7_0__°,∠4=_1_1_0__°.
利用邻补角与对顶角的性质求角度 5. 如图,直线AB,CD相交于点O,∠BOD=40°,
OA平分∠COE,求∠DOE的度数. 解:∵∠BOD=40°,
∴∠AOC=∠BOD=40°, ∵OA平分∠COE, ∴∠COE=2∠AOC=80°,
同学们,再见!
பைடு நூலகம்
∴∠DOE=180°-∠COE=100°.
6. (2023·湛江霞山区一模)如图,直线AB,CD相交于点 O,OE是∠AOD的平分线,∠AOC=26°,求∠AOE 的度数.
解:∵∠AOC=26°, ∴∠AOD=180°-∠AOC=154°. 又∵OE是∠AOD的平分线, ∴∠AOE= 12∠AOD=77°.
新人教版初中七年级数学下学期
第五章 相交线与平行线
第1课 相交线(1) 邻补角与对顶角
邻补角与对顶角的定义及性质
定义
图例 性质 几何语言
邻 有一条公共边,另一 补 边互为反向延长线的 角 两个角
∵∠1与∠2 邻补角 是邻补角, 互__补___ ∴∠__1_+__∠__2__
=__1_8_0_°______
对 有公共顶点,一角的 顶 两边与另一角的两边 角 互为反向延长线
对顶角 _相__等__
∵∠1与∠2 是对顶角, ∴∠__1_=__∠__2__
1. 下列图形中,∠1与∠2互为邻补角的是
( D)
2. (2023·东莞月考)下列四个图形中,∠1与∠2是对顶角
的是
( B)
3. 如图,直线a,b相交于点O. (1)∠1的对顶角是_∠__3_,∠1的邻补角是_∠__2_,__∠__4___; (2)(2023·东莞月考)∠2=140°,则∠1=___4_0_°_,∠3 =__4_0_°__.
人教版七年级数学下册练习题

人教版七年级数学下册练习题七年级数学第五章《相交线与平行线》班级:_______ 姓名:_________ 座号:_______ 成绩:_______一、选择题(每小题3分,共30分)1、如图所示,∠1和∠2是对顶角的是()A、12.B、12.C、12.D、122、如图AB∥CD可以得到()A、∠1=∠2.B、∠2=∠3.C、∠1=∠4.D、∠3=∠43、直线AB、CD、EF相交于O,则∠1+∠2+∠3=()A、90°。
B、120°。
C、180°。
D、140°4、如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6.②∠2=∠8.③∠1+∠4=180°。
④∠3=∠8其中能判断a∥b的条件的序号是()A、①②。
B、①③。
C、①④。
D、③④5、某角的补角是60°,则这个角的度数是()A、30°。
B、60°。
C、120°。
D、150°6、下列哪个图形是由左图平移得到的()A、D。
B、D。
C、D。
D、D7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD面积的比是()A、3:4.B、5:8.C、9:16.D、1:28、下列现象属于平移的是()①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走A、③。
B、②③。
C、①②④。
D、①②⑤9、下列说法正确的是()A、有且只有一条直线与已知直线平行B、垂直于同一条直线的两条直线互相垂直C、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
D、在平面内过一点有且只有一条直线与已知直线垂直。
10、直线AB∥CD,∠B=23°,∠D=42°,则∠E=()A、23°。
B、42°。
C、65°。
D、19°二、填空题(本大题共6小题,每小题3分,共18分)11、直线AB、CD相交于点O,若∠AOC=100°,则∠AOD=___________。
人教版七年级数学下册训练单(10-20分钟)(少一章)
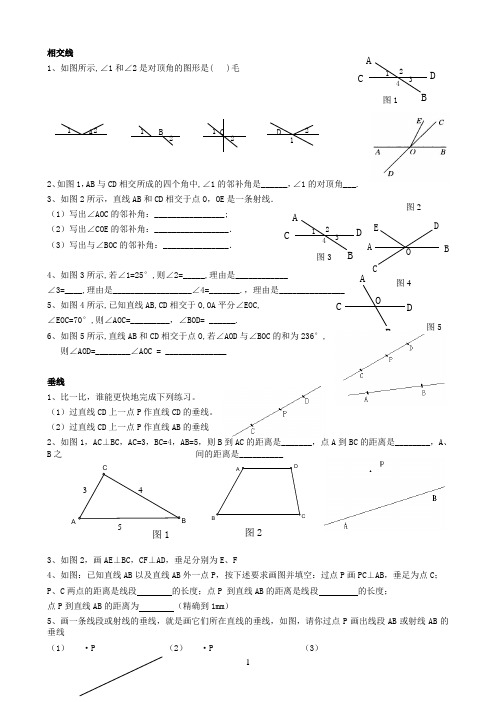
ODCBA34DCBA1234DCBA12相交线1、如图所示,∠1和∠2是对顶角的图形是( )毛121212212、如图1,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.3、如图2所示,直线AB和CD相交于点O,OE是一条射线.(1)写出∠AOC的邻补角:________________;(2)写出∠COE的邻补角:_________________.(3)写出与∠BOC的邻补角:_______________.4、如图3所示,若∠1=25°,则∠2=_____,理由是____________∠3=____,理由是__________________∠4=_______.,理由是_______________5、如图4所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠AOC=_________,∠BOD=•______.6、如图5所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOD=________∠AOC•= ______________垂线1、比一比,谁能更快地完成下列练习。
(1)过直线CD上一点P作直线CD的垂线。
(2)过直线CD上一点P作直线AB的垂线2、如图1,AC⊥BC,AC=3,BC=4,AB=5,则B到AC的距离是_______,点A到BC的距离是________,A、B之间的距离是__________3、如图2,画AE⊥BC,CF⊥AD,垂足分别为E、F4、如图:已知直线AB以及直线AB外一点P,按下述要求画图并填空:过点P画PC⊥AB,垂足为点C;P、C两点的距离是线段的长度;点P 到直线AB的距离是线段的长度;点P到直线AB的距离为(精确到1mm)5、画一条线段或射线的垂线,就是画它们所在直线的垂线,如图,请你过点P画出线段AB或射线AB的垂线OE DCBA图4图2A5图1A B C D图1图3图5图2相交线中的角1、如图,图中同位角有_____对,分别是 ,内错角有_____对,分别是 ,同旁内角有_____对,分别是_______________2、如图,与∠1是同位角的是_______________; 与∠2是内错角的是;与∠1是同旁内角的是__________________; 与∠2互为补角的是 ; ∠2的对顶角是 。
人教版数学七年级下册《5.1相交线》基础训练(含答案)

人教版数学七年级下册5.1相交线基础训练一、选择题1.邻补角是( D )A.和为180°的两个角B.有公共顶点且互补的两个角C.有一条公共边且互补的两个角D.有一条公共边,另一边互为反向延长线的两个角2.下列四个图形中,∠1和∠2互为对顶角的是( C )3.如图,OA⊥OB,若∠1=35°,则∠2的度数为( C )A.35 °B.45°C.55°D.70°4.如图,已知OA⊥OC,OB⊥OD, ∠BOC=50°,则∠AOD的度数为( C )A.100°B.120°C.130°D.140°5.如图,直线a,b被直线c所截,那么∠1的同位角是( C )A.∠2B.∠3C.∠4D.∠56.如图,内错角是( B )A.∠1和∠2B.∠3和∠4C.∠2和∠3D.∠1和∠47.如图所示,直线45,CD相交于点0,已知∠AOD= 160°,则∠B0C的大小为( D )A.20°B.60°C.70°D.160°8.下列各图中,过直线l外的点P画l的垂线CD,三角尺操作正确的是( D )9.下列图形中,∠1和∠2是同旁内角的是( A )10.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( B )A.∠4,∠2B.∠2,∠6C.∠5,∠4D.∠2,∠411.下列说法正确的有( B )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角一定不相等.A.1个B.2个C.3个D.4个12.如图,经过直线l外一点A画l的垂线,能画出( A )A.1条B.2条C.3条D.4条13.下列图形中,∠1与∠2是同位角的共有( A )A.1个B.2.个C.3个D.4个14.下列各图中,∠1与∠2互为邻补角的是( D )15.如图,点O为直线AB上一点,CO⊥AB于点O, OD在∠COB内,若∠COD=50°,则∠AOD的度数是( D )A.100°B.110°C.120°D.140°二、填空题16.如图,已知直线AB,CD,EF相交于点O.(1)∠AOD的对顶角是,∠EOC的对顶角是 ;(2)∠AOC的邻补角是,∠EOB的邻补角是 .答案:(1) ∠BOC ∠DOF;(2)∠AOD和∠BOC ∠AOE和∠BOF17.如图,直线AB,CD相交于点O, EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为______.答案:140°18.如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是 .答案:内错角19.如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE= 70°,则∠BOD= .答案:55°20.如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.解:∵OA⊥OB(已知)所以 =90°( )因为 =∠AOD-∠AOC, =∠BOC-∠AOC,∠AOD=∠BOC,所以 = (等量代换)所以 =90°所以OC⊥OD.答案:∠AOB 垂直的定义∠COD ∠AOB ∠COD ∠AOB∠COD21.(1)如图,直线AB,CD被DE所截,则∠1和是同位角,∠1和是内错角,∠1和是同旁内角;(2)在(1)中,如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由:因为∠5=∠1( ),∠5=∠3( ),所以∠1=∠3( ).答案:(1)∠3 ∠5 ∠2; (2)已知对顶角相等等量代换三、解答题22.如图,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.解析:因为∠2=65°,所以∠1=∠2=65°,又∠1=2∠3,所以∠3=32.5°,所以∠4=∠3=32.5°.23.根据下列要求画图.(1)如图1,过点P画AB的垂线;(2)如图2,过点P画OA,OB的垂线;(3)如图3,过点A画BC的垂线.答案:(1)如图1所示.(2)如图2所示.(3)如图3所示.24.如图,BE是AB的延长线,下面各组角是哪两条直线被哪一条直线所截而成的?它们各是什么位置关系的角?(1)∠A 与∠D;(2)∠A 与∠CBE;(3)∠C与∠CBE.答案:(1)∠A与∠D与是直线AB和直线CD被直线AD所截而成的同旁内角.(2)∠A与∠CBE是直线AD和直线BC被直线AE所截而成的同位角.(3)∠C与∠CBE是直线AE和直线CD被直线BC所截而成的内错角.。
人教版七年级数学下册第五章相交线与平行线复习训练题
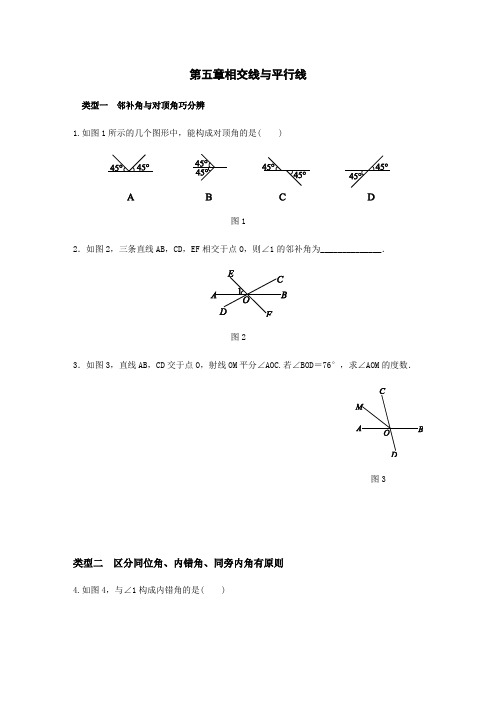
第五章相交线与平行线类型一邻补角与对顶角巧分辨1.如图1所示的几个图形中,能构成对顶角的是( )图12.如图2,三条直线AB,CD,EF相交于点O,则∠1的邻补角为______________.图23.如图3,直线AB,CD交于点O,射线OM平分∠AOC.若∠BOD=76°,求∠AOM的度数.图3类型二区分同位角、内错角、同旁内角有原则4.如图4,与∠1构成内错角的是( )图4A.∠2 B.∠3 C.∠4 D.∠55.如图5,直线DE经过点C,则∠A的内错角是________,∠A的同旁内角是________________.图56.如图6,E是AB延长线上一点,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?(1)∠A和∠D;(2)∠A和∠CBA;(3)∠C和∠CBE.图6类型三掌握相交的特殊情形——垂直7.如图7,已知AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=30°,则∠BOE等于( )图7A .30°B .60°C .120°D .130°8.如图8所示,在直角三角形ABC 中,∠ACB=90°,CD⊥AB 于点D ,则点A 到BC 的距离为线段______的长度;点A到CD 的距离为线段______的长度;点C 到AB 的距离为线段______的长度.图8类型四 平行线的判定和性质9.如图9,直线a ,b 被直线c 所截,下列说法正确的是( )A .当∠1=∠2时,一定有a∥bB .当a∥b 时,一定有∠1=∠2C .当a∥b 时,一定有∠1+∠2=90°D .当∠1+∠2=180°时,一定有a∥b10.如图10,已知AB∥CD,∠1=60°,则∠2=________°.图9图1011.如图11,不添加辅助线,请你写出一个能判定EB∥AC的条件:________________________.图1112.如图12,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,求∠2的度数.图1213.如图13,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,并说明理由.图1314.如图14所示,已知OP∥QR∥ST,连接PR,SR,猜想∠1,∠2,∠3三个角之间的关系,并说明理由.图14类型五命题与定理须细辨15.下列语句不是命题的是( )A.若a<0,b<0,则ab>0B.用三角板画一个60°的角C.对顶角相等D.互为相反数的两个数的和为016.下列命题中,是真命题的是( )A.对顶角相等B.同位角相等C.若a2=b2,则a=bD.若a>b,则-2a>-2b17.将下列命题改写成“如果……那么……”的形式.(1)直角都相等;(2)末位数字是5的整数能被5整除;(3)三角形的内角和是180°.类型六平移平移的特征:图形的平移变换中,图形的形状、大小、方向都不发生改变,只是改变了图形的位置;平移前后图形的对应点的连线平行(或在同一条直线上)且相等.18.下列现象中,不属于平移的是( )A.钟表的指针转动B.电梯的升降C.火车在笔直的铁轨上行驶D.传送带上物品的运动19.如图15,将周长为8的三角形ABC沿BC方向向右平移1个单位长度得到三角形DEF,则四边形ABFD的周长为( )图15A.6 B.8 C.10 D.12类型七方程思想在几何中的应用20.如图16,已知a∥b,∠1=(3x+70)°,∠2=(5x+22)°,求∠1的补角的度数.图16类型八开放型问题21.给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并说明理由.已知:如图17,________________________.结论:________________________.图17类型九探究型问题22.【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:如图18①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.理由如下:过点P作PQ∥AB.∴∠BAP+∠APQ=180°.∵AB∥CD,PQ∥AB,∴PQ∥CD,∴∠PCD+∠CPQ=180°.∴∠BAP+∠APC+∠PCD=∠BAP+∠APQ+∠CPQ+∠PCD=180°+180°=360°.【问题解决】(1)如图②,AB∥CD,点P在AB与CD之间,可得∠BAP,∠APC,∠PCD间的等量关系是________________________________________________________________________;(2)如图③,AB∥CD,点P ,E 在AB 与CD 之间,AE 平分∠BAP,CE 平分∠DCP,写出∠AEC 与∠APC 间的等量关系,并写出理由;(3)如图④,AB∥CD,点P ,E 在AB 与CD 之间,∠BAE=13∠BAP,∠DCE=13∠DCP ,可得∠AEC与∠APC 间的等量关系是________________________.图18答案1.D2.∠BOE 和∠AOF 3.解:∵∠BOD=76°, ∴∠AOC=∠BOD=76°. ∵射线OM 平分∠AOC,∴∠AOM=12∠AOC=12×76°=38°.4.B5.∠ACD ∠ACB,∠ACE 和∠B6.解:(1)∠A 和∠D 是直线AE ,DC 被直线AD 所截而成的同旁内角. (2)∠A 和∠CBA 是直线AD ,BC 被直线AE 所截而成的同旁内角. (3)∠C 和∠CBE 是直线DC ,AE 被直线BC 所截而成的内错角. 7.C 8.AC AD CD 9.D 10.12011.答案不唯一,如∠C=∠EBD 12.解:∵AB∥CD,∴∠2=∠BEG,∠BEF+∠1=180°. ∵∠1=50°,∴∠BEF=130°. ∵EG 平分∠BEF,∴∠BEG=12∠BEF=65°, ∴∠2=65°.13.解:∠ACB=∠DEB.理由:∵∠1+∠2=180°,∠1+∠DFE=180°,∴∠2=∠DFE,∴AB∥EF,∴∠DEF=∠BDE.∵∠DEF=∠A,∴∠A=∠BDE,∴AC∥DE,∴∠ACB=∠DEB.14.解:∠2+∠3=180°+∠1.理由:∵OP∥QR,∴∠2+∠QRP=180°,∴∠QRP=180°-∠2.∵QR∥ST,∴∠3=∠QRS=∠1+∠QRP=∠1+180°-∠2.∴∠2+∠3=180°+∠1.15.B16. A17.解:(1)如果几个角是直角,那么它们都相等.(2)如果一个整数的末位数字是5,那么它能被5整除.(3)如果一个图形是三角形,那么它的内角和是180°.18.A19. C20.解:如图,因为a∥b,所以∠1=∠3.又因为∠1=(3x+70)°,∠2=(5x+22)°,∠2+∠3=180˚,所以(3x +70)°+(5x+22)°=180°,解得x=11,所以∠1=(3x+70)°=103°.又因为180°-103°=77°,所以∠1的补角的度数为77°.21.解:答案不唯一,符合题意的情况有3种,即①②→③;①③→②;②③→①,任选其中一种即可.已知:如图17,∠B+∠D=180°,AB∥CD.结论:BC∥DE.理由:因为AB∥CD,所以∠B=∠C(两直线平行,内错角相等).又因为∠B+∠D=180°,所以∠C+∠D=180°,所以BC∥DE(同旁内角互补,两直线平行).22.解:(1)如图②,作PE∥AB,得∠APE=∠BAP.∵AB∥CD,AB∥PE,∴CD∥PE,∴∠CPE=∠PCD,∴∠APC=∠APE+∠CPE=∠BAP+∠PCD.故答案为∠APC=∠BAP+∠PCD.(2)∠APC=2∠AE C.理由:设∠EAB=∠EAP=x,∠ECD=∠ECP=y.由(1)可知:∠AEC=x+y,∠APC=2x+2y,∴∠APC=2∠AE C.(3)设∠EAB=a,∠DCE=b,则∠BAP=3a,∠DCP=3b. 由题意得∠AEC=a+b,∠APC+3a+3b=360°,∴∠APC+3∠AEC=360°.故答案为∠APC+3∠AEC=360°.。
初中数学同步训练必刷题(人教版七年级下册5

初中数学同步训练必刷题(人教版七年级下册5.1.1 相交线)一、单选题1.(2022七下·承德期末)下列四个图形中,∠1与∠2是对顶角的是()A.B.C.D.【答案】C【知识点】对顶角及其性质【解析】【解答】解:对顶角指的是有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,所以:A、两角没有公共顶点,不符合题意;B、两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;C、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;D、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;故答案为:C.【分析】有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角是对顶角,据此逐一判断即可.2.(2022七上·南海期中)直线AB和直线CD相交于点O,若∠AOC=40°,则∠BOC等于()A.140°B.60°C.40°D.160°【答案】A【知识点】邻补角【解析】【解答】解:∵∠AOC=40°,∴∠BOC=180°-∠AOC=180°-40°=140°, 故答案为:A .【分析】利用邻补角求出∠BOC 的度数即可。
3.(2022七下·崇川期末)如图,直线AB 与CD 相交于点O ,∠AOC :∠AOD =2:3,则∠BOD 等于( )A .36°B .72°C .60°D .75°(【答案】B【知识点】对顶角及其性质;邻补角【解析】【解答】解:∵∠AOC :∠AOD =2:3, ∴∠AOD =32∠AOC ,又∵∠AOC +AOD =180°,∴∠AOC +32∠AOC =180°,解得∠AOC =72°,∴∠BOD =∠AOC =72°(对顶角相等). 故答案为:B .【分析】根据角的比例关系得出∠AOD =32∠AOC ,结合∠AOC +AOD =180°,联立求出∠AOC 的度数,再根据对顶角的性质求出∠BOD 度数即可.4.(2022九上·南宁开学考)如图,直线AB ,CD 相交于点O ,OA 平分∠EOC ,∠EOC =110°,则∠BOC的度数是( )A .115°B .125°C .135°D .145°【答案】B【知识点】邻补角;角平分线的定义【解析】【解答】解:∵直线AB ,CD 相交于点O ,∠EOC =110°,∴∠DOE =180°﹣∠EOC =70°, 又∵OA 平分∠EOC ,∴∠AOE =12∠EOC =55°,∴∠BOC =∠AOD =∠AOE+∠DOE =55°+70°=125°. 故答案为:B .【分析】由邻补角定义求得∠DOE 的度数,由角平分线定义可得AOE=12∠EOC ,则∠BOC=∠AOD=∠AOE+∠DOE 可求解.5.(2022七下·承德期末)如图,小明手持手电筒照向地面,手电筒发出的光线CO 与地面AB 形成了两个角,∠BOC =8∠AOC ,则∠BOC 的度数是( )A .160°B .150°C .120°D .20°【答案】A【知识点】角的运算;邻补角【解析】【解答】解:∵∠AOC +∠BOC =180°,∠BOC =8∠AOC ,∴9∠AOC =180°, ∴∠AOC =20°,∴∠BOC =8×20=160°, 故答案为:A .【分析】由邻补角的定义可得∠AOC +∠BOC =180°,结合∠BOC =8∠AOC 即可求解.6.(2022七下·延庆期末)如图,直线AB,CD相交于点O,如果∠1=35°,那么∠2的度数是()A.35°B.55°C.145°D.165°【答案】A【知识点】对顶角及其性质【解析】【解答】解:由对顶角的性质可得:∠1=∠2,∵∠1=35°,∴∠2=35°,故答案为:A.【分析】根据对顶角相等解答即可.7.(2022七下·钦州期末)如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD =2:3,则∠BOD的度数为()A.40°B.37°C.36°D.35°【答案】C【知识点】对顶角及其性质;邻补角;角平分线的定义【解析】【解答】解:∵∠EOC∶∠EOD=2∶3,∠EOC+∠EOD=180°,∴∠EOC+32∠EOC=180°,∴∠EOC=72°,∵OA平分∠EOC,∴∠AOC=12∠EOC=12×72°=36°,∴∠BOD=∠AOC=36°.故答案为:C.【分析】根据邻补角的性质可得∠EOC+∠EOD=180°,结合已知条件可得∠EOC 的度数,由角平分线的概念可得∠AOC=12∠EOC ,由对顶角的性质可得∠BOD=∠AOC ,据此解答.8.(2022七下·东明期末)如图,直线AB 、CD 相交于点O ,且∠AOC +∠BOD =110°,则∠AOD 的度数为( )A .125°B .120°C .110°D .100°【答案】A【知识点】对顶角及其性质;邻补角【解析】【解答】解:∵∠AOC +∠BOD =110°,∠AOC =∠BOD ,∴∠AOC =∠BOD =55°, ∵∠AOC +∠AOD =180°,∴∠AOD =180°−∠AOC =180°−55°=125°.故答案为:A .【分析】由对顶角相等及∠AOC +∠BOD =110°,可得∠AOC =∠BOD =55°,然后根据邻补角的定义即可求解.9.(2022七下·青县期末)如图,直线AB 、CD 相交于点O ,下列描述一定正确的是( )A .∠1和∠2互为对顶角B .∠1和∠3互为邻补角C .∠1=∠2D .∠1=∠3【答案】D【知识点】对顶角及其性质;邻补角【解析】【解答】解:∵直线AB 、CD 相交于点O ,∴∠1和∠3互为对顶角;故A 、B 不符合题意;∴∠1=∠3;故D 符合题意; ∵∠1+∠2=180°,故C 不符合题意; 故答案为:D .【分析】根据对顶角的定义及性质、邻补角的定义进行判断即可.10.(2022七下·江油期中)如图,直线AB 、CD 相交于O ,OA 平分∠EOC ,若∠EOC =70°,那么∠BOD的度数是( )A .30°B .35°C .45°D .40°【答案】B【知识点】对顶角及其性质;角平分线的定义【解析】【解答】解∠∵OA 平分∠EOC ,∠EOC =70°, ∴∠AOC=12∠EOC=35°,∴∠BOD=∠AOC=35°, 故答案为:B .【分析】利用角平分线的定义求出∠AOC 的度数,再利用对顶角相等,可得到∠BOD 的度数.二、填空题11.(2022七下·五常期末)若∠1和∠2是对顶角,∠1=36°,则∠2的度数是 度. 【答案】36【知识点】对顶角及其性质【解析】【解答】解:∵∠1和∠2是对顶角,且∠1=36°,∴∠2=∠1=36°, 故答案为:36.【分析】根据对顶角的定义计算求解即可。
新人教版七年级下册数学(全册)同步练习随堂练习一课一练

新人教版七年级下册数学全册同步练习(课本配套,适合课堂小测、作业布置和知识强化训练)《相交线》同步练习如图,已知AB 是线1. 如图1所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.(1) (2) (3)2.如图1所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图2所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.4.如图3所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD=•______.5.对顶角的性质是______________________.6.如图4所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.(4)34D CBA 12OFED CB A OED CBAODC BA 12E OE DCBA7.如图5所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°, 则∠EOB=______________. 8.如图6所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________.1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2.如图7所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°(7) (8) (9) 3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等. A.1个 B.2个 C.3个 D.4个4.如图8所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( ) A.62° B.118° C.72° D.59°5.如图9所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30 C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°12121221OFE D CB A O DCBA 60︒30︒34l 3l 2l 1121. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.2. 如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.3. 如图所示,AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的 度数.4. 如图所示,直线AB 与CD 相交于点O,∠AOC:∠AOD=2:3,求∠BOD 的度数.OF EDCBA 1234l 3l 2l 112OE DCBA5. 如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.答案和解析一、填一填 1、 ∠2和∠4 ∠32、155° 25° 155°3、∠BOC ∠AOD 和∠COB 50° 130°4、 35°5、对顶角相等1,46、125° 55°ODCBAcba34127、147.5° 8、42° 二、选择 1、A 2、B 3、B 4、A 5、D 三、解答题1、∠2=60°2、∠4=36°3、∠BOD=120°,∠AOE=30°4、∠BOD=72°5、∠4=32.5°《垂线》同步练习如图,已知AB 是线1.如图所示,直线AB 与直线CD 的位置关系是_______,记作_______,此时,•∠AOD=∠_____=∠______=∠______=90°.2.过一点有且只有________直线与已知直线垂直.3.画一条线段或射线的垂线,就是画它们________的垂线.O DCBA4.直线外一点到这条直线的_________,叫做点到直线的距离.1.如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段(1) (2)2.如图1所示,能表示点到直线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条3.下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线; ②在平面内,过直线外一点有且只有一条直线垂直于已知直线; ③在平面内,过一点可以任意画一条直线垂直于已知直线; ④在平面内,有且只有一条直线垂直于已知直线. A.1个 B.2个 C.3个 D.4个4.如图2所示,AD ⊥BD,BC ⊥CD,AB=acm,BC=bcm,则BD 的范围是( ) A.大于acm B.小于bcmC.大于acm 或小于bcmD.大于bcm 且小于acm 5.到直线L 的距离等于2cm 的点有( ) A.0个 B.1个 C.无数个 D.无法确定6.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到 直线m 的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cmDCBADCBA1如图所示,直线AB,CD,EF 交于点O,OG 平分∠BOF,且CD ⊥EF,∠AOE=70°, 求∠DOG 的度数.2如图所示,村庄A 要从河流L 引水入庄,需修筑一水渠,请你画出修筑水渠的路线图.3.如图6所示,O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线. (1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说明理由.答案和解析一、填一填1、垂直 AB ⊥CD DOB BOC COA2、一条3、所在直线4、 35°5、垂线段的长度 二、选择6、C7、D8、CGOFEDCBA ODC BA9、D10、C11、D三、解答题1、∠DOG=55°2、解:如图3所示.3、解:(1)∵∠AOC+∠BOC=∠AOB=180°,∴13∠BOC+∠BOC=180°,∴43∠BOC=•1 80°,∴∠BOC=135°,∠AOC=45°,又∵OC是∠AOD的平分线,∴∠COD=∠AOC=45°.(2)∵∠AOD=∠AOC+∠COD=90°,∴OD⊥AB.《同位角内错角同旁内角》同步练习如图,已知AB是线1.如图,根据图形填空.(1)∠A和_________ 是同位角;(2)∠B和_________ 是内错角;l(3)∠A和_________ 是同旁内角.2.如图所示,与∠C构成同旁内角的有个.3.如图,与图中的∠1成内错角的角是.4.如图:△ABC中,∠A的同旁内角是.5.如图,直线MN分别交直线AB,CD于E,F,其中,∠AEF的对顶角是∠,∠BEF的同位角是∠____.6.如图:图中的∠1,∠2,∠3,∠4,∠5,∠6,∠7 中同位角有对.1.如图,∠1与∠2是()A.对顶角B.同位角C.内错角D.同旁内角2.如图,已知AB∥CD,与∠1是同位角的角是()A.∠2 B.∠3 C.∠4 D.∠5 3.如图,与∠1是同位角的是()A.∠2 B.∠3 C.∠4 D.∠5 4.如图,下列各语句中,错误的语句是()A.∠ADE与∠B是同位角 B.∠BDE与∠C是同旁内角C.∠BDE与∠AED是内错角D.∠BDE与∠DEC是同旁内角5.如图,在所标识的角中,同位角是()A.∠1和∠2 B.∠1和∠3 C.∠1和∠4 D.∠2和∠36.已知:如图,直线AB、CD被直线EF所截,则∠EMB的同位角是()A.∠AMF B.∠BMF C.∠ENC D.∠END7.如图,若直线MN与△ABC的边AB、AC分别交于E、F,则图中的内错角有()A.2对B.4对C.6对D.8对8.如图,下列说法中错误的是()A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠4是内错角1 如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?2.如图所示,BF、DE相交于点A,BG交BF于点B,交AC于点C.(1)指出ED、BC被BF所截的同位角,内错角,同旁内角;(2)指出ED、BC被AC所截的内错角,同旁内角;(3)指出FB、BC被AC所截的内错角,同旁内角.答案和解析一、填一填1、(1)∠A和∠ECD,∠BCD是同位角;(2)∠B和∠BCE是内错角;(3)∠A和∠ECA,∠BCA是同旁内角;2、33、∠BDC4、∠B和∠C5、∠BEM ∠DFN6、3二、选择12、B13、D14、C15、B16、C17、D18、C19、D三、解答题1解:左图:∠1与∠2是AB与CD被直线BD所截形成的内错角,∠3与∠4是直线AD与直线BC被直线BD所截形成的内错角;右图:∠1与∠2是AB与CD被直线BD所截形成的同旁内角,∠3与∠4是直线AD与直线BC被直线AB所截形成的同位角.2、解:(1)同位角:∠FAE和∠B;内错角:∠B和∠DAB;同旁内角:∠EAB和∠B;(2)内错角:∠EAC和∠BCA,∠DAC和∠ACG;同旁内角:∠EAC和∠ACG,∠DAC和∠BCA;(3)内错角:∠BAC和∠ACG,∠FAC和∠BCA;同旁内角:∠BAC和∠BCA,∠BAC和∠ABC,∠B和∠ACB,∠FAC和∠ACG.《平行线》同步练习如图,已知AB是线1.在同一平面内,不重合的两条直线的位置关系有_______种,分别是________.2.设a,b,c为平面内三条不同直线:(1)若a∥b,c⊥a,则b与c的位置关系是______;(2)若a∥b,b∥c,则a与c的位置关系是______.3.在同一平面内L1与L2没有公共点,则L1______L2.4.在同一平面内L1和L2有一个公共点,则L1与L2______.1.下列说法不正确的是()A.过马路的斑马线是平行线B.100米跑道的跑道线是平行线C.若a∥b,b∥d,则a⊥dD.过直线外一点有且只有一条直线与已知直线平行2.下列说法正确的是()A.同一平面内不相交的两线段必平行B .同一平面内不相交的两射线必平行C .同一平面内不相交的一条线段与一条直线必平行D .同一平面内不相交的两条直线必平行3.如图所示,在这些四边形AB 不平行于CD 的是( )A . ∠1和∠2B .∠1和∠3C .∠1和∠4D .∠2和∠31.在同一平面内三条直线交点有多少个?甲:同一平面三直线相交交点的个数为0个,因为a ∥b ∥c ,如图(1)所示. 乙:同一平面内三条直线交点个数只有1个,因为a ,b ,c 交于同一点O ,如图(2)所示.以上说法谁对谁错?为什么?2.如图所示,在5×5的网格中,AC 是网格中最长的线段,请画出两条线段与AC 平行并且过网格的格点.3.如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?答案和解析一、填一填1、2,相交,平行2、(1)b⊥C (2)a∥c3、∥4、相交二、选择20、C21、D22、D三、解答题1甲,乙说法都不对,各自少了三种情况.a∥b,c与a,b相交如图(1),a,b,•c两两相交如图(2),所以三条直线互不重合,交点有0个或1个或2个或3个,共四种情况.2、如图所示:EF∥AC,PQ∥AC,MN∥AC,且它们都过格点.3、(1)正面:AB∥EF,AE∥MF等等;上面:A′B′∥AB,C′D′∥CD等等;右侧: DD′∥HR,DH∥D′R(2)EF∥A′B′,CC′⊥DH《平行线的判定》同步练习1.已知三条不同的直线a,b,c在同一平面内,下列四个推理:①∵∥,∥,∴⊥;②∵∥,∥,∴∥;③∵⊥,⊥,∴⊥;④∵⊥,⊥,∴∥.其中正确的是.(填写所有正确的序号)2.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是______.3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.4.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.(1)由∠CBE=∠A可以判断______∥______,根据是_________.(2)由∠CBE=∠C可以判断______∥______,根据是_________.1.下列四幅图中都有∠1=∠2,其中能说明AB∥CD的是( ).A B C D2.如图,下列推理错误的是( ).A.∵∠1=∠2,∴∥B.∵∠1=∠4,∴∥C.∵∠2+∠3=180?,∴∥D.∵∠1=∠5,∴∥3.如图,下列条件不能判断AD∥EF的是( ).ED CBAA.∠D=∠EFCB.∠D+∠EFD=180?C.EF ∥BC ,AD ∥BCD.∠A+∠B=180?A . ∠1和∠2B .∠1和∠3C .∠1和∠4D .∠2和∠31.如图, , . 说明:AB ∥CD.2.如图,AD 是一条直线, . .说明:BE ∥CF.3. ①如图,哪两个角相等能判定直线AB ∥CD? ②如果∠1=∠2,能判定哪两条直线平行?③如果∠3=∠4,能判定哪两条直线平行?新课 标 第 一 网答案和解析一、填一填 1、②④ 2、相交 3、互相平行◆ 三、解答题 A BCD E G H123 4 54、(1)AD BC 同位角相等,两直线平行(2)CD AB 内错角相等,两直线平行二、选择23、C24、B25、D三、解答题1、∵∠1=70°∴∠3=∠1=70°∴∠1=∠2=70°∴ AB ∥CD2、∵∠2=115°∴∠BCF=65°∴∠1=∠BCF∴BE ∥CF3、①∠2=∠3 或∠4=∠5或∠1=∠2②AB ∥CD③EF∥ GD《平行线的性质》同步练习如图,已知AB是线1.如图1所示,直线a ∥b ,且a ,b 被c 所截,若∠1=40°,则∠2=______.图1 图2 图32.如图2所示,直线a ∥b ,且a ,b 被c 所截,若∠1=60°,则∠2=_______,•∠3=________.3.如图3所示,若AB ∥CD ,∠DEF=120°,则∠B=_______.4.如图4所示,砌墙师傅用重锤线检验砌的墙体是否与地面垂直,•墙体坚直线用a 表示,重锤线用b 表示,地平线用c 表示,当a ∥b 时,因为b ⊥c ,则a______c ,•这里运用了平行线的性质是_______.图4 图55.如图5所示,一块木板,AB ∥CD ,木工师傅量得∠B=80°,∠C=65°,则∠A=______,∠D=______.1.如图6所示,DE ∥BC ,DF ∥AC ,下列结论正确的个数为( ) ①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFBA.1个 B.2个 C.3个 D.4个图6 图72.如图7,在甲,乙两地之间修一条笔直公路,从甲地测得公路的走向是北偏东50°,甲,乙两地同时开工,若干天后,公路准确接通,则乙地所修公路走向是()A.北偏45° B.南北方向 C.南偏西50° D.以上都不对3.家住湖边的小海,帮爸爸用铁丝用网箱如图8所示,若AB∥CD,AC∥BD,•若∠1=α,则:①∠3=α;②∠2=180°-α;③∠4=α,其中正确的个数有()A.0个 B.1个 C.2个 D.3个4.如图9所示,AM平分∠BAC,AM∥EN,则与∠E•相等的角下列说法不正确的是()A.∠BAM B.∠ABC C.∠NDC D.∠MAC图8 图91.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?2.如图所示,若∠1+∠2=180°,∠3=110°,求∠4.3.(探究题)如图所示,若AB∥CD,且∠1=∠2,试判断AM与CN位置关系,•并说明理由.答案和解析一、填一填1、40°2、60°,120°3、60°4、⊥,两直线平行,同位角相等(同旁内角互补).5、115°,100°二、选择26、D27、C28、C29、B三、解答题1.可以,∵∠AED=60°,EF平分∠AED∴∠FED=30°又∵∠EDB=∠2=30°∴EF∥BD解题规律:证两直线平行,找内错角相等.2.设∠2对顶角为∠5,则∠2=∠5∵∠1+∠2=180°∴∠1+∠5=180°∴AB∥CD,∴∠3=∠4又∵∠3=110°∴∠4=110°解题规律:先判断AB∥CD,再运用平行线的性质定理. 3.因为AB∥CD所以∠EAB=∠ECD又因为∠1=∠2而∠EAM=∠EAB-∠1∠ACN=∠ACD-∠2即∠EAM=∠ACN所以AM∥CN(同位角相等,两直线平行).解题技巧:判断AM∥CN,①可证∠EAM=∠ECN,②证∠MAC+∠ACN=180°,都能达到目的.《命题定理证明》同步练习如图,已知AB是线1、每个命题都由__ __和两部分组成。
人教版七年级下册数学相交线练习题(含答案)
人教版七年级下册数学5.1相交线练习题(含答案)一、单选题1.如图,直线AB⊥CD于点O,直线EF经过点O,若⊥1=25°,则⊥2的度数是()A.25°B.65°C.55°D.64°2.下列图形中,⊥1与⊥2是对顶角的是()A.B.C.D.3.如图,下列各角与⊥A是同位角的是()A.⊥1B.⊥2C.⊥3D.⊥44.如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是()A.6B.8C.10D.4.85.如图,直线AB、CD相交于点O,下列描述:①⊥1和⊥2互为对顶角;②⊥1和⊥2互为邻补角;③⊥1=⊥2,④∠1=∠3,其中正确的是()A .①③B .②④C .②③D .①④6.如图,要把河中的水引到村庄A ,小凡先作AB ⊥CD ,垂足为点B ,然后沿AB 开挖水渠,就能使所开挖的水渠最短,其依据是( )A .两点确定一条直线B .两点之间线段最短C .在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D .连结直线外一点与直线上各点的所有线段中,垂线段最短7.如图,射线OC 的端点O 在直线AB 上,设⊥1的度数为x ,⊥2的度数为y ,且x 比y 的2倍多10°,则列出的方程组正确的是( )A .{x +y =180x =y +10B .{x +y =180x =2y +10C .{x +y =180x =10−2yD .{x +y =90y =2x −108.如图,若⊥1+⊥2=220°,则⊥3的度数为( )A .70°B .60°C .65°D .50°9.如图,直线 AB 、直线 CD 交于点 E , EF ⊥AB ,则 ∠CEF 与 ∠BED 的关系是( )A .互余B .相等C .对顶角D .互补10.如图所示,下列判断正确的是( )A.图(1)中∠1和∠2是一组对顶角B.图(2)中∠1和∠2是一组对顶角C.图(4)中∠1和∠2互为邻补角D.图(3)中∠1和∠2是一对邻补角11.如图,直线a,b被c所截,则∠1与∠2是()A.同位角B.内错角C.同旁内角D.邻补角12.两直线被第三条直线所截,⊥1与⊥2是同旁内角,且⊥1=30° ,则⊥2的度数为()A.150°B.30°C.30° 或150°D.无法确定二、填空题13.如果⊥A=135°,那么⊥A的邻补角的度数为°.14.如图,直线AB与CD相交于点O,过点O作OE⊥AB,若⊥EOC=55°,则⊥AOD=°.15.如图,直线AB,CD,EF相交于点O,若∠AOE:∠COE=1:2,AB⊥CD,则∠COF=度.16.如图,已知直线AB、CD相交于点O,EO⊥AB,若∠1=32°,则∠2=,∠4=.17.如图,在公园绿化时,需要把管道l中的水引到A,B两处.工人师傅设计了一种又快又节省材料的方案如下:画法:如图,⊥连接AB;⊥过点A画线段AC⊥直线l于点C,所以线段AB和线段AC即为所求.请回答:工人师傅的画图依据是.18.如图,已知直线AB和CD相交于点O,射线OE在∠COB内部,OE⊥OC,OF平分∠AOE,若∠BOD=40∘,则∠COF=度.19.如图,点A,B,C是直线l上的三点,点P在直线l外,PA⊥l,垂足为A,PA=5cm,PB=7cm,PC=6cm,则点P到直线l的距离是cm.20.已知A 、O、B 三点共线,⊥BOC=35°,作OD⊥OC,则⊥DOB=.三、作图题21.如图,某村庄计划把河中的水引到水池M中,怎样开的渠最短,为什么(保留作图痕迹,不写作法和证明)理由是:.四、解答题22.如图,直线AB、CD相交于点O,∠AOC=70°,过点O画EO⊥CD,O为垂足,求∠BOE 的度数.23.如图,直线AB和CD相交于点O,若∠BOD=40°,OA平分∠EOC,求∠EOD的度数.24.如图,直线AB,CD,EF相交于点O.如果⊥BOD=60°,EF垂直于AB于点O,求⊥AOD和⊥FOC的度数.25.如图,直线AB,CD相交于点O,∠BOC=125°,∠AOE=∠BOD,求∠DOE的度数.答案1.B 2.C 3.C 4.B 5.B 6.D 7.B 8.A 9.A 10.C 11.A 12.D 13.45 14.35 15.120 16.58°;122°17.两点之间,线段最短;垂线段最短18.25 19.5 20.125°或55°21.解:理由是:垂线段最短.作图如下:22.解:如图:∵⊥AOC=70°,∴⊥BOC=180°-70°=110°,∵EO⊥CD,∴⊥BOE=⊥BOC-⊥COE=20°;如图,∵⊥AOC=70°,∴⊥BOD=70°,∵EO⊥CD,∴⊥BOE=⊥BOD+⊥DOE=160°;综上:⊥BOE的度数为20°或160°.23.解:∵⊥BOD=40°,∴⊥AOC=⊥BOD=40°.∵OA平分⊥EOC,∴⊥AOE=⊥AOC=40°,∴∠EOD=180°−∠AOE−∠BOD=180°−40°−40°=100°.24.解:∵⊥BOD =60°∴⊥AOD =120°,⊥AOC =60°,∵EF垂直于AB于点O∴⊥AOF =90°,∴⊥FOC=⊥AOF+⊥AOC=90°+60°=150°.25.解:∵直线AB,CD相交于点O,∠BOC=125°,∴∠BOD=180°−∠BOC=180°−125°=55.又∵∠AOE=∠BOD,∴∠AOE=55°,∴∠DOE=180°−∠AOE−∠BOD=180°−55°−55°=70°.。
人教版七年级下册数学5.1.1相交线与平行线练习题(含答案)
第五章相交线与平行线5.1.1相交线知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( )3.下面四个图形中,∠1与∠2是邻补角的是( )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是,∠1的对顶角是.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( )A.120° B.90° C.60°D.30°7.如图,测角器测得工件(圆台)的角度是度,其测量角的原理是.第4题图第5题图第6题图第7题图8.在括号内填写依据:如图,因为直线a,b相交于点O,所以∠1+∠3=180°( ),∠1=∠2( ).AB9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是___________,∠EOC 的对顶角是___________②∠AOC 的邻补角是_________________,∠BOE 的邻补角是__________________. ③若∠AOC=50°,求∠BOD ,∠COB 的度数. 解:∵∠AOC=50° ∴∠BOD=__________=________( ); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠________( )=180°-________°=________°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.【综合训练】11.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( )A .62°B .118°C .72°D .59°第12题图 第13题图14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x = . 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为 . 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD=__________=________( );∵OE 平分∠AOD ∴∠AOE=21___________( ) ∵∠AOD+∠AOC=180°∴∠AOD=180°-∠________( )=_________________________=___________ ∠AOE=____________.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.20.探究题:(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有 个交点,最多有 个交点,对顶角有 对,邻补角有 对.OE DC BA第五章相交线与平行线5.1.1相交线答案知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( A )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( C )3.下面四个图形中,∠1与∠2是邻补角的是( D )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2,∠4,∠1的对顶角是∠3.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( A )A.120° B.90° C.60°D.30°AB 7.如图,测角器测得工件(圆台)的角度是40度,其测量角的原理是对顶角相等.8.在括号内填写依据:如图,因为直线a ,b 相交于点O , 所以∠1+∠3=180°(邻补角互补), ∠1=∠2(对顶角相等).9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是_∠BOC__,∠EOC 的对顶角是__∠DOF___ ②∠AOC 的邻补角是_∠AOD____,∠BOE 的邻补角是___∠AOE__. ③若∠AOC=50°,求∠BOD ,∠COB 的度数.解:∵∠AOC=50°∴∠BOD=_∠AOC_=_50°(对顶角相等); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠AOC (邻补角互补) =180°- 50° = 130°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.解:因为OA 平分∠EOC ,∠EOC =70°, 所以∠AOC =12∠EOC =35°.所以∠BOD =∠AOC =35°. 【综合训练】11.下列说法正确的有( B )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( C )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( A )A .62°B .118°C .72°D .59° 14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x=40或80. 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为135°. 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=140°.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD= ∠AOC = 120° (对顶角相等); ∵OE 平分∠AOD∴∠AOE=21∠AOD∵∠AOD+∠AOC=180°∴∠AOD=180°-∠AOC (邻补角互补)=180°-120°= 60° ∠AOE= 30°.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.解:因为∠AOE =∠BOE ,且∠AOE +∠BOE =180°, 所以∠AOE =∠BOE =90°. 因为∠DOE =50°,所以∠DOB =∠BOE -∠DOE =40°.因为OB 平分∠DOF ,所以∠DOF =2∠DOB =80°.OE DCBA19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数. 解:设∠1=∠2=x °,则∠3=8x °. 由∠1+∠2+∠3=180°,得 10x =180.解得x =18. 所以∠1=∠2=18°. 所以∠4=∠1+∠2=36°. 20.探究题:(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有1个交点,最多有n (n -1)2个交点,对顶角有n(n -1)对,邻补角有2n(n -1)对.解:(1)图略,对顶角有6对,邻补角有12对. (2)图略,对顶角有12对,邻补角有24对.。
人教版初中数学七年级下册相交线练习题附参考答案

人教版初中数学七年级下册相交线练习题附参考答案1.在两条直线相交所成的四个角中,( )不能判定这两条直线垂直A.对顶角互补 B.四对邻补角 C.三个角相等 D.邻补角相等答案:B说明:两条直线相交,已有四对邻补角,因此,选项B不足以判定这两条直线垂直;而根据垂直的定义,对顶角、邻补角的性质不难判断其它选项的说法都可以判定这两条直线垂直;所以答案为B.2.如图,在三角形ABC中,AC⊥BC,CD⊥AB于D,则下列关系不成立的是( )A.AB>AC>ADB.AB>BC>CDC.AC+BC>ABD.AC>CD>BC答案:D说明:由垂线段最短的性质,可知AB>AC,AB>BC,AC>AD,BC>CD都成立,即选项A、B中的关系都是正确的;再由两点之间线段最短,可知AB<AC+BC成立,所以选项C也正确;只有选项D中CD>BC不成立,答案为D.3.图中,∠1和∠2是同位角的是( )A B C D答案:D说明:由同位角的概念可知,一条直线与两条直线相交,同位角位置相同且有一边在同一直线上,这样可以判断选项A、B、C中的∠1与∠2都不是同位角,只有选项D中的∠1与∠2是同位角,答案为D.填空题:1.如图,直线a,b,c交于O,∠1 = 30º,∠2 = 50º,则∠3 =________.答案:100º说明:如图,∠3的对顶角为∠4,所以∠3 =∠4;又∠1+∠2+∠4 = 180º,∠1 = 30º,∠2 = 50º,所以∠4 = 180º−30º−50º = 100º,即∠3 = 100º.2.如图,直线AB、CD交于O,OA平分∠EOC,且∠EOD = 120º,则∠BOD =_______.答案:30º说明:因为∠BOD =∠COA,∠EOD+∠EOC = 180º,OA平分∠EOC,所以∠EOD+2∠COA = 180º,再由∠EOD = 120º,可得∠COA = 30º,即∠BOD = 30º.3.已知如图,①∠1与∠2是_______被_______所截成的_______角;②∠2与∠3是_______被_______截成的_______角;③∠3与∠A是_______被_______截成的_______角;④AB、AC被BE截成的同位角_______,内错角_______,同旁内角_______;⑤DE、BC被AB截成的同位角是_______,内错角_______,同旁内角_______.答案:①DE、BC;BE;内错角②AC、BC;BE;同旁内角③AB、BE;AC;同位角④不存在;∠ABE与∠3;∠ABE与∠AEB⑤∠ADE与∠ABC;不存在;∠EDB与∠DBC4.在三角形ABC中,AC⊥BC,CD⊥AB于D,如图,则在图中共有______对互余的角,______对互补的角,______对邻补角,点A到CD的距离是______,到BC的距离是______,到点B的距离是______,点C 到直线AB的距离是______.答案:有4对互余的角:∠ACD与∠A;∠A与∠B;∠B与∠BCD;∠BCD与∠ACD;有3对互补的角:∠CDA与∠CDB;∠ACB与∠CDA;∠ACB与∠CDB;有1对邻补角:∠CDA与∠CDB;点A到CD的距离是AD;点A到BC的距离是AC;点A到点B的距离是AB;点C到直线AB的距离是CD.解答题:1.如图,已知直线AB、CD、EF相交于O,OG⊥AB,且∠FOG = 32º,∠COE = 38º,求∠BOD.答案:因为AB、CD、EF交于O,所以∠FOD =∠COE =38º又因为OG⊥AB,所以∠BOD = 90º−∠FOD−∠FOG = 90º−32º−38º = 20º.2.如图,已知OA⊥OB,OC⊥OD,且∠AOD:∠BOC = 4:5,求∠BOC的度数.答案:因为OA⊥OB,OC⊥OD所以∠AOB =∠DOC =90º即∠AOD+∠BOC = 180º又因为∠AOD:∠BOC = 4:5所以∠BOC = ×180º = 100º.3.如图,直线AB、CD交于O,∠AOE = 30º,∠BOC = 2∠AOC,求∠DOF.解答:∵AB、CD交于O∴∠AOC+∠BOC = 180º又∵∠BOC = 2∠AOC∴3∠AOC = 180º∴∠AOC = 60º又∵∠AOE = 30º∴∠DOF = 30º。
人教版数学七年级下全册同步练习(答案全)

第五章相交线与平行线1相交线学习要求1.能从两条直线相交所形成的四个角的关系入手,理解对顶角、互为邻补角的概念,掌握对顶角的性质.2.能依据对顶角的性质、邻补角的概念等知识,进行简单的计算.课堂学习检测一、填空题1.如果两个角有一条______边,并且它们的另一边互为____________,那么具有这种关系的两个角叫做互为邻补角.2.如果两个角有______顶点,并且其中一个角的两边分别是另一个角两边的___________ ________,那么具有这种位置关系的两个角叫做对顶角.3.对顶角的重要性质是_________________.4.如图,直线AB、CD相交于O点,∠AOE=90°.(1)∠1和∠2叫做______角;∠1和∠4互为______角;∠2和∠3互为_______角;∠1和∠3互为______角;∠2和∠4互为______角.(2)若∠1=20°,那么∠2=______;∠3=∠BOE-∠______=______°-______°=______°;∠4=∠______-∠1=______°-______°=______°.5.如图,直线AB与CD相交于O点,且∠COE=90°,则(1)与∠BOD互补的角有________________________;(2)与∠BOD互余的角有________________________;(3)与∠EOA互余的角有________________________;(4)若∠BOD=42°17′,则∠AOD=__________;∠EOD=______;∠AOE=______.二、选择题6.图中是对顶角的是( ).7.如图,∠1的邻补角是( ).(A)∠BOC (B)∠BOC 和∠AOF (C)∠AOF(D)∠BOE 和∠AOF8.如图,直线AB 与CD 相交于点O ,若AOD AOC ∠=∠31,则∠BOD 的度数为( ). (A)30° (B)45° (C)60°(D)135°9.如图所示,直线l 1,l 2,l 3相交于一点,则下列答案中,全对的一组是( ).(A)∠1=90°,∠2=30°,∠3=∠4=60° (B)∠1=∠3=90°,∠2=∠4=30° (C)∠1=∠3=90°,∠2=∠4=60° (D)∠1=∠3=90°,∠2=60°,∠4=30° 三、判断正误10.如果两个角相等,那么这两个角是对顶角.( )11.如果两个角有公共顶点且没有公共边,那么这两个角是对顶角.( )12.有一条公共边的两个角是邻补角.( ) 13.如果两个角是邻补角,那么它们一定互为补角. ( ) 14.对顶角的角平分线在同一直线上.( ) 15.有一条公共边和公共顶点,且互为补角的两个角是邻补角.( )综合、运用、诊断一、解答题16.如图所示,AB ,CD ,EF 交于点O ,∠1=20°,∠BOC =80°,求∠2的度数.17.已知:如图,直线a ,b ,c 两两相交,∠1=2∠3,∠2=86°.求∠4的度数.18.已知:如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠DOE=4∶1.求∠AOF的度数.19.如图,有两堵围墙,有人想测量地面上两堵围墙内所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?拓展、探究、思考20.如图,O是直线CD上一点,射线OA,OB在直线CD的两侧,且使∠AOC=∠BOD,试确定∠AOC与∠BOD是否为对顶角,并说明你的理由.21.回答下列问题:(1)三条直线AB,CD,EF两两相交,图形中共有几对对顶角(平角除外)?几对邻补角?(2)四条直线AB,CD,EF,GH两两相交,图形中共有几对对顶角(平角除外)?几对邻补角?(3)m条直线a1,a2,a3,…,a m-1,a m相交于点O,则图中一共有几对对顶角(平角除外)?几对邻补角?2 垂线学习要求1.理解两条直线垂直的概念,掌握垂线的性质,能过一点作已知直线的垂线.2.理解点到直线的距离的概念,并会度量点到直线的距离.课堂学习检测一、填空题1.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线______,其中一条直线叫做另一条直线的______线,它们的交点叫做______.2.垂线的性质性质1:平面内,过一点____________与已知直线垂直.性质2:连接直线外一点与直线上各点的_________中,_________最短.3.直线外一点到这条直线的__________________叫做点到直线的距离.4.如图,直线AB,CD互相垂直,记作______;直线AB,CD互相垂直,垂足为O点,记作____________;线段PO的长度是点_________到直线_________的距离;点M到直线AB的距离是_______________.二、按要求画图5.如图,过A点作CD⊥MN,过A点作PQ⊥EF于B.图a 图b 图c6.如图,过A点作BC边所在直线的垂线EF,垂足是D,并量出A点到BC边的距离.图a 图b 图c7.如图,已知∠AOB及点P,分别画出点P到射线OA、OB的垂线段PM及PN.图a 图b 图c8.如图,小明从A村到B村去取鱼虫,将鱼虫放到河里,请作出小明经过的最短路线.综合、运用、诊断一、判断下列语句是否正确(正确的画“√”,错误的画“×”)9.两条直线相交,若有一组邻补角相等,则这两条直线互相垂直.( ) 10.若两条直线相交所构成的四个角相等,则这两条直线互相垂直.( ) 11.一条直线的垂线只能画一条.( ) 12.平面内,过线段AB外一点有且只有一条直线与AB垂直.( ) 13.连接直线l外一点到直线l上各点的6个有线段中,垂线段最短.( ) 14.点到直线的距离,是过这点画这条直线的垂线,这点与垂足的距离.( ) 15.直线外一点到这条直线的垂线段,叫做点到直线的距离.( )16.在三角形ABC 中,若∠B =90°,则AC >AB . ( )二、选择题17.如图,若AO ⊥CO ,BO ⊥DO ,且∠BOC =α,则∠AOD 等于( ).(A)180°-2α(B)180°-α (C)α2190+︒(D)2α-90°18.如图,点P 为直线m 外一点,点P 到直线m 上的三点A 、B 、C 的距离分别为P A =4cm ,PB =6cm ,PC =3cm ,则点P 到直线m 的距离为( ). (A)3cm(B)小于3cm(C)不大于3cm(D)以上结论都不对19.如图,BC ⊥AC ,CD ⊥AB ,AB =m ,CD =n ,则AC 的长的取值范围是( ).(A)AC <m (B)AC >n (C)n ≤AC ≤m(D)n <AC <m20.若直线a 与直线b 相交于点A ,则直线b 上到直线a 距离等于2cm 的点的个数是( ). (A)0(B)1(C)2(D)321.如图,AC ⊥BC 于点C ,CD ⊥AB 于点D ,DE ⊥BC于点E ,能表示点到直线(或线段)的距离的线段有( ). (A)3条 (B)4条 (C)7条(D)8条三、解答题22.已知:OA ⊥OC ,∠AOB ∶∠AOC =2∶3.求∠BOC 的度数.23.已知:如图,三条直线AB ,CD ,EF 相交于O ,且CD ⊥EF ,∠AOE =70°,若OG平分∠BOF .求∠DOG .拓展、探究、思考24.已知平面内有一条直线m 及直线外三点A ,B ,C ,分别过这三个点作直线m 的垂线,想一想有几个不同的垂足?画图说明.25.已知点M ,试在平面内作出四条直线l 1,l 2,l 3,l 4,使它们分别到点M 的距离是1.5cm .·M26.从点O 引出四条射线OA ,OB ,OC ,OD ,且AO ⊥BO ,CO ⊥DO ,试探索∠AOC与∠BOD 的数量关系.27.一个锐角与一个钝角互为邻角,过顶点作公共边的垂线,若此垂线与锐角的另一边构成75直角,与钝角的另一边构成直73角,则此锐角与钝角的和等于直角的多少倍?3 同位角、内错角、同旁内角学习要求当两条直线被第三条直线所截时,能从所构成的八个角中识别出哪两个角是同位角、内错角及同旁内角.课堂学习检测一、填空题1.如图,若直线a ,b 被直线c 所截,在所构成的八个角中指出,下列各对角之间是属于哪种特殊位置关系的角?(1)∠1与∠2是_______;(2)∠5与∠7是______; (3)∠1与∠5是_______;(4)∠5与∠3是______; (5)∠5与∠4是_______;(6)∠8与∠4是______; (7)∠4与∠6是_______;(8)∠6与∠3是______; (9)∠3与∠7是______;(10)∠6与∠2是______.2.如图2所示,图中用数字标出的角中,同位角有______;内错角有______;同旁内角有______.3.如图3所示,(1)∠B 和∠ECD 可看成是直线AB 、CE 被直线______所截得的_______角; (2)∠A 和∠ACE 可看成是直线_______、______被直线_______所截得的______角. 4.如图4所示,(1)∠AED 和∠ABC 可看成是直线______、______被直线______所截得的_______角;图2 图3 图4(2)∠EDB和∠DBC可看成是直线______、______被直线_______所截得的______角;(3)∠EDC和∠C可看成是直线_______、______被直线______所截得的______角.综合、运用、诊断一、选择题5.已知图①~④,图①图②图③图④在上述四个图中,∠1与∠2是同位角的有( ).(A)①②③④(B)①②③(C)①③(D)①6.如图,下列结论正确的是( ).(A)∠5与∠2是对顶角(B)∠1与∠3是同位角(C)∠2与∠3是同旁内角(D)∠1与∠2是同旁内角7.如图,∠1和∠2是内错角,可看成是由直线( ).(A)AD,BC被AC所截构成(B)AB,CD被AC所截构成(C)AB,CD被AD所截构成(D)AB,CD被BC所截构成8.如图,直线AB,CD与直线EF,GH分别相交,图中的同旁内角共有( ).(A)4对(B)8对(C)12对(D)16对拓展、探究、思考一、解答题9.如图,三条直线两两相交,共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?4 平行线及平行线的判定学习要求1.理解平行线的概念,知道在同一平面内两条直线的位置关系,掌握平行公理及其推论.2.掌握平行线的判定方法,能运用所学的“平行线的判定方法”,判定两条直线是否平行.用作图工具画平行线,从而学习如何进行简单的推理论证.课堂学习检测一、填空题1.在同一平面内,______的两条直线叫做平行线.若直线a与直线b平行,则记作______.2.在同一平面内,两条直线的位置关系只有______、______.3.平行公理是:_______________________________________________________________.4.平行公理的推论是如果两条直线都与______,那么这两条直线也______.即三条直线a,b,c,若a∥b,b∥c,则______.5.两条直线平行的条件(除平行线定义和平行公理推论外):(1)两条直线被第三条直线所截,如果____________,那么这两条直线平行.这个判定方法1可简述为:____________,两直线平行.(2)两条直线被第三条直线所截,如果____________,那么____________.这个判定方法2可简述为:____________,____________.(3)两条直线被第三条直线所截,如果____________,那么____________.这个判定方法3可简述为:____________,____________.二、根据已知条件推理6.已知:如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.(1)如果∠2=∠3,那么____________.(____________,____________)(2)如果∠2=∠5,那么____________.(____________,____________)(3)如果∠2+∠1=180°,那么____________.(____________,____________)(4)如果∠5=∠3,那么____________.(____________,____________)(5)如果∠4+∠6=180°,那么____________.(____________,____________)(6)如果∠6=∠3,那么____________.(____________,____________)7.已知:如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.(1)∵∠B=∠3(已知),∴______∥______.(____________,____________)(2)∵∠1=∠D(已知),∴______∥______.(____________,____________)(3)∵∠2=∠A(已知),∴______∥______.(____________,____________)(4)∵∠B+∠BCE=180°(已知),∴______∥______.(____________,____________)综合、运用、诊断一、依据下列语句画出图形8.已知:点P是∠AOB内一点.过点P分别作直线CD∥OA,直线EF∥OB.9.已知:三角形ABC及BC边的中点D.过D点作DF∥CA交AB于M,再过D点作DE∥AB交AC于N点.二、解答题10.已知:如图,∠1=∠2.求证:AB∥CD.(1)分析:如图,欲证AB∥CD,只要证∠1=______.证法1:∵∠1=∠2,(已知)又∠3=∠2,( )∴∠1=_______.( )∴AB∥CD.(___________,___________)(2)分析:如图,欲证AB∥CD,只要证∠3=∠4.证法2:∵∠4=∠1,∠3=∠2,( )又∠1=∠2,(已知)从而∠3=_______.( )∴AB∥CD.(___________,___________)11.绘图员画图时经常使用丁字尺,丁字尺分尺头、尺身两部分,尺头的里边和尺身的上边应平直,并且一般互相垂直,也有把尺头和尺身用螺栓连接起来,可以转动尺头,使它和尺身成一定的角度.用丁字尺画平行线的方法如下面的三个图所示.画直线时要按住尺身,推移丁字尺时必须使尺头靠紧图画板的边框.请你说明:利用丁字尺画平行线的理论依据是什么?拓展、探究、思考12.已知:如图,CD ⊥DA ,DA ⊥AB ,∠1=∠2.试确定射线DF 与AE 的位置关系,并说明你的理由.(1)问题的结论:DF ______AE .(2)证明思路分析:欲证DF ______AE ,只要证∠3=______. (3)证明过程:证明:∵CD ⊥DA ,DA ⊥AB ,( )∴∠CDA =∠DAB =______°.(垂直定义) 又∠1=∠2,( )从而∠CDA -∠1=______-______,(等式的性质) 即∠3=___.∴DF ___AE .(____,____)13.已知:如图,∠ABC =∠ADC ,BF 、DE 分别平分∠ABC 与∠ADC .且∠1=∠3. 求证:AB ∥DC .证明:∵∠ABC =∠ADC ,.2121ADC ABC ∠=∠∴( ) 又∵BF 、DE 分别平分∠ABC 与∠ADC ,.212,211ADC ABC ∠=∠∠=∠∴ ( ) ∴∠______=∠______.( ) ∵∠1=∠3,( ) ∴∠2=∠______.(等量代换) ∴______∥______.( )14.已知:如图,∠1=∠2,∠3+∠4=180°.试确定直线a 与直线c 的位置关系,并说明你的理由.(1)问题的结论:a______c.(2)证明思路分析:欲证a______c,只要证______∥______且______∥______.(3)证明过程:证明:∵∠1=∠2,( )∴a∥______.(________,________)①∵∠3+∠4=180°,( )∴c∥______.(________,________)②由①、②,因为a∥______,c∥______,∴a______c.(________,________)5 平行线的性质学习要求1.掌握平行线的性质,并能依据平行线的性质进行简单的推理.2.了解平行线的判定与平行线的性质的区别.3.理解两条平行线的距离的概念.课堂学习检测一、填空题1.平行线具有如下性质:(1)性质1:______被第三条直线所截,同位角______.这个性质可简述为两直线______,同位角______.(2)性质2:两条平行线__________________,_______相等.这个性质可简述为_____________,_____________.(3)性质3:__________________,同旁内角______.这个性质可简述为_____________,__________________.2.同时______两条平行线,并且夹在这两条平行线间的______________叫做这两条平行线的距离.二、根据已知条件推理3.如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.(1)如果AB∥EF,那么∠2=______.理由是____________________________________.(2)如果AB∥DC,那么∠3=______.理由是____________________________________.(3)如果AF∥BE,那么∠1+∠2=______.理由是______________________________.(4)如果AF∥BE,∠4=120°,那么∠5=______.理由是________________________.4.已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.(1)∵DE∥AB,( )∴∠2=______.(__________,__________)(2)∵DE∥AB,( )∴∠3=______.(__________,__________)(3)∵DE∥AB( ),∴∠1+______=180°.(______,______)综合、运用、诊断一、解答题5.如图,∠1=∠2,∠3=110°,求∠4.解题思路分析:欲求∠4,需先证明______∥______.解:∵∠1=∠2,( )∴______∥______.(__________,__________)∴∠4=______=______°.(__________,__________)6.已知:如图,∠1+∠2=180°.求证:∠3=∠4.证明思路分析:欲证∠3=∠4,只要证______∥______.证明:∵∠1+∠2=180°,( )∴______∥______.(__________,__________)∴∠3=∠4.(______,______)7.已知:如图,AB∥CD,∠1=∠B.求证:CD是∠BCE的平分线.证明思路分析:欲证CD是∠BCE的平分线,只要证______=______.证明:∵AB∥CD,( )∴∠2=______.(____________,____________)但∠1=∠B,( )∴______=______.(等量代换)即CD是________________________.8.已知:如图,AB∥CD,∠1=∠2.求证:BE∥CF.证明思路分析:欲证BE∥CF,只要证______=______.证明:∵AB∥CD,( )∴∠ABC=______.(____________,____________)∵∠1=∠2,( )∴∠ABC-∠1=______-______,( )即______=______.∴BE∥CF.(__________,__________)9.已知:如图,AB∥CD,∠B=35°,∠1=75°.求∠A的度数.解题思路分析:欲求∠A,只要求∠ACD的大小.解:∵CD∥AB,∠B=35°,( )∴∠2=∠______=_______°.(____________,____________)而∠1=75°,∴∠ACD=∠1+∠2=______°.∵CD∥AB,( )∴∠A+______=180°.(____________,____________)∴∠A=_______=______.10.已知:如图,四边形ABCD 中,AB ∥CD ,AD ∥BC ,∠B =50°.求∠D 的度数.分析:可利用∠DCE 作为中间量过渡. 解法1:∵AB ∥CD ,∠B =50°,( )∴∠DCE =∠_______=_______°. (____________,______) 又∵AD ∥BC ,( )∴∠D =∠______=_______°.(____________,____________)想一想:如果以∠A 作为中间量,如何求解? 解法2:∵AD ∥BC ,∠B =50°,( )∴∠A +∠B =______.(____________,____________) 即∠A =______-______=______°-______°=______°. ∵DC ∥AB ,( )∴∠D +∠A =______.(_____________,_____________) 即∠D =______-______=______°-______°=______°.11.已知:如图,AB ∥CD ,AP 平分∠BAC ,CP 平分∠ACD ,求∠APC 的度数.解:过P 点作PM ∥AB 交AC 于点M .∵AB ∥CD ,( )∴∠BAC +∠______=180°.( ) ∵PM ∥AB ,∴∠1=∠_______,( )且PM ∥_______.(平行于同一直线的两直线也互相平行) ∴∠3=∠______.(两直线平行,内错角相等) ∵AP 平分∠BAC ,CP 平分∠ACD ,( )∠=∠∴211______,∠=∠214______.( ) 90212141=∠+∠=∠+∠∴ACD BAC .( )∴∠APC =∠2+∠3=∠1+∠4=90°.( ) 总结:两直线平行时,同旁内角的角平分线______.拓展、探究、思考12.已知:如图,AB ∥CD ,EF ⊥AB 于M 点且EF 交CD 于N 点.求证:EF ⊥CD .13.如图,DE∥BC,∠D∶∠DBC=2∶1,∠1=∠2,求∠E的度数.14.问题探究:(1)如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的大小有何关系?举例说明.(2)如果一个角的两边与另一个角的两边分别垂直,那么这两个角的大小有何关系?举例说明.15.如图,AB∥DE,∠1=25°,∠2=110°,求∠BCD的度数.16.如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).6 命题学习要求1.知道什么是命题,知道一个命题是由“题设”和“结论”两部分构成的.2.对于给定的命题,能找出它的题设和结论,并会把该命题写成“如果……,那么……”的形式.能判定该命题的真假.课堂学习检测一、填空题1.______一件事件的______叫做命题.2.许多命题都是由______和______两部分组成.其中题设是____________,结论是______ _____.3.命题通常写成“如果……,那么…….”的形式.这时,“如果”后接的部分是______,“那么”后接的部分是______.4.所谓真命题就是:如果题设成立,那么结论就______的命题.相反,所谓假命题就是:如果题设成立,不能保证结论______的命题.二、指出下列命题的题设和结论5.垂直于同一条直线的两条直线平行.题设是___________________________________________________________;结论是___________________________________________________________.6.同位角相等,两直线平行.题设是___________________________________________________________;结论是___________________________________________________________.7.两直线平行,同位角相等.题设是___________________________________________________________;结论是___________________________________________________________.8.对顶角相等.题设是___________________________________________________________;结论是___________________________________________________________.三、将下列命题改写成“如果……,那么……”的形式9.90°的角是直角.__________________________________________________________________.10.末位数字是零的整数能被5整除.__________________________________________________________________.11.等角的余角相等.__________________________________________________________________.12.同旁内角互补,两直线平行.__________________________________________________________________.综合、运用、诊断一、下列语句哪些是命题,哪些不是命题?13.两条直线相交,只有一个交点.( ) 14. 不是有理数.( )15.直线a与b能相交吗?( ) 16.连接AB.( )17.作AB⊥CD于E点.( ) 18.三条直线相交,有三个交点.( )二、判断下列各命题中,哪些命题是真命题?哪些是假命题?(对于真命题画“√”,对于假命题画“×”)19.0是自然数.( )20.如果两个角不相等,那么这两个角不是对顶角.( )21.相等的角是对顶角.( )22.如果AC=BC,那么C点是AB的中点.( )23.若a∥b,b∥c,则a∥c.( )24.如果C是线段AB的中点,那么AB=2BC.( )25.若x2=4,则x=2.( )26.若xy=0,则x=0.( )27.同一平面内既不重合也不平行的两条直线一定相交.( )28.邻补角的平分线互相垂直.( )29.同位角相等.( )30.大于直角的角是钝角.( )拓展、探究、思考31.已知:如图,在四边形ABCD中,给出下列论断:①AB∥DC;②AD∥BC;③AB=AD;④∠A=∠C;⑤AD=BC.以上面论断中的两个作为题设,再从余下的论断中选一个作为结论,并用“如果……,那么……”的形式写出一个真命题.答:_____________________________________________________________________.32.求证:两条平行线被第三条直线所截,内错角的平分线互相平行.7 平移学习要求了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.课堂学习检测一、填空题1.如图所示,线段ON是由线段______平移得到的;线段DE是由线段______平移得到的;线段FG是由线段______平移得到的.2.如图所示,线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3),具有哪些性质.图a图b 图c(1)线段AB上所有的点都是沿______移动,并且移动的距离都________.因此,线段AB,A1B1,A2B2,A3B3的位置关系是____________________;线段AB,A1B1,A2B2,A3B3的数量关系是________________.(2)在平移变换中,连接各组对应点的线段之间的位置关系是______;数量关系是______.3.如图所示,将三角形ABC平移到△A′B′C′.图a 图b在这两个平移中:(1)三角形ABC的整体沿_______移动,得到三角形A′B′C′.三角形A′B′C′与三角形ABC的______和______完全相同.(2)连接各组对应点的线段即AA′,BB′,CC′之间的数量关系是__________________;位置关系是__________________.综合、运用、诊断一、按要求画出相应图形4.如图,AB∥DC,AD∥BC,DE⊥AB于E点.将三角形DAE平移,得到三角形CBF.5.如图,AB∥DC.将线段DB向右平移,得到线段CE.6.已知:平行四边形ABCD及A′点.将平行四边形ABCD平移,使A点移到A′点,得平行四边形A′B′C′D′.7.已知:五边形ABCDE及A′点.将五边形ABCDE平移,使A点移到A′点,得到五边形A′B′C′D′E′.拓展、探究、思考一、选择题8.如图,把边长为2的正方形的局部进行如图①~图④的变换,拼成图⑤,则图⑤的面积是( ).(A)18 (B)16 (C)12 (D)8二、解答题9.河的两岸成平行线,A,B是位于河两岸的两个车间(如图).要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法如下:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB.EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.试说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.10.以直角三角形的三条边BC,AC,AB分别作正方形①、②、③,如何用①中各部分面积与②的面积,通过平移填满正方形③?你从中得到什么结论?第六章 实数6.1平方根学习要求1. 理解算术平方根和平方根的含义。
新人教版七年级数学下册各章知识点练习

七年级数学人教版下学期期末总复习资料第五章 相交线与平行线一、知识回顾:1、 如果A ∠与B ∠是对顶角,则其关系是:2、 如果C ∠与D ∠是邻补角,则其关系是: 如果α∠与β∠互为余角,则其关系是⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩定义_____________________________1 过一点____________________2 垂直性质 2 连接直线外一点与直线上各点的所有线段中,___________最短 3、点到直线距离是:__________________两点间的距离是:_________________ 两平行线间的距离是指:_____________________________________________ 4、在同一平面内,两条直线的位置关系有_____种,它们是_____________ 5、平行公理是指:_________________________如果两条直线都与第三条直线平行,那么_________________________________ 6、平行线的判定方法有:①、 ②、__________________________________ ③、___________________________________ 7、平行线的性质有:①、___________________________________②、___________________________________ ③、___________________________________8、命题是指____________________________每一个命题都可以写成_______________的形式,“对顶角相等”的题设是_______________________,结论是 ___________ 9、平移:①定义:把一个图形整体沿着某一_____移动_______,图形的这种移动,叫做平移变换,简称平移 ②图形平移方向不一定是水平的③平移后得到的新图形与原图形的_________和________完全相同 ④新图形中的每一点与原图形中的对应点的连线段________且_________ 二、练习:1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )B EDA CF87654321DCBAA .50°B .60°C .140°D .160°2、如图2,已知AB ∥CD ,∠A =70°,则∠1的度数是( )A .70°B .100°C .110°D .130°3、已知:如图3,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠ 与2∠的关系一定成立的是( ) A .相等 B .互余C .互补D .互为对顶角图1 图2 图34、如图4,AB DE ∥,65E ∠=o,则B C ∠+∠=( )A .135oB .115oC .36oD .65o图4 图5 图6 5、如图5,小明从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20o方向行走至C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )A .右转80°B .左转80°C .右转100°D .左转100° 6、如图6,如果AB ∥CD ,那么下面说法错误的是( )A .∠3=∠7;B .∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠87、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30ο,那么这两个角是( ) A . 42138οο、;B . 都是10ο;C . 42138οο、或4210οο、;D . 以上都不对8、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )A .①、②是正确的命题;B .②、③是正确命题;C .①、③是正确命题 ;D .以上结论皆错DBAC1ab1 2OABCD EF2 1 OabMP N123A B Ca b1 2 3A BE9、下列语句错误的是( )A .连接两点的线段的长度叫做两点间的距离;B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等 10、如图7,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=( ) A .180oB .270oC .360oD .540o 图711、如图8,直线a b ∥,直线c 与a b ,相交.若170∠=o,则2_____∠=o.图8 图9 图10 12、如图9,已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒.13、如图10,已知AB ∥CD ,BE 平分∠ABC ,∠CDE =150°,则∠C =______ 14、如图11,已知a b ∥,170∠=o,240∠=o,则图11 图12 15、如图12所示,请写出能判定CE ∥AB 的一个条件 . 16、如图13,已知AB CD //,∠α=____________ 17、推理填空:(每空1分,共12分)如图: ① 若∠1=∠2,则 ∥ ( ) 若∠DAB+∠ABC=1800,则 ∥ ( ) ②当 ∥ 时,∠ C+∠ABC=1800 ( ) 当 ∥ 时,∠3=∠C ( )1 2bac bac d 123 4ABCDE321DCBA18、如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数.19、已知:如图AB ∥CD ,EF 交AB 于G ,交CD 于F ,FH 平分∠EFD ,交AB 于H ,∠AGE=500,求:∠BHF 的度数.20、观察如图所示中的各图,寻找对顶角(不含平角):(1)如图a ,图中共有___对对顶角;(2)如图b ,图中共有___对对顶角; (3)如图c ,图中共有___对对顶角.(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n 条直线相交于一点,则可形成多少对对顶角?21、已知,如图,CD ⊥AB ,GF ⊥AB ,∠B =∠ADE ,试说明∠1=∠2.第六章 平面直角坐标系一、知识回顾:HG FEDBAABCDO123EFF21GE DCB A1、平面直角坐标系:在平面内画两条___________、____________的数轴,组成平面直角坐标系2、平面直角坐标系中点的特点:①坐标的符号特征:第一象限(),++,第二象限( ),第三象限( )第四象限( ) 已知坐标平面内的点A (m ,n )在第四象限,那么点(n ,m )在第____象限 ②坐标轴上的点的特征:x 轴上的点______为0,y 轴上的点______为0; 如果点P (),a b 在x 轴上,则b =___; 如果点P (),a b 在y 轴上,则a =______如果点P ()5,2a a +-在y 轴上,则a =__ __,P 的坐标为( ) 当a =__时,点P (),1a a -在横轴上,P 点坐标为( ) 如果点P (),m n 满足0mn =,那么点P 必定在__ __轴上③象限角平分线上的点的特征:一三象限角平分线上的点___________________;二四象限角平分线上的点______________________;如果点P (),a b 在一三象限的角平分线上,则a =_ ____; 如果点P (),a b 在二四象限的角平分线上,则a =____ _ 如果点P (),a b 在原点,则a =___ __=__ __已知点A (3,29)b b -++在第二象限的角平分线上,则b = ______ ④平行于坐标轴的点的特征:平行于x 轴的直线上的所有点的______坐标相同,平行于y 轴的直线上的所有点的______坐标相同 如果点A (),3a -,点B ()2,b 且AB//x 轴,则_______ 如果点A ()2,m ,点B (),6n -且AB//y 轴,则_______3、 点P (),x y 到x 轴的距离为_______,到y 轴的距离为______,到原点的距离为____________;4、 点P (),a b -到,x y 轴的距离分别为___ __和_ ___5、 点A ()2,3--到x 轴的距离为_ _,到y 轴的距离为_ _ 点B ()7,0-到x 轴的距离为_ _,到y 轴的距离为__ __点P ()2,5x y -到x 轴的距离为_ _,到y 轴的距离为_ _点P 到x 轴的距离为2,到y 轴的距离为5,则P 点的坐标为___________________________ 4、对称点的特征:①关于x 轴对称点的特点_______不变,______互为相反数 ②关于y 轴对称点的特点_______不变,______互为相反数 ③关于原点对称点的特点_______、 ______互为相反数点A (1,2)-关于y 轴对称点的坐标是______,关于原点对称的点坐标是______,关于x 轴对称点的坐标是______点M (),2x y -与点N ()3,x y +关于原点对称,则______,______x y ==5、平面直角坐标系中点的平移规律:左右移动点的_____坐标变化,(向右移动____________,向左移动____________),上下移动点的______坐标变化(向上移动____________,向下移动____________) 把点A (4,3)向右平移两个单位,再向下平移三个单位得到的点坐标是_________ 将点P (4,5)-先向____平移___单位,再向____平移___单位就可得到点()/2,3P -6、平面直角坐标系中图形平移规律:图形中每一个点平移规律都相同:左右移动点的_____坐标变化,(向右移动____________,向左移动____________),上下移动点的______坐标变化(向上移动____________,向下移动____________)已知V ABC 中任意一点P (2,2)-经过平移后得到的对应点1(3,5)P ,原三角形三点坐标是A (2,3)-,B (4,2)--,C ()1,1- 问平移后三点坐标分别为_______________________________ 二、练习:1.已知点P(3a-8,a-1).(1) 点P 在x 轴上,则P 点坐标为 ;(2) 点P 在第二象限,并且a 为整数,则P 点坐标为 ; (3) Q 点坐标为(3,-6),并且直线PQ ∥x 轴,则P 点坐标为 . 2.如图的棋盘中,若“帅” 位于点(1,-2)上, “相”位于点(3,-2)上,则“炮”位于点___ 上.3.点)1,2(A 关于x 轴的对称点'A 的坐标是 ;点)3,2(B 关于y 轴的对称点'B 的坐标是 ;点)2,1(-C 关于坐标原点的对称点'C 的坐标是 . 4.已知点P 在第四象限,且到x 轴距离为52,到y 轴距离为2,则点P 的坐标为_____. 5.已知点P 到x 轴距离为52,到y 轴距离为2,则点P 的坐标为 . 6. 已知),(111y x P ,),(122y x P ,21x x ≠,则⊥21P P 轴,21P P ∥ 轴;7.把点),(b a P 向右平移两个单位,得到点),2('b a P +,再把点'P 向上平移三个单位,得到点''P ,则''P 的坐标是 ;8.在矩形ABCD 中,A (-4,1),B (0,1),C (0,3),则D 点的坐标为 ; 9.线段AB 的长度为3且平行与x 轴,已知点A 的坐标为(2,-5),则点B 的坐标为_____. 10.线段AB 的两个端点坐标为A (1,D(3,0),则线段AB 与线段CD A.平行且相等 B.平行但不相等三、解答题:1.已知:如图,)3,1(-A ,)0,2(-B2.已知:)0,4(A ,),3(y B ,点C ⑴ 求点C 的坐标;⑵ 若10=∆ABC S ,求点B 的坐标.3.已知:四边形ABCD 各顶点坐标为A(-4,-2),B(4,-2),C(3,1),D(0,3). (1)在平面直角坐标系中画出四边形ABCD ; (2)求四边形ABCD 的面积.(3)如果把原来的四边形ABCD 各个顶点横坐标减2,纵坐标加3,所得图形的面积是多少?4. 已知:)1,0(A ,)0,2(B ,)3,4(C .⑴ 求△ABC 的面积;⑵ 设点P 在坐标轴上,且△ABP 与△ABC 的面积相等, 求点P 的坐标.5.如图,是某野生动物园的平面示意图. 建立适当的直角 坐标系,写出各地点的坐标,并求金鱼馆与熊猫馆的实际距离.6.如图,平移坐标系中的△ABC ,使AB 平移到11B A 的位 置,再将111C B A ∆向右平移3个单位,得到222C B A ∆,第5题图画出222C B A ∆,并求出△ABC 到222C B A ∆的坐标变化.第七章 三角形一、知识回顾:二、练习:1.一个三角形的三个内角中 ( )⎧⎪⎨⎪⎩⎧⎨⎩⎧⎪⎨⎪⎩定义:由不在______三条线段______所组三角形 成的图形表示方法:_________________________三角形两边之和_____第三边三角形三边关系三角形两边之差_____第三边中线________________三角形的三条重要线段高线________________三角形角平分线____________内角和__三角形的内角和与外角和多边形⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎨⎪⎩⎪⎪⎪⎩⎪⎪⎪⎪⎩__________1________外角性质2________外角和____________三角形面积:______________________________三角形具有____性,四边形__________性多边形定义_______________________________多边形n 边形内角和为__________多⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎨⎪⎩⎧⎪⎪⎨⎪⎪⎩⎩边形外角和为____从n 边形一个顶点可作出_____条对角线定义:__________________________________能用一图形镶嵌地面的有_________________平面镶嵌能用两种正多边形镶嵌地面的有_____和___________和_______;_______和_____________⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪A 、至少有一个钝角B 、至少有一个直角C 、至多有一个锐角D 、 至少有两个锐角2.下列长度的三条线段,不能组成三角形的是 ( )A 、a+1,a+2,a+3(a>0)B 、 3a,5a,2a+1(a>0)C 、三条线段之比为1:2:3D 、 5cm ,6cm ,10cm 3.下列说法中错误的是 ( )A 、一个三角形中至少有一个角不少于60°B 、三角形的中线不可能在三角形的外部C 、直角三角形只有一条高D 、三角形的中线把三角形的面积平均分成相等的两部分 4.图中有三角形的个数为 ( )A 、 4个B 、 6个C 、 8个D 、 10个5.如图,点P 有△ABC 内,则下列叙述正确的是( )A 、︒=︒yx B 、x °>y° C 、x °<y °D 、不能确定 6.已知,如图,AB∥CD ,∠A=700,∠B=400,则∠ACD=( ) A 、 550 B 、 700 C 、 400 D 、 11007.下列图形中具有稳定性有 ( )A 、 2个B 、 3个C 、 4个D 、 5个8.一个多边形内角和是10800,则这个多边形的边数为 ( )A 、 6B 、 7C 、 8D 、 99.如图所示,已知△ABC 为直角三角形,∠C=90,若烟图中虚线剪去∠C ,则∠1+∠2 等于( )A 、90°B 、135°C 、270°D 、315°第(4)题E DCBA(1)(2)(3)(4)(5)(6)第(6)题DCBA第(5)题P y 0x 0CBA第(9)题 第(10)题10. 如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于,点P ,若∠A=500 ,则 ∠BPC 等于( )A 、90°B 、130°C 、270°D 、315°11.用正三角形和正方形能够铺满地面,每个顶点周围有______个正三角形和_____个正方形。
