数据结构第7章_图_7.1~
合集下载
数据结构7-图 完整版
A E C D B
其中： V2={A, B, C, D, E} VR2={（A,B）,（A,C),(E,C), (E,D),(D,B) }
5
有向图、无向图示例
A D C
G1
B
1 3
2 4 6
G2
E
5
下列形式的图本章不作讨论
6
完全图、稀疏图与稠密图
n:图中顶点的个数; e:图中边或弧的数目。
2
1 0 3 (a) 1 2 3 (b) 0
q图的应用广泛:
ü ü ü
电路网络分析、交通运输、管理与线路的铺设 印刷电路板与集成电路的布线、社会网络、WEB链接图 工程进度的安排、课程表的制订、关系数据库的设计
2
7.1 图的定义和术语 一、图的结构定义:
q 图是由一个顶点集 V 和一个顶点间的关系集合弧集VR
（边的集合）构成的数据结构。
ü 可以用二元组定义为： Graph = (V, VR ) ü 其中，VR＝{<v,w>| v,w∈V 且 P(v,w)} ü 谓词 P(v,w) 定义了弧 <v,w>的意义或信息。
T5,T6不是有向树
22
● 有向图的生成树/生成森林:
含有图的全部顶点，但只有足以构成若干互不相交的有向树的弧。
A F
B E
G
C D
A F
B E
F1
C D
A
D B
F2
？
F E
C
A F
B E
T1
C D
？
D C B
T2
A E A F E
T3
D B C
F
23
图的抽象数据类型定义
q
其中： V2={A, B, C, D, E} VR2={（A,B）,（A,C),(E,C), (E,D),(D,B) }
5
有向图、无向图示例
A D C
G1
B
1 3
2 4 6
G2
E
5
下列形式的图本章不作讨论
6
完全图、稀疏图与稠密图
n:图中顶点的个数; e:图中边或弧的数目。
2
1 0 3 (a) 1 2 3 (b) 0
q图的应用广泛:
ü ü ü
电路网络分析、交通运输、管理与线路的铺设 印刷电路板与集成电路的布线、社会网络、WEB链接图 工程进度的安排、课程表的制订、关系数据库的设计
2
7.1 图的定义和术语 一、图的结构定义:
q 图是由一个顶点集 V 和一个顶点间的关系集合弧集VR
（边的集合）构成的数据结构。
ü 可以用二元组定义为： Graph = (V, VR ) ü 其中，VR＝{<v,w>| v,w∈V 且 P(v,w)} ü 谓词 P(v,w) 定义了弧 <v,w>的意义或信息。
T5,T6不是有向树
22
● 有向图的生成树/生成森林:
含有图的全部顶点，但只有足以构成若干互不相交的有向树的弧。
A F
B E
G
C D
A F
B E
F1
C D
A
D B
F2
？
F E
C
A F
B E
T1
C D
？
D C B
T2
A E A F E
T3
D B C
F
23
图的抽象数据类型定义
q
数据结构第七章图PPT课件
第7章 图
CAC - 2
CAC - 3
7.1 图的定义和术语
7.1.1 图的定义和术语
1. 图的定义（graph）
图G由两个集合构成，记作G=<V,E> ，其中V是顶点的非空有限集合，
E是顶点间关系----边的有限集合，边是顶点的无序对或有序对集合。 。
【例】 V0
V1
V2
V3
V4
无序对(vi,vj)： 用连接顶点vi、vj的线段
V0
V1
V0
V1
V2
V3
V2
V3
两个强连通分量
CAC - 17
练习
具有n个顶点的强连通图至少有多少条边？是什么形状？
分析：强连通图是针对有向图而言的。由于强连通图要求 图中任何2个顶点之间能够连通，因此每个顶点至少要有一条 以该顶点为终点（弧头）和出发点（弧尾）的弧，每个顶点 的入度和出度至少各为1，即顶点的度至少为2。
边或弧
G2=<V2,E2> V2={ v0 ,v1,v2,v3 } E2={ <v0,v1 > , <v0,v2 >, <v2,v3 >,<v3,v0 > }
CAC - 6
7.1.1 图的定义和术语
2. 图的相关术语 （1）无向图：若图G中所有边是没有方向的，则称G为无向图。 （2）有向图：若图G中所有顶点间的连线是有方向的，则称G为有向图。 （3）顶点：数据元素Vi称为顶点。 （4）边和弧：P(Vi,Vj)表示在顶点Vi和Vj之间有线相连，如果是无向图， 则称该线为边；在有向图中，则称该连线为弧。边用顶点的无序偶对(Vi， Vj)表示，弧用有序偶对< Vi，Vj >表示。 （5）弧头和弧尾：有序偶对的第一个结点称为始点（或弧尾，即不带箭 头的一端），有序偶对的第二个结点称为终点（或弧头，即带箭头的一 端）。
CAC - 2
CAC - 3
7.1 图的定义和术语
7.1.1 图的定义和术语
1. 图的定义（graph）
图G由两个集合构成，记作G=<V,E> ，其中V是顶点的非空有限集合，
E是顶点间关系----边的有限集合，边是顶点的无序对或有序对集合。 。
【例】 V0
V1
V2
V3
V4
无序对(vi,vj)： 用连接顶点vi、vj的线段
V0
V1
V0
V1
V2
V3
V2
V3
两个强连通分量
CAC - 17
练习
具有n个顶点的强连通图至少有多少条边？是什么形状？
分析：强连通图是针对有向图而言的。由于强连通图要求 图中任何2个顶点之间能够连通，因此每个顶点至少要有一条 以该顶点为终点（弧头）和出发点（弧尾）的弧，每个顶点 的入度和出度至少各为1，即顶点的度至少为2。
边或弧
G2=<V2,E2> V2={ v0 ,v1,v2,v3 } E2={ <v0,v1 > , <v0,v2 >, <v2,v3 >,<v3,v0 > }
CAC - 6
7.1.1 图的定义和术语
2. 图的相关术语 （1）无向图：若图G中所有边是没有方向的，则称G为无向图。 （2）有向图：若图G中所有顶点间的连线是有方向的，则称G为有向图。 （3）顶点：数据元素Vi称为顶点。 （4）边和弧：P(Vi,Vj)表示在顶点Vi和Vj之间有线相连，如果是无向图， 则称该线为边；在有向图中，则称该连线为弧。边用顶点的无序偶对(Vi， Vj)表示，弧用有序偶对< Vi，Vj >表示。 （5）弧头和弧尾：有序偶对的第一个结点称为始点（或弧尾，即不带箭 头的一端），有序偶对的第二个结点称为终点（或弧头，即带箭头的一 端）。
数据结构课后习题答案第七章
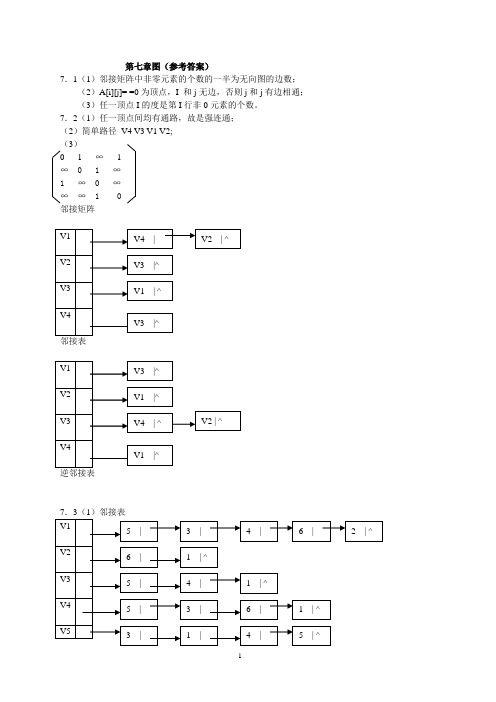
第七章图（参考答案）7．1（1）邻接矩阵中非零元素的个数的一半为无向图的边数；（2）A[i][j]= =0为顶点，I 和j无边，否则j和j有边相通；（3）任一顶点I的度是第I行非0元素的个数。
7．2（1）任一顶点间均有通路，故是强连通；（2）简单路径V4 V3 V1 V2;（3）0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表（2）从顶点4开始的DFS序列：V5,V3,V4,V6,V2,V1（3）从顶点4开始的BFS序列：V4,V5,V3,V6,V1,V27．4（1）①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j，则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路，退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if （!visited[k]）dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略，本算法判断一邻接表为存储结构的图g种，是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf （” 顶点”,i,”和顶点”,j,”有路径”）；else printf （” 顶点”,i,”和顶点”,j,”无路径”）；}// void connect_DFS(2)宽度优先遍历全程变量，调用函数与（1）相同，下面仅写宽度优先遍历部分。
数据结构(C语言版) 第七章 图
路径与连通性
路径、简单路径、回路(环)、简单回路
顶点之间的连通性、无向连通图、有向强连通
图
4/46
7.1 图的定义和术语(3)
路径与连通性
对于有向图G1
V1V3V4V1V2 是从V1 到V2 的路径, 不是简单路径；
V1V2是简单路径; V1V3V4V1V3V4V1是环,不是简单环; V1V3V4V1是简单环。
3/46
7.1 图的定义和术语(2)
有向图
弧<v,w> ∊ E (v,w ∊V)，w为弧头, v为弧尾; 顶点v
邻接到顶点w，顶点w 邻接自顶点v，弧< v, w >和 顶点v、w相关联。
顶点v 的入度是以v 为弧头的弧的数目,记为ID(v); v 的出度是以v为弧尾的弧的数目,记为OD(v); v 的度是TD(v) = ID(v) + OD(v)。
}VNode, AdjList[MAX_VERTEX_NUM];
这种存储结构适合于进行first_adj(G,v) 找v的第一个邻接点的操作
邻接矩阵的方法适合存储稠密图
26/46
7.2.2 邻接表--- 链式存储结构
邻接表是一种顺序存储与链式结构相结 合的存储方式，类似于树的孩子链表。
对每个顶点建立一个单链表，第i个单链 表中的结点表示依附于顶点vi的边。
邻接矩阵
从邻接矩阵M中可以看出该图 共有（ ）个顶点；如果是有 向图该图共有（ ）条弧，如 果是无向图，则共有（ ）边。
AB CD
G
25/46
邻接矩阵存储的特点
无向图的邻接矩阵是对称的，对n个顶 点的无向图只需要存入下三角矩阵，即 需要n(n-1)/2个存储单元。
有向图的邻接矩阵所需要的存储单元不 一定，需要N*N个存储单元
数据结构-第7章图答案
7.3 图的遍历 从图中某个顶点出发游历图，访遍图中其余顶点， 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发，访问此顶点，然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图，直至图中所有和V0有路径相通的顶点都被访 问到，若此时图中尚有顶点未被访问，则另选图中 一个未曾被访问的顶点作起始点，重复上述过程， 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
数据结构第七章--图(严蔚敏版)
9个顶点 个顶点
8个顶点的无向图最多有 条边且该图为连通图 个顶点的无向图最多有28条边且该图为连通图 个顶点的无向图最多有 连通无向图构成条件:边 顶点数 顶点数-1)/2 顶点数*(顶点数 连通无向图构成条件 边=顶点数 顶点数 顶点数>=1,所以该函数存在单调递增的单值反 顶点数 所以该函数存在单调递增的单值反 函数,所以边与顶点为增函数关系 所以28个条边 函数 所以边与顶点为增函数关系 所以 个条边 的连通无向图顶点数最少为8个 所以28条边的 的连通无向图顶点数最少为 个 所以 条边的 非连通无向图为9个 加入一个孤立点 加入一个孤立点) 非连通无向图为 个(加入一个孤立点
28
无向图的邻接矩阵为对称矩阵
2011-10-13
7.2
图的存储结构
Wij 若< vi,vj > 或<vj,v i > ∈E(G)
若G是网（有权图），邻接矩阵定义为 是网（有权图）， ），邻接矩阵定义为
A [ i，j ] = ， 0或 ∞
如图： 如图：
V1
若其它
V2
3 4
2
V3
2011-10-13
C
A
B
D 2011-10-13 (a )
3
Königsberg七桥问题
• Königsberg七桥问题就是说，能否从某点出发 通过每桥恰好一次回到原地？
C
C
A B
．
A D
B
D (a)
2011-10-13
(b)
4
第七章 图
7.1 图的定义 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
2011-10-13
8个顶点的无向图最多有 条边且该图为连通图 个顶点的无向图最多有28条边且该图为连通图 个顶点的无向图最多有 连通无向图构成条件:边 顶点数 顶点数-1)/2 顶点数*(顶点数 连通无向图构成条件 边=顶点数 顶点数 顶点数>=1,所以该函数存在单调递增的单值反 顶点数 所以该函数存在单调递增的单值反 函数,所以边与顶点为增函数关系 所以28个条边 函数 所以边与顶点为增函数关系 所以 个条边 的连通无向图顶点数最少为8个 所以28条边的 的连通无向图顶点数最少为 个 所以 条边的 非连通无向图为9个 加入一个孤立点 加入一个孤立点) 非连通无向图为 个(加入一个孤立点
28
无向图的邻接矩阵为对称矩阵
2011-10-13
7.2
图的存储结构
Wij 若< vi,vj > 或<vj,v i > ∈E(G)
若G是网（有权图），邻接矩阵定义为 是网（有权图）， ），邻接矩阵定义为
A [ i，j ] = ， 0或 ∞
如图： 如图：
V1
若其它
V2
3 4
2
V3
2011-10-13
C
A
B
D 2011-10-13 (a )
3
Königsberg七桥问题
• Königsberg七桥问题就是说，能否从某点出发 通过每桥恰好一次回到原地？
C
C
A B
．
A D
B
D (a)
2011-10-13
(b)
4
第七章 图
7.1 图的定义 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
2011-10-13
《数据结构教学课件》第7章.ppt
❖设图 A = (V, E) 有 n 个顶点，则图的邻接矩阵是一个二维数 组 A.Edge[n][n]，定义为：
1, 如果< i, j > E 或者 (i, j则
例1：
v1
v2
A
v3
v4
v5
顶点表： （ v1 v2 v3 v4 v5 ）
邻接矩阵： 0 10 0 01 0 v1
与v2是连通的。如果图中任意一对顶点都是连通的, 则称此图是连通图。 非连通图的极大连通子图叫做连通分量。
7
强连通图：在有向图中, 若对于每一对顶点vi和vj, 都存在一条
从vi到vj和从vj到vi的路径, 则称此图是强连通图。 非强连通图的极大强连通子图叫做强连通分量。
有两类图形 不在本章讨 论之列：
顶点的入度=第i列元素之和。ID( Vi )= A.Edge[ j ][i ] 顶点的度=第i行元素之和+第i列元素之和, 即：TD(Vi)=OD( Vi ) + ID( Vi )
有向图中，边数接近n(n-1)
子 图： 设有两个图 G＝(V, E) 和 G’＝(V’, E’)。若 V’ V 且
E’ E, 则称 图G’ 是 图G 的子图。
6
带权图：即边上带权的图。其中权是指每条边可以标上 具有某种含义的数值（即与边相关的数）。
网 络：＝带权图
连通图： 在无向图中, 若从顶点v1到顶点v2有路径, 则称顶点v1
无向完全图
无向图(树)
有向图 有向完全图
n(n-1)/2 条边
n(n-1) 条边
G1的顶点集合为V(G1)={0,1,2,3} 边集合为E(G1)={(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)}
数据结构课件
while (i>0)
{
/*读入顶点对号,建立边表*/
e++；
/*合计边数 */
p = (pointer)malloc(size(struct node))；/*生成新旳邻接点序号为j旳表结点*/
p-> vertex = j;
p->next = ga->adlist[i]．first；
ga->adlist[i].first = p；
三个强连通分量
第七章 图
权：图旳边具有与它有关旳数, 称之为权。这种带 权图叫做网络。
10
1
6
15
27 5
12
3 76
9
8
6 3
4
16
7
有向权图
60
AB 40 80 C源自307535
D
E
45
无向权图
第七章 图
生成树：连通图G旳一种子图假如是一棵包 括G旳全部顶点旳树，则该子图称为G旳生成
树；显然，n个顶点旳生成树具有n-1条边
scanf (“%d”， &(ga->n))；
for (i =1; i<= ga->n; i++)
{
/*读入顶点信息，建立顶点表*/
scanf (“ \n %c”， &( ga->adlist［i］．data) )
；
ga->adlist［i］．first = NULL； ｝
e = 0； /*开始建邻接表时，边数为0*/
ga->edges[i][j] = 0；
for (k = 0；k<ga->e；k++) /*读入边旳顶点编号和权值，建立邻接矩阵*/
相关主题