C样条
样条曲线如何变成多段线 c语言

一、概述样条曲线在计算机图形学和数学建模中被广泛应用,其优雅的曲线形状和高阶平滑性使其成为数字化设计领域的重要工具。
然而,计算机处理样条曲线需要离散化的数据结构,这就需要将样条曲线表示成多段线段。
在C语言中,实现样条曲线向多段线的转换是一个常见的问题,而解决这个问题可以加深我们对样条曲线和多段线的理解,并为更复杂的图形处理算法奠定基础。
二、样条曲线和多段线的概念1. 样条曲线样条曲线是由一系列插值点确定的平滑曲线,通常使用一个或多个多项式函数来逼近实际曲线。
根据插值点的不同分布和连接方式,可以得到不同类型的样条曲线,如自然样条、Hermite样条等。
2. 多段线多段线是由一系列线段组成的曲线,每个线段由起点和终点确定,相邻线段之间有一定的连接条件。
多段线通常用于离散表示曲线,在计算机图形学中得到广泛应用。
三、从样条曲线到多段线的转换1. 分割样条曲线我们需要将样条曲线分割成若干个小段。
这一步通常使用离散化算法,将曲线上的点均匀取样或按照一定规则选取插值点,然后通过连接相邻插值点来得到线段。
2. 近似曲线分割得到的线段通常是容易计算的、直线性质的线段,为了得到更接近原曲线的多段线,我们需要进行线段间的平滑处理。
通常的方法是通过插值算法,在相邻线段的连接处进行平滑处理,使得转换后的多段线与原样条曲线尽可能接近。
3. 实现算法在C语言中,我们可以利用数值计算库和线性代数库来实现样条曲线到多段线的转换算法。
通过对插值点的处理、线段间的连接和平滑处理,我们可以编写一段高效、可靠的代码来实现这一转换过程。
四、问题与挑战1. 数据精度在样条曲线到多段线的转换过程中,我们需要考虑数据的精度和误差问题。
特别是在高阶样条曲线和复杂曲线形状的情况下,数据的精度要求更高,这就需要我们在算法实现中考虑如何避免数据丢失和精度损失的问题。
2. 算法效率样条曲线到多段线的转换是一个复杂的计算过程,特别是在处理大规模数据时,算法的效率成为一个关键问题。
二次样条插值及其C语言的实现

for(i=1;i<11;i++)
{
u[i]=(x[i]-x[i-1])/(x[i+1]-x[i-1]); //μ1~μ10的求解公式
v[i]=1-u[i]; //λ1~λ10的求解公式
g[i]=(6/(x[i+1]-x[i-1]))*((y[i+1]-y[i])/(x[i+1]-x[i])-(y[i]-y[i-1])/(x[i]-x[i-1])); //g1~g10的求解公式
}
for(i=0;i<11;i++)
{
printf("[ %.2f, %.2f ] :\n",x[i],x[i+1]);
printf("S= %fx^3+%fx^2+%fx+%f\n",X3[i+1],X2[i+1],X1[i+1],X0[i+1]);
printf("\n");
}
}
、最小二乘拟合函数:
int i,j=0;
int AllD=1; //三角对阵的行列式
double Mv=1,Mu=1; //Mv表示λ1*λ2*…*λ10,Mu表示μ1*μ2*…*μ10
double M[12],X3[11],X2[11],X1[11],X0[11]; //M[12]用于存放M0~M11,X3[11]用于存放x^3的系数,X2[11]用于存放x^2的系数,
}
g[0]=(6/(x[1]-x[0]))*((y[1]-y[0])/(x[1]-x[0])-0.75); //g0的求解公式
(完整)三次样条插值的C程序(很全啊)

三次样条插值 C/C++程序(自己整理的) 具体推导看书<<数值分析〉〉 code:#include <iostream> using namespace std;(完整)三次样条插值的 C 程序(很全啊)const int MAXN = 100;int n; double x[MAXN], y[MAXN]; //下标从 0。
n double alph[MAXN], beta[MAXN], a[MAXN], b[MAXN]; double h[MAXN]; double m[MAXN]; //各点的一阶导数;inline double sqr(double pa) { return pa * pa;}double sunc(double p, int i) {[i]return (1 + 2 * (p — x[i]) / (x[i + 1] - x[i])) * sqr((p - x[i + 1]) / (x[i + 1] — x[i])) * y+ (1 + 2 * (p — x[i + 1]) / (x[i] - x[i + 1])) * sqr((p - x[i]) / (x[i + 1] — x [i])) * y[i + 1]+ (p - x[i]) * sqr((p — x[i + 1]) / (x[i] - x[i + 1])) * m[i] + (p — x[i + 1]) * sqr((p — x[i]) / (x[i + 1] — x[i])) * m[i + 1]; }int main() { int i, j;double xx;(完整)三次样条插值的 C 程序(很全啊)freopen("threeInsert.in", "r", stdin);scanf(”%d", &n);for (i = 0; i <= n; i++) scanf(”%lf%lf”, &x[i], &y[i]);// scanf("%lf%lf”, &m[0], &m[n]);for (i = 0; i <= n - 1; i++) h[i] = x[i + 1] - x[i];//第一种边界条件//alph[0] = 0; alph[n] = 1; beta[0] = 2 * m[0]; beta[n] = 2 * m[n];//第二种边界条件alph[0] = 1; alph[n] = 0; beta[0] = 3 * (y[1] — y[0]) / h[0]; beta[n] = 3 * (y[n] - y[n — 1] / h [n — 1]);for (i = 1; i 〈= n - 1; i++) { alph[i] = h[i — 1] / (h[i - 1] + h[i]); beta[i] = 3 * ((1 - alph[i]) * (y[i] — y[i — 1]) / h[i - 1] + alph[i] * (y[i + 1] — y[i]) / h[i]);} a[0] = — alph[0] / 2; b[0] = beta[0] / 2;for (i = 1; i <= n; i++) { a[i] = — alph[i] / (2 + (1 — alph[i]) * a[i — 1]); b[i] = (beta[i] - (1 — alph[i]) * b[i - 1]) / (2 + (1 - alph[i]) * a[i — 1]);} m[n + 1] = 0;for (i = n; i 〉= 0; i--) { m[i] = a[i] * m[i + 1] + b[i];} scanf("%lf”, &xx);for (i = 0; i < n; i++) { if (xx 〉= x[i] && xx <= x[i + 1]) break;} printf(”%lf\n", sunc(xx, i));return 0; }(完整)三次样条插值的 C 程序(很全啊)#include<iostream〉 #include<iomanip〉 using namespace std;const int MAX = 50; float x[MAX], y[MAX], h[MAX];//变量设置:x 为各点横坐标;y 为各点纵坐标;h 为步长 float c[MAX], a[MAX], fxym[MAX];float f(int x1, int x2, int x3)/*****************求差分函数(含三个参数)**** ************************/ {float a = (y[x3] — y[x2]) / (x[x3] — x[x2]); float b = (y[x2] — y[x1]) / (x[x2] - x[x1]); return (a - b)/(x[x3] — x[x1]); }void cal_m(int n)/***********************用追赶法求解出弯矩向量 M…… ***************************/ {float B[MAX]; B[0] = c[0] / 2;for(int i = 1; i 〈 n; i++)(完整)三次样条插值的 C 程序(很全啊)B[i] = c[i] / (2 - a[i]*B[i-1]);//fxym[0] = fxym[0] / 2; for(i = 1; i 〈= n; i++)fxym[i] = (fxym[i] - a[i]*fxym[i-1]) / (2 - a[i]*B[i-1]); for(i = n—1; i >= 0; i--)fxym[i] = fxym[i] — B[i]*fxym[i+1]; } void printout(int n);int main(){int n,i; char ch;do{cout〈〈"请输入已知断点个数:”;cin〉>n;for(i = 0; i 〈= n; i++){cout<<"Please put in X"〈〈i〈〈’:’;cin〉>x[i];//cout<<endl;cout〈<"Please put in Y”<〈i<〈’:’;cin>>y[i]; //cout<〈endl;}(完整)三次样条插值的 C 程序(很全啊)for(i = 0; i < n; i++) //求步长;其数组值较之 x,y 个数少一 h[i] = x[i+1] - x[i];cout<<”Please 输入边界条件\n 1: 已知两端的一阶导数\n 2:两端的二阶 导数已知\n 默认:自然边界条件\n”;int t; float f0, f1; cin>〉t; switch(t) { case 1:cout<<"Please put in Y0\' Y”<〈n<〈”\'\n";//显示数据为 Y0' 至 Yn’,即断点的一阶导数cin>>f0>〉f1; c[0] = 1; a[n] = 1; fxym[0] = 6*((y[1] - y[0]) / (x[1] - x[0]) - f0) / h[0]; fxym[n] = 6*(f1 — (y[n] - y[n—1]) / (x[n] - x[n—1])) / h[n—1]; break; case 2:cout〈<”Please put in Y0\" Y”<〈n<〈"\”\n”;//显示数据为 Y0” 至 Yn”,即断点的二阶导数 cin>>f0>>f1; c[0] = a[n] = 0; fxym[0] = 2*f0; fxym[n] = 2*f1; break; default:cout<<"不可用\n";//待定};//switch(完整)三次样条插值的 C 程序(很全啊)for(i = 1; i 〈 n; i++)fxym[i] = 6 * f(i—1, i, i+1);//调用差分函数(only!)for(i = 1; i < n; i++){a[i] = h[i—1] / (h[i] + h[i-1]);c[i] = 1 — a[i];}a[n] = h[n—1] / (h[n—1] + h[n]);cal_m(n);//调用弯矩函数(only!)cout〈<"\n 输出三次样条插值函数:\n”;printout(n);//调用求解三次样条插值函数;函数输出cout〈<"Do you to have anther try ? y/n :"; cin〉>ch; } while(ch == ’y' || ch == ’Y’); return 0; } void printout(int n)/***************求三次样条插值函数(因已知断点个数 而异)***********************/ { cout〈〈setprecision(6);//通过操作器 setprecision()设置有效位数;其为头文件 〈iomanip。
二次样条插值及其C语言的实现范文

if(s == NULL)
{
printf("内存分配失败\n");
exit (0);
}
t = (double *)calloc(n,sizeof(double));
if(t == NULL)
{
printf("内存分配失败\n");
exit (0);
}
b = (double *)calloc(n,sizeof(double));
if(b == NULL)
{
printf("内存分配失败\n");
exit (0);
}
z = 0;
for(i=1;i<=n;i++)
z=z+x[i-1]/n;
b[0]=1;
d1=n;
p=0;
c=0;
for(i=1;i<=n;i++)
if(j%4==0) printf("\n");
}
printf("\n");
j=0;
printf("g(0) to g(11):\n");
for(i=0;i<12;i++)
{
printf(" %f ",g[i]);
j++;
if(j%4==0) printf("\n");
}
for(i=1;i<=12;i++)
return(1);
}
4、上机调试说明:
、三次样条差值函数:
塑料标准样条四个标准

面积不小于10*10,厚度3-6.4
UL-94
阻燃样条
长:125±5宽:13.0±0.5厚:最大不超过13mm,0.75+0.05,1.5+0.1,3.0+0.2,
ISO
拉伸样条
长:大于150 宽:10.0±0.2厚:4.0±0.2
弯曲样条
简支梁:长:80±2 宽:10.0±0.2 厚:4.0±0.2跨距:16±1厚度
热变形样条
长:120.0±10.0 厚:3.0-4.2 宽:9.8-15
长:80±2.0 厚:4±0.2 宽:10±0.2
洛氏硬度
厚度:至少6mm面积:至少可以测试五个点,点与点之间距离不少于10mm,点离样片边缘不少于10mm
测试标准号对照
项目
ASTM标准
项目
ISO标准
项目
DIN标准
项目
GB标准
TS:
冲击样条
长:64±2.0 厚:12.70±0.20 宽:3.0-12.7
缺口剩余厚度:10.2±0.05 缺口底角半径:0.25R±0.05 缺口弧度:45。±1.
洛氏硬度样块
面积不小于50*50,厚度不小于六毫米
维卡样条
面积不小于10*10,厚度:3-6.5
热变形样条
长:127±2 宽: 13±0.2 厚3-13
MI
DIN EN ISO1133
MI
GB3682
HDT
D648
HDT
ISO75
HDT
DIN EN ISO75
HDT
GB1643
维卡
D1525
维卡
ISO306
维卡
DIN ENISO306
塑料三大标准(美标 ISO 国标)测试样条规格
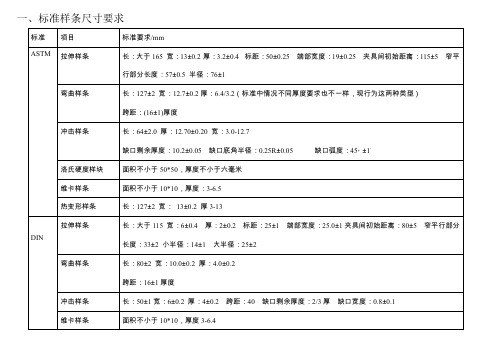
项目
TS: EL: FS: FM: 缺口冲击 无缺口冲 击 MI HDT 维卡 密度 洛氏硬度
ISO 标准
ISO527 ISO527 ISO178 ISO178 ISO180/ISO179 ISO180 ISO1133 ISO75 ISO306 ISO1183 ISO2039/2
项目
TS: EL: FS: FM: 缺口冲击 无缺口冲 击 MI HDT 维卡 密度 洛氏硬度
阻燃性
阻燃性
简支梁:长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:16±1 厚度
冲击样条
长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:62-0.0+0.5 长:80±2 宽:10.0±0.2 宽:4.0±0.2(悬臂梁 长:80±2 宽:10.0±0.2 宽:4.0±0.2(悬臂梁 无缺口) 缺口)缺口剩余厚度:8.0±0.2
DIN 标准
DIN EN ISO527 DIN EN ISO527 DIN EN ISO178 DIN EN ISO178 DIN EN ISO180/ISO179 DIN EN ISO180 DIN EN ISO1133 DIN EN ISO75 DIN EN ISO306 DIN EN ISO1183 /
长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:16±1 厚度
冲击样条 维卡样条
长:50±1 宽:6±0.2 厚:4±0.2 面积不小于 10*10,厚度 3-6.4
跨距:40
缺口剩余厚度:2/3 厚
缺口宽度:0.8±0.1
UL-94 ISO
阻燃样条 拉伸样条 弯曲样条
长:125±5 宽:13.0±0.5 厚:最大不超过 13mm ,0.75+0.05,1.5+0.1,3.0+0.2, 长:大于 150 宽:10.0±0.2 厚:4.0±0.2
塑料标准样条(四个标准)
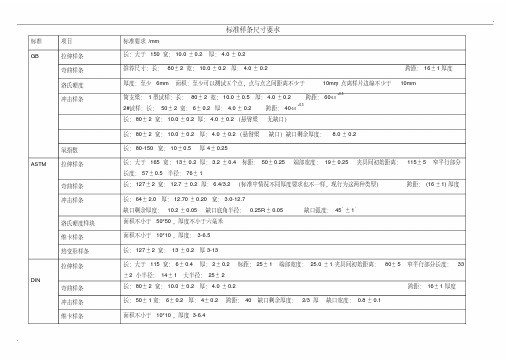
标准样条尺寸要求标准项目标准要求/mmGB 拉伸样条长:大于150 宽:10.0±0.2厚:4.0±0.2弯曲样条推荐尺寸:长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:16±1厚度洛氏硬度厚度:至少6mm 面积:至少可以测试五个点,点与点之间距离不少于10mm,点离样片边缘不少于10mm冲击样条简支梁:1型试样:长:80±2 宽:10.0±0.5 厚:4.0±0.2 跨距:60-0.0+0.52#试样:长:50±2 宽:6±0.2 厚:4.0±0.2 跨距:40-0.0+0.5长:80±2 宽:10.0±0.2厚:4.0±0.2(悬臂梁无缺口)长:80±2 宽:10.0±0.2 厚:4.0±0.2(悬臂梁缺口)缺口剩余厚度:8.0±0.2氧指数长:80-150 宽:10±0.5 厚4±0.25ASTM 拉伸样条长:大于165 宽:13±0.2厚:3.2±0.4标距:50±0.25 端部宽度:19±0.25 夹具间初始距离:115±5 窄平行部分长度:57±0.5 半径:76±1弯曲样条长:127±2 宽:12.7±0.2厚:6.4/3.2(标准中情况不同厚度要求也不一样,现行为这两种类型)跨距:(16±1)厚度冲击样条长:64±2.0 厚:12.70±0.20 宽:3.0-12.7缺口剩余厚度:10.2±0.05 缺口底角半径:0.25R±0.05 缺口弧度:45。
±1.洛氏硬度样块面积不小于50*50,厚度不小于六毫米维卡样条面积不小于10*10,厚度:3-6.5热变形样条长:127±2 宽: 13±0.2 厚3-13DIN 拉伸样条长:大于115 宽:6±0.4厚:2±0.2 标距:25±1 端部宽度:25.0±1夹具间初始距离:80±5 窄平行部分长度:33±2 小半径:14±1 大半径:25±2弯曲样条长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:16±1厚度冲击样条长:50±1宽:6±0.2 厚:4±0.2 跨距:40 缺口剩余厚度:2/3厚缺口宽度:0.8±0.1维卡样条面积不小于10*10,厚度3-6.4UL-94 阻燃样条长:125±5宽:13.0±0.5厚:最大不超过13mm ,0.75+0.05,1.5+0.1,3.0+0.2,ISO 拉伸样条长:大于150 宽:10.0±0.2厚:4.0±0.2弯曲样条简支梁:长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:16±1厚度冲击样条长:80±2 宽:10.0±0.2 厚:4.0±0.2 跨距:62-0.0+0.5 长:80±2 宽:10.0±0.2宽:4.0±0.2(悬臂梁无缺口)长:80±2 宽:10.0±0.2 宽:4.0±0.2(悬臂梁缺口)缺口剩余厚度:8.0±0.2维卡样条厚:3-6.5 面积:不少于10mm2热变形样条长:120.0±10.0 厚:3.0-4.2 宽:9.8-15长:80±2.0 厚:4±0.2 宽:10±0.2洛氏硬度厚度:至少6mm 面积:至少可以测试五个点,点与点之间距离不少于10mm,点离样片边缘不少于10mm测试标准号对照项目ASTM标准项目ISO标准项目DIN标准项目GB标准TS:D638 TS:ISO527 TS:DIN EN ISO527 TS:GB1040 EL:D638 EL:ISO527 EL:DIN EN ISO527 EL:GB1040 FS:D790 FS:ISO178 FS:DIN EN ISO178 FS:GB9341 FM:D790 FM:ISO178 FM:DIN EN ISO178 FM:GB9341IS1/4“D256 缺口冲击ISO180/ISO179 缺口冲击DIN ENISO180/ISO179 缺口冲击GB1043/GB1843(D)IS/18”D256 无缺口冲击ISO180 无缺口冲击DIN EN ISO180 无缺口冲击GB1043/GB1843(D)MI D1238 MI ISO1133 MI DIN EN ISO1133 MI GB3682 HDT D648 HDT ISO75 HDT DIN EN ISO75 HDT GB1643 维卡D1525 维卡ISO306 维卡DIN EN ISO306 维卡GB1633 密度D792 密度ISO1183 密度DIN EN ISO1183 密度GB1033洛氏硬度D785 洛氏硬度ISO2039/2 洛氏硬度/ 洛氏硬度GB9342 收缩率D955 收缩率ISO294 收缩率/ 收缩率GB/T1037 吸水率D570 吸水率ISO62 吸水率/ 吸水率GB/T1034球压痕硬度/ 球压痕硬度ISO2039/1 球压痕硬度DIN ENISO2039/1 球压痕硬度GB3398阻燃性UL-94 阻燃性ISO1210阻燃性DIN EN ISO1210阻燃性GB2048(水)TL 1010(大众标准)GB2049(垂)。
带钢C翘样条有限元法

(7)
其中
Cin ( x) =
k = −1
∑ cos(
n +1
n +1 2ikπ 2ikπ )j j ( x) , Sin ( x) = ∑ sin( )j j ( x) n n k = −1
为样条基函数组成的正交函数系。 pij 等为正交函数的插值系数,根据实测数据可快速计算出,然后再转化 为标准样条插值系数。 由此可以得到
(11)
(12)
T 而 ∫∫ N x N x dxdy 等矩阵的结果可以解析的得到,见文献[8][9]等。 Ω
( i , j = x, y , z )
(3)
将(1)带入上式,可以将本构关系简化为 E1 Eν E1 Eν = σx (ε x + νε y ) + 1 12 c0 + f x , = σy (ε y + νε x ) + 1 12 c0 + f y (1 −ν 12 ) (1 −ν 1 ) (1 −ν 12 ) (1 −ν 1 ) ,σz = τ xy Gγ xy + f xy =
T fx Nx + f xy N T y 1 T T P= − ∫∫ f y N y + f xy N x 2Ω fz T Nx NCx + N T y NC xy 1 T − ∫∫ N T dxdy = y NC y + N x NC xy dxdy 2Ω NCz
+ 1 ( f x ε x + f y ε y + f z c0 + f xy γ xy )d Ω 2 ∫∫ Ω
Hale Waihona Puke (5)4C 翘分析的样条有限元
塑料标准样条(四个标准)
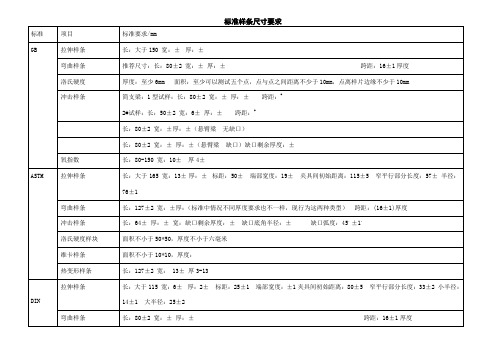
维卡样条
厚: 面积:不少于10mm2
热变形样条
长:± 厚: 宽:
长:80± 厚:4± 宽:10±
洛氏硬度
厚度:至少6mm面积:至少可以测试五个点,点与点之间距离不少于10mm,点离样片边缘不少于10mm
测试标准号对照
项目
ASTM标准
项目
ISO标准
项目
DIN标准
项目
GB标准
TS:
D638
TS:
ISO527
TS:
DIN EN ISO527
TS:
GB1040
EL:
D638
EL:
ISO527
EL:
DIN EN ISO527
EL:
GB1040
FS:
D790
FS:
ISO178
FS:
DIN EN ISO178
FS:
GB9341
FM:
D790
FM:
ISO178
2#试样:长:50±2 宽:6± 厚:± 跨距:+
长:80±2 宽:±厚:±(悬臂梁 无缺口)
长:80±2 宽:± 厚:±(悬臂梁 缺口)缺口剩余厚度:±
氧指数
长:80-150 宽:10± 厚4±
ASTM
拉伸样条
长:大于165 宽:13±厚:±标距:50± 端部宽度:19± 夹具间初始距离:115±5 窄平行部分长度:57± 半径:76±1
维卡样条
面积不小于10*10,厚度
UL-94
阻燃样条
长:125±5宽:±厚:最大不超过13mm,+,+,+,
ISO
三次C—Cardinal样条曲线及曲面

个参数 可调 整曲线 的形状 : 一 O时极限 曲线 为通常 当 的 F ruo eg sn曲线、B z r fi 曲线 、 e B样条曲线。
近年来 , _ ̄i c B z r曲线的研究有 了进一步 的发展 , e 已从
三次推广到 四次 、 五次及 一般 的 ”次 曲线[ ; 2 曲线 可方便 ] 地表示圆弧[ , 5 也可用于构造工程 曲面 。 ] j 2 ( B样条曲线/ 曲面也有进一步 的研究 、 推广[ 及一 7 ]
文献标识码 : A
函数 , 经适 当变换 , 得到一组基 函数 。以此构 造的 曲线 , 除
1 引言
C 曲线是用 {i ,O ,, } . s tCStt 1 为基底构 造 的一 系列 曲 n 线[ 包括 CF ruo ”, - eg s n曲线 、 - i 曲线 、 Cl e  ̄z r C B样条 曲线
维普资讯
C 31 5 / P N4-2 8 T
I S 1 0 — 3 X S N 0 7 1 0
计算机工程与科学
C M P E NG NE R NG 8 C E E O UT R E I E I L I NC S
20 0 6年第 2 卷第 2期 8
了首末两个型 值点外 , 插值所 有 其它 型值 点 ; 可 曲线 达到 C 连续 , 们称之 为 C C r i l 条 曲线 。与 以往 C 插 我 - adn 样 a 1 值 的曲线 不同的是 , 曲线 的每一 端有两 个可调参数 与 , 可对 曲线进行局部调整 而不影响 曲线 的连续性 , 有更好 具
meh d t p o et n lg u i ec r e x mpe h w ta h u v s r c a eU e Ofe- r c re to .I rp r i a ao o sw t t u v .E a lss o h t ec r e/ u f ec n b S d t ef m u s s ys hh t a r o v
c4d样条动力学,样条分裂扩散

c4d样条动力学,样条分裂扩散C4D样条动力学,即利用样条曲线进行物体运动与变形的技术,是计算机图形学中常用的技术之一。
该技术可以模拟真实物体在运动中产生的弯曲和弹性效果,使得图形的形态更加自然逼真。
本文将介绍样条动力学技术的基本原理及样条分裂扩散的应用。
一、样条动力学的基本原理样条动力学技术通过对曲线进行数学建模,模拟物体在运动中的弹性和形变。
在计算机图形学中,常用的样条曲线包括贝塞尔曲线、B 样条曲线和样条插值曲线等。
这些曲线可以用来描述物体的运动轨迹,并通过物理引擎的计算,实现相应的动态效果。
在样条动力学中,物体的形变可以通过对样条曲线进行控制点的调整来实现。
通过改变控制点的位置和弹性参数,可以使物体在运动过程中产生弹性效果。
同时,还可以通过添加约束条件,实现物体的碰撞检测和碰撞反应,使得物体之间的交互更加真实。
二、样条分裂扩散的应用样条分裂扩散是样条动力学技术中的一种常见应用,通过对样条曲线进行分裂和扩散,实现复杂形状的自动生成。
该技术广泛应用于计算机游戏、影视特效和工程模拟等领域。
在游戏开发中,样条分裂扩散可以用来生成树木、草地、山峰等自然景物。
通过对样条曲线的分裂和扩散,可以形成树木的枝干和叶子,使得游戏场景更加真实。
同时,还可以通过调整样条曲线的参数,控制树木的生长速度和形态,实现树木的动态变化。
在影视特效中,样条分裂扩散可以用来生成爆炸、火焰、液体等特效。
通过对样条曲线的分裂和扩散,可以模拟物体在爆炸或流动过程中的形变和变形。
同时,还可以通过调整样条曲线的参数,控制特效的形态和运动轨迹,实现逼真的视觉效果。
在工程模拟中,样条分裂扩散可以用来生成管道、线缆、绳索等模型。
通过对样条曲线的分裂和扩散,可以生成具有弯曲和弹性效果的模型。
同时,还可以通过添加约束条件,实现模型的稳定和真实的物理行为。
样条动力学技术是计算机图形学中常用的技术之一,通过对样条曲线进行数学建模,实现物体运动和变形的效果。
塑料三大标准 美标 ISO 国标 测试样条规格

二、测试标准号对照
项目 ASTM 标准 项目
ISO 标准
项目
DIN 标准
项目
GB 标准
TS: EL: FS: FM: IS1/4“
IS/18” MI HDT 维卡 密度
洛氏硬度
D638 D638 D790 D790 D256
D256 D1238 D648 D1525 D792 D785
TS: EL: FS: FM:
ISO527 ISO527 ISO178 ISO178
TS: EL: FS: FM:
缺口冲击 无缺口冲
击
ISO180/ISO179 ISO180
缺口冲击 无缺口冲
击
MI
ISO1133
MI
HDT
ISO75
HDT
维卡
ISO306
维卡
密度
ISO1183
密度
洛氏硬度 ISO2039/2 洛氏硬度
DIN EN ISO527 DIN EN ISO527 DIN EN ISO178 DIN EN ISO178 DIN EN ISO180/ISO179
收缩率
吸水率 球压痕硬
度
阻燃性
GB/T1037 GB/T1034
GB3398 GB2048(水) GB2049(垂)
跨距:(16±1)厚度
冲击样条
长:64±2.0 厚:12.70±0.20 宽:3.0-12.7 缺口剩余厚度:10.2±0.05 缺口底角半径:0.25R±0.05
缺口弧度:45。±1.
洛氏硬度样块
面积不小于 50*50,厚度不小于六毫米
维卡样条
面积不小于 10*10,厚度:3-6.5
热变形样条
cad样条曲线用途

cad样条曲线用途
CAD(计算机辅助设计)样条曲线是一种数学曲线,由一系
列相邻曲线段组成,通过插值和逼近方法得到。
它在CAD软
件中的应用非常广泛,具有以下几个主要用途:
1. 几何造型:CAD样条曲线可以用于绘制各种几何形状,如
曲线、曲面和体素模型等。
通过调整样条曲线的控制点或参数,可以创建出各种自然、流畅的几何形状,实现精确的造型设计。
2. 动画和影视特效:在计算机动画和影视特效制作中,CAD
样条曲线常用于描述物体的运动轨迹和形变变化。
通过调整样条曲线的参数或控制点,可以实现物体的平滑移动、形变和变形效果,使电影、电视剧和游戏中的动画更加真实和流畅。
3. 工程设计:CAD样条曲线在工程设计中广泛应用于各种产
品的造型设计和分析。
通过对样条曲线的参数进行调整,可以优化产品的曲线形状,提高其外观和性能。
同时,样条曲线还可用于分析产品的强度和变形等工程问题。
4. 数字雕刻和3D打印:在数字雕刻和3D打印领域,CAD样
条曲线常用于生成复杂的曲线和曲面模型。
通过对样条曲线进行插值和逼近,可以生成平滑、流畅的曲线和曲面,为后续的雕刻和打印操作提供准确的模型数据。
总之,CAD样条曲线是CAD软件中的重要工具,它可以用于造型设计、动画和影视特效、工程设计、数字雕刻和3D打印
等各个领域,帮助用户实现各种几何形状的绘制和分析。
Silverlight认证题(选择题)

0一、基础题(每题2分)1. 以下关于Silverlight应用程序的特点的说法,错误的是(D )A 支持丰富的数据格式和网络通信方式B 高质量的视频和音频C 使用现有的编程工具和.NET Framework编程模型D 和Flash一样,不支持搜索引擎优化(SEO)2 以下关于Silverlight应用程序的结构的说法,正确的是(A )A Silverlight 应用程一个派生自序必须有Application的类,负责初始化应用程序B Silverlight 应用程序最终编译成.xap文件,该文件符合W3C的XML标准、、Xaml文件符合C Silverlight 应用程序中必须有一个Page类,用于显示用户界面D Silverlight 应用程序必须运行在Aspxyem环境中3 以下关于Silverlight 应用程序的生命周期的说法,错误的是( B)A Silverlight 应用程序必须运行在本身的Runtime环境中B 先在客户端创建应用程序的执行环境,再下载Silverlight应用程序包(.xap文件)C 如果用户浏览器没有安装Silverlight.exe,则会提示用户下载安装D 在Silverlight 应用程序运行前,允许用户自定义启动画面4 以下关于XAML 的依赖属性的说法,错误的有是( A)A 依赖属性的访问方式与其他属性没有区别,通过"."运算符访问B 依赖属性必须由Static修饰C 依赖属性可以节约资源D 依赖属性必须使用DependencyProperty.Register()实现注册5 以下不属于XAML特性的是(D )A XAML 中的元素(标记)都对应.NET Framework中的某个类型B XAML 可以创建节点树C XAML 中通过元素和元素属性实现的功能都可以使用后台代码实现D XAML 中的元素不能被继承6 以下关于内容控件的说法,正确的是(A )A 内容控件都具有Content属性B ContentControl类直接派生自FormworkElement类C Border是内容控件D TextBlock是内容控件7 以下关于Grid控件的说法,错误的是( D)A Grid控件中的<RowDefinition>具有Height属性而没有Width属性B Grid控件中的<ColumnDefinition>具有Width属性而没有Height属性C Grid控件的布局作用类似于HTML中的<table>D Grid控件中必须有行和列的定义,才可以放置其他控件8 以下关于DataContext属性的说法,错误的是( C)A DataContext属性可以被一个元素的内部元素继承B 每个元素都具有DataContext属性C 如果父元素和子元素都具有DataContext属性,则父元素会覆盖子元素的属性值D 非列表控件在设置了DataContext属性之后才可以进行数据绑定9 以下关于数据绑定的描述,错误的是(B )A INotifyPropertyChanaged接口用于在数据源发生变化时通知Bind对象B Silverlight中的数据绑定与中的数据绑定没有区别C OneWay和TwoWay绑定模式必须实现INotifyPropertyChanged接口D 可以将数据对象作为XAML中的静态资源进行绑定10 以下对控件的描述,正确的有( B)A Popup控件ToolTip控件都用于为UI元素创建提示信息,并且可以自动隐藏B DataGrid控件中的列可以自动生成或在XAML中进行设计C ComboBox控件中的下拉列表项只能是静态创建的<ComboBoxItem>元素D Image元素的Source属性只能指向Silverlight程序中的图片11 以下关于全局样式的说法,错误的是(D )A 全局样式被定义为全局的静态资源B 全局样式和页面级别样式都通过Setter设置样式属性的值C Key属性值在全局样式中不能重复D 一种类型的控件只能定义一个全局样式12 以下关于控件模板的说法,错误的是(A )A 控件模板需要在App.xaml文件中定义,且必须作为全局静态资源进行定义B 控件模板能够使控件的外观,内容和结构保持一致C 控件模板可以使控件重用性更高, 有利于代码的维护D 控件只要具有Template属性,就可以定制模板13 以下关于路由事件的描述,不正确的有(C )A Silverlight中的路由事件就是事件冒泡B 路由事件是父控件接收和处理来自子控件的事件C 路由事件是子控件接收和处理来自父控件的事件D 鼠标事件MouseLeftButtonDown允许路由事件14 以下关于Silverlight用户控件的说法,不正确的有(C )A 所有的Silverlight用户界面都是由用户控件呈现B 用户控件只能被追加到其他的用户控件中进行呈现C 用户控件只能在当前应用程序中重用D 用户控件可以单独呈现15 以下关于自定义控件的说法,不正确的有(D )A 自定义控件可以在Silverlight类库创建,在任何Silverlight应用程序中重用B 自定义控件如果派生自Control类,则除非定制了控件模板,否则不会呈现任何UI界面C 自定义控件可以派生自现有的任何内置控件D 自定义控件不允许用户自己通过Content属性添加内容16 以下关于Path对象的描述,正确的有(AB )A Path可以绘制任何的Shape形状B Path对象的Data属性只能使用几何图形呈现内容C Path对象的Data属性中mini-language不区分大小写,例如,H和h绘制的水平线相同D Path对象在Data属性中通过mini-language绘制路径,C表示绘制二次方的贝赛尔曲线//注释C表示三次方的贝塞尔曲线,Q表示二次方贝塞尔曲线,A:椭圆曲线,Z结束命令17 以下关于画刷的描述,正确的有(B )A 图片刷ImageBrush必须与图片元素Image结合使用B 视频刷必须与MediaEelement元素结合使用C 线性渐变刷和径向渐变刷的作用完全相同D SolidColorBrush可以使用多种颜色填充元素18 以下关于Geometry图形和Shape形状之间的区别,说法正确的是(A )A Shape可以自我呈现B Geometry可以自我呈现C Geometry可以单独存在D Shape和Geometry绘制的都是3D图形19 以下关于元素变换的说法,错误的是( A)A RotateTransform默认按照逆时针方向进行旋转变换默认顺时针方向B ScaleTransform的ScaleX属性按照指定的比例沿X轴方向缩放变换C 矩阵变换通过修改结构体Matrix的矩阵实现D TransformGroup允许嵌套TransformGroup20 以下关于Image元素的Stretch属性的描述,错误的是( C)A 取值为None时,不拉伸图像B 取值为Uniform时,图像按比例拉伸,不破坏图像比例C 取值为Fill时,图像会填满规定的尺寸区域,不破坏图像比例D 取值为UniformToFill时,图像会被裁剪,但比例不会破坏21 以下关于WCF服务契约的描述,错误的是(D )A 服务契约必须以ServiceContact特性标识B 服务契约一般以接口定于C 服务契约中定义了服务操作,这些操作以OperationContract特性标识D 在一个WCF服务中可以没有服务契约22 以下关于WCF的终结点EndPoint的描述,正确的有( A)A WCF可以有一个或多个终结点B 地址指定了外部能够访问的操作契约指定了外部能够访问的操作BC说反了C 契约指定了终结点的位置地址制定了终结点的位置D 终结点中的绑定指定了它与外界通信的协议23 创建和调用WCF的步骤,正确的有(B )A 创建服务契约-> 自我承载服务-> 创建服务-> 客户端调用服务B 创建服务契约-> 创建服务-> 自我承载服务-> 客户端调用服务C 创建服务契约-> 创建服务-> 客户端调用服务-> 自我承载服务D 创建服务契约-> 创建服务-> 客户端调用服务-> IIS承载服务24 以下关于Silverlight调用WCF服务的说法,错误的是( BC)A Silverlight总是异步调用WCF服务B Silverlight只能调用同域的WCF服务// 注释,可以快于,加XMl文件C Silverlight调用的WCF服务必须寄宿在WEB服务器//注释,还可以自己承载D Silverlight默认不能跨域调用WCF服务25以下关于WCF服务器端配置的说法,错误的是( A)如果WCF服务由IIS承载,则不需要添加配置如果WCF服务是自我承载,可以通过配置或者托管代码监听和对外公开元数据如果文件可以是web.config,也可以是app.config配置文件中的endpoint节点用于配置服务器端终结点,包括地址绑定契约26 Silverlight中使用WebClient 对象与使用HttpWebRequest对象的区别在于( C)A WebClient是抽象类,HttpWebRequest不是抽象类// WebClient是实体类,HttpWebRestpuset是抽象类B HttpWebRequest通过事件实现异步调用C WebClient通过事件实现异步调用D WebClient回调函数运行在非UI线程上,所以回调函数中不能处理Silverlight控件27 以下关于用户独立存储空间的说法,不正确的是(A)A 操作系统独立存储空间的类位于System.IO命名空间下、、注释:SystemIO.IsolatedStorageFile中B 独立存储空间可以将数据永久存储在用户计算机中C 独立存储空间使用文件流保存文件D 独立存储空间存储在服务器端28 以下对于JSON数据序列化和反序列化的解释,错误的有(C )A Json数据可以使用第三方插件序列化B 反序列化是指将Json封装为实体对象C 序列化是指将Json封装为实体对象、、注释:序列化是将对象转化为Json 格式的字符串。
cad样条曲线围成的封闭区间的面积

一、概念解释在计算机辅助设计(CAD)中,样条曲线是一种由插值或者逼近算法生成的光滑曲线。
而样条曲线围成的封闭区间,即为由样条曲线所包围的闭合区域。
在CAD设计中,对于这样的封闭区间,我们通常需要计算其面积,以便进行后续的工程设计和分析。
二、样条曲线的特性1.光滑性:样条曲线通常具有很好的光滑性,能够较好地描述实际曲线和曲面的形状。
2.灵活性:样条曲线的控制点和节点参数的调节能够灵活地改变曲线的形状和特性。
3.精度:通过调整样条曲线的阶数和节点参数,能够达到所需的曲线拟合精度。
4.封闭性:多个样条曲线可以围成封闭区间,形成封闭的曲线区域。
三、计算封闭区间面积的方法在CAD设计中,计算样条曲线围成的封闭区间的面积通常可以采用数值计算的方法进行。
一种常用的方法是将封闭区间分割成若干小区域,然后利用数值积分的方法对每个小区域的面积进行计算,最后将所有小区域的面积相加得到封闭区间的总面积。
在实际的CAD软件中,通常会提供相应的功能模块来进行这样的计算。
四、个人观点和理解在CAD设计中,样条曲线围成的封闭区间的面积计算是一个常见而且重要的问题。
掌握好这一计算方法,能够帮助工程师更好地进行曲线和曲面的设计和分析工作。
对于CAD软件的开发和改进也具有一定的指导意义。
总结回顾通过本文的讨论,我们了解了CAD中样条曲线围成的封闭区间面积的计算方法,以及样条曲线的特性和应用。
对这一问题的深入理解,对于CAD工程设计和软件开发都具有一定的重要性。
在CAD设计中,样条曲线围成的封闭区间面积的计算是一个常见而且重要的问题。
掌握好这一计算方法,能够帮助工程师更好地进行曲线和曲面的设计和分析工作。
对于CAD软件的开发和改进也具有一定的指导意义。
希望本文的内容能够对你有所帮助,如有任何问题或意见,欢迎与我交流讨论。
样条曲线在CAD设计中有着广泛的应用,它不仅能够精确地描述曲线和曲面的形状,还能够通过调节控制点和节点参数来改变曲线的特性,具有较好的灵活性和精度。
c4d样条约束模型变形

c4d样条约束模型变形
在C4D(Cinema 4D)软件中,样条约束是一种常用的变形工具,可以用于对模型进行精确的控制。
通过样条约束,我们可以将模型沿着样条路径进行变形,从而实现各种复杂的动画效果。
下面是使用C4D样条约束模型变形的步骤:
1. 创建样条路径:首先,我们需要在C4D中创建一条样条路径。
这可以通过“样条工具”或“贝塞尔曲线工具”来完成。
样条路径可以是直线、曲线或任意形状的路径。
2. 添加样条约束:选中需要变形的模型,然后点击“添加样条约束”按钮,将样条路径拖拽到模型上。
这样,模型就被沿样条路径进行了约束。
3. 编辑样条路径:在样条约束的标签页中,我们可以对样条路径进行编辑,如调整控制点、改变样条类型等。
这些操作将实时反映在模型变形上。
4. 调整样条约束参数:在样条约束的标签页中,我们可以调整各种参数,如缩放、旋转、平移等,以实现对模型变形的精确控制。
5. 预览和调整:在完成样条约束设置后,我们可以预览动画效果,并根据需要对样条路径和约束参数进行调整,以达到理想的效果。
通过以上步骤,我们就可以使用C4D样条约束工具对模型进行变形了。
在实际操作中,还可以结合其他变形工具和技巧,如FFD(基本体素变形器)、网格变形器等,来实现更丰富的模型变形效果。
CAD中利用样条曲线进行平滑绘制技巧

CAD中利用样条曲线进行平滑绘制技巧在CAD设计中,我们经常需要绘制各种曲线,使设计更加流畅和美观。
其中,使用样条曲线是一种常见的技巧,能够帮助我们绘制出更加平滑的曲线。
下面将介绍如何在CAD软件中利用样条曲线进行平滑绘制的技巧。
首先,打开你的CAD软件,并选择画线工具。
然后,在命令行输入“spl”来调出样条曲线命令。
接下来,我们需要确定曲线的控制点。
控制点是决定曲线形状的重要因素。
你可以点击鼠标左键来设置控制点,根据你的需求设置多个点来确定曲线的形状。
在选择控制点时,要注意控制点的位置和数量。
过多或过少的控制点可能会导致曲线形状不理想。
一般来说,4-6个控制点之间可以绘制出平滑的曲线。
确定好控制点后,可以按回车键或点击鼠标右键来结束样条曲线命令。
此时,你将看到绘制出的样条曲线,它会根据你的控制点形成一条平滑的曲线。
如果你觉得曲线不够平滑或不满意,你可以使用修改命令来调整曲线的形状。
选择曲线对象,然后输入“splinedit”命令,你将看到一系列的控制点和曲线段。
你可以调整控制点的位置,来改变曲线的形状。
点击控制点,然后拖动它们到你想要的位置。
你还可以使用删除、添加和移动控制点的工具来对曲线进行更精确的调整。
另外,你还可以使用校正命令来平滑曲线。
选择曲线对象,然后输入“splinefit”命令。
CAD会自动平滑曲线,并重新定义控制点。
绘制完成后,你可以使用修剪命令来修剪曲线的多余部分,使它们符合你的设计要求。
选择修剪命令,然后选择需要修剪的曲线段和边界,按下回车键或右键来完成修剪。
最后,你可以选择曲线对象并进行进一步的修改,例如调整线型、颜色和线宽等。
根据你的需要,你还可以将曲线转换为实体或进行其他操作。
通过使用样条曲线技巧,你可以在CAD中绘制出更加平滑和自然的曲线。
这种技巧对于设计曲线较多的产品、图纸和建筑等领域非常有用。
尝试使用这些技巧,让你的设计更加出色!。
creo样条曲线标注角度

creo样条曲线标注角度
(最新版)
目录
1.Creo 样条曲线简介
2.样条曲线标注角度的方法
3.样条曲线标注角度的应用实例
4.总结
正文
一、Creo 样条曲线简介
Creo 是一款由美国 PTC 公司开发的计算机辅助设计(CAD)软件,广泛应用于工程领域。
在 Creo 中,样条曲线是一种常见的曲线类型,它具有通过指定控制点和调整参数来控制曲线形状的特点。
样条曲线可以实现较为复杂的曲线设计,因此在工程设计中有着广泛的应用。
二、样条曲线标注角度的方法
在 Creo 中,标注样条曲线角度的方法主要有以下两种:
1.使用“标注”命令:首先,在 Creo 中创建或打开样条曲线。
然后,选择“标注”命令,在样条曲线上点击,并输入所需的角度数值。
最后,点击“完成”按钮即可完成样条曲线角度的标注。
2.使用“几何尺寸”命令:首先,在 Creo 中创建或打开样条曲线。
然后,选择“几何尺寸”命令,在样条曲线上点击,并选择“角度”选项。
接着,输入所需的角度数值,并点击“完成”按钮。
此时,样条曲线的角度便被成功标注。
三、样条曲线标注角度的应用实例
在实际工程设计中,样条曲线标注角度具有重要意义。
例如,在某机
械零件设计中,需要标注样条曲线的轴线方向,以便于加工和装配。
此时,可以通过上述方法标注样条曲线角度,从而确保零件加工和装配的准确性。
四、总结
总之,在 Creo 中,样条曲线标注角度的方法有多种,用户可以根据实际需求选择合适的方法。
标注样条曲线角度在工程设计中具有重要意义,可以有效提高设计质量和加工效率。
样条的标准尺寸

2缺口冲击样条包括弯曲样条
h
b
L
其中L为长度=80±2mm;b为宽度=10.0±0.2mm; h为厚度=4.0±0.2mm;样条1/3的长度内各处厚度与厚度平均值的偏差不应大于2%,宽度与平均值的偏差不应大于3%,样条截面面应是矩形且无倒角。
3防火样条尺寸
Rmax 1.3mm
b
L
其中样条L长度=125±5mm;b宽度=13.0±0.5mm,边缘应平滑同时倒角半径不应超过1.3mm。其厚度可定为3.2mm;1.6mm;0.8mm三个等级。
4色板尺寸
以上为色板的尺寸图,其中a区标识,上面有公司名称与联系方式;b区的表面为光面;c区为三个不同种等级的磨沙面组成。
样条采样原理

样条采样原理什么是样条采样样条采样是一种常用的插值方法,用于从有限数量的数据点中生成平滑的曲线。
样条采样的原理是通过基函数的线性组合来逼近曲线,从而得到一个连续的函数。
在计算机图形学、数值计算和数据拟合等领域都广泛应用到样条采样。
本文将详细探讨样条采样的原理及相关概念。
样条插值方法通常情况下,我们需要从给定的数据点中计算曲线的插值问题。
样条插值方法将曲线划分为若干小段,并在每个小段上构造一个局部插值函数。
这些局部插值函数要满足一定的条件,使得整个曲线能够平滑地连接起来。
自然样条插值自然样条插值是一种特殊的样条插值方法。
它要求在给定数据点的端点处,曲线的二阶导数为零。
这意味着曲线在数据点的两侧呈现出平滑的曲线段。
自然样条插值的优点是能够在给定数据点处生成最平滑的曲线。
样条基函数在样条插值中,基函数起着非常重要的作用。
它们决定了如何将各个局部插值函数组合成整个曲线。
常用的样条基函数有三次样条、五次样条等。
这些基函数通常具有局部支撑性质,即一个数据点的影响范围仅限于其相邻的一些小段上。
样条插值的计算方法在实际计算中,我们需要给定一组数据点和相应的函数值。
根据这些数据点,我们可以构造一个线性方程组,求解得到每个小段上的系数。
通过这些系数,我们可以得到整个曲线的插值函数。
其中,使用矩阵求逆的方法是一种常用的计算方法。
三次样条插值算法三次样条插值是最常用的样条插值方法之一。
它具有较高的精度和平滑性。
在三次样条插值中,每个小段上的插值函数是一个三次多项式,它的系数可以通过求解线性方程组得到。
同时,为了保证整条曲线的平滑性,我们需要在两个相邻数据点的连接处设置一定的边界条件。
边界条件的选择在样条插值中,边界条件的选择对最终的结果具有重要影响。
常用的边界条件有自然边界条件、固定边界条件和周期边界条件等。
不同的边界条件会导致不同的插值函数形式和性质。
数值计算误差分析样条插值是一种数值计算方法,因此存在一定的计算误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们已经详细介绍过低次(二次、三次)的Hermite 插值样条,它是基于端点的位置矢量和曲线在两端点的切矢建立的,但有时候我们不需要输入曲线斜率值或其他几何信息就能生成样条曲线,因此就出现了Cardinal 样条,这种基于Hermite 样条的变化形式,它不需要输入曲线控制点上的导数值,而是采用控制点的坐标位置来计算导数。
下面我们来详细介绍一下Cardinal 样条
Cardinal 样条跟Hermite 样条一样,也是分段三次插值样条,一段Cardinal 样条曲线完全由4个连续的控制点给出。
中间两个控制点是曲线端点,另外两个控制点用来计算终点斜率。
如图1所示,设P(t)是两控制点k p 和1p k +间的参数函数式,则从1k p -到2k p +间的4个控制点用于建立Cardinal 样条曲线段的边界条件:
011
'011'121/2(1)()1/2(1)()
k
k k k k k p p p p p ts p p p ts p p ++-+===--=--
则控制点k p 和1p k +处的斜率分别与弦112k k k k p p p p -++和成正比,如图2所示。
参数ts 称为张力参数,因为ts 控制Cardinal 样条曲线与输入控制点间的松紧程度,如图3说明了张力ts 取很小值和很大值时Cardinal 样条曲线的形状。
特别地,ts=0时,这类曲线称为Catmull-Rom 样条曲线或Overhauser 样条曲线。
ts<0
Ts>0
将上面的4个方程代入三次Hermite样条曲线的方程,并将之转换成矩阵形式,如下:
(2)
其中, Cardinal矩阵是:
(3)
其中s = (1 - ts) / 2
将矩阵方程(2)展开成多项式形式,可以得到
P(u) = P k-1(-su3+ 2su2 - su) + P k[(2 - s)u3 + (s - 3)u2 + 1] + P k+1[(s - 2)u3 + (3 – 2s)u2 + su] + P k+2(su3 - su3)。
